Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
DifferentiationA puppy weighs 2 0 pounds at birth and 3 5 pounds two months later If the weight of the puppy during its first 6 months is increasing at a rate proportional to its weight then how much will the puppy weigh when it is 3 months old OA 4 2 pounds OB 5 6 pounds C 6 5 pounds D 4 6 pounds E 4 8 pounds
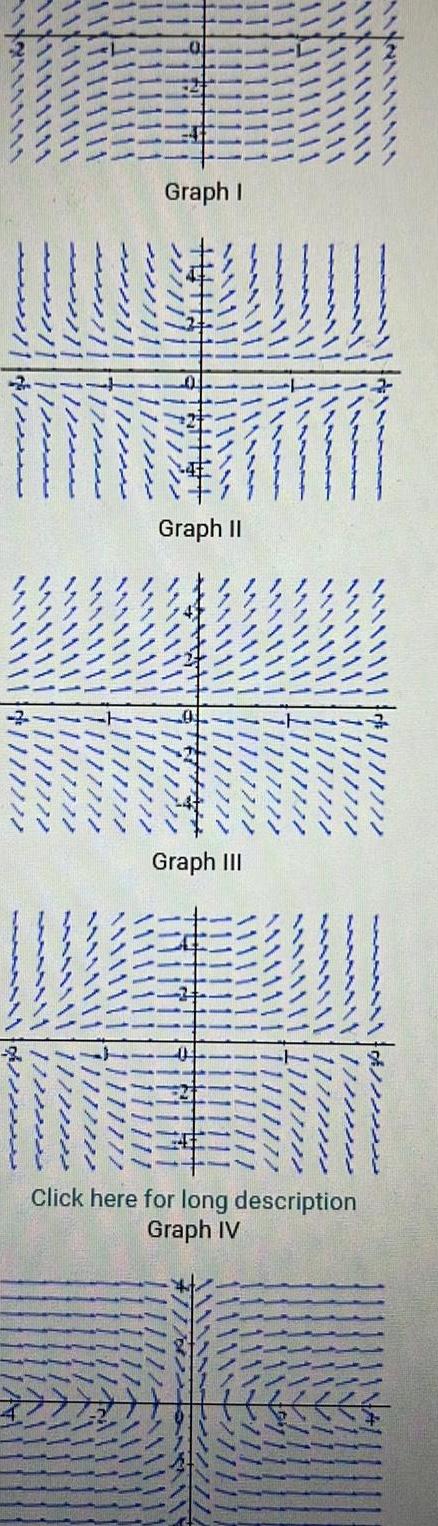
Calculus
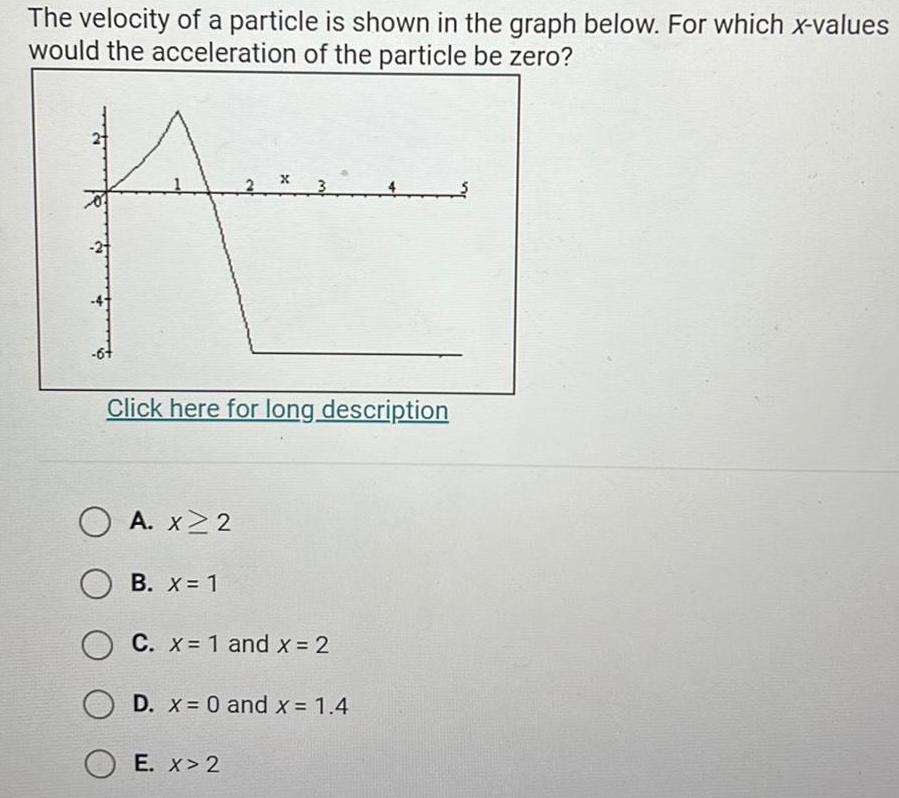
DifferentiationThe velocity of a particle is shown in the graph below For which x values would the acceleration of the particle be zero Click here for long description OA x 22 X B X 1 OC x 1 and x 2 OD x 0 and x 1 4 OE x 2

Calculus
Application of derivativesX y The sides of the rectangle above increase in such a way 1 and da d 3d At the instant when x 4and y 3 what is the value of dt dt A 5 B 5 C 2 Z D 3 E 1

Calculus
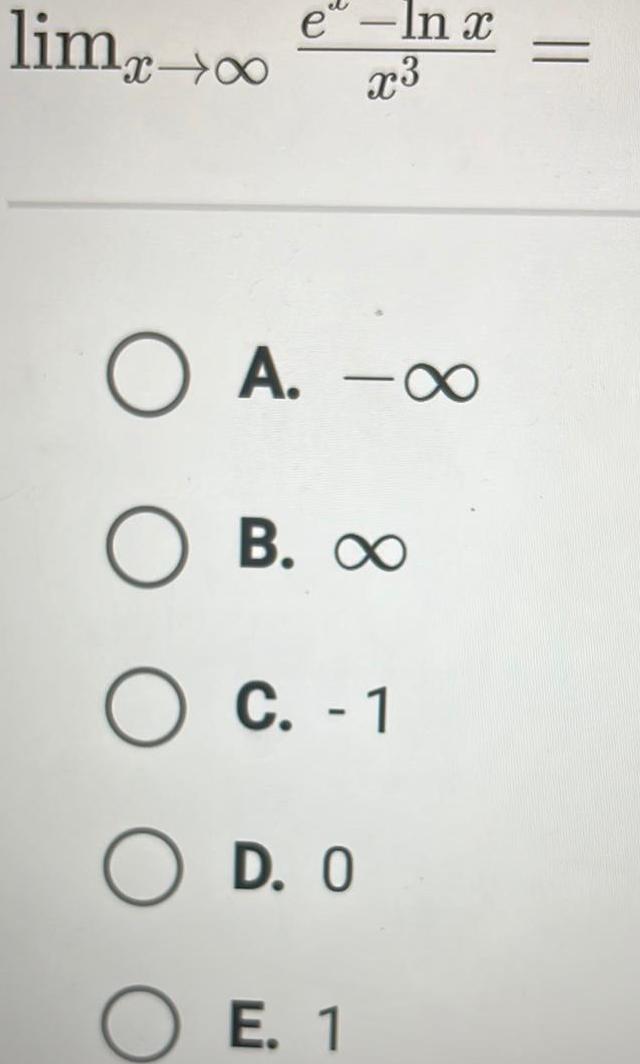
Limits & ContinuityThe absolute minimum value of f x x 3x 12 on the closed interval 2 4 occurs at x OA 4 OB 2 O C 0 O D 1 OE 2
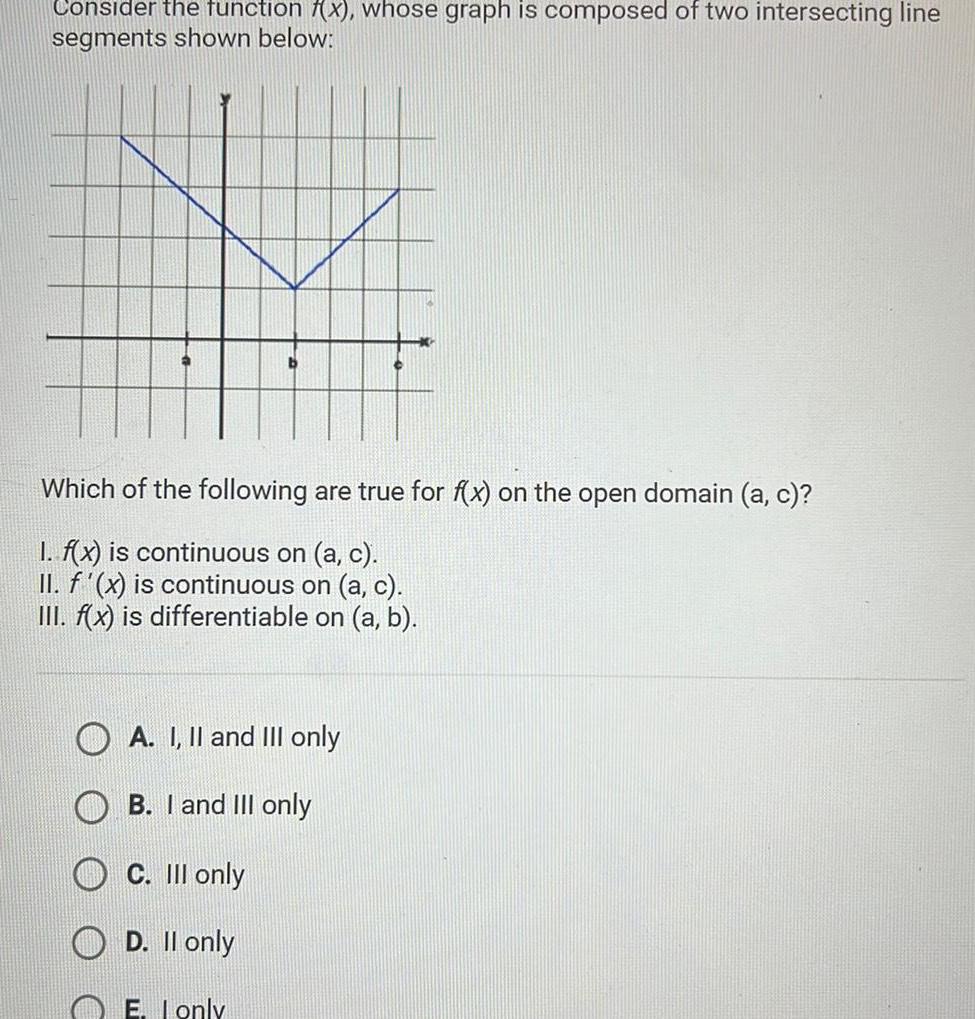
Calculus
Application of derivativesConsider the function x whose graph is composed of two intersecting line segments shown below Which of the following are true for f x on the open domain a c I f x is continuous on a c II f x is continuous on a c III f x is differentiable on a b A I II and III only B I and III only C III only D II only E I only

Calculus
Indefinite IntegrationIf f x sin there exists a number c in the interval x 3 that satisfies the conclusion of the Mean Value Theorem Which of the following could be c O A 2T B 5T C T D 3 4 3 2

Calculus
Application of derivativesWater is pouring into a container at a rate given by ri t t gallons hour water is pouring out of the same container at a rate given by ro t et gallons hour OA 41 608 B 10 402 OC 89 598 If there are 100 gallons of water at time t 0 how many gallons of water will be in the container at t 4hours D 110 402 2 OE 141 608 and

Calculus
DifferentiationThe graph of y is concave downward for all values of x such that A x 2 OB x 0 O C x 0 OD x 2 OE x 5

Calculus
DifferentiationIf fis a differentiable function f a is given by which of the following lim 0 f a h f a h f x f a limx a x a limx a f x h f x h OA I only OB II only OC I and II only OD I and III only E I II and III
Calculus
DifferentiationThe region enclosed by the curve y ex the x axis and the lines x 0 and x 1 is revolved about the x axis Find the volume of the resulting solid formed A 2 1 T B 3T O C T 2 O D e 1 2 E e
Calculus
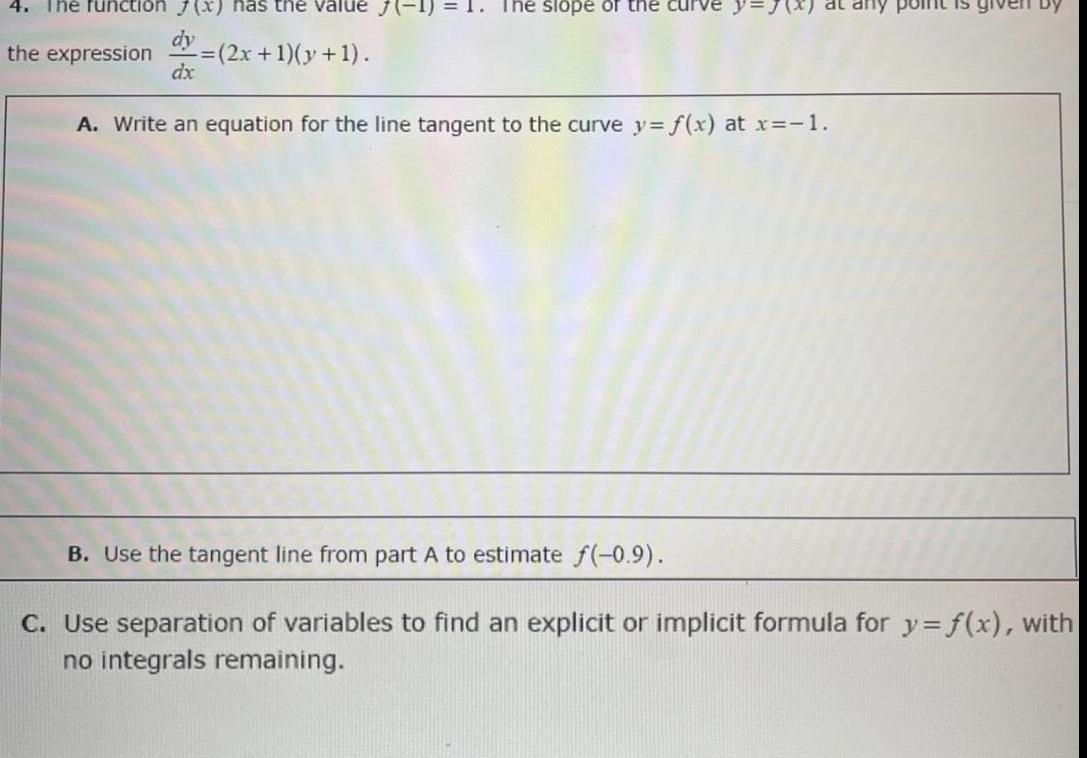
Limits & Continuity4 The function 7 x has the value J 1 dy the expression 2x 1 y 1 dx The slope of the curve at any point is A Write an equation for the line tangent to the curve y f x at x 1 B Use the tangent line from part A to estimate f 0 9 C Use separation of variables to find an explicit or implicit formula for y f x with no integrals remaining

Calculus
Application of derivativesAn equation of the line tangent to the graph of f x x 1 2x at the point 1 1 is A y 6x 5 B y 2x 1 C y 2x 3 D y 7x 6 E y 7x 8

Calculus
Application of derivativesIf the function f is continuous for all real numbers and if f x x 2 then f 2 A 0 B 2 C 1 D 4 E 2 x 4 x 2 when
Calculus
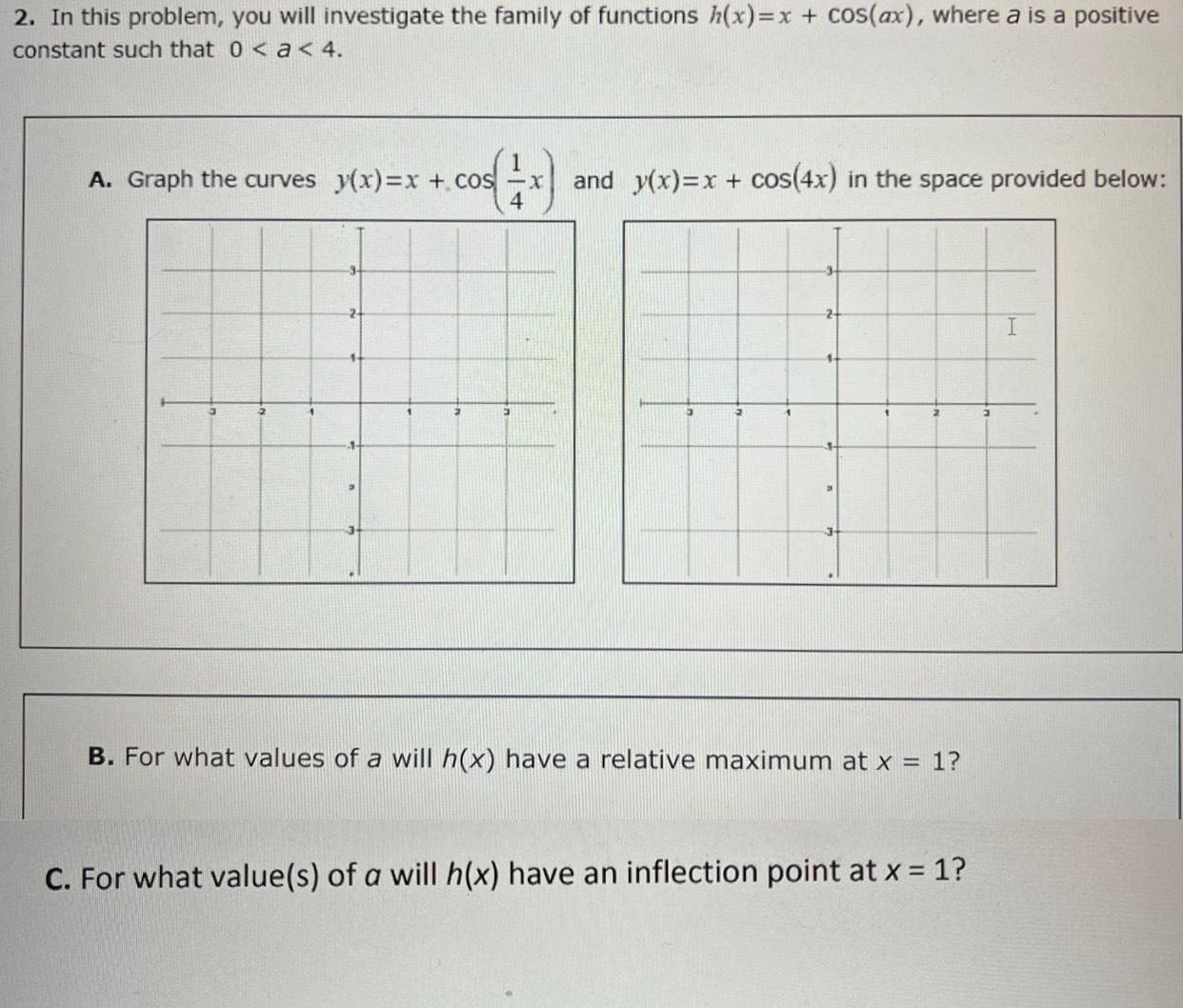
Application of derivatives2 In this problem you will investigate the family of functions h x x cos ax where a is a positive constant such that 0 a 4 A Graph the curves y x x cos x and y x x cos 4x in the space provided below 4 B For what values of a will h x have a relative maximum at x 1 C For what value s of a will h x have an inflection point at x 1 I
Calculus
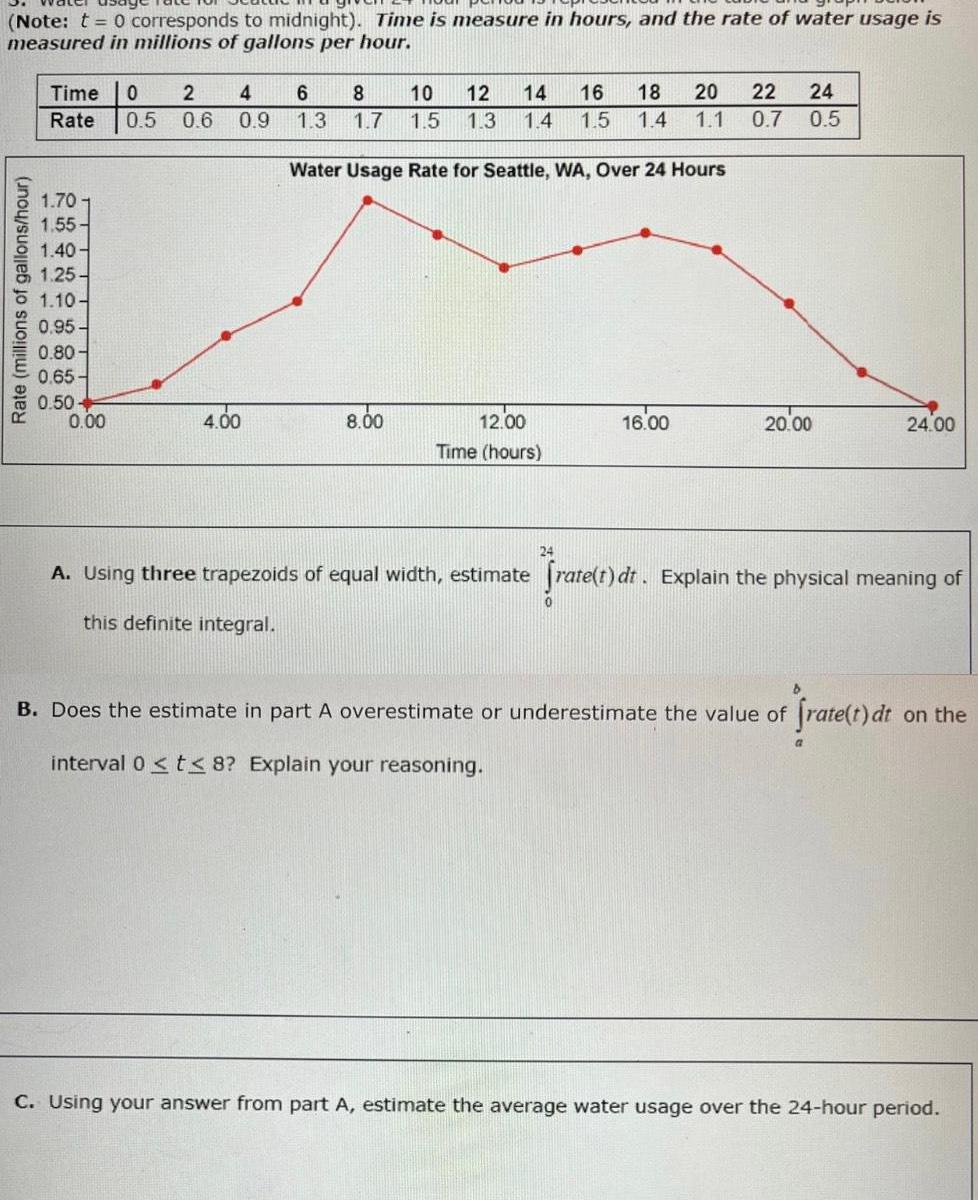
Application of derivativesNote t 0 corresponds to midnight Time is measure in hours and the rate of water usage is measured in millions of gallons per hour Rate millions of gallons hour Time 0 Rate 0 5 1 70 1 55 1 40 1 25 1 10 0 95 0 80 0 65 0 50 0 00 2 0 6 4 0 9 4 00 6 8 1 3 1 7 10 12 14 16 18 20 22 24 1 5 1 3 1 4 1 5 1 4 1 1 0 7 0 5 Water Usage Rate for Seattle WA Over 24 Hours 8 00 12 00 Time hours 16 00 20 00 24 00 24 A Using three trapezoids of equal width estimate frate t dt Explain the physical meaning of fratel t dt this definite integral B Does the estimate in part A overestimate or underestimate the value of frate t dt on the interval 0 t 8 Explain your reasoning a C Using your answer from part A estimate the average water usage over the 24 hour period

Calculus
DifferentiationThe tank s base diameter is 40 m and a height of 10 m A Write an expression for the rate of change of the water level with respect to time in terms of h the water s height in the tank h B Assume that at t 0 the tank of water is empty Find the water level h as a function of the time t
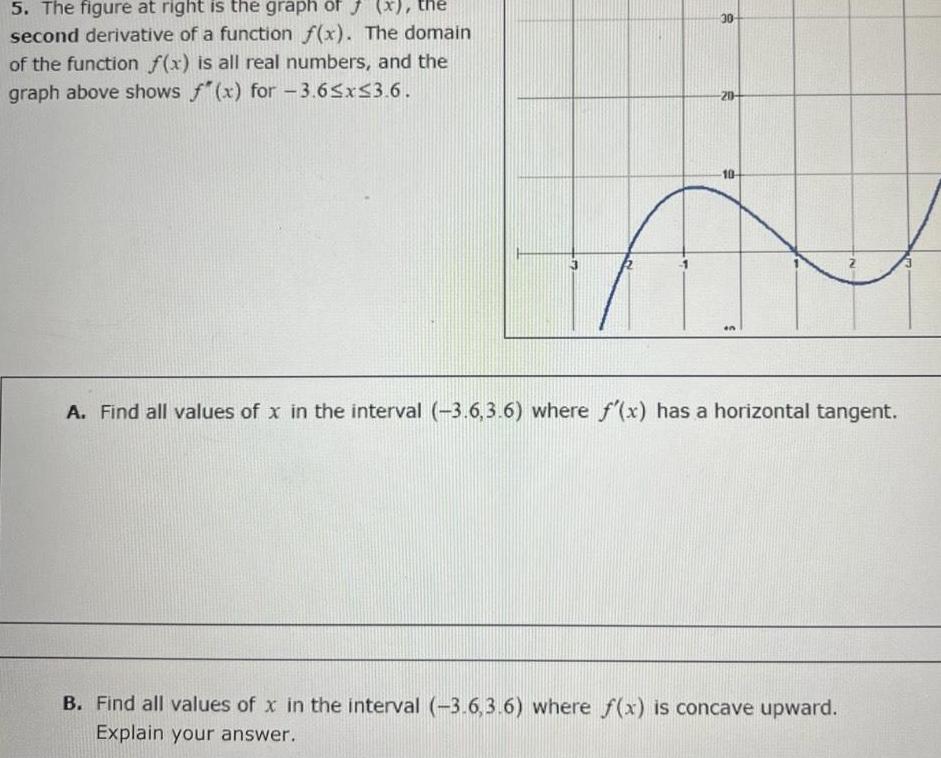
Calculus
Application of derivatives5 The figure at right is the graph of f x the second derivative of a function f x The domain of the function f x is all real numbers and the graph above shows f x for 3 6 x 3 6 30 20 10 A Find all values of x in the interval 3 6 3 6 where f x has a horizontal tangent B Find all values of x in the interval 3 6 3 6 where f x is concave upward Explain your answer
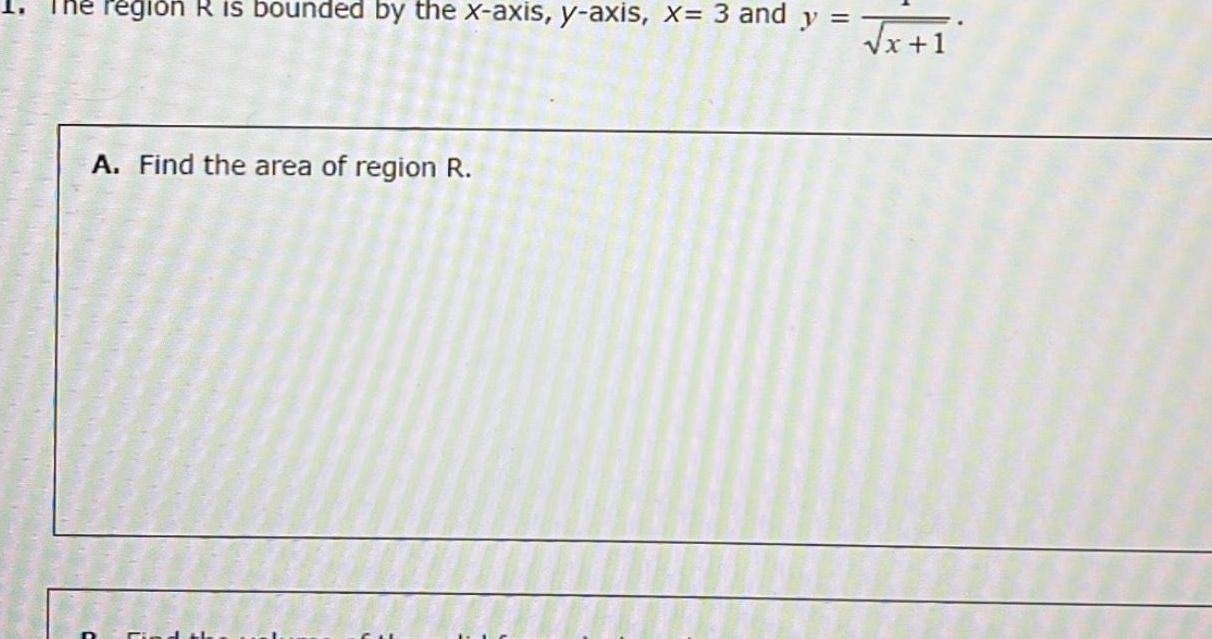
Calculus
Limits & ContinuityPegion R is bounded by the x axis y axis x 3 and y A Find the area of region R x 1

Calculus
Application of derivativesHow many critical points does the function f x x 1 6 x 5 have O A 6 OB 13 O C 1 OD 7 OE 3
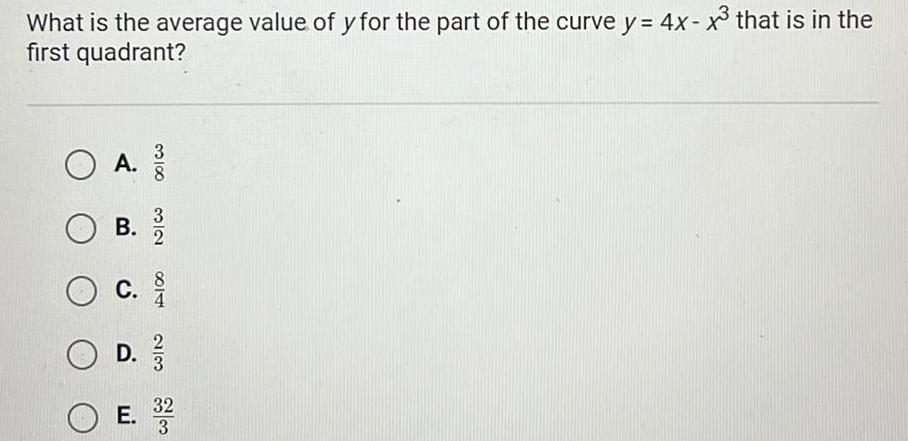
Calculus
Application of derivativesWhat is the average value of y for the part of the curve y 4x x that is in the first quadrant O A B 3 2 O c D 2 3 E 3 2 2

Calculus
Limits & ContinuityIf limx 3 f x 7 which of the following must be true 1 f is continuous at x 3 II f is differentiable at x 3 III f 3 7 A None B II only C III only OD I and III only OE I II and III

Calculus
Application of derivativesThe slope of the line normal to the graph of y 2 ln sec x at x is OA 2 OB 1 2 OC 2 D nonexistent E OE 1 2

Calculus
Application of derivativesIn an experiment to study the growth of bacteria a medical student measured 5000 bacteria at time 0 and 8000 at time 10 minutes Assuming that the number of bacteria grows exponentially how many bacteria will be present after 30 minutes A 14000 bacteria B 29333 bacteria C 24332 bacteria D 20480 bacteria E 17830 bacteria

Calculus
DifferentiationThe volume of the solid obtained by revolving the region enclosed by the ellipse x 9y2 9 about the x axis is OA 2 OB 4T OC 9T OD 6TT E 12T
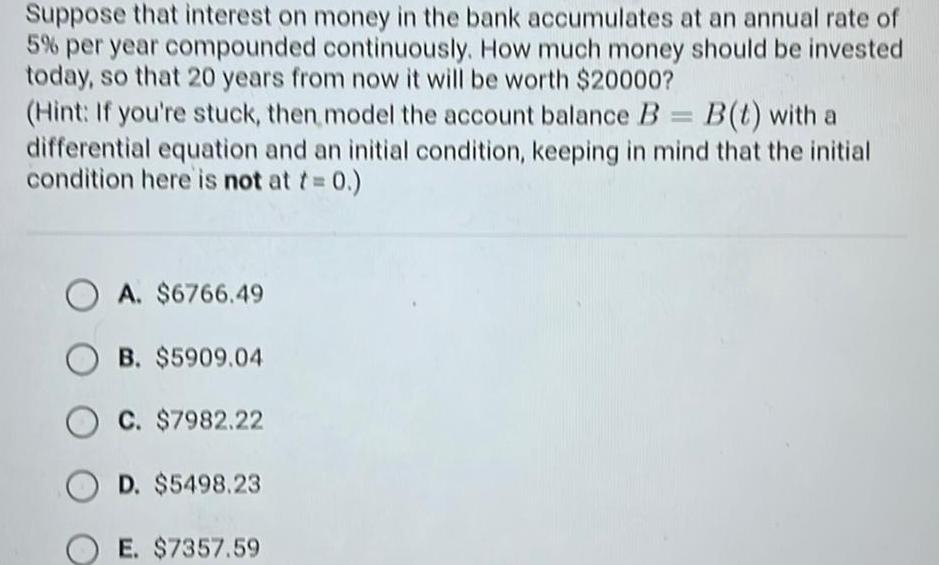
Calculus
Vector CalculusSuppose that interest on money in the bank accumulates at an annual rate of 5 per year compounded continuously How much money should be invested today so that 20 years from now it will be worth 20000 Hint If you re stuck then model the account balance B B t with a differential equation and an initial condition keeping in mind that the initial condition here is not at t 0 OA 6766 49 OB 5909 04 C 7982 22 OD 5498 23 E 7357 59
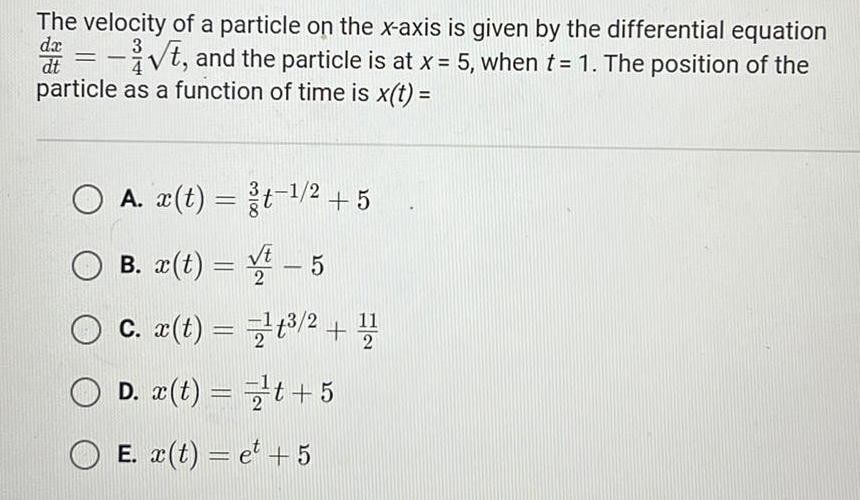
Calculus
Application of derivativesThe velocity of a particle on the x axis is given by the differential equation 3 da t and the particle is at x 5 when t 1 The position of the dt particle as a function of time is x t O A x t gt 2 5 B x t t 5 c x t 1 12 D x t t 5 E x t et 5

Calculus
Limits & ContinuitySuppose an experimental population of amoeba increases according to the law of exponential growth There were 100 amoeba after the second day of the experiment and 300 amoeba after the fourth day Approximately how many amoeba were in the original sample A 10 B Not enough information to determine C 5 D 33 E 71
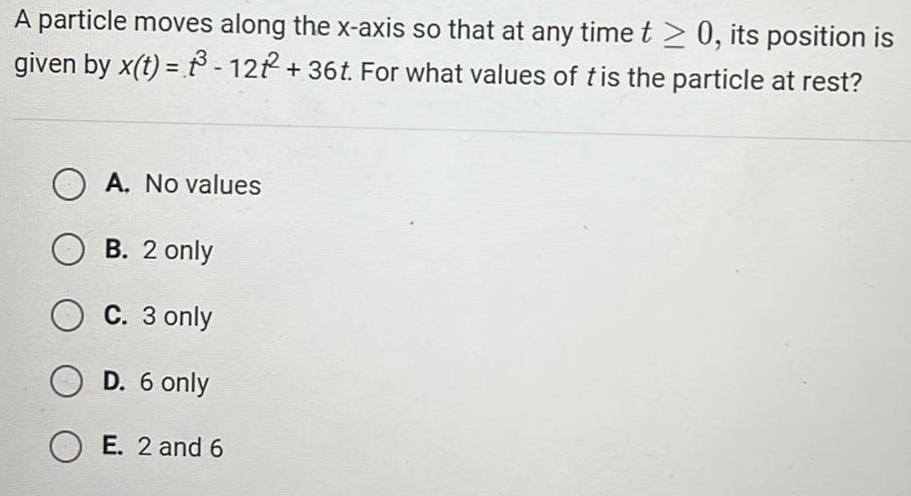
Calculus
Differential equationsA particle moves along the x axis so that at any time t 0 its position is given by x t 3 12 2 36t For what values of t is the particle at rest A No values OB 2 only O C 3 only O D 6 only OE 2 and 6
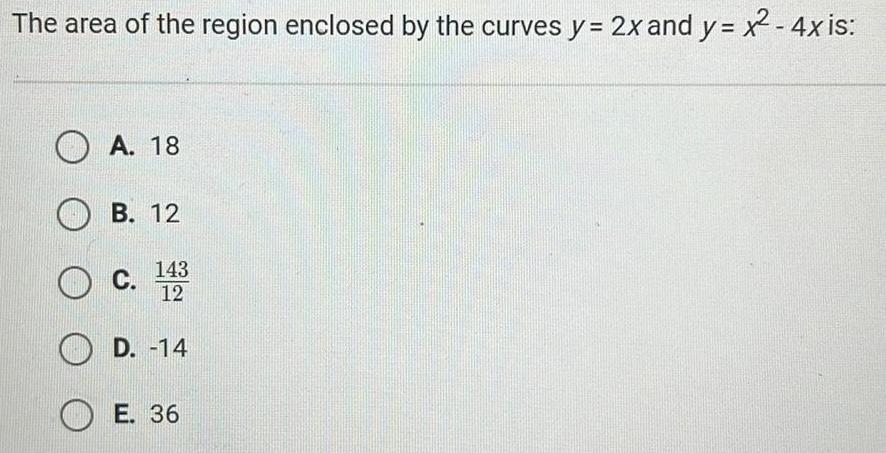
Calculus
Application of derivativesThe area of the region enclosed by the curves y 2x and y x 4x is A 18 B 12 143 O C 12 D 14 E 36

Calculus
Definite IntegralsIf the definite integral e da is first approximated by using two inscribed f rectangles of equal width and then by using the trapezoidal rule with n 2 the difference between the two approximations is OA 26 80 OB 53 60 OC 27 80 OD 12 78 O E 30 51
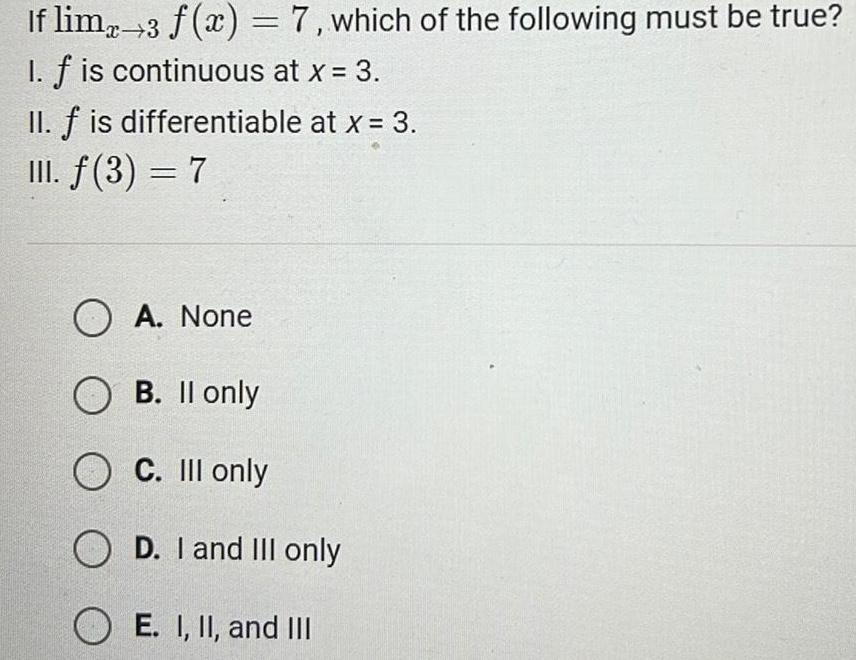
Calculus
Application of derivativesIf limx 3 f x 7 which of the following must be true I f is continuous at x 3 II f is differentiable at x 3 III f 3 7 OA None O B II only O C III only OD I and III only OE I II and III
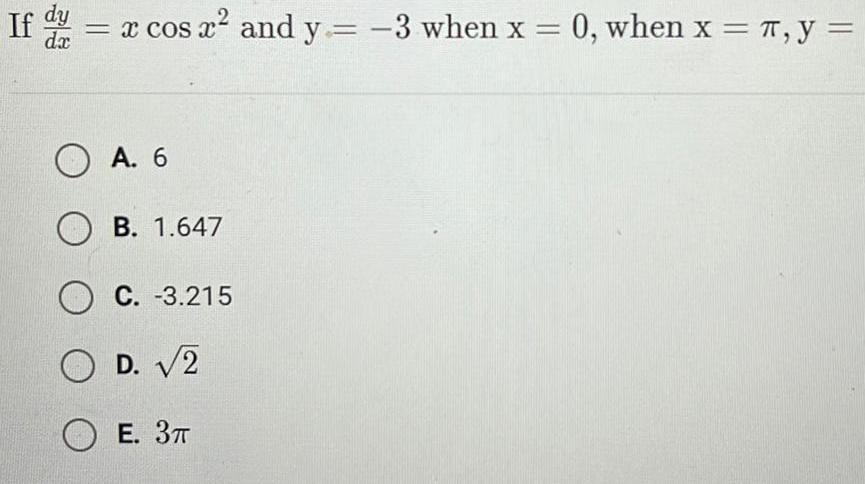
Calculus
Differential equationsIf d dy x cos x and y 3 when x 0 when x y dx A 6 OB 1 647 OC 3 215 OD 2 OE 3T
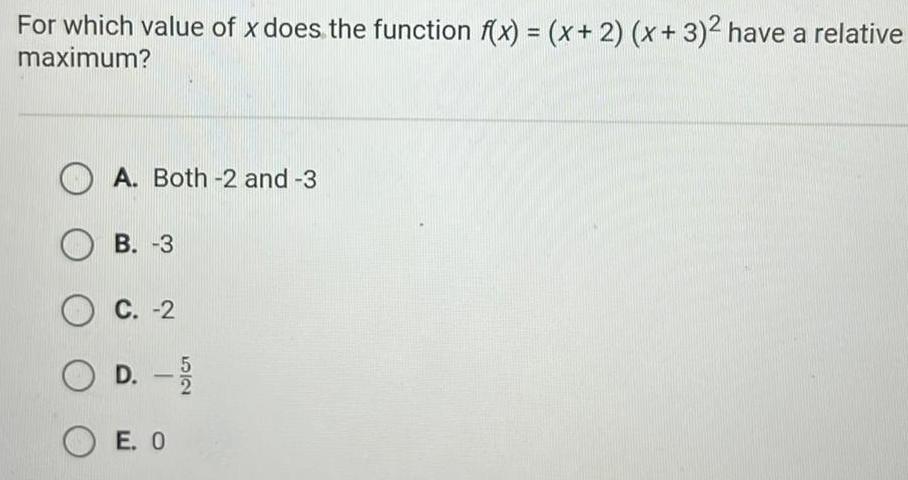
Calculus
Definite IntegralsFor which value of x does the function f x x 2 x 3 have a relative maximum A Both 2 and 3 B 3 C 2 OD 5 2 OE O

Calculus
Application of derivativesWhich of the following is a right hand endpoint Riemann sum approximation to f f x dx with six equal subdivisions A 1 5 2 f 2 5 f 3 3 5 4 O B O c f 1 f 1 5 f 2 f 2 5 f 3 f 3 5 f 1 f 1 5 f 2 f 2 5 f 3 f 3 5 O D f 1 f 1 5 f 2 f 2 5 f 3 f 3 5 E 1 5 f 2 f 2 5 3 f 3 5 f 4
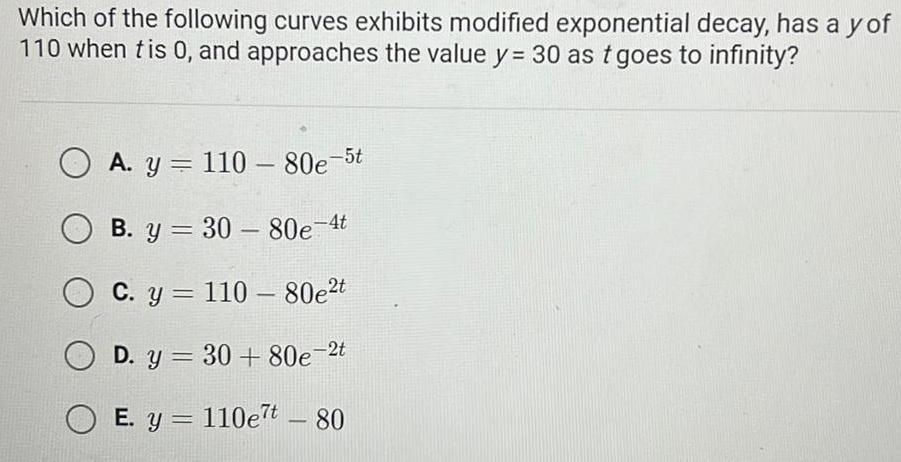
Calculus
Application of derivativesWhich of the following curves exhibits modified exponential decay has a y of 110 when tis 0 and approaches the value y 30 as t goes to infinity OA y 110 80e 5t B y 30 80e 4t OC y 110 80e t OD y 30 80e 2t OE y 110e t 80
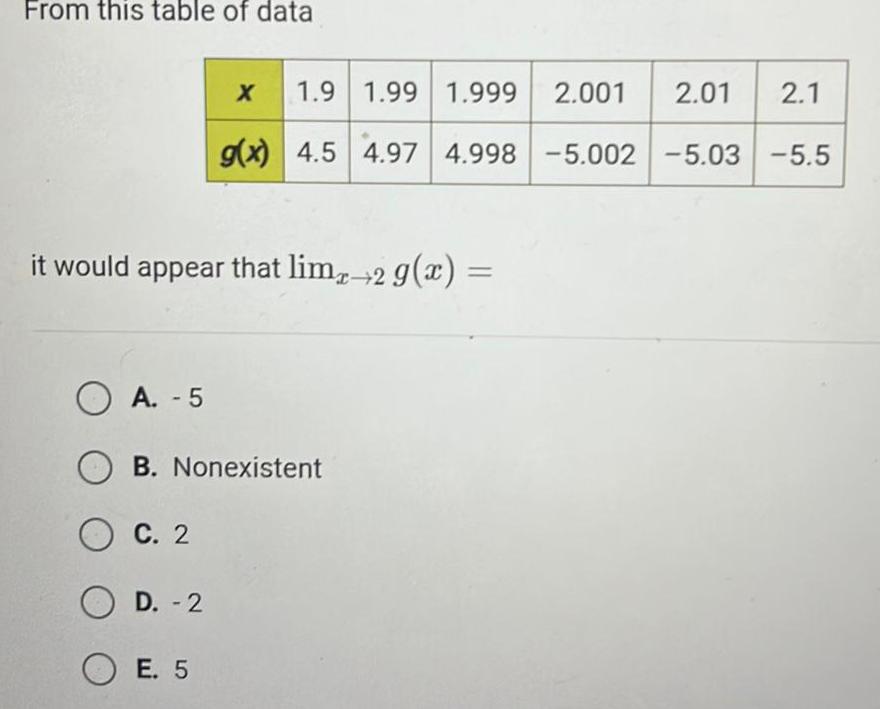
Calculus
Differential equationsFrom this table of data 1 9 1 99 1 999 2 001 2 01 2 1 g x 4 5 4 97 4 998 5 002 5 03 5 5 X it would appear that limx 2 g x O A 5 OB Nonexistent OC 2 OD 2 OE 5
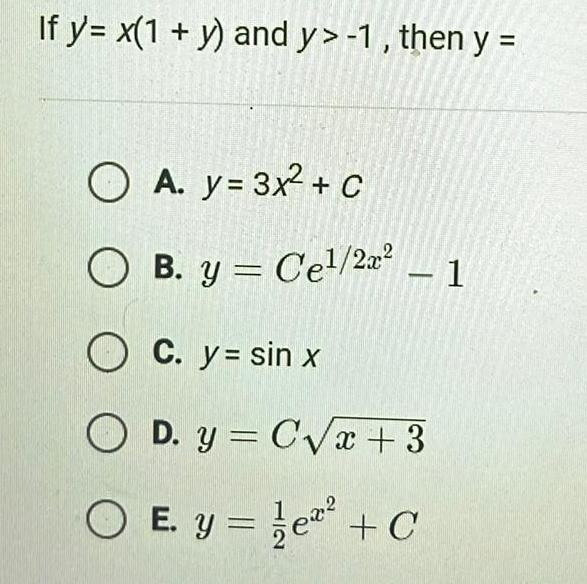
Calculus
Differential equationsIf y x 1 y and y 1 then y OA y 3x C OB y Cel 2x 1 O C y sin x OD y C x 3 OE y C

Calculus
Definite Integrals3 Solve the following Initial Value Problems IVP and find the interval of validity for the solution of each problem a y c y dy b e sec y 1 1 y 0 0 dt e 3x 4x 4 2y 4 dy dt 3 xy 1 x dy d 6y x y 1 dx y 1 3 y 0 1 1 25 y sint y 0 1 5 5 5 5 5
Calculus
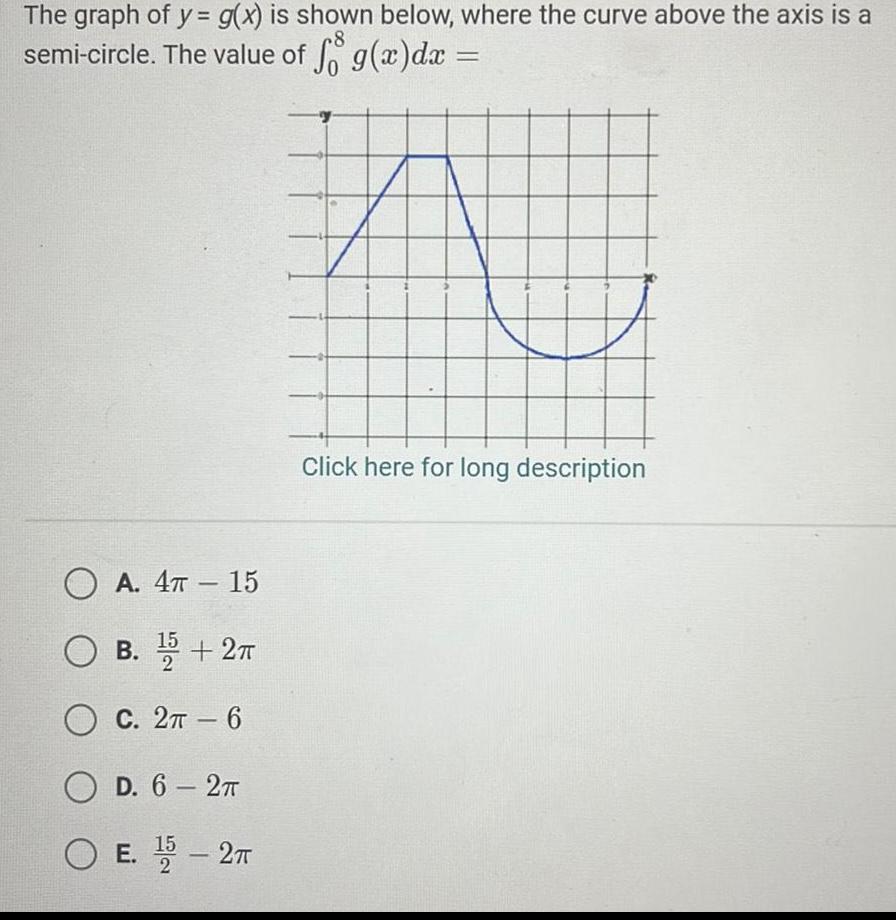
Differential equationsThe graph of y g x is shown below where the curve above the axis is a semi circle The value of fog x dx OA 4T 15 O B 5 2 OC 2 6 OD 6 2TT O E 5 2T 15 Click here for long description

Calculus
Application of derivativesThe rate of change of P with respect to tis directly proportional to 10 and inversely proportional to the cube root of P The differential equation that models this situation is O A d OB c de dt k 10 t 1 T kv P 10 t 10 t P dP O D dt k 10 t VP O E k 10 t P

Calculus
Differential equationsSuppose the number of bacteria in a culture increases by 50 every hour if left on its own Assuming that biologists decide to remove approximately one thousand bacteria from the culture every ten minutes which of the following equations best models the population P P t of the bacteria culture where tis in hours O A 1 5P 1000 dt OB 1 5P 6000 O c 5P 1000 OD 5P 5P 1000 OE dP dt dP dt dP dt F 5P 6000
Calculus
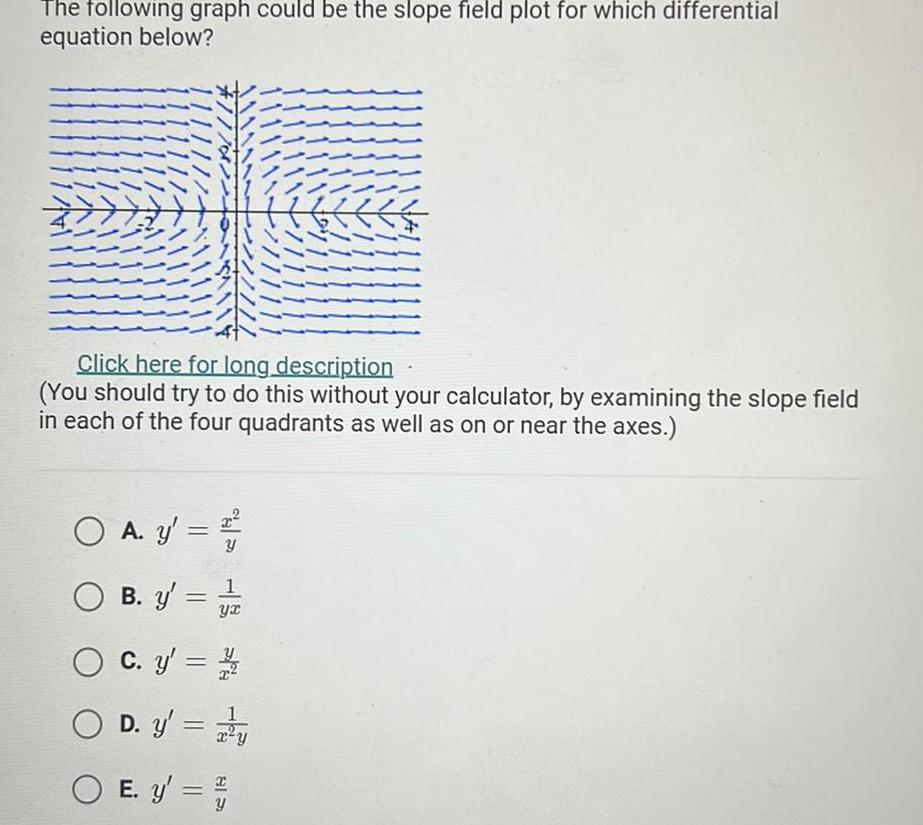
Application of derivativesThe following graph could be the slope field plot for which differential equation below X 2 O A y Y Click here for long description You should try to do this without your calculator by examining the slope field in each of the four quadrants as well as on or near the axes O B y 1 yx O O D y O E y C y 1 2 1111111 Go I 1 1 1 1 1 1 1 1 1 11 11

Calculus
Differential equationsUsing separation of variables technique solve the following differential equation with initial condition 1 and y 3 5 The solution is dy yx 5x dz O A In y 5 ln x 1 O B ln y 5 arctan3 n10 arctan 3 C y ln x 1 50 In 10 O D y In x 1 25 In 10 O E In y 5 ln x 1 ln 10

Calculus
Differential equationsSuppose you want to find an equation for a curve whose slope at any point x y is x 6y2 You d need to solve the differential equation x 6y Using separation of variables to solve this equation you get where C is an arbitrary constant of integration O A y x C B 3y 2x C C 2y x C O D 2y x C E 6y x C
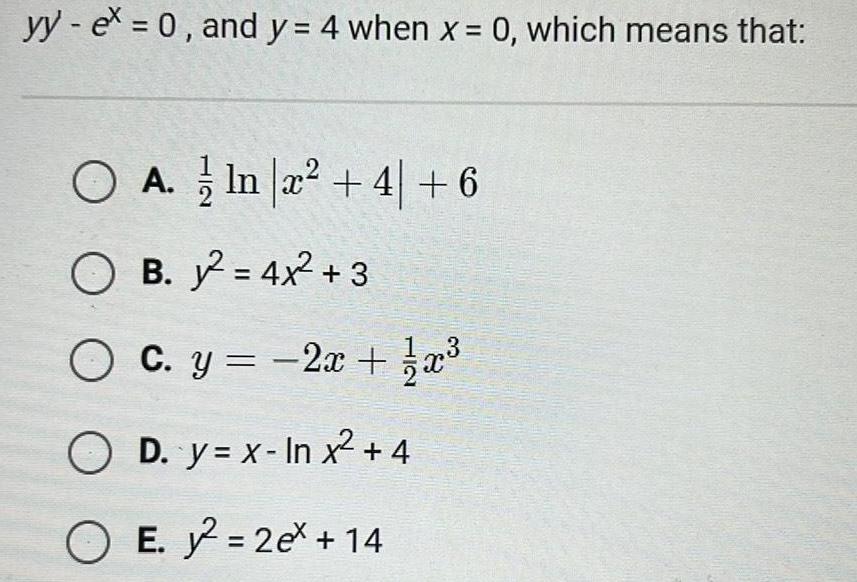
Calculus
Differential equationsyy ex 0 and y 4 when x 0 which means that O A In x 4 6 OB 2 4x 3 O c y 2x x OD y x In x 4 O E 2 2ex 14

Calculus
DifferentiationWhich of the following differential equations with initial condition yields a solution curve that exhibits modified exponential growth such that y goes to negative infinity as t goes to positive infinity Hint Check each one by solving the differential equation quickly Remember to solve the differential equation the quick and easy way recall the fact that the solution to the differential equation k y a is y Aekt Aekt a So you just need to write the differential equation in the proper form first Then of course you must solve for the constant A using the initial condition OA 2 y 200 with initial condition y 0 B 38 38 100 D dy dt 2 y 200 with initial condition y 0 50 dy O C c 3 5 y 123 with initial condition y 0 100 dy 3 5 y 123 with initial condition y 0 50 dt E 2 y 200 with initial condition y 0 50

Calculus
Application of derivativesSolve the following differential equation with initial conditions y e 2t 10e t y 0 1 y 0 0 The solution is 5 4t O A y e e 3t O B y e 2t 54 2 O C y 4e 2t 16e t 6t 19 OD y e 2t e4t 1 O E y 2t e t 2t 4t 8

Calculus
Application of derivativeshe acceleration of a particle moving along the x axis at time tis given by a t 6t 2 If the velocity is 25 when t 3 and the position is 10 when t 1 the position x t A t t 4t 6 B 36t 4t2 77t 55 O c 9t 1 D t3 t 9t 20 OE 3t 2t 4