Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
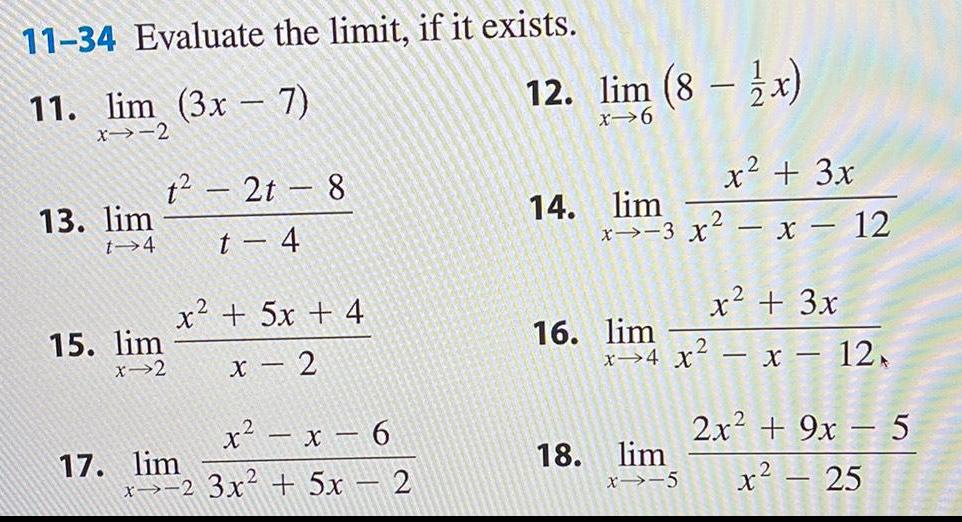
Calculus
Limits & Continuity11 34 Evaluate the limit if it exists 11 lim 3x 7 x 2 13 lim t 4 1 2t 8 t 4 15 lim x 2 17 lim x2 5x 4 x 2 x x 6 x2 3x 5x 2 12 lim 8 x x 6 14 lim x 3 x x 12 16 lim x 4 X 18 lim x 5 x 3x 2 2 x 3x x 12 2x 9x 5 x 25

Calculus
DifferentiationIn Seattle on September 30 the temperature in F t hours after midnight was given by the function Temp t 60 12 sin t 11 What was the average temperature over the period from 8 A M until 10 P M OA 76 39 F OB 60 F O c 56 05 F OD 76 39 F OE 65 48 F

Calculus
Definite IntegralsFind the area of the region in quadrant I bounded by the curves y x 2 y x 2 y 1 and y 3 1 2 You get O A 3 O B 2 3 O c 2 3 O D 2 3 32 O E 3 3 8 coco

Calculus
Definite IntegralsFind the area between the curves y f x x 3x and y g x x 4x x on the interval 0 x 2 O A 200 OB B 83 O C 4 O D O E

Calculus
Definite IntegralsFind the area of the region bounded by the curves 3 y sin x y csc x x 4 and x You get O A 2 2 OB 2 2 O c 2 2 OD 2 2 OE 2 2

Calculus
Application of derivativescertain chemical involved in the reaction changes at a rate that s inversely proportional to the product of the mass of the chemical present in grams and the time elapsed since the reaction began in seconds A The mass m m t of this chemical is modeled with what differential equation for time 12 1 second B The solution to the differential equation modeling the mass m of the chemical at time t seconds is m t 2kInt C for t 1 where k and C are undetermined constants Show how this equation is derived from your answer in part A C Suppose that the amount of this chemical involved in the reaction is 40 grams at time t 1 second and 30 grams at time t 10 seconds Find an explicit equation for the mass m of the chemical as a function of t for t 1 Your equation should not involve any unknown constants or any calculator numbers D According to your equation for m t in part Cat what time
Calculus
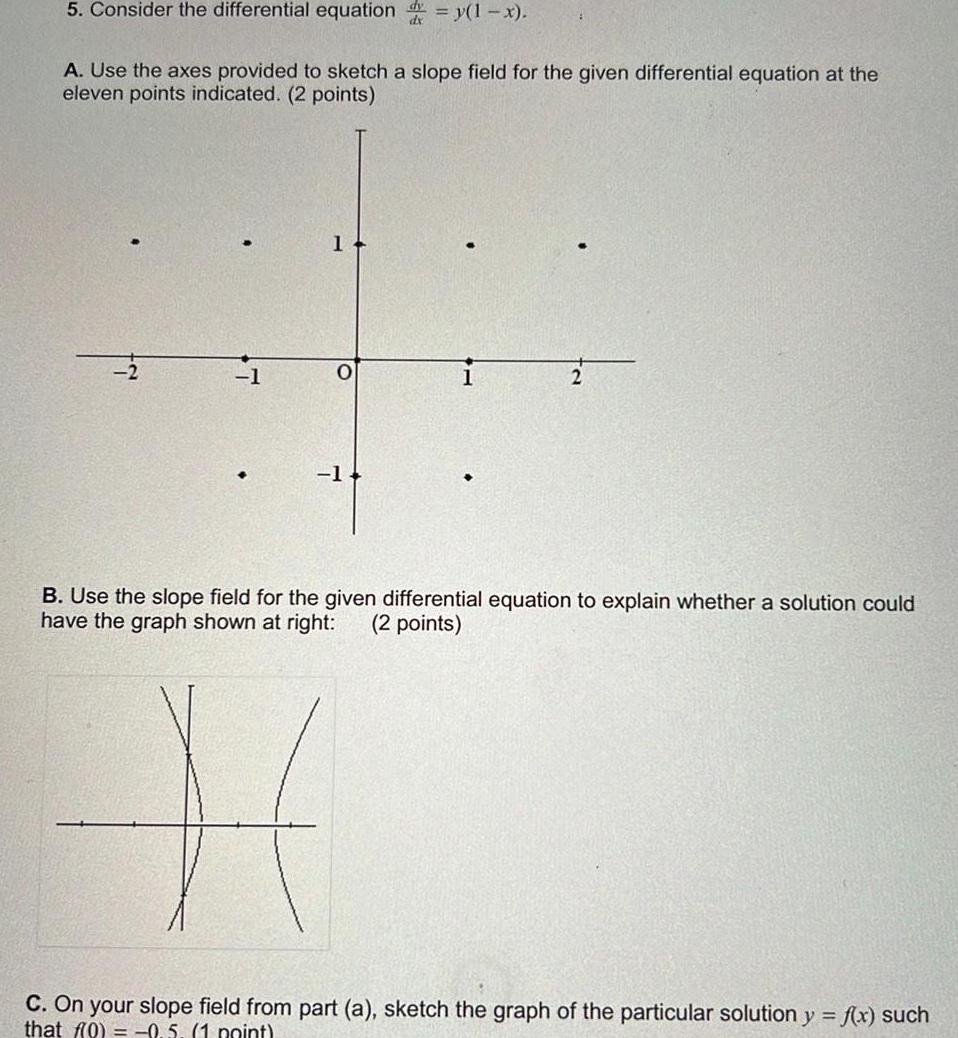
Differential equations5 Consider the differential equation y 1 x A Use the axes provided to sketch a slope field for the given differential equation at the eleven points indicated 2 points 1 1 1 B Use the slope field for the given differential equation to explain whether a solution could have the graph shown at right 2 points H C On your slope field from part a sketch the graph of the particular solution y f x such that f 0 0 5 1 point

Calculus
Application of derivatives3 9 Evaluate the limit and justify each step by indicating the appropriate Limit Law s 3 lim 4x 5x x 5 5 lim v 2v 2v 5 v 2 7 lim 9 u 2u 2 9 lim 1 2t5 5t 4 3 4 lim 2x 6x 9 x 3 3t 1 7t 5t 2 6 lim 8 lim x 5 2x 3x X 3 I

Calculus
Differential equations4 At high temperatures nitrogen dioxide NO2 decomposes into NO and O2 If y t is the concentration of NO2 in moles per liter then at 600 K y t changes according to the reaction law 05y for time t in seconds A Express y in terms of t and the initial concentration y B Assuming that the concentration of NO is twice as high at t 20 seconds as it is at 100 seconds find the exact initial concentration of the NO Reminder Exact means no

Calculus
Definite Integrals1 The popu present population A Model the population P P 1 of the bacteria population with a differential equation B Solve the differential equation that models the population P P t of the bacteria population t C Suppose the population at time 0 hours is 1000 Derive an equation for the population P as an explicit function of time t in hours Your equation should contain no undetermined constants D What s the population of the bacteria culture at the end of 10 hours After 100 hours
Calculus
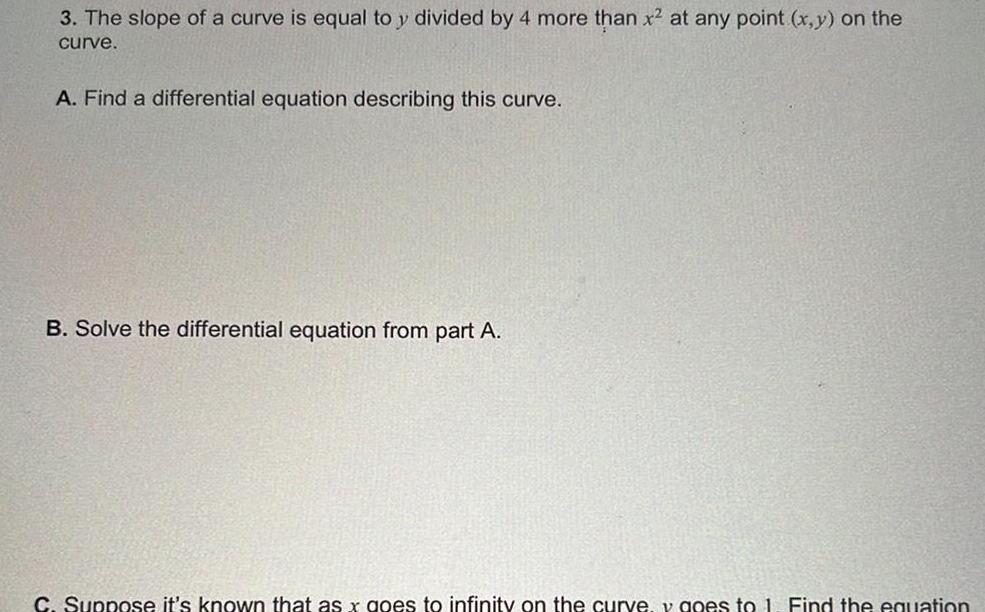
Application of derivatives3 The slope of a curve is equal to y divided by 4 more than x at any point x y on the curve A Find a differential equation describing this curve B Solve the differential equation from part A C Suppose it s known that as x goes to infinity on the curve v goes to 1 Find the equation

Calculus
Definite Integrals1 Consider the curve y f x 2 1 A Find the exact area of the region in the first quadrant bounded by the curves y f x 2x and y x Exact area means no calculator numbers
Calculus
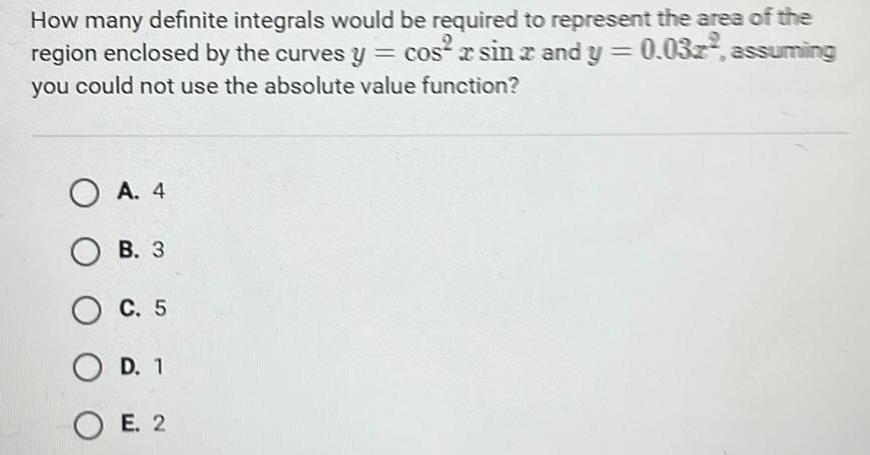
Limits & ContinuityHow many definite integrals would be required to represent the area of the region enclosed by the curves y cos sin and y cos xsin 2 and y 0 03z assuming you could not use the absolute value function OA 4 OB 3 O C 5 O D 1 OE 2
Calculus
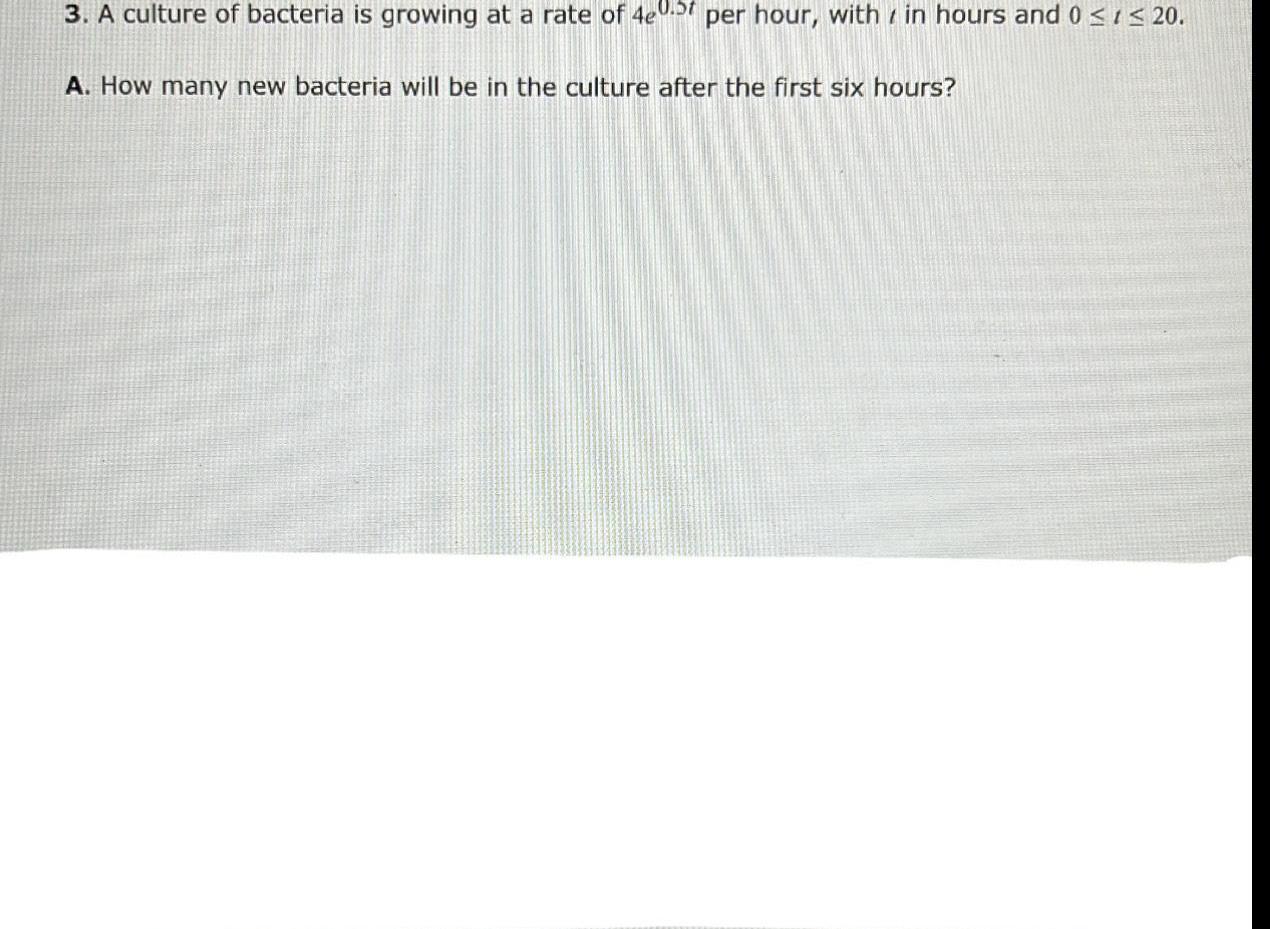
Definite Integrals3 A culture of bacteria is growing at a rate of 4e0 5 per hour within hours and 0 1 20 A How many new bacteria will be in the culture after the first six hours
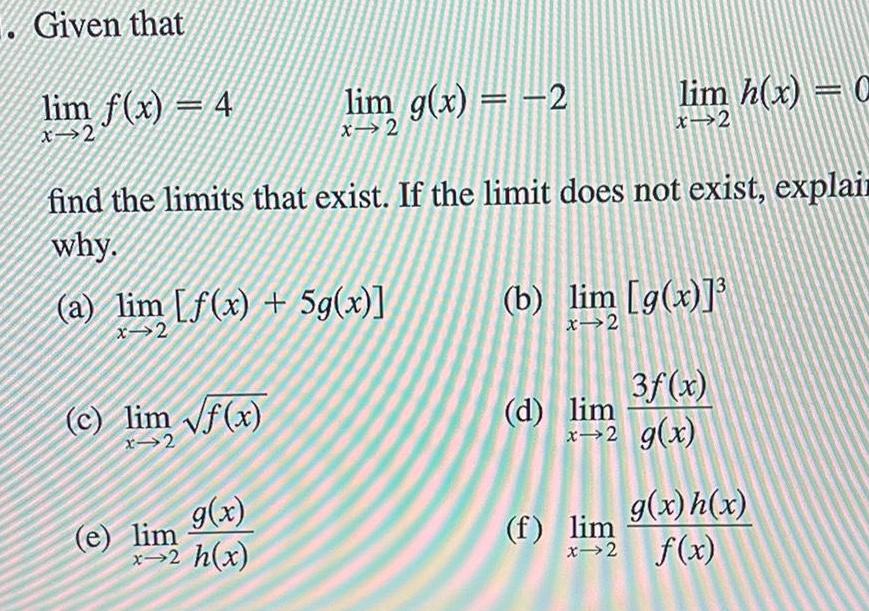
Calculus
Limits & ContinuityGiven that lim f x 4 x 2 find the limits that exist If the limit does not exist explain why a lim f x 5g x x 2 c lim f x x 2 lim g x 2 x 2 g x x 2 h x e lim lim h x C x 2 b lim g x x 2 3f x x 2 g x d lim f lim g x h x x 2 f x
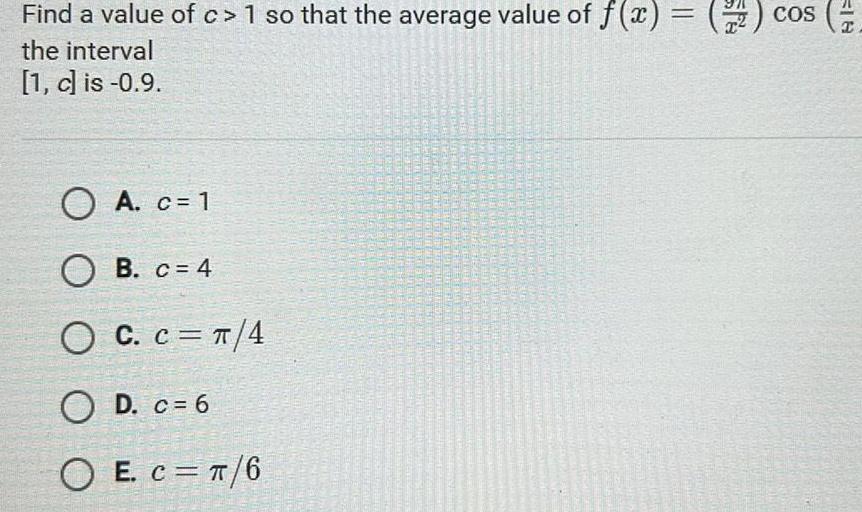
Calculus
Definite IntegralsFind a value of c 1 so that the average value of f x the interval 1 c is 0 9 A c 1 OB c 4 OC C 4 OD c 6 O E C 6 Cos 18

Calculus
Indefinite IntegrationA Find the exact area of the region in the first quadrant bounded by the curves y f x 2x 1 and y x Exact area means no calculator numbers B Find the inverse function y f x C Using part A and the notion of symmetry between a function and its inverse find the exact area of the region in the first quadrant bounded by the curves y f x and y x Explain your reasoning Hint Think graphically and little or no math will need to be done D Find a value for a such that the average value of the function f x on the interval 0 a is equal
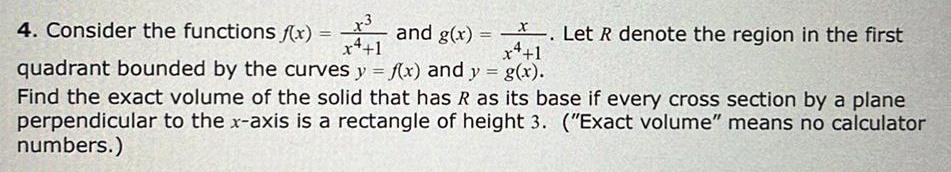
Calculus
Application of derivatives4 Consider the functions f x x3 x4 1 and g x Let R denote the region in the first x 1 quadrant bounded by the curves y f x and y g x Find the exact volume of the solid that has R as its base if every cross section by a plane perpendicular to the x axis is a rectangle of height 3 Exact volume means no calculator numbers

Calculus
Application of derivatives2 A particle moves on a coordinate line with an acceleration at time seconds of et 2 m sec2 At 1 0 the particle is at the origin and its velocity is 4 m seci A Find a function v t that gives the velocity of the particle at time t B At what exact time is the velocity of the particle 0 m s C Set up an expression which may contain integrals but not absolute values to find the total distance traveled by the particle from time 0 to 1 6 You do not have to solve your
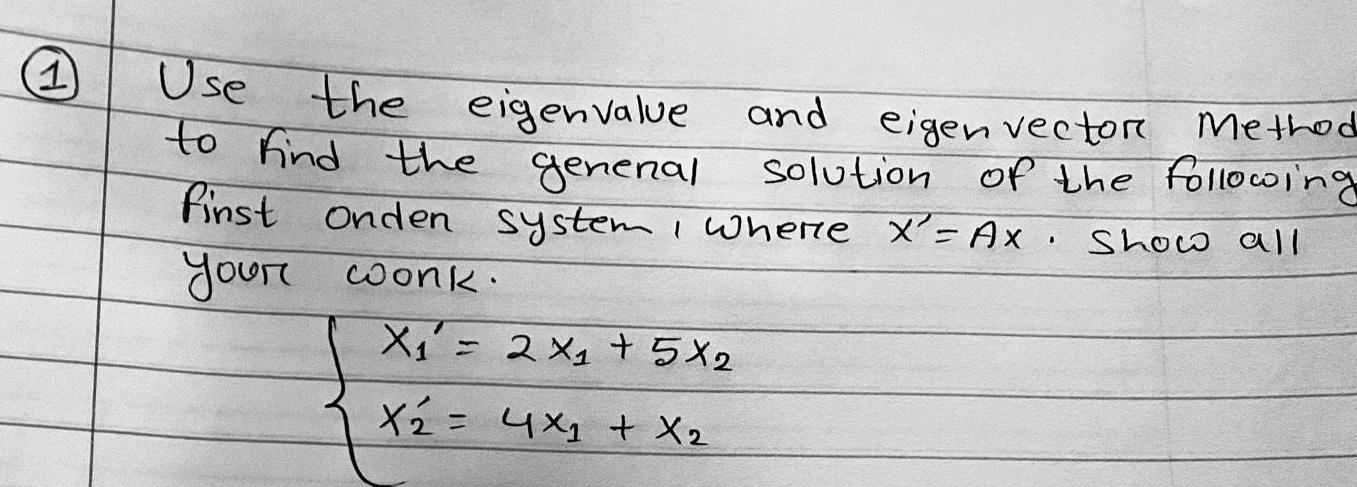
Calculus
Differentiation1 Use the eigenvalue to find the general Method and eigen vector solution of the following finst onden system where x Ax Show all your work X 2X 5X2 X 4x X

Calculus
Differentiation7 Solve the following initial value phroblem the Laplace Transform Alternate Use Show all work do not X x 12X 12x 0 10 Or methods

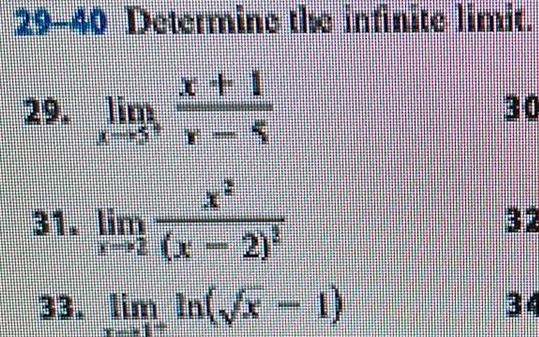

Calculus
Indefinite IntegrationPowen to the following differential equation you do not senies to find the powen senies solution need to find the nadius do not need to find the familiare function You of convengence You Use Powen senies to solve and express final solution as a power senies won k must Your all

Calculus
Definite Integralshind the Invense function show Laplace Thansform as of Variable to fully simplity as all your work F s S 5 d 3 3 2s 2 16

Calculus
Application of derivativesthe given nonlinear system and associated critica Point find the Jacobian Matnix and use eigenvalues to classify the critical point in terms of type an Stability Then wonite out the linearization to the system Show all your work dy 21 64 4x4 dt dx x 2x xy dt at 0 3
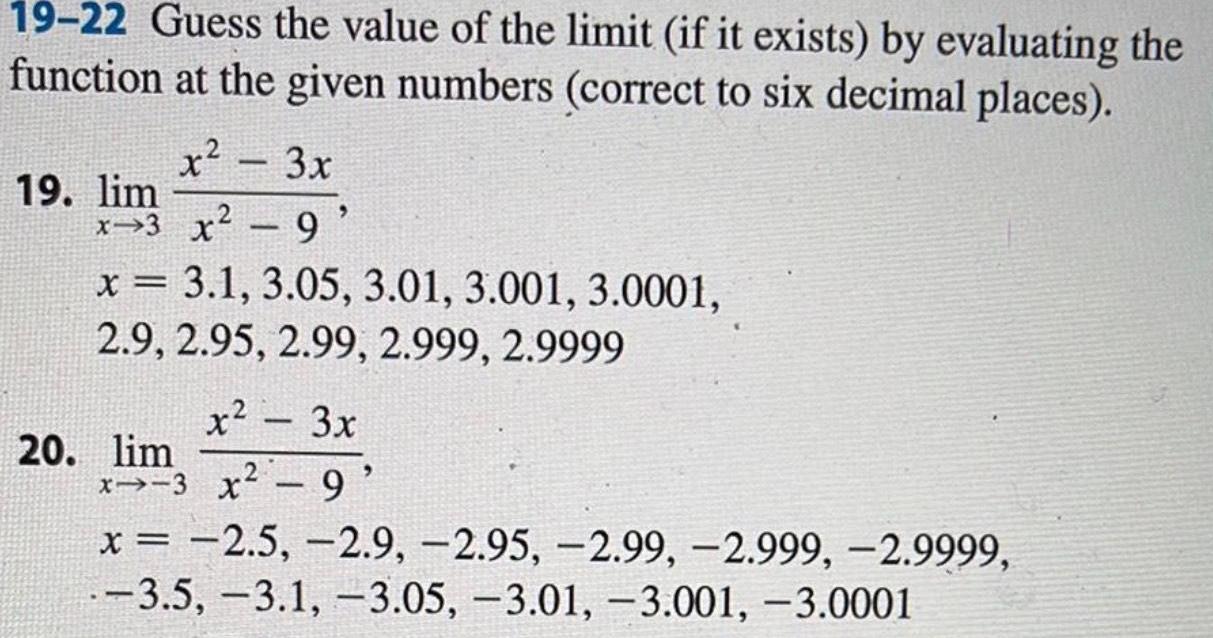
Calculus
Application of derivatives19 22 Guess the value of the limit if it exists by evaluating the function at the given numbers correct to six decimal places x 3x x 3 x 9 19 lim x 3 1 3 05 3 01 3 001 3 0001 2 9 2 95 2 99 2 999 2 9999 x 3x x3 x 9 20 lim x 2 5 2 9 2 95 2 99 2 999 2 9999 3 5 3 1 3 05 3 01 3 001 3 0001

Calculus
Application of derivatives12 A race car is running practice laps in preparation for an upcoming race To judge how the car is performing the crew takes measurements of the car s speed S t in miles per hour or mph every minute The measurements are given in the table below t minutes S t mph 0 201 1 205 208 214 218 212 219 223 220 221 217 218 216 3 5 6 7 8 10 11 12 A Use the trapezoid rule with 4 equal subdivisions to approximate the total distance the car traveled in miles over the first 12 minutes B Find one approximation for S 6 including the units Explain what this quantity means in the context of the problem
Calculus
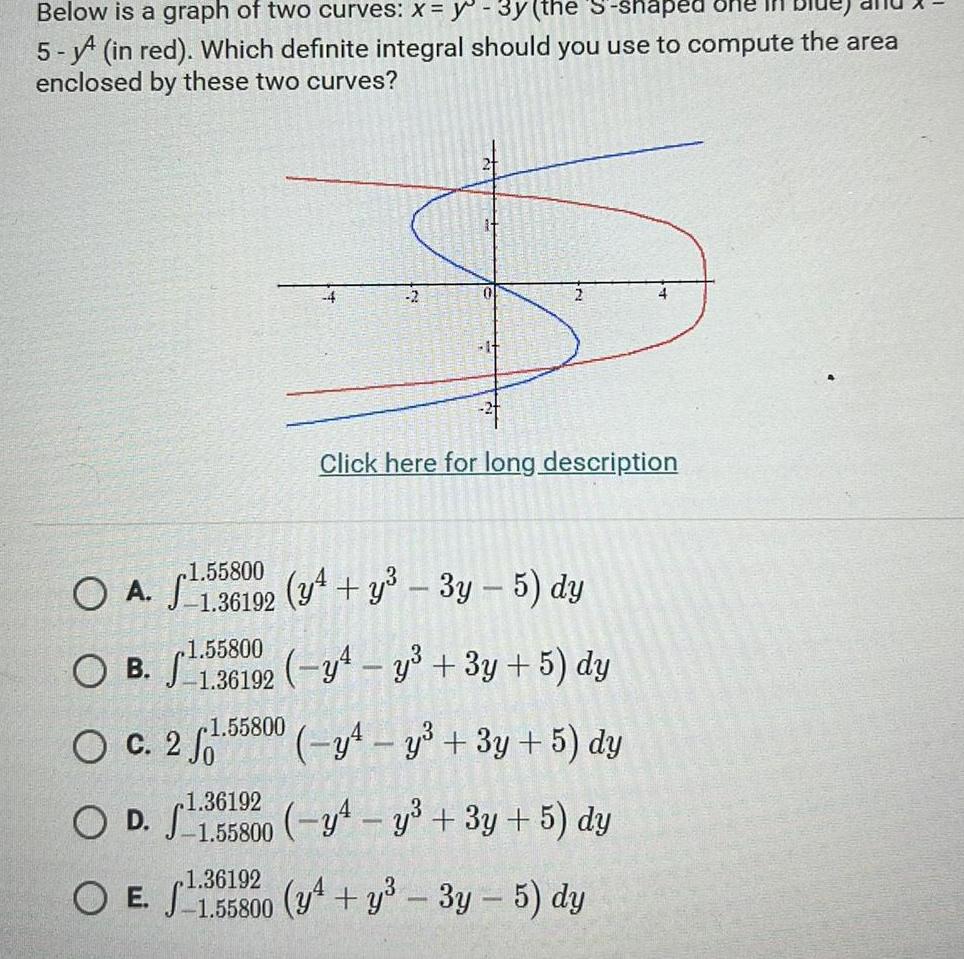
Limits & ContinuityBelow is a graph of two curves x y 3y the S shaped 5 in red Which definite integral should you use to compute the area enclosed by these two curves A OA O B O c 2 1 36192 OD 1 55800 0 Click here for long description 1 55800 1 36192 y y 3y 5 dy 1 55800 1136192 y4 y 3y 5 dy 1 55800 y y 3y 5 dy y y 3y 5 dy 1 36192 OE 1 55800 y y 3y 5 dy

Calculus
Vector Calculus15 Water is draining from a small cylindrical tank into a larger one below it The small cylindrical tank has a radius of 4 feet and a height of 6 feet the large cylindrical tank has a radius of 8 feet and a height of 16 feet The small tank is initially full of water and the water drains out at a rate of cubic feet per second Note The volume of a cylinder is V r h A Find the volume Vs of the water remaining in the small tank as a function of time B How long does it take for the small tank to completely empty C Let z be the depth of the water in the large tank which is initially empty Compute D What fraction of the total amount of water is in the large tank at time t 6

Calculus
Definite Integralshe formal integral Calculus definition Thans form to find the of the and Use of the Laplace Laplace Show all woonk FH eat Transform 1 following funct all propen nota

Calculus
DifferentiationYou may use your calculator on the following three questions 11 Consider a curve given implicitly by the equation 1 x y xy 85 0 A Calculated at a general point x y B Write the equation of the tangent line to the curve at the point 3 1 C At 3 1 y x is defined implicitly as a function of x Let g x be the inverse function of y x Compute g 1

Calculus
Differential equations12200 4 Consider a lake of constant volume 12200 km3 which at time contains an amount y t tons of y 1 pollutant evenly distributed throughout the lake with a concentration tons km Assume that fresh water enters the lake at a rate of 67 1 km yr and that water leaves the lake at the same rate Suppose that pollutants are added directly to the lake at a constant rate of 550 tons yr Among the many simplifying assumptions that must be made to model such a complicated real world process is that the pollutants coming into the lake are instantaneously evenly distributed throughout the lake A Write a differential equation for y t B Solve the differential equation for initial condition y 0 200000 to get an expression for y t Use your solution y t to describe in practical terms what happens to the amount of pollutants in the lake as goes from 0 to infinity
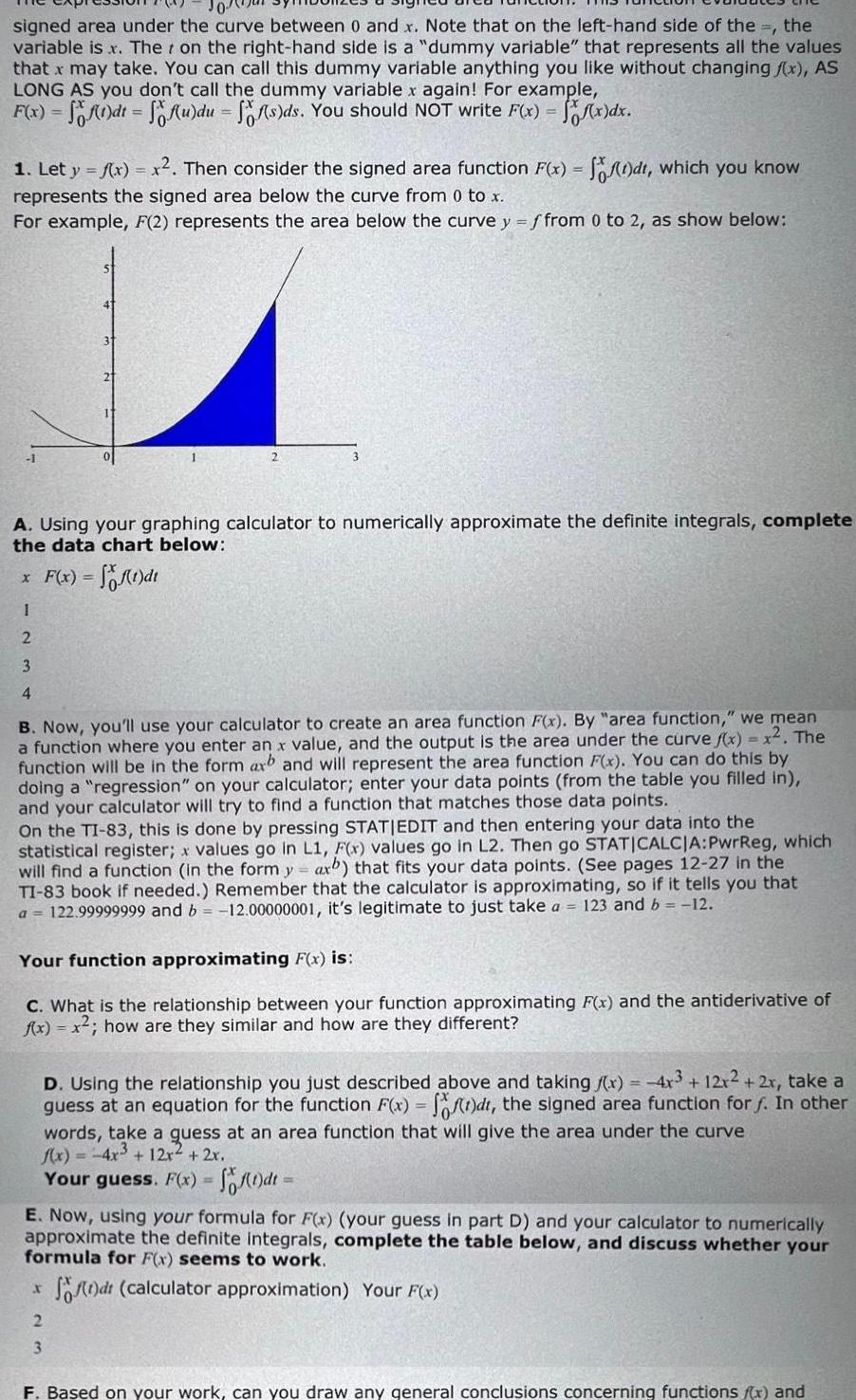
Calculus
Vector Calculussigned area under the curve between 0 and x Note that on the left hand side of the the variable is x Ther on the right hand side is a dummy variable that represents all the values that x may take You can call this dummy variable anything you like without changing f x AS LONG AS you don t call the dummy variable x again For example F x f 1 dt f u du ff s ds You should NOT write F x f x dx 1 Let y f x x Then consider the signed area function F x f t dt which you know represents the signed area below the curve from 0 to x For example F 2 represents the area below the curve y f from 0 to 2 as show below A Using your graphing calculator to numerically approximate the definite integrals complete the data chart below x F x f 1 dt I 2 3 4 B Now you ll use your calculator to create an area function F x By area function we mean a function where you enter an x value and the output is the area under the curve f x x The function will be in the form axb and will represent the area function F x You can do this by doing a regression on your calculator enter your data points from the table you filled in and your calculator will try to find a function that matches those data points On the TI 83 this done by pressing STATIEDIT and then entering your data into the statistical register x values go in L1 F x values go in L2 Then go STATICALCJA PwrReg which will find a function in the form y ax that fits your data points See pages 12 27 in the TI 83 book if needed Remember that the calculator is approximating so if it tells you that a 122 99999999 and b 12 00000001 it s legitimate to just take a 123 and b 12 Your function approximating F x is C What is the relationship between your function approximating F x and the antiderivative of f x x how are they similar and how are they different D Using the relationship you just described above and taking x 4x3 12x2 2x take a guess at an equation for the function F x f t dt the signed area function for f In other words take a quess at an area function that will give the area under the curve f x 4x 12x 2x Your guess F x f 1 dt E Now using your formula for F x your guess in part D and your calculator to numerically approximate the definite integrals complete the table below and discuss whether your formula for F x seems to work f dt calculator approximation Your F x r 2 3 F Based on your work can you draw any general conclusions concerning functions f x and
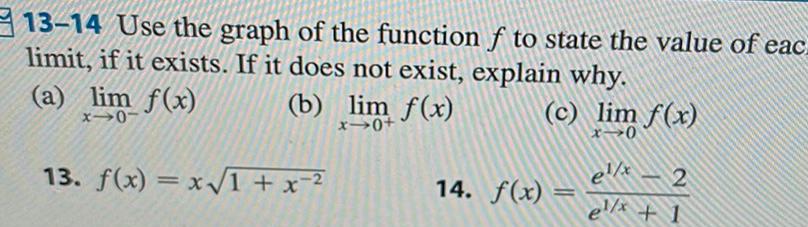
Calculus
Differential equations13 14 Use the graph of the function f to state the value of eac limit if it exists If it does not exist explain why a lim f x x10 b lim f x x40 13 f x x 1 x c lim f x x 0 14 f x 2 el x e x 1

Calculus
Differential equations17 Consider the differential equation given by A On the axes provided below sketch a slope field for the given differential equation at the nine points indicated B Let y f x be the particular solution to the given differential equation with the initial condition Based on your slope field how does the value of f 0 2 compare to f 0 Justify your answer C Find the particular solution y f x to the given differential equation with the initial condition f 0 3 Use your solution to find 0 2 y 1 3 2 dy xy dx 2 1 X

Calculus
Differentiation16 Suppose that f has a continuous second derivative for all x and that f 0 1 f 0 2 and f 0 0 A Does f have an inflection point at x 0 Explain your answer B Let g x 3x 2 f x x 2x 5 f x The point 0 5 is on the graph of g Write the equation of the tangent line to g at this point C Use your tangent line to approximate g 0 3 D Find q 0
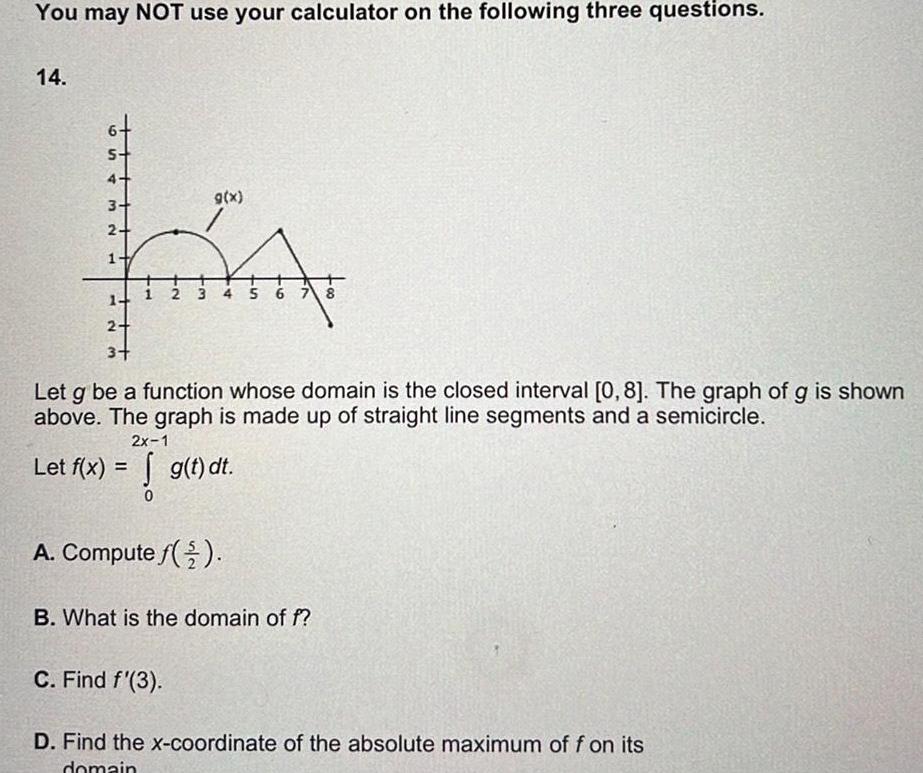
Calculus
DifferentiationYou may NOT use your calculator on the following three questions 14 S 4 3 2 H Let f x M 2 3 1 g x Let g be a function whose domain is the closed interval 0 8 The graph of g is shown above The graph is made up of straight line segments and a semicircle 3 4 5 6 7 8 2x 1 g t dt A Compute f C Find f 3 B What is the domain of f D Find the x coordinate of the absolute maximum of f on its domain

Calculus
Differentiationvelocity by time it hits the ground By measuring the impact you determine that this terminal velocity is 49 m sec A Write the equation representing the velocity 1 of the object at time seconds given the initial velocity vo and the fact that acceleration due to gravity is 9 8 m sec2 Here assume you re modeling the falling body with the differential equation g kv and use the resulting formula for v 1 found in the Tutorial Of course you can derive it if you d like dv dt B Determine the value of k the continuous percentage growth rate from the velocity equation by utilizing the information given concerning the terminal velocity

Calculus
Differentiation3 Biologists stocked a lake with 800 fish and estimated the carrying capacity of the lake to be 20000 In the first year the number of fish doubled Use a logistic model to model the fish population and answer the questions below A Find an expression for the size of the fish population P P t at time in years You may approximate the constant to six decimal places B How long will it take for the fish population to reach 10000
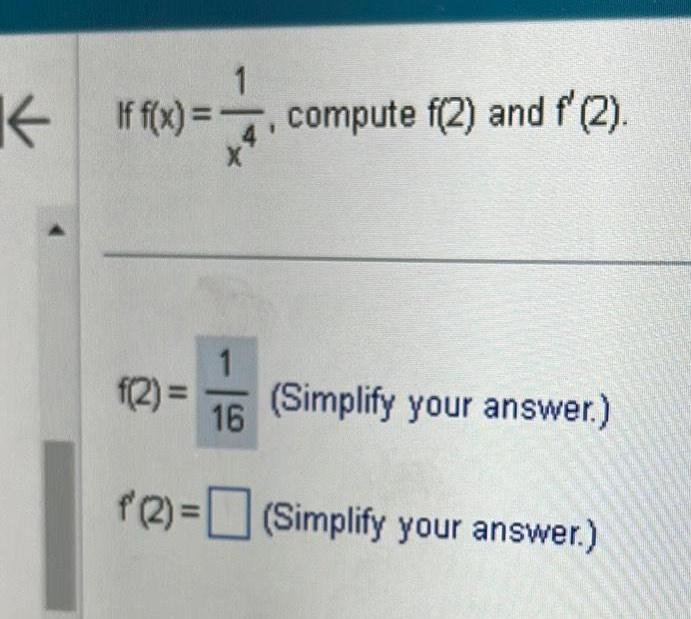
Calculus
DifferentiationK if f x 4 1 If f x compute f 2 and f 2 9 f 2 Simplify your answer 1 16 f 2 Simplify your answer
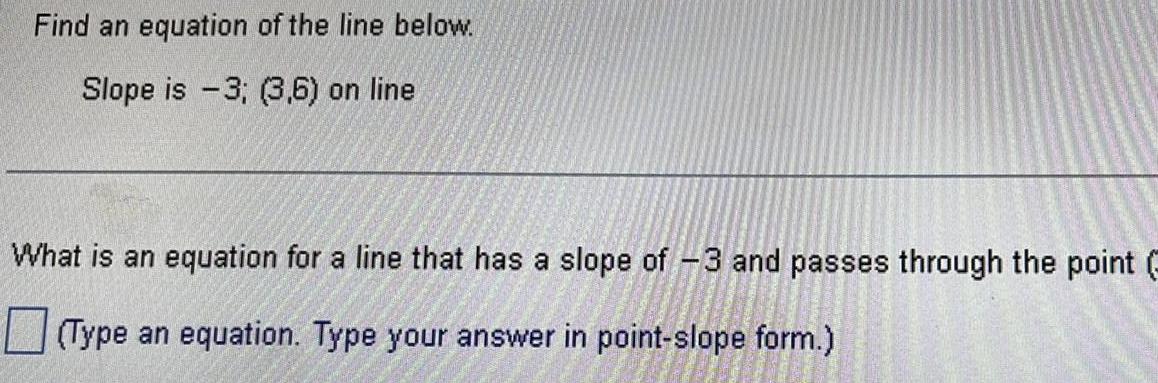
Calculus
Differential equationsFind an equation of the line below Slope is 3 3 6 on line What is an equation for a line that has a slope of 3 and passes through the point Type an equation Type your answer in point slope form
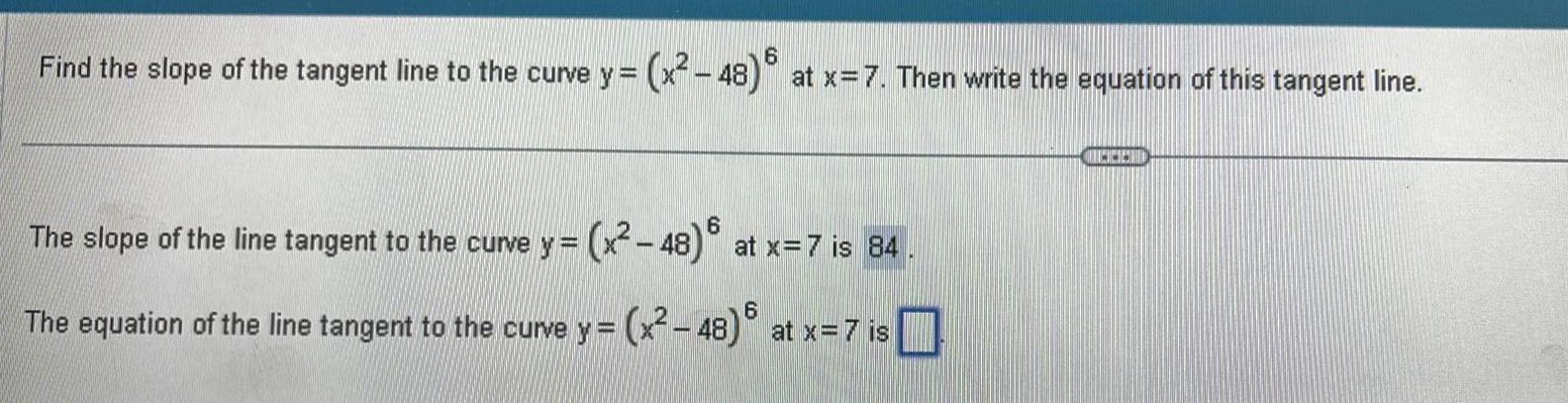
Calculus
Application of derivatives6 Find the slope of the tangent line to the curve y x 48 at x 7 Then write the equation of this tangent line 6 x 48 at x 7 is 84 The slope of the line tangent to the curve y 6 The equation of the line tangent to the curve y x 48 at x 7 is CHCES

Calculus
Vector Calculussomething that is happening in the world over the last month I would like you to find something other than the fire in Maui Create a slides presentation Find 2 current events dig deeper than the first site you find on google o They can be happening in Vegas The US or the World o One slide for each event On you slide you need o A summary of the events IN YOUR OWN WORDS This should be 3 4 sentences o A personal response 3 sentences Why did you choose this event why is the event important how do you feel about this event what action would you take to either solve highlight this event Add a picture s of the event Share will people sitting at your table One two people will share their event s with class

Calculus
Definite IntegralsConsider the cost function C x 5x 14x 16 thousand dollars a What is the marginal cost at production level x 4 b Use the marginal cost at x 4 to estimate the cost of producing 4 25 units c Let R x x 51x 51 denote the revenue in thousands of dollars generated from the production of x units What is the break even point Recall that the break even point is when the revenue is equal to the cost d Compute and compare the marginal revenue and marginal cost at the break even point Should the company increase production beyond the break even point a The marginal cost at production level x 4 is
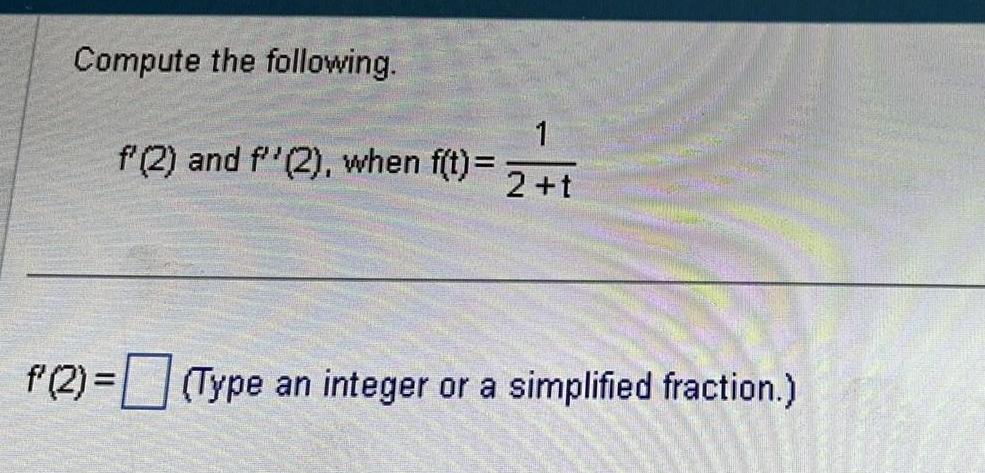
Calculus
DifferentiationCompute the following 1 f 2 and f 2 when f t 2 t f 2 Type an integer or a simplified fraction
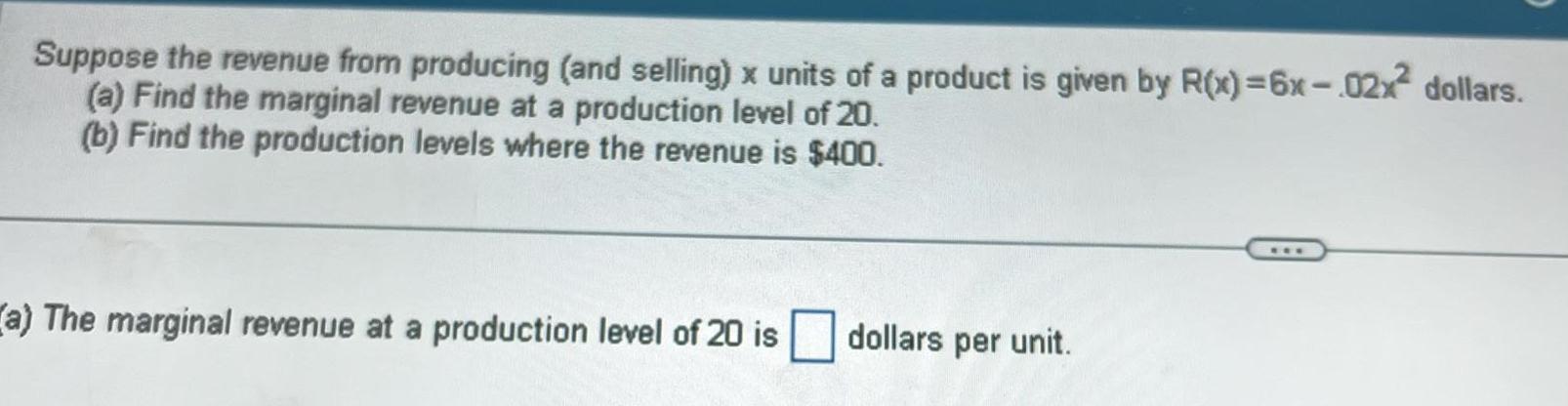
Calculus
DifferentiationSuppose the revenue from producing and selling x units of a product is given by R x 6x 02x dollars a Find the marginal revenue at a production level of 20 b Find the production levels where the revenue is 400 a The marginal revenue at a production level of 20 is dollars per unit
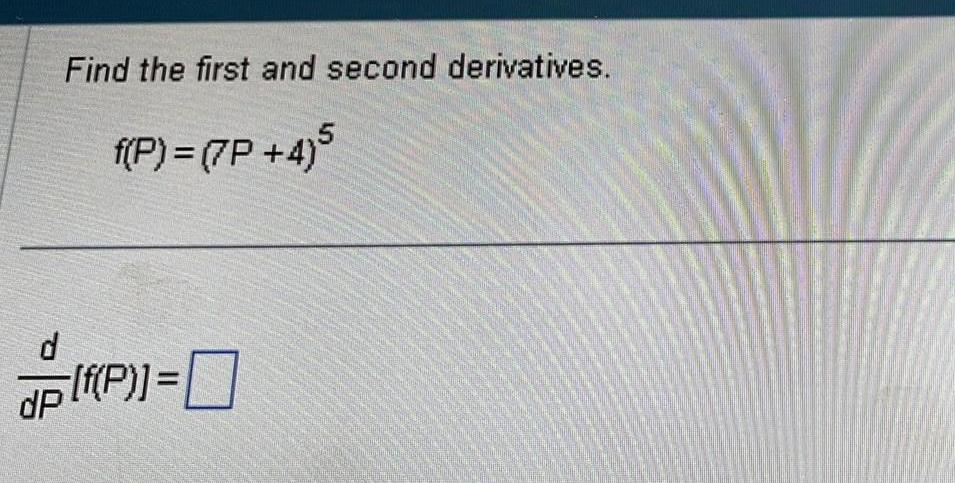


Calculus
Vector Calculuse 4 t cos 3 t 2 3 e 4 t sin 3 t e answer above is NOT correct 1 point Find the inverse Laplace transform f t F s of the function F s f 1 C 1 s 2 5 85 25 e 4t cos 3t 2 3e 4t sin3t e cos 31 sin 3 t 3 s 2 s 8s 25 help formulas inco