Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
Limits & ContinuityMeasurements of a lake s width were taken at 15 foot intervals as show 0 f x 0 Estimate 120 If x dx f x dx with n 4 using each of the following methods 0 A Left hand approximation 15 30 45 60 75 90 105 120 15 18 20 19 23 24 22 12 B Right hand approximation C Trapezoidal approximation
Calculus
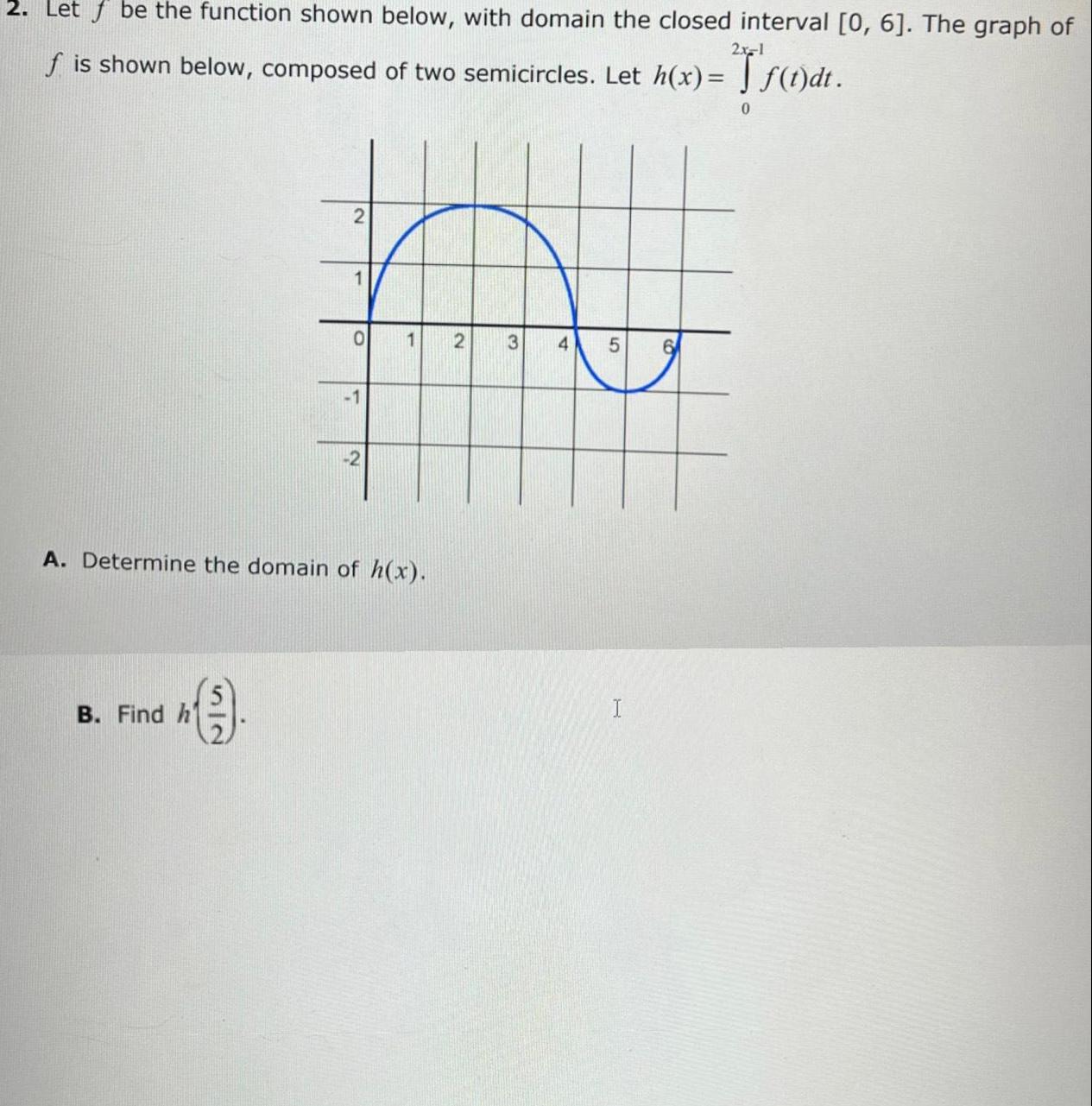
Application of derivatives2x 1 2 Let be the function shown below with domain the closed interval 0 6 The graph of f is shown below composed of two semicircles Let h x f t dt B Find h 1 9 O 1 2 A Determine the domain of h x 1 2 3 4 5 6 0

Calculus
Indefinite Integration3 The base of a solid is a right triangle whose base side has length a and whose perpendicular side has length a Find the volume of the solid if cross sections perpendicular to the base of the triangle are semicircles

Calculus
Limits & ContinuityThe domain of the function f x arccos 3x2 2 is O A all x in the interval 1 3 U 1 OB all x in the interval 0 1 OC all x in the interval O D all real numbers OE all x in the interval 1 1
Calculus
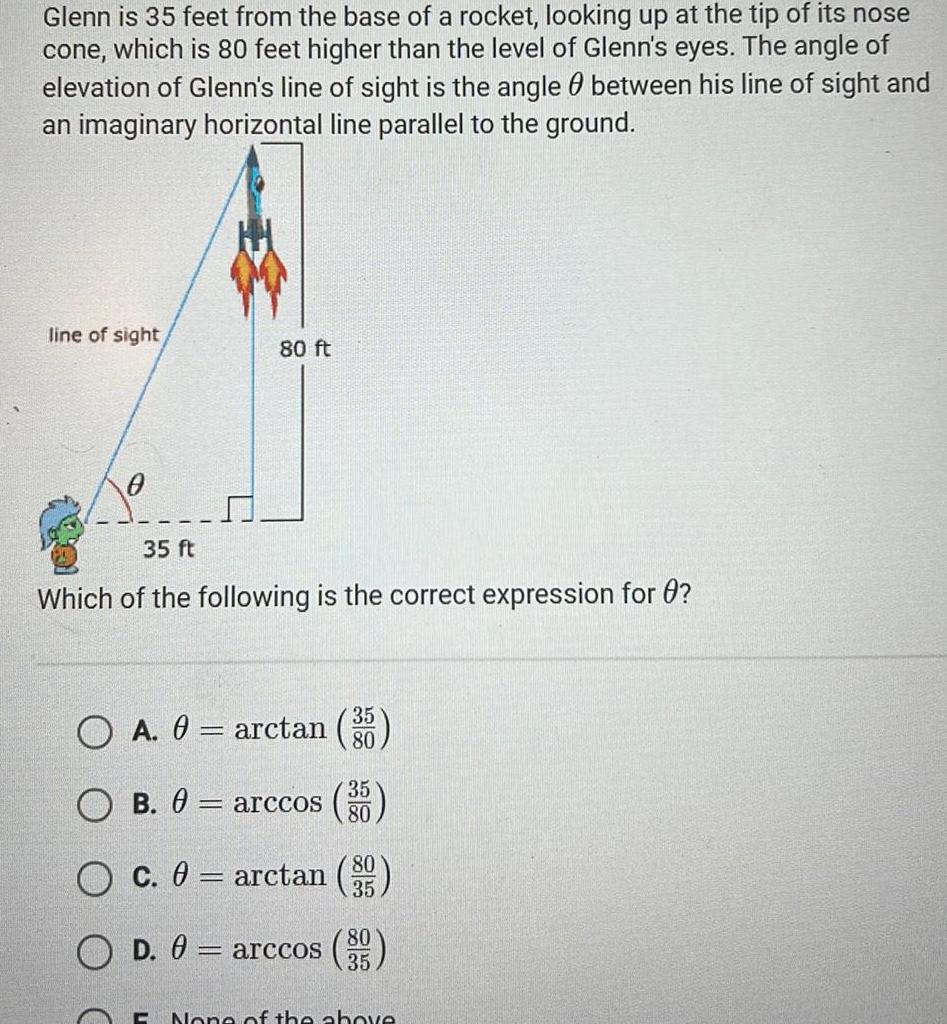
Application of derivativesGlenn is 35 feet from the base of a rocket looking up at the tip of its nose cone which is 80 feet higher than the level of Glenn s eyes The angle of elevation of Glenn s line of sight is the angle between his line of sight and an imaginary horizontal line parallel to the ground line of sight 80 ft 35 ft Which of the following is the correct expression for 0 O A 0 arctan g B 0 arccos O c 0 arctan O D 0 arccos 395 80 35 80 35 C None of the above

Calculus
Application of derivativesConsider the function f x x 4x 5 x 2 You have that f x 1 O A where x and y are related by the equation y x 4x 5 x 2 2y 4 for x 1 OB O C d da O E 1 2x 4 1 2x 4 for x 2 D 2y4 where x and y are related by the equation y x 4x 5 x 2 where x and y are related by the equation satisfy th equation x y 4y 5 x 1 1 2y 4

Calculus
Application of derivativesA tetrahedron has three mutually perpendicular faces and three mutually perpendicular edges of lengths 2 3 and 4 cm respectively Find its volume

Calculus
Vector Calculusx 2 The base of a solid is a region bounded by the curve 82 18 1 an ellipse with the major and minor axes of lengths 16 and 8 respectively Find the volume of the solid if every cross section by a plane perpendicular to the major axis x axis has the shape of an isosceles triangle with height equal to the length of the base

Calculus
Application of derivatives4 A solid has as its base the region bounded by the curves y 21 2 and y x 1 Find the volume of the solid if every cross section of a plane perpendicular to the x axis is a trapezoid with lower base in the xy plane upper base equal to the length of the lower base and height equal to 2 times the length of the lower base
Calculus
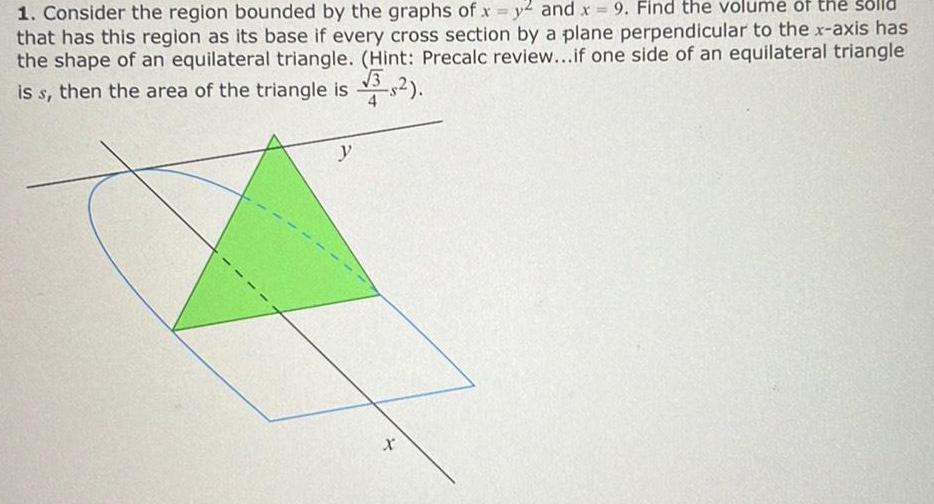
Application of derivatives1 Consider the region bounded by the graphs of x y2 and x 9 Find the volume of the solld that has this region as its base if every cross section by a plane perpendicular to the x axis has the shape of an equilateral triangle Hint Precalc review if one side of an equilateral triangle 3 is s then the area of the triangle is 3 2 y X
Calculus
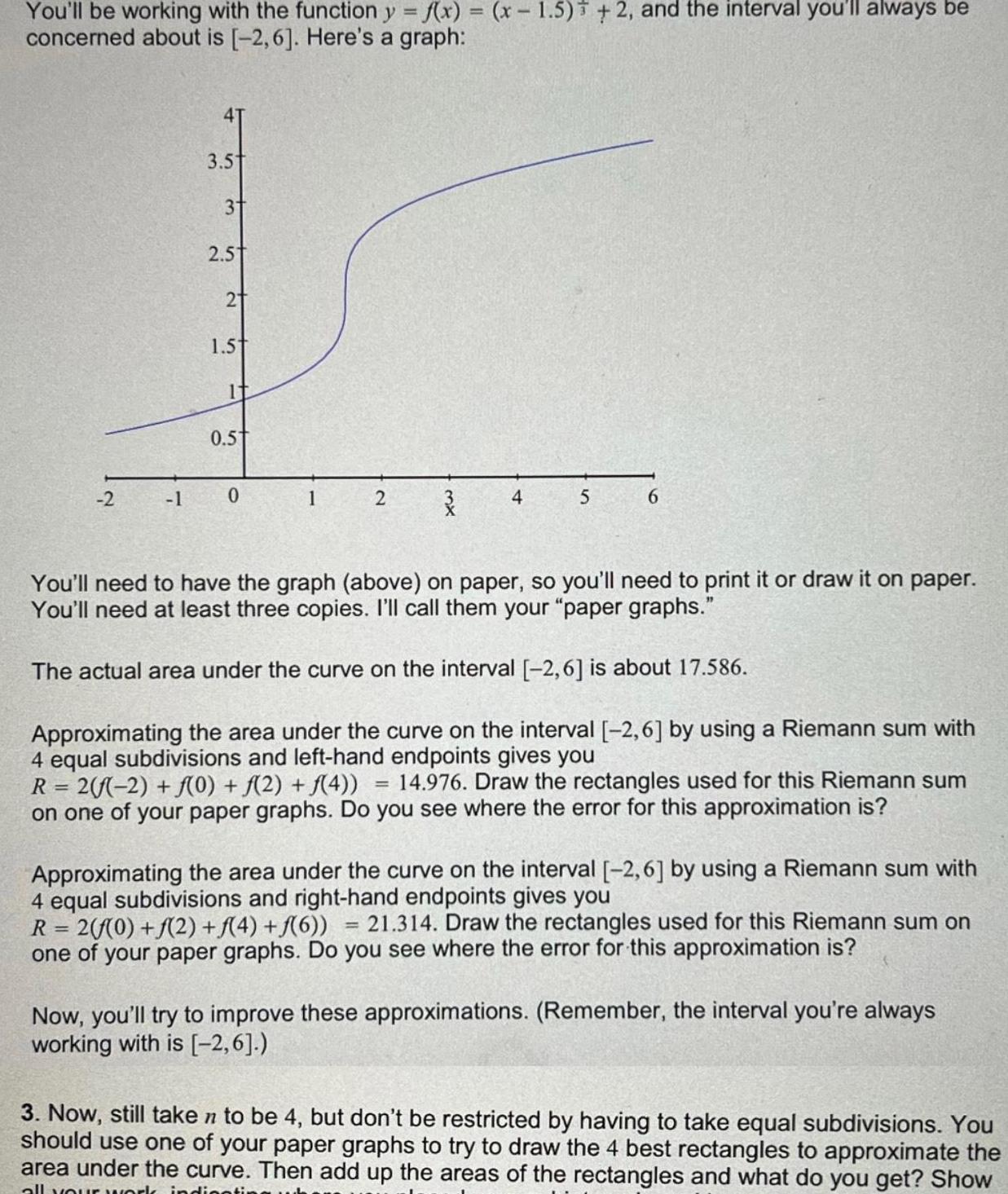
Vector CalculusYou ll be working with the function y f x x 1 5 2 and the interval you ll always be concerned about is 2 6 Here s a graph 2 1 3 5 3 2 5 2 1 5t It 0 5 0 1 2 4 5 6 You ll need to have the graph above on paper so you ll need to print it or draw it on paper You ll need at least three copies I ll call them your paper graphs The actual area under the curve on the interval 2 6 is about 17 586 Approximating the area under the curve on the interval 2 6 by using a Riemann sum with 4 equal subdivisions and left hand endpoints gives you R 2 f 2 f 0 f 2 f 4 14 976 Draw the rectangles used for this Riemann sum on one of your paper graphs Do you see where the error for this approximation is Approximating the area under the curve on the interval 2 6 by using a Riemann sum with 4 equal subdivisions and right hand endpoints gives you R 2 f 0 f 2 f 4 f 6 21 314 Draw the rectangles used for this Riemann sum on one of your paper graphs Do you see where the error for this approximation is Now you ll try to improve these approximations Remember the interval you re always working with is 2 6 3 Now still taken to be 4 but don t be restricted by having to take equal subdivisions You should use one of your paper graphs to try to draw the 4 best rectangles to approximate the area under the curve Then add up the areas of the rectangles and what do you get Show all your work indig

Calculus
DifferentiationA Find the equation of the normal line to the curve In y3 2x 1 at the point 1 1 I
Calculus
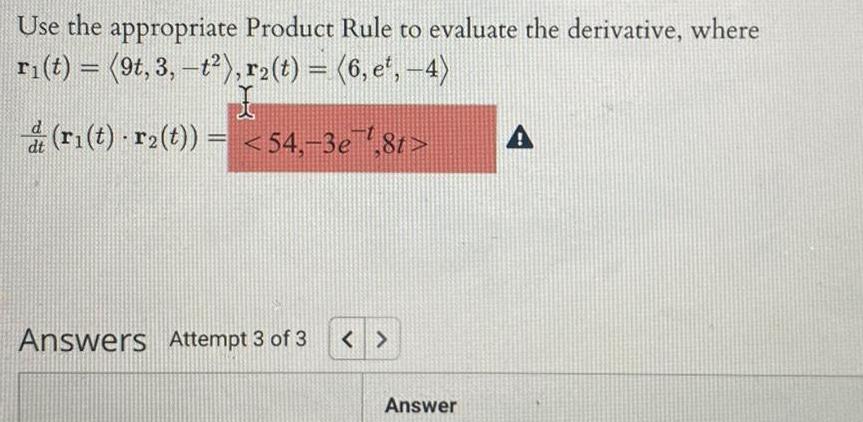
Vector CalculusUse the appropriate Product Rule to evaluate the derivative where ri t 9t 3 t r t 6 e 4 dt r t r t 54 3e 8t Answers Attempt 3 of 3 Answer
Calculus
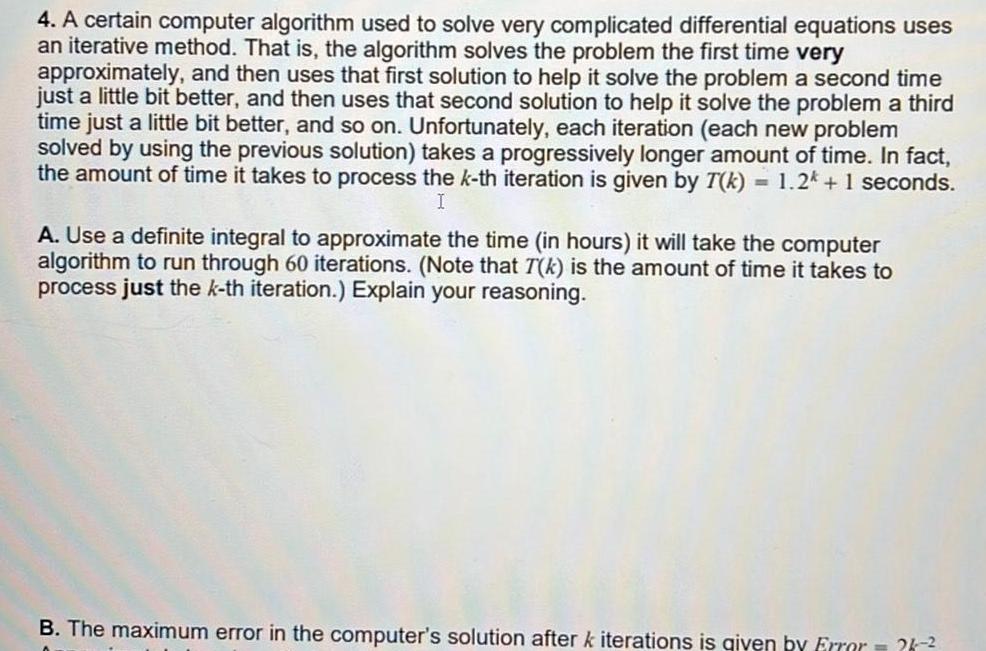
Limits & Continuity4 A certain computer algorithm used to solve very complicated differential equations uses an iterative method That is the algorithm solves the problem the first time very approximately and then uses that first solution to help it solve the problem a second time just a little bit better and then uses that second solution to help it solve the problem a third time just a little bit better and so on Unfortunately each iteration each new problem solved by using the previous solution takes a progressively longer amount of time In fact the amount of time it takes to process the k th iteration is given by T k 1 2k 1 seconds I A Use a definite integral to approximate the time in hours it will take the computer algorithm to run through 60 iterations Note that T k is the amount of time it takes to process just the k th iteration Explain your reasoning B The maximum error in the computer s solution after k iterations is given by Error 26
Calculus
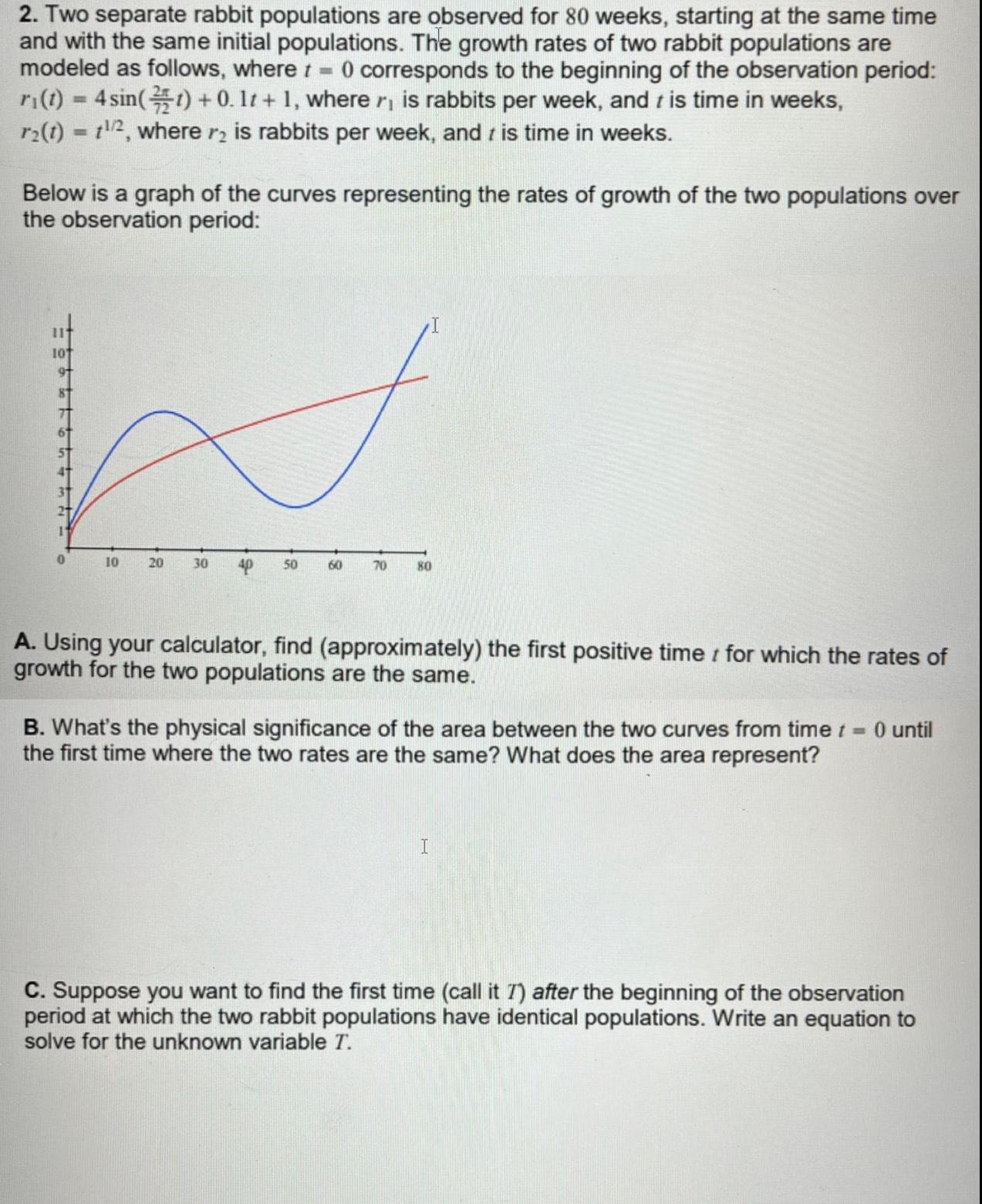
Indefinite Integration2 Two separate rabbit populations are observed for 80 weeks starting at the same time and with the same initial populations The growth rates of two rabbit populations are modeled as follows where t 0 corresponds to the beginning of the observation period ri t 4 sin t 0 11 1 where r is rabbits per week and is time in weeks r2 t t 2 where r is rabbits per week and is time in weeks Below is a graph of the curves representing the rates of growth of the two populations over the observation period 10 20 30 50 60 70 80 A Using your calculator find approximately the first positive time for which the rates of growth for the two populations are the same B What s the physical significance of the area between the two curves from time t 0 until the first time where the two rates are the same What does the area represent I C Suppose you want to find the first time call it 7 after the beginning of the observation period at which the two rabbit populations have identical populations Write an equation to solve for the unknown variable T

Calculus
DifferentiationFind a parameterization for the circle of radius 4 in the xy plane centered at the origin clockwise r t y t z t 9
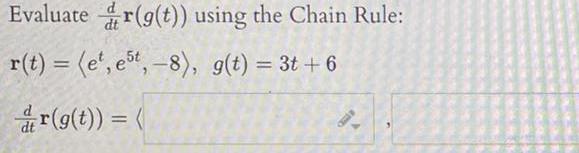
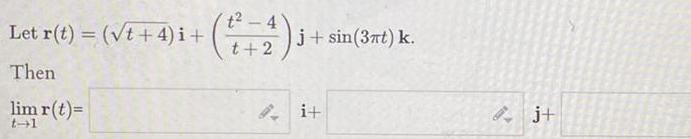
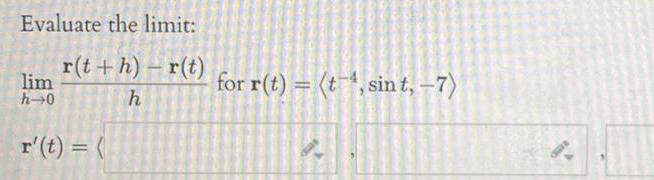


Calculus
Differentiationcustomer is using while a kilowatt hour is one kilowatt of power being used for one hour For constant power use the number of kilowatt hours used is calculated by kilowatt hours kilowatts time in hours Thus if customers use 5 kilowatts for 30 minutes they ll have used 5 kilowatts hours 2 5 kilowatt hours Suppose the power use of a customer over a 30 day period is given by the continuous function P f t where P is kilowatts is time in hours and 0 corresponds to the beginning of the 30 day period A Approximate with a Riemann sum the total number of kilowatt hours used by the customer in the 30 day period and explain why your Riemann sum is an approximation of the desired property B Derive an expression representing the total number of kilowatt hours used by the customer in the 30 day period and explain your reasoning This expression should not be an approximation C Consider the following table of data for the function 1 f 1 0 2 3 2 5 2 1 3 9 3 6 5 5 4 5 7 5 6 8 1 2 9 1 0 10 1 8 3 4 I Recall that r represents the number of kilowatts being used by a customer at timer hours

Calculus
Indefinite Integrationlowing is not true OA Figuring the volume of a solid can involve slicing it into cross sections B In a solid of revolution the cross sections are circles or washers C A solid of revolution is obtained by revolving a region about a line D You can figure the volume of a solid by slicing it into cross sections figuring the individual volumes and adding them up E You can figure the exact volume of a solid by slicing it into cross sections figuring the individual volumes by multiplying cross sectional area times thickness and adding them up

Calculus
Application of derivativesIf g x f x on the interval a b then the area between the curves for a x bis given by O A f f x g x dx O B f g x f x dx O c f A x dx OD Both f f x g x dx and o f x dx f g x dx ob E f f x dx f g x dx
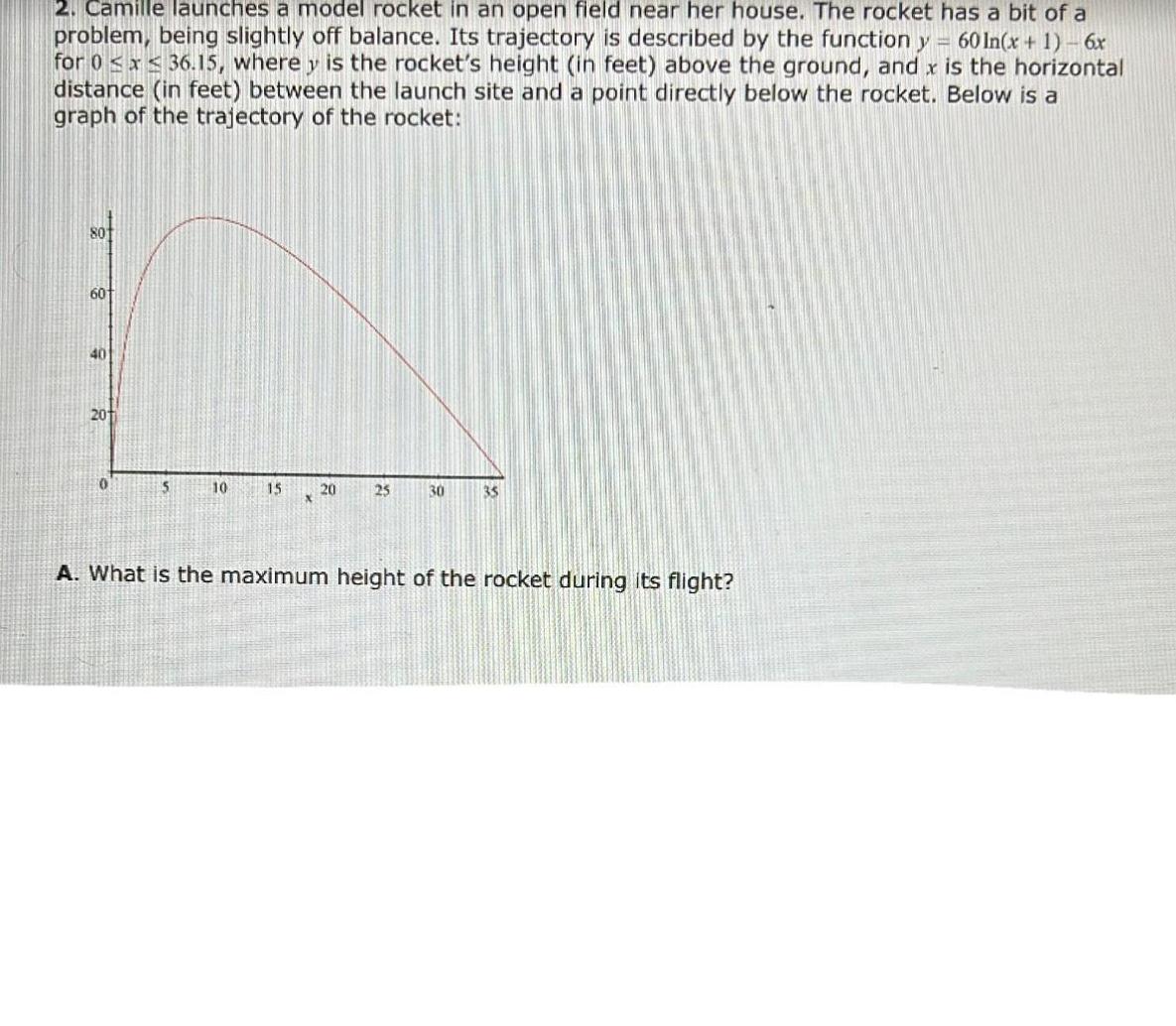
Calculus
Differential equations2 Camille launches a model rocket in an open field near her house The rocket has a bit of a problem being slightly off balance Its trajectory is described by the function y 60 In x 1 6x for 0 x 36 15 where y is the rocket s height in feet above the ground and x is the horizontal distance in feet between the launch site and a point directly below the rocket Below is a graph of the trajectory of the rocket 801 60 40 201 0 5 10 15 20 25 30 35 A What is the maximum height of the rocket during its flight

Calculus
Differentiation1 Consider the function f x x e 2x for x 0 where n is some unknown constant greater than 2 A Find the constant for which the function f x attains its maximum value at x 3 Make certain to justify that a maximum is attained I
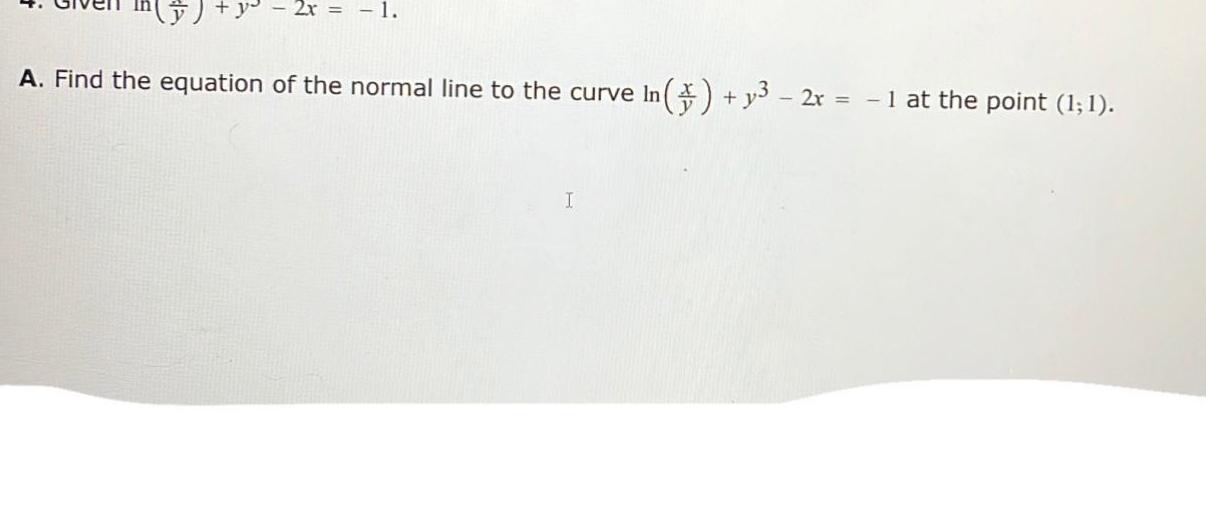
Calculus
DifferentiationA Find the equation of the normal line to the curve In y 2x 1 at the point 1 1 1

Calculus
Differentiation3 The position of a particle in rectilinear motion is given by s t tln for t 0 where is in seconds Find the time 0 at which the velocity of the particle is 0 and find the particle s acceleration at that time as well You must find exact values don t approximate with a calculator

Calculus
Vector CalculusThe graph of the equation 2x y from A 0 0 to B 2 2 is revolved about the x axis The surface area of the resulting solid is in square units and to three decimal places is A 3 3934 OB 18 088 O C 22 062 O D 18 585 OE 21 322

Calculus
Definite IntegralsThe area of the region enclosed by the curves y given by which of the following expressions O A S O C OE 0 28166 1 67738 2 26296 2 26296 O B S 1 67738 2 x 3x dx 1 67738 0 28166 x 3x 2 dx 2 x 3x dx 1 67738 x 3x 2 dx 2 26296 028108 2 2 3 32 0 28166 9 85917 2 26296 O D 1 67738 2 26296 228296 0 28166 2 x x 3x 2 dx 0 28166 1 67738 3x dx dx x 3x 2 dx 2 x 3x dx 3 and y 1
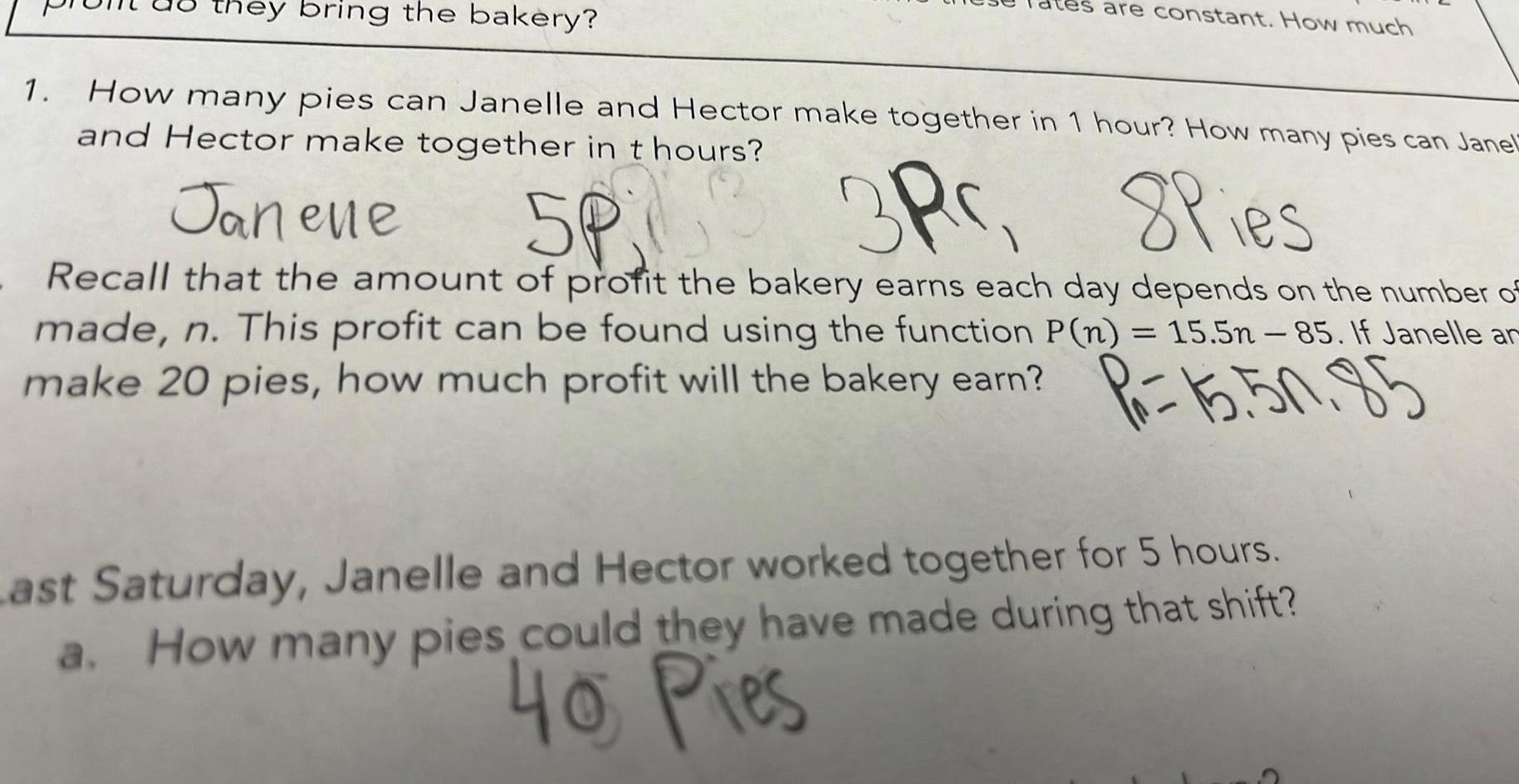
Calculus
Vector Calculusthey bring the bakery 1 How many pies can Janelle and Hector make together in 1 hour How many pies can Janel and Hector make together in t hours are constant How much Janene 5P 3P 8Pies Recall that the amount of profit the bakery earns each day depends on the number of made n This profit can be found using the function P n 15 5n 85 If Janelle ar make 20 pies how much profit will the bakery earn Pr 15 50 85 Last Saturday Janelle and Hector worked together for 5 hours a How many pies could they have made during that shift 40 Pies
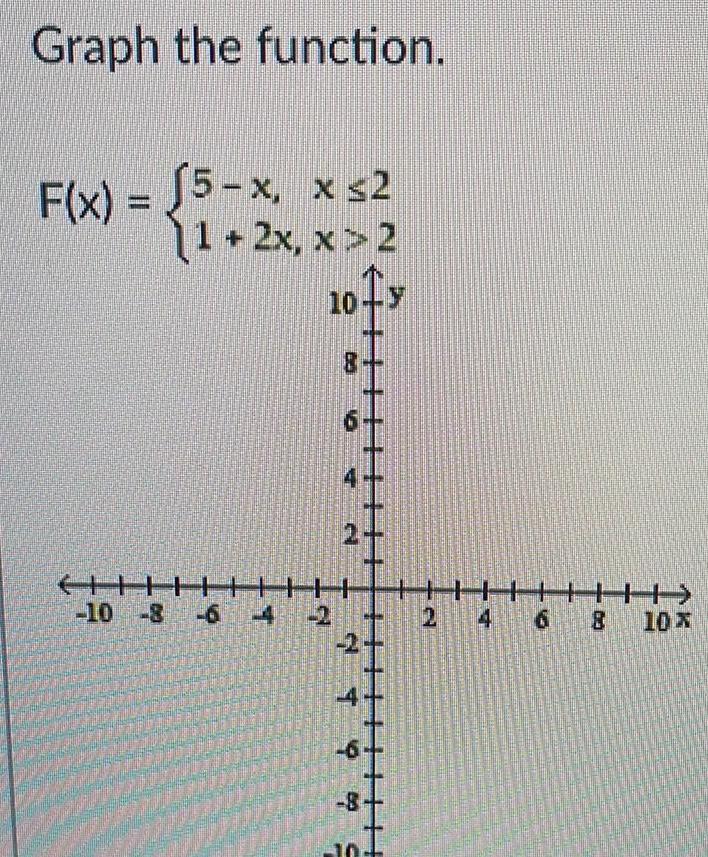
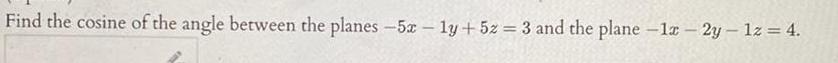
Calculus
Vector CalculusFind the cosine of the angle between the planes 5x 1y 5z 3 and the plane 12 2y 1z 4
Calculus
Application of derivativesA child wanders slowly down a circular staircase from the top of a tower With z y z in feet and the origin at the base of the tower her position t minutes from the start is given by x 30 cost y 30 sint 90 5t a How tall is the tower height ft b When does the child reach the bottom time minutes c What is her speed at time t speed ft min d What is her acceleration at time t acceleration ft min2


Calculus
Vector CalculusFind the velocity and acceleration vectors for the motion described by v t a t 9 9 x 7 2t y 4 2t z 7 2t

Calculus
Vector CalculusLet r t t 1 t 4t Calculate the derivative of r t a t at t 2 assuming that a 2 6 3 3 and a 2 9 7 3 d dt r t a t t 2
Calculus
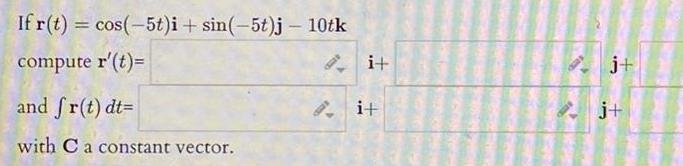
DifferentiationIf r t cos 5t i sin 5t j 10tk compute r t and fr t dt with C a constant vector i i j j
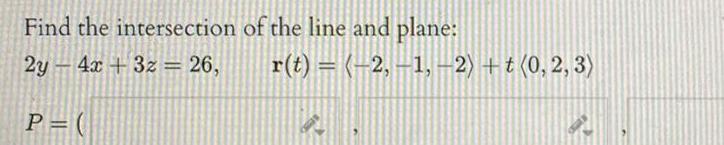

Calculus
Vector Calculus1 point If r t cos 3t i sin 3t j 7tk compute A The velocity vector v t B The acceleration vector a t i i j Ij
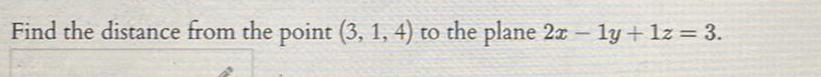

Calculus
Vector CalculusFind the vector equation for the line of intersection of the planes 4x 3y 5z 0 and 4x 5z 1 0 t 15
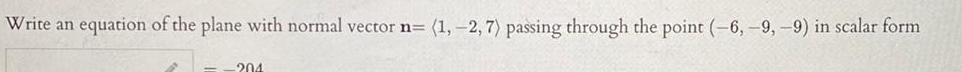
Calculus
Definite IntegralsWrite an equation of the plane with normal vector n 1 2 7 passing through the point 6 9 9 in scalar form 204

Calculus
Application of derivativesFind r t and v t given acceleration initial velocity and initial position v t r t 1 a t t 1 v 0 6 6 r 0 0 0

Calculus
Application of derivativesFind v t given the acceleration and initial condition v t Usage To enter a vector for example x y z type x y z a t 4i v 0 j

Calculus
Vector CalculusFind an equation of a plane containing the three points 5 3 2 3 6 3 3 7 1 in which the coefficient of a is 7 0

Calculus
Application of derivativesFind the equation of the plane which passes through O and is parallel to 3y 2x z 6 y z 8 x

Calculus
Application of derivativesFind a vector n normal to the plane with the equation y 3x3z 4 n 3
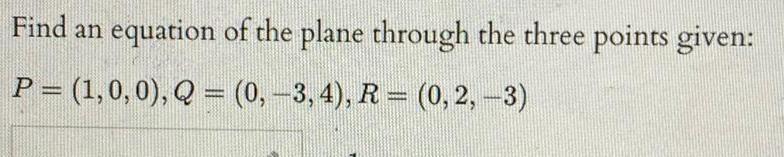
Calculus
Vector CalculusFind an P 1 0 0 Q 0 3 4 R 0 2 3 equation of the plane through the three points given
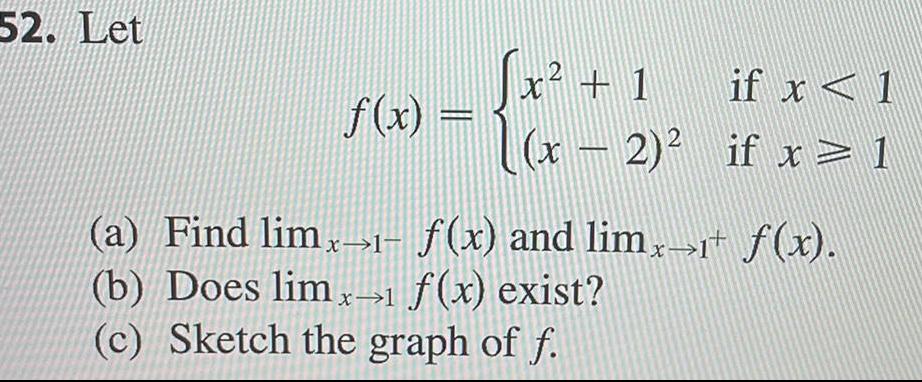
Calculus
Limits & Continuity52 Let f x x 1 if x 1 x 2 if x 1 a Find limx f x and limx f x b Does limx 1 f x exist c Sketch the graph of f
Calculus
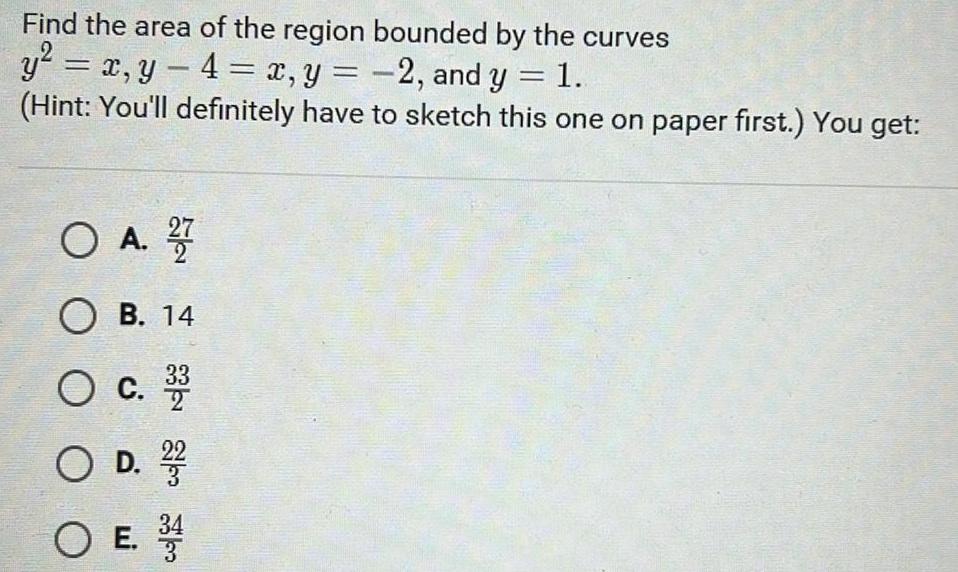
Definite IntegralsFind the area of the region bounded by the curves y x y 4 x y 2 and y 1 Hint You ll definitely have to sketch this one on paper first You get O A 27 OB 14 O C 2 O D 22 O E 3 4