Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
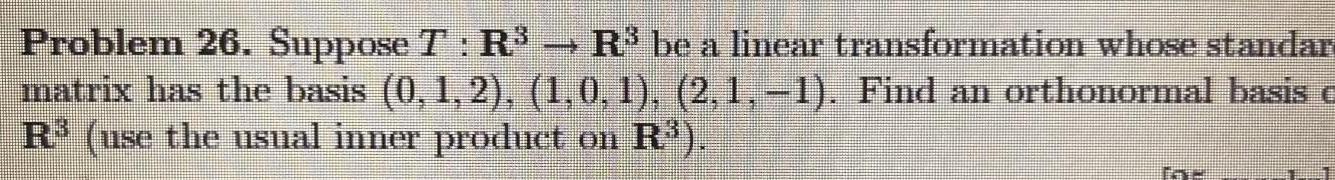
Calculus
DifferentiationProblem 26 Suppose 7 R R be a linear transformation whose standar matrix has the basis 0 1 2 1 0 1 2 1 1 Find an orthonormal basis R use the usual inner product on R THE
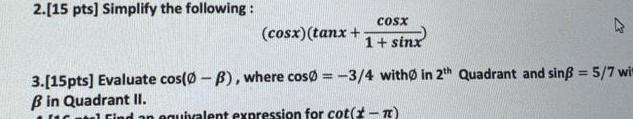
Calculus
Limits & Continuity2 15 pts Simplify the following cosx tanx COSX 1 sinx 3 15pts Evaluate cos 0 3 where cos0 3 4 with in 2th Quadrant and sin 5 7 wi B in Quadrant II 16 Find an equivalent expression for cot t

Calculus
Application of derivatives5 15 pts If tanx 1 6 and x is in the fourth quadrant 6 18 pts Prove the following tan x sin x tan xsin x

Calculus
Indefinite IntegrationGiven S is a surface for a part of the sphere x y z 4 that lies above the cone z x y Find a parametric representation for the surface S in term of o and 8 Then determine the domain of and 0 Based on the expression written previously show that rx rell 4 sin o Hence compute the surface integral of ffs ds where the surface S is given parametrically by r 0 0 Let C is the boundary curve along the bottom of the upper half of the sphere thus use Stokes theorem to compute the line integral of fo F dr where F x y z xzi yzj xyk and upwards orientation

Calculus
Limits & ContinuityFind a power series for the function centered at c 5x x 3x g x I g x C 0 100 n 2 1 1 1 n 0 Determine the interval of convergence Enter your answer using interval notation 1 1

Calculus
DifferentiationFind the partial fraction decomposition of the rational function x 14 x 2x 8 2 x 2 3 2 2 2
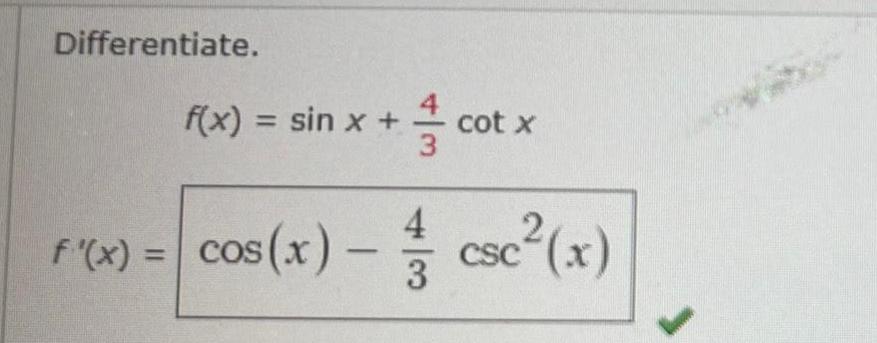
Calculus
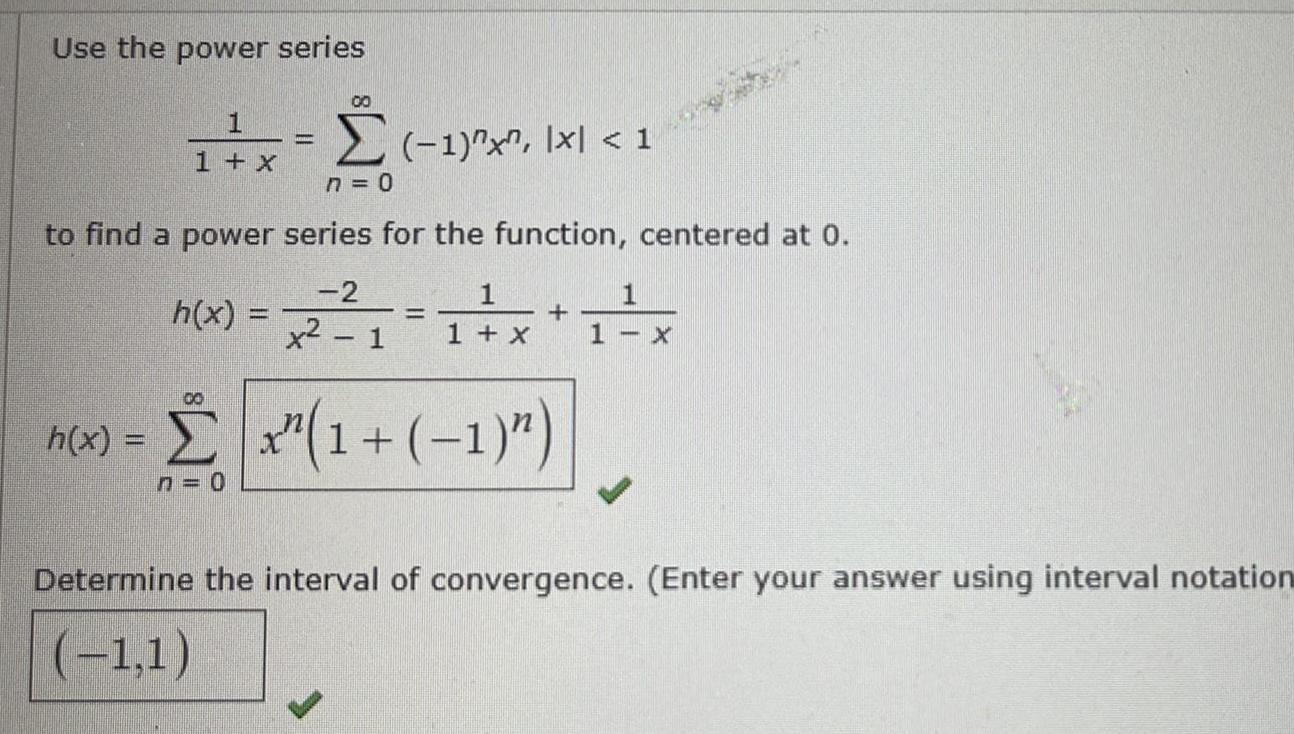
Limits & ContinuityUse the power series 1 1 x to find a power h x h x 00 n 0 00 1 x Ixl 1 n 0 series for the function centered at 0 2 x 1 x 1 1 1 1 x 1 X Determine the interval of convergence Enter your answer using interval notation 1 1

Calculus
Differential equationsFind each equilibrium solution x t x of the given second order differential equation x f x x 0 Use a computer or graphing calculator to construct a phase portrait and direction field for the equivalent first order system x f x y Thereby ascertain whether the critical point 0 looks like a center a saddle point or a spiral point of t system x x x 0 Comp The equilibrium solution s is are x t Type an integer or a fraction Use a comme to separate answers as needed

Calculus
Application of derivatives3 The asymptotic expression f n O g n means there exists a constant c 0 and an integer No such that for all nz No f n sc g n Consider f n n and g n gn It is a fact that n O lg Determine the smallest positive constant No such that for all n No f n sc g n given that c 32 Be careful The floor over the log makes this problem interesting 5 points

Calculus
Limits & ContinuityFind the radius of convergence of the power series If you need to use co or co enter INFINITY or INFINITY respectively 1 n 0 n 9

Calculus
Limits & ContinuityFind the interval of convergence of the power series Be sure to include a check for convergence at the endpoints of the interval If the answer is an interval enter your answer using interval notation If the answer is a finite set of values enter your answers as a comma separated list of values 1 4x 1 n 1 n 1 11 11

Calculus
Application of derivativesind the interval of convergence of the power series Be sure to include a check for convergence at the endpoints of the interval If the answer is an interval enter your answer using interval notation If the answer is a finite set of values enter nswers as a comma separated list of values 1 x 2 n8n n 1 6 10
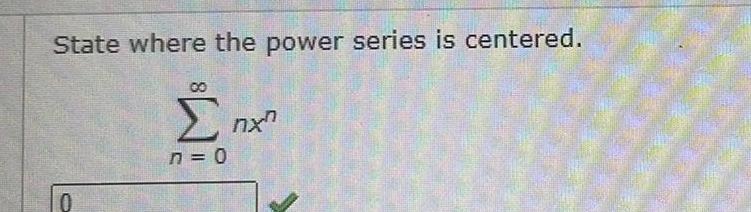


Calculus
Vector CalculusGiven a generic point M in the Argand diagram representing the complex number z and let 8 iz 61 zi s t Re U 0 Determined the circle representing the locus of M Find the locus of M whenever the complex number U is real
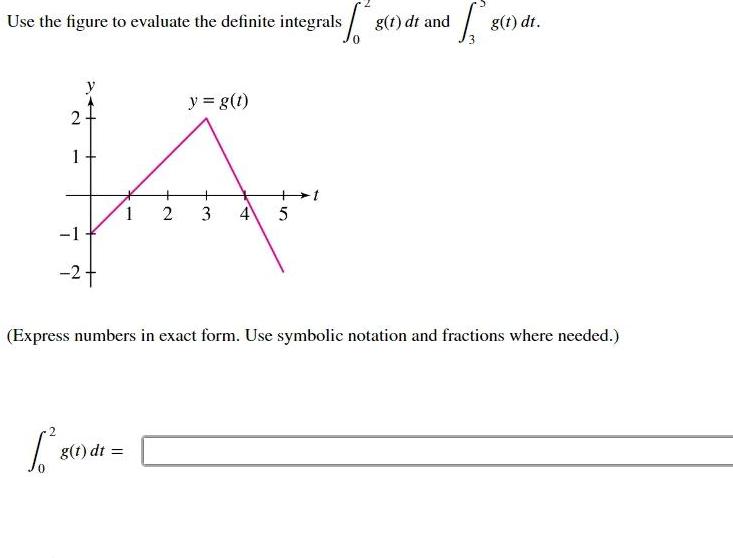
Calculus
Definite IntegralsUse the figure to evaluate the definite integrals g 1 dt and 2 1 2 8 1 a 1 g t dt y g t 2 3 4 5 8 Express numbers in exact form Use symbolic notation and fractions where needed g t dt

Calculus
Application of derivativesThe function f x 16x 4 is one to one a Find the inverse of f and check the answer b Find the domain and the range of f and f c Graph f f1 and y x on the same coordinate axes
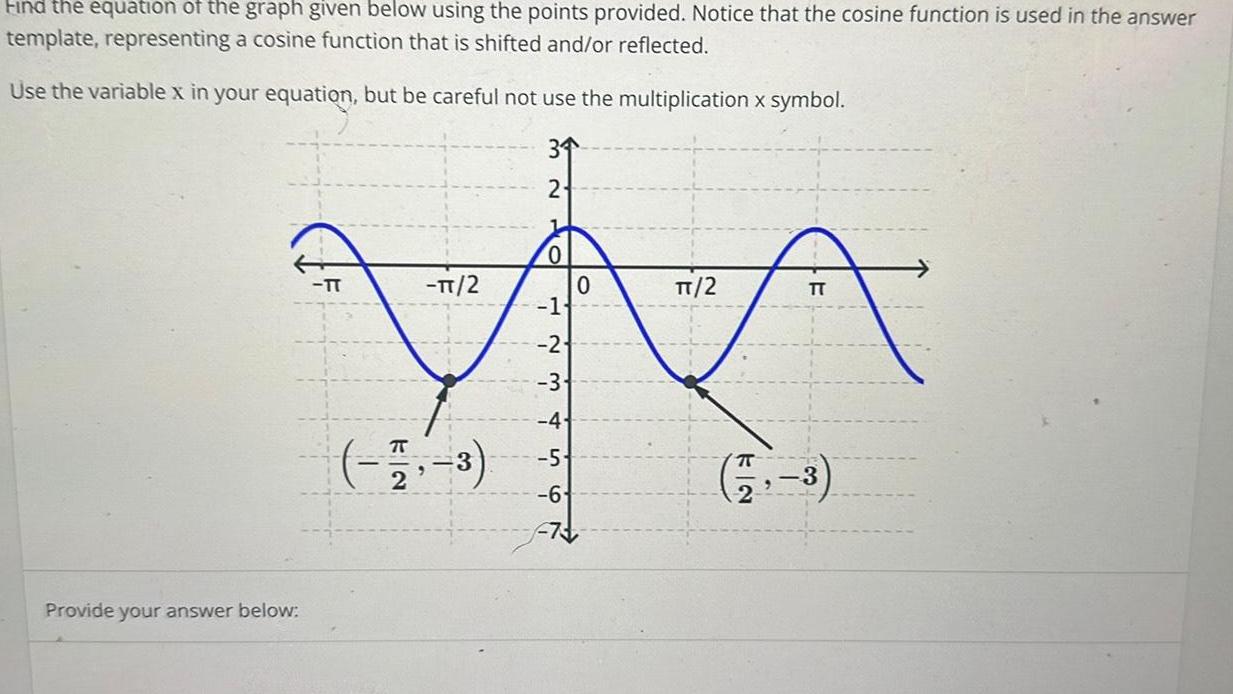
Calculus
Application of derivativesFind the equation of the graph given below using the points provided Notice that the cosine function is used in the answer template representing a cosine function that is shifted and or reflected Use the variable x in your equation but be careful not use the multiplication x symbol 34 2 Provide your answer below N TT TT 2 2 3 0 1 2 3 6 0 TT 2 E 3 t
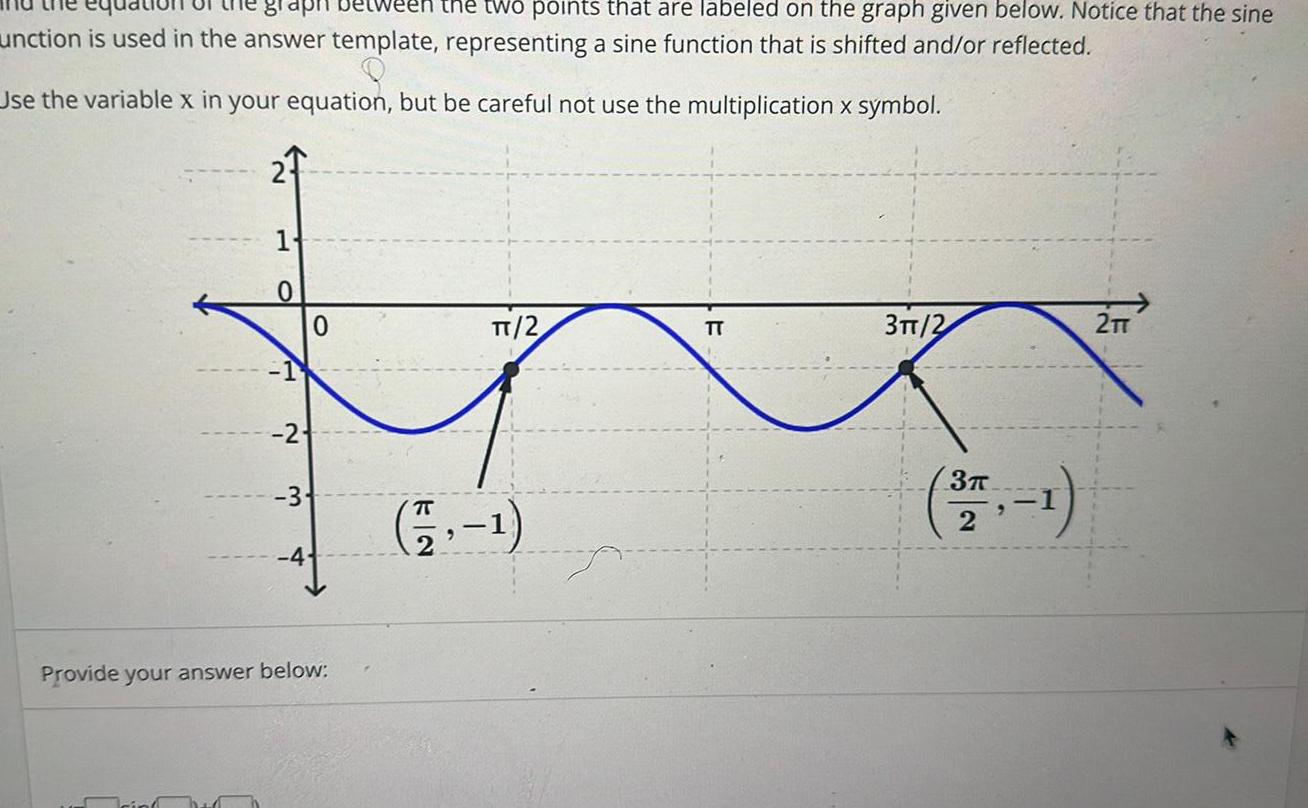
Calculus
Vector Calculusgraph be the two points that are labeled on the graph given below Notice that the sine unction is used in the answer template representing a sine function that is shifted and or reflected Use the variable x in your equation but be careful not use the multiplication x symbol 2 1 0 1 2 3 0 4 Provide your answer below TT 2 57 TT 3TT 2 3T 2 2TT
Calculus
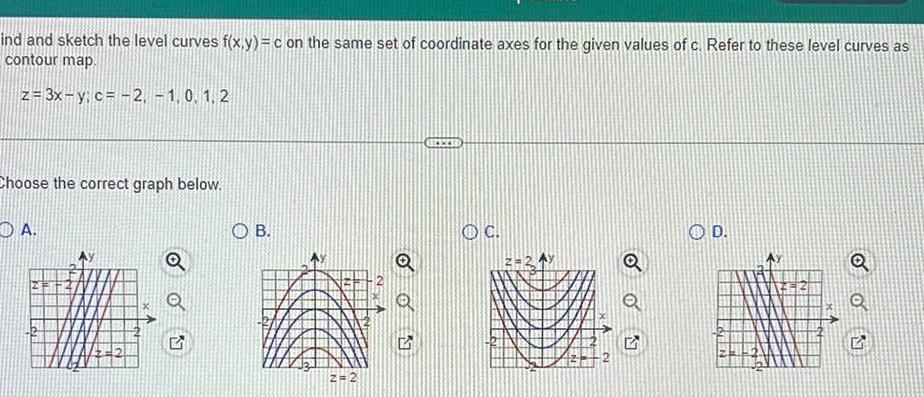
Vector Calculusind and sketch the level curves f x y c on the same set of coordinate axes for the given values of c Refer to these level curves as contour map z 3x y c 2 1 0 1 2 Choose the correct graph below A O 2 OB 2 2 Q Q 5 OC 1 Q 5 OD 2 O OU
Calculus
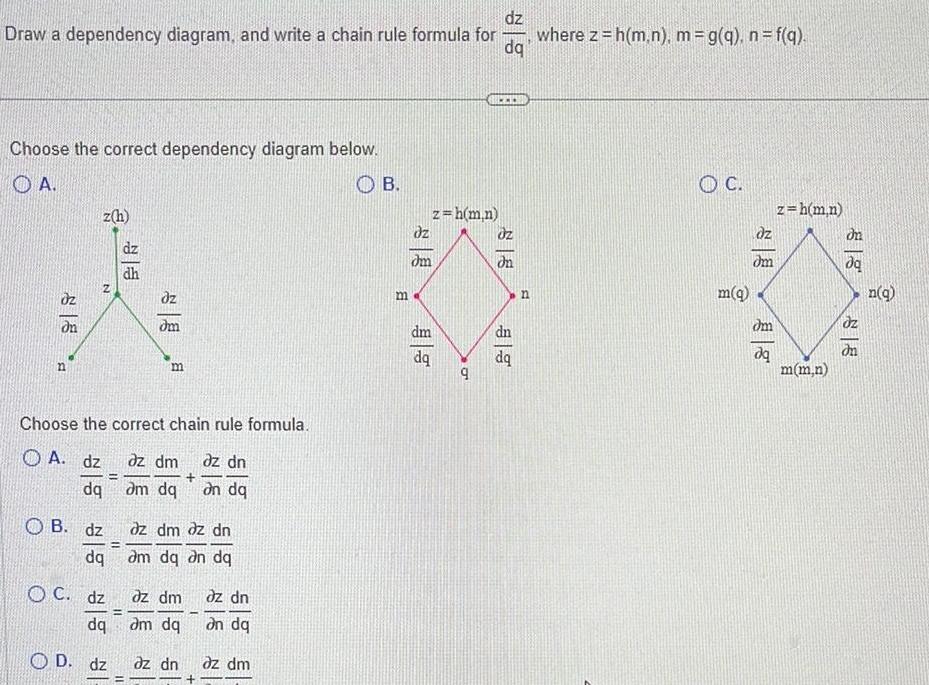
Application of derivativesdz Draw a dependency diagram and write a chain rule formula for where z h m n m g q n f q dq Choose the correct dependency diagram below OA dn n z h N OB dz dq Choose the correct chain rule formula A dz dq OC dz dq OD dz 11 dz dh dm m az dm az dn am dq on dq dz dm dz dn am dq an dq dz dm dz dn am dq an dq az dn az dm I B m z h m n dz dm dm dq 9 Uz on dn B n C m q dz dm dm dq z h m n m m n dq dz n q
Calculus
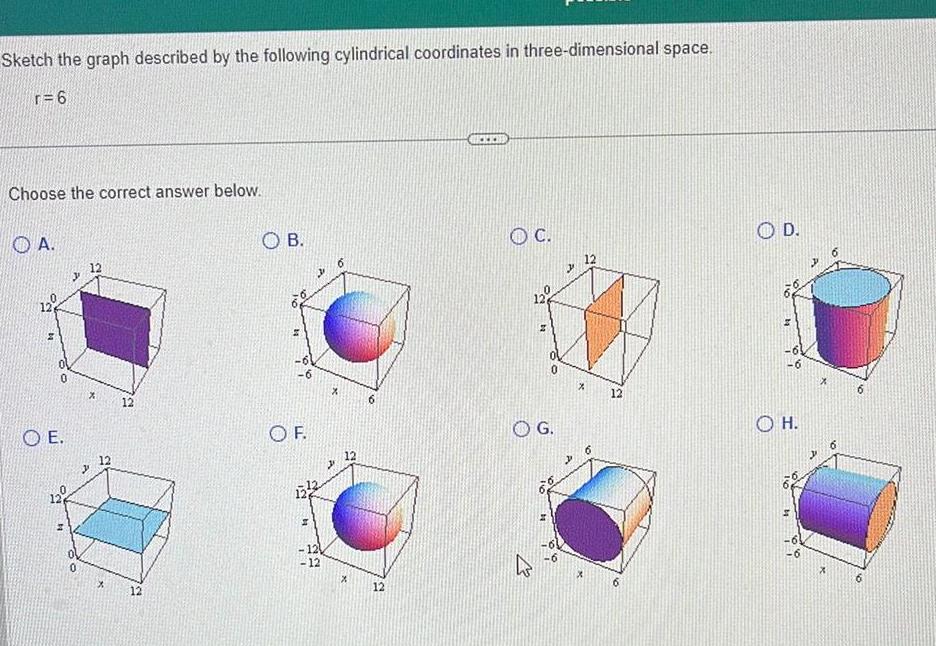
Application of derivativesSketch the graph described by the following cylindrical coordinates in three dimensional space r 6 Choose the correct answer below A 12 OE 12 12 12 OB 11 6 OF 126 H 12 12 X 12 X 12 O C 12 0 O G X 12 OD OH X
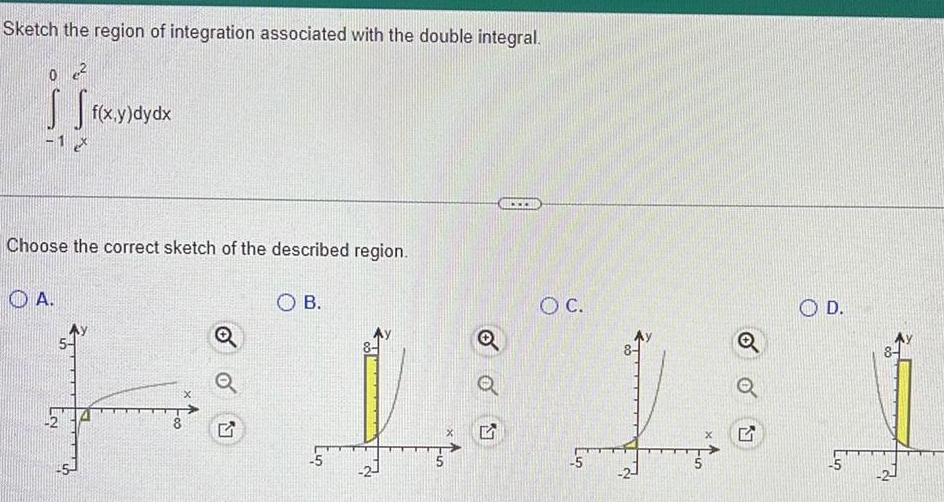
Calculus
Definite IntegralsSketch the region of integration associated with the double integral S S f x y 1 X Choose the correct sketch of the described region OA f x y dydx N 00 M OB 2 15 OC 5 Q 27 OD 5
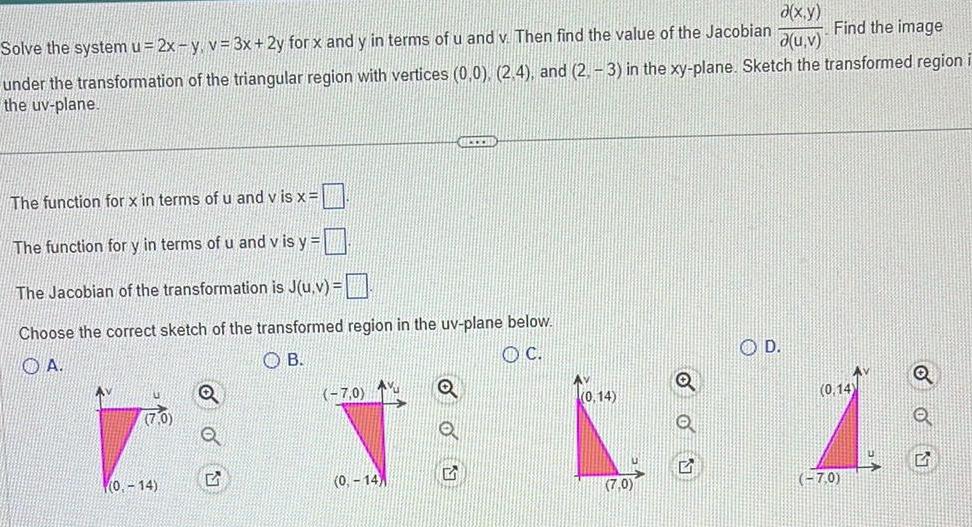
Calculus
Application of derivativesa x y Find the image d u v Solve the system u 2x y v 3x 2y for x and y in terms of u and v Then find the value of the Jacobian under the transformation of the triangular region with vertices 0 0 2 4 and 2 3 in the xy plane Sketch the transformed region the uv plane The function for x in terms of u and vis x The function for y in terms of u and v is y The Jacobian of the transformation is J u v Choose the correct sketch of the transformed region in the uv plane below OA OB OC 0 14 OU 7 0 0 14 ELTER Q Q 0 14 7 0 D 0 14 7 0 ON
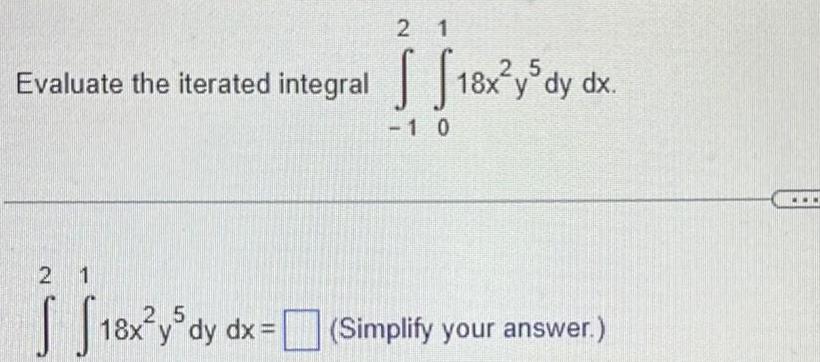
Calculus
Application of derivativesEvaluate the iterated integral 2 1 25 S S 18x y dy dx 21 5 18x y dy 1 0 dx x Simpaty Simplify your answer


Calculus
Indefinite IntegrationUse integration by parts together with the techniques of this section to evaluate the integral Use C for the constant of integration x tan tan x dx


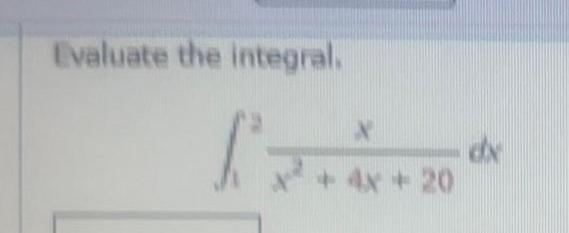

Calculus
Application of derivativesOn the graph of f x sec x and the interval 2 0 for what value of x does f x 1 Choose all answers that apply Select all that apply 2 0 37 IT 32


Calculus
Differentiationa Write out the form of the partial fraction decomposition of the function as in this example Do not determine the numerical values of the coefficients x6 x2 4 b x x 1 x 8

Calculus
DifferentiationProblem 6 Sketch a graph of the function f that satisfies the following conditions f is continuous on f 2 1 f 0 0 f 2 1 f 0 0 f x 0 on 0 f x 0 on 0 f 2 0 f 2 0 f x 0 on 2 and 2 00 f x 0 on 2 2 lim f x 2 lim f x 2 8118 218 Solution

Calculus
Application of derivatives6 A patient is injected with a drug and t hours later the concentration of the drug remaining in the patient s mg cm What is the average concentration of drug during the 3t bloodstream is given by C t 1 36 first 8 hours after the injection 10pts Use substitution
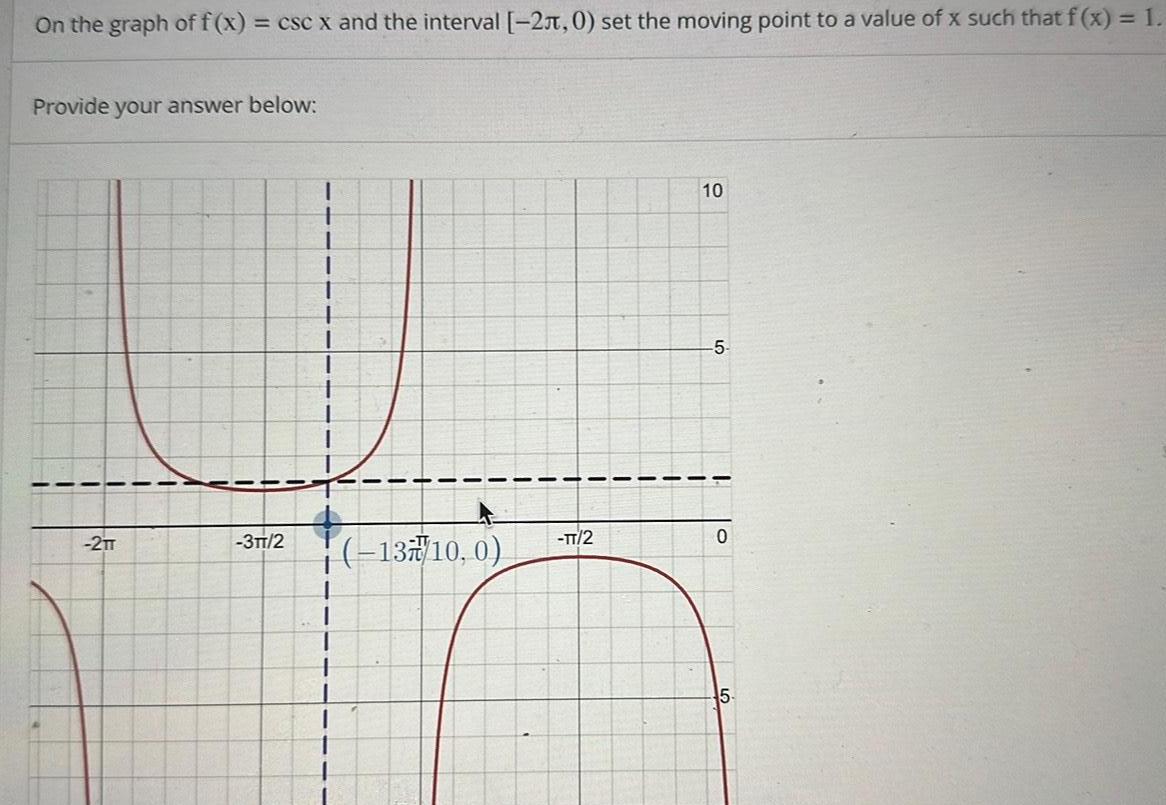
Calculus
Application of derivativesOn the graph of f x csc x and the interval 2 0 set the moving point to a value of x such that f x 1 Provide your answer below 2 T 3TT 2 I 1 1 1 I 13 10 0 1 TT 2 1 I 10 5 0 5
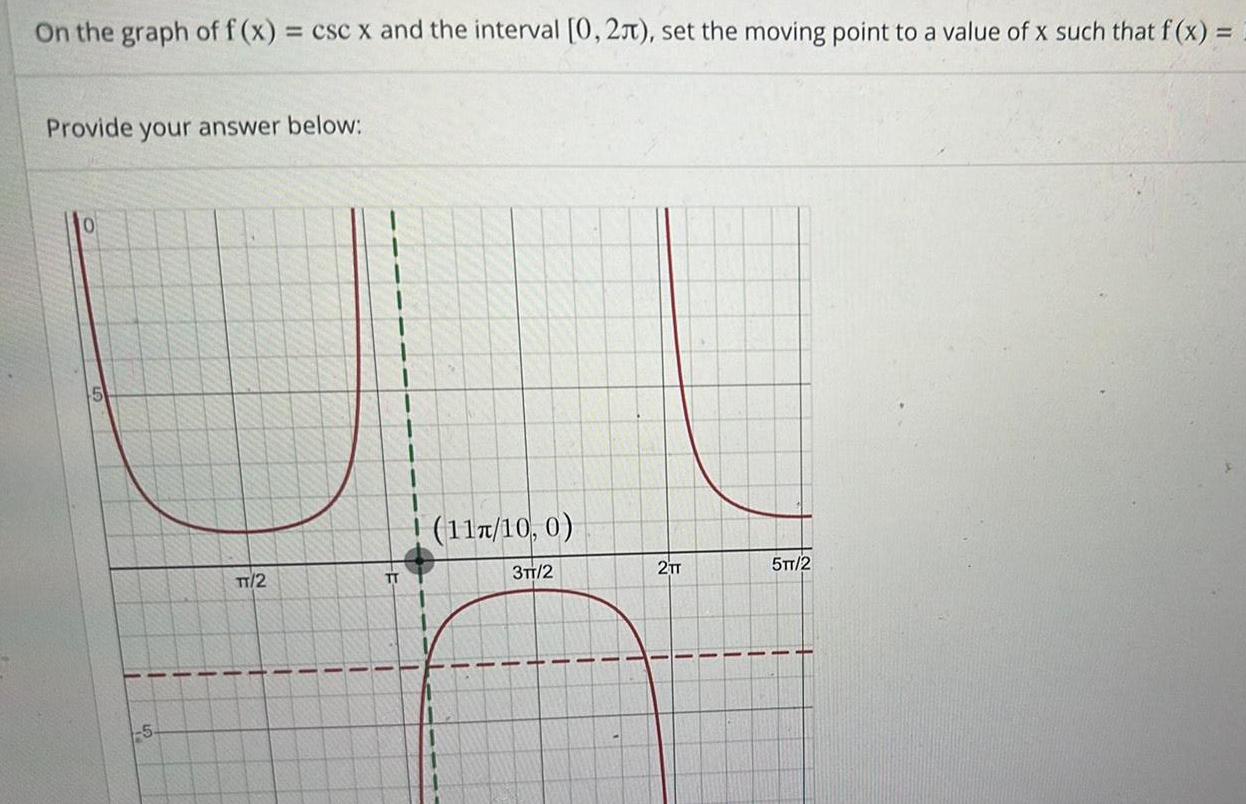
Calculus
Limits & ContinuityOn the graph of f x csc x and the interval 0 2 set the moving point to a value of x such that f x Provide your answer below 5 TT 2 1 11 11 1 TT 11 11 11 10 0 11 11 3TT 2 11 JE 11 THE 2TT 11 11 11 5TT 2

Calculus
Application of derivativesThe equation T 0 6sin 2 t 8 101 4 describes the body temperature of a cow in Fahrenheit where t is time in 2 Do not include the units in your hours What is the temperature of the cow to the nearest tenth of a degree when t answer NOTE The angle is in radians

Calculus
Definite Integralsa b c d dx X 7 S Since the function y Since the function y Since the function y Since the integral dx x 9 Since the integral Since the function y Since the function y Since the integral 8 S Since the function y Since the integral tan x dx 8 5 Since the integral Since the integral ex dx X Since the integral 10 Since the integral 1 Since the function y 1 Since the function y Since the function y 1 Since the function y tan x has an infinite discontinuity at x 0 the integral is a Type 2 improper integral Since the function y tan x has an infinite discontinuity at x the integral is a Type 2 improper integral 2 Since the function y tan x has an infinite discontinuity at x 1 the integral is a Type 2 improper integral 1 X 7 00 dx 1 has an infinite discontinuity at x 1 the integral is a Type 2 improper integral x 7 1 has an infinite discontinuity at x 7 the integral is a Type 2 improper integral X 7 X 00 dx has an infinite interval of integration it is a Type 1 improper integral x 9 has an infinite interval of integration it is a Type 2 improper integral x 9 dx 1 dx X 7 1 1 has an infinite discontinuity at x 9 the integral is a Type 1 improper integral x 9 1 has an infinite discontinuity at x 8 the integral is a Type 1 improper integral x 9 1 has an infinite discontinuity at x 7 the integral is a Type 1 improper integral x2 has an infinite discontinuity at x 9 the integral is a Type 2 improper integral 9 has an infinite interval of integration it is a Type 1 improper integral has an infinite interval of integration it is a Type 2 improper integral tan x dx has an infinite interval of integration it is a Type 1 improper integral tan x dx has an infinite interval of integration it is a Type 2 improper integral X X ex has an infinite discontinuity at x 1 the integral is a Type 1 improper integral X has an infinite discontinuity at x 0 the integral is a Type 1 improper integral ex has an infinite discontinuity at x 0 the integral is a Type 2 improper integral X X ex dx has an infinite interval of integration it is a Type 1 improper integral ex dx has an infinite interval of integration it is a Type 2 improper integral

Calculus
Definite Integralsc tan x dx 11 Since the function y tan x has an infinite discontinuity at x 0 the integral is a Type 2 improper integral Since the function y tan zx has an infinite discontinuity at x the integral is a Type 2 improper integral Since the function y tan x has an infinite discontinuity at x 1 the integral is a Type 2 improper integral O Since the integral tan x dx has an infinite interval of integration it is a Type 1 improper integral tan x dx has an infinite interval of integration it is a Type 2 improper integral Since the integral
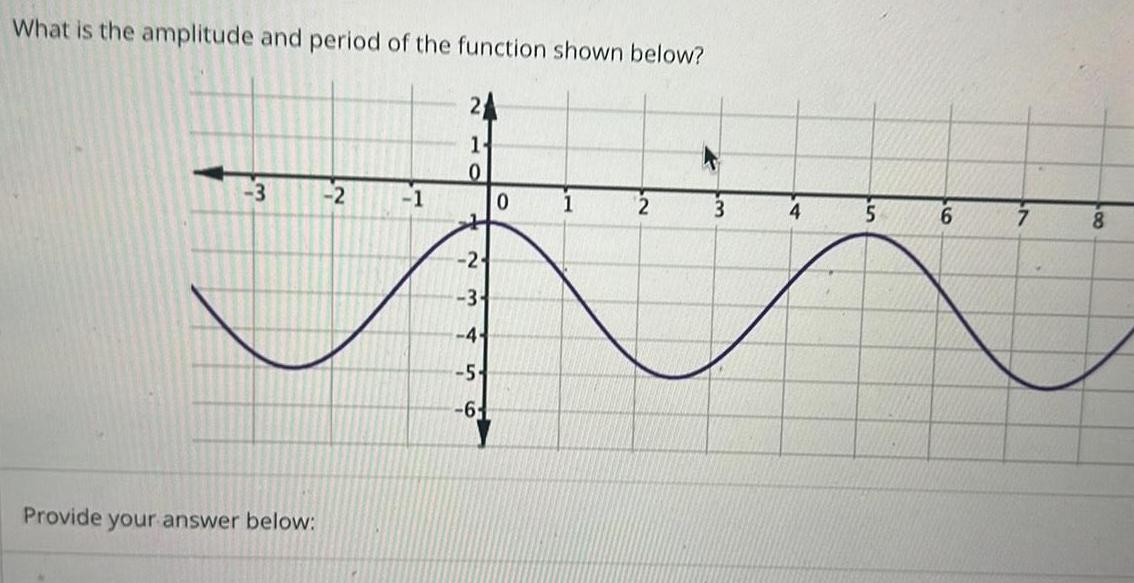
Calculus
Application of derivativesWhat is the amplitude and period of the function shown below 3 Provide your answer below 2 1 1 0 1 24 3 4 5 56 6 0 2 3 4 5 6 8
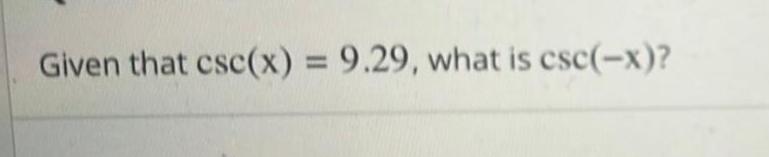

Calculus
Application of derivativesExplain why each of the following integrals is improper s dx x 7 O Since the function y O Since the function y O Since the integral 1 O Since the function y O Since the integral dx x 9 O Since the function y O Since the function y O Since the function y 500 1 x 7 has an infinite discontinuity at x7 the integral is a Type 1 improper integral O Since the integral O Since the integral I 1 x 7 1 X dx dx x 7 has an infinite discontinuity at x 1 the integral is a Type 2 improper integral has an infinite discontinuity at x 7 the integral is a Type 2 improper integral has an infinite interval of integration it is a Type 1 improper integral has an infinite interval of integration it is a Type 2 improper integral 1 has an infinite discontinuity at x 9 the integral is a Type 1 improper integral x 9 1 x 9 1 9 has an infinite discontinuity at x 9 the integral is a Type 2 improper integral dx x 9 dx 9 has an infinite discontinuity at x 8 the integral is a Type 1 improper integral has an infinite interval of integration it is a Type 1 improper integral has an infinite interval of integration it is a Type 2 improper integral

Calculus
Application of derivativesa Sketch the garden use INSERT SHAPES and INSERT DRAW b How many meters of stone do you need to create the border FO 12 9 Danielle wants to create a patio in her backyard She would like it to be 6 ft by 12 ft What is the area of the patio Sketch the patio INSERT SHAPES and INSERT DRAW C 13 10 A basketball with a diameter 24 cm is packaged so that it just fits into a cube shaped box Calculate the amount of empty space in the box round to 1 decimal place T 17
Calculus
Application of derivativesAmerican General offers a 18 year annuity with a guaranteed rate of 6 47 compounded annually How much sho you pay for one of these annuities if you want to receive payments of 1300 annually over the 18 year period How much should a customer pay for this annuity Round to the nearest cent
Calculus
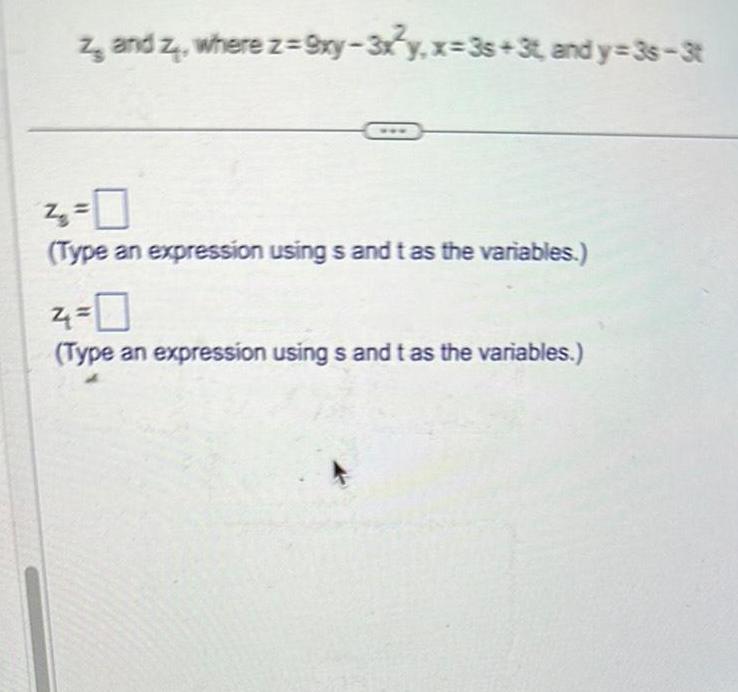
Application of derivativesz and z where z 9xy 3x y x 3s 3t and y 3s 3t 4 0 Type an expression usings and t as the variables 4 0 Type an expression using s and t as the variables
Calculus
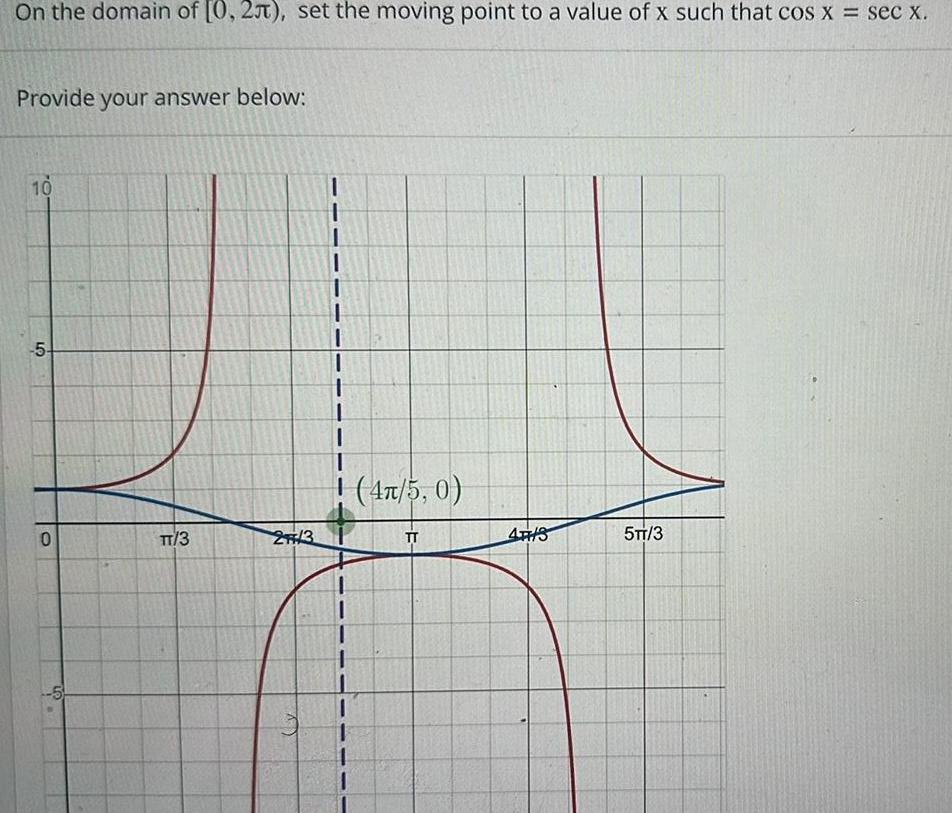
Application of derivativesOn the domain of 0 2 set the moving point to a value of x such that cos x sec x Provide your answer below 10 5 0 5 TT 3 27 3 y 13 I 1 1 T 4 5 0 TT 4TH 3 5TT 3