Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
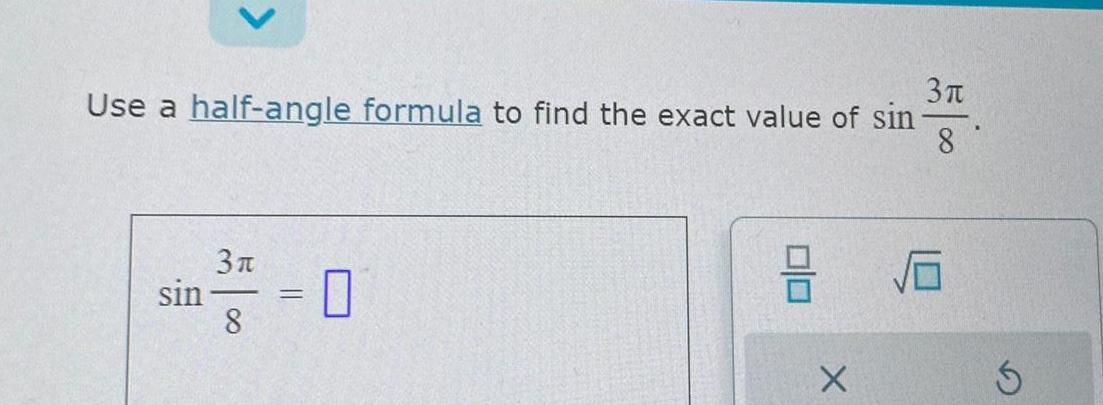
Application of derivativesQuestion The equation d 5sin 24t measures the displacement of a swinging pendulum in simple harmonic motion t is measured in seconds and d is measured in centimeters What is the displacement to the nearest centimeter when t 4 NOTE The angle is in radians Provide your answer below
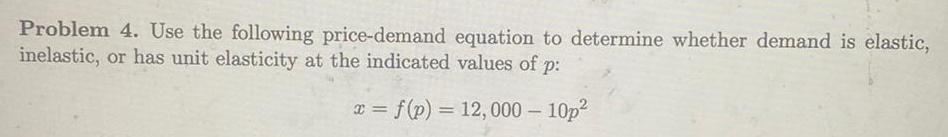
Calculus
Application of derivativesProblem 4 Use the following price demand equation to determine whether demand is elastic inelastic or has unit elasticity at the indicated values of p x f p 12 000 10p
Calculus
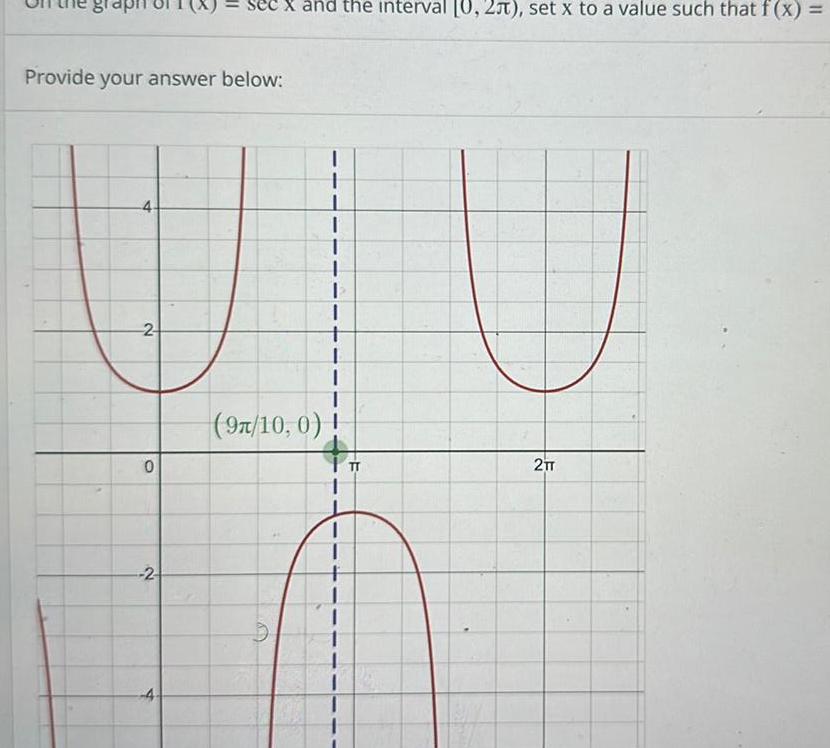
Limits & ContinuityProvide your answer below 4 2 O 2 and the interval 0 2 set x to a value such that f x I 1 9 10 0 1 1 TT 2TT
Calculus
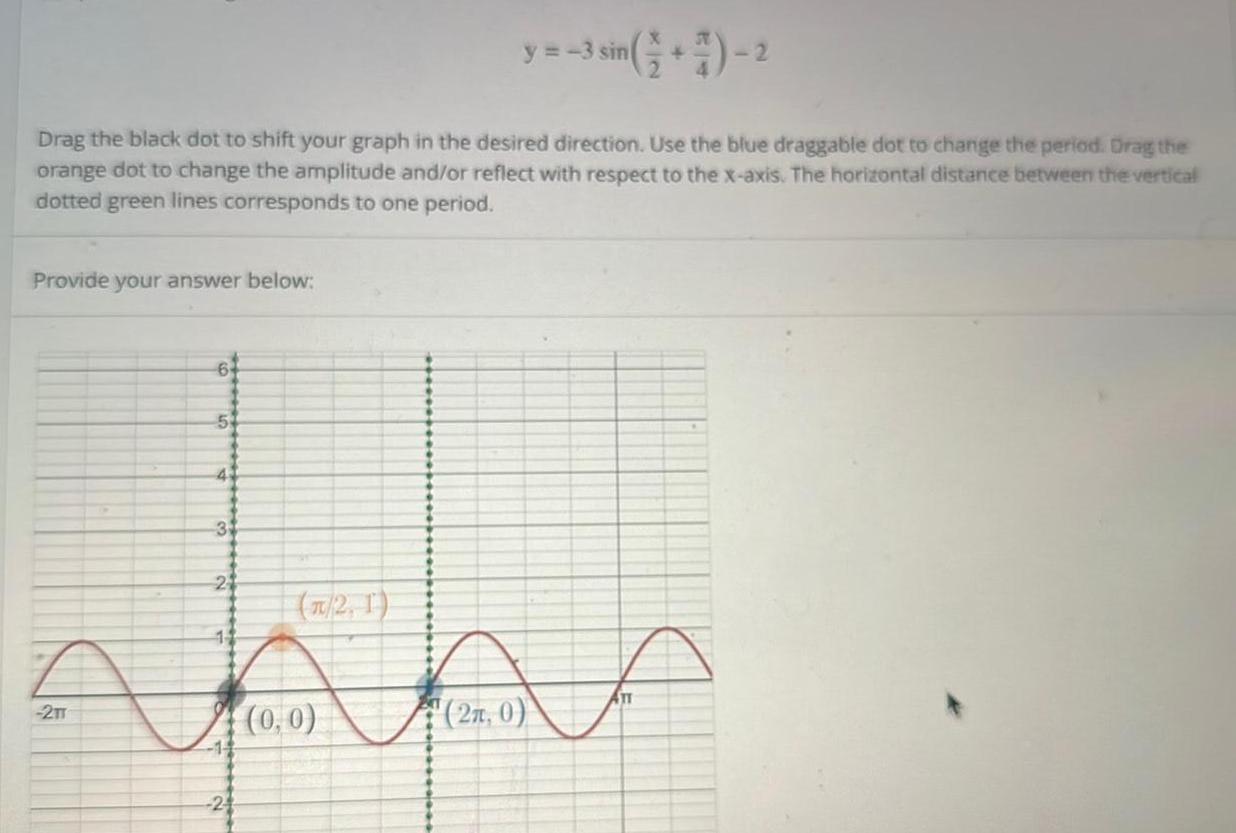
Vector Calculusy 3 sin 2 Drag the black dot to shift your graph in the desired direction Use the blue draggable dot to change the period Drag the orange dot to change the amplitude and or reflect with respect to the x axis The horizontal distance between the vertical dotted green lines corresponds to one period Provide your answer below 64 2TT 51 41 4 31 2 2 1 Amm 0 0 14 24 21 0 f ATT

Calculus
Definite IntegralsThe population densities of a rectangular county are shown in the figure to the right a Use the fact that population population density x area to estimate the population of the county b Explain how the calculation of part a is related to Riemann sums integrals a The population of the county is 3 2 3 2 Population densities have people per square m 350 450 250 1 2 100 450 250 3 2 100 250 100

Calculus
Application of derivativesProblem 3 A 7 ft tall person is walking away from a 20 ft tall lamppost at a rate of 5 ft sec Assume the scenario can be modeled with right triangles At what rate is the length of the person s shadow changing when the person is 16 ft from the lamppost
Calculus
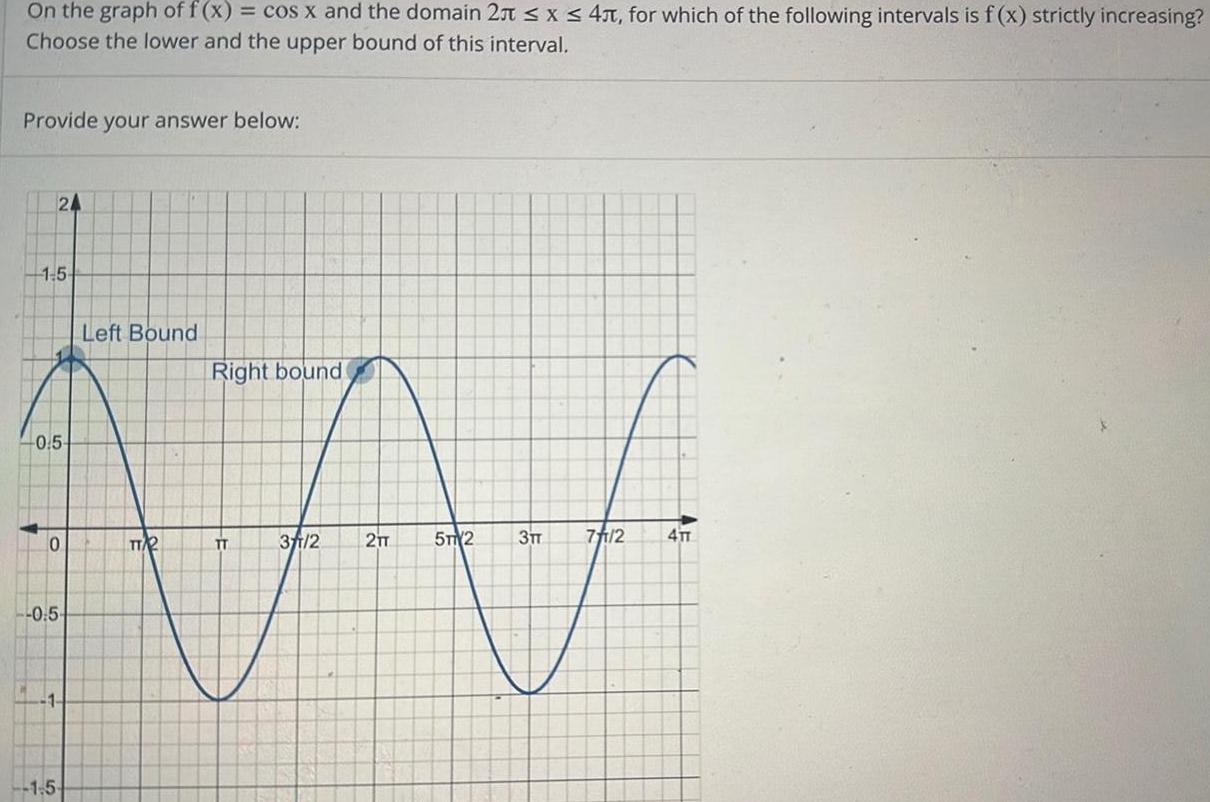
Application of derivativesOn the graph of f x cos x and the domain 2 x 4 for which of the following intervals is f x strictly increasing Choose the lower and the upper bound of this interval Provide your answer below 24 1 5 0 5 0 0 5 1 1 5 Left Bound TT2 Right bound TT 31 2 2TT 5T2 3TT 7 11 2 4TT
Calculus
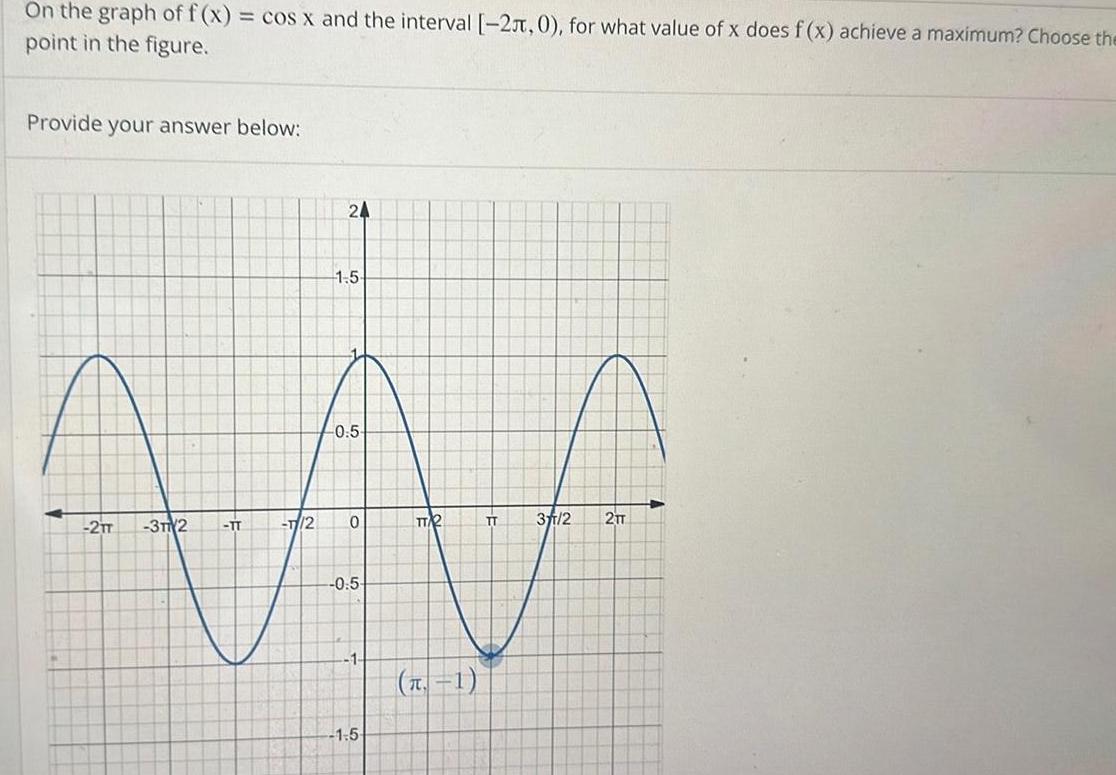
DifferentiationOn the graph of f x cos x and the interval 2 0 for what value of x does f x achieve a maximum Choose the point in the figure Provide your answer below 24 2TT 1 5 0 5 AAA 3T 2 TT T 2 0 5 1 n 1 1 5 3f1 2 2TT
Calculus
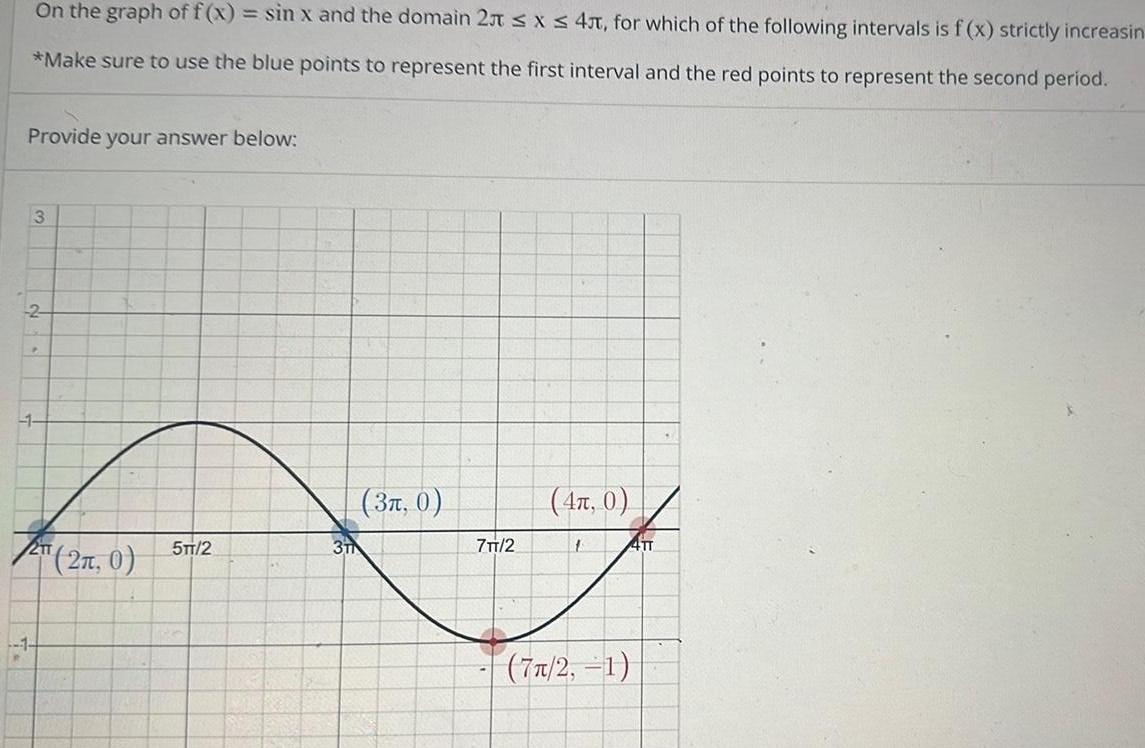
Application of derivativesOn the graph of f x sin x and the domain 2 x 4 for which of the following intervals is f x strictly increasin Make sure to use the blue points to represent the first interval and the red points to represent the second period Provide your answer below 3 2 1 2T 2n 0 1 5TT 2 3 0 7TT 2 4 0 1 4TT 77 2 1

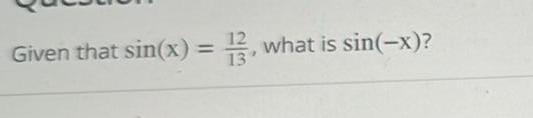

Calculus
Application of derivativesFind the surface area of revolution about the x axis of y 4x 7 over the interval 0 x
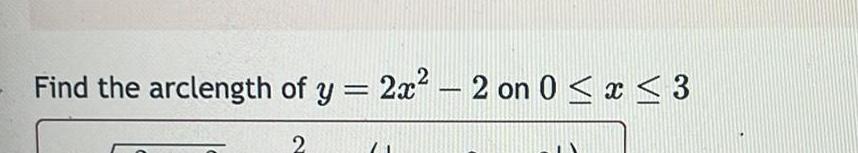
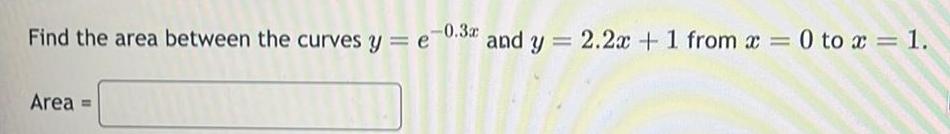
Calculus
Differential equationsFind the area between the curves y e 0 3 and y 2 2x 1 from x 0 to x 1 Area
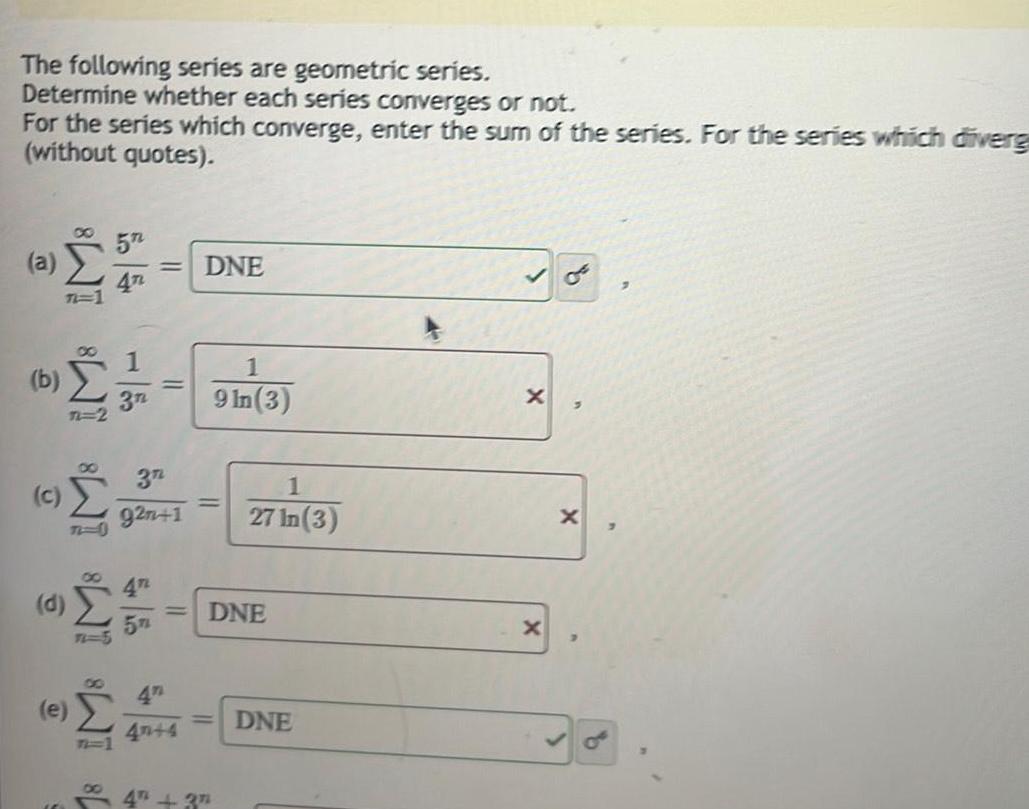
Calculus
Application of derivativesThe following series are geometric series Determine whether each series converges or not For the series which converge enter the sum of the series For the series which diverg without quotes a b c O 18 IM8 IM8 IM8 M8 IM8 n 2 e 5 4T 1 3n 3n 92n 1 40 4 DNE 1 9 In 3 4 37 1 27 In 3 DNE DNE X X 3 X 7
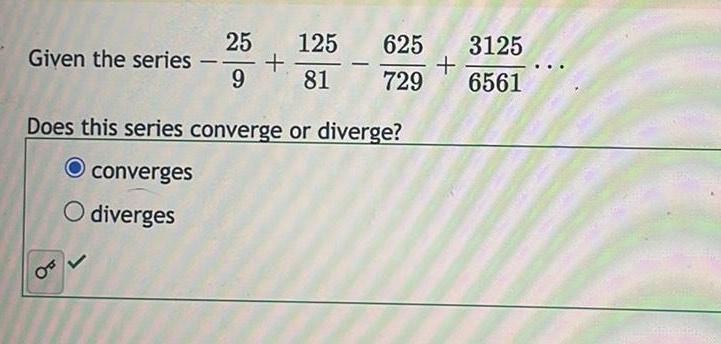
Calculus
Application of derivativesGiven the series OF 25 125 9 81 625 3125 729 6561 Does this series converge or diverge O converges O diverges
Calculus
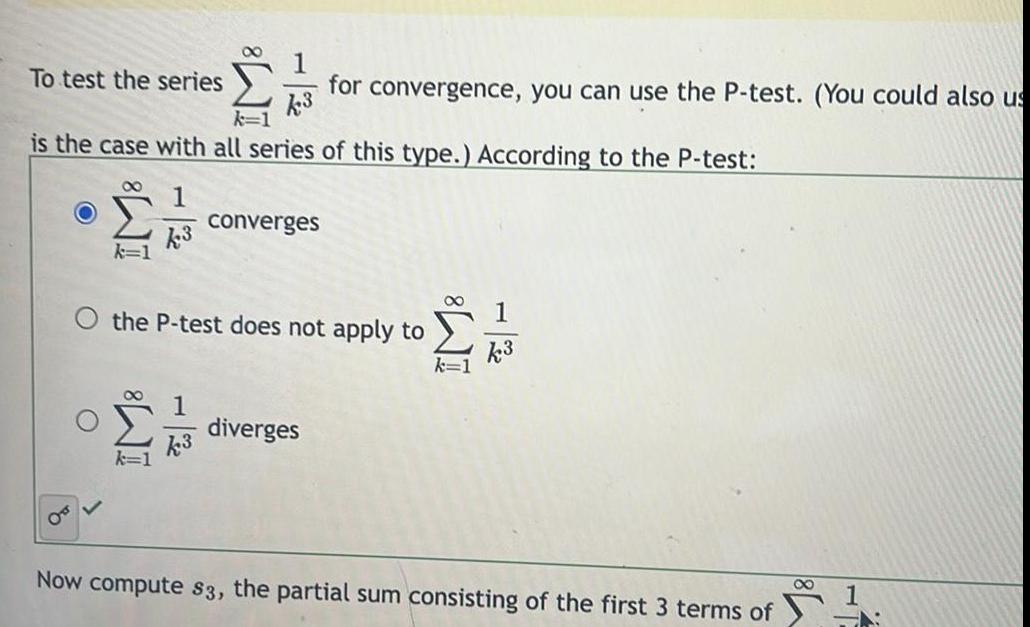
Definite IntegralsTo test the series is the case with all series of this type According to the P test 8 k 1 1 k3 1 for convergence you can use the P test You could also us k3 1 k3 converges the P test does not apply to diverges k3 Now compute s3 the partial sum consisting of the first 3 terms of 8

Calculus
Application of derivativesFind the limit of the sequence 1n 8n 5 2n 8n 6 an 2 n 8n 5 2 1 X syntax incomplete
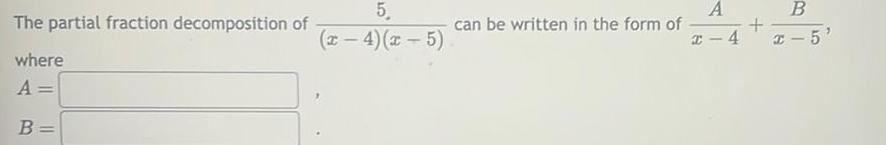
Calculus
Application of derivativesThe partial fraction decomposition of where A B 5 x 4 x 5 can be written in the form of I A 4 B x 5
Calculus
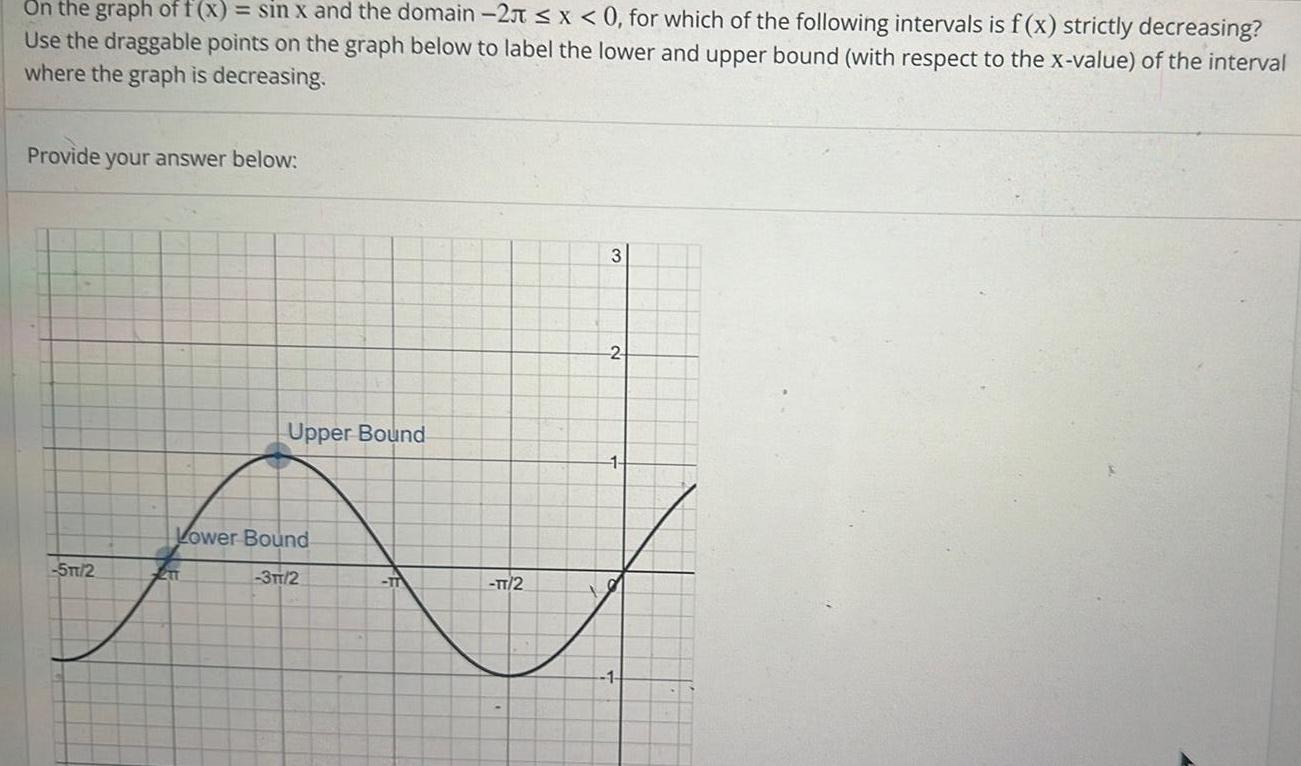
Application of derivativesOn the graph of f x sin x and the domain 2 x 0 for which of the following intervals is f x strictly decreasing Use the draggable points on the graph below to label the lower and upper bound with respect to the x value of the interval where the graph is decreasing Provide your answer below 5m 2 Upper Bound Lower Bound 3TT 2 4TT TT 2 3 2

Calculus
Definite Integrals4 A population P of bacteria is growing at the rate of dp dt 3000 1 25t b What is the population after 3 days where t is the time in days When t the population is 1000 a Find a model for the population Hint integrate dP dt and find the particular solution
Calculus
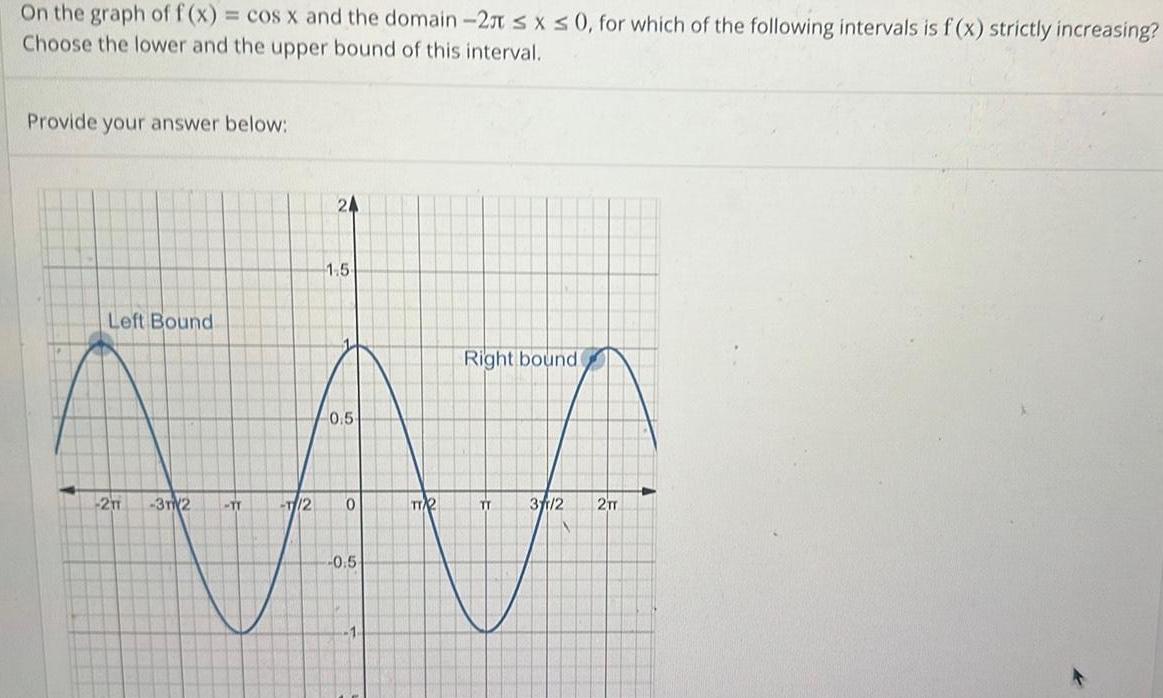
Application of derivativesOn the graph of f x cos x and the domain 2 x 0 for which of the following intervals is f x strictly increasing Choose the lower and the upper bound of this interval Provide your answer below Left Bound 2TT 32 TT T 2 24 1 5 0 5 0 0 5 TT 2 Right bound TT 3 1 2 2TT

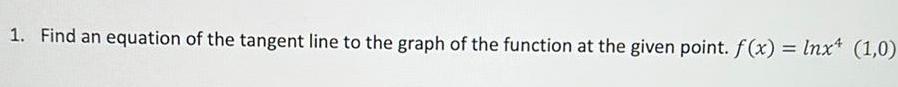
Calculus
Application of derivatives1 Find an equation of the tangent line to the graph of the function at the given point f x Inx4 1 0
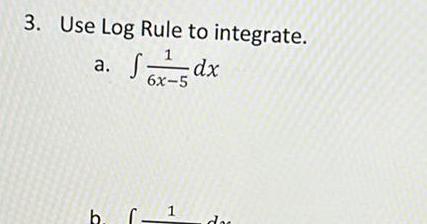
Calculus
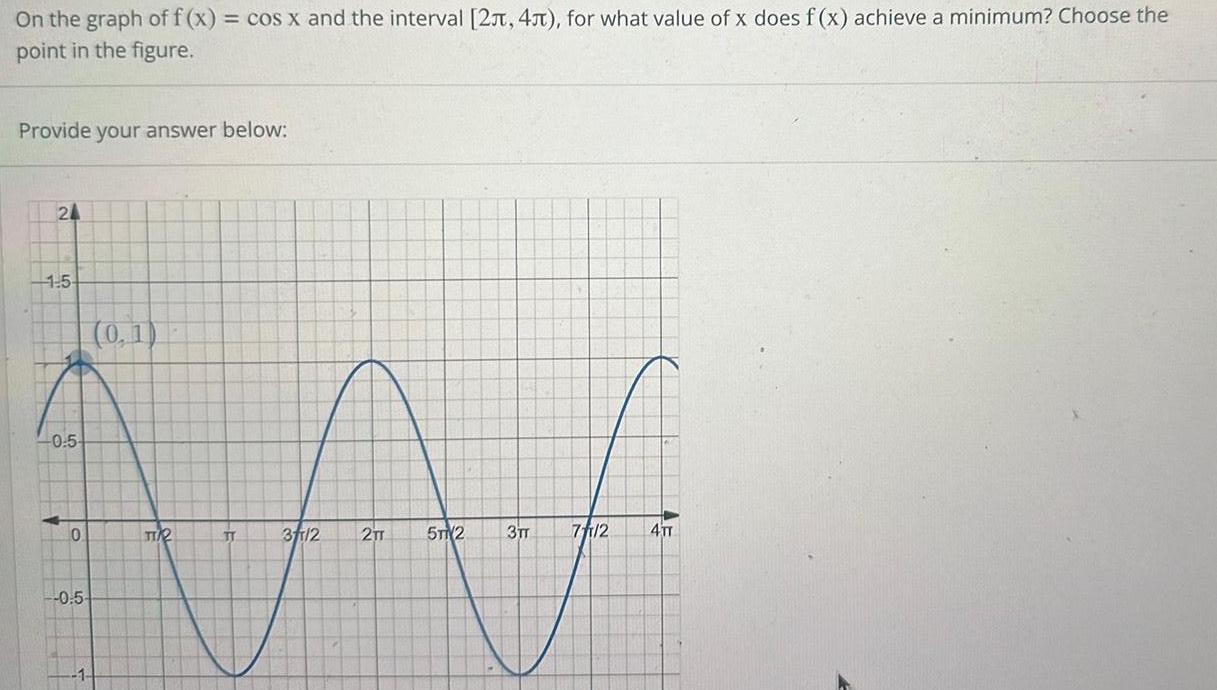
DifferentiationOn the graph of f x cos x and the interval 2 4 for what value of x does f x achieve a minimum Choose the point in the figure Provide your answer below 24 1 5 4 0 5 0 0 5 0 1 TI TT 31 2 2TT 5TM2 3TT 71 2 4TT
Calculus
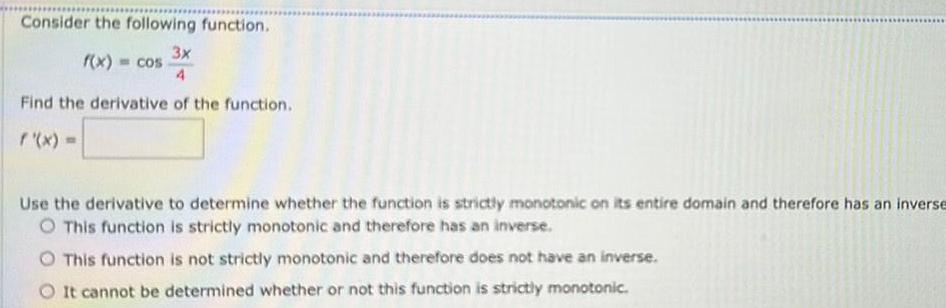
Application of derivativesConsider the following function 3x 4 Find the derivative of the function f x f x cos Use the derivative to determine whether the function is strictly monotonic on its entire domain and therefore has an inverse O This function is strictly monotonic and therefore has an inverse This function is not strictly monotonic and therefore does not have an inverse It cannot be determined whether or not this function is strictly monotonic

Calculus
Application of derivativesdentify the real numbers X0 X X2 X3 and x4 in the figure such that each of the following is true Select all that appl a f x 0 xo 0x1 0x2 b 3 XA none of these F x 0 O xo 0x1 0x2 3 X4 Onone of these d c f x does not exist O xo 0x 0x2 X3 X4 none of these f has a relative maximum 0 0 Xo 0x1 X2 X3 X4 none of these e f has a point of inflection xo 0 x1 n X3 X

Calculus
DifferentiationA cylindrical package to be sent by a postal service can have a maximum combined length and girth perimeter of a cross section of 108 inches Find the dimensions of the package of maximum volume that can be sent The cross section is circular radius length in in

Calculus
Application of derivativesThe velocity of an automobile starting from rest is given by the equation below where v is measured in feet per second and t is the time in seconds Round your answers to three decimal pla v t 95t 6t 18 a Find the acceleration at 5 seconds ft sec b Find the acceleration at 10 seconds ft sec2 c Find the acceleration at 20 seconds ft sec
Calculus
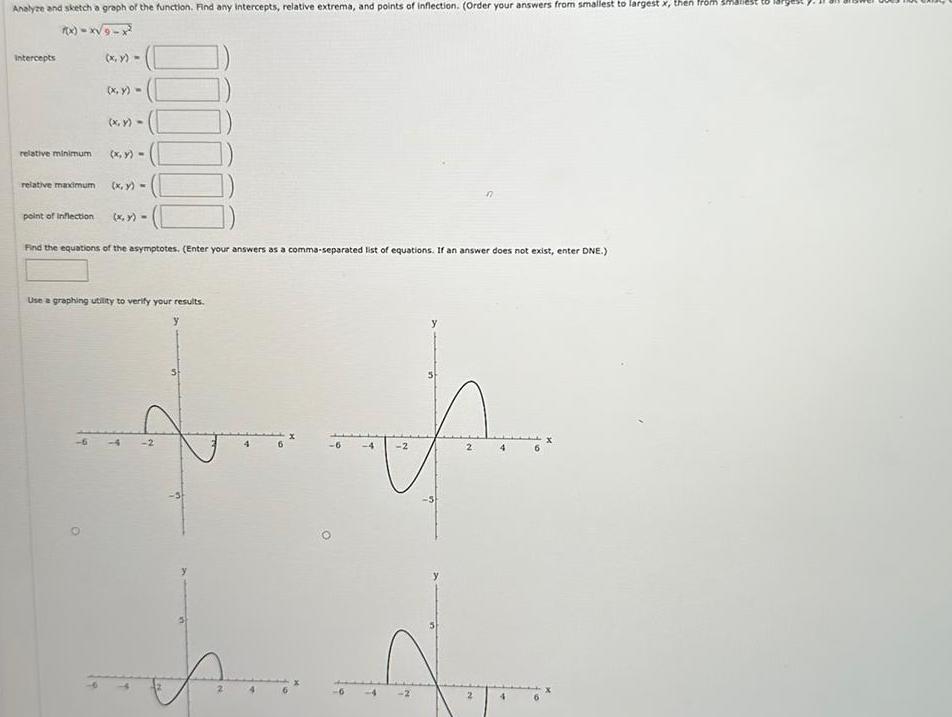
Application of derivativesAnalyze and sketch a graph of the function Find any intercepts relative extrema and points of inflection Order your answers from smallest to largest x then from smallest to 7x x 9 x Intercepts relative minimum relative maximum point of Inflection x y x y x y x y Find the equations of the asymptotes Enter your answers as a comma separated list of equations If an answer does not exist enter DNE Use a graphing utility to verify your results sults 5 t 3 N 2 4

Calculus
DifferentiationConsider the following function f x 6x 4x Find the limit lim Ar 0 f x Ax f x Ax

Calculus
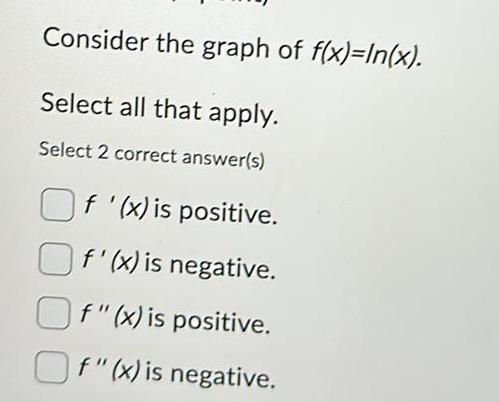
Application of derivativesConsider the graph of f x In x Select all that apply Select 2 correct answer s Of x is positive f x is negative Of x is positive Of x is negative

Calculus
Application of derivativesFind the nth Maclaurin polynomial for the function 4x 3 f x x 1 n 4 P4 x 3 7x 7x 7x 7x

Calculus
Application of derivativesFind the nth Taylor polynomial for the function centered at c f x In x n 4 c 3 1 P4 x ln 3 x 3 8 x 3 x 3 324 x 3 4 18
Calculus
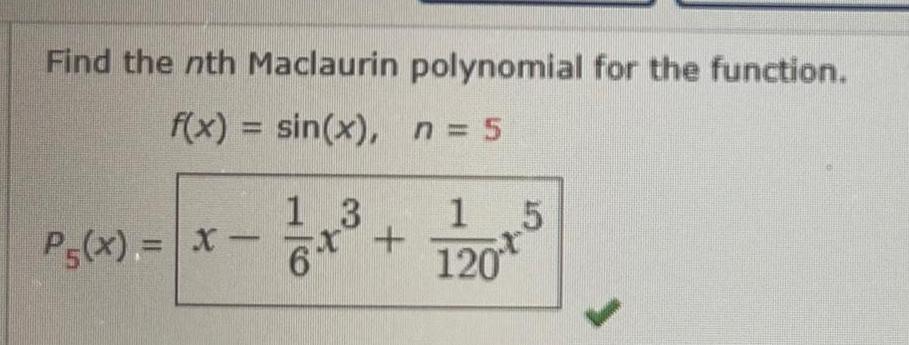
DifferentiationFind the nth Maclaurin polynomial for the function f x sin x n 5 Ps x x 3 1 x 1 5 120 t

Calculus
Application of derivativesA parent function is given by y 2 The following transformations took place Vertical shift 3 units upwards Horizontal shift 4 units to the right Reflection about the y axis Vertical compression by a factor of 1 3 Give the equation of the transformed function Indicate where each transformation occurs in your equation Sketch a graph of the transformed function and include a table of values State the domain and range of the transformed function C 8
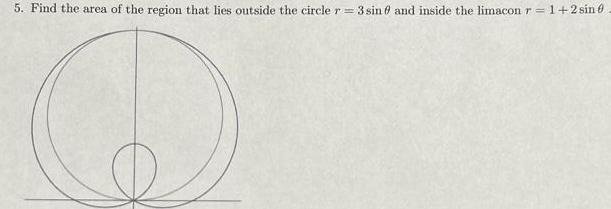
Calculus
Indefinite Integration5 Find the area of the region that lies outside the circle r 3 sin 0 and inside the limacon r 1 2 sin
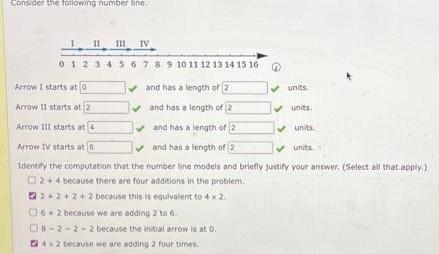
Calculus
Application of derivativesConsider the following number line III 0 1 2 3 4 5 Arrow I starts at 0 Arrow II starts at 2 Arrow III starts at IV 6 7 8 9 10 11 12 13 14 15 16 and has a length of 2 and has a length of 2 and has a length of 2 units Arrow IV starts at and has a length of 2 units Identify the computation that the number line models and briefly justify your answer Select all that apply 02 4 because there are four additions in the problem 2 2 2 2 because this is equivalent to 4 x 2 6 2 because we are adding 2 to 6 D8 2 2 2 because the initial arrow is at 0 142 because we are adding 2 four times units units

Calculus
Application of derivatives2 Obtuse triangle ARST is shown below along with line m Point S lies on m Lines are drawn in from the vertices of RST that are perpendicular to line m a Using a compass only draw the image of ARST i e AR S T after a reflection in line m Leave all relevant construction marks b Why are points S and S coincident i e lie in the same spot R T c Draw segment TT Why is ASTT isosceles If you don t remember what isosceles means look it up S m

Calculus
Definite IntegralsUse the transformation u 4x 2y v x 2y to evaluate the given integral for the region R bounded by the lines y 2x 2 y 2x 3 y 2x and y x x 1 2x 5xy 2y dx dy R 2x 5xy 2y dx dy R Type an integer or a simplified fraction

Calculus
Definite IntegralsT Find the volume of the portion of the solid sphere p 5 that lies between the cones 4 The volume is Type an exact answer using and radicals as needed 3 and 4

Calculus
Limits & Continuitypatient per hour now many milligrams of medication are delivered in 30 seconds Round to two decimal place Answer 2 A pediatric vitamin drug product contains the equivalent of 0 25 mg of fluoride ion in each milliliter How many milligrams of fluoride ion would be provided by a dropper that delivers 0 6 mL Round to two decimal place Answer 3 COLCRYS scored tablets each contain 0 6 mg of colchicine How many micrograms of colchicine would a patient take by administering one half tablet Round to the whole number Answer 4 An intravenous solution contains 500 g of a drug substance in each milliliter How many milligrams of the drug would a patient receive from the intravenous infusion of a liter of the solution Round to the whole number Answer
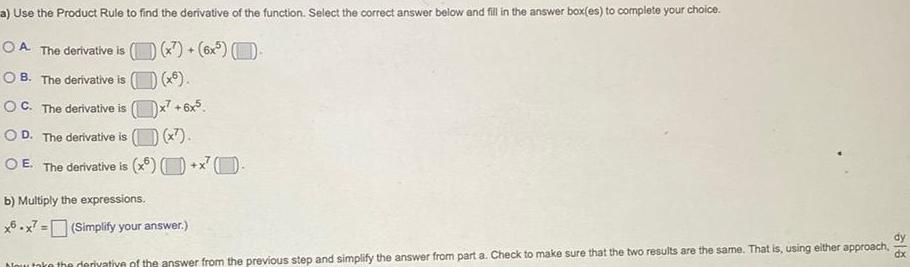
Calculus
Differentiationa Use the Product Rule to find the derivative of the function Select the correct answer below and fill in the answer box es to complete your choice OA The derivative is x 6x OB The derivative is OC The derivative is OD The c ne derivative is O E The derivative is x6 x6 6x5 x b Multiply the expressions x6x7 Simplify your answer Now take the derivative of the answer from the previous step and simplify the answer from part a Check to make sure that the two results are the same That is using either approach dy dx

Calculus
Vector Calculusshould be injected to receive 40 units of insulin Answer 2 A formula for 1250 tablets contains 6 25 grams of diazepam How many grams of diazepam should be used in preparing 550 tablets Round to three significant figures Answer 3 If 100 capsules contain 400 mg of an active ingredient how many milligrams of the ingredient will 48 capsules contain Answer 4 A cough syrup contains 10 mg of dextromethorphan hydrobromide per 5 mL How many milligrams of the drug are contained in a 120 mL container of the syrup Answer
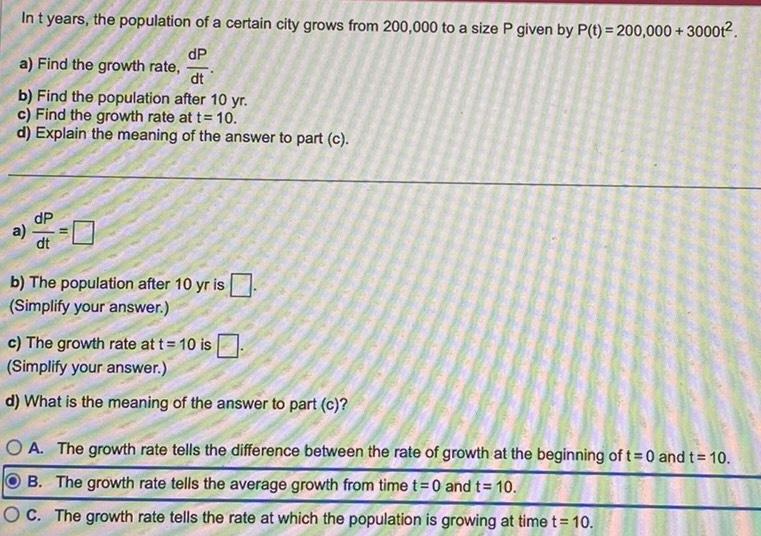
Calculus
DifferentiationIn t years the population of a certain city grows from 200 000 to a size P given by P t 200 000 30001 dP a Find the growth rate dt b Find the population after 10 yr c Find the growth rate at t 10 d Explain the meaning of the answer to part c a b The population after 10 yr is Simplify your answer c The growth rate at t 10 is Simplify your answer d What is the meaning of the answer to part c OA The growth rate tells the difference between the rate of growth at the beginning of t 0 and t 10 B The growth rate tells the average growth from time t 0 and t 10 OC The growth rate tells the rate at which the population is growing at time t 10
Calculus
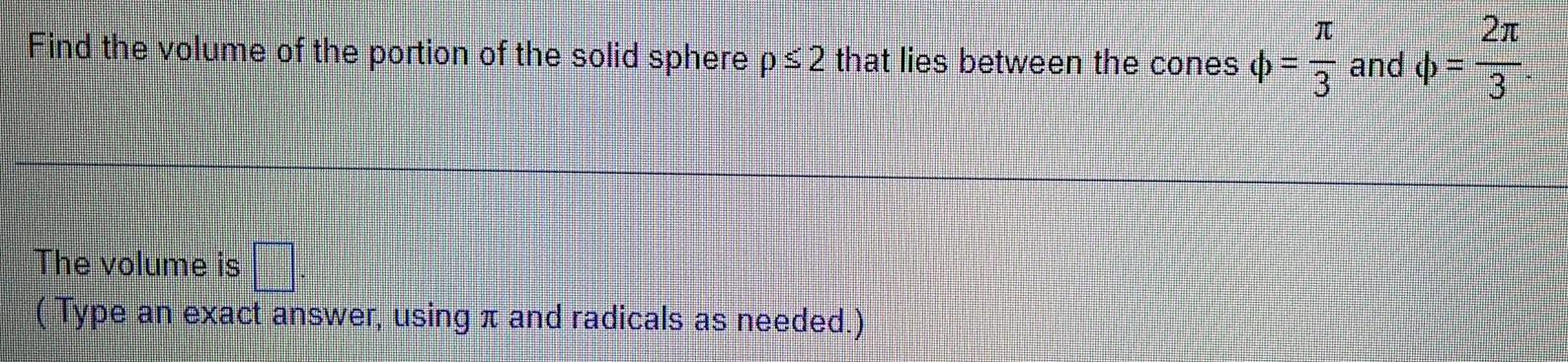
Definite IntegralsT 2T Find the volume of the portion of the solid sphere p 2 that lies between the cones 3 and 3 The volume is Type an exact answer using and radicals as needed