Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
Application of derivativesregulation size by the International Football Association FIFA field is variable if it is between 100 and 110 m long and between 64 and 73 m wide it is considered DA 50 Part a A particular field is 108 5 m long and 68 5 m wide What is the area of this field in square meters A sin cotan m cos asin tan 7 8 9 9 HOME acos E TAL 4 S 6 Grade Summary Deductions Potential 0 100 Submissions Attempts remaining 10
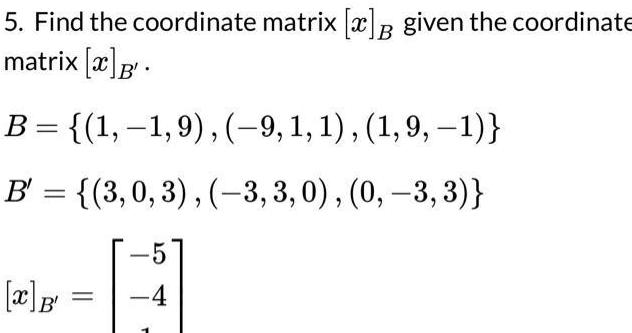
Calculus
Definite Integrals5 Find the coordinate matrix x given the coordinate matrix x B 1 1 9 9 1 1 1 9 1 B 3 0 3 3 3 0 0 3 3 x B 5 4
Calculus
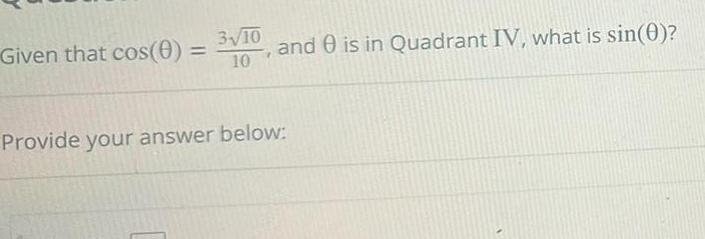
Application of derivativesGiven that cos 0 3 10 10 and is in Quadrant IV what is sin 0 Provide your answer below

Calculus
Definite IntegralsUse a reference angle to write cos Provide your answer below 43 36 in terms of the cosine of a positive acute angle in radians
Calculus
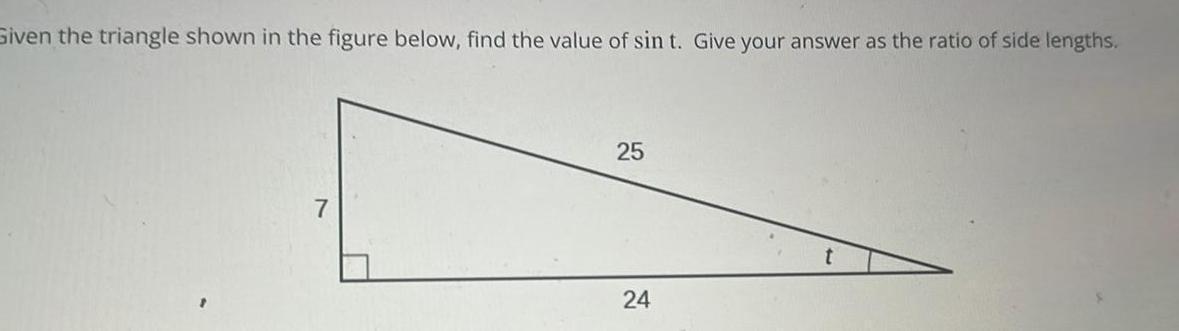
Application of derivativesGiven the triangle shown in the figure below find the value of sin t Give your answer as the ratio of side lengths 25 24
Calculus
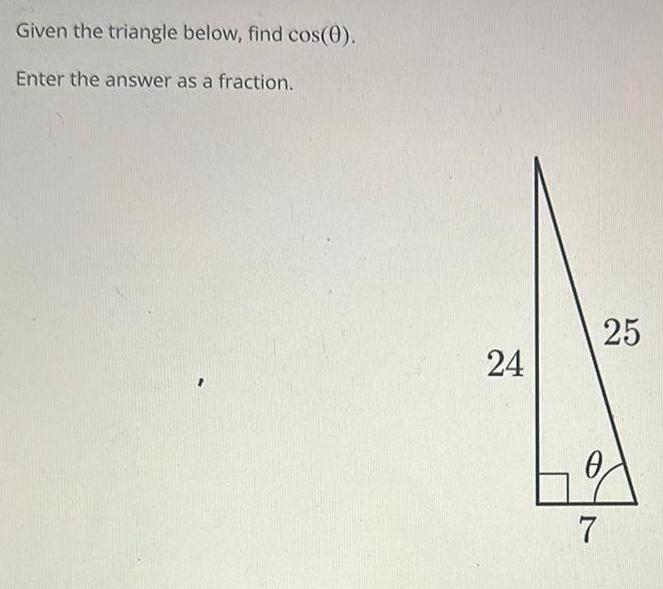
Application of derivativesGiven the triangle below find cos 0 Enter the answer as a fraction 24 7 25
Calculus
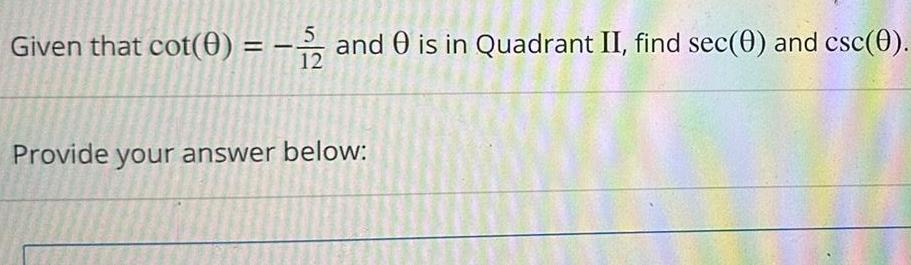
Differential equationsGiven that cot 0 and 0 is in Quadrant II find sec 0 and csc 0 12 Provide your answer below

Calculus
Application of derivatives0 Provide your answer below 65 ft A hiker is standing on the ground looking up to the top of a tree with an angle of elevation of 0 54 The figure shown above represents the situation where the base of the triangle is the eye level of the hiker and the vertical side is the tree Based on the dimensions shown in the figure what is the distance a in feet from the hiker to the base of the tree Rounc one decimal place

Calculus
Vector CalculusWrite sec 325 in terms of the secant of a positive acute angl Sorry that s incorrect Try again

Calculus
Application of derivativesIn terms of the cotangent of a positive acute angle what is the expression for cot 55
Calculus
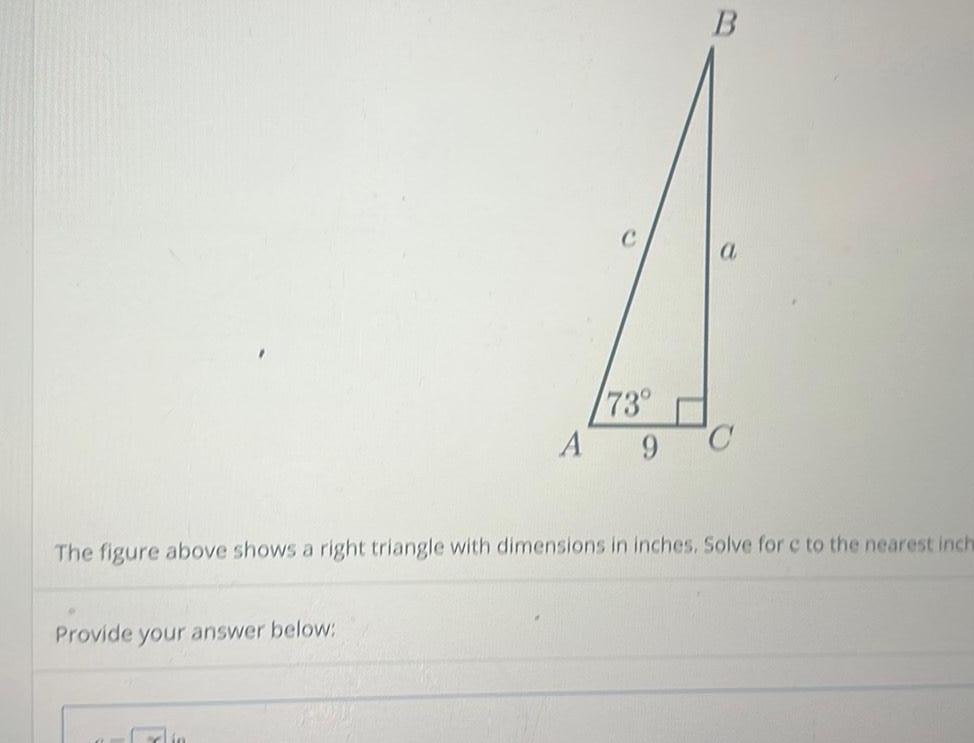
Application of derivativesProvide your answer below B The figure above shows a right triangle with dimensions in inches Solve for c to the nearest inch Erlin 73 A 9 C

Calculus
DifferentiationCompute the following using a calculator sin 13 Round your answer to two decimal places
Calculus
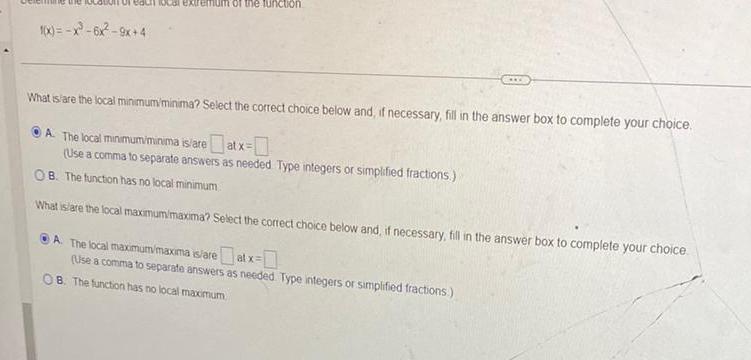
Application of derivatives1 x x 6x 9x 4 of the function What is are the local minimum minima Select the correct choice below and if necessary fill in the answer box to complete your choice A The local minimum minima is are atx Use a comma to separate answers as needed Type integers or simplified fractions B The function has no local minimum What is are the local maximum maxima Select the correct choice below and if necessary fill in the answer box to complete your choice A The local maximum maxima is areat x Use a comma to separate answers as needed Type integers or simplified fractions OB The function has no local maximum
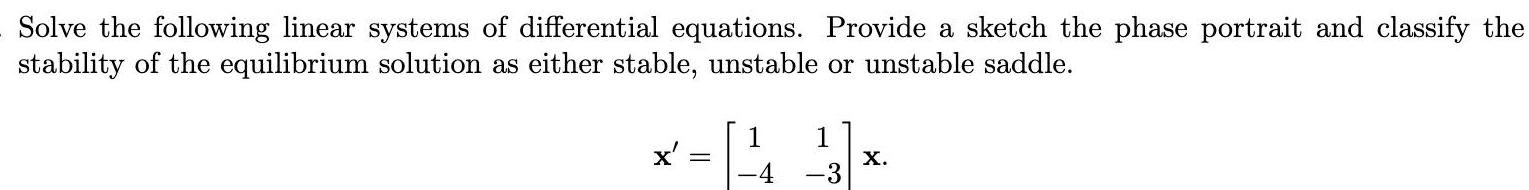
Calculus
Application of derivativesSolve the following linear systems of differential equations Provide a sketch the phase portrait and classify the stability of the equilibrium solution as either stable unstable or unstable saddle x 1 3 X
Calculus
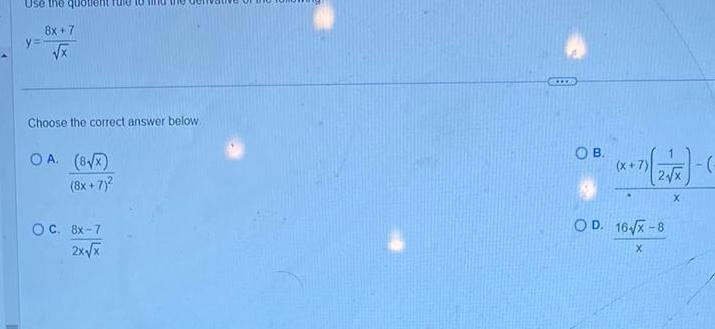
DifferentiationUse the quotient to miu 8x 7 x y Choose the correct answer below OA 8 x 8x 7 OC 8x 7 2x x OB 7 2 xX x 7 OD 16 X 8 X X

Calculus
Vector CalculusCompute the following using a calculator cos Round your answer to two decimal places

Calculus
Application of derivatives2 Evaluate cos 8 B where sine with in the second quadrant and tan with B in the fourth quadrant

Calculus
Application of derivativesWhat is the value of cot 0 if the terminal side of angle 0 intersects the unit circle in the first quadrant at x 45
Calculus
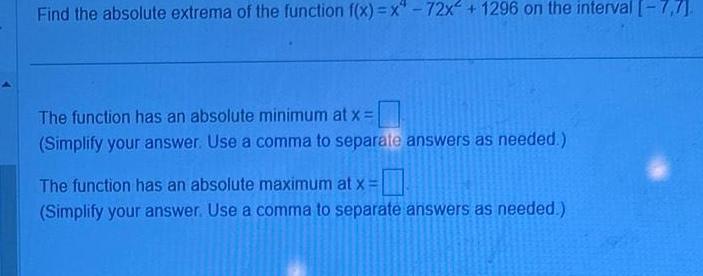
Application of derivativesFind the absolute extrema of the function f x x 72x 1296 on the interval 7 7 The function has an absolute minimum at x Simplify your answer Use a comma to separate answers as needed The function has an absolute maximum at x Simplify your answer Use a comma to separate answers as needed


Calculus
DifferentiationThe function s t 612 91 2 gives the distance from a starting point at time t of a particle moving along a line Find the velocity and acceleration functions Then find the velocity and acceleration at t 0 and t 5 Assume that time is measured in seconds and distance is measured in centimeters Velocity will be in centimeters per second cm sec and acceleration in centimeters per second per second cm soc v t Do not factor a t v 0 cm sec v 5 cm sec a 0 cm sec a 5 cm sec EIIE

Calculus
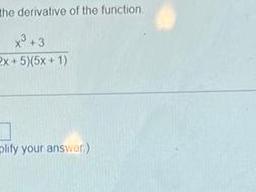
Limits & Continuityf x 14x 7 at 3 7 given point he equation of the tangent line to the graph of f x at the given point is
Calculus
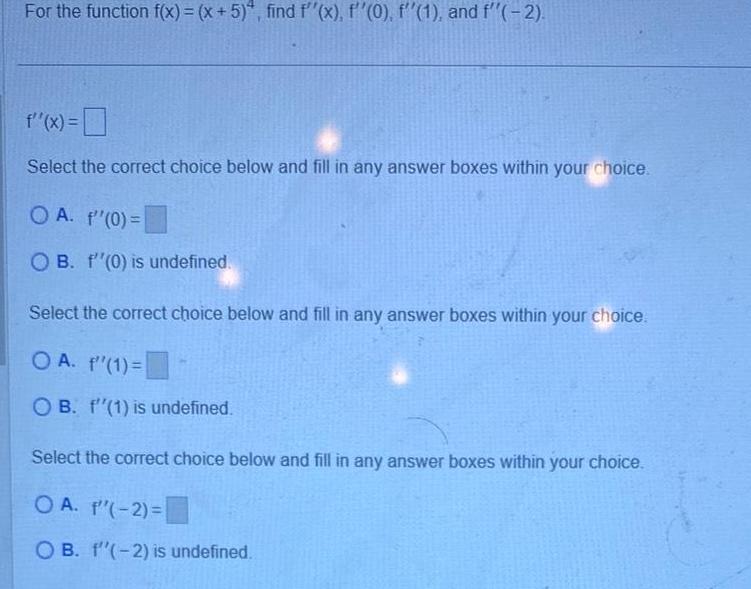
DifferentiationFor the function f x x 5 find f x f 0 f 1 and f 2 f x Select the correct choice below and fill in any answer boxes within your choice OA f 0 OB f 0 is undefined Select the correct choice below and fill in any answer boxes within your choice OA f 1 OB f 1 is undefined Select the correct choice below and fill in any answer boxes within your choice OA f 2 OB f 2 is undefined
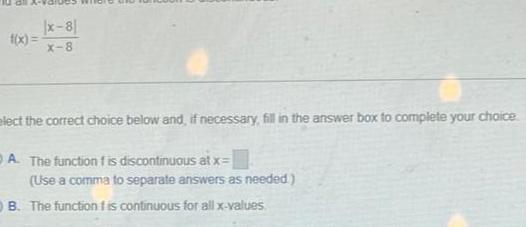
Calculus
Limits & Continuityx 8 X 8 elect the correct choice below and if necessary fill in the answer box to complete your choice A The function f is discontinuous at x Use a comma to separate answers as needed B The function f is continuous for all x values

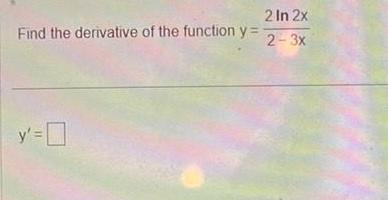
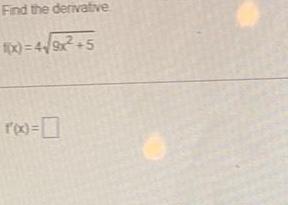

Calculus
Application of derivativesGiven the triangle below find cos 0 Enter an exact answer in fraction form 7 24 25
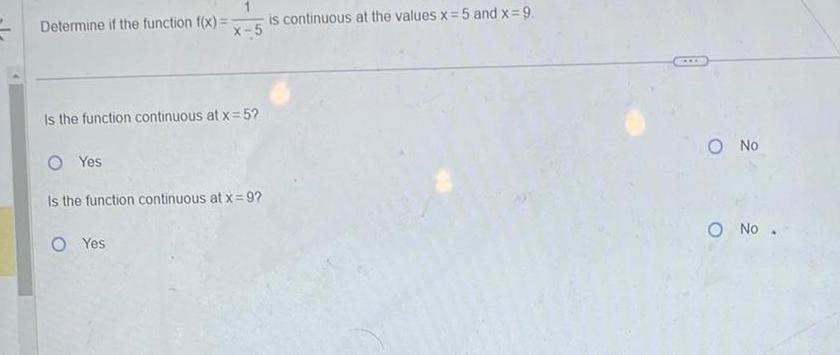
Calculus
Limits & ContinuityDetermine if the function f x is continuous at the values x 5 and x 9 X 5 Is the function continuous at x 5 Yes Is the function continuous at x 9 O Yes O No O No
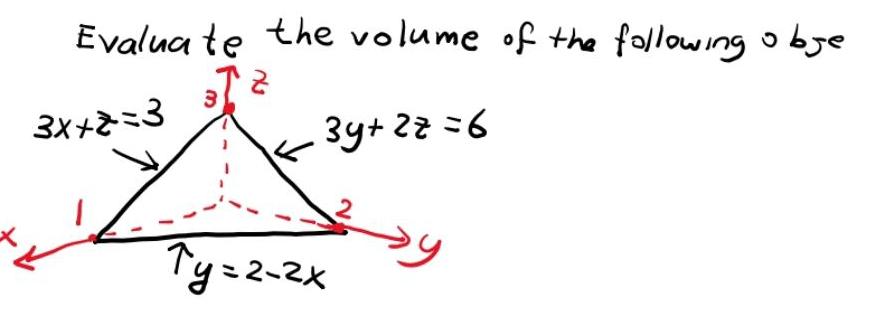
Calculus
DifferentiationFind i the net area and ii the area of the region bounded by the graph of f and the x axis on the given interval You may find it useful to sketch the region f x 5x 5x on 0 3 1 The net area is Type an exact answer using radicals as needed ii The area of the region bounded by the curve and the x axis is GITE
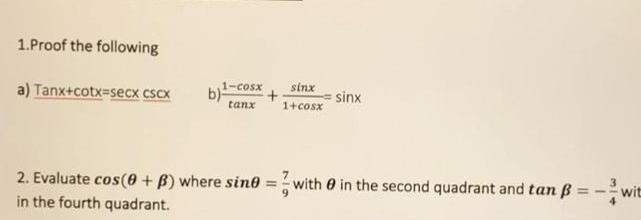
Calculus
Application of derivatives1 Proof the following a Tanx cotx secx cScx 1 cosx tanx b sinx 1 cosx sinx 2 Evaluate cos 0 B where sine with in the second quadrant and tan B wit in the fourth quadrant
Calculus
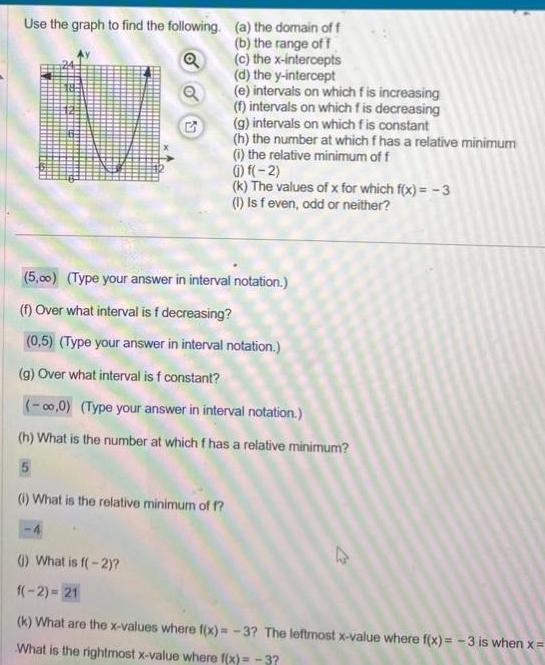
DifferentiationUse the graph to find the following a the domain off G b the range of f c the x intercepts d the y intercept e intervals on which f is increasing f intervals on which fis decreasing g intervals on which f is constant h the number at which f has a relative minimum i the relative minimum of f 1 What is the relative minimum of f 1 f 2 k The values of x for which f x 3 1 Is f even odd or neither 5 00 Type your answer in interval notation f Over what interval is f decreasing 0 5 Type your answer in interval notation g Over what interval is f constant 0 0 Type your answer in interval notation h What is the number at which f has a relative minimum 1 What is f 2 1 2 21 k What are the x values where f x 3 The leftmost x value where f x 3 is when x What is the rightmost x value where f x 3
Calculus
Vector Calculus16 Round your answer to two decimal places 9 Compute the following using a calculator cos

Calculus
Limits & ContinuityA cold metal bar at 80 C is submerged in a pool maintained at a temperature of 40 C After 55 seconds the temperature of the bar is 20 C How long will it take for the bar to attain a temperature of 30 C Use decimal notation Give your answer to one decimal place Round any intermediate calculations if needed to no less than four decimal places t seconds
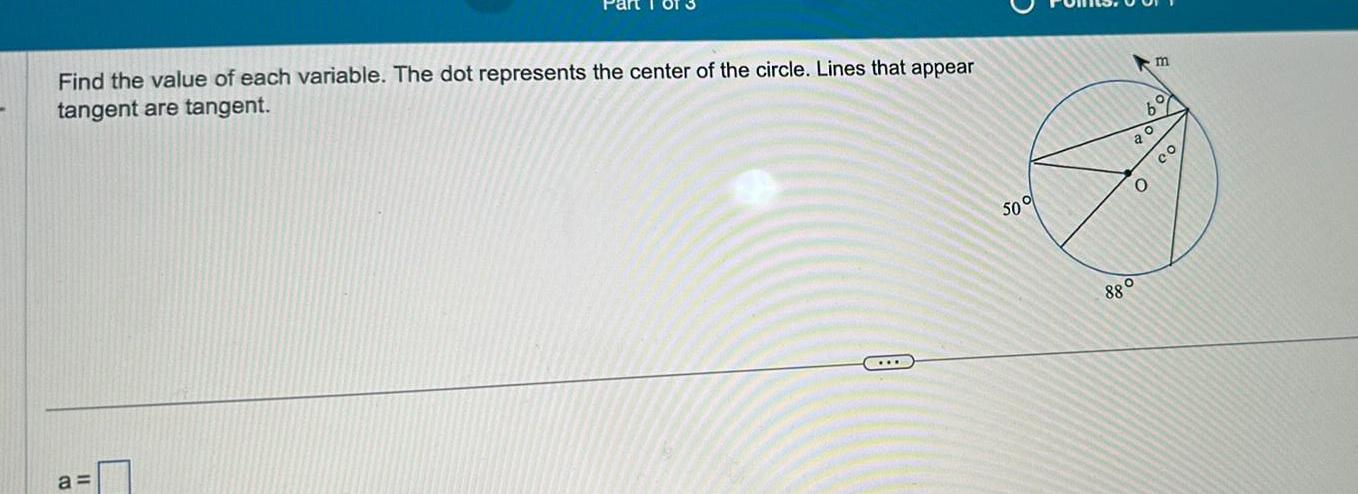
Calculus
Limits & ContinuityFind the value of each variable The dot represents the center of the circle Lines that appear tangent are tangent a 50 a 880 m b O O CO
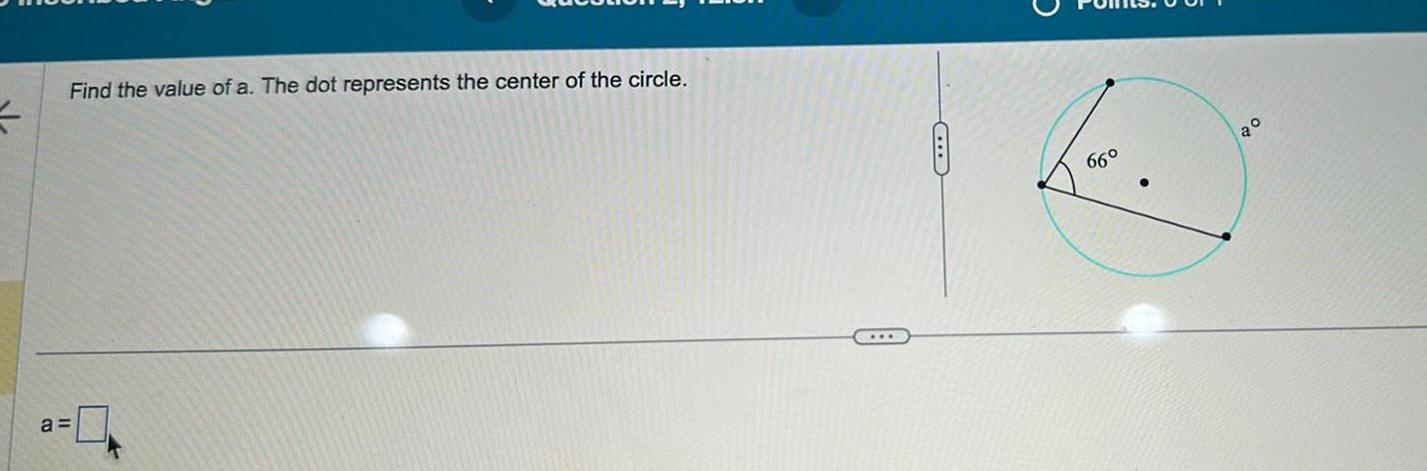
Calculus
Differentiation4 Find the value of a The dot represents the center of the circle a CHEB L 66 20

Calculus
Vector CalculusGiven the triangle below find csc 0 Enter your answer as a ratio of sides 3 5 0
Calculus
Definite Integralss 16 Round your answer to two decimal places 9 Compute the following using a calculator cos
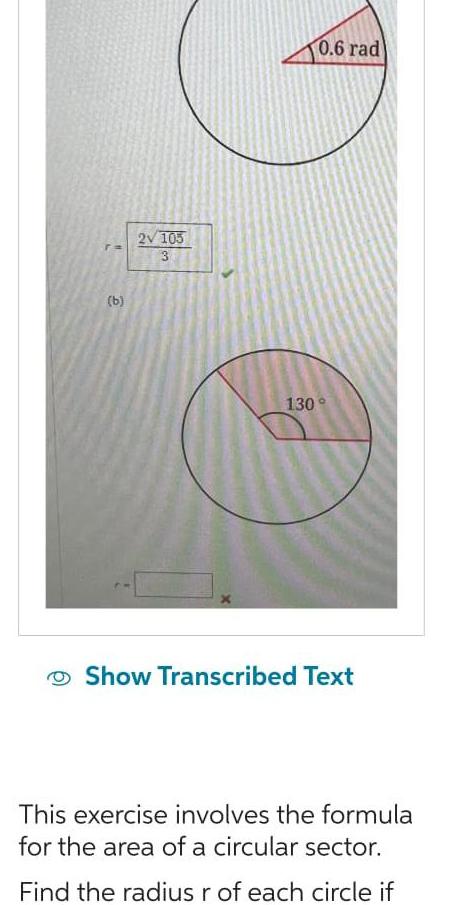
Calculus
Application of derivativesb 2V 105 3 0 6 rad 130 Show Transcribed Text This exercise involves the formula for the area of a circular sector Find the radius r of each circle if
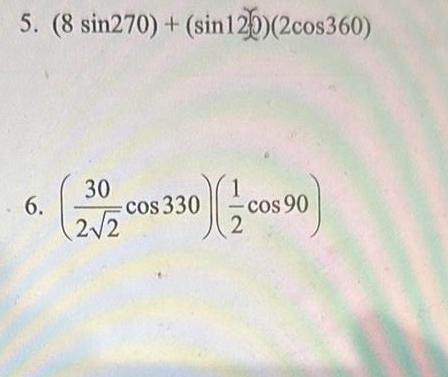

Calculus
DifferentiationDetermine the exact values of sin 0 and cos if the terminal side of angle intersects the unit circle in the first quadrant Provide your answer below

Calculus
Application of derivativesFind the coordinates of the point on the unit circle at an angle of 3 4 Give your answer in the form x y and leave any fractions in fraction form
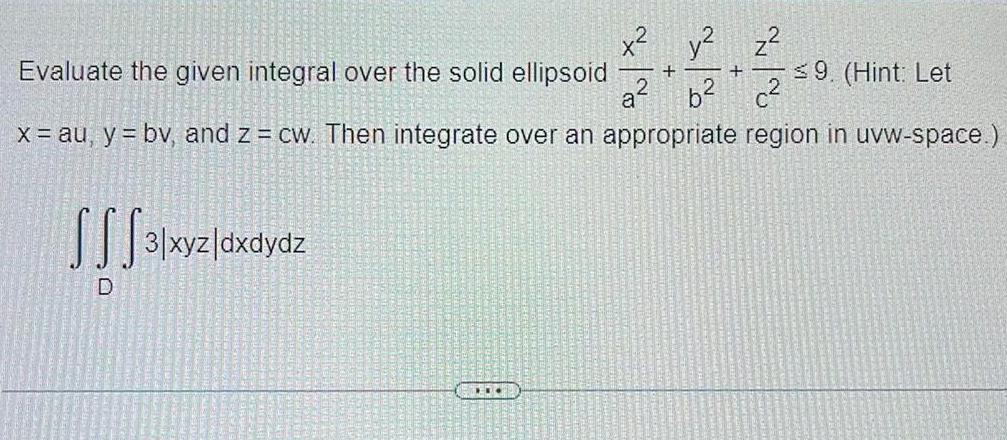
Calculus
Application of derivatives9 Hint Let c x au y bv and z cw Then integrate over an appropriate region in uvw space Evaluate the given integral over the solid ellipsoid a b SSS3 xyz dx dydz x y z D HI
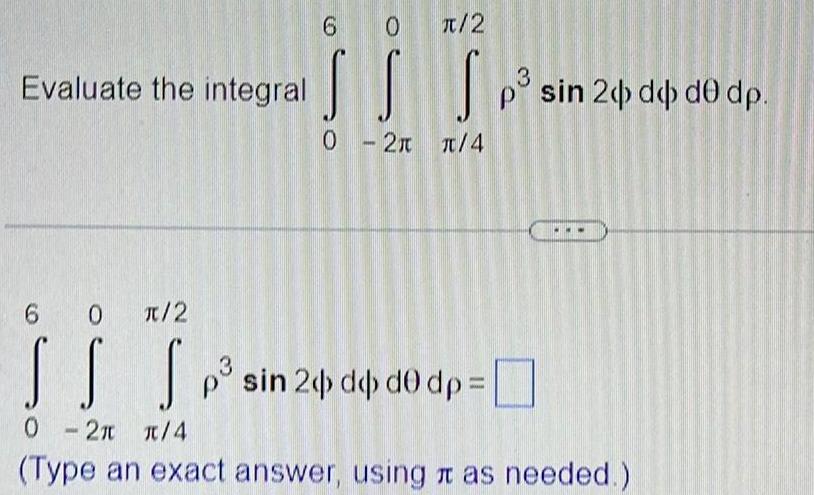
Calculus
Definite IntegralsEvaluate the integral 6 0 2 SS 0 2x 4 Sp 3 p sin 20 d d0 dp 6 0 2 SS S 0 2 4 Type an exact answer using as needed p sin 2 dbd0 dp
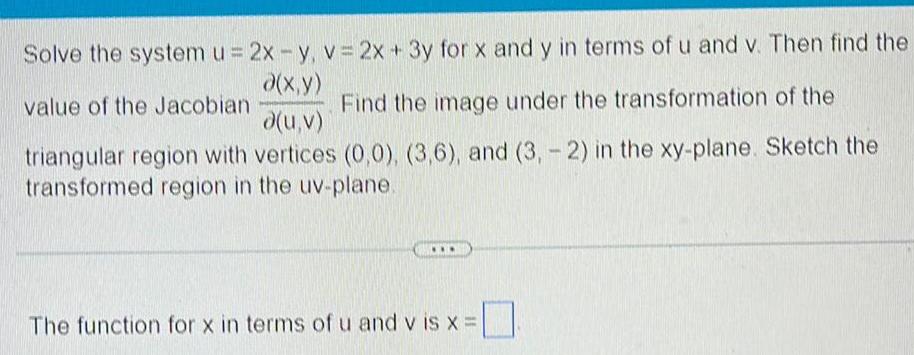
Calculus
Application of derivativesSolve the system u 2x y v 2x 3y for x and y in terms of u and v Then find the x y value of the Jacobian Find the image under the transformation of the d u v triangular region with vertices 0 0 3 6 and 3 2 in the xy plane Sketch the transformed region in the uv plane The function for x in terms of u and vis x
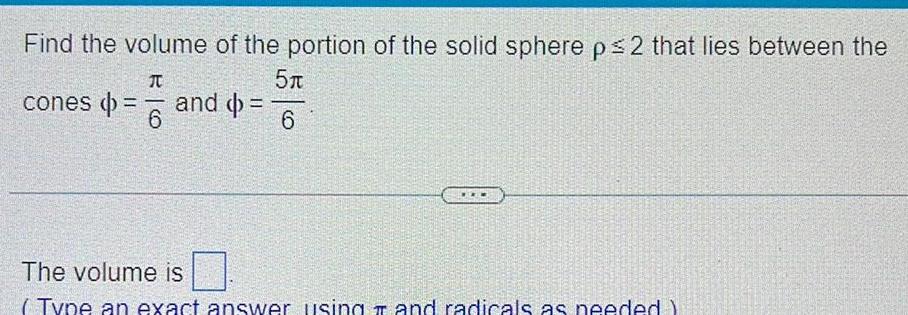
Calculus
Definite IntegralsFind the volume of the portion of the solid sphere p 2 that lies between the T 5 6 cones 6 and The volume is Type an exact answer using and radicals as needed

Calculus
Indefinite IntegrationIn a Use a substitution to find f Show your work and final answer in the provided area using HTML Editor s Insert Math Equation function an da