Algebra Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Algebra
Quadratic equationsEvaluate the determinants in Exercises 1 and 2 1 2 5 2 i 3 If A 82 cos 0 sin 0 4 iii 4 If A 0 1 8 If i 4 sin 0 cos e MATHEMATICS 6 IfA 2 5 Evaluate the determinants 3 1 2 i 0 0 1 3 5 0 A 6 2 X 2 18 X of be rep 004 1 0 2 1 0 3 2 3 0 1 1 54 9 7 Find values of x if 2 4 5 1 2 then show that 2A 4 A T 2 3 N 6 2x 4 4 X 6 2 18 6 ii then show that 3 A 27 A find A x x 1 x 1 B 6 11 Rationalised 2023 24 then x is equal to 2 iv 0 3 1 2 3 1 4 TK ber 5 1 2 2 1 3 5 0 4 3 Area of a Triangle In earlier classes we have studied that the area of 2 13 31 12 x x y 1 X 3 1 X Y x 1 x 35 2x 5 olished triangle whose vertices a x 3 x vz V x y x y and x y is given by the expression x3 Now this expression can be written in the form of a determinant as Remarks i Since area is a positive quantity we always take the absolute value of th 1

Algebra
Quadratic equations80 a31 a32 a 1 a 2 a33 a32 a 13 a22 a 1 a23 a 1 a32 a3 a A a 1 a 12 a33 a21 932 913 a23 a31 a12 a11 a22 a33 913 931 922 Expansion along first Column C By expanding along C we get A a 1 1 922 MATHEMATICS a11 912 a13 A a21 922 923 a31 a32 A33 iii Let A 923 a32 a33 t to me jepub 2 2 23 4 0 a12 a21 a33 a12 923 a31 and B 921 1 1 Rationalised 2023 24 1 20 a31 a 13 a 12 a13 931 1 1 922 923 a 1 a 2 a33 a23 a32 a21 a 12 a 33 a 3 a32 a31 a 12 a23 a13 a22 13 a22 a31 a 13 A a a22 a33 a 11 a23 a32 a21 a 12 a33 a31 a 13 a22 a 1 a 22 a33 a 11 a 23 a32 a 12 a21 A33 A 2 A23 A31 a 13 a21 a32 12 A 0 8 8 and B 0 2 2 Observe that A 4 2 2 B or A square matrices A and B 912 a13 a32 a33 1 24 3 0 4 1 0 a23 a11 a32 a13 a31922 3 Clearly values of A in 1 2 and 3 are equal It is left as an exercise to the reader to verify that the values of A by expanding along R C and C are equal to the value of A obtained in 1 2 or 3 Hence expanding a determinant along any row or column gives same value Remarks i For easier calculations we shall expand the determinant along that row or column which contains maximum number of zeros Example 3 Evaluate the determinant A 1 a13 a21 a32 a21 a 13 a32 ii While expanding instead of multiplying by 1 we can multiply 1 or 1 according as i j is even or odd 2 a31 a 12 a23 verify that A 2B Also In general if A kB where A and B are square matrices of order n then A k B where n 1 2 3 where n 2 is the order of

Algebra
Permutations and CombinationsExpansion along first Row R 11 Step 1 Multiply first element a of R by 1 1 1 sum of suffixes in a11 and with the second order determinant obtained by deleting the elements of first row R and first column C of A as a lies in R and C i e 922 923 1 a 932 A33 Step 2 Multiply 2nd element a of R by 1 2 1 sum of suffixes in a order determinant obtained by deleting elements of first row R and 2nd column C of A as a 12 lies in R and C i e 1 2 a 2 Step 3 Multiply third element a 3 of R by 1 3 1 sum of suffixes in a and the second order determinant obtained by deleting elements of first row R and third column C of A as a 3 lies in R and C3 or 1 3a13 250 1951 i e Step 4 Now the expansion of determinant of A that is A written as sum of all three terms obtained in steps 1 2 and 3 above is given by 145 a31 932 922 a23 1 det A A 1 32 33 1 3 a a21 922 931 932 A a a22 a33 a32a23 12 a 1 a33 a31a23 a13 a 1 a32 931 922 a13 a 1 a22 A33 11 a 13 a31 a22 Note We shall apply all four steps together Expansion along second row R Expanding along R we get A 1 1 a Rationalised 2023 24 a11 a32a23 a 12 a21 a 33 a11 A a21 a 31 923 921 a32 A33 1 a12 a13 1 all a31 912 1 3 a21 a12 a33 a32 a 13 a22 a23 a11 a32 a31 9 2 a12 932 a 1 2 912 923 931 933 a13 22 23 a32 a33 RT 922 aus de 912 and the second all a13 a31 DETERMINANTS 79 a12 a31 a23 a13 a21 a32 a31 a 13 1 published
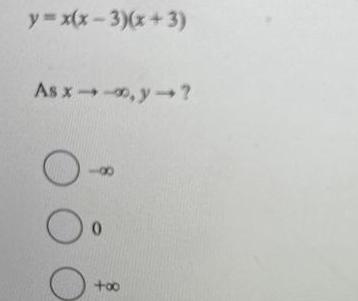

Algebra
Matrices & Determinantsa32a33 Cofactor of a21 A 1 M 1 a 2a33a 3 a Remark Expanding the determinant A in Example 21 along R a2 2 1 1 A 1 a 1 a32 86 911 1 2 a A a 2A 2 a13A 3 where A is cofactor of a 11 12 sum of product of elements of R with their corresponding cofactors Similarly A can be calculated by other five ways of expansion that is along R R C C and C Hence A sum of the produ of elements of any row or column with their corresponding cofactors MATHEMATICS Note If elements of a row or column are multiplied with cofactors of any other row or column then their sum is zero For example A a A 1 a 2 A22 a13 A23 a12 913 a32 6 0 5 Solution We have M M 2 1 1 all a12 a13 a11 a12 a13 a31 932 933 Similarly we can try for other rows and columns M 3 M M 2 M 3 a23 a33 5 16 64 1 II 12 33 943 a33 4 and verify that a A3 a 2 A32 a 3 A33 0 31 2 a 12 Example 11 Find minors and cofactors of the elements of the determinant 2 3 5 5 921 923 a31 a33 1 2 10 4 Rationalised 2023 24 7 21 2 RT 0 since R and R are identical a21 922 1 3 a3 a31 932 9 1 a13 a31 933 30 0 30 a12933 a13a32 we have 4 a 13 14 5 19 10 3 13 1 3 0 20 20 A 1 20 20 42 4 46 A 1 2 46 46 a11 a12 a31 a32 1 2 19 19 A23 1 3 13 13 perance

Algebra
Quadratic equationsand Now So II 1 i 18 3 7 21 25 21 25 4 3 22 M32 M 33 ON62 12 1 31 10 545 1 0 0 2 1 0 1 0 00 1 30 0 30 0 5 If A 21 14 5 19 a11 912 12 0 12 CERT 8 30 22 0 18 18 ii be requalis a 2 a 2 3 a 3 5 A 12 A2 22 A 18 12 13 31 a 1 A31 a12 A32 a13 A33 2 12 3 22 5 18 24 66 90 0 a13 1 0 4 ii 35 1 0 1 2 EXERCISE 4 3 Write Minors and Cofactors of the elements of following determinants 2 4 0 3 a b d a31 a32 a33 A a A a A a 4 4 1 2 2 19 19 A23 1 3 13 13 Rationalised 2023 24 A 1 12 12 A32 1 3 2 22 22 B A33 1 3 18 18 4 Using Cofactors of elements of third column evaluate 5 3 8 3 Using Cofactors of elements of second row evaluate A 20 1 3 DETERMINANTS ignas yz A a A a A ZX Z xy 87 then value of A is given by

Algebra
Matrices & DeterminantsRemarks i Since area is a positive quantity we always take the absolute value of the determinant in 1 ii If area is given use both positive and negative values of the determinant for calculation iii The area of the triangle formed by three collinear points is zero Example 6 Find the area of the triangle whose vertices are 3 8 4 2 and 5 1 Solution The area of triangle is given by 38 A 4 5 This gives 2 1 1 1 3 2 1 8 4 5 1 4 10 61 2 1 3 72 14 Example 7 Find the equation of the line joining A 1 3 and B 0 0 using determinants and find k if D k 0 is a point such that area of triangle ABD is 3sq units Solution Let P x y be any point on AB Then area of triangle ABP is zero Why So 1 0 0 2 1 3 y Rationalised 2023 24 X This gives which is the equation of required line AB Also since the area of the triangle ABD is 3 sq units we 3 1 10 0 13 y 3x 0 or y 3x k 0 0 3k 3 i e k F 2 2 EXERCISE 4 2 DETERMINANTS 83 iii 2 3 3 2 1 8 e reputished 1 Find area of the triangle with vertices at the point given in each of the following i 1 0 6 0 4 3 ii 2 7 1 1 10 8 2 Show that points A a b c B b c a C c a b are collinear 3 Find values of k if area of triangle is 4 sq units and vertices are i k 0 4 0 0 2 ii 2 0 0 4 0 k 4 i Find equation of line joining 1 2 and 3 6 using determinants ii Find equation of line joining 3 1 and 9 3 using determinants 5 If area of triangle is 35 sq units with vertices 2 6 5 4 and k 4 Then k is

Algebra
Matrices & DeterminantsIn the previous chapter we have studied inverse of a matrix In this section we shall discuss the condition for existence of inverse of a matrix To find inverse of a matrix A i e A we shall first define adjoint of a matrix 4 5 1 Adjoint of a matrix n Definition 3 The adjoint of a square matrix A a is defined as the transpose of the matrix A where A is the cofactor of the element a Adjoint of the matrix A is denoted by adj A 1 n y Let 88 a11 912 913 A 9 1 922 923 a31 32 33 Hence MATHEMATICS A11 A12 A13 Then adj A Transpose of A21 A22 A23 A31 A32 A33 Rationalised 2023 24 3 Example 12 Find adj A for A 4 Solution We have A 4 A 1 A 3 A 2 2 Let Remark For a square matrix of order 2 given by adj A AA 42 A22 1 adj A A of The adj A can also be obtained by interchanging a a 2 and a212 i e anl a21 911 912 921 a22 where I is the identity matrix of order n Verification A11 A21 A31 A12 A22 A32 A13 A23 A33 a12 Change sign Interchange We state the following theorem without proof Theorem 1 If A be any given square matrix of order n then a11 912 a13 A 921 922 923 then adj A A adj A adj A A A I A21 a a 12 3 and by changing signs Autished All A21 A31 A12 A22 A32

Algebra
Matrices & Determinantsusing minors and cofactors Definition 1 Minor of an element a of a determinant is the determinant obtained by deleting its ith row and jth column in which element a lies Minor of an element a IS denoted by M ij Remark Minor of an element of a determinant of order n n 2 is a determinant of order n 1 1 2 3 Example 8 Find the minor of element 6 in the determinant A 4 5 6 8 Solution Since 6 lies in the second row and third column its minor 1 M23 3 8 14 6 obtained by deleting R and C in A is defined by Definition 2 Cofactor of an element denoted A 1 M where M is minor Example 9 Find minors and cofactors of all the elements of the determinant Solution Minor of the element Here a 1 So M Minor of a 3 M 2 Minor of the element a 2 4 M 1 Minor of the element a21 2 M 2 Minor of the element a 1 Now cofactor of a is A So A 1 M 1 3 3 A 2 1 2 M 1 4 4 A 1 1 M 1 2 2 A 2 1 2 M 2 1 1 1 Minor of a M Minor of a M Rationalised 2023 24 Example 10 Find minors and cofactors of the elements a a in the determinant a11 912 a13 a23 a31 a32 a33 Solution By definition of minors and cofactors we have 922 a23 a32 933 a22 a33a23 a32 Cofactor of a A 1 M A22 A33 A23 a32 11 11 11 a12 A 921 922 is given by a13 a a a 3 A32 21 DETERMINANTS 85 ed

Algebra
Permutations and CombinationsTheorem 1 If A be any given square matrix of order n then A adj A adj A A A I where I is the identity matrix of order n Verification a13 a23 931 932 933 Since sum of product of elements of a row or a column with corresponding cofactors is equal to A and otherwise zero we have Let 911 912 A 9 1 922 A adj A Let 2 A11 A21 A31 then adj A A12 A22 A32 A13 A23 A33 Rationalised 2023 24 A 0 0 0 A 0 0 A 0 A 0 1 Similarly we can show adj A A A I Hence A adj A adj A A A I Definition 4 A square matrix A is said to be singular if A 0 For example the determinant of matrix A Hence A is a singular matrix Definition 5 A square matrix A is said to be non singular if A oto A Then 4 hed 2 3 4 A 5 48 3 Hence A is a nonsingular matrix We state the following theorems without proof 00 A Remark We know that adj A A A I 0 0 00 1 0 A I is zero Theorem 2 If A and B are nonsingular matrices of the same order then AB and BA are also nonsingular matrices of the same order Theorem 3 The determinant of the product of matrices is equal to product of their respective determinants that is AB A B where A and B are square matrices of the same order DETERMINANTS 89 A 0 0 Writing determinants of matrices on both sides we have O 0 A 0 A 0 0 A


Algebra
Quadratic equationsAs x y O 0 oo Question 19 1 point What are the x intercepts of y x x 3 x 3 0 3 3 3 0 3

Algebra
Quadratic equationsUse the vertex formula to find the vertex of the quadratic function f x x 4x 7 The vertex is Type an ordered pair Simplify your answer

Algebra
Quadratic equationsSelect the correct answer The quadratic function which has a vertex h k 1 4 and contains the point x y 2 6 IS Of 2 2 x 1 4 Of x 2x 4x 6 Of x x 1 4 Of x 2 x 1 4 f x x 3x 2

Algebra
Quadratic equationsA ball is thrown directly upward from a height of 5 ft with an initial velocity of 20 ft sec The function s t 16t 20t 5 gives the height of the ball in feet t seconds after it has been thrown Determine the time at which the ball reaches its maximum height and find the maximum height The ball reaches its maximum height of Type integers or decimals ft sec s after the ball is thrown C

Algebra
Complex numbersPerform the indicated operation 5 6i 5 i 5 6i 5 i Type your answer in the form a bi Use integers or fractions for any numbers in the expression

Algebra
Quadratic equationsWrite an equation for a parabola with x intercepts 2 0 and 5 0 which passes through the point 3 30 Write the equation 7
Algebra
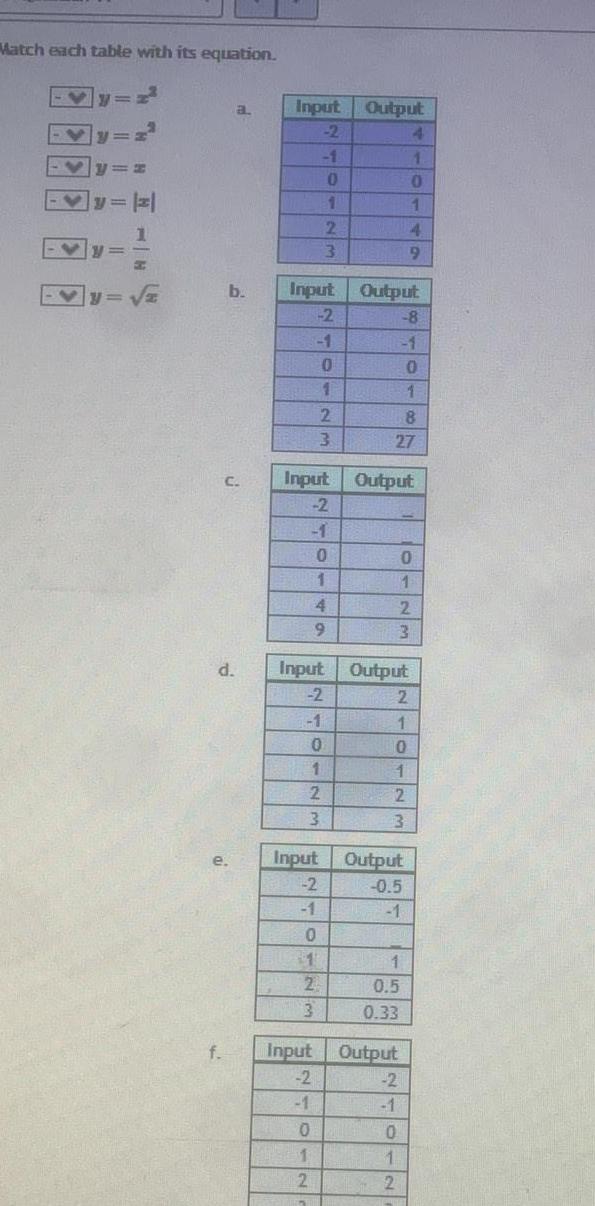
Quadratic equationsMatch each table with its equation A E A 11 d e f a b Input 2 1 0 1 2 3 Input 2 1 1 0 1 2 3 0 1 4 Input 2 1 0 1 2 3 Input 2 1 Input Output 2 0 1 2 3 Input 2 1 0 1 2 Output 4 1 0 Output 8 0 1 8 27 1 4 9 1 0 1 2 3 Output 2 1 0 1 12 3 Output 0 5 1 0 5 0 33 Output 2 1 0 1 2

Algebra
Complex numbersQuestion 10 HIA Match each graph with its equation v z 2 y 2 y 1 1 y y 1 H EA 4 4 a b C d 3 2 1 34 3 2 1 34 3 2 1 5 4 3 2 1 5 4 3 2 1 34 E 1 E 2 E 4 5 5 3 In 2 3 2 2 2 7 1 1 2 3 4 a 1 2 3 4 5 23 4 5

Algebra
Quadratic equationsMicah found the vertex for the function y 9 5x 47 5x 63 as shown Find and correct Micah s error X X X b 2a 47 5 2 9 5 47 5 19 x 2 5 x 2 5 y 9 5 2 5 47 5 2 5 63 y 59 375 118 75 63 y 115 125 Explain the error O A Micah should have found a positive value when he simplified the 9 5 2 5 term B Micah used the wrong sign for b in the formula x b 2a C Micah should have evaluated the function with x 0 to find the y coordinate OD Micah did not use the correct order of operations dividing 47 5 by 2 9 5 The correct vertex is Type an ordered pair


Algebra
Quadratic equationsm 4 The distance s that an object falls varies directly with the square of the time t of the fall If an object falls 16 feet in one second how long for it to fall 144 feet Follow these steps to help you solve the question a Write a function s t and use k as the proportionality constant b Find the constant of proportionality k and write the function s t If necessary round the value of k to two decimal places c Use your function from part b to answer the question



Algebra
Quadratic equationsQuestion 8 Suppose f x 22 2x 7 Compute the following A f 4 f 4 B f 4 f 4 Question Help Video

Algebra
Quadratic equationsZ at Q 20000 6000 8 20000 7 6000 202000 Z at R 10500 34500 8 x 10500 7 34500 325500 Z at S 5000 40000 8 5000 7 40000 320000 Z at T 0 40000 7 40000 280000 Now observe that the profit is maximum at x 10500 and y 34500 and the maximum profit is 325500 Hence the manufacturer should produce 10500 bottles of M medicine and 34500 bottles of M medicine in order to get maximum profit of 325500 Example 6 Suppose a company plans to produce a new product that incur some costs fixed and variable and let the company plans to sell the product at a fixed price Prepare a mathematical model to examine the profitability Solution Step 1 Situation is clearly identifiable 204 MATHEMATICS Rationalised 2023 24 Step 2 Formulation We are given that the costs are of two types fixed and variable The fixed costs are independent of the number of units produced e g rent and rates while the variable costs increase with the number of units produced e g material Initially we assume that the variable costs are directly proportional to the number of units produced this should simplify our model The company earn a certain amount of money by selling its products and wants to ensure that it is maximum For convenience we assume that all units produced are sold immediately The mathematical model Let x number of units produced and sold C total cost of production in rupees I income from sales in rupees P profit in rupees Our assumptions above state that C consists of two parts i fixed cost a in rupees ii variable cost b rupees unit produced Then C a bx Also income I depends on selling price s rupees unit Thus I Sx The profit P is then the difference between income and costs So s b x a ott be published independent dependent 1 3 We now have a mathematical model of the relationships 1 to 3 between the variables x C I P a b s These variables may be classified as 2 X C I P parameters a b s The manufacturer knowing x a b s can determine P Step 3 From 3 we can observe that for the break even point i e make neither profit units a nor loss he must have P 0 i e x s b Stens 4 and 5 In view of the break even point one may conclude that if the company
Algebra
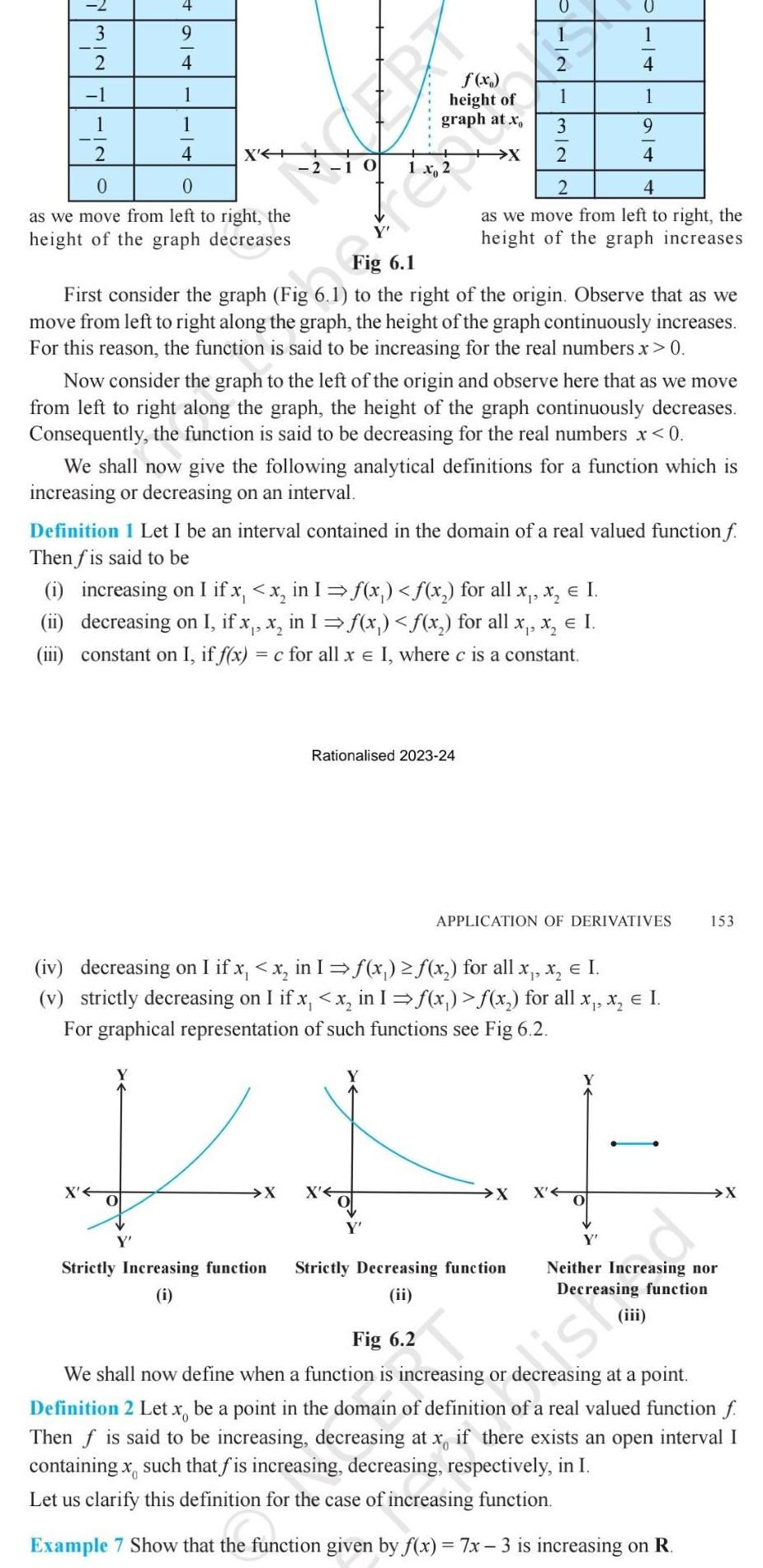
Permutations and Combinations32 4 1 1 4 0 as we move from left to right the height of the graph decreases 2 1 X J X f x height of graph at x O PINN Fig 6 1 First consider the graph Fig 6 1 to the right of the origin Observe that as we move from left to right along the graph the height of the graph continuously increases For this reason the function is said to be increasing for the real numbers x 0 Strictly Increasing function i 1 Now consider the graph to the left of the origin and observe here that as we move from left to right along the graph the height of the graph continuously decreases Consequently the function is said to be decreasing for the real numbers x 0 Rationalised 2023 24 X X 2 We shall now give the following analytical definitions for a function which is increasing or decreasing on an interval 3 Definition 1 Let I be an interval contained in the domain of a real valued function f Then f is said to be i increasing on I if x x in 1 f x x for all x x I ii decreasing on I if x x in I x x for all x x I iii constant on I if f x c for all x I where c is a constant 2 Fig 6 2 2 4 as we move from left to right the height of the graph increases iv decreasing on I if x x in I f x x for all x x I v strictly decreasing on I if x x in 1 x x for all x x I For graphical representation of such functions see Fig 6 2 Strictly Decreasing function ii 4 1 9 4 APPLICATION OF DERIVATIVES X X O 153 ist X Neither Increasing nor Decreasing function 20 We shall now define when a function is increasing or decreasing at a point Definition 2 Let x be a point in the domain of definition of a real valued function f Then f is said to be increasing decreasing at x if there exists an open interval I containing x such that fis increasing decreasing respectively in I Let us clarify this definition for the case of increasing function Example 7 Show that the function given by f x 7x 3 is increasing on R



Algebra
Quadratic equationsMacmillan Learning Follow the four step process to sketch the graph of the rational function R x Use the graphing utility to plot zeros graph asymptotes and create a sign diagram for the given rational function R x x 1 x x 1 x 2 1 Plot any zeros Select the zero button then click the graph to place a apro if th Reset step x 1 x x 1 x 2 10 Next step


Algebra
Complex numbersThe function f is defined as follows f x 2x 2 if x 0 if x 0 a Find the domain of the function b Locate any intercepts c Graph the function d Based on the graph find the range OC d Based on the graph find the range Select the correct choice below and fill in the answer box es to complete your choice OA The range consists exclusively of one or more isolated values It can be described as Use a comma to separate answers as needed B The range has at least one isolated value It can be described as the union of the interval s Use a comma to separate answers as needed www The range does not have any isolated values It can be described by Type your answer in interval notation and the set

Algebra
Sequences & SeriesUse the nth term test for divergence to show that the series is divergent or state that the test is inconclusive 8 COS n 1 19 n Choose the correct answer below O A The test is inconclusive because lim cos n 19 OB The series diverges because lim cos n nx O c The series diverges because lim cos nix O D The series diverges because lim cos n18 19 n 19 n 19 n o and fails to exist exists and is equal to and fails to exist

Algebra
Matrices & DeterminantsA matrix is said to be a column matrix if it has only one column 3 For example A 1 1 2 In general A a mx is a column matrix of order m 1 ii Row matrix 1 A matrix is said to be a row matrix if it has only one row For example B J1x4 In general B b x is a row matrix of order 1 n ii Square matrix 40 For example A is a column matrix of order 4 1 2 A matrix in which the number of rows are equal to the number of columns is said to be a square matrix Thus an m n matrix is said to be a square matrix if m n and is known as a square matrix of order n 4 MATHEMATICS 5 23 3 1 0 3 3 2 1 3 v Scalar matrix In general A a mxm Note If A a is a square matrix of order n then elements entries a a is a row matr 1 3 are said to constitute the diagonal of the matrix A Thus if A 2 4 3 5 Then the elements of the diagonal of A are 1 4 6 is a square matrix of order 3 is a square matrix of order m For example A 4 B Rationalised 2023 24 of order 1 2 3 respectively 1 olished iv Diagonal matrix A square matrix B b mxm is said to be a diagonal matrix if all its non diagonal elements are zero that is a matrix B b xm is said to be a diagonal matrix if b 0 when i j y 1 1 0 0 C 0 20 0 03 b 0 when i j y 1 1 6 a nn he are diagonal matrices A diagonal matrix is said to be a scalar matrix if its diagonal elements are equal that is a square matrix B b nxn is said to be a scalar matrix

Algebra
Quadratic equations26 Represent the above information in the form of a 3 2 matrix What does the entry in the third row and second column represent 38 MATHEMATICS Solution The information is represented in the form of a 3 x 2 matrix as follows 30 25 A 25 31 27 26 The entry in the third row and second column represents the number of women workers in factory III Rationalised 2023 24 Example 2 If a matrix has 8 elements what are the possible orders it can have Solution We know that if a matrix is of order m n it has mn elements Thus to find all possible orders of a matrix with 8 elements we will find all ordered pairs numbers whose product is 8 Thus all possible ordered pairs are 1 8 8 1 4 2 2 4 Hence possible orders are 1 8 8 1 4 2 2 4 Now Example 3 Construct a 3 2 matrix whose elements are by aj Solution In general a 3 2 matrix is given by Therefore 21 11 i 3j i 1 a11 13 3 11 0 3 and j 1 2 912 1 3 2 a32 921 922 a31 a32 2 12 3 11 4 12 3 21 2 Hence the required matrix is given by A 21 2 H 0 52 2 3x2 2 1 11 3 3x2 noxto be ravishe 3 i 3jl

Algebra
Sequences & SeriesMalika has 17 00 in quarters dimes and nickels She has 10 more dimes than quarters If Malika has 130 coins in all how many of each type of coin does she have 2 WRITE THE SYSTEM OF EQUATIONS 1 d 11 3 q d n DECLARE YOUR VARIABLES SOLVE THE SYSTEM EQ 19 EQ 2 EQ 3 EXPLAIN YOUR PROCESS Which method did you use to solve the problem Explain your process

Algebra
Quadratic equationsDallas needs 4 liter of milk for a recipe and there is 10 of a liter of milk left in the carton How much is left after Dallas makes his recipe

Algebra
Quadratic equationsx 5 2 The general geometric series is a ar ar n Write out the first few terms of the geometric series n 0 series Then express the inequality r 1 in terms of x and find the values of x for which the inequality holds and the series converges ar arm to find a and r and find the sum of the 3 What is the first term of the given series

Algebra
Quadratic equationsIndicate whether the series converges or diverges If it converges find its sum k k k 1 106k Select the correct choice below and if necessary fill in the answer box within your choice OA The series diverges because it is a geometric series with r 1 O B The series converges because it is a geometric series with r 1 The sum of the series is Type an integer or a simplified fraction O C O D k k 106k The series diverges because lim 0 or fails to exist k k 106k The series converges because lim 0 The sum of the series is

Algebra
Quadratic equationsThen the sum of the two matrices A and B is defined as a matrix C c c a b for all possible values of i and j Example 6 Given A 1 3 she A B defined 1 5 1 1 1 5 and B KARN Since A B are of the same order 3 Therefore addition of A and B is defined and is given by 2 3 2 2 3 3 0 2 5 1 1 2 3 2 3 B Note 1 We emphasise that if A and B are not of the same order then A B is not xample if A 1 5 0 1 2 This can be represented in the matrix 6 10 Rationalised 2023 24 23 e 31 2 We may observe that addition of matrices is an example of binary operation on the set of matrices of the same order 3 4 2 Multiplication of a matrix by a scalar Now suppose that Fatima has doubled the production at a factory A in all categories refer to 3 4 1 Girls 60 65 85 where then A B is not defined Previously quantities in standard units produced by factory A were Boys 80 75 90 Revised quantities produced by factory A are as given below Boys Girls 1 2 80 2x 60 2 2x75 2 65 32x90 2x85 MATRICES 170 olshed 45 We observe that the new matrix is obtained by multiplying each element of the previous matrix by 2 In general we may define multiplication of a matrix by a scalar as follows if A a is a matrix and k is a scalar then kA is another matrix which is obtained by multiplying each element of A by the scalar k mx n

Algebra
Complex numbersDoes the sequence converge or diverge Give a reason for your answer 2 1 2 an Select the correct answer below and if necessary fill in the answer box to complete your choice O A an diverges because it is nondecreasing and it has no upper bound O B a converges because it is nondecreasing and has a least upper bound of Simplify your answer Type an exact answer using radicals as needed OC a converges because it is nonincreasing and has a greatest lower bound of Simplify your answer Type an exact answer using radicals as needed O D a diverges because it is nonincreasing and it has no lower bound OE a diverges because it has no upper bound and no lower bound OF a diverges because when n is odd the limit of the sequence is therefore the limit does not exist sequence is and when n is even the limit of the

Algebra
Permutations and CombinationsIn other words kA k a mxn k a mx n that is i j th element of kA is ka for all possible values of i and j For example if 46 notto MATHEMATICS For example let 1 5 7 2 Example 7 If A Solution We have 3A 3 5 Negative of a matrix The negative of a matrix is denoted by A We define A 1 A 1 2 3 2 31 0 5 3 1 1 5 7 3 2 0 5 2A B 2 1 5 3 21 2 och mot 3 1 A 1 A 1 5 X Difference of matrices If A a B b are two matrices of the same order say mxn then difference A B is defined as a matrix D d where d a b for all value of i and j In other words D A B A 1 B that is sum of the matrix A and the matrix B and B then Rationalised 2023 24 3 A 5 9 3 4 5 3 5 21 9 6 0 15 1 2 3 2 3 3 1 1 0 2 4 6 462 3 then A is given by 2 3 1 1 3 H 1 1 0 2 then find 2A B A B a b a b X 2 3 4 1 6 3 1 3 4 1 6 0 2 2 5 60 5 3 4 3 Properties of matrix addition tion The addition of matrices satisfy the following properties i Commutative Law If A a B b are matrices of the same order say mx n then A B B A Now blished b a addition of numbers is commutative b a B A ii Associative Law For any three matrices A a B b C c of the same order say mx n A B C A B C

Algebra
Quadratic equationsDetermine whether the series n 0 DIR OB The series diverges because lim n O C converges or diverges If it converges find its sum Select the correct choice below and if necessary fill in the answer box within your choice The series converges because it is a geometric series with r 1 The sum of the series is Type an exact answer O A The series converges because lim n T T 0 or fails to exist n 0 The sum of the series is Type an exact answer OD The series diverges because it is a geometric series with r 21

Algebra
Quadratic equationsExample 9 Find X and Y if X Y or Solution We have X Y X Y or Also or or 1 or 20 8 10 4 25 6 5 12 or or or i e X X Y Y X Y X Y 2 2x 3 10 4 14 1 2y 6 2 X 2x 3 7 N 2x 7 3 4 2 x 2 5 2 0 9 Y 5 GSH Y 3 0 5 2 8 3 9 88 8 113 52 3 0 9 2 6 X X X Y 5 3 2 1 0 188 210 Example 10 Find the values of x and y from the following equation and and 12 14 31 7 and X Y and and 7 6 15 14 2X 3 4 3 4 210 731 60 2 0 10 Rationalised 2023 24 6 9 6 9 Solution We have 5 4 7 6 2x 10 3 6 H 2 6 1 2 4 4 7 y 3 15 2y 6 2Y 15 6 1 0 2 5 6 14 y 2x 3 6 2y 4 15 2y 4 14 2y 18 4 y 9 18 2 31 7 3 3 14 3 T 41 10 what to shed 7 7 6 1 is 14 15 Why MATRICES 6 49 Example 11 Two farmers Ramkishan and Gurcharan Singh cultivates only three varieties of rice namely Basmati Permal and Naura The sale in Rupees of these varieties of rice by both the farmers in the month of September and October are given hu the follo A ond R

Algebra
Sequences & SeriesB IS 52 nk 3 then Cik For example if C The matrix C Ciklmxp is the product of A and B 2 7 1 MATHEMATICS and is given by CD Entry in first row first column Entry in first row second column 0 Entry in second row first column 1 1 0 3 Thus CD AB Example 12 Find AB 1 entry is the sum of the products across some row of C with the corresponding entries down some column of D These four computations are 2 1 4 13 2 17 13 1 2 34 3 1 34 1 0 3 4 a 22k 2 N 4 Rationalised 2023 24 2 and D 1 5 2 1 2 1 5 second column 03 43 lish Entry in second row a 3 D3k 1 5 4 7 1 5 4 2 2 3 1 100 12 63 36 81 0 72 4 21 12 27 0 24 This is a 2 x 2 matrix in which each 1 in 1 2 1 1 2 5 27 13 1 2 4 then the product CD is defined 13 1 7 1 1 260 3 and B 28 79 to be 6 2 9 7 6 6 9 9 6 0 9 8 2 2 3 7 2 6 3 9 2 0 3 8 Solution The matrix A has 2 columns which is equal to the number of rows of B Hence AB is defined Now 2 0 7 3 1 4 4 2 75 117 72 25 39 24

Algebra
Quadratic equationsRamkishan Gurcharan Singh Thus in October Ramkishan receives 100 200 and 120 as profit in the sale of each variety of rice respectively and Grucharan Singh receives profit of 400 200 and 200 in the sale of each variety of rice respectively 5 8 10 11 100 400 3 4 5 Multiplication of matrices Suppose Meera and Nadeem are two friends Meera wants to buy 2 pens and 5 story books while Nadeem needs 8 pens and 10 story books They both go to a shop to enquire about the rates which are quoted as follows Pen 5 each story book 50 each How much money does each need to spend Clearly Meera needs 5 2 50 5 that is 260 while Nadeem needs 8 x 5 50 10 that is 540 In terms of matrix representation we can write the above information as follows Requirements Prices per piece in Rupees Money needed in Rupees 260 5 50x50 340 50 200 200 2 5 8 10 2 5 8 10 120 200 Suppose that they enquire about the rates from another shop quoted as follows pen 4 each story book 40 each de f Now the money required by Meera and Nadeem to make purchases will be respectively 4 2 40 5 208 and 8 4 10 40 432 Rationalised 2023 24 4 40 5x2 5x50 8x5 10x50 5 4 50 40 Again the above information can be represented as follows Requirements Prices per piece in Rupees Money needed in Rupees MATRICES 51 Now the information in both the cases can be combined and expressed in terms of matrices as follows Requirements Prices per piece in Rupees Money needed in Rupees 208 8 4 10 40 432 260 208 5x2 5x50 4x2 40 5 8x5 10x50 8 4 10 40 The above is an example of multiplication of matrices We observe that for multiplication of two matrices A and B the number of columns in A should be equal to the number of rows in B Furthermore for getting the elements of the product matrix we take rows of A and columns of B multiply them element wise and take the sum Formally we define multiplication of matrices as follows HOUT The product of two matrices A and B is defined if the number of columns of A is equal to the number of rows of B Let A a be an m n matrix and B b be an nxp matrix Then the product of the matrices A and B is the matrix C of order m p To get the i k th element c of the matrix C we take the ith row of A and kth column of B multiply them elementwise and take the sum of all these products In other words if A almx B bl xp then the ith row of A is a a a and the kth column of

Algebra
Quadratic equationsYour business requests a 3 month loan for 500 000 What will be the interest paid at the end of the term if the business risk percentage is assessed at 2 0 and LIBOR is at 1 8 interest paid

Algebra
Quadratic equationsO Macmillan Learning Graph the rational function R x follow R x x 3x x3 3x2 9 y 8 7 6 5 4 3 18x 40 18x 40 using the graphing utility Use the graph to answer the questions that PAR 201

Algebra
Quadratic equationsIdentify the graph of a rational function consistent with the given information There is more than one correct answer Vertical asymptotes x 4 and x 4 and no horizontal asymptote 4 3 y 6 3 0 3 6 9 0 4 8 3 4 6 8 9 12 8 4 Y 12 0 12 8 0 4 4 8 8 12 x x