Algebra Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
Algebra
Quadratic equations3 Consider the IVP y t 1 y t 3 1 1 1 t 6 a Write out the iterative relation difference equation of Euler s method for this IVP with a ste size h b Using h0 5 to 1 and wo to y t 2 1 use two steps of Euler s method to compute an approximatio

Algebra
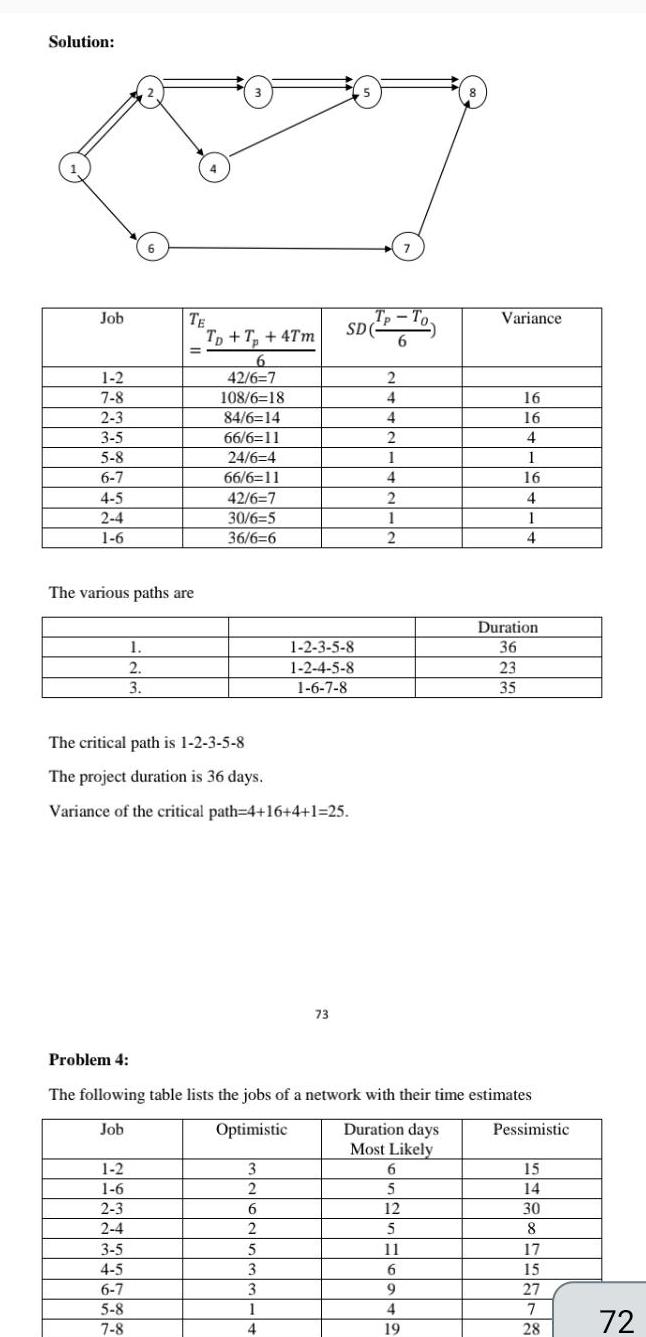
Quadratic equationsproblem has no solution using graphical method 2 If the maximum value of z appears only at o then the problem has unbounded solution 3 If the maximum value of z appears at 2 points there exists infinite number of solutions to the LPP Problem 4 Find the maximum value of z to the following LPP using graphical method Max z 5x 7x2 subject to x x2 4 3x1 8x2 24 10x 7x 35 and x 0 Vi 1 2 Solution The given problem contains only two variables x and x So graphical method is possible Consider the equations we get X X 4 3x 8x 24 Now to find the points Consider x x 4 Put x 0 x 4 10x 7x 35 and x 0 x 4 Therefore 0 4 and 4 0 are the pts Similarly consider 3x 8x 24 We get 0 3 and 8 0 are the pts Consider 10x 7x 35 We get 0 5 and 3 5 0 are the pts The graphical representation is

Algebra
Quadratic equationsA shop has 4 workers and 4 works to be performed The estimate of time man hours each man will take to perform each project is given in the following table How should the works to be allotted so as to optimise the total work 1 2 3 4 1 2 3 1 4 19 2 3 4 Solution Step 1 Given matrix is 1 1 8 2 13 3 4 38 19 8 13 38 19 26 0 9 23 28 4 26 9 26 24 10 Step 2 Here the given matrix is a square matrix Hence the assignment problem is a balanced problem Subtracting minimum cost of each row of the cost matrix we obtain the following matrix 17 2 3 4 11 26 17 11 18 15 28 4 26 1 2 3 4 19 18 15 26 24 10 18 24 4 16 9 3 0 22 3 0 28 14 0 Step 3 Subtracting minimum cost of each column of the modified cost matrix we obtain the following matrix 12 3 4

Algebra
Matrices & DeterminantsLinear Linear programming can be used in a variety of situations In most of the business or economical situation resources will be limited The problem there will be to make use of the available resources in such a way that to maximise the production or to minimize the expenditure These datas can be formulated as linear programming models The objective of the linear programming problem is to maximize the profit and minimize the total cost inng Froblem The LPP is to determine the values of the decision variables such that all the constraints are satisfied and gives the maximum or minimum value for the objective function The maximum or minimum value of the objective function is called an Optimum value Formulation of LPP resources The formulation of any situation to a LPP is based on the following guidelines 1 Identification of decision variables 2 Formation of objective function which is to be either maximize or minimize 3 The various constraints involved due to the limited availability of Mathematical Formulation of LPP The general form of LPP is as follows Max or Min z C x C X Cnxn Subject to a 1x A 2X2 nxn b a21x1 a22x2 a2nxn b am1x1 am 2x2 amn n bm x 0 V

Algebra
Permutations and CombinationsIntroduction A inventory may be defined as an idle resources that possesses economic value It is an item stored or reserved for meeting future demand Such items may be materials machines many or even human resources Reasons for holding storks The main reasons are 1 To ensure sufficient goods one are available to meet anticipated demands 2 To absorb variations in demand and production 3 To prove a buffer between production processor 4 To take advantage of bulk purchasing discounts 5 To meet possible shortages in the future 6 To enable produces process to flow smoothly and efficiently 7 As deliberate investment policy particularly in times of inflation or possible shortages The Objective of Inventory Control The objective of inventory control is to maintain stock levels so that the combined costs mentioned earlier are at amenities This is done by establishing two sectors how to order When to order Inventory control terminologies 1 Demand The amount of quantity required by sales or products usually expressed as the rate of demand for week or month or year etc 2 Economic order quantity EOQ This is a calculated ordering quantity which minimized the balance between inventory holding costs and re order costs 3 Lead time The period of time between ordering and replenishment 4 Butter stock or safety stock It is a stock allowance to cover errors in forecasting the lead time on the demand during the lead time 54 5 Maximum stock A stock level as the maximum desirable which is used as an indicator 6 Reorder level The level of stock of which culture replacement order should be placed The re order level 9 independent upon the lead time and the demand upon the lead time and the demand during the lead time Types of Inventory Models There are two types of models can be used for inventory control They are i deterministic model ii stochastic model

Algebra
Permutations and CombinationsP t AP t 2P 1 t n 0 Po t AP t n 0 Po t At Po t lim At At 0 1 0 1 Multiplying both sides of A by z and taking summation for n 1 2 00 we get En0 Pn t z En 1 Pn t z En 1 Pn 1 t 2 Log P z t M z 1 t E To determine E we put t 0 to get Log P z 0 E P z 0 02 P 0 P z t ed 2 1 Now Pn t can be defined as P z t P t dp z t 0 P z t at e at n P z t P 1 2 n 0 P z t P z t AP t In general P t Classification of queueing models I Probabilistic queueing models 00 P t zn R 0 46 z 1 Model I Erlang Model This model is symbolically represented by MIMI co FCFS this denotes poisson arrival exponential inter arrival poisson departure exponential service time single server infinite capacity and first come first served service discipline Model II General Erlang Model Although this model is also represented by MIMI 00 FCFS but this is a general queueing model in which the rate of arrival and service depend on the length n of the line Model III this model represented by MIMI NFCFS In this model capacity of the system is limited finite say n Obviously the number of arrivals will not exceed the number N in any case Model IV This model is represented by MMS 0o FCFS in which the number of stations is s in parallel 46
Algebra
Permutations and CombinationsSolution Job 1 2 7 8 2 3 3 5 5 8 6 7 4 5 2 4 1 6 6 The various paths are 1 2 3 1 2 1 6 2 3 TE 2 4 3 5 4 5 6 7 5 8 7 8 Tp T 4Tm 6 42 6 7 108 6 18 84 6 14 66 6 11 24 6 4 66 6 11 42 6 7 30 6 5 36 6 6 The critical path is 1 2 3 5 8 The project duration is 36 days Variance of the critical path 4 16 4 1 25 3 2 6 2 5 3 3 SD TP 1 2 3 5 8 1 2 4 5 8 1 6 7 8 1 4 73 2 4 4 2 1 4 2 1 2 Problem 4 The following table lists the jobs of a network with their time estimates Job Optimistic Duration days Most Likely 7 6 6 5 12 5 11 6 9 4 19 Variance 16 16 4 1 16 4 1 4 Duration 36 23 35 Pessimistic 15 14 30 8 17 15 27 7 28 72

Algebra
Matrices & DeterminantsSuppose there are n jobs J1J2Jn which are to be processed in two machines say M and M in order M M M first and M next Let tij be the processing time for ith job in jih machine The list of jobs along with their processing times can be summarized as in the following table Jobs Processing time in M Processing time in M J t11 t21 J t12 above t22 Let x2j be the time for which the machine M remains idle after completing the j 1 th job and before starting jth job A job is assigned to machine My first and after it has been completely processed in machine M it is assigned to the machine M If the machine M is not free at any moment for processing a particular job then that job has to wait in a waiting line for its turn on the machine M In other words passing is not allowed Hence machine My will always be busy and will process the n jobs one by one After processing all the n jobs the machine My remains idle until all the n jobs are completed in the machine M However M may remain idle after the completion of some of the m jobs and before starting the next job The sequencing problem is to minimize the total idle time of the second machine M Jn tin 32 tzn Hence the total idle time for machine M is E 1X2j Thus the sequencing problem is to minimize E1 X2 The total elapsed time T is given by T Processing time idle time i e T Ej 1t2j j 1 X2j Here some of the x2 may be zeros We observe that E 1 t2 is constant Hence minimizing T is equivalent to minimizing j1 X2j Algorithm to find the optimum sequence for n jobs in 2 machines Step 1 List the jobs along with their processing times in a table as given Step 2 Find the minimum tij t2j for all j 1 2 n Step 3 If the smallest processing time is for the first machine M then place the corresponding job in the first available position in the sequence If it is for the second machine M then place the corresponding job in the last available position in the sequence Step 4 If there is a tie in the minimum of all the processing times then there arises three cases Case i Minimum among all processing times is same for the two machines i e minimum t j t2j t t2s then place the rth job in the first available position in the sequence and the sth job in the last available position in the sequence Case ii If the tie is for the minimum among the processing times tij on machine M only then place the jobs arbitrarily one after the other in the last available positions in the sequence Case iii If the tie is for the minimum among the processing times t2j on machine M only then place the jobs arbitrarily one after the other in the last available positions in the sequence Stan 5 Remove the assigned jobs from the table If the table becomes

Algebra
Complex numbersP t AP t 2P 1 t n 0 Po t AP t n 0 P z 0 02 P 0 lim At 0 1 0 1 Po t At Po t At P z t ed 2 1 Now Pn t can be defined as P t d z n dz t 0 Log P z t z 1 t E To determine E we put t 0 to get Log P z 0 E at e at n Multiplying both sides of A by z and taking summation for n 1 2 00 we get 0 Pr t 2 n 1 Pn t 2 1 Pn 1 t 2 P z t P t z P z t P z t 00 P z t P t z n 0 In general P t Classification of queueing models I Probabilistic queueing models 00 P t n 0 46 z 1 Model I Erlang Model This model is symbolically represented by MIMI o FCFS this denotes poisson arrival exponential inter arrival poisson departure exponential service time single server infinite capacity and first come first served service discipline Model II General Erlang Model Although this model is also represented by MIMI 00 FCFS but this is a general queueing model in which the rate of arrival and service depend on the length n of the line Model III this model represented by MIMI NIFCFS In this model capacity of the system is limited finite say n Obviously the number of arrivals will not exceed the number N in any case Model IV This model is represented by MIMIS 0o FCFS in which the number of stations is s in parallel Model V This model is represented by MEI 0o FCFS that is poisson arrivals Erlangian service time for k phases and a single server 46

Algebra
Complex numbersservice rate per busy service is u Therefore over all service rate when there are n units in the system may be obtained in the following two situations i And If n s all the customers may be served simulataneously There will be no queue s n number of servers may remain idle and then Hn nu n 0 1 2 s ii If n s all the servers are busy maximum number of customers waiting in queue will be n s then nu MODEL IV B MMS NIFCFS In model IV A if the maximum number in the system is limited to N then as in model III sp P 0 2n P su Where Po may be written as sp n s 1 p sp sp n s Virtually the same relationships hold between P and Po as in model IV A with infinite capacity Therefore Po 51 s 1 for 0 n N forn N sp Pon for o n s S pr Po s 0 for n N n 1 nu for 0 n s for s n N for s n N SP sp s s s 1 sp n n n s 1 p s 1 1 1 p N s 1 p 1 This queueing modrl with limited waiting room is valuable because of its relevance to many real situations and the fact that changes may be made to its properties by adjusting the number of servers or the capacity of the waiting room However while poission arrivals are common in practice negative exponential service times are less so and it is the second assumption in the system MIMs that limits its usefulness Example
Algebra
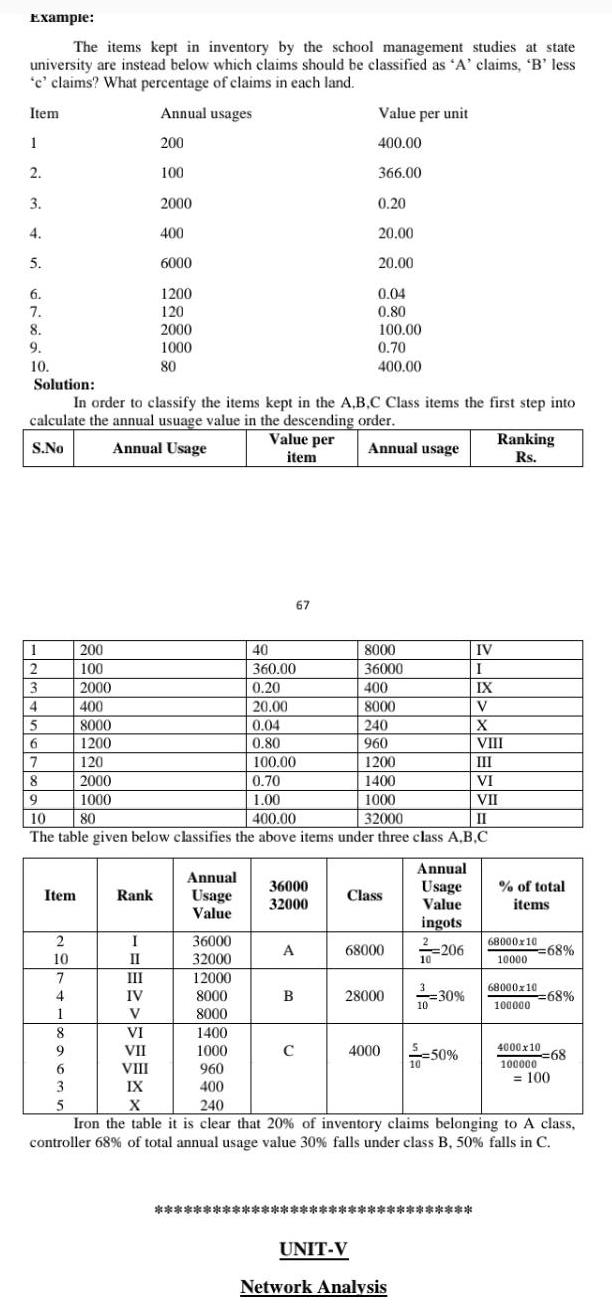
Matrices & DeterminantsExample The items kept in inventory by the school management studies at state university are instead below which claims should be classified as A claims B less c claims What percentage of claims in each land Item Annual usages 1 200 2 3 4 5 6 7 8 9 10 Item 2 10 7 4 1 8 9 200 100 2000 400 8000 1200 120 2000 1000 6 3 5 Solution In order to classify the items kept in the A B C Class items the first step into calculate the annual usuage value in the descending order Value per item Annual Usage S No Annual usage Rank 100 I II 2000 400 6000 1200 120 2000 1000 80 III IV V 1 40 2 360 00 3 0 20 400 4 20 00 8000 5 0 04 240 6 0 80 960 7 100 00 1200 8 0 70 1400 9 1 00 1000 10 80 400 00 32000 The table given below classifies the above items under three class A B C Annual Usage Value 36000 32000 12000 8000 8000 1400 1000 960 400 36000 32000 A 67 B Value per unit 400 00 C 366 00 0 20 20 00 20 00 0 04 0 80 100 00 0 70 400 00 8000 36000 Class UNIT V 68000 28000 Annual Usage Value ingots 206 10 3 10 Network Analysis 30 4000 50 10 IV VI VII VIII IX X 240 Iron the table it is clear that 20 of inventory claims belonging to A class controller 68 of total annual usage value 30 falls under class B 50 falls in C Ranking Rs I IX V X VIII III VI VII II of total items 68000x10 10000 68000x10 100000 68 68 4000x10 10000068 100

Algebra
Matrices & DeterminantsThe various paths are 1 2 3 Job 1 2 The critical path is 1 2 3 5 8 and 1 6 7 8 The project duration is 36 days Variance of the critical path 4 16 16 36 Exercises 1 A project consists of 12 jobs Draw a project network and determine the critical path 2 3 2 4 3 4 3 5 4 6 5 8 Activity 1 2 1 3 3 5 3 4 4 6 5 6 6 7 6 8 7 8 8 9 Duration 2 7 3 3 5 3 5 1 2 4 5 8 1 2 3 5 8 1 6 7 8 2 Consider the following project whose activities along with PERT time estimates the optimistic time a most likely time m and the pessimistic time b are given as follows a days 12 7 4 36 12 6 9 6 4 8 Job 6 7 75 6 10 7 9 8 9 9 10 m days 14 10 6 Duration 23 36 36 40 15 8 12 10 5 10 Duration 8 4 4 1 7 b days 21 16 10 60 24 12 18 15 7 14

Algebra
Complex numbersGive a property of real numbers associative commutative addition or multiplication that justifies each step in the following equation 3x 1 2x 7 x 22 1 3x 2x 1 7 x 22 2 x 3 2 6 x 22 Sr 6 x 22 3 5x 6 6 x 22 6 Sr x 28 4 5r r r 28 r Solve the following equations for x show all steps 1 3 x 2 x 4 6 x 2 2 5 7 6 3 15 4 3 4 5 25 4 Part II Properties of Real Numbers Use the indicated properties of real numbers to complete the blanks of the following statements 73 1 50 43 Commutative property of Addition Associative property of Addition Additive Identity 2 1 6 7 8 5 7 11 14 16 4 fation 2x 1 5 X 3 Bu fat pitatiand w Multiplicative Inverse Commutative property of Multiplication Associative property of Multiplication Distributive property

Algebra
Sequences & Series2 c Clearly by a and b above f is neither increasing nor decreasing in 0 2 Example 10 Find the intervals in which the function f given by f x x 4x 6 is a increasing b decreasing Solution We have or f x x 4x 6 f x 2x 4 156 Therefore f x 0 gives x 2 Now the point x 2 divides the real line into two disjoint intervals namely 2 and 2 Fig 6 3 In t 4 0 interval 2 f x 2x Therefore f is decreasing in this interval Also in the interval 2 f x 0 and so the function f is increasing in this interval Solution We have Example 11 Find the intervals in which the function fgiven by f x 4x 6x 72x 30 is a increasing b decreasing f x 4x 6x 72x 30 12x 12x 72 12 x x 6 12 x 3 x 2 Therefore f x 0 gives x 2 3 The points x 2 and x 3 ides the real line into three disjoint intervals namely 2 2 3 and 3 00 or 80 MATHEMATICS Interval 2 2 3 3 00 8 Rationalised 2023 24 Sign of f x 0 0 0 pun you Fig 6 4 3 In the intervals 2 and 3 f x is positive while in the interval 2 3 f x is negative Consequently the function is increasing in the intervals 2 and 3 0 while the function is decreasing in the interval 2 3 However fis neither increasing nor decreasing in R Example 12 Find intervals in which the function given by f x a increasing b decreasing Nature of function f fis increasing fis decreasing fis increasing o Sin 3x xe 0 1 is
Algebra
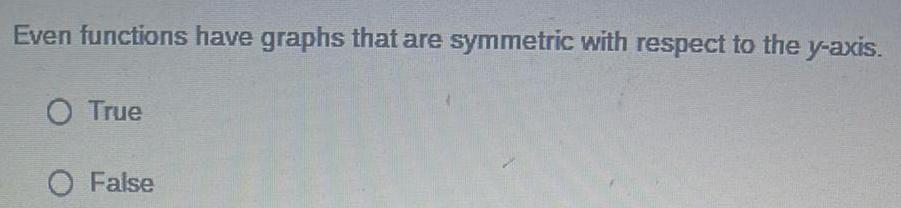
Quadratic equationsEven functions have graphs that are symmetric with respect to the y axis O True O False

Algebra
Matrices & Determinants10 Prove that the logarithmic function is increasing on 0 11 Prove that the function fgiven by f x x x 1 is neither strictly increasing nor decreasing on 1 1 TU 12 Which of the following functions are decreasing on 0 2 A cos x B cos 2x C cos 3x D tan x 13 On which of the following intervals is the function fgiven by f x x 00 sin x 1 decreasing A 0 1 D None of these 14 For what values of a the function f given by f x x ax 1 ncreasing on 1 2 15 Let I be any interval disjoint from 1 1 Prove that the function f given by 1 f x x is increasing on I X 16 Prove that the function fgiven by f x log TC TU B TC C 0 2 2 decreasing on 160 increasing on TC T TU 2 37 3 2 a Ge MATHEMATICS 17 Prove that the function fgiven by f x log cos x is decreasing on 0 0 7 ar is increasing on thenERPo 0 1 18 Prove that the function given by f x x 3x 3x 100 is increasing in R 19 The interval in which y x e is increasing is A B 2 0 C 2 Rationalised 2023 24 and D 0 2 6 4 Maxima and Minima In this section we will use the concept of derivatives to calculate the maximum or minimum values of various functions In fact we will find the turning points of the graph of a function and thus find points at which the graph reaches its highest or and lowest locally The knowledge of such points is very useful in sketching the graph of a given function Further we will also find the absolute maximum and absolute minimum of a function that are necessary for the solution of many applied problems Let us consider the following problems that arise in day to day life 1 The profit from a grove of orange trees is given by P x ax bx where a b are constants and x is the number of orange trees per acre How many trees per acre will maximise the profit ii A ball thrown into the air from a building 60 metres high travels along a path

Algebra
Permutations and Combinations154 MATHEMATICS Proof a Let x x a b be such that x x Then by Mean Value Theorem Theorem 8 in Chapter 5 there exists a point c between and X x such that i e i e Thus we have Rationalised 2023 24 f x f x f c x x f x f x 0 f x f x X x Hence f is an increasing function in a b f x f x for all x x a b is increasing on R Solution Note that The proofs of part b and c are similar It is left as an exercise to the Remarks There is a more generalised theorem which states that if f x for x in an interval excluding the end points and fis continuous in the interval then fis increasing Similarly if f x 0 for x in an interval excluding the end points and fis continuous in the interval then fis decreasing Example 8 Show that the function f given by f x 3x 6x 4 as f c 0 given 3 x 2x 1 1 t to be po hod 3 x 1 1 0 in every interval of R Therefore the function fis increasing on R Example 9 Prove that the function given by f x cos x is a decreasing in 0 b increasing in 1 2 and c neither increasing nor decreasing in 0 2

Algebra
Complex numbers158 or f is decreasing in MATHEMATICS Interval T T 5T 4 4 5 4 2 a increasing in 0 0 7 Sign of f x T 5T 4 4 Rationalised 2023 24 c 2x 9x 12x 1 e x 1 x 3 7 Show that y log 1 x 0 0 0 EXERCISE 6 2 1 Show that the function given by f x 3x 17 is increasing on 2 Show that the function given by f x e x is increasing on R 3 Show that the function given by f x Nature of function f is increasing 6 7 9m f is decreasing f is increasing sin x is c neither increasing nor decreasing in 0 4 Find the intervals in which the function f given by f x 2x 3x is a increasing b decreasing 5 Find the intervals in which the function f given by f x 2x 3x 36x 7 a increasing b decreasing 6 Find the intervals in which the following functions are strictly increasing decreasing a x 2x 5 b decreasing b 10 6x 2x d 6 9x x 2x x 1 is an increasing function of 2 x throughout its domain 8 Find the values of x for which y x x 2 is an increasing function 4 sin 0 9 Prove that y A is an increasing function of in

Algebra
Complex numbersf x 3cos 3x Therefore f x 0 gives cos 3x 0 which or 3 0 17 2 into two disjoint intervals 0 implies 3x 0 Now f x 0 all xe T T fis increasing on or as x 2 Solution We have So x Therefore fis increasing in 0 0 is increasing or decreasing namely The points x BI6 Note that TC TU 4 TU 2 TC and x Ra R6 5T 3x TU Also the given function is continuous at x 0 and x 6 T The point x 6 B N 3 2 and decreasing on Rationalised 2023 24 and decreasing in T as 0 x 0 3x 6 Example 13 Find the intervals in which the function f given by f x sin x cos x 0 x 2 Now f x 0 gives sin x cos x which gives that 0 7 7 5 and ST 27 4 4 4 gives TU TU 6 2 f x sin x cos x f x cos x sin x TC x 0 if x 0 ST 3x 0 2 3 0 T 4 2 2 divides the interval 0 APPLICATION OF DERIVATIVES T T 6 2 as x 0 B 6 Fig 6 5 0 3x and f x 0 for 2 4 0 7 E2 ROBN TC T 5T 4 Fig 6 6 Therefore by Theorem 1 157 as 0 x 2 27 into three disjoint intervals e rejushed 2
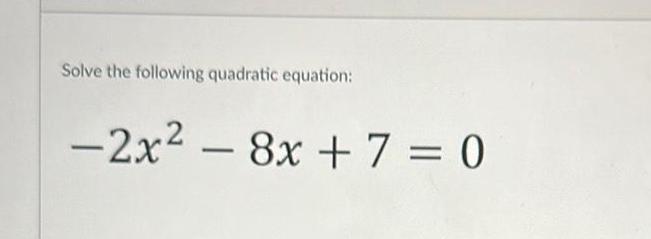

Algebra
Sequences & Seriesprovided this limit exists Derivative of fat c is denoted by f c or dx function defined by wherever the limit exists is defined to be the derivative off The derivative of fis d dy dx dx denoted by f x or f x or if y f x by or y The process of finding derivative of a function is called differentiation We also use the phrase differentiate f x with respect to x to mean find f x The following rules were established as a part of algebra of deriva 1 ut v u v 2 uv u v uv Leibnitz or product rule 3 U lim h 0 120 u v uv its answer If lim h 0 wherever v 0 Quotient rule The following table gives a list of derivatives of rtain standard functions Table 5 3 f x f x tan x sin x sec x Whenever we defined derivative we had put a caution provided the limit exists Now the natural question is what if it doesn t The question is quite pertinent and so is f c h f c h does not exist we say that fis not differentiable at c In other words we say that a function fis differentiable at a point c in its domain if both f c h f c f c h f c h are finite and equal A function is said h to be differentiable in an interval a b if it is differentiable at every point of a b As in case of continuity at the end points a and b we take the right hand limit and left hand limit which are nothing but left hand derivative and right hand derivative of the function at a and b respectively Similarly a function is said to be differentiable in an interval a b if it is differentiable at every point of a b f x lim h 0 MATHEMATICS Therefore But for x c we have nx 1 and lim h 0 f x h f x h lim X C sin x Rationalised 2023 24 COS X f x f c Theorem 3 If a function f is differentiable at a point c then it is also continuous at that point Proof Since fis differentiable at c we have f x f c X C blish lim f x f c lim X C X C COS X f x f c X C f c 5 co J x c The x c f x f c X C 7 x c ed

Algebra
Permutations and CombinationsIs the function f defined by 2x 3 if x 2 2x 3 if x 2 6 f x x 8 f x x 0 continuous at x 0 At x 1 At x 2 Find all points of discontinuity off where fis defined 10 f x if x 0 if x 0 x 1 if x 1 x 1 if x 1 udenly she x 0 1 if x 1 12 f x if x 1 13 Is the function defined by a continuous function f x User f x x if x 1 2 if x 1 16 f x 2x if 1 x 1 2 if x 1 5 if x 1 x 3 if x 3 f x 2x if 3 x 3 6x 2 if x 3 11 f x 9 f x x x 5 if x 1 x 5 if x 1 Rationalised 2023 24 x if x 0 1 1 if x 0 x 3 if x 2 x 1 if x 2 CONTINUITY AND DIFFERENTIABILITY Discuss the continuity of the function f where f is defined by 3 if 0 x 1 14 f x 4 if 1 x 3 5 if 3 x 10 2x if x 0 15 f x 0 if 0 x 1 4x if x 1 is continuous at x 3 18 For what value of 2 is the function defined by 17 Find the relationship between a and b so that the function f defined by ax 1 if x 3 f x bx 3 if x 3 2 x 2x if x 0 4x 1 117 olished f x continuous at x 0 What about continuity at x 1 19 Show that the function defined by g x x x is discontinuous at all integral points Here x denotes the greatest integer less than or equal to x 20 Is the function defined by f x x sin x 5 continuous at x

Algebra
Permutations and Combinations4 9 is continuous at x c provided g c 0 Proof We are investigating continuity of f g at x c Clearly it is defined at x c We have 114 lim f g x lim f x g x X C MATHEMATICS Hence f g is continuous at x c Proofs for the remaining parts are similar and left as an exercise to the reader lim f x lim g x X C X C function defined by f c g c f g c Rationalised 2023 24 Remarks 1 As a special case of 3 above if f is a constant function i e f x 2 for some real number then the function 2 g defined by g x g x is also continuous In particular if 1 the continuity of fimplies continuity of f ii As a special case of 4 above if f is the constant function f x 2 then the 2 g you by definition of f g by the theorem on limits as fand g are continuous by definition of f g 2 2 x is also continuous wherever g x 0 In g x g particular the continuity of g implies continuity of g The above theorem can be exploited to generate many continuous functions They also aid in deciding if certain functions are continuous or not The following examples illustrate this Example 16 Prove that every rational function is continuous Solution Recall that every rational function fis given by Bird q x 0 P x f x 9 x where p and q are polynomial functions The domain off is all real numbers except points at which q is zero Since polynomial functions are continuous Example 14 fis continuous by 4 of Theorem 1 Example 17 Discuss the continuity of sine function Solution to see this we use the following facts lim sin x 0 X 0 We have not proved it but is intuitively clear from the graph of sin x near 0 Now observe that f x sin x is defined for every real number Let c be a real xc we know that h 0 Therefore number Put x c h lim f x lim sin x X C X C lim sin c h h 0 blishe lim sin ccos h cosc sin h h 0 lim sinc cos h lim cos c sin h

Algebra
Quadratic equationsDescribe how to transform x5 into an expression with a rational exponent Make sure you respond with complete sentences CCC CO
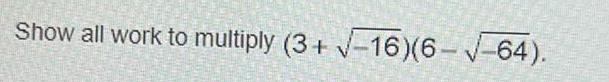

Algebra
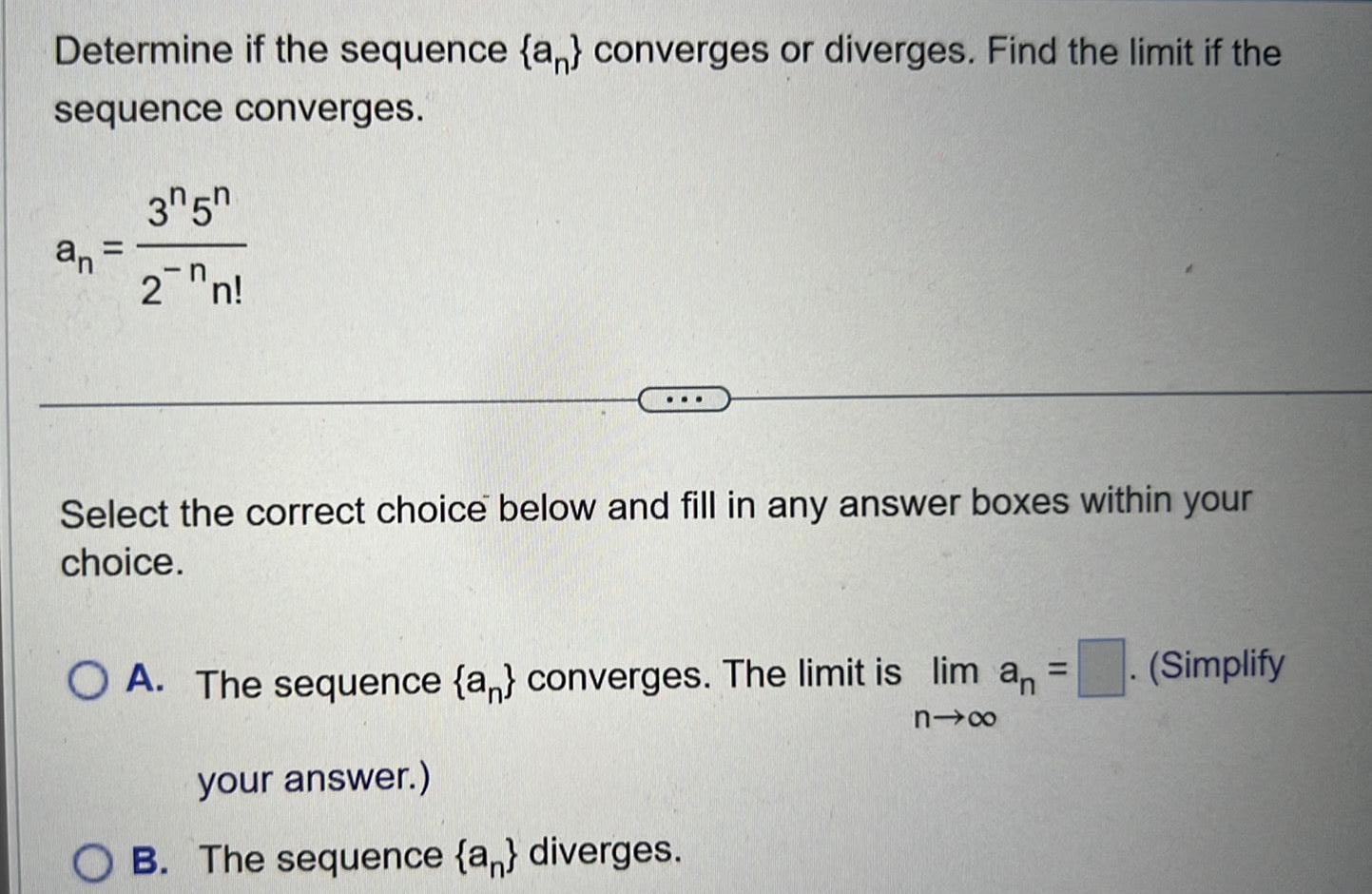
Quadratic equationsSolve the equation x 6 2 6 for the variable Show each step of your solution process
Algebra
Quadratic equationsDetermine if the sequence an converges or diverges Find the limit if the sequence converges 35 an 2n Select the correct choice below and fill in any answer boxes within your choice OA The sequence a converges The limit is lim a n your answer OB The sequence a diverges Simplify

Algebra
Matrices & DeterminantsX C Now let c be a real number such that c 0 Then f c c Also lim f x lim x c X C X C Since lim f x f c f is continuous is continuous at all points Example 8 Discuss the continuity of the function f given by f x x x 1 Solution Clearly fis defined at every real number c and its value at c is c c 1 We also know that fis a continuous function Thus lim f x f c and hence fis continuous at every real number This means X C Solution Fix any non zero real number c we have 1 1 Example 9 Discuss the continuity of the function f defined by f x x 0 X lim x x 1 c c 1 X C explanatory lim f x lim X C X f x X C X 1 Also since for c 0 f c we have lim f x f c and hence fis continuous X C at every point in the domain off Thus fis a continuous function 1 1 3 333 Rationalised 2023 24 0 3 0 2 5 We take this opportunity to explain the concept of infinity This we do by analysing 1 X the function f x near x 0 To carry out this analysis we follow the usual trick of finding the value of the function at real numbers close to 0 Essentially we are trying to find the right hand limit of fat 0 We tabulate this in the following Table 5 1 Table 5 1 0 3 0 2 0 1 10 0 01 10 5 10 100 10 0 001 10 10 f x 13 333 1000 10 10 We observe that as x gets closer to 0 from the right the value of f x shoots up higher This may be rephrased as the value of f x may be made larger than any given number by choosing a positive real number very close to 0 In symbols 1 lim f x x 0 to be read as the right hand limit of f x at 0 is plus infinity We wish to emphasise that is NOT a real number and hence the right hand limit of fat 0 does not exist as a real number Similarly the left hand limit of f The following table is self hed C real numbers Hence f CONTINUITY AND DIFFERENTIABILITY 109 Table 5 2 0 may be fou 10 10 10 10 3 10 10 2 10

Algebra
Quadratic equationspoint For the function f x f x h f x h f w f x W X h 0 14x 7h 9 7 x2 simplify each expression as much as possible x w

Algebra
Complex numbers1 Write out the first 4 terms of the series show that diverges n 2 1 to show how the series starts Then find the sum of the series or 4

Algebra
Matrices & Determinantsfunction defined by wherever the limit exists is defined to be the derivative off The derivative of fis d dy denoted by f x or f x or if y f x by or y The process of finding dx dx derivative of a function is called differentiation We also use the phrase differentiate f x with respect to x to mean find f x 3 The following rules were established as a part of algebra of deriva 1 ut v u v 2 uv u v uv Leibnitz or product rule lim h 0 120 u v uv wherever v 0 Quotient rule The following table gives a list of derivatives of rtain standard functions Table 5 3 its answer If lim h 0 f x 2 I f x f c h f c h f x lim h 0 Therefore MATHEMATICS sec x Whenever we defined derivative we had put a caution provided the limit exists Now the natural question is what if it doesn t The question is quite pertinent and so is f c h f c does not exist we say that f is not differentiable at c h In other words we say that a function f is differentiable at a point c in its domain if both are finite and equal A function is said to be differentiable in an interval a b if it is differentiable at every point of a b As in case of continuity at the end points a and b we take the right hand limit and left hand limit which are nothing but left hand derivative and right hand derivative of the function at a and b respectively Similarly a function is said to be differentiable in an interval a b if it is differentiable at every point of a b f x h f x h and lim h 0 But for x c we have sin x f c h f c h lim X C COS X Rationalised 2023 24 f x f c lim f x f c X C f x f c X C Theorem 3 If a function f is differentiable at a point c then it is also continuous at that point Proof Since f is differentiable at c we have blish C COS X lim X C sin x f x f c X C f c 560 3 x c f x f c X C tan x x c COT ed

Algebra
Matrices & DeterminantsExample 18 Prove that the function defined by f x tan x is a continuous function Solution The function f x tan x sin x COS X TU that cos x 0 i e x 2n 1 2 We have just proved that both sine and cosine functions are continuous Thus tan x being a quotient of two continuous functions is continuous wherever it is defined This is defined for all real numbers such An interesting fact is the behaviour of continuous functions with respect to composition of functions Recall that if fand g are two real functions then fog x f g x is defined whenever the range of g is a subset of domain off The following theorem stated without proof captures the continuity of composite functions Theorem 2 Suppose fand g are real valued functions such that fog is defined at c If g is continuous at c and if fis continuous at g c then fog is continuous at c The following examples illustrate this theorem Example 19 Show that the function defined by f x sin x is a continuous function Solution Observe that the function is defined for every real number The function f may be thought of as a composition g o h of the two functions g and h where g x sin x and h x x Since both g and h are continuous functions by Theorem 2 it can be deduced that fis a continuous function Example 20 Show that the function f defined by f x 11 x x where x is any real number is a continuous function Solution Define 116 MATHEMATICS h 1 x x 1 x x f x In Example 7 we have seen that h is a continuous function Hence g being a sum of a polynomial function and the modulus function is continuous But then f being a composite of two continuous functions is continuous g x 1 x x and h by h x x for all real x Then hog x h g x Rationalised 2023 24 EXERCISE 5 1 1 Prove that the function f x 5x 3 is continuous at x 0 at x 3 and at x 5 2 Examine the continuity of the function f x 2x 1 at x 3 3 Examine the following functions for continuity a f x x 5 b f x 1 x 5 x 5

Algebra
Permutations and Combinations4 is continuous at x c provided g c 0 8 Proof We are investigating continuity of f g at x c Clearly it is defined at x c We have 114 im f g x lim f x g x X C MATHEMATICS Hence f g is continuous at x c Proofs for the remaining parts are similar and left as an exercise to the reader function defined by lim f x limg x X C X C f c g c f g c Rationalised 2023 24 Remarks i As a special case of 3 above iffis a constant function i e f x 2 for some real number 2 then the function 2 g defined by 2 g x 2 g x is also continuous In particular if 1 the continuity of fimplies continuity of f ii As a special case of 4 above if f is the constant function f x 2 then the x is also continuous wherever g x 0 In g x a 2 2 g 8 not 1 particular the continuity of g implies continuity of g The above theorem can be exploited to generate many continuous functions They also aid in deciding if certain functions are continuous or not The following examples illustrate this by definition of f g by the theorem on limits as fand g are continuous by definition of f g Example 16 Prove that every rational function is continuous Solution Recall that every rational function fis given by q x 0 f x P x 9 x where p and q are polynomial functions The domain offis all real numbers except points at which q is zero Since polynomial functions are continuous Example 14 fis continuous by 4 of Theorem 1 Example 17 Discuss the continuity of sine function Solution to see this we use the following facts lim sin x 0 x 0 We have not proved it but is intuitively clear from the graph of sin x near 0 Now observe that f x sin x is defined for every real number Let c be a real number Put x c h If x c we know that h 0 Therefore lim f x X C lim sin x X C lim sin c h h 0 blishe lim sin c cos h cosc sinh h 0

Algebra
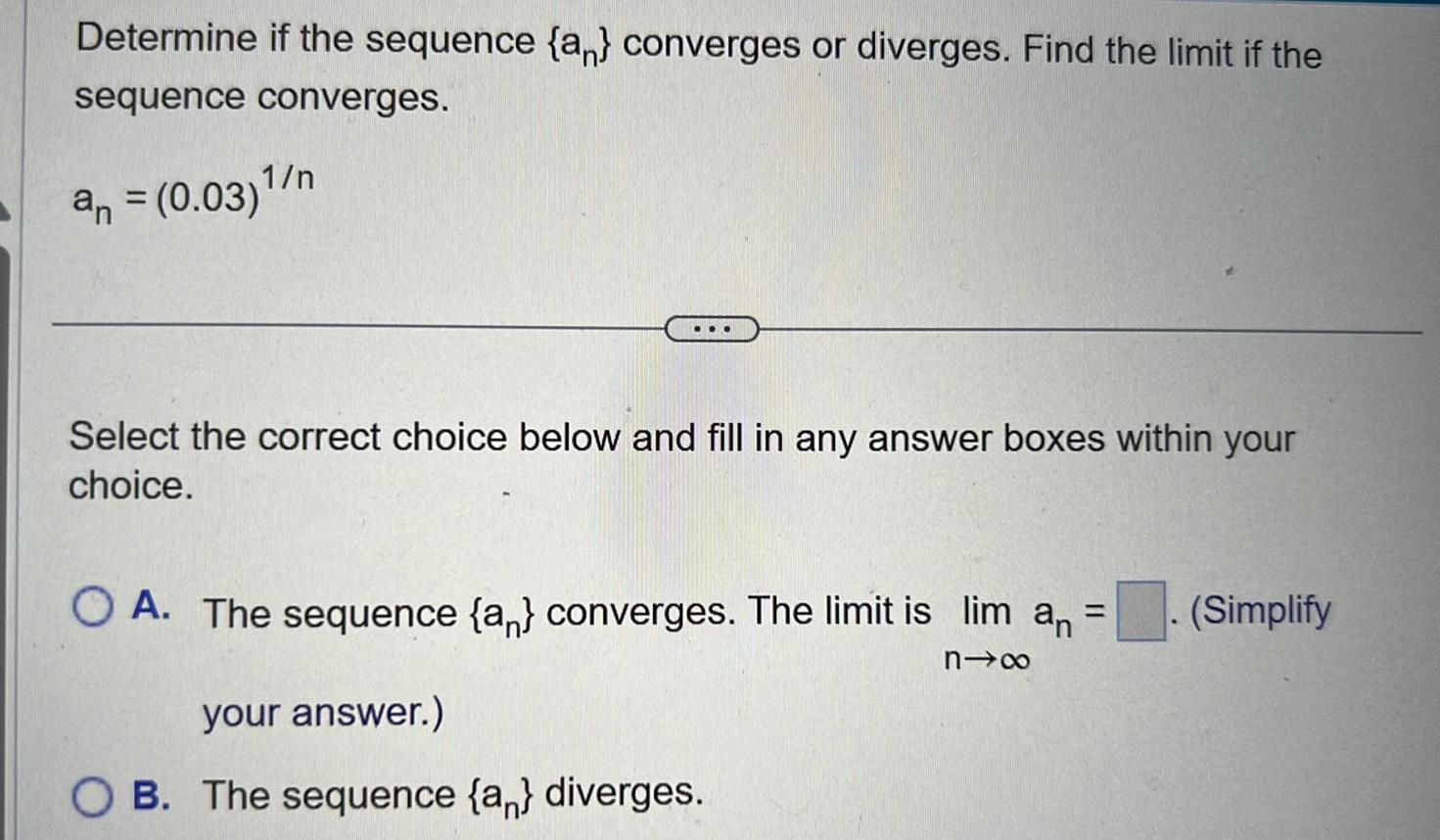
Quadratic equationsIs the function defined by 2x 3 if x 2 2x 3 if x 2 6 f x x 8 f x x 0 continuous at x 0 At x 1 At x 2 Find all points of discontinuity off where fis defined 10 f x if x 0 if x 0 NO x 1 if x 1 x 1 if x 1 x 0 1 if x 1 12 f x if x 1 13 Is the function defined by a continuous function f x User uden she f x x if x 1 2 if x 1 16 f x 2x if 1 x 1 2 if x 1 5 if x 1 x 3 if x 3 f x 2x if 3 x 3 6x 2 if x 3 11 f x 9 f x x x 5 if x 1 x 5 if x 1 Rationalised 2023 24 x if x 0 1 1 if x 0 x 3 if x 2 x 1 if x 2 CONTINUITY AND DIFFERENTIABILITY Discuss the continuity of the function f where fis defined by 3 if 0 x 1 14 f x 4 if 1 x 3 5 if 3 x 10 2x if x 0 15 f x 0 if 0 x 1 4x if x 1 is continuous at x 3 18 For what value of 2 is the function defined by 17 Find the relationship between a and b so that the function f defined by ax 1 if x 3 f x bx 3 if x 3 2 x 2x if x 0 4x 1 117 olished f x continuous at x 0 What about continuity at x 1 19 Show that the function defined by g x x x is discontinuous at all integral points Here x denotes the greatest integer less than or equal to x 20 Is the function defined by f x x sin x 5 continuous at x
Algebra
Sequences & SeriesDetermine if the sequence a converges or diverges Find the limit if the sequence converges an 0 03 n Select the correct choice below and fill in any answer boxes within your choice O A The sequence a converges The limit is lim an 81x your answer OB The sequence an diverges Simplify

Algebra
Permutations and Combinationsii No element of E is related to any element of O and vice versa iii E and O are disjoint and Z EUO The subset E is called the equivalence class containing zero and is denoted by 0 Similarly O is the equivalence class containing 1 and is denoted by 1 Note that 0 1 0 2r and 1 2r 1 r Z Infact what we have seen above is true for an arbitrary equivalence relation R in a set X Given an arbitrary equivalence relation R in an arbitrary set X R divides X into mutually disjoint subsets A called partitions or subdivisions of X satisfying i all elements of A are related to each other for all i ii no element of A is related to any element of A iii UA X and A A 0 i j The subsets A are called equivalence classes The interesting part of the situation is that we can go reverse also For example consider a subdivision of the set Z given by three mutually disjoint subsets A A and A hose union is Z with A x Z x is a multiple of 3 6 3 0 3 6 A x Z x 1 is a multiple of 3 5 2 1 4 7 A x Z x 2 is a multiple of 3 4 1 2 5 8 Define a relation R in Z given by R a b 3 divides a b Following the arguments similar to those used in Example 5 we can show that R is an equivalence relation Also A coincides with the set of all integers in Z which are related to zero A coincides with the set of all integers which are related to 1 and A coincides with the set of all integers in Z which are related 2 Thus A 0 A 1 and A 2 In fact A 3r A 3r 1 and A 3r 2 for all r Z Example 6 Let R be the relation defined in the set A 1 2 3 4 5 6 7 by R a b both a and b are either odd or even Show that R is an equivalence relation Further show that all the elements of the subset 1 3 5 7 are related to each other and all the elements of the subset 2 4 6 are related to each other but no element of the subset 1 3 5 7 is related to any element of the subset 2 4 6 Rationalised 2023 24 RELATIONS AND FUNCTIONS E Solution Given any element a in A both a and a must be either odd or even so that a a e R Further a b R both a and b must be either odd or even b a R Similarly a b R and b c R all elements a b c must be either even or odd simultaneously a c R Hence R is an equivalence relation Further all the elements of 1 3 5 7 are related to each other as all the elements of this subset are odd Similarly all the elements of the subset 2 4 6 are related to each other as all of them are even Also no element of the subset 1 3 5 7 can be related to any element of 2 4 6 as elements of 1 3 5 7 are odd while elements of 2 4 6 are even EXERCISE 1 1 1 Determine whether each of the following relations are reflexive syr transitive 5 1 Relation R in the set A 1 2 3 13 14 defined R x y 3x y 0 ii Relation R in the set N of natural numbers defined as

Algebra
Matrices & DeterminantsTeration 8 Show that the relation R in the set A 1 2 3 4 5 given by R a b ab is even is an equivalence relation Show that all the elements of 1 3 5 are related to each other and all the elements of 2 4 are related to each other But no element of 1 3 5 is related to any element of 2 4 9 Show that each of the relation R in the set A x Z 0 x 12 given by i R a b a b is a multiple of 4 ii R a b a b is an equivalence relation Find the set of all elements relate 10 Give an example of a relation Which is elle 1 Symmetric but neither reflexive nor transitive ii Transitive but neither reflexive nor symmetric iii Reflexive and symmetric but not transitive iv Reflexive and transitive but not symmetric v Symmetric and transitive but not reflexive 11 Show that the relation R in the set A of points in a plane given by R P Q distance of the point P from the origin is same as the distance of the point Q from the origin is an equivalence relation Further show that the set of all points related to a point P 0 0 is the circle passing through P with origin as centre 12 Show that the relation R defined in the set A of all triangles as R T T T is similar to T is equivalence relation Consider three right angle triangles T with sides 3 4 5 T with sides 5 12 13 and T with sides 6 8 10 Which triangles among T T and T are related ollec 13 Show that the relation R defined in the set A of all polygons as R P P P and P have same number of sides is an equivalence relation What is the set of all elements in A related to the right angle triangle T with sides 3 4 and 5 1 in each case 14 Let L be the set of all lines in XY plane and R be the relation in L defined as R L L L is parallel to L Show that R is an equivalence relation Find the set of all lines related to the line y 2x 4 Rationalised 2023 24 11 RELATIONS AND FUNCTIONS 7 15 Let R be the relation in the set 1 2 3 4 given by R 1 2 2 2 1 1 4 4 1 3 3 3 3 2 Choose the correct answer A R is reflexive and symmetric but not transitive B R is reflexive and transitive but not symmetric C R is symmetric and transitive but not reflexive D R is an equivalence relation 16 Let R be the relation in the set Ngiven by R a b a b 2 b 6 Choose the correct answer A 2 4 ER B 3 8 R C 6 8 R D 8 7 R 1 3 Types of Functions The notion of a function along with some special functions like identity function constant function polynomial function rational function modulus function signum function etc along with their graphs have been given in Class XI
Algebra
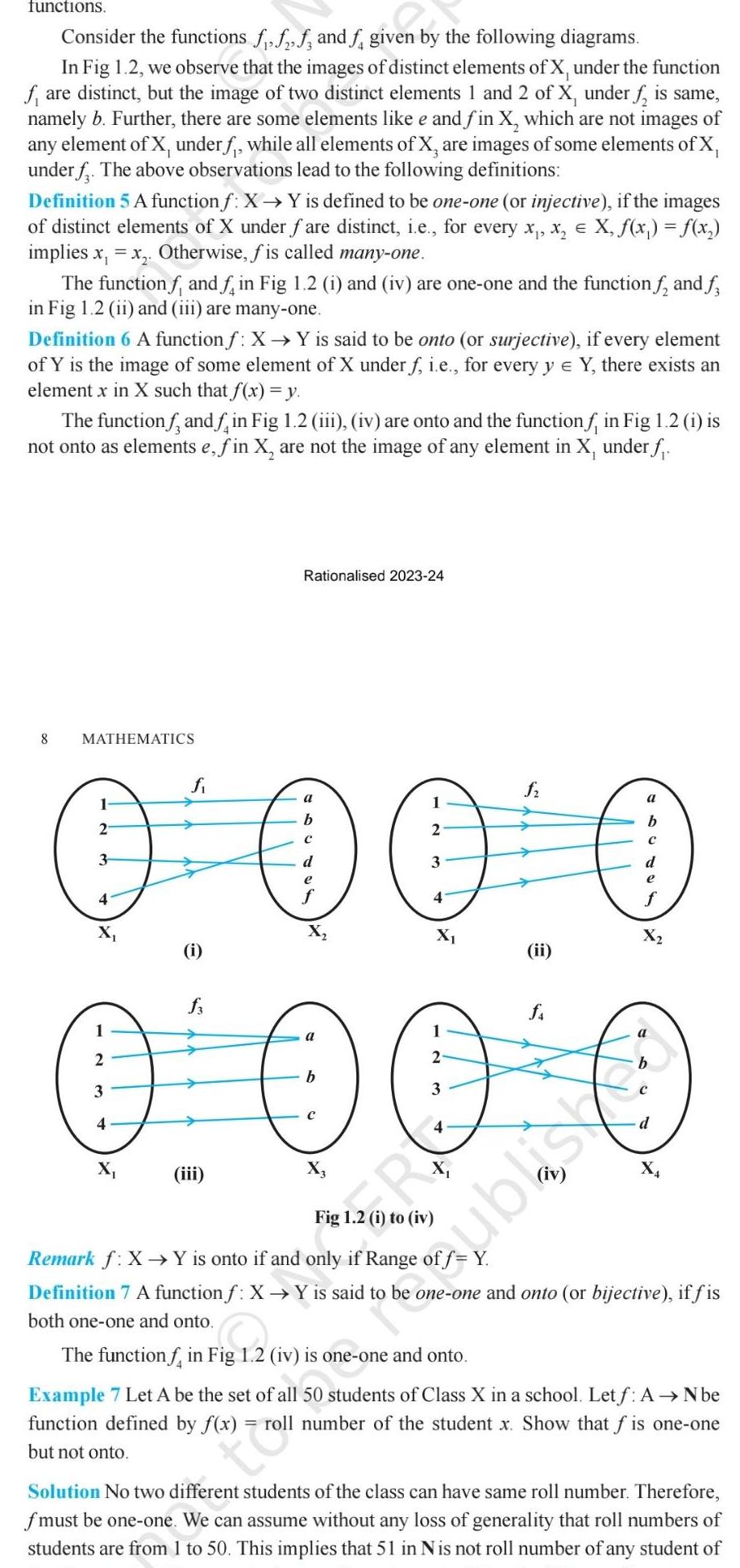
Permutations and Combinationsfunctions Consider the functions fff and f given by the following diagrams In Fig 1 2 we observe that the images of distinct elements of X under the function fare distinct but the image of two distinct elements 1 and 2 of X under f is same namely b Further there are some elements like e and fin X which are not images of any element of X under f while all elements of X are images of some elements of X under f The above observations lead to the following definitions Definition 5 A function f X Y is defined to be one one or injective if the images of distinct elements of X under fare distinct i e for every x x X f x f x implies x x Otherwise fis called many one The function f and f in Fig 1 2 i and iv are one one and the function f and f in Fig 1 2 ii and iii are many one Definition 6 A function f X Y is said to be onto or surjective if every element of Y is the image of some element of X under f i e for every y Y there exists an element x in X such that f x y The function and in Fig 1 2 iii iv are onto and the function f in Fig 1 2 i is not onto as elements e fin X are not the image of any element in X under f 8 MATHEMATICS fi a 1 1 a b 2 2 3 d 3 e e 4 4 X X O O O O 0 0 0 0 a 2 2 b 3 3 4 4 iii Rationalised 2023 24 i ii shari Remark f X Y is onto if and only if Range of f Y Definition 7 A function f X Y is said to be one one and onto or bijective if fis both one one and onto The function f in Fig 1 2 iv is one one and onto Example 7 Let A be the set of all 50 students of Class X in a school Let f A N be function defined by f x roll number of the student x Show that f is one one but not onto troll Solution No two different students of the class can have same roll number Therefore fmust be one one We can assume without any loss of generality that roll numbers of students are from 1 to 50 This implies that 51 in Nis not roll number of any student of

Algebra
Permutations and Combinationsthe class so that 51 can not be image of any element of X under f Hence fis not onto Example 8 Show that the function f N N given by f x 2x is one one but not onto Solution The function f is one one for f x f x 2x 2x x x Further fis not onto as for 1 N there does not exist any x in N such that f x 2x 1 X Rationalised 2023 24 Example 9 Prove that the functionf R R given by f x 2x is one one and onto Solution f is one one as f x f x 2x 2x x x Also given any real number y in R there exists in R such that f 2 2 1 y Hence f is onto 12 02 f x Y Example 10 Show that the function f N N for every x 2 is onto but not one one O is both one one and onto RELATIONS AND FUNCTIONS x 1 if x is odd x 1 if x is even CERT y f x 2x Example 11 Show that the function f R R defined as f x x is neither one one nor onto Solution Since f 1 1 f 1 f is not one one Also the element 2 in the co domain Ris not image of any element x in the domain R Why Therefore f is not onto X Example 12 Show that f N N given by X Solution fis not one one as f 1 f 2 1 But fis onto as given any y N y 1 we can choosex as y 1 such that f y 1 y 1 1 y Also for 1 N we have f 1 1 f 1 2 1 and f x x 1 1 1 x 1 Published O 9 f x x f 1 1 x 1 Y The image of 1 and 1 under f is 1 Fig 1 4

Algebra
Permutations and CombinationsSolution Suppose f x f x Note that if x is odd and x is even then we will have x 1 x 1 i e x x 2 which is impossible Similarly the possibility of x being even and x being odd can also be ruled out using the similar argument Therefore both x and x must be either odd or even Suppose both x and x are odd Then f x f x x 1 x 1 x x Similarly if both x and x are even then also f x f x x 1 x 1 x x Thus fis one one Also any odd number 2r 1 in the co domain N is the image of 2r 2 in the domain N and any even number 2r in the co domain N is the image of 2r 1 in the domain N Thus fis onto Example 13 Show that an onto function f 1 2 3 1 2 3 is always one one Solution Suppose fis not one one Then there exists two elements say 1 and 2 in the domain whose image in the co domain is same Also the image of 3 under f can be only one element Therefore the range set can have at the most two elements of the co domain 1 2 3 showing that f is not onto a contradiction Hence fmust be one one Example 14 Show that a one one function f 1 2 3 1 2 3 must be onto Solution Since fis one one three elements of 1 2 3 must be taken to 3 different elements of the co domain 1 2 3 under f Hence fhas to be onto Remark The results mentioned in Examples 13 and 14 are also true for an arbitrary finite set X i e a one one function f X X is necessarily onto and an onto map f X X is necessarily one one for every finite set X In contrast to this Examples 8 and 10 show that for an infinite set this may not be true In fact this is a characteristic difference between a finite and an infinite set EXERCISE 1 2 1 Show that the function f R R defined by f x iii f R iv f N N x where R is the set of all non zero real numbers Is the result true if the domain R is replaced by N with co domain being same as R 1 2 Check the injectivity and surjectivity of the following functions i f N N given by f x x ii f Z Z given by f x x Rationalised 2023 24 is one one and onto R given by f x x given by f x x v f Z Z given by f x x 3 Prove that the Greatest Integer Function f R R given by f x x is neither one one nor onto where x denotes the greatest integer less than or equal to x 1 if x 0 f x 0 if x 0 1 if x 0 RELATIONS AND FUNCTIONS 11 4 Show that the Modulus Functionf R R given by f x x is neither one one nor onto where x is x if x is positive or 0 and x is x if x is negative 5 Show that the Signum Function f R R given by is neither one one nor onto 6 Let A 1 2 3 B 4 5 6 7 and let f 1 4 2 5 3 6 be a function from A to B Show that fis one one

Algebra
Quadratic equationsThe table shows the percent of each type of doughnut sold at a bakery A store clerk put all of the cream filled and powdered sugar doughnuts on a display in the front of the store Both of these types of doughnuts completely sold out on Tuesday morning rt A If the clerk put 108 doughnuts in the front of store how many doughnuts were there in all at beginning of the day on Tuesday Type of Doughnut Cream Filled Glazed Maple Bacon Powdered Sugar Percen t 20 45 10 25
Algebra
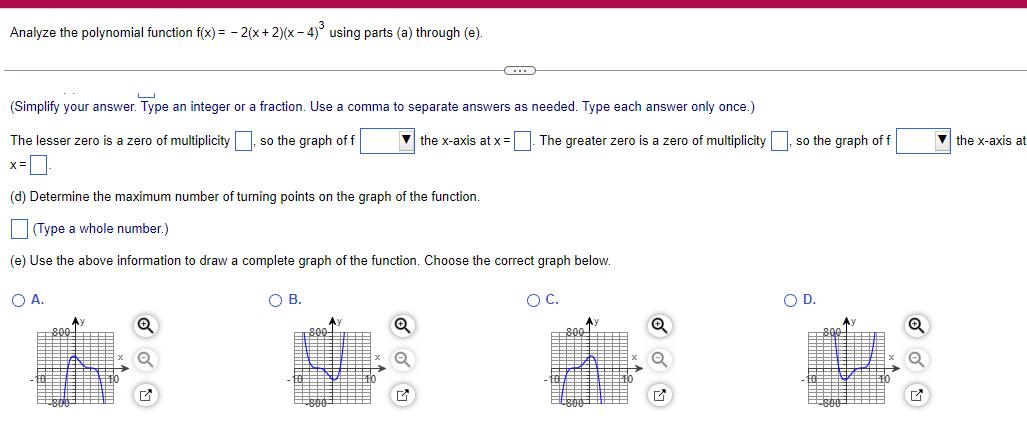
Quadratic equationsAnalyze the polynomial function f x 2 x 2 x 4 using parts a through e Simplify your answer Type an integer or a fraction Use a comma to separate answers as needed Type each answer only once The lesser zero is a zero of multiplicity so the graph of f the x axis at x The greater zero is a zero of multiplicity x d Determine the maximum number of turning points on the graph of the function Type a whole number e Use the above information to draw a complete graph of the function Choose the correct graph below O C OA Ay OB 800 C Ay G so the graph of f O D Q the x axis at

Algebra
Quadratic equationsFind the average rate of change for the function f x x 3 3 between xa and x a h 0 8 of 64
Algebra
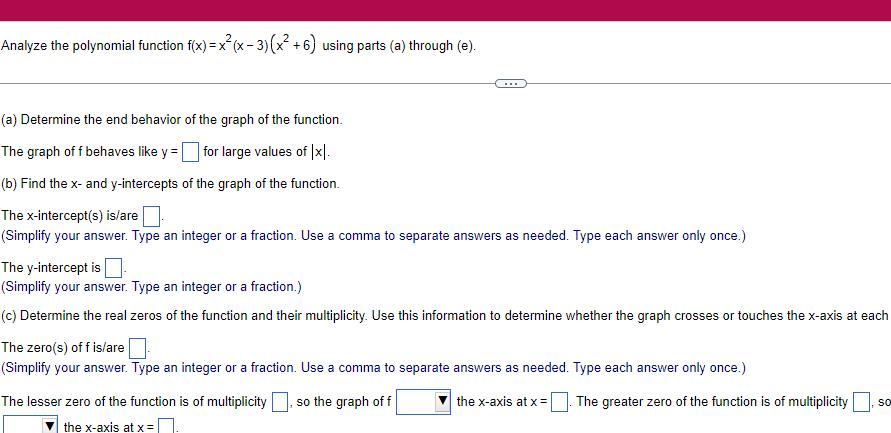
Complex numbersAnalyze the polynomial function f x x x 3 x 6 using parts a through e a Determine the end behavior of the graph of the function The graph of f behaves like y for large values of Ix b Find the x and y intercepts of the graph of the function The x intercept s is are Simplify your answer Type an integer or a fraction Use a comma to separate answers as needed Type each answer only once The y intercept is Simplify your answer Type an integer or a fraction c Determine the real zeros of the function and their multiplicity Use this information to determine whether the graph crosses or touches the x axis at each The zero s of f is are Simplify your answer Type an integer or a fraction Use a comma to separate answers as needed Type each answer only once so the graph of f the x axis at x The lesser zero of the function is of multiplicity the x axis at x The greater zero of the function is of multiplicity SO

Algebra
Matrices & DeterminantsWhat is AL 1 Draw any Why better to use wuring the lengt 4 FAB DE WO Exercise 5 1 ying in between A BC a AC s AB Note A that AC bele disadvantage in ervation 200 p between hut oder veget ay ABC Mre the length of All three points and AC mpang Ine segments that aru whle Venty whether the mid poid SHE mad poet of AC and is the m where A B C D on a straight ine say why A of Bo R D the mid point of AC D where A B C C07 uth that Buch Draw ve triangles and measure the sides Checke each case tsunof the length any he desi is the mid point of raight line say why All mast 309 id 1209 0 10 2 Where will the hand of a clock of a revolus a starts at 12 and make d starts at 2 and makes starts at 5 and makes a revolutions dockwise ution clock d starts at 5 and minesofaolution dockwise and make Nouth and Should ir this What part you stand facing la st ant tu the south and sum clock and tum Exercise 5 2 4 1001 tWhat fraction of a clockaine revolution does the four E How many right hand of a clock tum through when it goes from 710 58103 une full revolution specify dockwise of a lon Why noth evolution have you tume h Land Find the number of night angles uned through y hour hand dock when it gowe from 1355 028 wou and tum D north and tum ckase to fo west and tum to west id south and sam to north intiff in 1266 to weat wise to nas NURAY wit the hour hand of a clock stop fi i om 6 and tans through 1 night angle on and tuma through 2 right angles 0 from 10 and tums through 3 right angles 7 and tuma through 2 straight angles Exercise 5 3 DRO shes ange Clanuly each tight we than one outh more 1 Write down the measu a some acute angies some obtuse aigles hall noon ution blowing for eve walton of Exercise 5 4 What is the measure of a right ang70straight angle 2 Say True or The measure of an acute angle 90 b The measure of an abuse angle 30 fet The measure of a refox ange 180 da sight The measure of one complete revoto 360 e Itin A3 and mc 30 thn m CA mc Give at least two examples of nach 4 Messu the angles given below using the protractor and writs down the measure Wichangs Fland that mere Measure of ap L From these anges which has larger me Ea and then countem by meaning them 7 4 Menu ofangels Fin the banks with a ghaght 4 Ann whose messus is less than that of a Ito An angin whose measure is greater than that of a i An angle whose measures the sum of the of two night ang When the sum of the me res of two anges in that a When the sum of the measures of two gles is that s straight angis and if one of them is acute other should be then Find the First mure of the angle shown in each figurs mate with your eyes and then find the actual

Algebra
Quadratic equationsett a he 9 Find the angle between the hands of the och in sch figure 9 00 am 1 00 pm 10 te in the given figure the angle mease 20 Look at the same figure through a magnifying Dose change angle becomes laiger Does the suk of the angle 200 Measure and classify each angis CACH CADC Doc DOR 2008 Exercise 5 5 Me 6 00 pm a The adjacent edges of a table tap b The lines of a railway track c The line segments forming the leta 1 d The letter V from 1 Which of the following are modelsforperpendicular lines LR PLUS Pperverse to the the night Land XV esact in the peshtA Wer measure of Y 1 There are two ses ages in your the measures of the angles that a S comen Do they have any angle mat i perpine somman dy the digrom The is GE EGY b Door PE bes CO c dentify any e segments for which P Herpendicular tisector AC FG CD GHBC H Exercise 5 6 t Nams the types of owing ge a Tiangle with length of sides 7 cm 8 mand by BC with AB 87 cm AC 7 om and BC c APOR the PQ OR PR S5om id ADEF with eD 90 n SKYZ with mY 90 and XYYZ ALMN with 1 30 mM 70 and mN 80 Match the following Measure of Triangle 3 sides of equal lengt a Scale 8 2 sides of equal length b iscsperes right Types of Triangle angled Al sides of different Otae angled lingh v 3 acute anges v 1 night angin vi 1 obtuse angle vejt nght angle with two sides of equal length 0 Right angled e Equilateral Acute angled gosceias 3 Nemesach of the folowing triangies in two difer ways You may judge the nature of angle t obation MI Try to construct triangles ung machacks Some are shown here Can you make a tangle with a 3 matchto e 5 matates 1 6 matchwo Remember you have to use the matchats in each case i Nams the type of trade think of reasons for you cannot matang think of masons for b 4 match Exercise 5 7 1 Say true or false a Each angle of rectangle ght ange b The opposite sides of a rectangle an equal m lingh ght of a 10 Souess scans a d At the side of a mombus se of equal length 0 All the sides of a paralelogram are of soul length 4 Sepas pieselwigram 3 Ap regard d length and wipes angun meur Can you identify the requ The opposite sides of a trapanum um paralle 2 Give reasons for the following a Asquare can be thought of as a special rectangle A rectangle can be thought of special paralelogram mamb Exercise 5 8 Examine wheme the og epolygons among these say wh M 2 Namech polygon Make two more examples of each of the c The diagonale of a squarere perpendicular to 3 Draw a rough skich of a regular hexagon Connectin one another any time of vertices throw thangle identify th type of the triangle you uveden Drawough skach of a regula octagun Um aquared paper if you wan D rectangle joiningscy four of the vertices of the antagon 5 Adagol segment that joins any two vertic polygon arut is e side of the polygon Dram rough sch of a pentagon and draw is diegonale

Algebra
Complex numbersOne pair of parallel sides are et different lengths vi Kite and V Shaped Kite Remember A square is also a rectangle as it has opposite sides squal A parallelogram has 2 thombus are special type en parallelogram A 2 pairs of adjacent equal sides Triangle Properties of Kite A Diagonals of a kite are perpendicular to each other One of the diagonals divides the kite into two modes A kite may or ay not be a parallelogram The sum of internal angles of a quadrilaterali 360 A square ra rectangle can be divided into two right angled triangles of equal sine by joining any two opposite vertices diagonally Opposite angles of a parallelogram are equal 3 Polygons A closed plane figure having more than 2 sides is a polygon in regular polygons all sides and all angles are equal Diagonals of a regular polygon are pal All polygons are classified according to the number of their sides Quadrilateral 4 ofequial and parallel sides so all rectangles guares and Dwap 30 In your day to day life you can see different types of polygon all around you In nature bectives are the best examples of hesagons A design of pentagon can be seen in football and hout Stop sight and wall clocks have wight sides so they are regalar tagms An opmed umbrella and star s a symbol of decagon STOP If a polygon has all tissides equal it called a regular polygos A regular polygim has all angles angles in it Let s Practice 1 Select any there objects having a flat tops Measure all sides of the sip using a divider and a ruler 2 What is the angle mame for half a relution What is the angle name for one fourth revolution 4 Draw five other situations of one fourth half and the fourth revolution on a clock The hour hand of a clock moves from 12 to 5 is the revolution of the hour hand more than one right angle What does the angle made by the hour hand of the clock look like when it moves from 577 is the angle mereed more than 1 night angle 7 Draw the following and check the angle with your RA tester 00 going from 12 to 2 from 6107 v trum 21052 from 4 to 8 List five situations where the angles made are 1 acute i obtuse angles are made 0 right angles v refles angles may be seen

Algebra
Matrices & DeterminantsA perpendicular line segment All that passes through the mid point of another linea called the perpendicular bisector of PQ Classification of Triangles You know now that a portion covered by three line segments is called a triangle Look at adjoining figures of triangles in the first fig a three sides are equal in the second Some Special Quadrilaterals b two of the sides are equal But in the third fig c all three sides are unequal Here are some special quadrilaterals Square A equal sides b 4 right angles 4 WI GA 4 In the same way in fig d triangle has all three acute angles fig e contains a right angle and triangle has an obtuse angle Hence all triangles can be named on the basis of measurement of sides or angles Types of Triangles at the Basis of Sides 0 A triangle that has all three its sides unequal is called a scalerie triangle Fig c A triangle that has two of its sides equal is called isosceles triangle Fig b i A triangle that has all three sides are equal is called equilateral triangle Fig a Types of Triangles at the Basis of Angles 1 If each of a triangle is less than 90 then the triangle is called an acute angled triang Fig d i If any one angle in a triangle is right angle ie of 90 then the triangle is called a angled triangle Fig e i If any one angle in a triangle is an obtuse is larger than then the triangle is an obtuse angled triangle fig f Quadrilaterals A polygon made of four straight edges and four corners vertices is called a quadrilateral Given polygon ABCD is a quadrilateral as it has four 0 Sides AB BC CD DA i Angles ZA ZB ZC ZD i Vertices A B C D When you look around yourself you find many quadrilateral figures in your daily life Examples Your study table on which you study and acquire knowledge the picture frame which your picture looks attractive bedsheet which you use to have a sound sleep or a kite alla in the quadrilateral shape 52 Properties of a Square a Diagonals of square are equal b Diagonals of square are perpendicular to each other c Diagonals bisect each other i Rectangle X a 2 pairs of opposite equal sides b 4 night angles Properties of Rectangle a Opposite sides of a rectangle are equal and parallel b Diagonals of a rectangle are equal e Diagonals of a rectangle bisect each other ii Khombus a 4 equal sides b Opposite sides are parallel c Opposite angles are equal Properties of Rhombus A Opposite angles of a rhombus are equal 6 The diagonals of a shombus are perpendicular bisector of each other iv Parallelogram a 2 pairs of opposite equal sides b Opposite siden are parallel c Opposite angles are equal Properties of a Parallelogram a Opposite sides of a parallelogram are equal b Opposite angles of a parallelogram are equal c Diagonals of a parallelogram bisect each other Do You Know Square is a special kindvof parallelogram