Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
DifferentiationFor a function f x we know that f 19 65 and f 19 2 Estimate f 20 f 18 and f 25 f 20 f 18 25 IM Mi

Calculus
Differential equationsx 5 MR 6 5 36 66 When Hence the required marginal revenue is 66 EXERCISE 6 1 1 Find the rate of change of the area of a circle with respect to its radius r when a r 3 cm b r 4 cm 2 The volume of a cube is increasing at the rate of 8 cm s How fast is the surface area increasing when the length of an edge is 12 cm 3 The radius of a circle is increasing uniformly at the rate of 3 cm s Find the rate at which the area of the circle is increasing when the radius is 10 cm 4 An edge of a variable cube is increasing at the rate of 3 cm s How fast is the volume of the cube increasing when the edge is 10 cm long 5 A stone is dropped into a quiet lake and waves move in circles at the speed of 5 cm s At the instant when the radius of the circular wave is 8 cm how fast is the enclosed area increasing Rationalised 2023 24 APPLICATION OF DERIVATIVES 151 6 The radius of a circle is increasing at the rate of 0 7 cm s What is the rate of increase of its circumference 7 The length x of a rectangle is decreasing at the rate of 5 cm minute and the width y is increasing at the rate of 4 cm minute When x 8cm and y 6cm find the rates of change of a the perimeter and b the area of the rectangle 8 A balloon which always remains spherical on inflation is being inflated by pumping in 900 cubic centimetres of gas per second Find the rate at which the radius of the balloon increases when the radius is 15 cm 9 A balloon which always remains spherical has a variable radius Find the rate at which its volume is increasing with the radius when the later is 10 cm 10 A ladder 5 m long is leaning against a wall The bottom of the ladder is pulled along the ground away from the wall at the rate of 2cm s How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall 11 A particle moves along the curve 6y x 2 Find the points on the curve at which the y coordinate is changing 8 times as fast as the x coordinate the 12 The radius of an air bubble is increasing at the rate of cm s At what rate is the volume of the bubble increasing when the radius is 1 cm 3 2 2x 1 13 A balloon which always remains spherical has a variable diameter Find the rate of change of its volume with respect to x 14 Sand is pouring from a pipe at the rate of 12 cm s The falling sand forms a cone on the ground in such a way that the height of the cone is always one sixth of the radius of the base How fast is the height of the sand cone increasing when the height is 4 cm 15 The total cost C x in Rupees associated with the production of x units of an item is given by C x 0 007x 0 003x 15x 4000 Find the marginal cost when 17 units are produced 16 The total revenue in Rupees received from the sale of x units of a product is given by

Calculus
Differential equationsdt Thus the enclosed area is increasing at the rate of 80 cm s when dy Note is positive if y increases as x ncreases and negative if y decreases dx as x increases Example 4 The length x of a rectangle is decreasing at the rate of 3 cm minute and the width y is increasing at the rate of 2cm minute When x 10cm and y 6cm find the rates of change of a the perimeter and b the area of the rectangle Solution Since the length x is decreasing and the width y is increasing with respect to time we have and a The perimeter P of a rectangle is given by P 2 x y dP dt b The area A of the rectangle is given by A x y 150 dx dt Therefore When not be MATHEMATICS 2 dA dt dx dy dt dt dy dt Marginal Revenue When dx dt 3 6 10 2 as x 10 cm and y 6 cm 2 cm min y x Rationalised 2023 24 cost MC 2 cm min dy dt Example 5 The total cost C x in Rupees associated with the production of x units of an item is given by 2 3 2 2 cm min C x 0 005x 3 0 02 x 30x 5000 Find the marginal cost when 3 units are produced where by marginal cost we mean the instantaneous rate of change of total cost at any level of output dC dx Solution Since marginal cost is the rate of change of total cost with respect to the output we have Marginal 10 cm 0 005 3x 0 02 2x 30 x 3 MC 0 015 3 0 04 3 30 0 135 0 12 30 30 015 Hence the required marginal cost is 30 02 nearly Example 6 The total revenue in Rupees received from the sale of x units of a product is given by R x 3x 36x 5 Find the marginal revenue when x 5 where by marginal revenue we mean the rate of change of total revenue with respect to the number of items sold at an instant p rd Solution Since marginal revenue is the rate of change of total revenue with respect to the number of units sold we have dR dx x 5 MR 6 5 36 66 MR 6x 36

Calculus
Differential equationswhich its volume is increasing with the radius when the later is 10 cm 10 A ladder 5 m long is leaning against a wall The bottom of the ladder is pulled along the ground away from the wall at the rate of 2cm s How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall 11 A particle moves along the curve 6y x 2 Find the points on the curve at which the y coordinate is changing 8 times as fast as the x coordinate 12 The radius of an air bubble is increasing at the rate of cm s At what rate is the volume of the bubble increasing when the radius is 1 cm 3 2x 1 13 A balloon which always remains spherical has a variable diameter 2x Find the rate of change of its volume with respect to x 14 Sand is pouring from a pipe at the rate of 12 cm s The falling sand forms a cone on the ground in such a way that the height of the cone is always one sixth of the radius of the base How fast is the height of the sand cone increasing when the height is 4 cm 15 The total cost C x in Rupees associated with the production of x units of an item is given by x in Rupe C x 0 007x 0 003x 15x 4000 Find the marginal cost when 17 units are produced 16 The total revenue in Rupees received from the sale of x units of a product is given by Find the marginal revenue when x 7 Choose the correct answer for questions 17 and 18 17 The rate of change of the area of a circle with respect to its radius r at r 6 cm is A 10T B 12 C 8T D 11T 152 MATHEMATICS 18 The total revenue in Rupees received from the sale of x units of a product is given by R x 3x 36x 5 The marginal revenue when x 15 is A 116 B 96 C 90 D 126 6 3 Increasing and Decreasing Functions In this section we will use differentiation to find out whether a function is increasing or decreasing or none Values left to origin f x x R x 13x 26x 15 Consider the function f given by f x x x R The graph of this function is a parabola as given in Fig 6 1 X 2 3 2 1 1 2 4 9 4 Rationalised 2023 24 1 1 4 X 0 0 as we move from left to right the height of the graph decreases f x height of graph at x EX 2 10 Values right to origin f x x X 0 10 132 0 1 4 1 9 4 2 4 as we move from left to right the height of the graph increases
Calculus
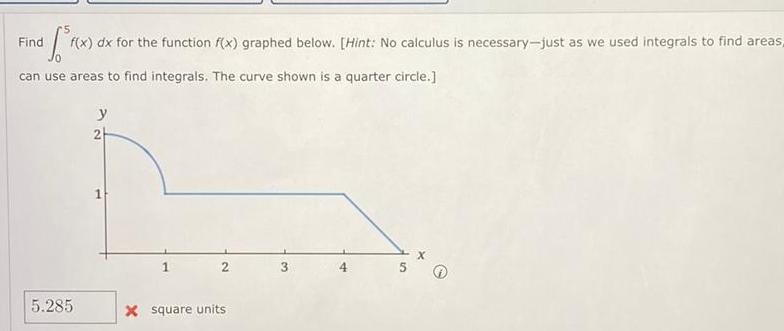
Differentiationaf f x f x dx for the function f x graphed below Hint No calculus is necessary just as we used integrals to find areas can use areas to find integrals The curve shown is a quarter circle Find 5 285 y 2 1 1 2 x square units
Calculus
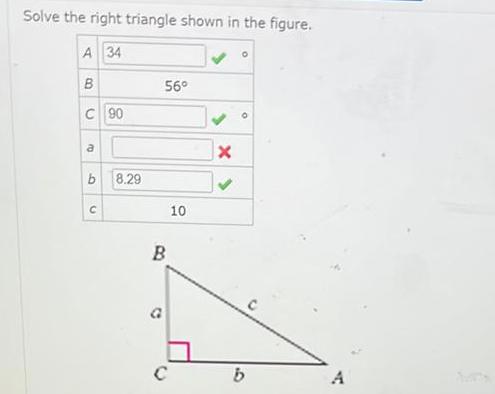
Application of derivativesSolve the right triangle shown in the figure A 34 B C 90 E b 8 29 C 56 B C 10 X 0 b
Calculus
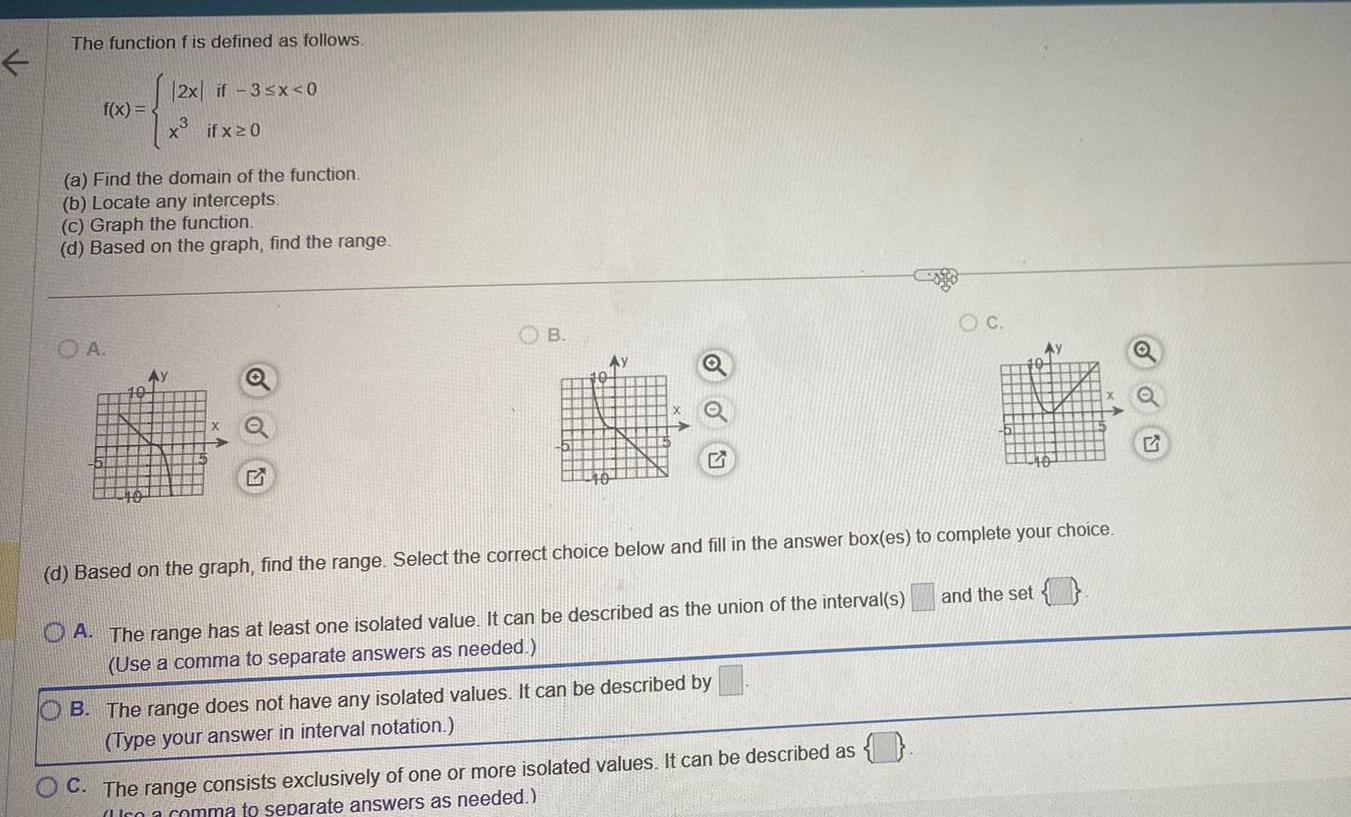
Limits & ContinuityThe function f is defined as follows f x 2x 3 O A if 3 x 0 if x20 a Find the domain of the function b Locate any intercepts c Graph the function d Based on the graph find the range OB Ay OB The range does not have any isolated values It can be described by Type your answer in interval notation OC C The range consists exclusively of one or more isolated values It can be described as co a comma to separate answers as needed d Based on the graph find the range Select the correct choice below and fill in the answer box es to complete your choice A The range has at least one isolated value It can be described as the union of the interval s Use a comma to separate answers as needed AY 40 and the set OU
Calculus
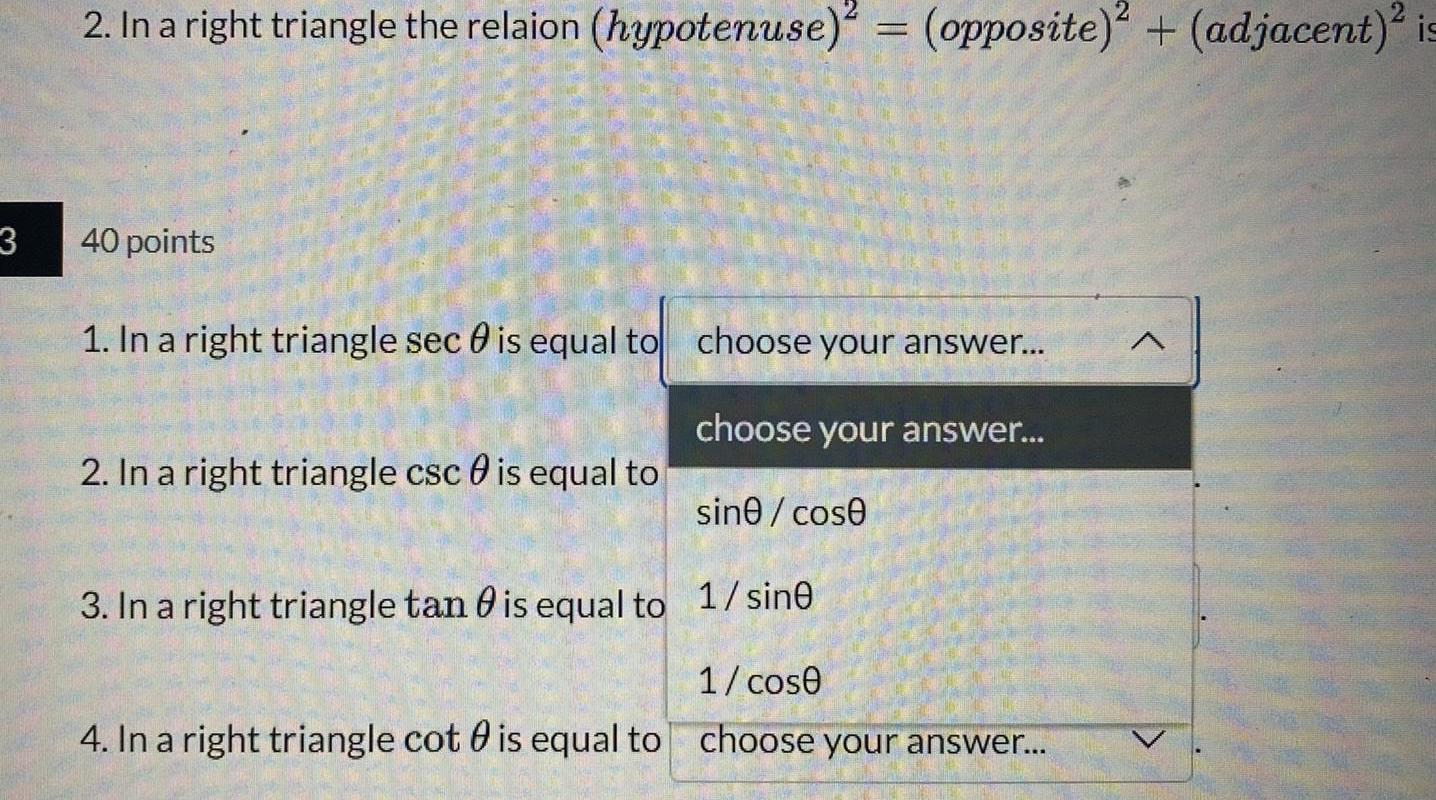
Application of derivatives3 2 In a right triangle the relaion hypotenuse opposite adjacent is 40 points 1 In a right triangle sec 0 is equal to choose your answer choose your answer 2 In a right triangle csc is equal to sine cose 3 In a right triangle tan 0 is equal to 1 sine 1 cose 4 In a right triangle cot is equal to choose your answer
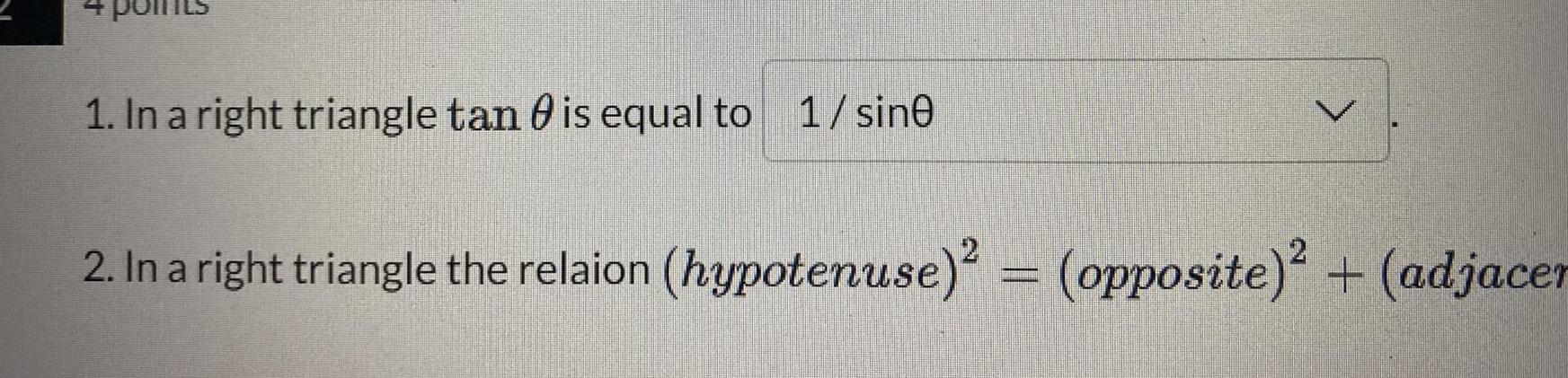
Calculus
Differentiation1 In a right triangle tan is equal to 1 sine L 2 In a right triangle the relaion hypotenuse opposite adjacer
Calculus
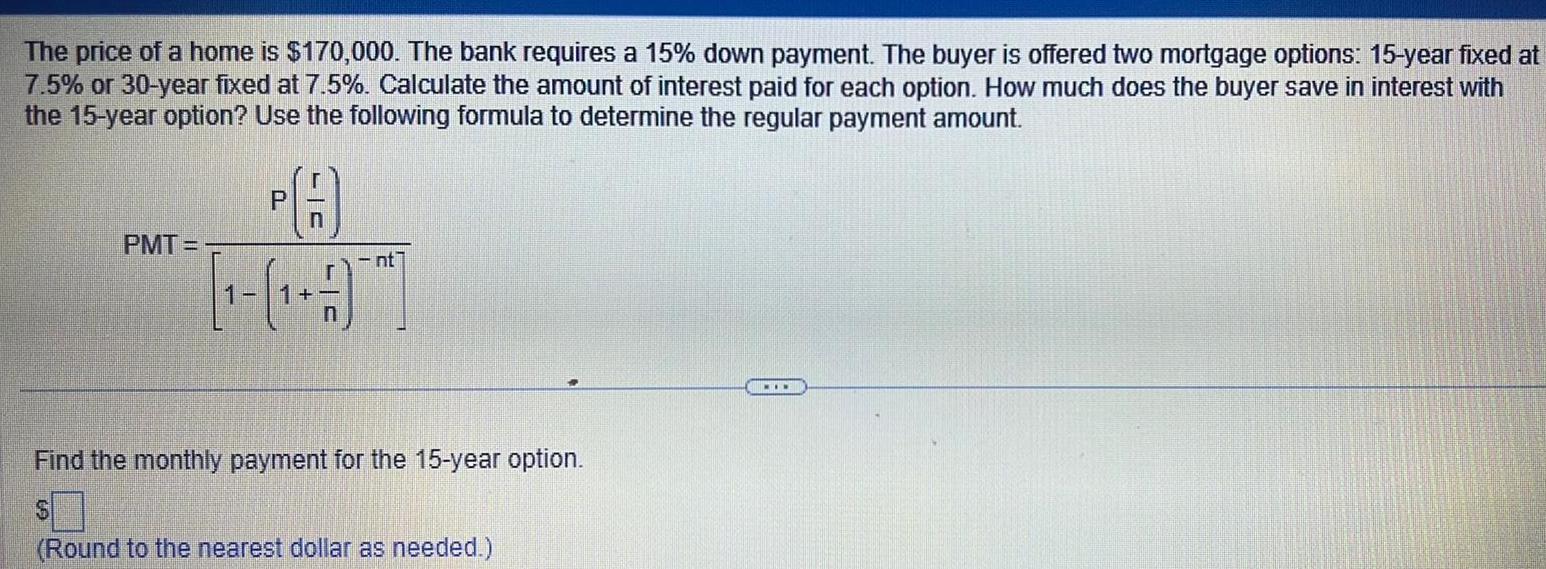
Vector CalculusThe price of a home is 170 000 The bank requires a 15 down payment The buyer is offered two mortgage options 15 year fixed at 7 5 or 30 year fixed at 7 5 Calculate the amount of interest paid for each option How much does the buyer save in interest with the 15 year option Use the following formula to determine the regular payment amount PMT P LC nt Find the monthly payment for the 15 year option Round to the nearest dollar as needed MIN

Calculus
DifferentiationEvaluate if possible the six trigonometric functions of the real number t If not possible enter IMPOSSIBLE 7 6 sin t cos t tan t t m csc t sec t cot t

Calculus
DifferentiationEach time your heart beats your blood pressure increases then decreases as the heart rests between beats A certain person s blood pressure is modeled by the function p t 115 25 sin 160nt where p t is the pressure in mmHg millimeters of mercury at time t measured in p t minutes Find the amplitude and period of O O amplitude 25 period O n amplitude 115 period 80 amplitude 115 period amplitude 25 period 80 10 80 H 80

Calculus
Application of derivativesMatch the right triangle definition with its trigonometric function a hyp adj b c d e f opp adj opp hyp adj opp hyp opp adj hyp Select Select Select Select Select 33 Select


Calculus
Limits & ContinuityFind a formula for the nth partial sum of the series and use it to find the series sum if the series converges 5 5 36 216 5 5 6 5 67 1 The formula for the nth partial sum sn of the series is

Calculus
Vector CalculusThe price of a condominium is 89 000 The bank requires a 5 down payment and one point at the time of closing The cost of the condominium is financed with a 30 year fixed rate mortgage at 9 Use the following formula to determine the regular payment amount Complete parts a through e below FA PMT C a Find the required down payment
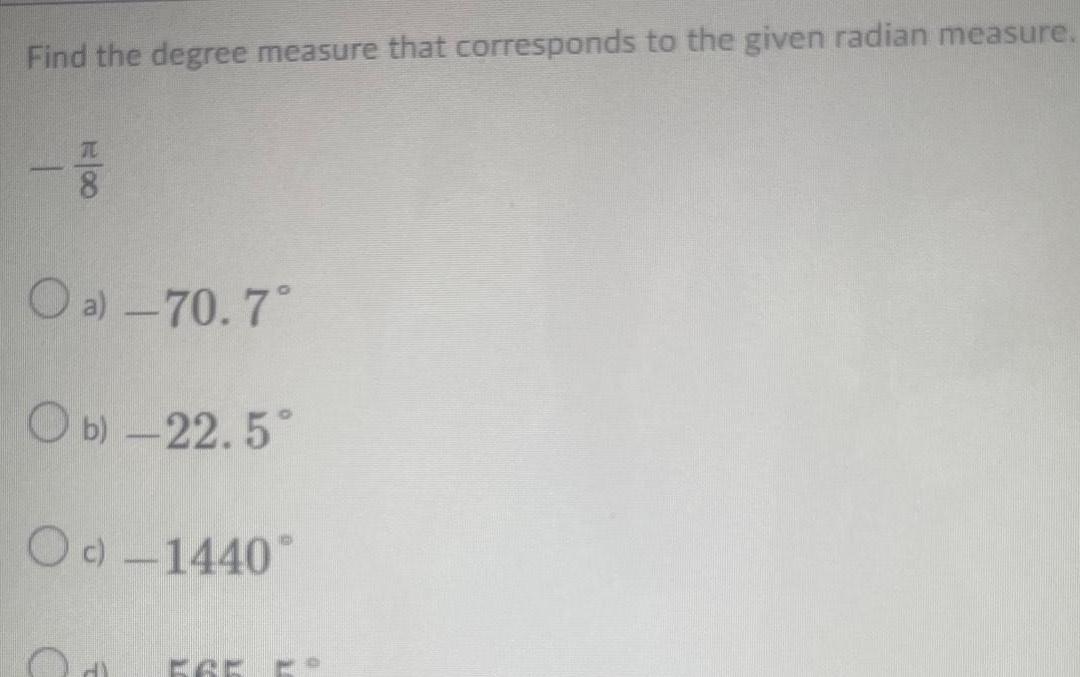
Calculus
Application of derivativesFind the degree measure that corresponds to the given radian measure E00 O a 70 7 Ob 22 5 Oc 1440 HY CAM

Calculus
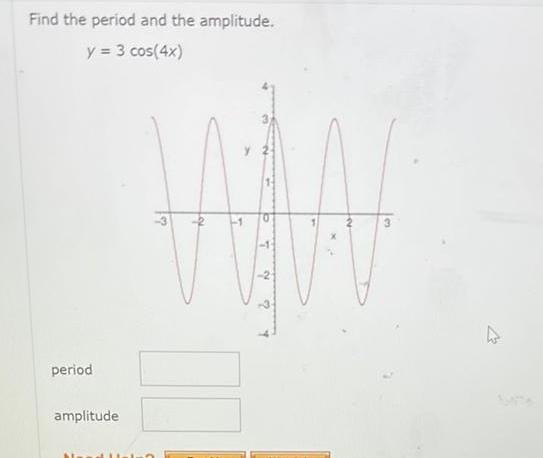
DifferentiationListen State the amplitude A and period T of the trigonometric function f x 3 sin x OA 3 T T OA T 3 OA 3 T 2 A 3 T 4T 1

Calculus
Application of derivativesGiven side a 24 side b 28 and side c 30 find the area of triangle A 285 316 336 909

Calculus
Application of derivativesA central angle in a circle of radius 2 5 cm is subtended by an arc of length 7 cm Find the measure of in degrees Recall In a circle of radius r the length of an arc that subtends a central angle of radians is S TO O a 160 4 Ob 2 8 Od 4 8 Od 35 7
Calculus
Indefinite IntegrationFind the exact value of the expression belo cos sin Oa0 Ob 3 b 001 12 200
Calculus
Application of derivativesGive the quadrant and reference angle of an angle that measures O a Quadrant II Reference Angle Angle Ob Quadrant I Reference Angle O c Quadrant I Reference Angle O d Quadrant II H 6 TL Reference Angle 6
Calculus
Definite Integrals4Listen If the point 3 5 of Cost and tant a cost b cost 05 20 O d 5 is the terminal point of t on the unit circle tant tant cost 3 4 3 Od cost 1 tant 4130 31 10 tant 3
Calculus
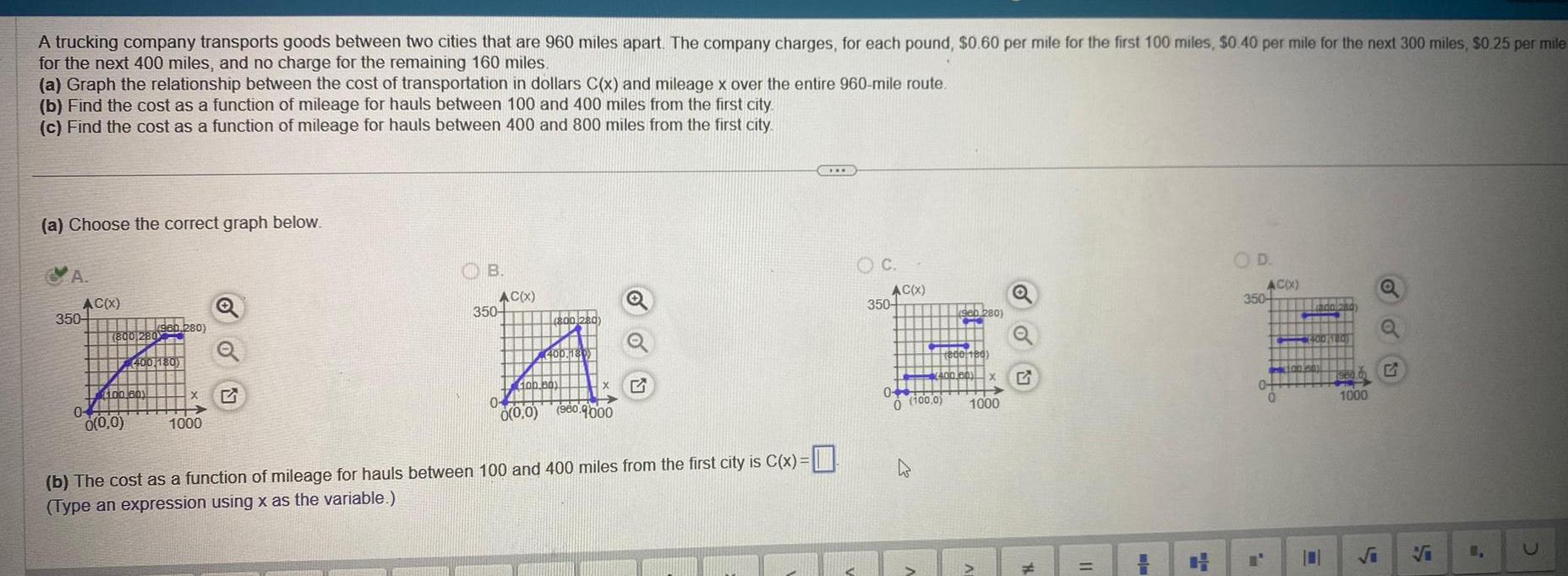
Application of derivativesA trucking company transports goods between two cities that are 960 miles apart The company charges for each pound 0 60 per mile for the first 100 miles 0 40 per mile for the next 300 miles 0 25 per mile for the next 400 miles and no charge for the remaining 160 miles a Graph the relationship between the cost of transportation in dollars C x and mileage x over the entire 960 mile route b Find the cost as a function of mileage for hauls between 100 and 400 miles from the first city c Find the cost as a function of mileage for hauls between 400 and 800 miles from the first city a Choose the correct graph below A AC x 350 04 800 280 100 18011 0 0 0 960 280 400 180 X 1000 OB 350 AC x 800 280 0 0 0 400 180 Gab bay 960 9000 b The cost as a function of mileage for hauls between 100 and 400 miles from the first city is C x Type an expression using x as the variable C OC 350 AC X 04 0 100 0 D Seb 280 FA 800 180 400 00 10011 X x 1000 Q 11 OD AC X 350 0 0 Lada 280 4400 1180 100 jen 0 Q L Q 2006 G 1000 1 U
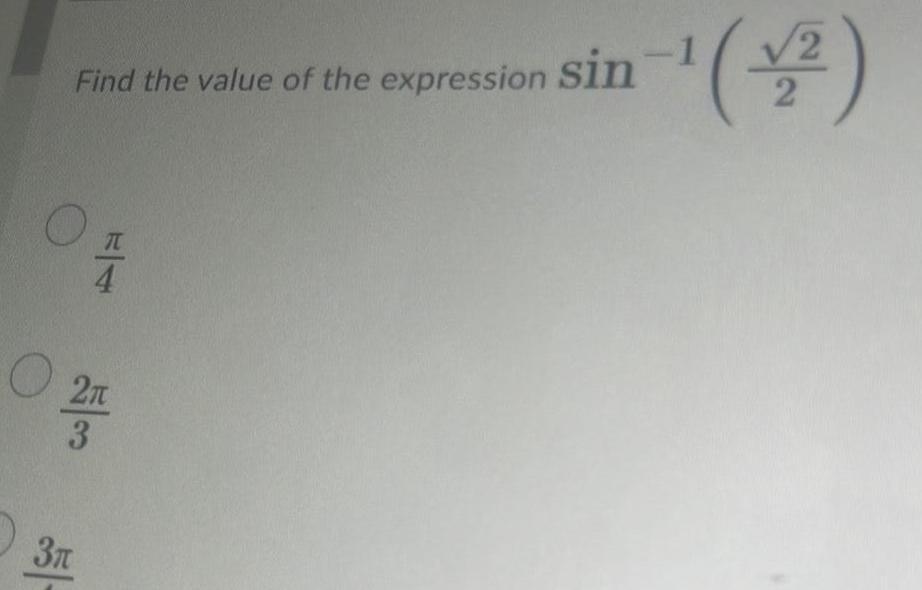

Calculus
Definite IntegralsGivensin e cot 0 0 3 103 00 3 v3 3 CY 0 2 3 for an angle in quadrant IV find the exact value of

Calculus
Definite IntegralsWhich angle below is NOT co terminal with the angle O a Ob 13m 4 O c 4 3n Od 21 4

Calculus
Application of derivativesA trigonometric function is given Find the amplitude period and horizontal shift of the function sin x 4 y 2 sin x Oa amplitude 2 period 2 horizontal shift units to the right Ob amplitude 2 period 4 horizontal shift 2 units to the right Od amplitude 2 period 2 horizontal shift units to the left Od amplitude 2 period 2 horizontal shift units to the right

Calculus
Differential equationsListen Find the degree measure that corresponds to the giv 5t 6 a 216 b 216 c 150 T d 150

Calculus
Definite IntegralsTo find the distance across a canyon from point B to point C a surveying team locates points A and B on one side of the canyon and point C on the other side of the canyon The distance between A and B is 93 yards The angle CAB is 67 and the angle CBA is 89 Find the distance across the canyon from point B to point C round to the nearest yard 230 yards 150 yards 210 yards 350 yards

Calculus
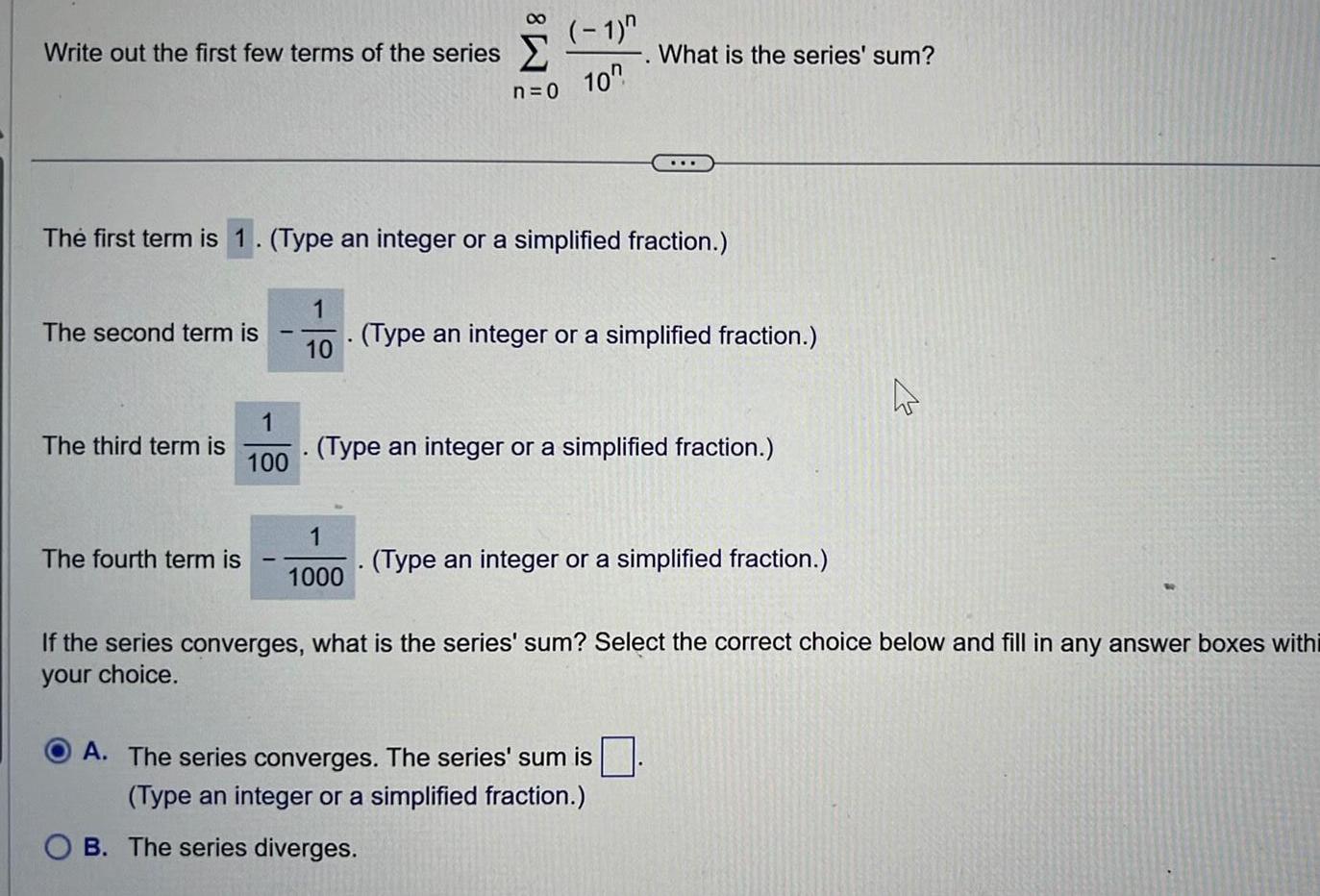
Application of derivativesWrite out the first few terms of the series The second term is The third term is The fourth term is The first term is 1 Type an integer or a simplified fraction 1 100 1 10 8 n 0 1 1000 1 10 What is the series sum Type an integer or a simplified fraction Type an integer or a simplified fraction Type an integer or a simplified fraction A The series converges The series sum is Type an integer or a simplified fraction B The series diverges A If the series converges what is the series sum Select the correct choice below and fill in any answer boxes withi your choice

Calculus
DifferentiationFind the radian measure that corresponds to the given degree measure 315 O a 56700 O b 7 n 4 c 7 T

Calculus
Differential equationsListen Which of the following angles is co terminal with an angle that measures Select all that apply a 120 b 960 c 60 d 360 240
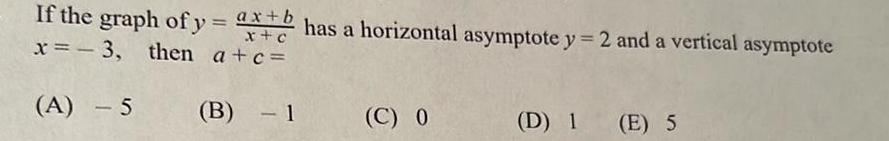
Calculus
Definite IntegralsIf the graph of y ax b x c x 3 then a c A 5 B 1 1 has a horizontal asymptote y 2 and a vertical asymptote C 0 D 1 E 5
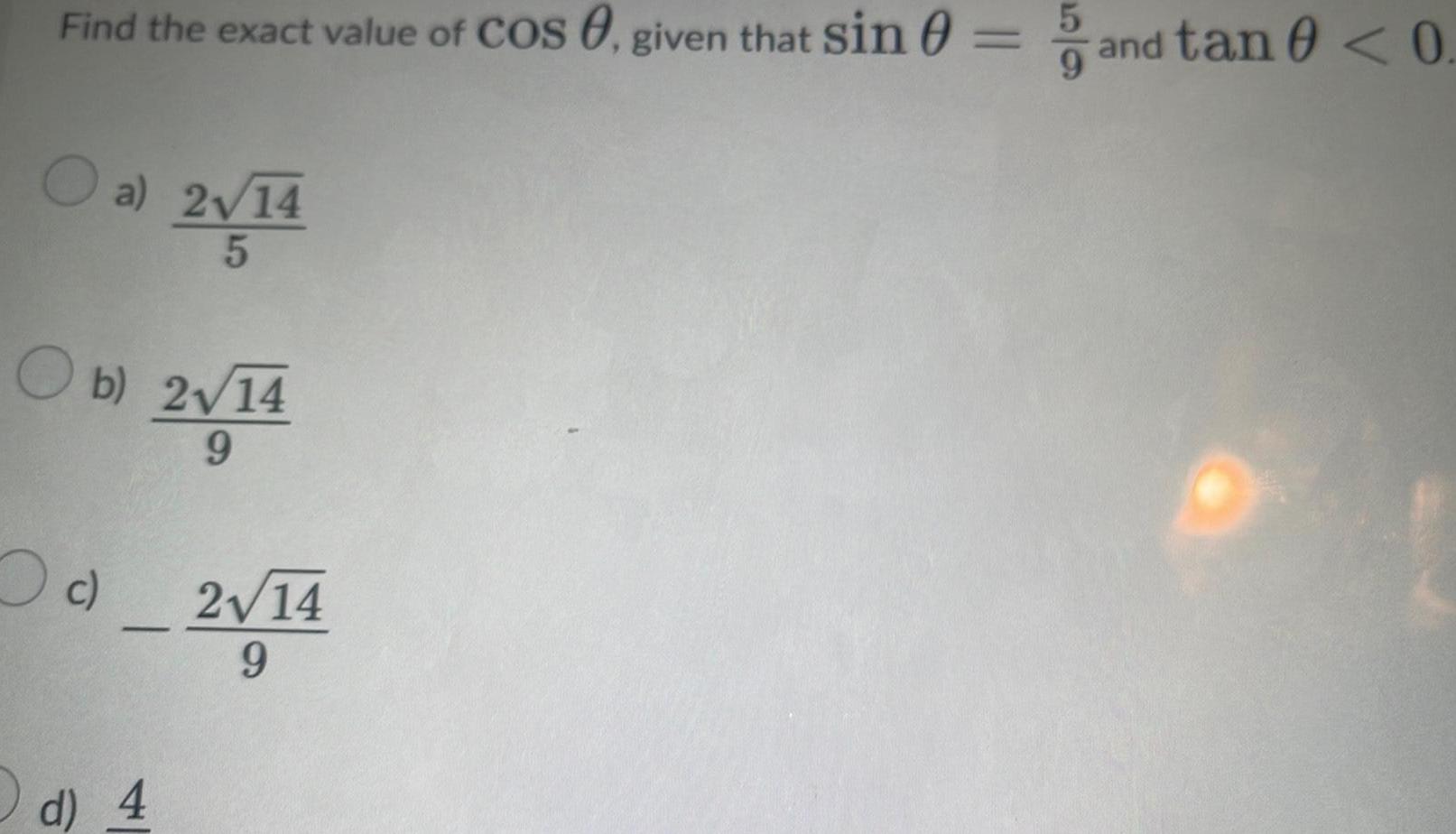
Calculus
DifferentiationFind the exact value of Cos 0 given that sin and tan 0 0 a 2 14 2 14 5 O b 2 14 2 14 9 c d 4 2 14 9
Calculus
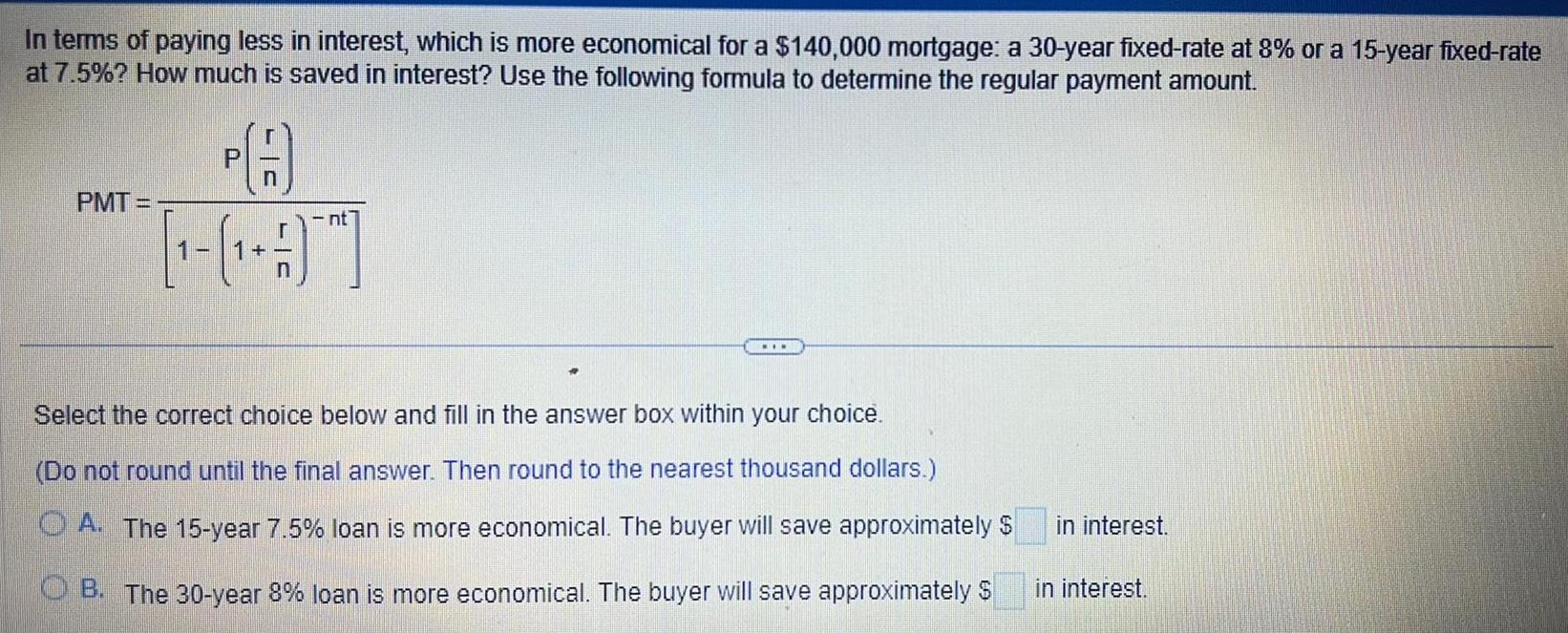
Vector CalculusIn terms of paying less in interest which is more economical for a 140 000 mortgage a 30 year fixed rate at 8 or a 15 year fixed rate at 7 5 How much is saved in interest Use the following formula to determine the regular payment amount PMT PA 1 nt Select the correct choice below and fill in the answer box within your choice Do not round until the final answer Then round to the nearest thousand dollars A The 15 year 7 5 loan is more economical The buyer will save approximately OB The 30 year 8 loan is more economical The buyer will save approximately in interest in interest
Calculus
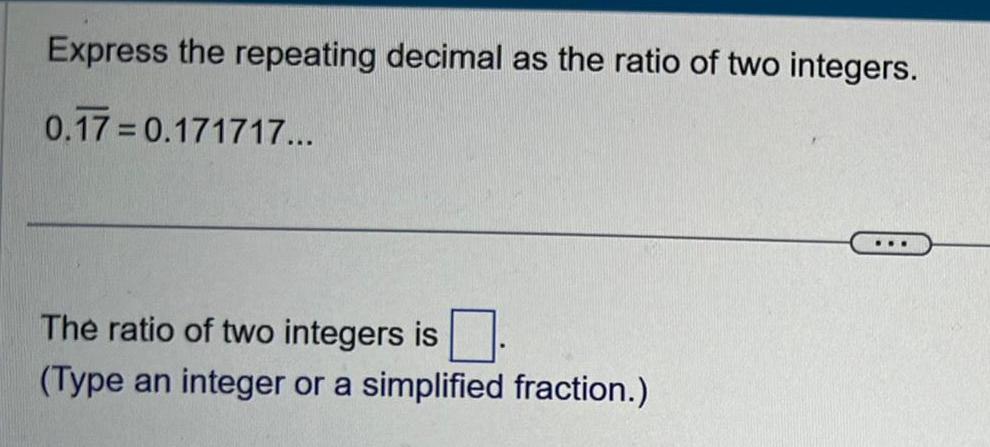
Definite IntegralsExpress the repeating decimal as the ratio of two integers 0 17 0 171717 The ratio of two integers is Type an integer or a simplified fraction

Calculus
Application of derivativesFind the values of x for which the given geometric series converges Also find the sum of the series as a function of x for those values of x n 3 n 0 x 4 Find the values of x for which the given geometric series converges Type an inequality or a compound inequality Use integers or fractions for any numbers in the inequality
Calculus
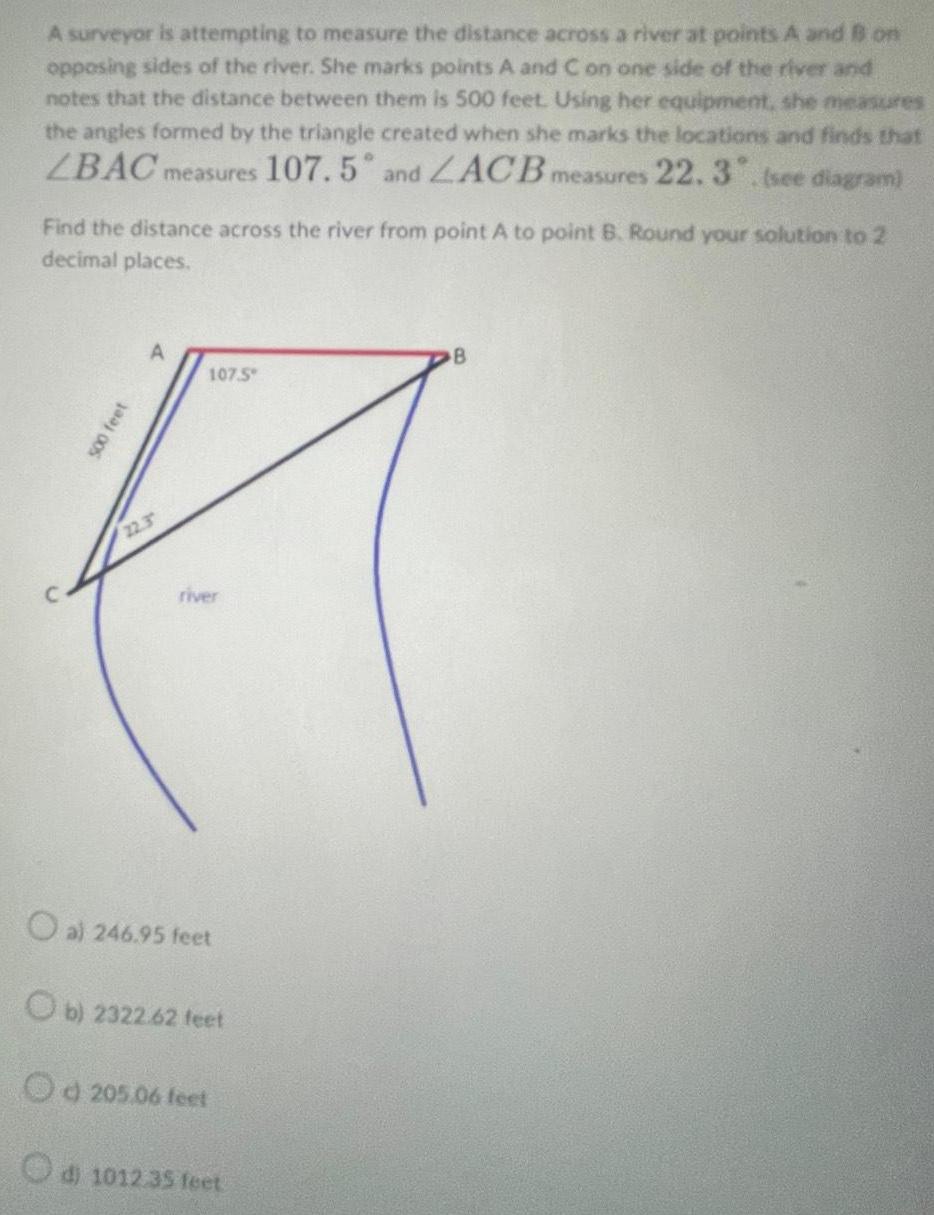
Application of derivativesA surveyor is attempting to measure the distance across a river at points A and B on opposing sides of the river She marks points A and C on one side of the river and notes that the distance between them is 500 feet Using her equipment she measures the angles formed by the triangle created when she marks the locations and finds that LBAC measures 107 5 and ZACB measures 22 3 see diagram Find the distance across the river from point A to point B Round your solution to 2 decimal places 500 feet 22 3 107 5 river O al 246 95 feet Ob 2322 62 feet Od 205 06 feet d 1012 35 feet B

Calculus
Application of derivativesDetermine if the geometric series converges or diverges If a series converges find its sum O A 9 Select the correct choice below and fill in any answer boxes in your choice 9 3 0 9 Simplify your answer OB The series diverges 5

Calculus
Application of derivativesWrite out the first few terms of the series The first term is 1 10 n 0 What is the series sum Type an integer or a simplified fraction
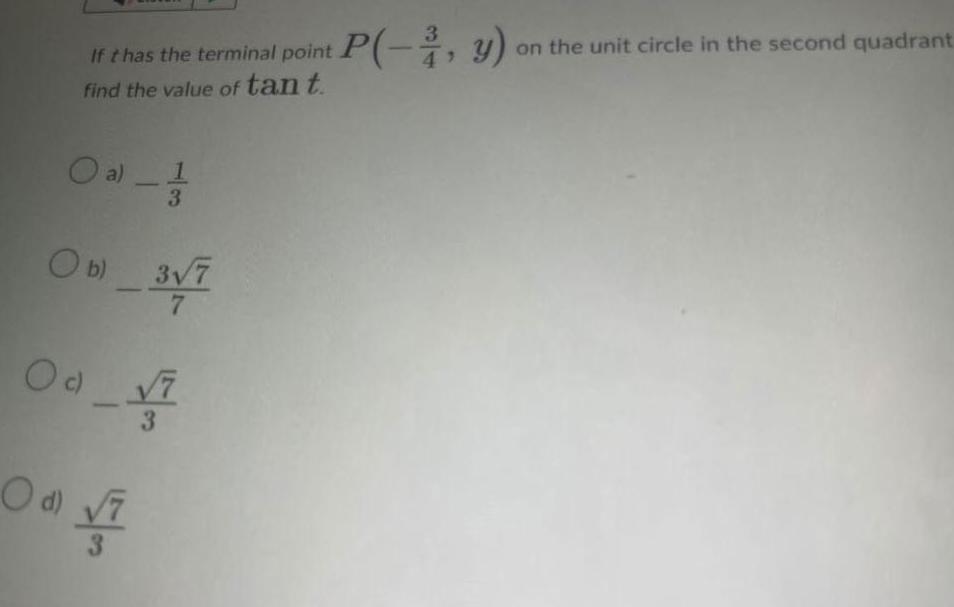
Calculus
Application of derivativesIf t has the terminal point find the value of tan t ON 13 10 a Ob 3 7 3VF 7 O c O d V 3 3 P 3 y on the unit circle in the second quadrant 4
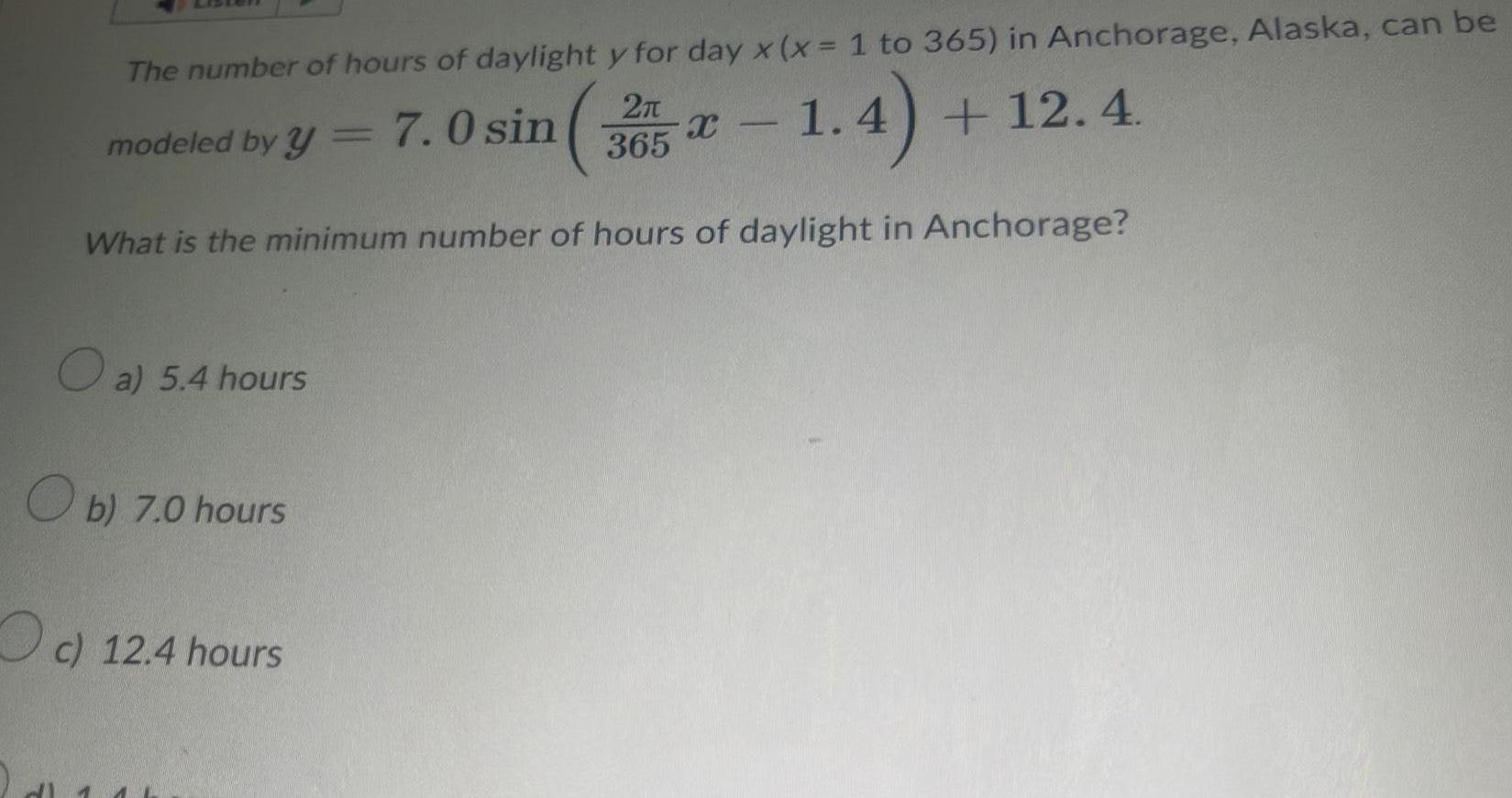
Calculus
Application of derivativesThe number of hours of daylight y for day x x 1 to 365 in Anchorage Alaska can be 1 4 12 4 What is the minimum number of hours of daylight in Anchorage modeled by y 7 0 sin a 5 4 hours b 7 0 hours c 12 4 hours 2 365 X
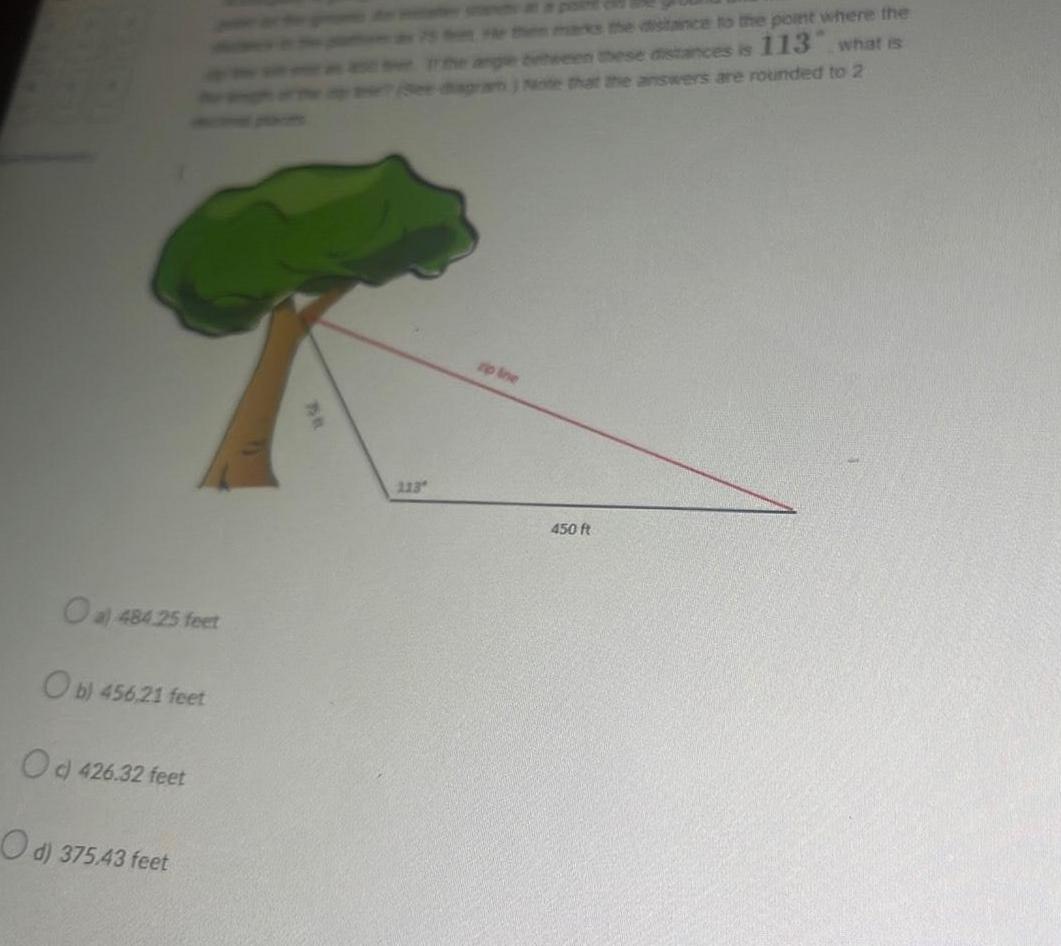
Calculus
Application of derivativesOa 484 25 feet Ob 456 21 feet Oc 426 32 feet Od 375 43 feet 113 the marks the distance to the point where the angebween these distances is 113 what is apran Note that the answers are rounded to 2 450 ft
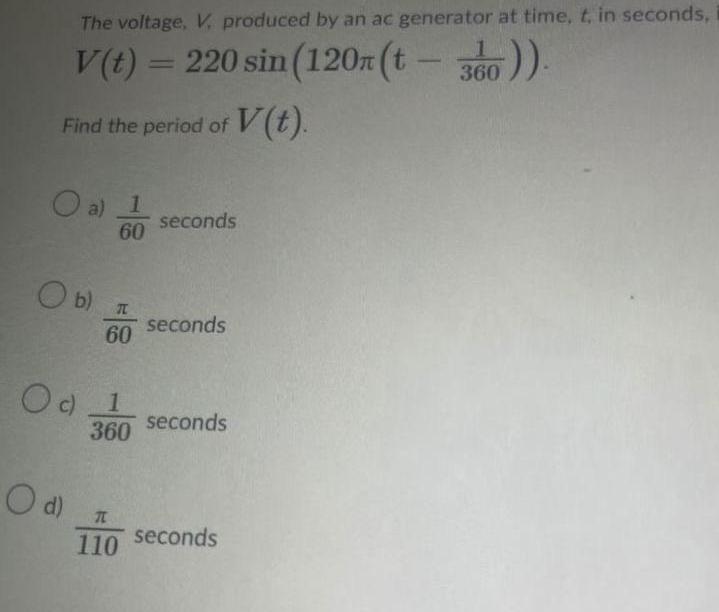
Calculus
Application of derivativesThe voltage V produced by an ac generator at time t in seconds V t 220 sin 120n t 360 360 V t Find the period of O a 1 60 O b O d T 60 Od 1 360 T 110 seconds seconds seconds seconds
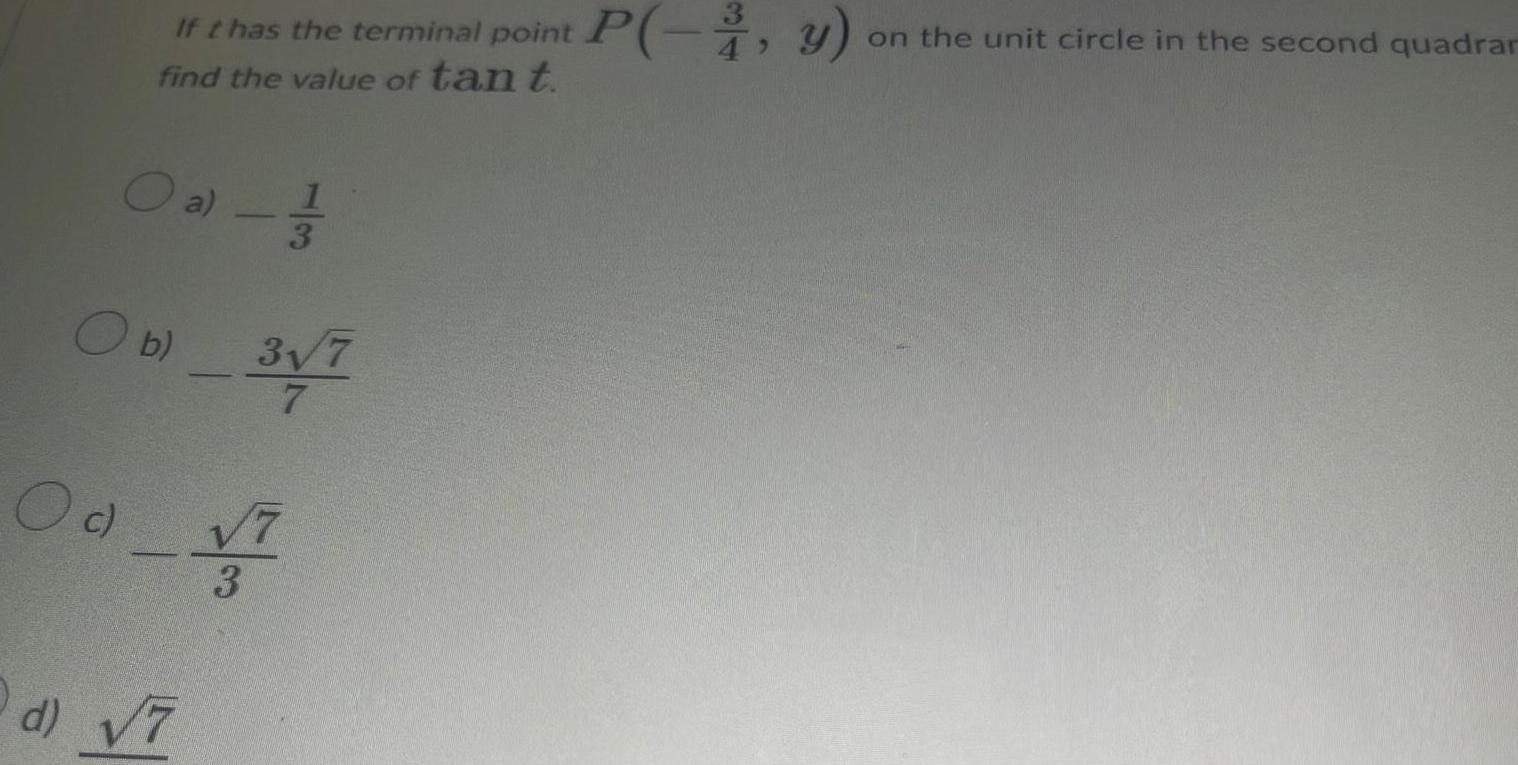
Calculus
Application of derivativesIf t has the terminal point P y on the unit circle in the second quadrar find the value of tan t Oa 1 1 20 3 O b 3 7 Od V 3 d 7

Calculus
Definite IntegralsIf the point P 20 of CSc t O a 20 21 Ob 21 20 c 29 21 la 21 29 29 d 29 20 is the terminal point of t on the unit circle find the v

Calculus
Application of derivativesConvert the angle measure from degrees to radians Round your answer to three decimal places 177 3 Trad