Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
Application of derivativesFor the cost function C x O O Cave x Cave x Cave I 2000 X 2000 x 10 10 3x 6 2 3 2000 10x 3x find Cave x
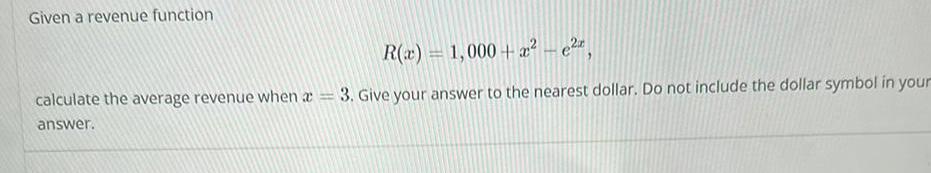
Calculus
Application of derivativesGiven a revenue function calculate the average revenue when a 1 answer R x 1 000 x 3 Give your answer to the nearest dollar Do not include the dollar symbol in your
Calculus
Application of derivativesK The function f is defined as follows f x 3 X if x 0 if x20 a Find the domain of the function b Locate any intercepts A c Graph the function d Based on the graph find the range B Ay M d Based on the graph find the range Select the correct choice below and fill in the answer box es to complete your choice OA The range does not have any isolated values It can be described by Type your answer in interval notation B The range has at least one isolated value It can be described as the union of the interval s Use a comma to separate answers as needed OC The range consists exclusively of one or more isolated values It can be described as and the set Points 0 5 of 1 D
Calculus
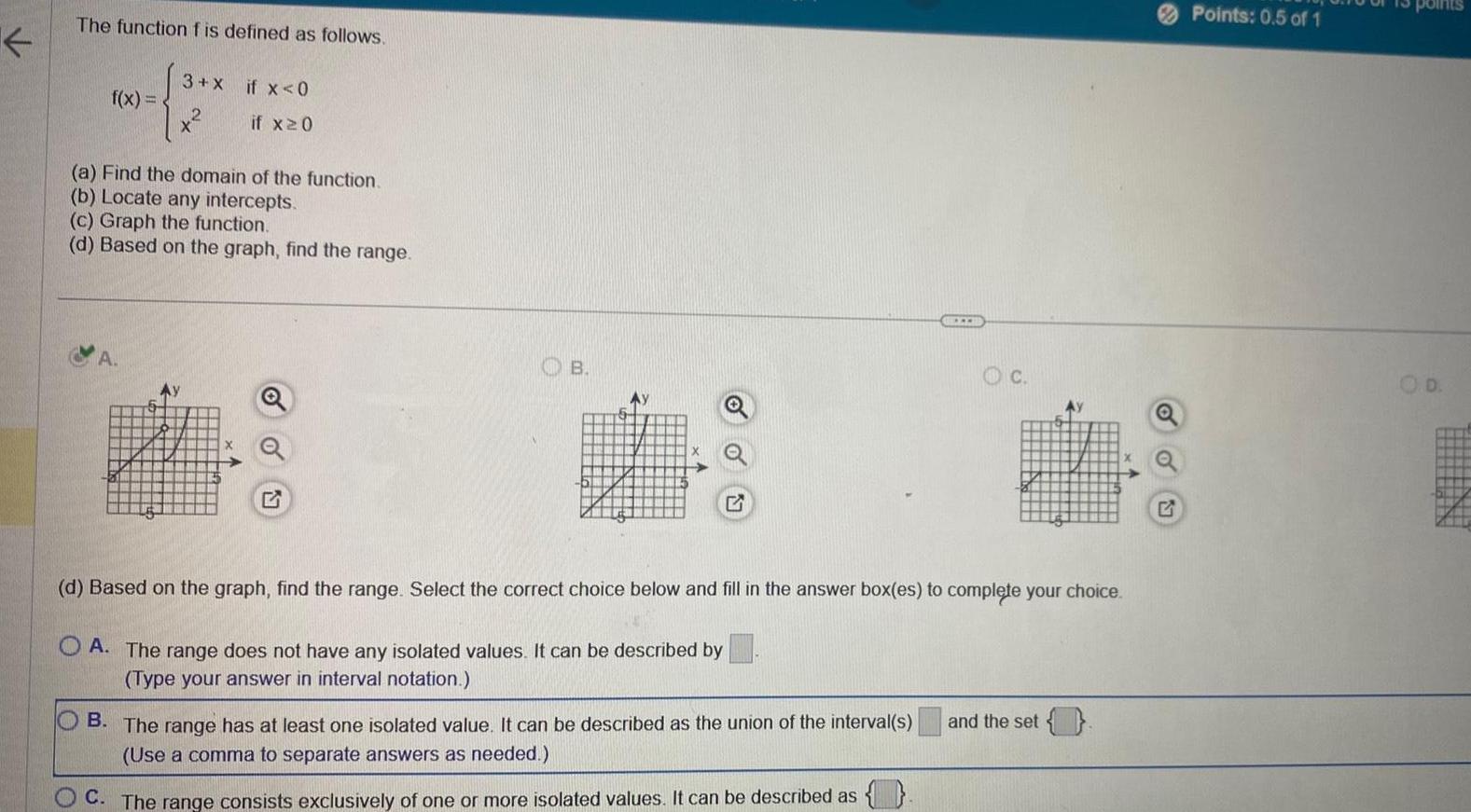
Application of derivativesilon t is defined as follows 2x 5 if x 1 4x 1 if x 1 a Find the domain of the function b Locate any intercepts c Graph the function d Based on the graph find the range f x C Choose the correct graph below OA B Ay O C d Based on the graph find the range Select the correct choice below and fill in the answer box es to complete your choice OA The range consists exclusively of one or more isolated values It can be described as O Use a comma to separate answers as needed B The range has at least one isolated value It can be described as the union of the interval s and the set Use a comma to separate answers as needed OC The range does not have any isolated values It can be described by
Calculus
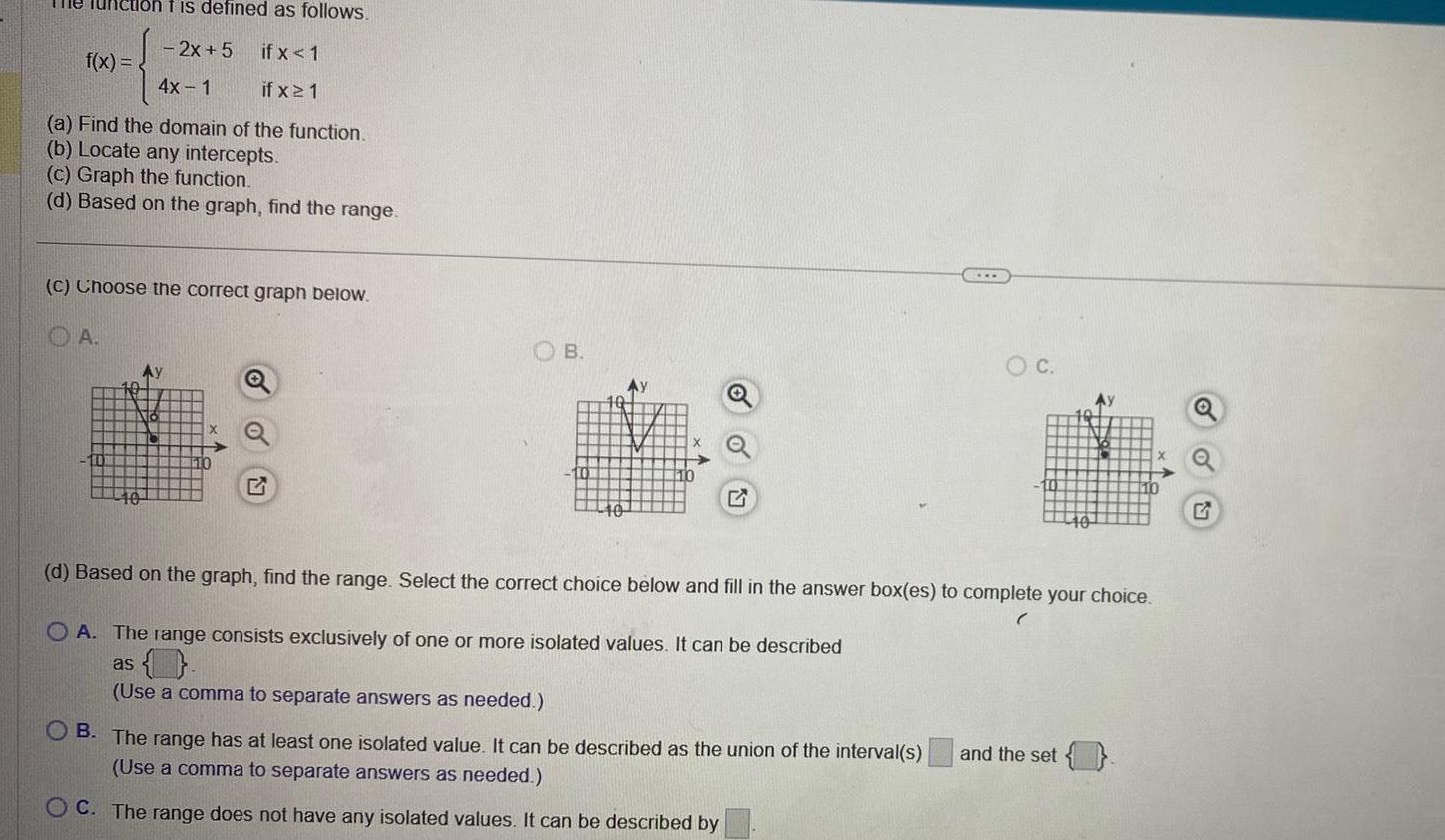
Vector Calculusf x 3 X if x 0 x if x20 a Find the domain of the function b Locate any intercepts c Graph the function d Based on the araph find the range Type your answer in interval notation b Locate any intercepts Select the correct choice below and if necessary fill in the answer box to complete your choice A The intercept s Ware 0 0 3 0 Type an ordered pair Use a comma to separate answers as needed OB There are no intercepts c Choose the correct graph of f x below O A Ay OB o c OU
Calculus
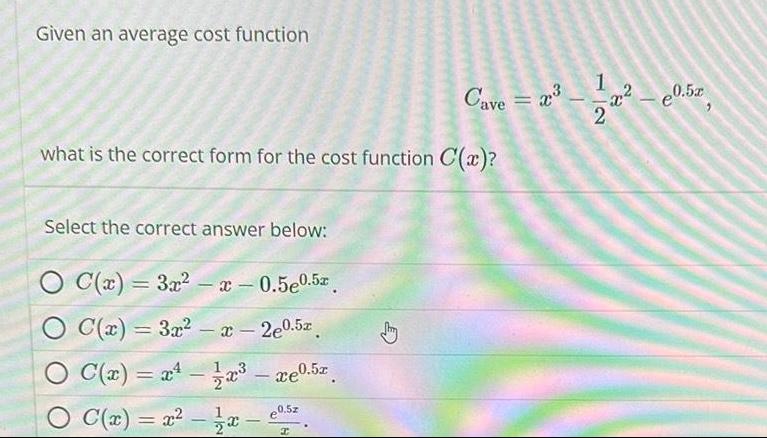
Application of derivativesGiven an average cost function Cave what is the correct form for the cost function C x Select the correct answer below O C x 3x x 0 5e0 5x O C x 3x x 2e0 5x O C x x 11x 723 xe0 5x C x x x e0 5z I 203 1 22 10 57
Calculus
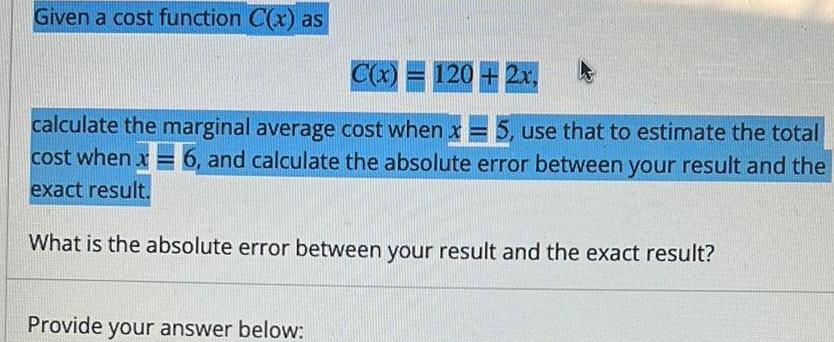
Application of derivativesGiven a cost function C x as C x 120 2x calculate the marginal average cost when x 5 use that to estimate the total cost when x6 and calculate the absolute error between your result and the exact result What is the absolute error between your result and the exact result Provide your answer below
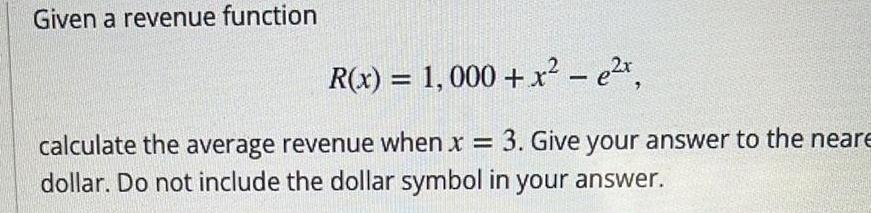
Calculus
Application of derivativesGiven a revenue function R x 1 000 x x calculate the average revenue when x 3 Give your answer to the neare dollar Do not include the dollar symbol in your answer
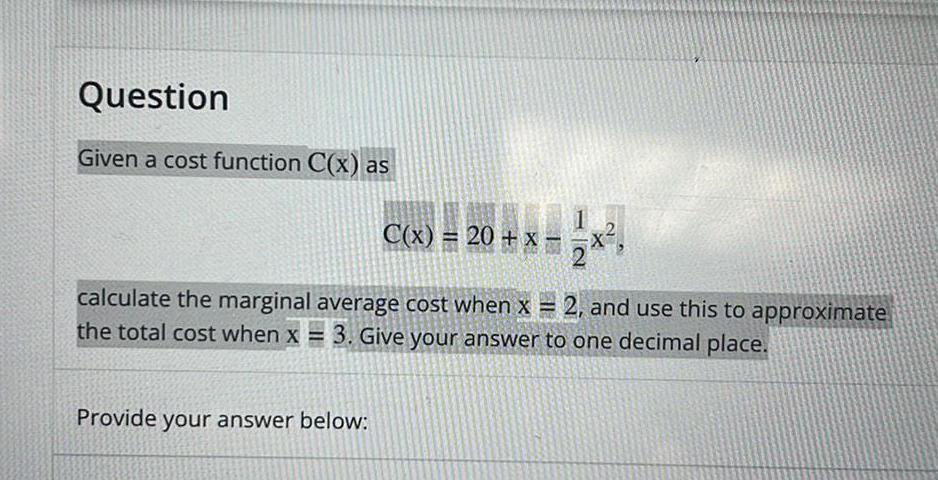
Calculus
Application of derivativesQuestion Given a cost function C x as C x 20 x Provide your answer below 1 calculate the marginal average cost when x 2 and use this to approximate the total cost when x 3 Give your answer to one decimal place
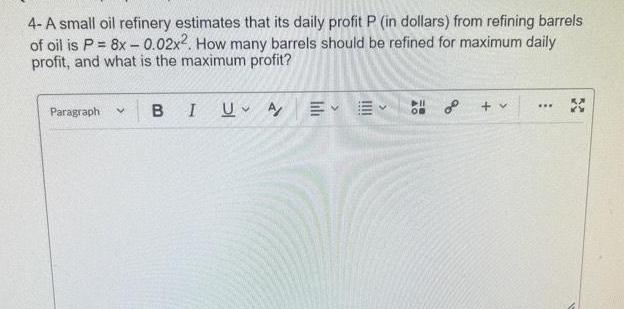
Calculus
Differential equations4 A small oil refinery estimates that its daily profit P in dollars from refining barrels of oil is P 8x 0 02x2 How many barrels should be refined for maximum daily profit and what is the maximum profit Paragraph V BI U A DII OB EE
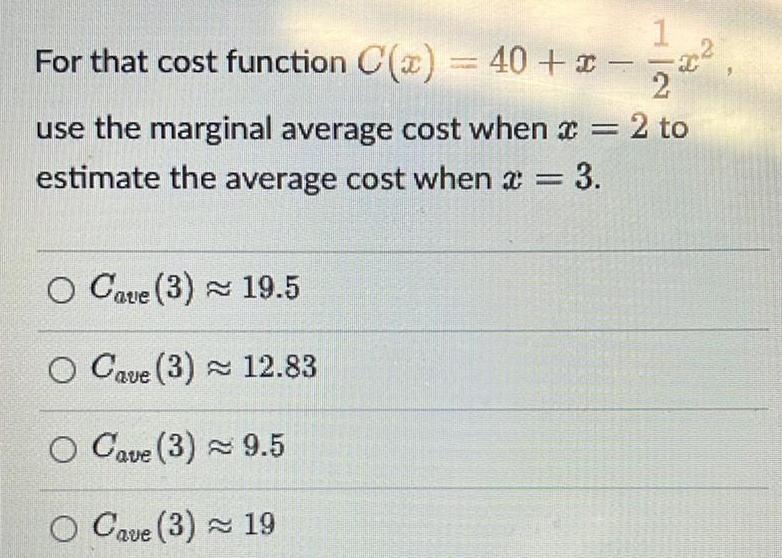
Calculus
Application of derivativesFor that cost function C x 40 x C 2 use the marginal average cost when 2 to estimate the average cost when x 3 O Cave 3 19 5 O Cave 3 12 83 O Cave 3 9 5 O Cave 3 19
Calculus
Definite IntegralsQuestion 5 10 points 5 A rectangular hole is to be cut in a wall for a vent If the perimeter of the hole is 48 cm and the length of the diagonal is a minimum what are the dimensions of the hole Paragraph v BI U A v 11 OB o v X
Calculus
Application of derivativesQuestion 7 15 points 7 Factories A and B are 8 0 km apart with factory B emitting eight times the pollutants into the air as factory A If the number n of particles of pollutants is inversely proportional to the square of the distance from a factory at what point between A and B is the pollution the least Paragraph V B I UA 2 v
Calculus
Differential equationswide is being filled at the rate of 0 80 m min At one end it is 1 0 m deep and at the other end it is 2 5 m deep with a constant slope between ends How fast is the height of water rising when the depth of water at the deep end is 1 0 m Paragraph M B I U A EE PIL o v
Calculus
Application of derivatives2 Find the coordinates of the local maximum and minimum points in the following function y 3x 15x Paragraph V B I U A E COB v www
Calculus
Application of derivatives3 Sketch the graphs of the given functions by determining the appropriate information and points from the first and second derivatives a y 12x 2x b y 2x 6x 5 Paragraph v BIU A BE 00 v

Calculus
Definite IntegralsQuestion 8 10 points 8 A race track 400 m long is to be built around an area that is a rectangle with a semicircle at each end Find the open side of the rectangle if the area of the rectangle is to be a maximum Paragraph B I U A lih

Calculus
Vector Calculuswrite O following a 4 1 r down the sequences rezt first three 4 terms of each of the a 3 8 b 1 1 b un S 2 ne zt
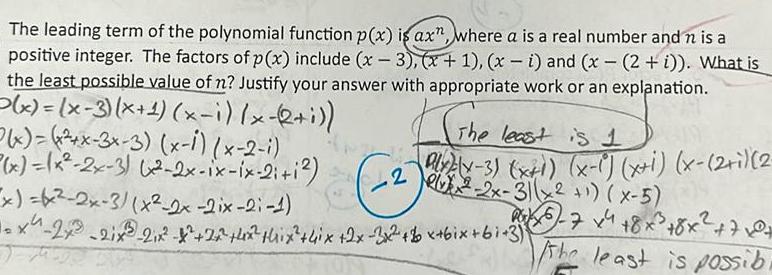
Calculus
Vector CalculusThe leading term of the polynomial function p x is ax where a is a real number and n is a positive integer The factors of p x include x 3 x 1 xi and x 2 i What is the least possible value of n Justify your answer with appropriate work or an explanation x x 3 x x i x 2 i x x x 3x 3 x 1 x 2 i x x 2x 3 x 2x ix ix 2i 1 x x 2x 3 x 2x 2ix 2 1 x 2x3 21x 2 8 X 26 4x thix 4ix 2x 3x2 bx 6ix bi 3 2 The least is 1 PLX x 3 x 1 x 1 x i x 2 i 2 xx 2x 3 x 1 x 5 2015 7 x 4 8 x 8 2 70 the least is possibi

Calculus
Differentiation18 A box with a square base and open top must have a volume of 32 000 cm Find the dimensions of the box that minimize the amount of material used

Calculus
Vector Calculus10 The rate in mg carbon m h at which photosynthesis takes place for a species of phytoplankton is modeled by the function P 100I 1 I 4 where I is the light intensity measured in thousands of foot candles For what light intensity in
Calculus
Vector Calculus4 The sum of two positive numbers is 16 What is the smallest possible value of the sum of their squares


Calculus
Application of derivatives3 City urbanization City planners model the size of their city using 1 the function A 1 2r 20 for 0 t 50 where A 50 is measured in square miles and t is the number of years after 2010 a Compute A t What units are associated with this derivative and what does the derivative measure b How fast will the city be growing when it reaches a size of 38 mi c Suppose the population density of the city remains constant from year to year at 1000 people mi Determine the growth rate of the population in 2030

Calculus
Definite Integrals41 Height estimate The distance an object falls when released from rest under the influence of Earth s gravity and with no air resis tance is given by d t 16r where d is measured in feet and t is measured in seconds A rock climber sits on a ledge on a verti cal wall and carefully observes the time it takes for a small stone to fall from the ledge to the ground a Compute d t What units are associated with the derivative and what does it measure b If it takes 6 s for a stone to fall to the ground how high is the ledge How fast is the stone moving when it strikes the ground
Calculus
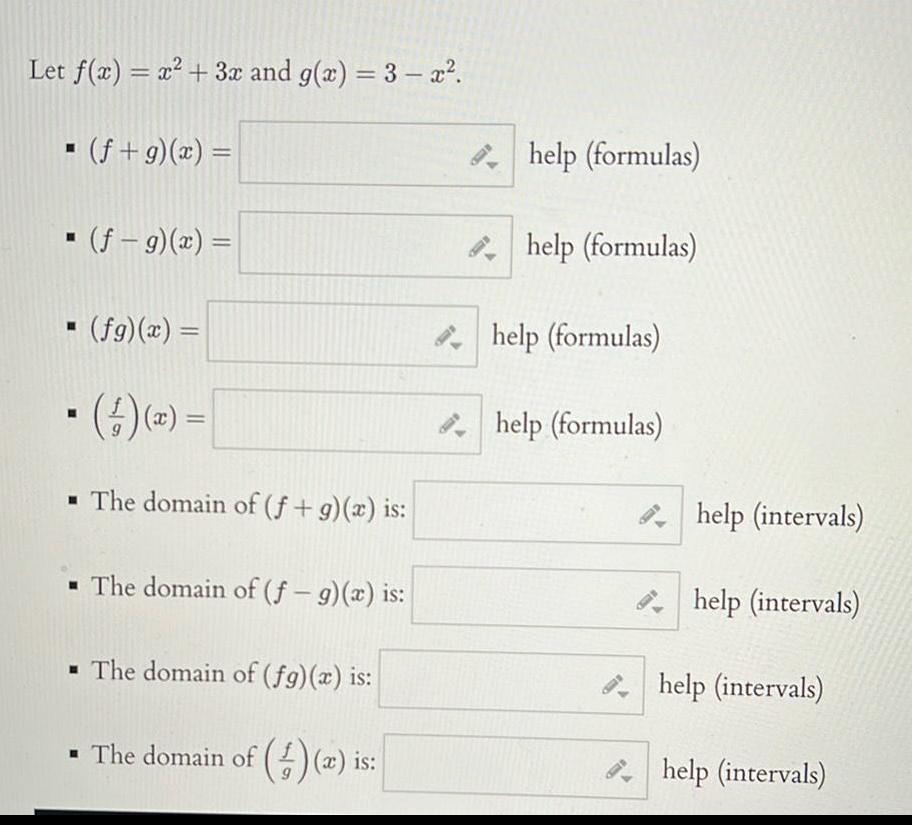
Vector CalculusLet f x x 3x and g x 3 x f g x f g x fg x 4 x The domain of f g x is The domain of f g x is The domain of fg x is The domain of x is help formulas help formulas help formulas help formulas help intervals help intervals help intervals help intervals
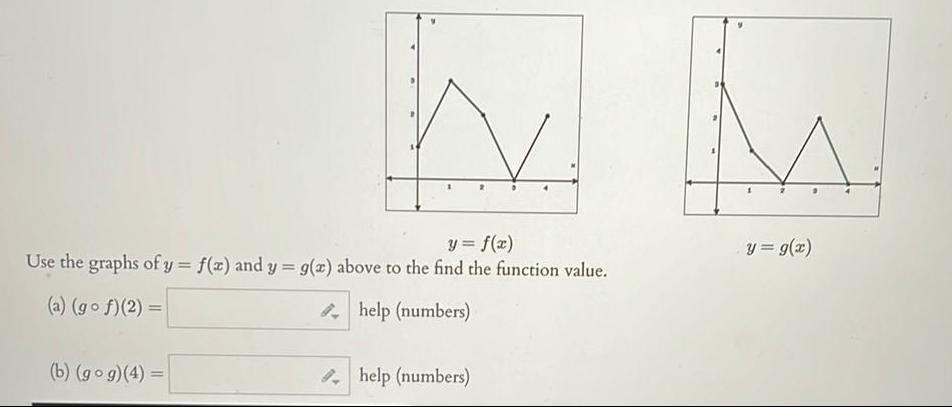
Calculus
Application of derivativesy f x Use the graphs of y f z and y g x above to the find the function value a gof 2 help numbers b gog 4 help numbers y g x
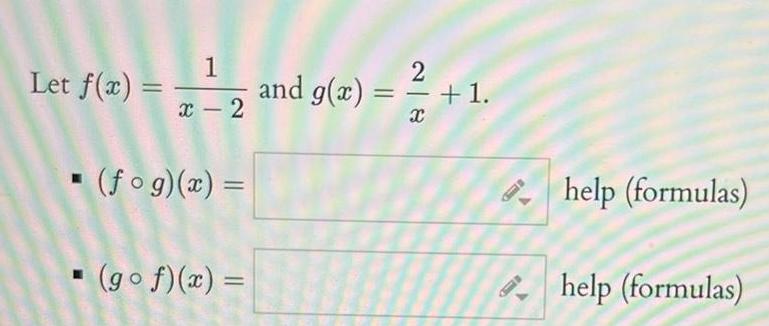
Calculus
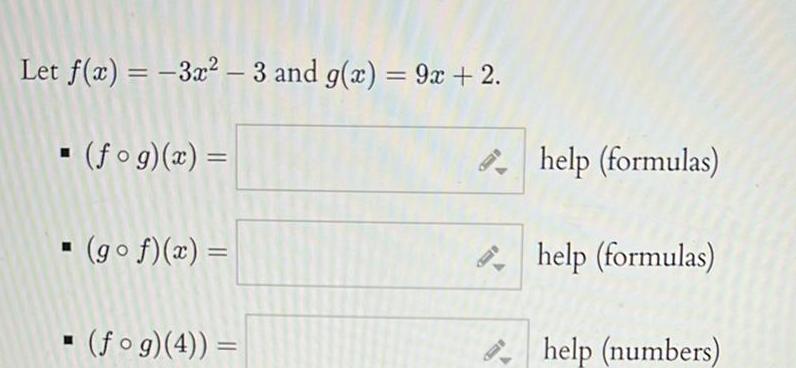
Differentiation8 1 2 3 4 5 6 7 8 9 3 f x 4 2 247622 g x 3 92 9 5 3 27 6 Use the table to evaluate the expression fog 1 help numbers

Calculus
Vector CalculusLet f x 5x and g x x 1 f g x f g x fg x 4 The domain of f g x is The domain of f g x is The domain of fg x is The domain of is help formulas help formulas help formulas help formulas help intervals help intervals help intervals help intervals
Calculus
Vector CalculusLet f x 3x 3 and g x 9x 2 fog x gof x fog 4 BI help formulas help formulas help numbers
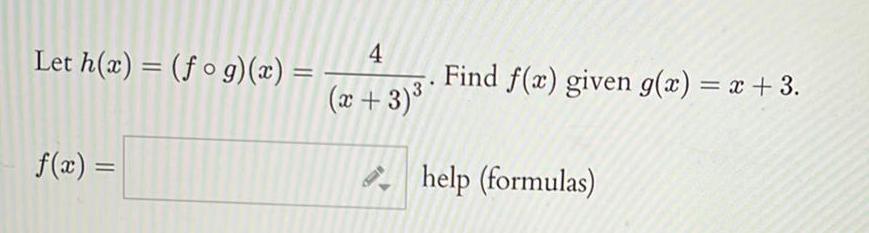


Calculus
Application of derivativesGiven that f x x and g x 5x 2 calculate a fog x b go f x c fo f x d go g x P FI E A
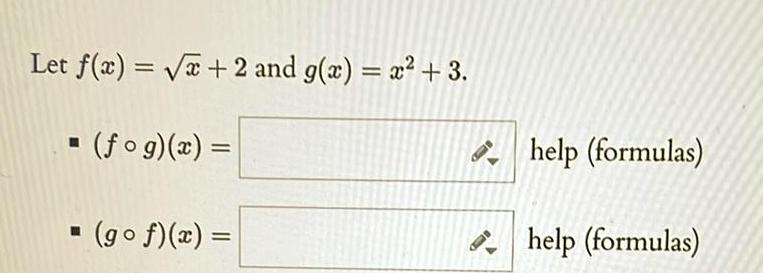
Calculus
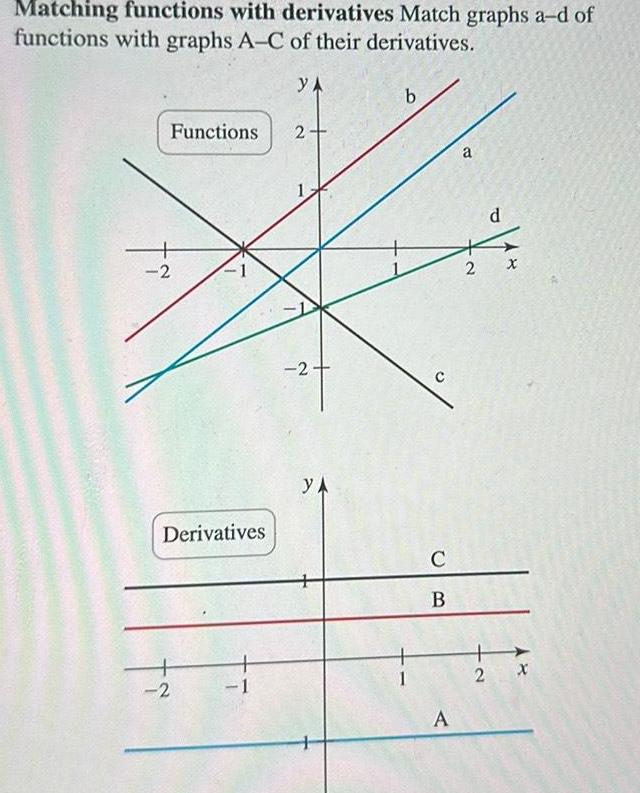
DifferentiationMatching functions with derivatives Match graphs a d of functions with graphs A C of their derivatives YA Functions 2 Derivatives 2 1 2 2 YA b C B A a d 2 X 2 x

Calculus
Vector CalculusA function f x has a local maximum if the curve changes from increasing to decreasing O True False

Calculus
Application of derivativesWhich of the following is an equivalent expression to fog x O g f x O f x g x Of x g x Of g x

Calculus
Definite IntegralsOn a hot summer afternoon a city s electricity consumption is 3t2 18t 10 units per hour where it is the number of hours after noon 0 ts 6 Find the total consumption of electricity between the hours of 1 p m and 6 p m units
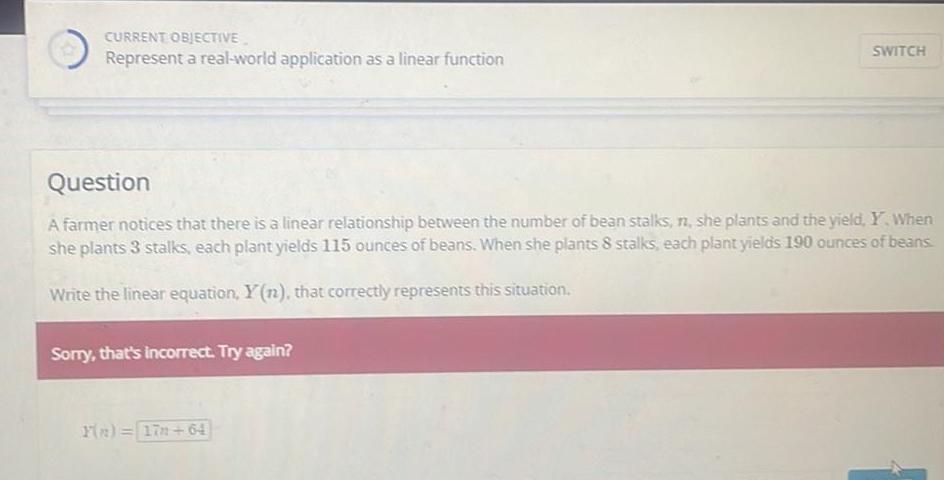
Calculus
Application of derivativesCURRENT OBJECTIVE Represent a real world application as a linear function Question A farmer notices that there is a linear relationship between the number of bean stalks n she plants and the yield Y When she plants 3 stalks each plant yields 115 ounces of beans When she plants 8 stalks each plant yields 190 ounces of beans Write the linear equation Y n that correctly represents this situation Sorry that s incorrect Try again SWITCH Y n 17 64

Calculus
Definite IntegralsA graphing calculator is recommended For the function do the following f x 32 3x from x 1 to x 2 a Integrate by hand to find the area under the curve between the given x values square units b Verify your answer to part a by having your calculator graph the function and find the area using a comman Fnint or f x dx square units

Calculus
Differential equations4 is continuous at x g Proof We are investigating continuity of f g at x c Clearly it is defined at x c We have 114 lim f g x MATHEMATICS provided g c 0 lim f x g x X C lim f x lim g x X C X C f c g c f g c Hence f g is continuous at x c Proofs for the remaining parts are similar and left as an exercise to the reader Rationalised 2023 24 Remarks i As a special case of 3 above iffis a constant function i e f x for some real number 2 then the function 2 g defined by 2 g x 2 g x is also continuous In particular if 1 the continuity of fimplies continuity of f ii As a special case of 4 above if f is the constant function f x 2 then the 2 2 2 function defined by x is also continuous wherever g x 0 In g g x g particular the continuity of g implies continuity of g by definition of f g by the theorem on limits as fand g are continuous by definition of f g The above theorem can be exploited to generate many continuous functions They also aid in deciding if certain functions are continuous or not The following illustrate this examples Example 16 Prove that every rational function is continuous Solution Recall that every rational function fis given by q x 0 p x q x f x where p and q are polynomial functions The domain offis all real numbers except points at which qis zero Since polynomial functions are continuous Example 14 fis continuous by 4 of Theorem 1 Example 17 Discuss the continuity of sine function Solution to see this we use the following facts We have not proved it but is intuitively clear from the graph of sin x near 0 Now observe that f x sin x is defined for every real number Let c be a real xc we know that h 0 Therefore number Put x c h lim f x lim sin x X C X C oblishe lim sin c h h 0 lim sinc cos h cos c sin h h 0 lim Isin c cos hl lim cosc sin hl
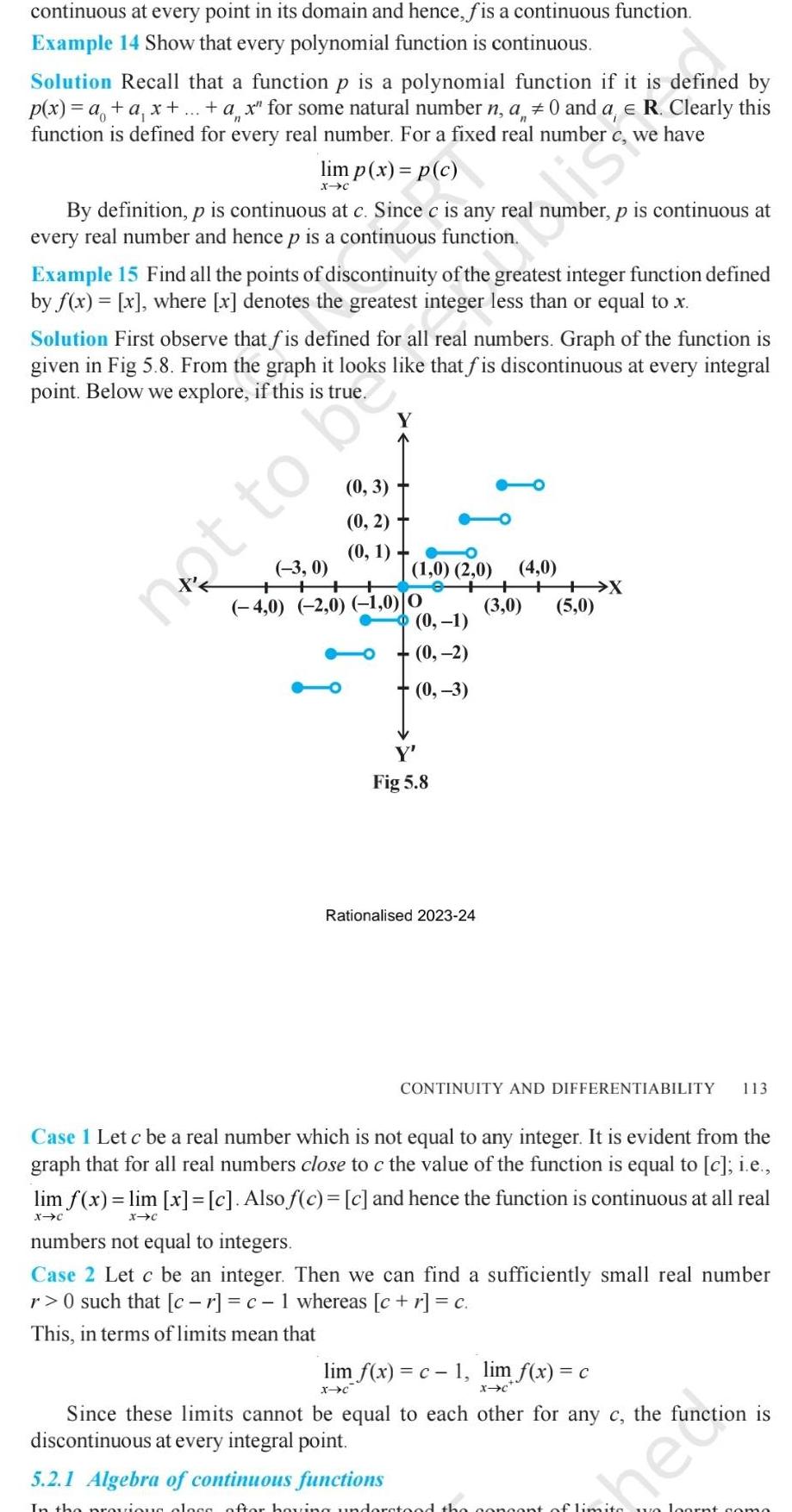
Calculus
Differential equationscontinuous at every point in its domain and hence f is a continuous function Example 14 Show that every polynomial function is continuous Solution Recall that a function p is a polynomial function if it is defined by p x a a x ax for some natural number n a 0 and a e R Clearly this function is defined for every real number For a fixed real number c we have lim p x p c X C By definition p is continuous at c Since c is any real number p is continuous at every real number and hence p is a continuous function Example 15 Find all the points of discontinuity of the greatest integer function defined by f x x where x denotes the greatest integer less than or equal to x Solution First observe that fis defined for all real numbers Graph of the function is given in Fig 5 8 From the graph it looks like that fis discontinuous at every integral point Below we explore if this is true Y 0 3 0 2 0 1 3 0 4 0 2 0 1 0 0 1 0 2 0 not to b 0 1 0 2 0 3 Y Fig 5 8 Rationalised 2023 24 4 0 3 0 X 5 0 CONTINUITY AND DIFFERENTIABILITY 113 Case I Let c be a real number which is not equal to any integer It is evident from the graph that for all real numbers close to c the value of the function is equal to c i e lim f x lim x c Also f c c and hence the function is continuous at all real X C X C numbers not equal to integers Case 2 Let c be an integer Then we can find a sufficiently small real number r 0 such that cr c 1 whereas c r c This in terms of limits mean that lim f x c 1 lim f x c X C X C Since these limits cannot be equal to each other for any c the function is discontinuous at every integral point 5 2 1 Algebra of continuous functions In the previous clogs after having understood the concept of limits we loont como he Anction

Calculus
Definite IntegralsFrom the Table 5 2 we deduce that the value of f x may be made smaller than any given number by choosing a negative real number very close to 0 In symbols we write lim f x 0 x 0 to be read as the left hand limit of f x at 0 is minus infinity Again we wish to emphasise that is NOT a real number and hence the left hand limit of fat 0 does not exist as a real number The graph of the reciprocal function given in Fig 5 3 is a geometric representation of the above mentioned facts 110 MATHEMATICS Rationalised 2023 24 f x lim f x lim x 2 c 2 f c X C X C Thus fis continuous at all points x 1 Case 3 If c 1 then the left hand limit of fat x 1 is Example 10 Discuss the continuity of the function f defined by x 2 if x 1 x 2 if x 1 lim f x lim x 2 1 2 3 x l x l The right hand limit of fat x 1 is f x 2 2 lim f x lim x 2 1 2 1 x 1 x 1 1 1 2 2 lim f x lim x 2 1 2 3 x 1 The right hand limit of fat x 1 is lim f x lim x 2 1 2 1 x 1 x 1 Since the left and right hand limits of fat x 1 Solution The function fis defined at all points of the real line Case 1 If c 1 then f c c 2 Therefore lim f x lim x 2 c 2 x c Thus fis continuous at all real numbers less than 1 Case 2 If c 1 then f c c 2 Therefore 3 1 3 3 2 1 2 2 1 1 1 3 3 Y X C 1 O X 1 2 3 Y Fig 5 3 ERT publiced 2 1 2 Example 11 Find all the points of discontinuity of the function f defined by x 2 if x 1 0 if x 1 x 2 if x 1 Solution As in the previous example we find that f is continuous at all real numbers x 1 The left hand limit of fat x 1 is 1 3 Since the left and right hand limits of fat x 1 do not coincide f is not continuous at x 1 Hence Fig 5 4 x 1 is the only point of discontinuity off The graph of the function is given in Fig 5 4 2 1 1 1 O 3 1 3 X 1 O 1 1 X F X 2 3
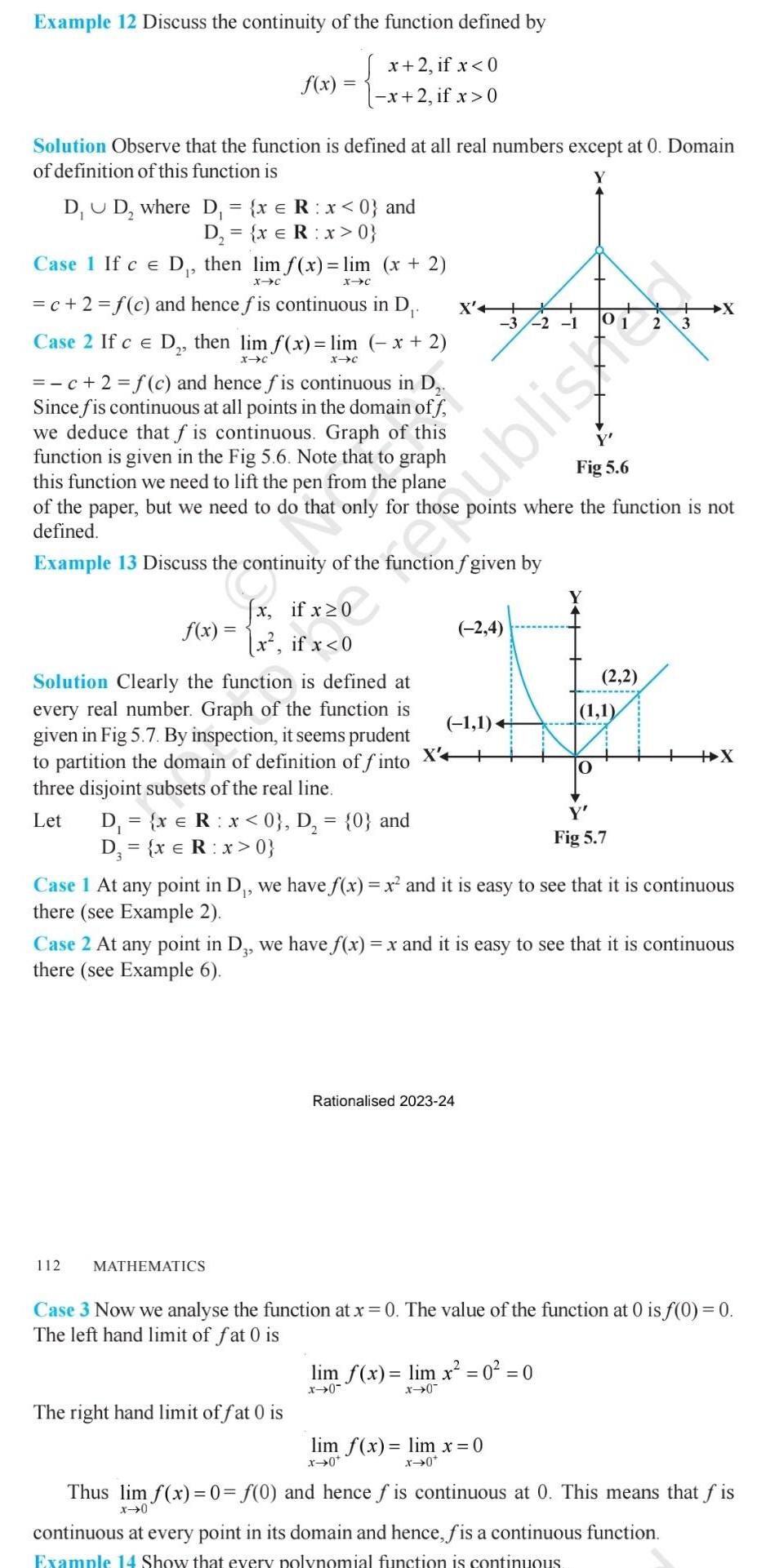
Calculus
Application of derivativesExample 12 Discuss the continuity of the function defined by x 2 if x 0 x 2 if x 0 Solution Observe that the function is defined at all real numbers except at 0 Domain of definition of this function is D D where D x R x 0 and D x R x 0 Case 1 If ce D then lim f x lim x 2 X C X C f x c 2 f c and hence fis continuous in D Case 2 If c E D then lim f x lim x 2 X C X C c 2 f c and hence fis continuous in D Since fis continuous at all points in the domain off we deduce that f is continuous Graph of this function is given in the Fig 5 6 Note that to graph this function we need to lift the pen from the plane of the paper but we need to do that only for thos defined Example 13 Discuss the continuity of the function f given by f x x x if x 0 if x 0 Solution Clearly the function is defined at every real number Graph of the function is given in Fig 5 7 By inspection it seems prudent to partition the domain of definition of finto three disjoint subsets of the real line 112 Let D x R x 0 D 0 and D x R x 0 MATHEMATICS X 3 2 1 The right hand limit of fat 0 is 2 4 1 1 Rationalised 2023 24 y Fig 5 6 points where the function is not Fig 5 7 Case 1 At any point in D we have f x x and it is easy to see that it is continuous there see Example 2 2 2 1 1 0 Case 2 At any point in D3 we have f x x and it is easy to see that it is continuous there see Example 6 lim f x lim x 0 0 x 0 x 0 Persiane lim f x lim x 0 x 0 x 0 X X Case 3 Now we analyse the function at x 0 The value of the function at 0 is f 0 0 The left hand limit of fat 0 is Thus lim f x 0 f 0 and hence fis continuous at 0 This means that fis x 0 continuous at every point in its domain and hence fis a continuous function Example 14 Show that every polynomial function is continuous

Calculus
Limits & Continuity4 Which Series converge or diverge give reasons for your answer If it converges find the sum 3 a 1 1 b 1 n 2 8 n 1 n 1

Calculus
DifferentiationFind a formula for the nth term of the sequence in terms of n 1 2 22 23 24 10 15 20 25 30 an for n 1

Calculus
Limits & Continuity3 Tell if the sequence converges or diverges If it converges find it s limit n 1 a a b an n 2n 1 1 3 n 1 1 n c a 70 4n d a 2 11 2 2