Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
Application of derivativesFind positive numbers x and y satisfying the equation xy 25 such that the sum 5x y is as small as possib Let S be the given sum What is the objective function in terms of one number x S 5x 25 X Type an expression The interval of interest of the objective function is 0 0 Simplify your answer Type your answer in interval notation The numbers are x 5 and y 5 5
Calculus
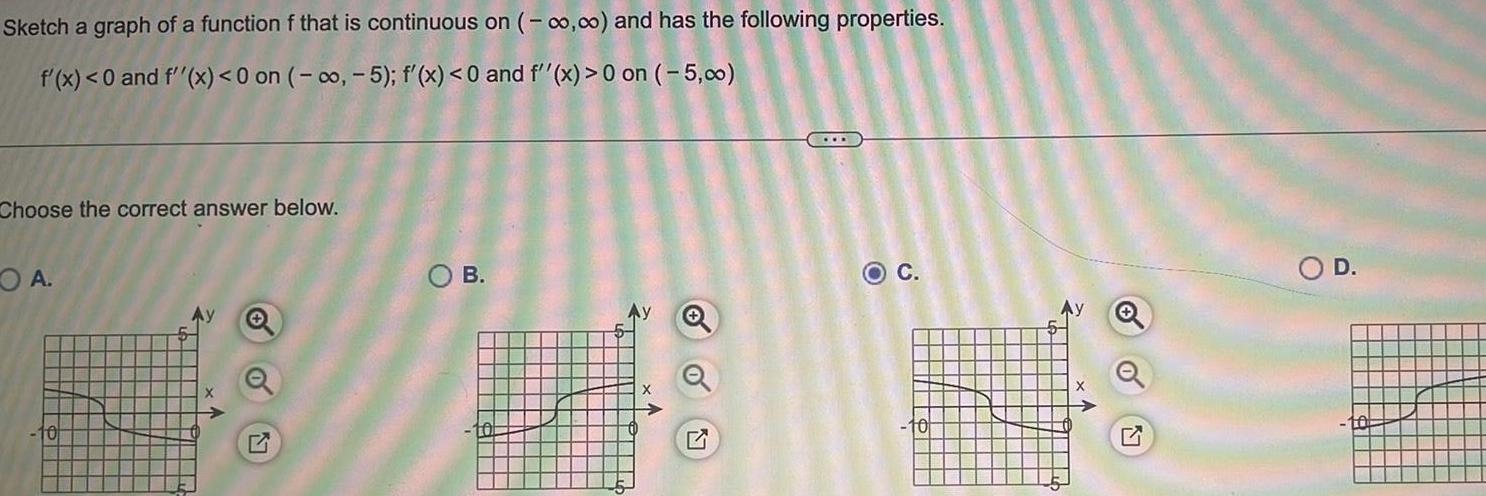
Application of derivativesSketch a graph of a function f that is continuous on 00 00 and has the following properties f x 0 and f x 0 on 5 f x 0 and f x 0 on 5 00 Choose the correct answer below OA Ay O B O D

Calculus
Application of derivativesA long jumper leaves the ground at an angle of 22 above the horizontal at a speed of 11 m s The height of the jumper can be modeled by x 0 053x 0 364x where it is the jumper s height in meters and x is the horizontal distance from the point of launch Part 0 3 Part 1 of 3 a At what horizontal distance from the point of launch does the maximum height occur Round to 2 decimal places The long jumper reaches a maximum height when the horizontal distance from the point of launch is approximately meters

Calculus
Limits & ContinuityQUESTION 13 got your water for your tea boiling to 212 F You prefer to drink your tea at a temperature of 100 F If you set it aside in a room where the temperature is 72 F how long until you can drink it Use Newton s Law Cooling to answer the question The k value is known to be 0 118 relative to time in minutes kt 6 T
Calculus
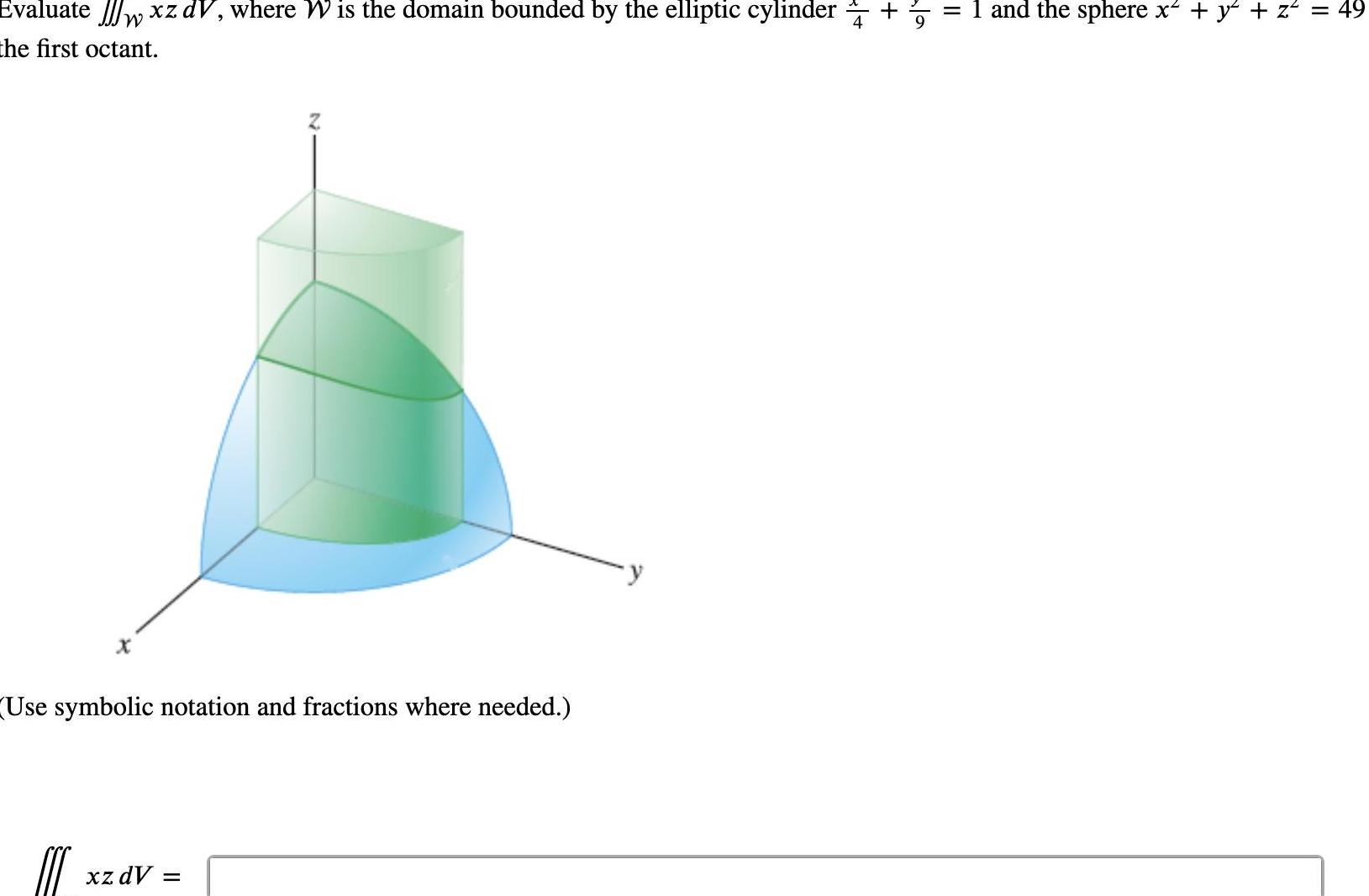
Indefinite IntegrationEvaluate w xz dV where W is the domain bounded by the elliptic cylinder the first octant W Use symbolic notation and fractions where needed C xz dV II and the sphere x y z
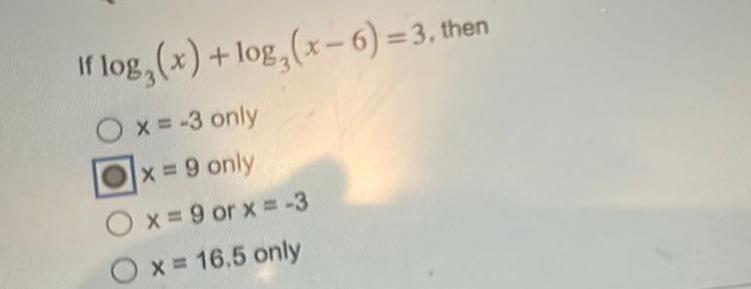
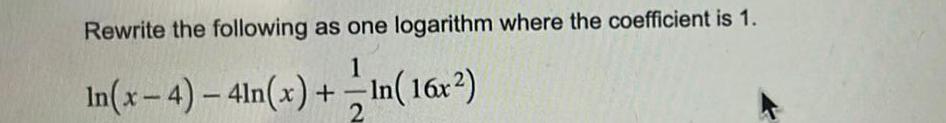
Calculus
Application of derivativesRewrite the following as one logarithm where the coefficient is 1 1 In x 4 4ln x In 16x 2

Calculus
Application of derivativesOne way to model exponential growth and decay is with percentages Doing so we can use the following equation where a is the starting value r and its sign is the growth decay rate as a decimal and t is the time A a 1 r Note that the time and percent need to have the same respective units of time a Vehicles are known to depreciate at a rate of approximately 16 per year Write a model for the depreciation of a brand new 35 000 vehicle over time b In what year will your vehicle be worth 10 000


Calculus
Application of derivativesA scientist begins with 250 grams of a radioactive substance After 340 minutes the sample has decayed to 32 grams a Rounding to five decimal places write an exponential equation representing this situation b To the nearest minute what is the half life of this substance
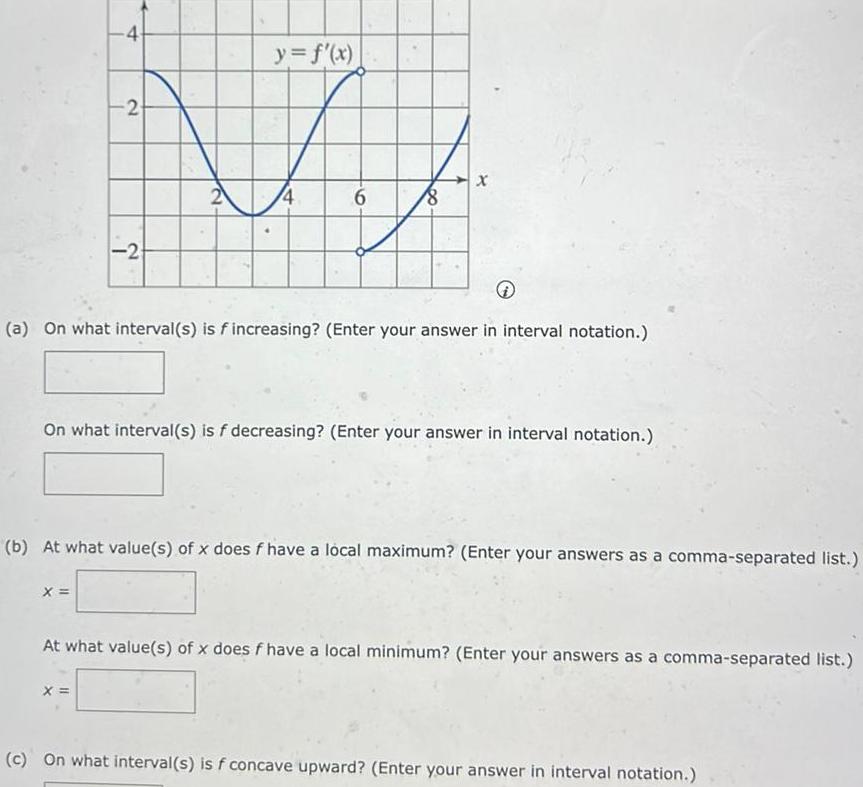
Calculus
Application of derivatives4 2 X 2 2 X y f x 6 8 a On what interval s is f increasing Enter your answer in interval notation x On what interval s is f decreasing Enter your answer in interval notation b At what value s of x does f have a local maximum Enter your answers as a comma separated list At what value s of x does f have a local minimum Enter your answers as a comma separated list c On what interval s is f concave upward Enter your answer in interval notation


Calculus
Application of derivativesA certain biological compund is known to have exponential growth The initial measurement show there is 3 grams of the compound One day later there is 3 7 grams of th compound Thinking of the exponential equation A Aek find the value of k kt O a k 0 1769 Ob k 1 1935 Ock 0 2097 d k 1 1564

Calculus
Application of derivativesTutorial Exercise Find the limit Use l Hospital s Rule where appropriate If there is a more elementary method consider using it lim X 0 cos x 1 x 4x4
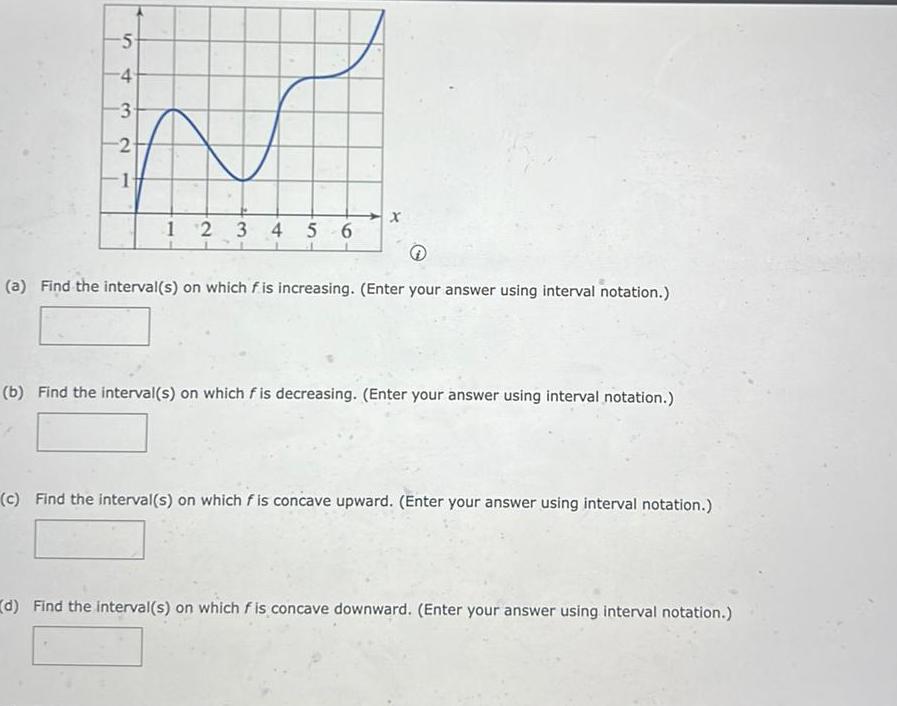
Calculus
Application of derivatives5 4 3 2 1 12 3 4 5 6 x a Find the interval s on which f is increasing Enter your answer using interval notation b Find the interval s on which f is decreasing Enter your answer using interval notation c Find the interval s on which fis concave upward Enter your answer using interval notation d Find the interval s on which fis concave downward Enter your answer using interval notation

Calculus
Application of derivativesFor each of the following state the aysmptote Be sure to state it as the equation of a line a y 2 2 b y in x 2 C y In x 1 d y 2x 2

Calculus
Limits & ContinuityApproximate the following logarithms given log 2 0 3562 log 3 0 5646 a log 60 b log 106 c log 1 d 10 b 100 11 log 5 0 8271

Calculus
Application of derivativesThe logistic growth function describes the number of people in a particular community who believe an internet conspiracy days after its initial post 12 000 y 1 199e 0 625t a How many people believed shared the conspiracy initially b How many people believed in the conspiracy after the 4th day c What is the carrying capacity and what does it mean

Calculus
Application of derivativesAngle has a measure of of 32 Provide your answer below What is its measure in degrees

Calculus
Application of derivativesConvert the angle 200 into radians Enter an exact fraction that contains the symbol

Calculus
Application of derivativesWhat is the radian measure of 210 Enter an exact fraction that contains the symbol

Calculus
Limits & ContinuityFind an angle A that is coterminal with an angle measuring 470 where 0 A 360 Do not include the degree symbol in your answer For example if your answer is 20 you would enter 20 Provide your answer below

Calculus
Application of derivatives3 A bee is flying around and its velocity function is given by v t 1 e 3t and has initial position at the point 2 1 0 Where does the bee hit the surface of th parabolic cylinder z x 9 and what is the speed at which the bee hits this surface Us technology to help approximate the solutions
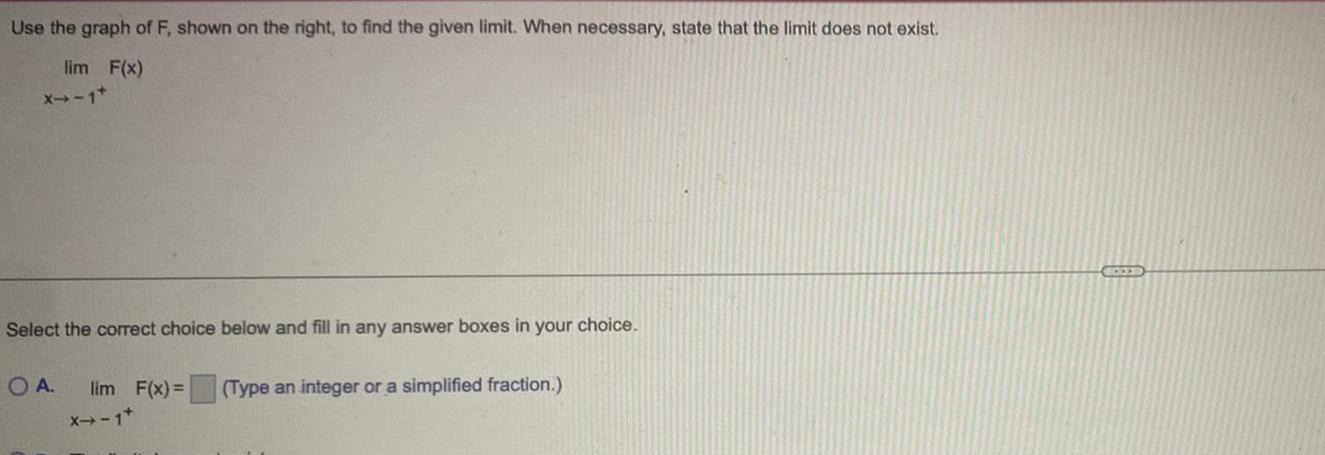
Calculus
Limits & ContinuityUse the graph of F shown on the right to find the given limit When necessary state that the limit does not exist lim F x X 1 Select the correct choice below and fill in any answer boxes in your choice OA lim F x Type an integer or a simplified fraction X 1

Calculus
Limits & ContinuityThe average price of a ticket to a baseball game can be approximated by p x 0 03x 0 42x 6 69 where x is the number of years after 1991 and p x is in dollars a Find p 5 b Find p 15 c Find p 15 p 5 d Find P 15 p 5 15 5 and interpret this result a p 5 Simplify your answer b p 15 Simplify your answer c p 15 p 5 Simplify your answer p 15 p 5 15 5 Simplify your answer Which of the following is the appropriate interpretation of this result d OA The result tells us that the price of a baseball ticket in 2016 is this amount more than in 2006 B From 1996 to 2006 the price of baseball tickets increased by this amount per year OC This amount was the average price difference of a baseball ticket from 1996 to 2006 OD From 1996 to 2006 the average price for a ticket increased on average by this amount per year
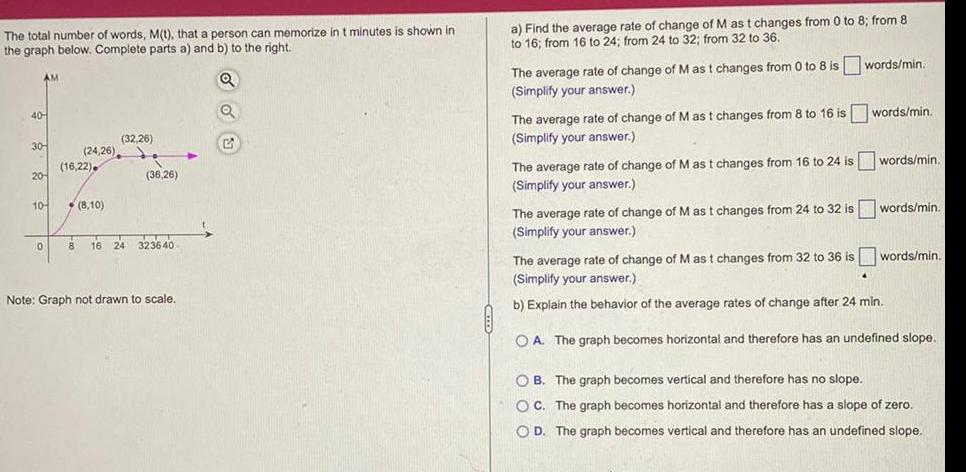
Calculus
Application of derivativesThe total number of words M t that a person can memorize in t minutes is shown in the graph below Complete parts a and b to the right 40 AM 30 20 10 0 24 26 16 22 8 10 32 26 8 16 24 36 26 323640 Note Graph not drawn to scale t Q 5 a Find the average rate of change of M as t changes from 0 to 8 from 8 to 16 from 16 to 24 from 24 to 32 from 32 to 36 The average rate of change of M as t changes from 0 to 8 is Simplify your answer The average rate of change of M as t changes from 8 to 16 is words min Simplify your answer The average rate of change of M as t changes from 16 to 24 is Simplify your answer words min The average rate of change of M as t changes from 24 to 32 is Simplify your answer words min words min words min The average rate of change of M as t changes from 32 to 36 is Simplify your answer b Explain the behavior of the average rates of change after 24 min OA The graph becomes horizontal and therefore has an undefined slope OB The graph becomes vertical and therefore has no slope OC The graph becomes horizontal and therefore has a slope of zero OD The graph becomes vertical and therefore has an undefined slope

Calculus
Indefinite IntegrationCalculate the following antiderivatives a 13 b 13t5t 2 dt S c 1 u9 4 1 504 4 u du C dx C C

Calculus
Application of derivativesWe can now use the substitution u sin 8 so du 8 sec 4 u Step 4 sec sin 8 Jn 3 15 4 We have determined that if we let u sin 8 then du cos 8 de on the interval 4 cos 8 de sin 0 du 15 4 5 2 Step 5 We can now evaluate the integral 15 4 5 2 1 15 4 U 2 cos 8 15 4 24 cos 8 du de Once more we must also make a substitution for the limits of integration When 8 TT 15 VS VTS Applying the substitution gives us the following result
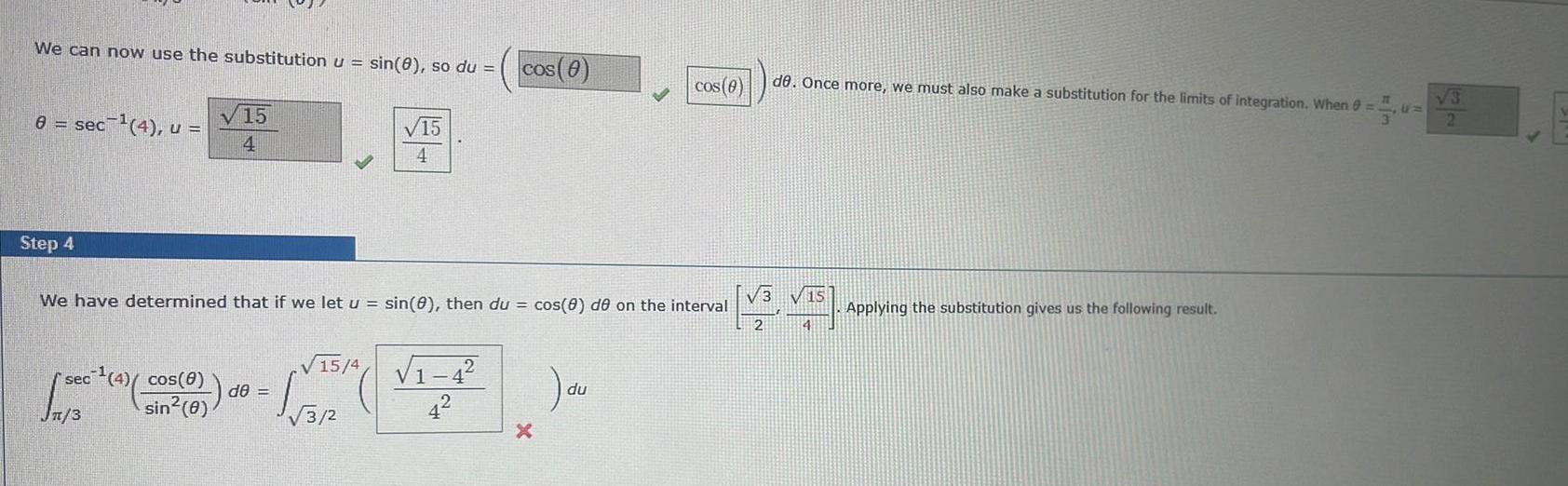
Calculus
Definite IntegralsWe can now use the substitution u sin 8 so du 8 sec ec 4 u Step 4 sec 4 cos 0 sin 0 15 4 JAS 4 We have determined that if we let u sin 8 then du cos 8 de on the interval V15 4 V1 1 329 4 de cos 0 cos 0 du de Once more we must also make a substitution for the limits of integration When 0 V3 v15 2 14 Applying the substitution gives us the following result 15

Calculus
Definite IntegralsStep 3 So far we have the following 10metric integral we put everything in terms of sin 0 and cos 0 Doing so gives the following result cos 8 sec 4 sec 0 tan e de tan 8 3 Step 4 8 sec 4 u sec 4 3 3 We can now use the substitution u sin 0 so du cos 8 sin 8 sec 4 cos 8 sin 0 4 de 15 4 sec 2007 4 Jn 3 15 4 de 3 2 15 4 sin 0 cos 8 We have determined that if we let u sin 0 then du cos 8 de on the interval sin 0 du cos 6 de de Once more we must also make a substitution for the limits of integration When 15 Applying the substitution gives us the following result
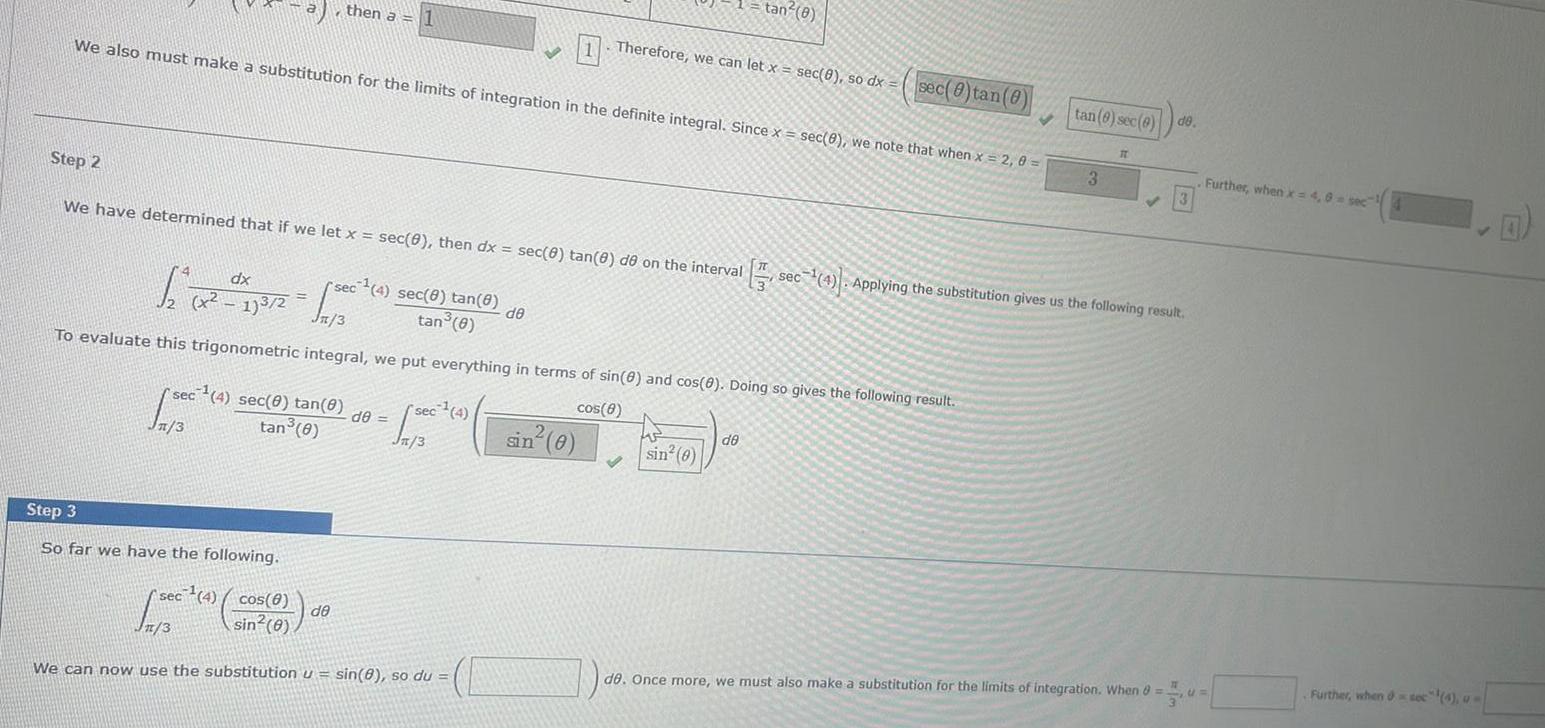
Calculus
Definite IntegralsWe also must make a substitution for the limits of integration in the definite integral Since x sec 8 we note that when x 2 0 then a 1 Step 2 We have determined that if we let x sec 0 then dx sec 8 tan 8 de on the interval sec 4 sec 0 tan 0 1 3 tan 0 Step 3 So far we have the following rsec 4 sec 8 tan 8 tan 0 dx 1 x x 173 2 1500 Jn 3 To evaluate this trigonometric integral we put everything in terms of sin 8 and cos 0 Doing so gives the following result cos 8 de de sec 4 Jn 3 sec 4 cos 8 Jn 3 sin 0 We can now use the substitution u sin 8 so du de Therefore we can let x sec 0 so dx sin 0 tan 8 V sin 0 de sec 0 tan 0 tan 6 sec 0 de 3 IT 3 sec 4 Applying the substitution gives us the following result de Once more we must also make a substitution for the limits of integration When 8 CI Further when x 4 8 sec Further when soc 4 u

Calculus
Definite IntegralsWe note that x 1 3 2 x 1 Therefore the following entry from the Table of Trigonometric Substitutions is appropriate Expression x a If x 1 x a then a 1 Submit x a sec 8 0 0 Substitution dx 12 12 X17 2 100 0 S sec 4 sec 8 tan 8 tan 8 0 1 or or 8 2 We also must make a substitution for the limits of integration in the definite integral Since x sec 0 we note that when x 2 0 sec 4 sec 8 tan e de tan 0 Skip you cannot come back sec 4 Jn 3 2 1 Step 2 We have determined that if we let x sec 8 then dx sec 8 tan 8 de on the interval sec 4 Applying the substitution gives us the following result 3 2 de n 3 To evaluate this trigonometric integral we put everything in terms of sin 0 and cos 8 Doing so gives the following result cos 8 Identity sec 0 1 tan 0 Therefore we can let x sec 0 so dx sec 0 tan 0 de tan 8 sec 8 de 3 TL 3 Further when x 4 8 sec 4
Calculus
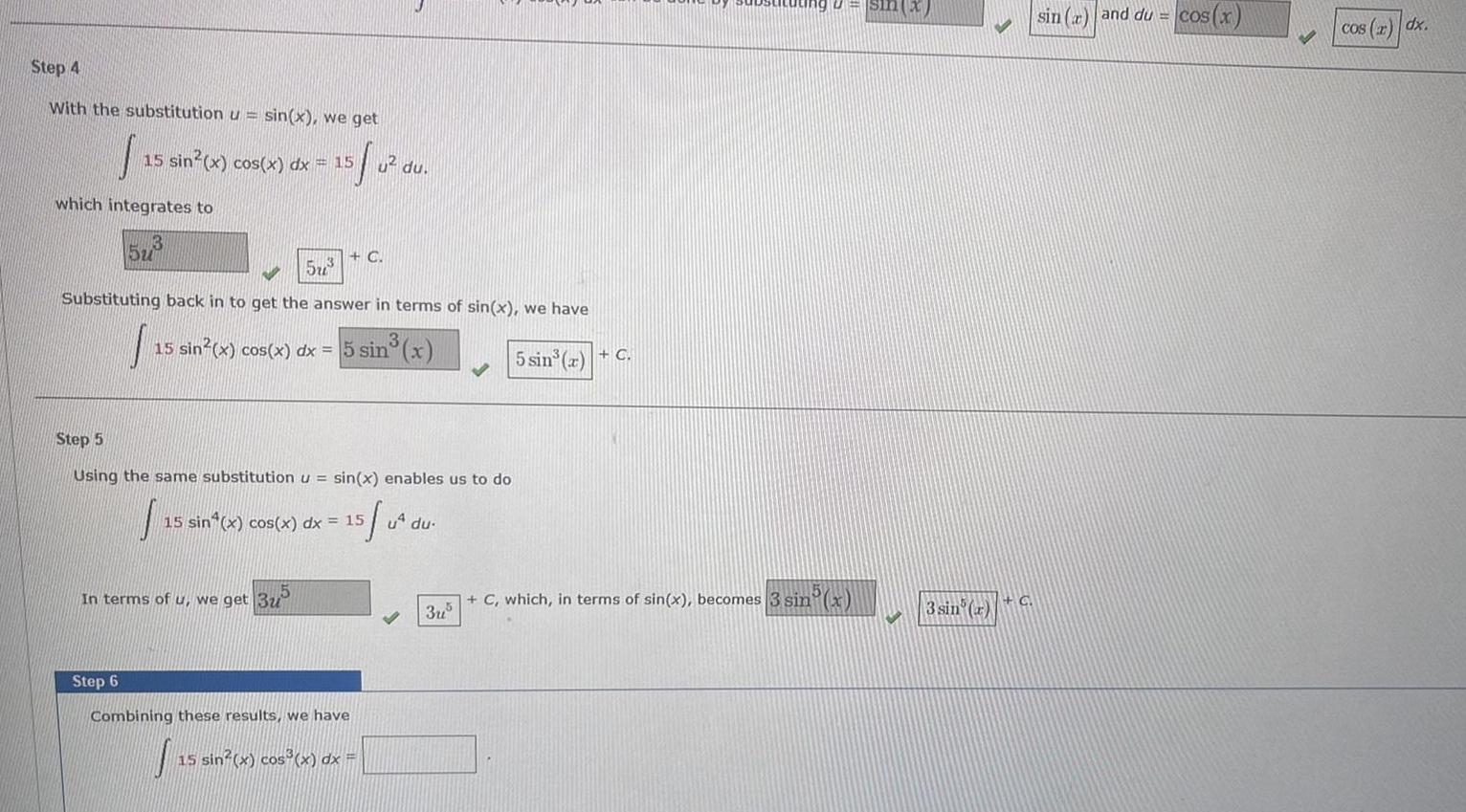
Indefinite IntegrationStep 4 With the substitution u sin x we get 15 sin x cos x dx 15 S which integrates to 13 5u 573 u du G Substituting back in to get the answer in terms of sin x we have sin x In terms of u we get 3u 15 sin x cos x dx 5 sin Step 5 Using the same substitution u sin x enables us to do 15 sin x cos x dx 15 Step 6 Combining these results we have J 15 sin x cos x dx 5 u du 3u 5 sin a C sin x C which in terms of sin x becomes 3 sin x 3 sin x C sin r and du cos x cos x dx
Calculus
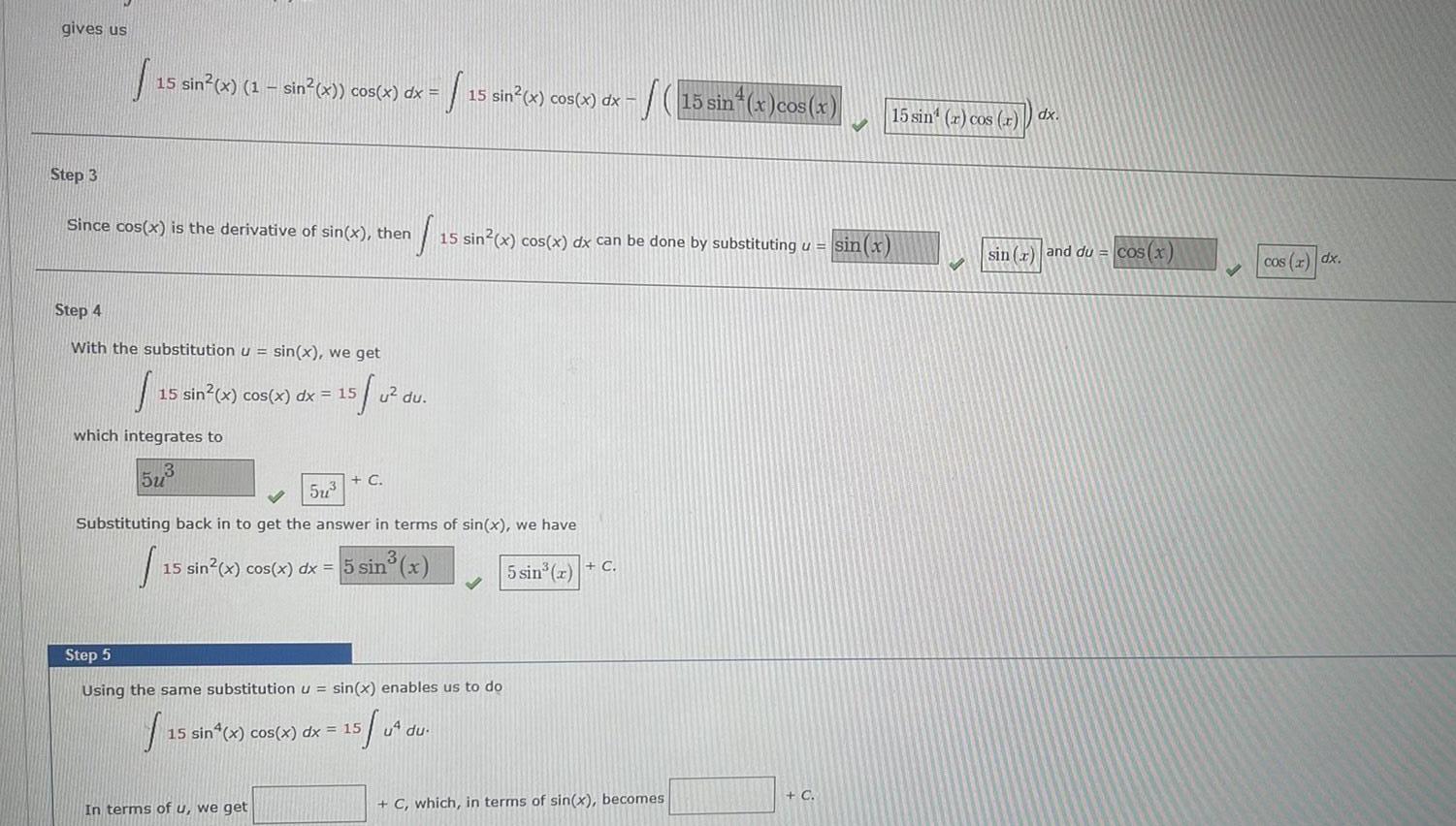
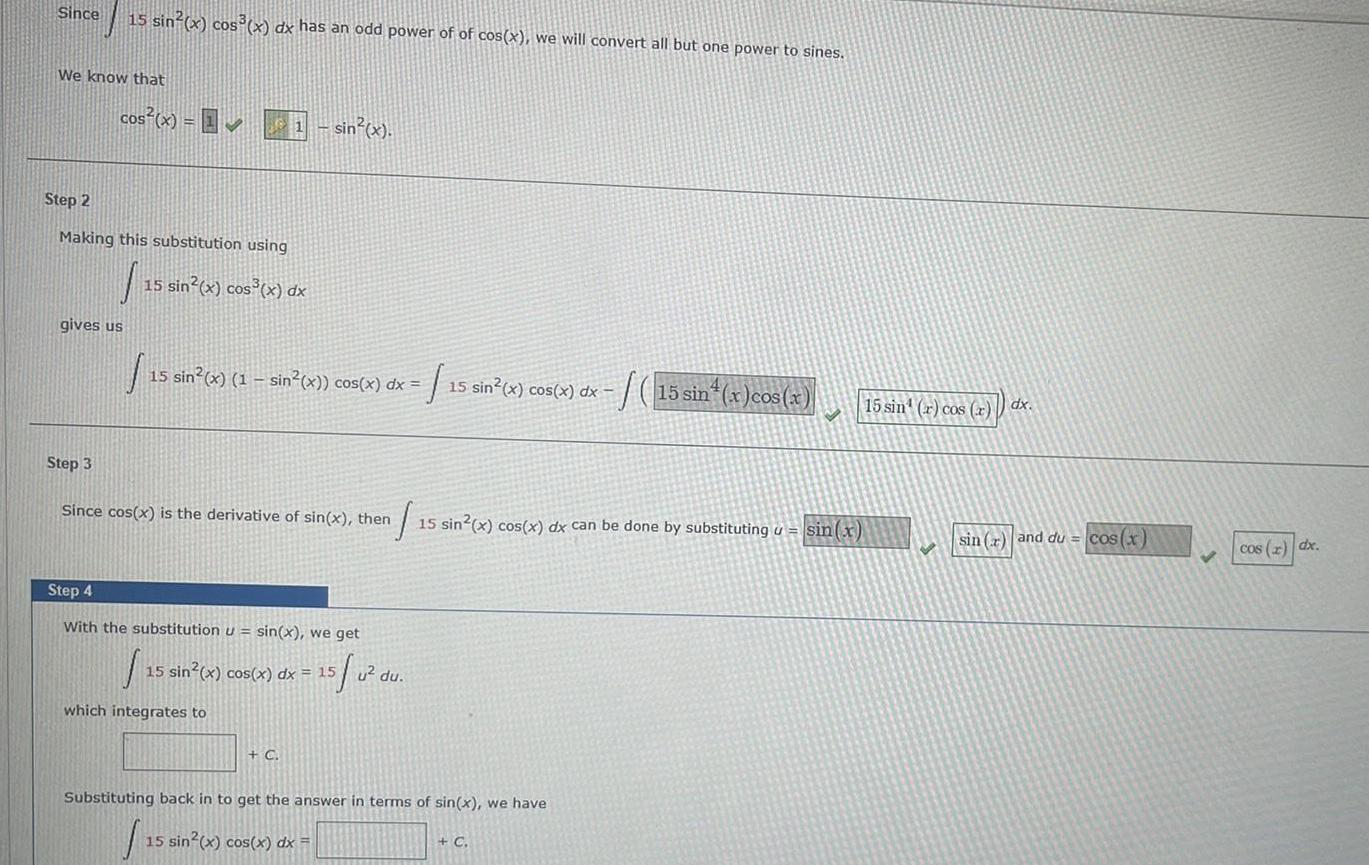
Indefinite Integrationgives us Step 3 15 sin x 1 sin x cos x dx 15 sin x cos x dx Since cos x is the derivative of sin x then S 15 sin x cos x dx can be done by substituting u sin x Step 4 With the substitution u sin x we get 15 0 15 which integrates to 15 sin x cos x dx 15 5u u du C 5u Substituting back in to get the answer in terms of sin x we have 15 sin x cos x dx 5 sin x 5 sin x C In terms of u we get Step 5 Using the same substitution u sin x enables us to do f 15 15 sin x cos x dx 15 5 04 S 15 sin x cos x u du C which in terms of sin x becomes C 15 sin r cos r dx sin x and du cos x cos x dx


Calculus
Application of derivativesConsider the following dt Let t 9 tan 8 and determine the following a r9 1 dt V 81 t t 0 8 sec 0 9 sec t 9 8 X 0 T 4 Evaluate the integral 2 1 X de
Calculus
Indefinite IntegrationSince We know that 15 sin x cos x dx has an odd power of of cos x we will convert all but one power to sines cos x Step 2 Making this substitution using 15 sin x cos x dx gives us Step 3 15 sin x 1 sin x cos x dx 15 sin x cos x dx sin x Since cos x is the derivative of sin x then Step 4 With the substitution u sin x we get 15 0 which integrates to 15 sin x cos x dx 15 C 15 15 sin x cos x dx can be done by substituting u sin x u du Substituting back in to get the answer in terms of sin x we have 15 sin x cos x dx 15 sin x cos x C 15 sin r cos r dx sin r and du cos x cos x dx

Calculus
Indefinite IntegrationConsider the following function 3 JO R 64 dx a Determine an appropriate trigonometric substitution Use x 8 sin 0 where 1 0 1 since the integrand contains the expression 82 x 2 Use x 8 tan 8 where x3 64 x IT 2 0x dx S 0 O Use x 8 sec 0 where 0 0 0 or 0 31 TT 2 TT since the integrand contains the expression 8 x 2 b Apply the substitution to transform the integral into a trigonometric integral Do not evaluate the integral 8 sin 0 8 cos 0 X since the integrand contains the expression 8 x de
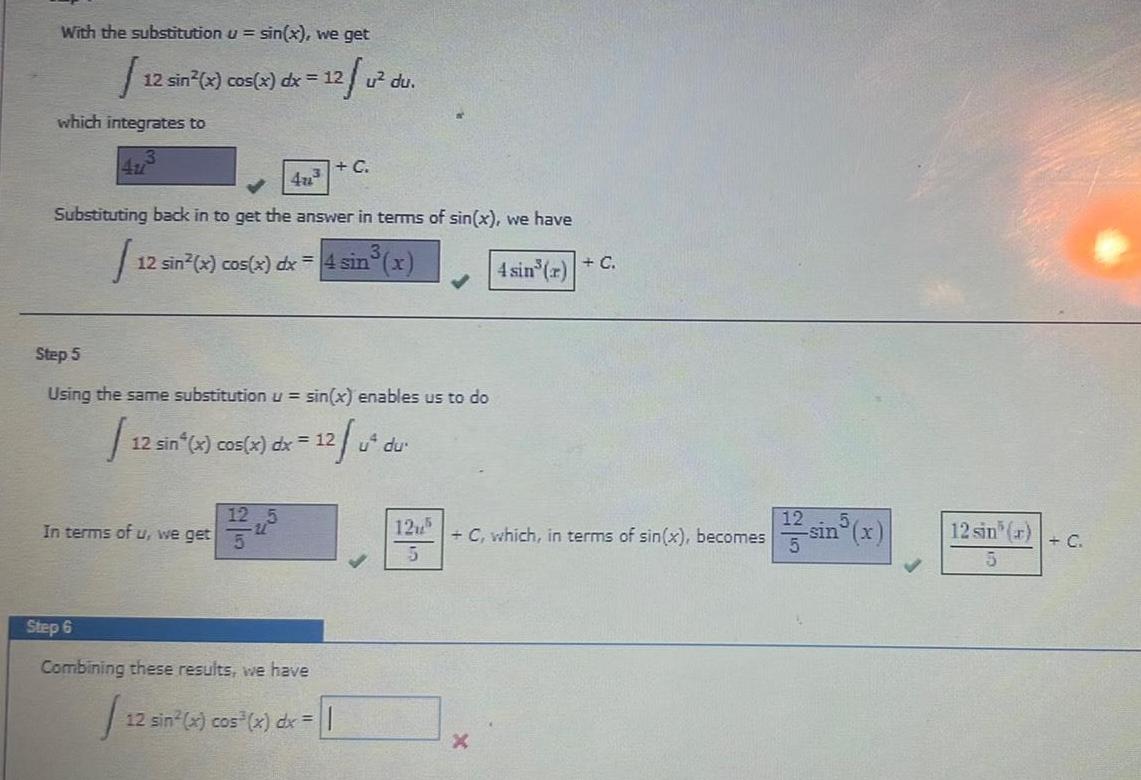
Calculus
Indefinite IntegrationWith the substitution u sin x we get J which integrates to 12 sin x cos x dx 12 u du Substituting back in to get the answer in terms of sin x we have I 12 sin x cos x dx 4 sin x 4 sin r C 12 sin 4u Step 5 Using the same substitution u sin x enables us to do 12 u dur 12 sin x cos x dx 12 In terms of u we get 12 C Step 6 Combining these results we have 12 sin x cos x dx 125 5 C which in terms of sin x becomes 12 sin r 5 C
Calculus
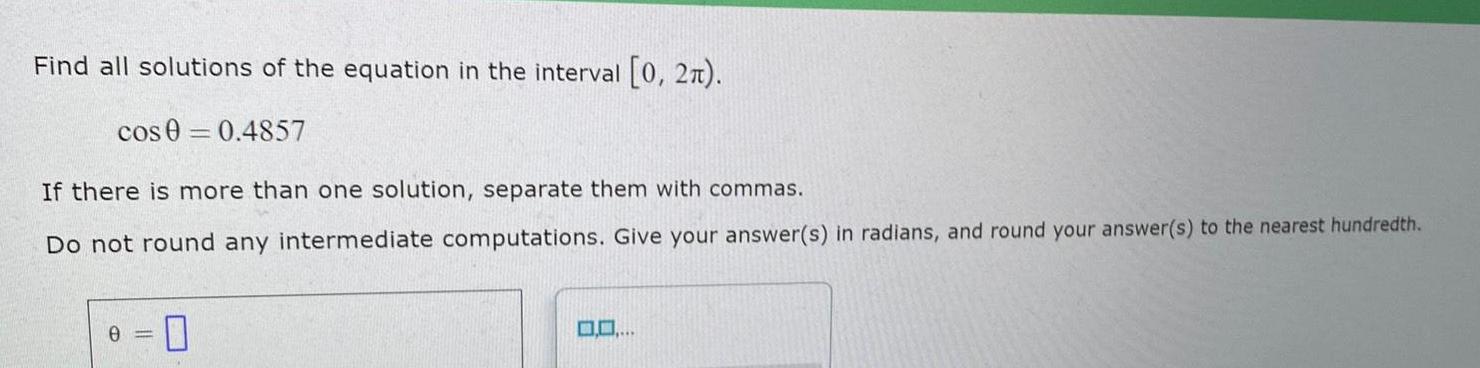
DifferentiationFind all solutions of the equation in the interval 0 2 cos 0 0 4857 If there is more than one solution separate them with commas Do not round any intermediate computations Give your answer s in radians and round your answer s to the nearest hundredth 0 0 0 0
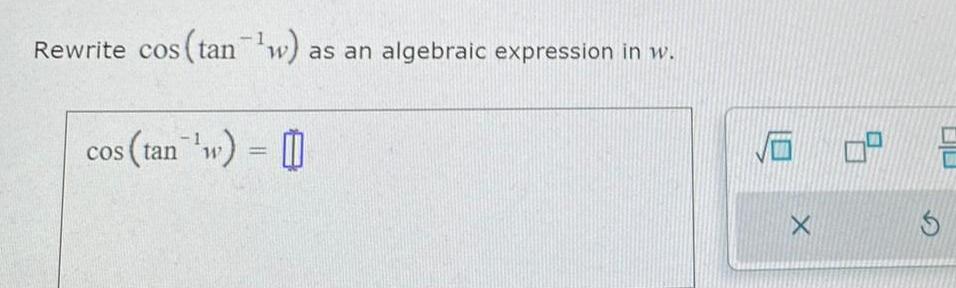
Calculus
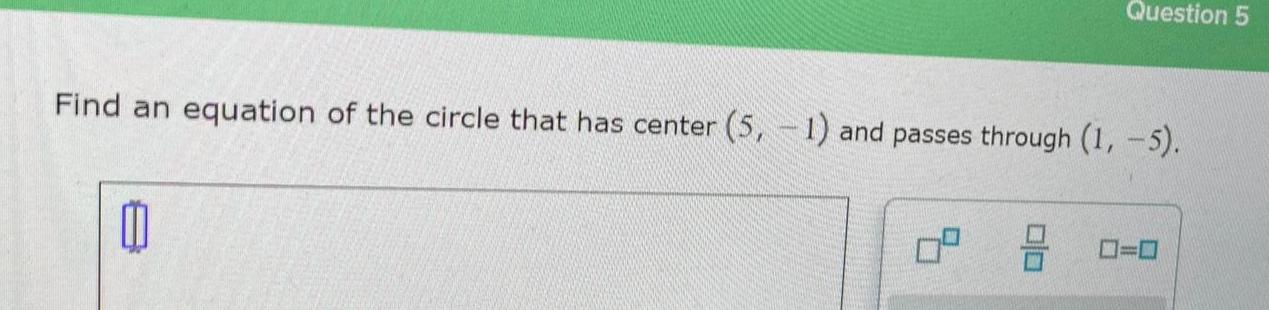
Application of derivativesQuestion 5 Find an equation of the circle that has center 5 1 and passes through 1 5 0
Calculus
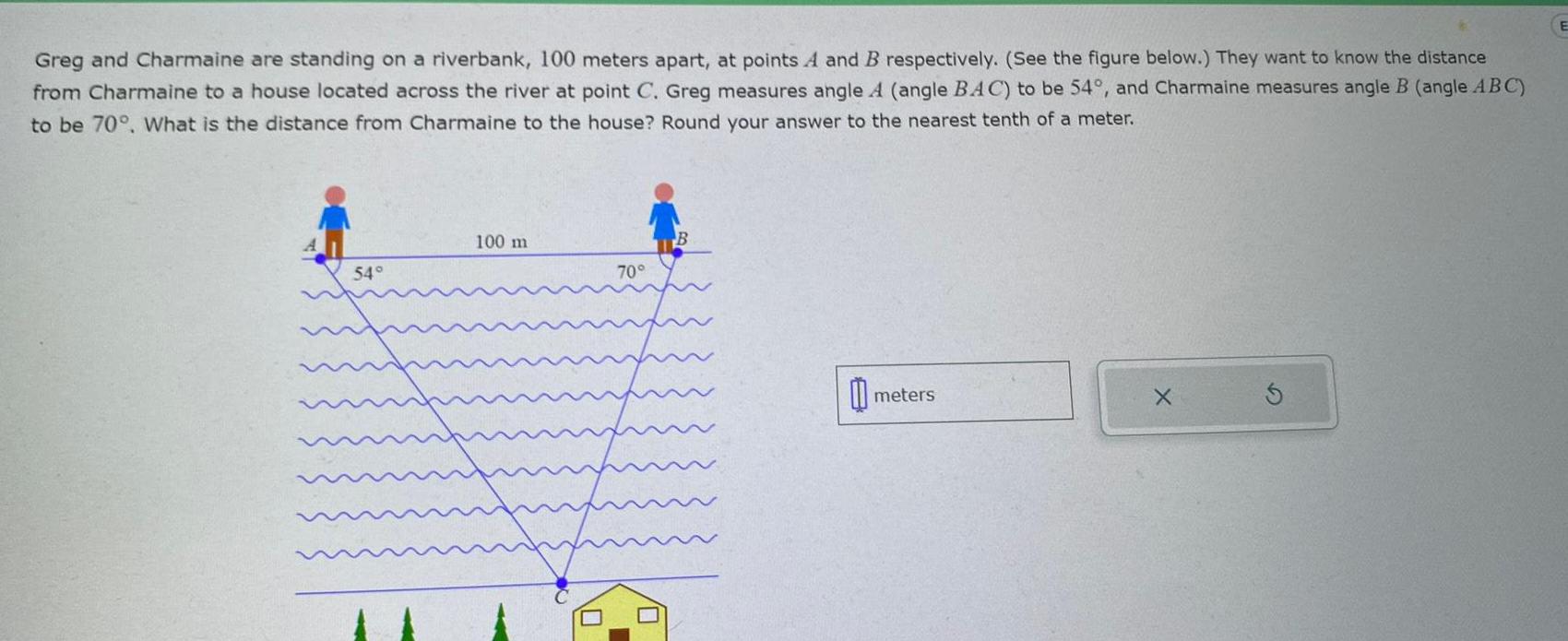
Vector CalculusGreg and Charmaine are standing on a riverbank 100 meters apart at points A and B respectively See the figure below They want to know the distance from Charmaine to a house located across the river at point C Greg measures angle A angle BAC to be 54 and Charmaine measures angle B angle ABC to be 70 What is the distance from Charmaine to the house Round your answer to the nearest tenth of a meter 54 100 m 70 B meters X E


Calculus
Application of derivativesConsider the following y 7x In x 1 7 Find an equation of the tangent line to the graph of the function at the given point Use a graphing utility to graph function and its tangent line at the point and use the tangent feature of a graphing utility to confirm your results y

Calculus
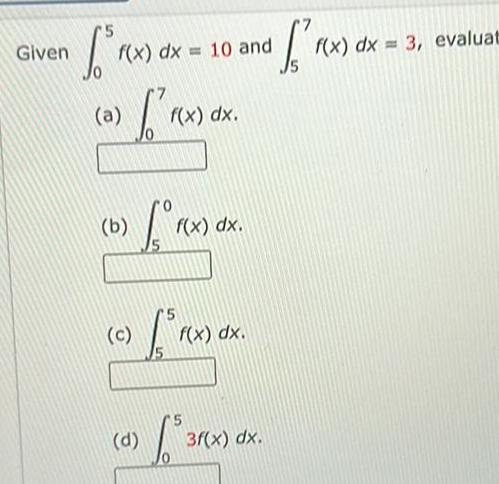
Definite IntegralsGiven r x a f x dx 10 and b f c f x dx d f x dx f x dx S af rex 3f x dx f x dx 3 evaluat