Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
Differential equationsFind the simple interest on the loan Round your answer to the nearest dollar 6750 at 4 5 for 8 months

Calculus
Application of derivativesMaximize Subject to Maximum is X y z 4x 3y 3x 7y 5x 3y X Y 56 50 0 0
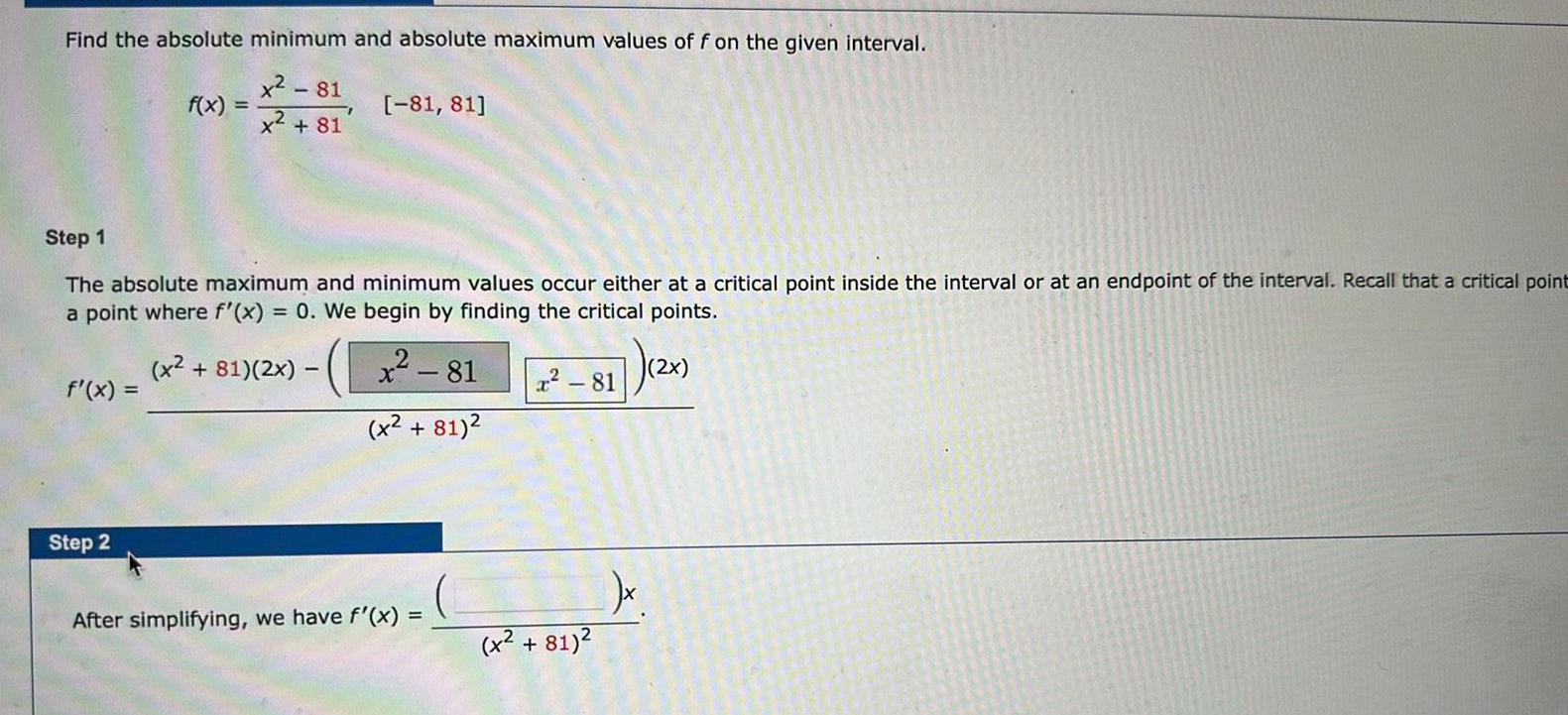
Calculus
DifferentiationFind the absolute minimum and absolute maximum values of f on the given interval 281 81 81 Step 1 The absolute maximum and minimum values occur either at a critical point inside the interval or at an endpoint of the interval Recall that a critical point a point where f x 0 We begin by finding the critical points x2 81 2x x 81 x 81 f x f x Step 2 After simplifying we have f x x 81 x 81 7 2x
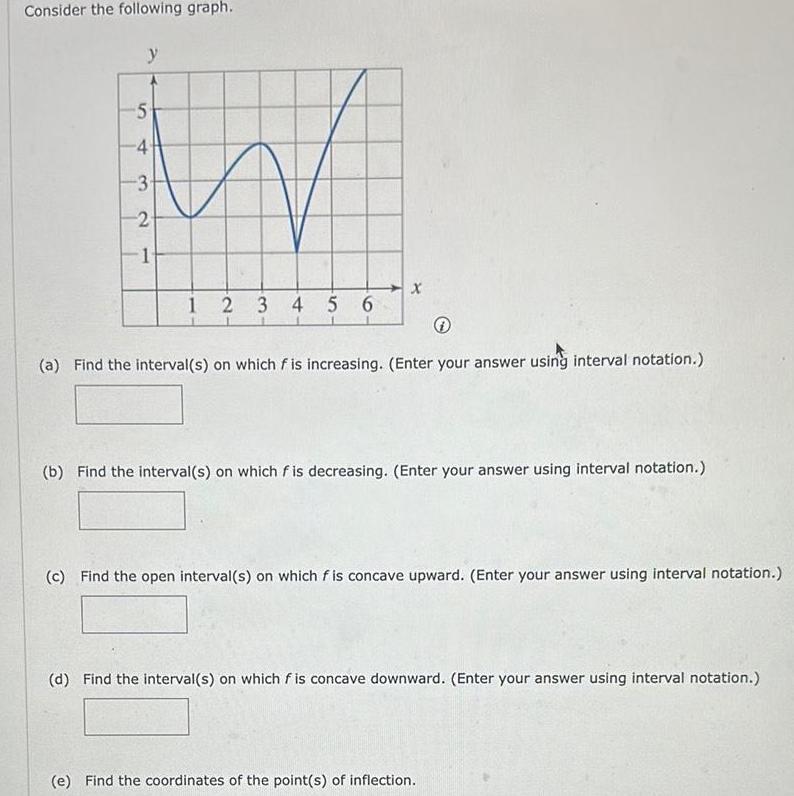
Calculus
Limits & ContinuityConsider the following graph y 5 4 3 2 1 1 2 3 4 5 6 X a Find the interval s on which f is increasing Enter your answer using interval notation b Find the interval s on which fis decreasing Enter your answer using interval notation c Find the open interval s on which fis concave upward Enter your answer using interval notation d Find the interval s on which fis concave downward Enter your answer using interval notation e Find the coordinates of the point s of inflection

Calculus
DifferentiationF x x4 5 x 9 X Enter your answers as a comma separated list If an answer does not exist enter DNE Enhanced Feedback To find critical numbers of a differentiable function you need to differentiate the given function F x and solve for x in the equation F x 0 All solutions as we not differentiable are the critical numbers Make sure that you use the Product Rule when differentiating the function

Calculus
Application of derivativesUse the graph of the derivative f of a continuous function f is shown Assume f continues to co y 4 X 2 2 X 2 y f x a On what interval s is f increasing Enter your answer using interval notation 4 On what interval s is f decreasing Enter your answer using interval notation b At what value s of x does f have a local maximum Enter your answers as a comma separated list At what value s of x does f have a local minimum Enter your answers as a comma separated list c On what interval s is f concave upward Enter your answer using interval notation On what interval s is concave downward Enter your answer using interval notation

Calculus
Definite IntegralsProblem 66 Summarize the pertinent information obtained by applying the graphing strategy and sketch the graph of f x 3x5 5x Domain Range Increasing Decreasing interval s Concavity or concavities Inflection point s Max and or min Asymptotes

Calculus
Application of derivativesFind the critical numbers of the function Enter your answers as a comma separated list If an answer does not exist enter DNE 1 2 2 f x 9 1 X 5

Calculus
Application of derivativesC Problem 70 Summarize the pertinent information as in previous problem obtained by applying the graphing strategy and sketch the graph of f x 2e0 5x e 0 5x


Calculus
Application of derivatives4 T shirt manufacturer is planning to expand its workforce It estimates that the number of T shirts produced by hiring x new workers is given by T x 0 25x 3x 0 x 9 When is the rate of change of T shirt production increasing and when is it decreasing What is the point of diminishing returns and the maximum rate of change for T shirt production Graph T and T on the same coordinate system The rate of change of T shirt production is increasing on Type your answer in interval notation
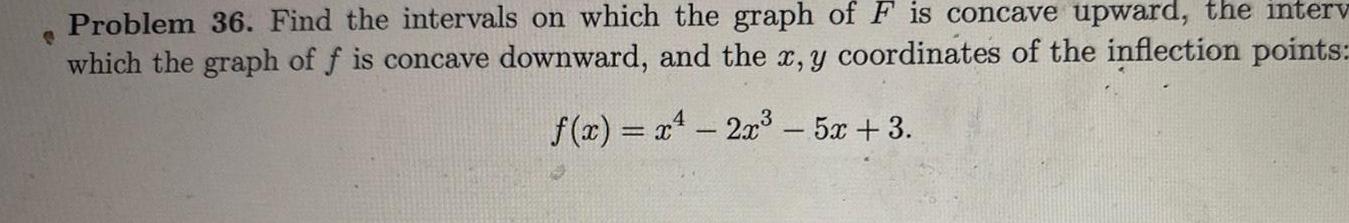
Calculus
Application of derivativesC Problem 36 Find the intervals on which the graph of F is concave upward the interv which the graph of f is concave downward and the x y coordinates of the inflection points f x x 2x 5x 3

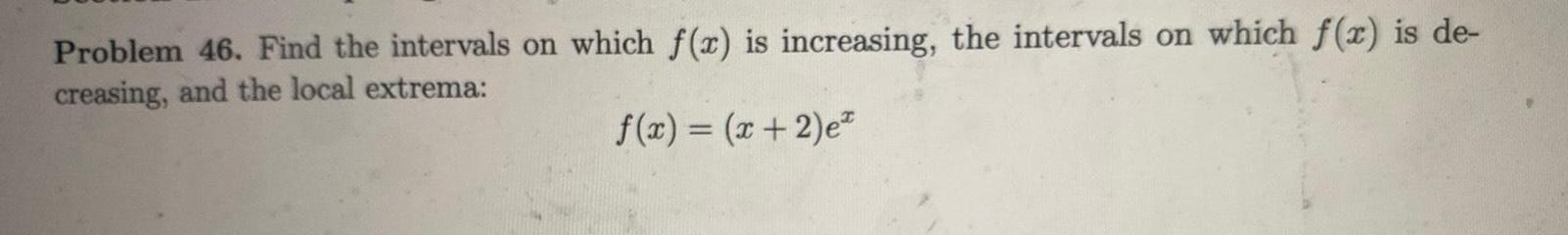
Calculus
Application of derivativesProblem 46 Find the intervals on which f x is increasing the intervals on which f x is de creasing and the local extrema f x x 2 e

Calculus
Limits & ContinuitySection 11 3 L Hopital s Rule Problem 26 Use L Hopital s rule to find the limit x 1 x1 ln x3 lim
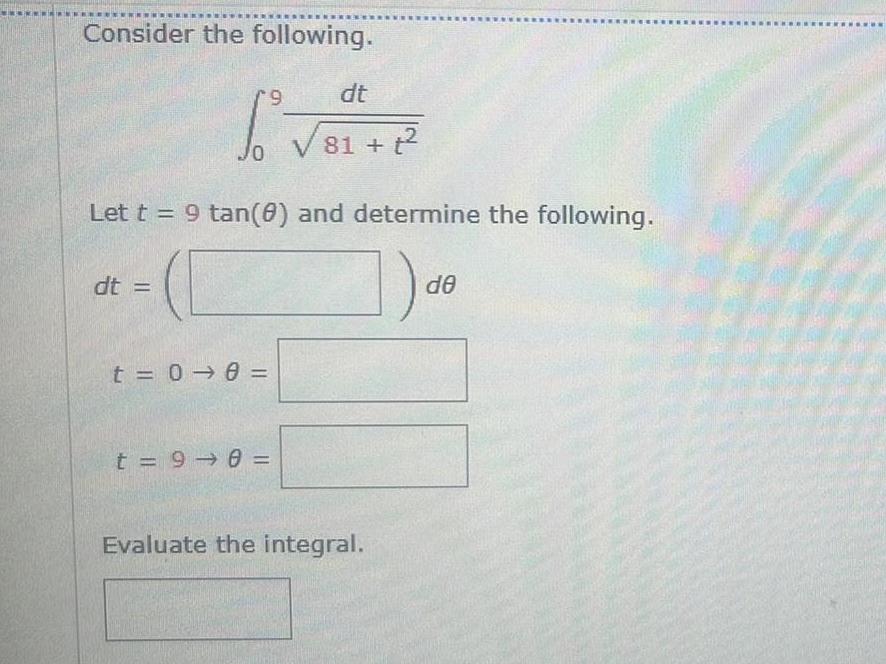
Calculus
Indefinite IntegrationConsider the following 9 6 3 Let t 9 tan 0 and determine the following a dt t 0 0 dt 81 2 t 9 0 Evaluate the integral de

Calculus
Differentiationx 1 Step 1 Recall the Inverse Substitution Rule where f and g are differentiable functions and g is one to one R x dx We are given the following dx 1 2 x x37 2 If f g t g t dt We note that x 1 2 x 1 Therefore the following entry from the Table of Trigonometric Substitutions is appropriate Expression It x a x a sec 8 0 8 or 0 3 2 2 1 2 a Substitution then a Identity sec 0 1 tan 0 Therefore we can let x sec 0 so dx de We also must make a substitution for the limits of integration in the definite integral Since x sec 8 we note that when x 2 0 Further when x 4 8 sec
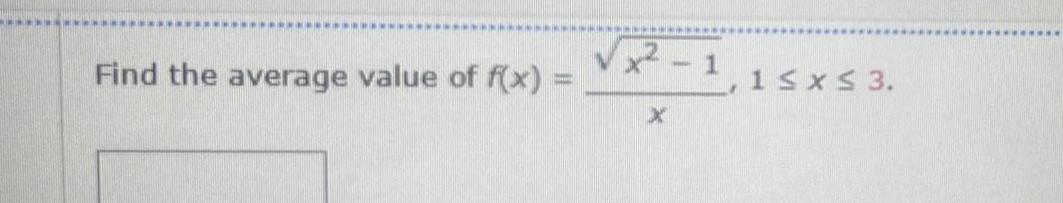
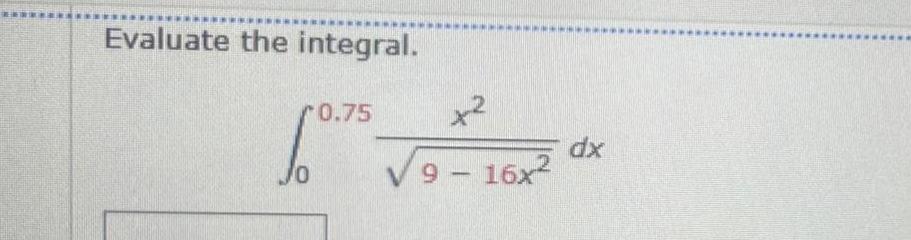

Calculus
Application of derivativesConsider the following function 3 dx a Determine an appropriate trigonometric substitution O Use x 8 sin 0 where O Use x 8 tan 0 where 1 IT 2 IT 2 since the integrand contains the expression 8 2 8 TT 2 since the integrand contains the expression 82 x O Use x 8 sec 0 where 0 0 or 0 3 2 since the integrand contains the expression 8 x 2 b Apply the substitution to transform the integral into a trigonometric integral Do not evaluate the integral x3 J dx 64 x de
Calculus
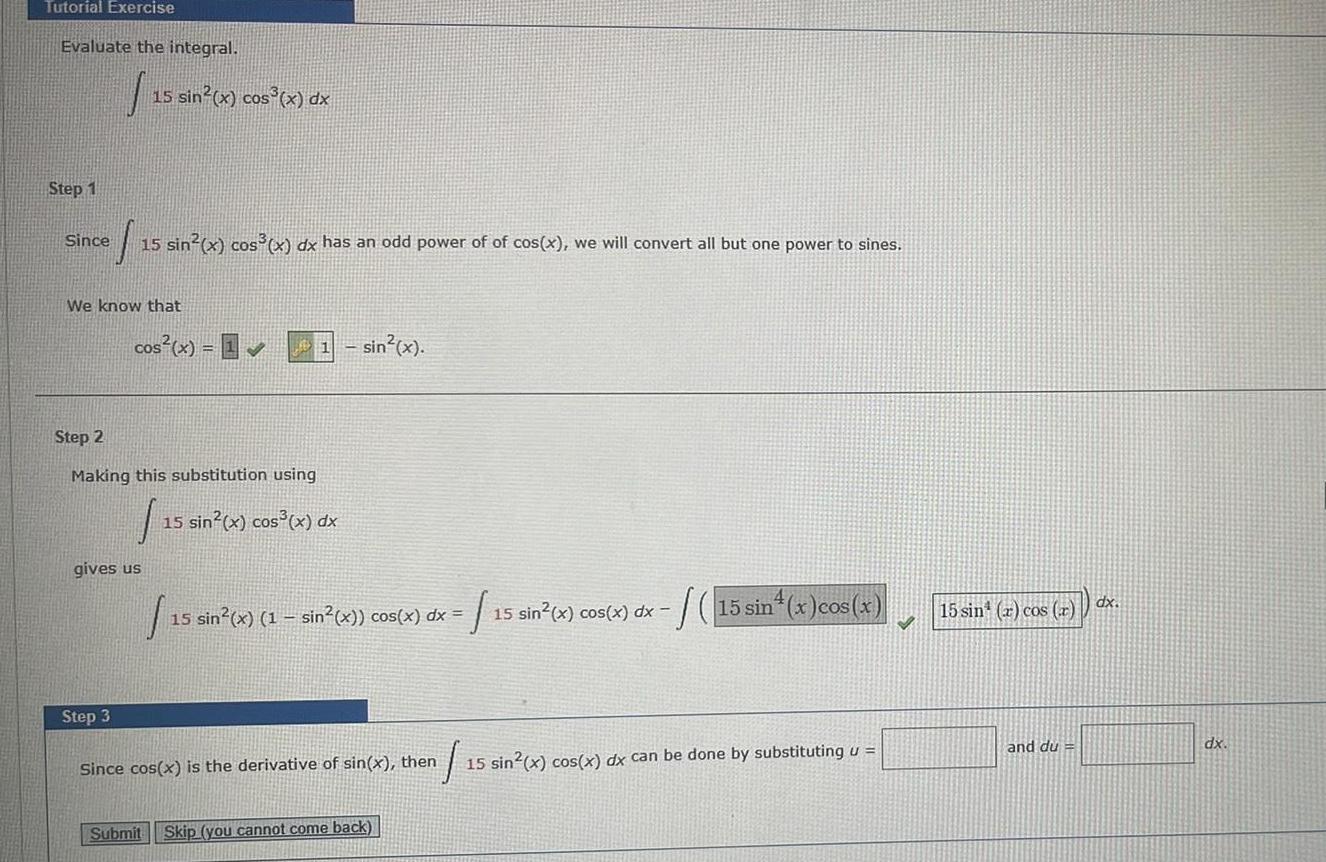
Indefinite IntegrationTutorial Exercise Evaluate the integral Step 1 Since S 15 sin x cos x dx has an odd power of of cos x we will convert all but one power to sines We know that 15 sin x cos x dx cos x 1 11 sin x Step 2 Making this substitution using 1 15 sin x cos x dx gives us Step 3 Submit 15 15 sin x 1 sin x cos x dx 1 Skip you cannot come back 1 15 sin x cos x dx Since cos x is the derivative of sin x then 1 15 sin x cos x dx can be done by substituting u 15 sin x cos x 15 sin r cos r and du dx dx
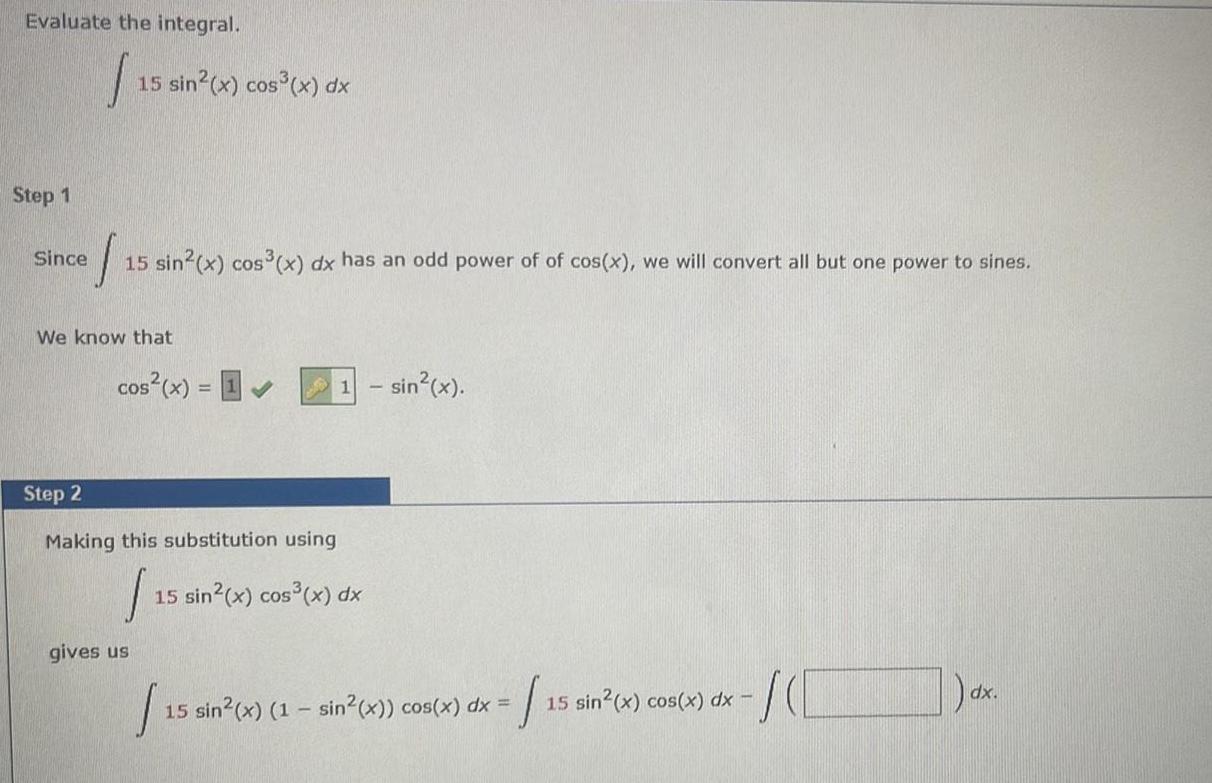
Calculus
Indefinite IntegrationEvaluate the integral I Step 1 15 sin x cos x dx Since 1 15 sin x cos x dx has an odd power of of cos x we will convert all but one power to sines We know that cos x 1 Step 2 Making this substitution using 1 gives us 1 sin x 15 sin x cos x dx 15 sin 15 sin x 1 sin x cos x dx 15 sin x cos x dx 155 SCC dx

Calculus
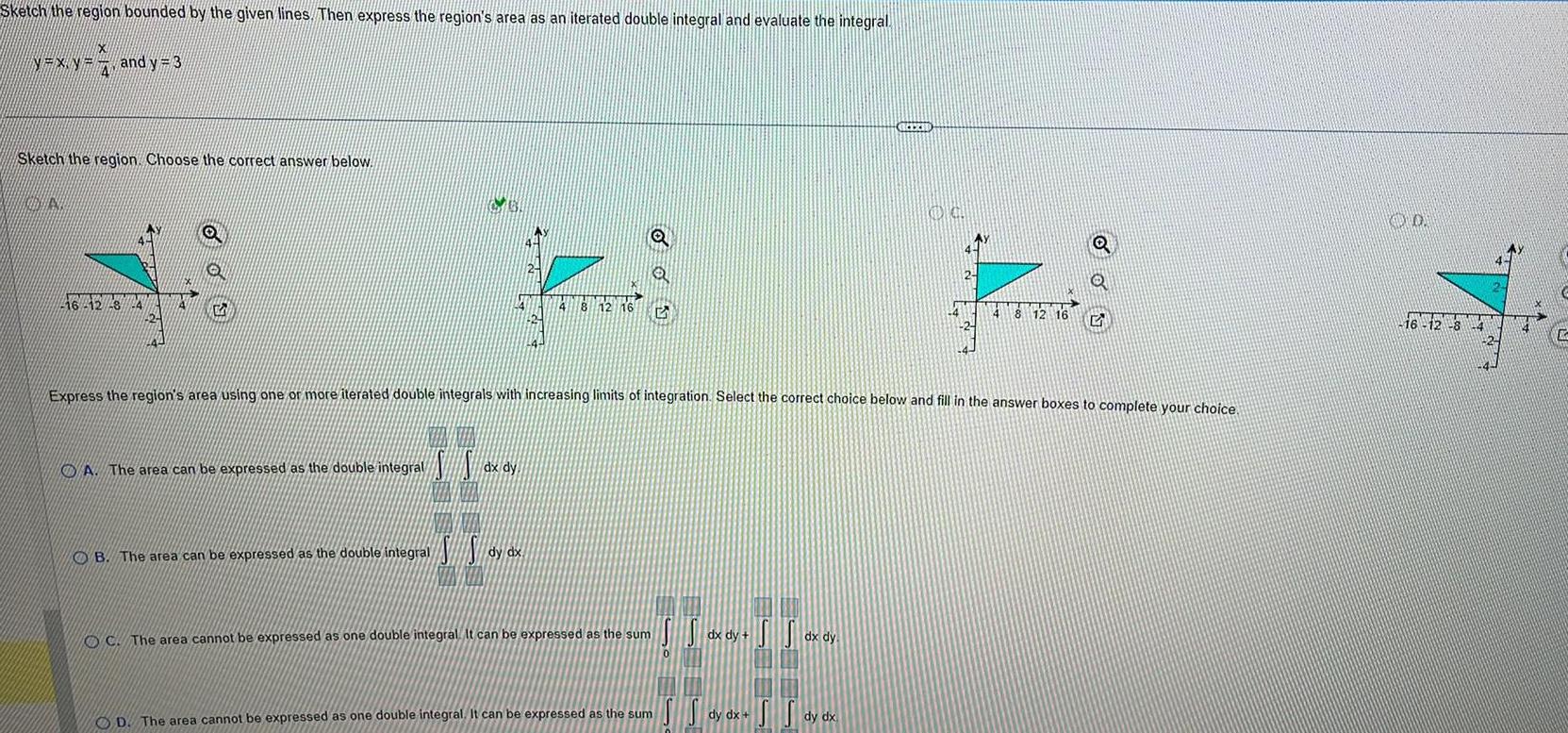
Definite IntegralsSketch the region bounded by the given lines Then express the region s area as an iterated double integral and evaluate the integral N XN X NXX and y 3 4 Sketch the region Choose the correct answer below N 46 42 8 24 O Q G A The area can be expressed as the double integral I l dx dy 8 12 16 O B The area can be expressed as the double integral SS dy dx OC The area cannot be expressed as one double integral It can be expressed as the sum D The area cannot be expressed as one double integral It can be expressed as the sum dx dy Express the region s area using one or more iterated double integrals with increasing limits of integration Select the correct choice below and fill in the answer boxes to complete your choice dx dy REEZID SS dy dx dy dx OG 4 2 Q 4 8 12 16 5 20 16 12 8 14 C
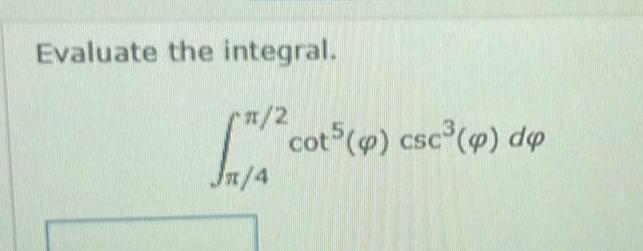

Calculus
Indefinite IntegrationTutorial Exercise Evaluate the integral 15 Step 1 15 sin x cos x dx Since J 15 sin x cos x dx has an odd power of of cos x we will convert all but one power to sines We know that cos x sin x
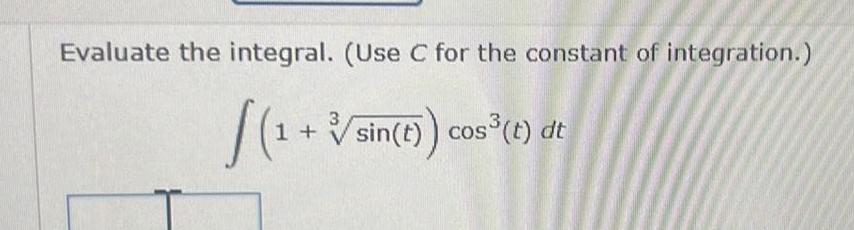
Calculus
Indefinite IntegrationEvaluate the integral Use C for the constant of integration 1 sin t cos t dt
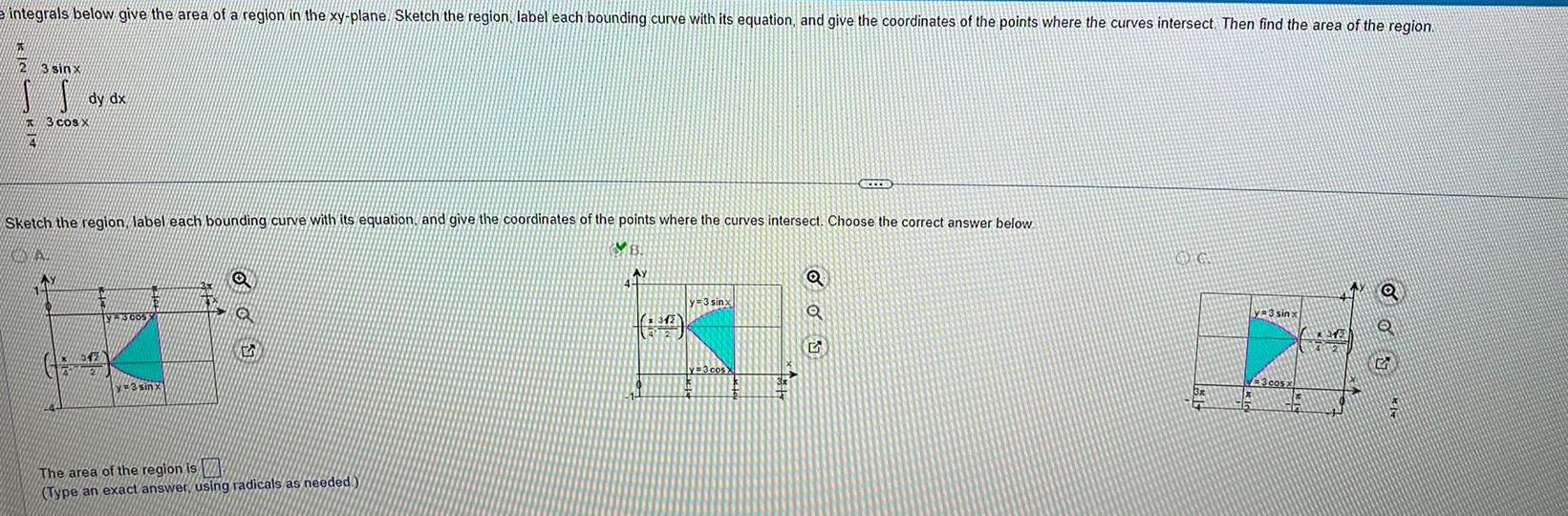
Calculus
Definite Integralsintegrals below give the area of a region in the xy plane Sketch the region label each bounding curve with its equation and give the coordinates of the points where the curves intersect Then find the area of the region 4 3 sinx dy dx 3 cos x Sketch the region label each bounding curve with its equation and give the coordinates of the points where the curves intersect Choose the correct answer below KINIS 342 VE3005 y 3 sinx 5 The area of the region is Type an exact answer using radicals as needed AY 6 y 3 sinx y 3 cos X SECES Q Q 5 OG 3x 1x 16 y 3 sinx 3 cos X thr Q Q G
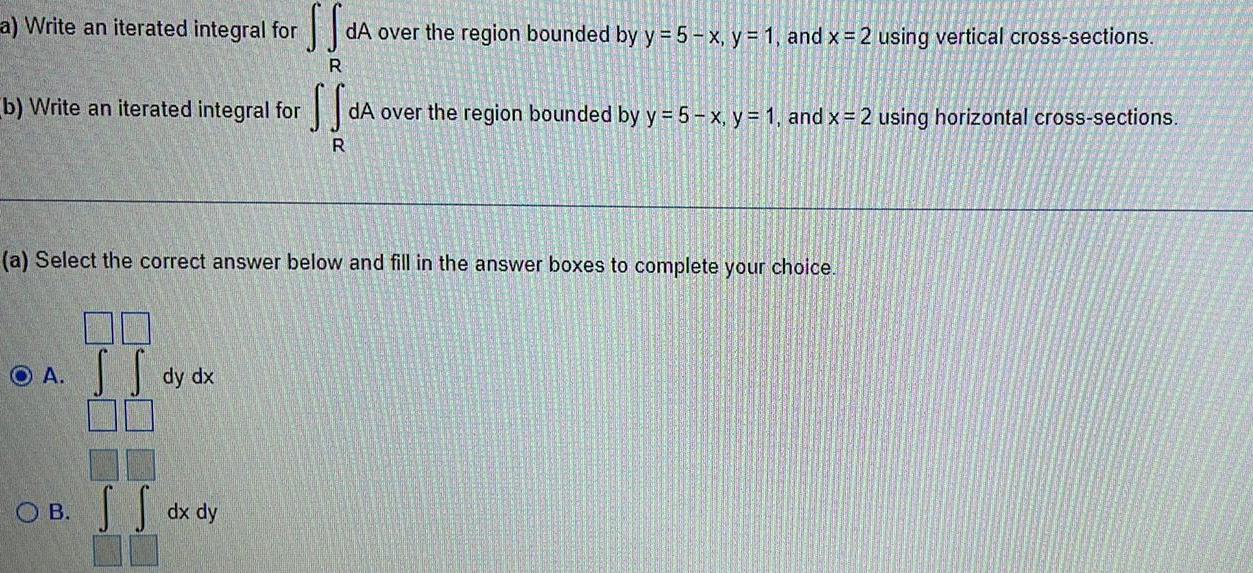
Calculus
Definite Integralsa Write an iterated integral for b Write an iterated integral for f R O A a Select the correct answer below and fill in the answer boxes to complete your choice S S SS dA over the region bounded by y 5 x y 1 and x 2 using vertical cross sections R dy dx OB dx dy dA over the region bounded by y 5 x y 1 and x 2 using horizontal cross sections
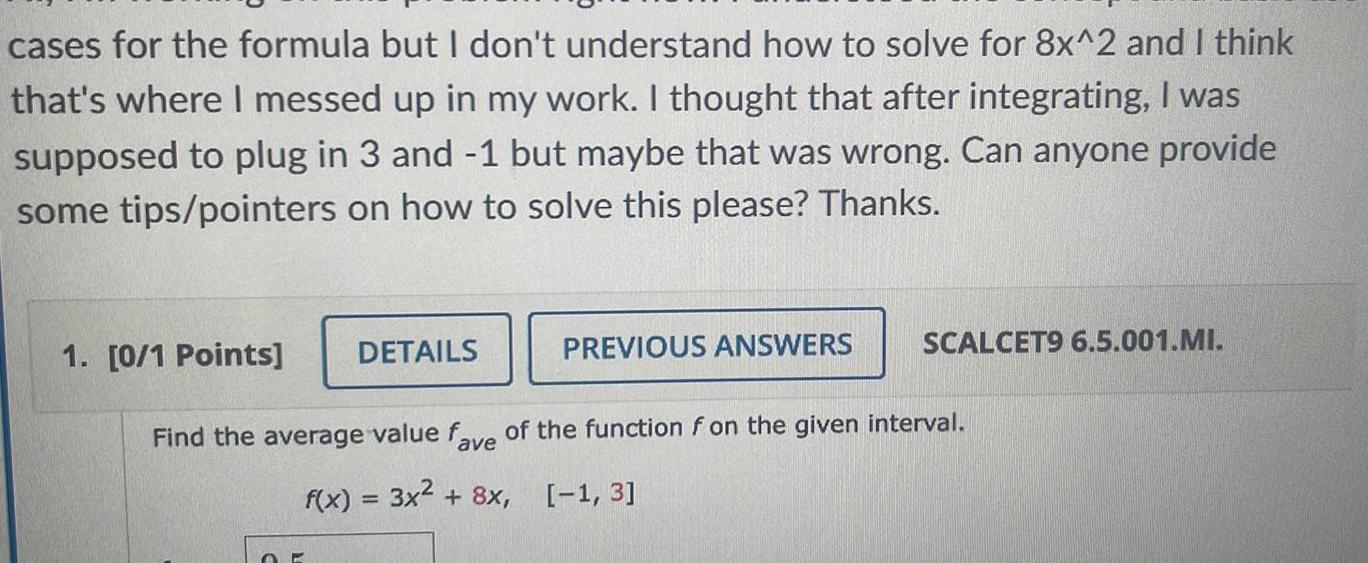
Calculus
Definite Integralscases for the formula but I don t understand how to solve for 8x 2 and I think that s where I messed up in my work I thought that after integrating I was supposed to plug in 3 and 1 but maybe that was wrong Can anyone provide some tips pointers on how to solve this please Thanks 1 0 1 Points DETAILS O PREVIOUS ANSWERS SCALCET9 6 5 001 MI Find the average value fave of the function f on the given interval f x 3x 8x 1 3

Calculus
Definite IntegralsTV 4 1 sin5 x dx 0 At first I divided sin5 x dx to sin4 x sin x dx And I changed sin x to 1 cos x in terms of the Cosine function After that I solved it by using integral rules But I couldn t solve it Can anyone give me a hint to solve it I attached my calculations below

Calculus
Definite IntegralsQuestion Find the average value fave of the function fon the given interval f x 3x 4x 1 5 At first I calculated using the two formulas The average value of function f over the interval a b and the Power Rule that I wrote in the picture but couldn t solve it I attached the picture below Can anyone give me a hint of what I missed B
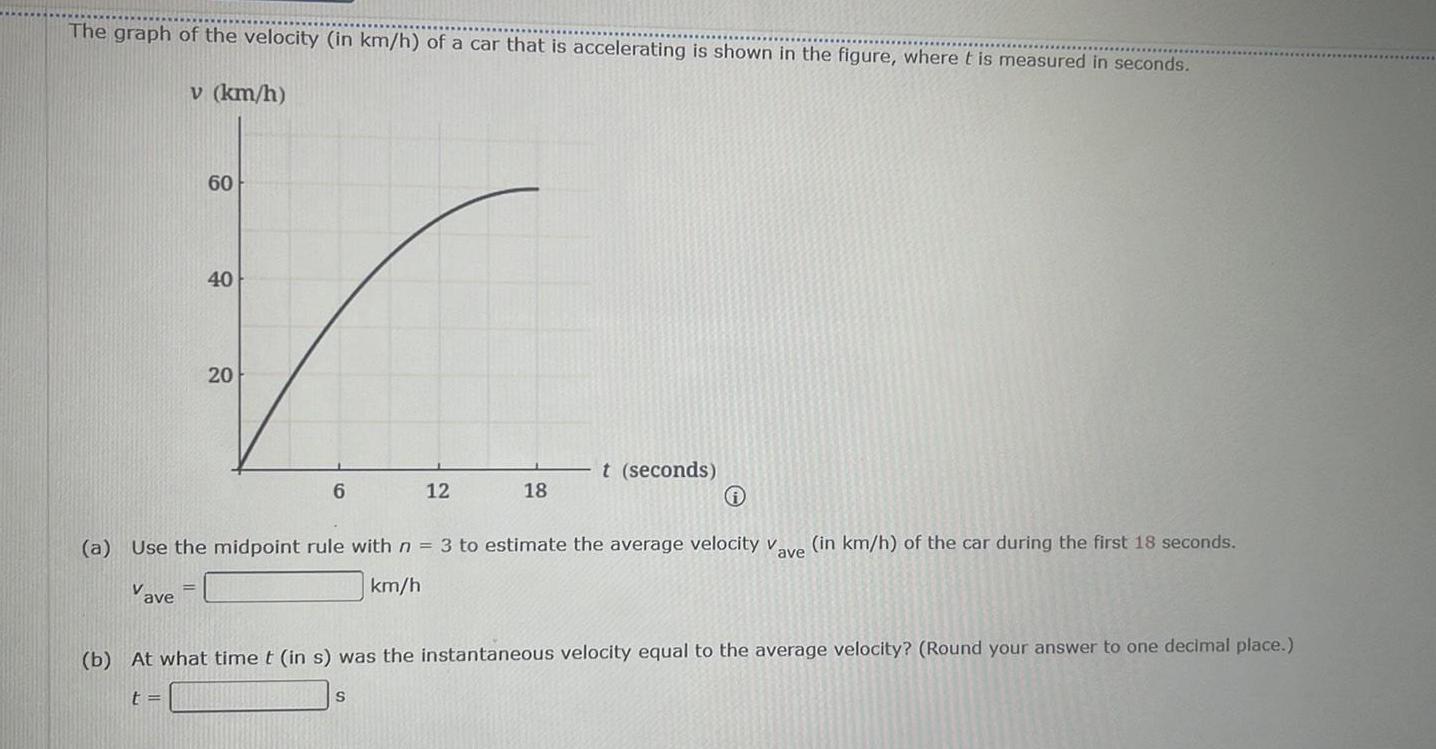
Calculus
Definite IntegralsThe graph of the velocity in km h of a car that is accelerating is shown in the figure where t is measured in seconds v km h Vave 60 40 20 6 12 i a Use the midpoint rule with n 3 to estimate the average velocity va in km h of the car during the first 18 seconds ave km h 18 S t seconds b At what time t in s was the instantaneous velocity equal to the average velocity Round your answer to one decimal place t
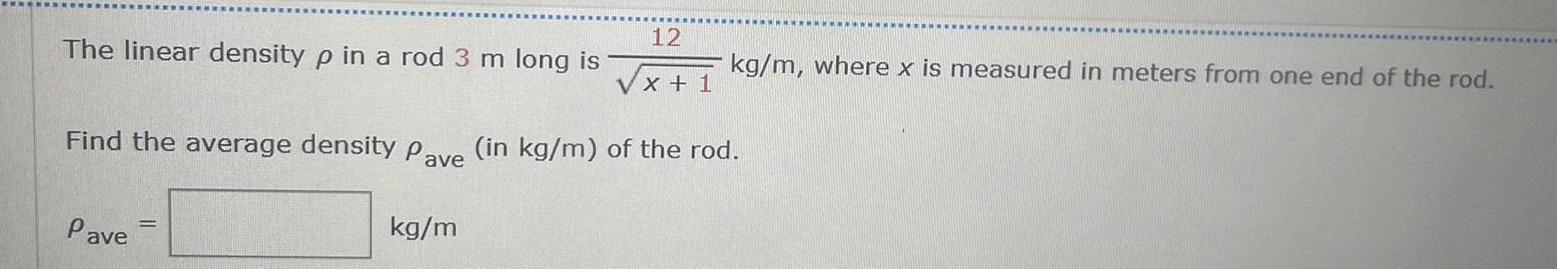
Calculus
Definite Integrals12 x 1 Find the average density Pave in kg m of the rod The linear density p in a rod Pave kg m m long is kg m where x is measured in meters from one end of the rod

Calculus
Definite IntegralsFind the average value h have ave 0 3238 of the function h on the given interval h u In u 1 5 U
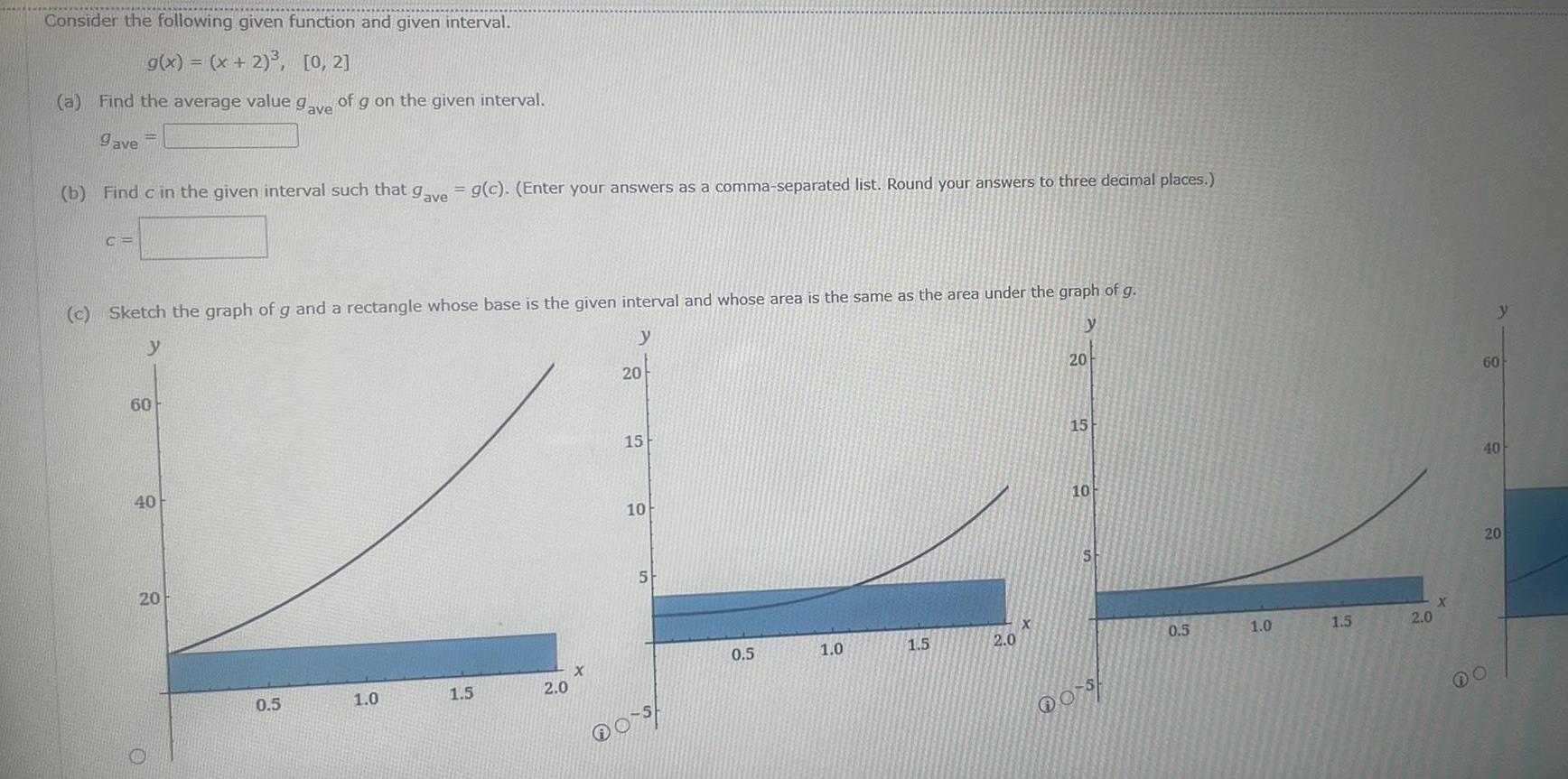
Calculus
Application of derivativesConsider the following given function and given interval g x x 2 0 2 a Find the average value gave C b Find c in the given interval such that gave g c Enter your answers as a comma separated list Round your answers to three decimal places 60 c Sketch the graph of g and a rectangle whose base is the given interval and whose area is the same as the area under the graph of g y y y 40 20 gave O of of g on the given interval 0 5 1 0 1 5 2 0 20 15 10 5 O S 0 5 1 0 1 5 2 0 20 15 10 S os 0 5 1 0 1 5 2 0 X 60 40 20
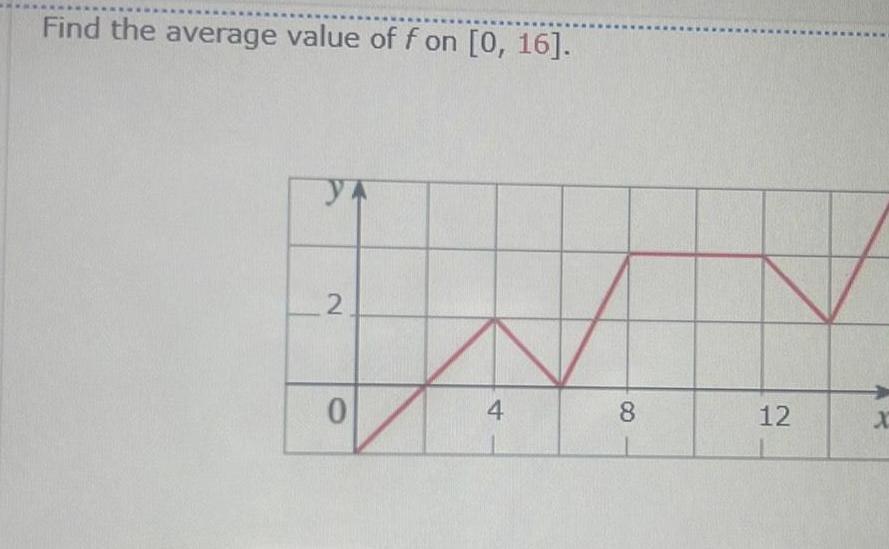

Calculus
Application of derivativesIf 5000 is invested at 7 annual simple interest how long does it take to be worth 8150 yr

Calculus
Application of derivativesFIne the area enclosed by the given ellipse x asint y bcost 0 t 2pi The area is
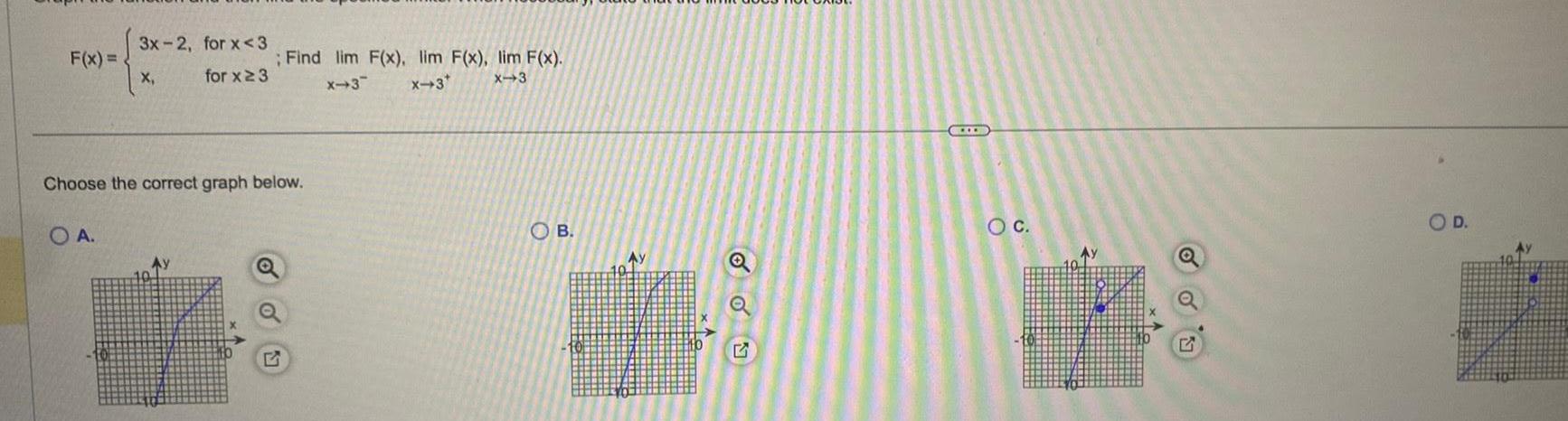
Calculus
Limits & ContinuityF x 3x 2 for x 3 for x 3 OA X Choose the correct graph below Find lim F x lim F x lim F x X 3 X 3 x 3 Ay OB Ay Q D O C O D
Calculus
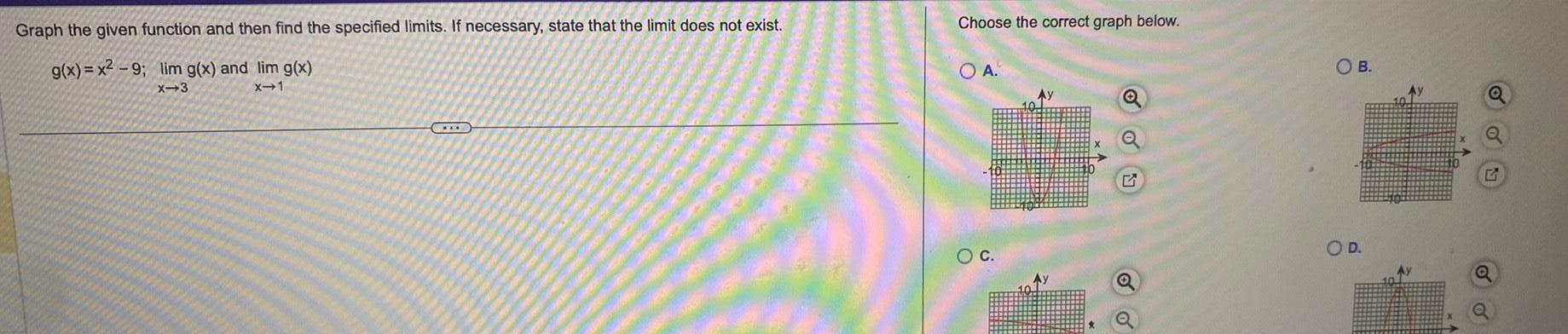
Application of derivativesGraph the given function and then find the specified limits If necessary state that the limit does not exist g x x 9 lim g x and lim g x X 3 x 1 Choose the correct graph below OA O C OB O D Ay Q Q
Calculus
Application of derivativesFind an equation of the line tangent to the graph of f x 5 6x at 5 145 The equation of the tangent line to the graph of f x 5 6x at 5 145 is y Type an expression using x as the variable
Calculus
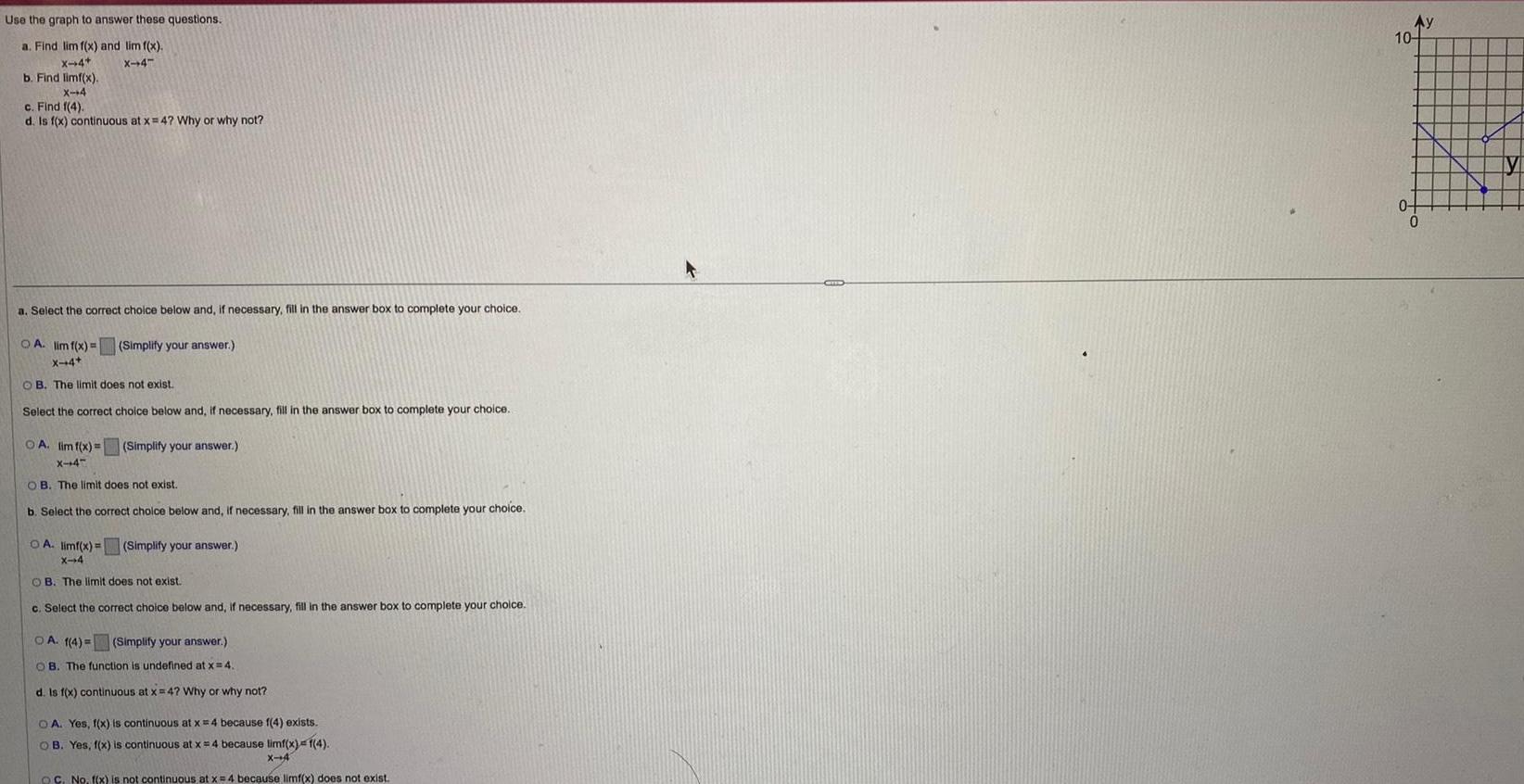
Limits & ContinuityUse the graph to answer these questions a Find lim f x and lim f x X 4 X 4 b Find limf x X 4 c Find 1 4 d Is f x continuous at x 4 Why or why not a Select the correct choice below and if necessary fill in the answer box to complete your choice OA lim f x X 4 OB The limit does not exist Select the correct choice below and if necessary fill in the answer box to complete your choice Simplify your answer OA lim f x Simplify your answer X 4 OB The limit does not exist b Select the correct choice below and if necessary fill in the answer box to complete your choice OA limf x Simplify your answer X 4 OB The limit does not exist c Select the correct choice below and if necessary fill in the answer box to complete your choice OA 1 4 Simplify your answer OB The function is undefined at x 4 d Is f x continuous at x 4 Why or why not OA Yes f x is continuous at x 4 because f 4 exists OB Yes f x is continuous at x 4 because limf x 1 4 X 4 OC No f x is not continuous at x 4 because limf x does not exist F Ay 10 04 0 y
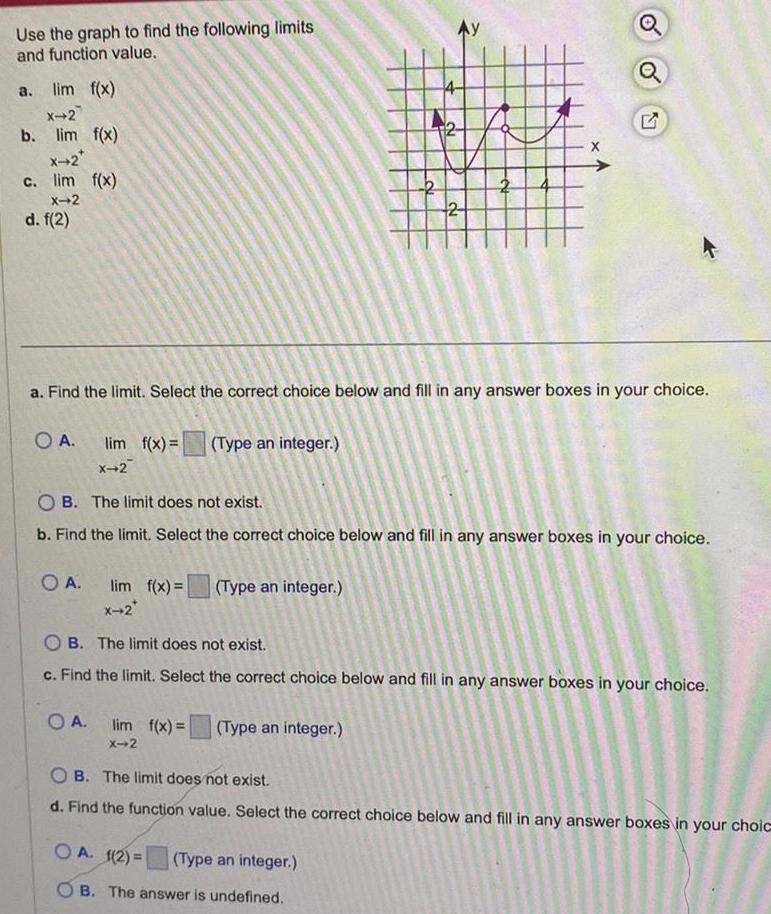
Calculus
Application of derivativesUse the graph to find the following limits and function value a lim f x X 2 b lim f x X 2 c lim f x X 2 d f 2 O A O A lim f x Type an integer X 2 a Find the limit Select the correct choice below and fill in any answer boxes in your choice OA lim f x Type an integer X 2 2 OB The limit does not exist b Find the limit Select the correct choice below and fill in any answer boxes in your choice lim f x Type an integer X 2 2 2 OA 1 2 X OB The limit does not exist c Find the limit Select the correct choice below and fill in any answer boxes in your choice Type an integer B The answer is undefined 57 OB The limit does not exist d Find the function value Select the correct choice below and fill in any answer boxes in your choic

Calculus
Definite Integralsketch the region bounded by the given line and curve Then express the region s area as an iterat and evaluate the integral 2 The parabola x y and the line y x 2 A The area can be expressed as the double integral dy dx B The area cannot be expressed as one double integral It can be expressed as the sum s so dy dx x S S dy dx C The area can be expressed as the double integral OD The value of the integral is dx dy 1 y The area cannot be expressed as one double integral It can be expressed as the sum S S dx dy SS S dx dy 2 y 2 Simplify your answer Type an integer or a fraction

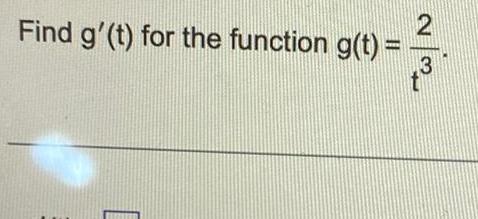

Calculus
Application of derivativesFind H x for the given function H x 3 x 8 H x Type an exact answer using radicals as needed
