Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
Calculus
Indefinite IntegrationA commercial cherry grower estimates from past records that if 23 trees are planted per acre then each tree will yield an average of 37 pounds of cherries per season If for each additional tree planted per acre up to 23 additional trees the average yield per tree is reduced by 1 pound how many trees should be planted per acre to obtain the maximum yield per acre What is the maximum yield In order to get the highest yield of pounds trees should be planted per acre
Calculus
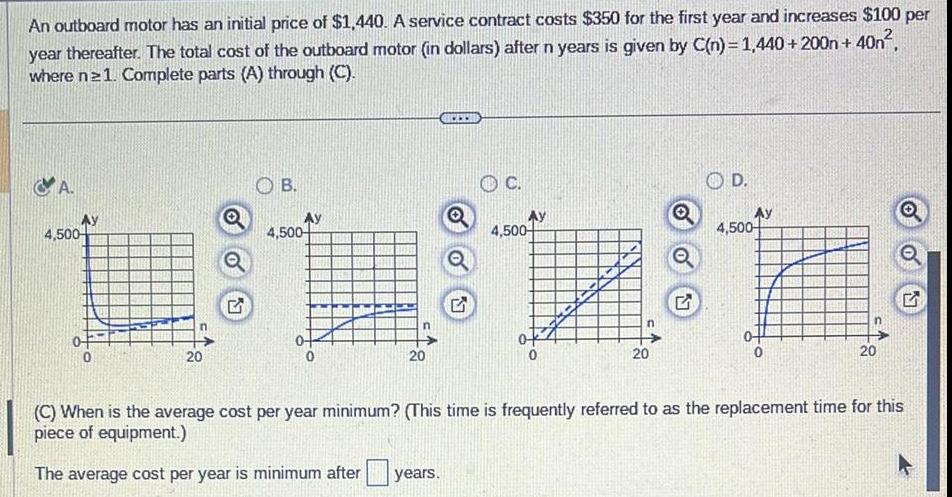
Differential equationsAn outboard motor has an initial price of 1 440 A service contract costs 350 for the first year and increases 100 per year thereafter The total cost of the outboard motor in dollars after n years is given by C n 1 440 200n 40n where ne 1 Complete parts A through C A Ay 4 500 20 OB Ay 4 500 20 C 4 500 20 Q OD 4 500 20 C When is the average cost per year minimum This time is frequently referred to as the replacement time for this piece of equipment The average cost per year is minimum after years 17
Calculus
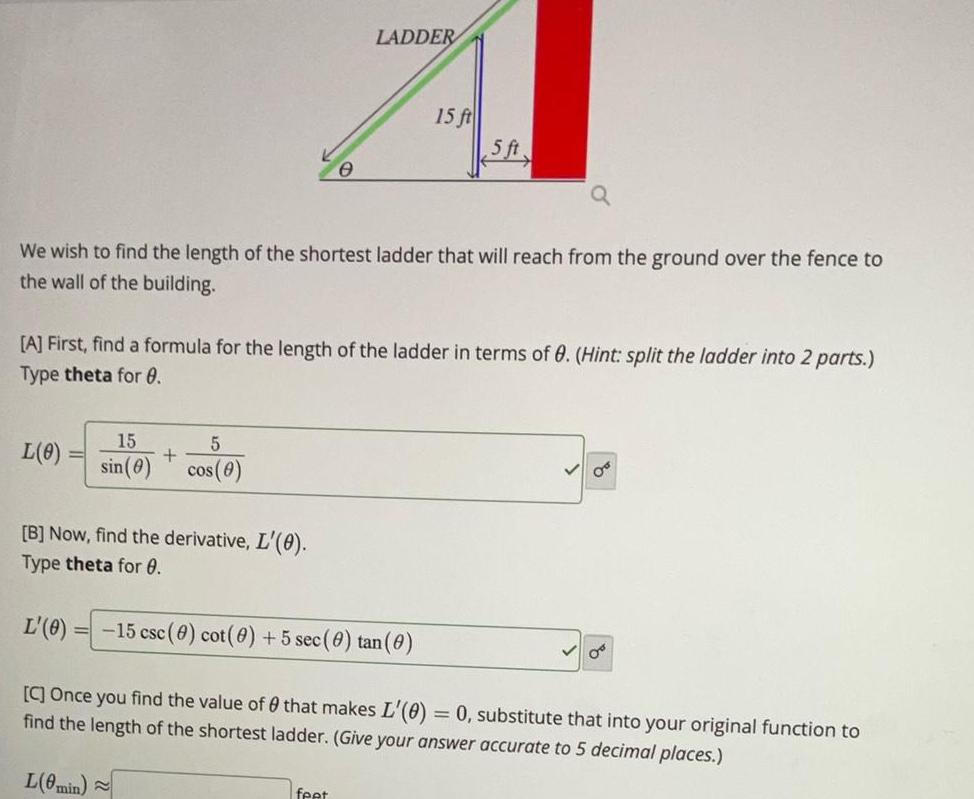
Differential equationsL 0 We wish to find the length of the shortest ladder that will reach from the ground over the fence to the wall of the building 15 5 sin 0 cos 0 B Now find the derivative L 0 Type theta for 0 L 0 0 A First find a formula for the length of the ladder in terms of 0 Hint split the ladder into 2 parts Type theta for 0 LADDER 15 ft 15 csc 0 cot 0 5 sec 0 tan 0 feet 5 ft C Once you find the value of that makes L 0 0 substitute that into your original function to find the length of the shortest ladder Give your answer accurate to 5 decimal places L 0min

Calculus
Application of derivativesLet F x y f x y g x y be defined on R Find and graph the streamlines for the vector field F y 5 Oy 10x C Oy 10 OA C Choose the correct graph below Q 5 OB CHICCO OC 5 OD Q G KKERRE 22222 X
Calculus
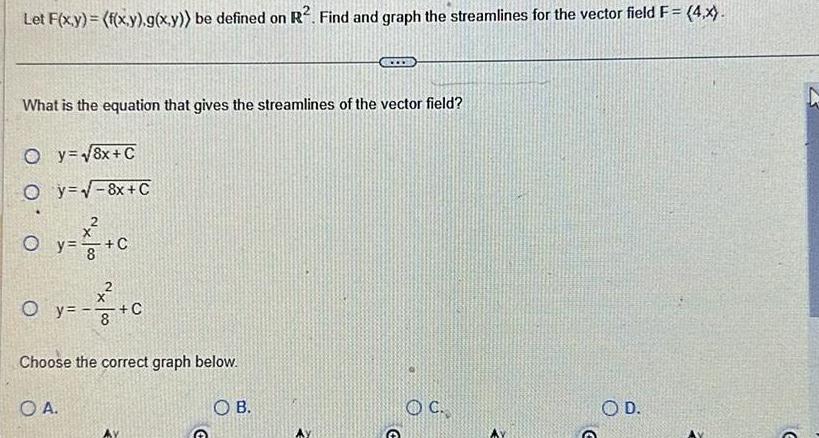
Application of derivativesLet F x y f x y g x y be defined on R Find and graph the streamlines for the vector field F 4 x What is the equation that gives the streamlines of the vector field Oy 8x C Oy 8x C x O y O y C OA x 8 C Choose the correct graph below OB OC O D G

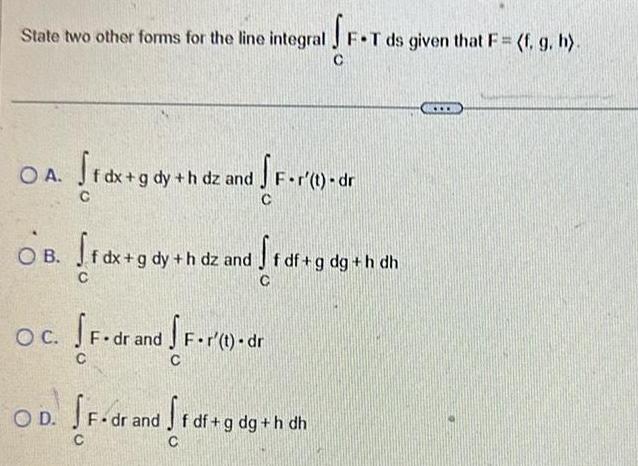
Calculus
Indefinite IntegrationState two other forms for the line integral J F T ds given that F f g h SF T OA Srdx gdy hdz and f F r t dr C OB 1 dx gdy h dz and 1 df g dg h dh C C OC SF dr and OD F dr and F r t dr C F dr and f df g dg h din dh C C
Calculus
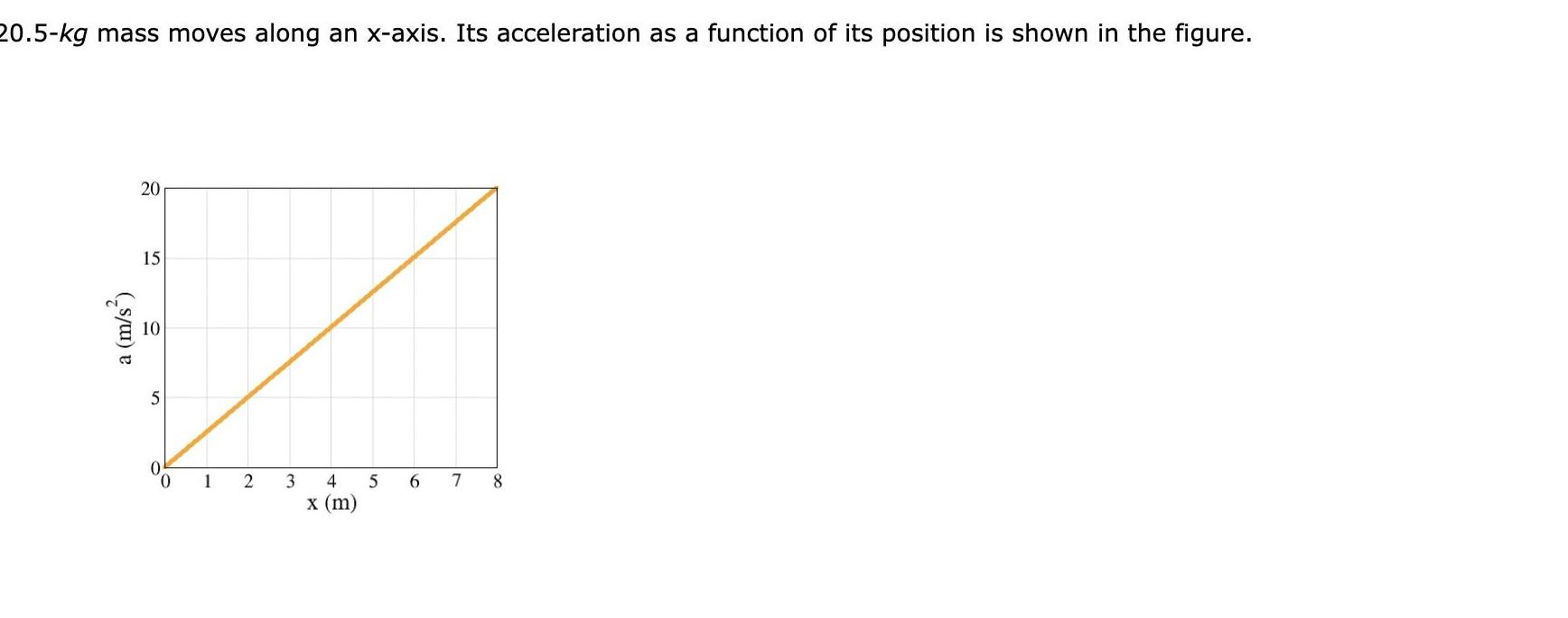
Application of derivatives20 5 kg mass moves along an x axis Its acceleration as a function of its position is shown in the figure a m s 20 15 10 5 1 2 3 4 x m 5 6 7 8
Calculus
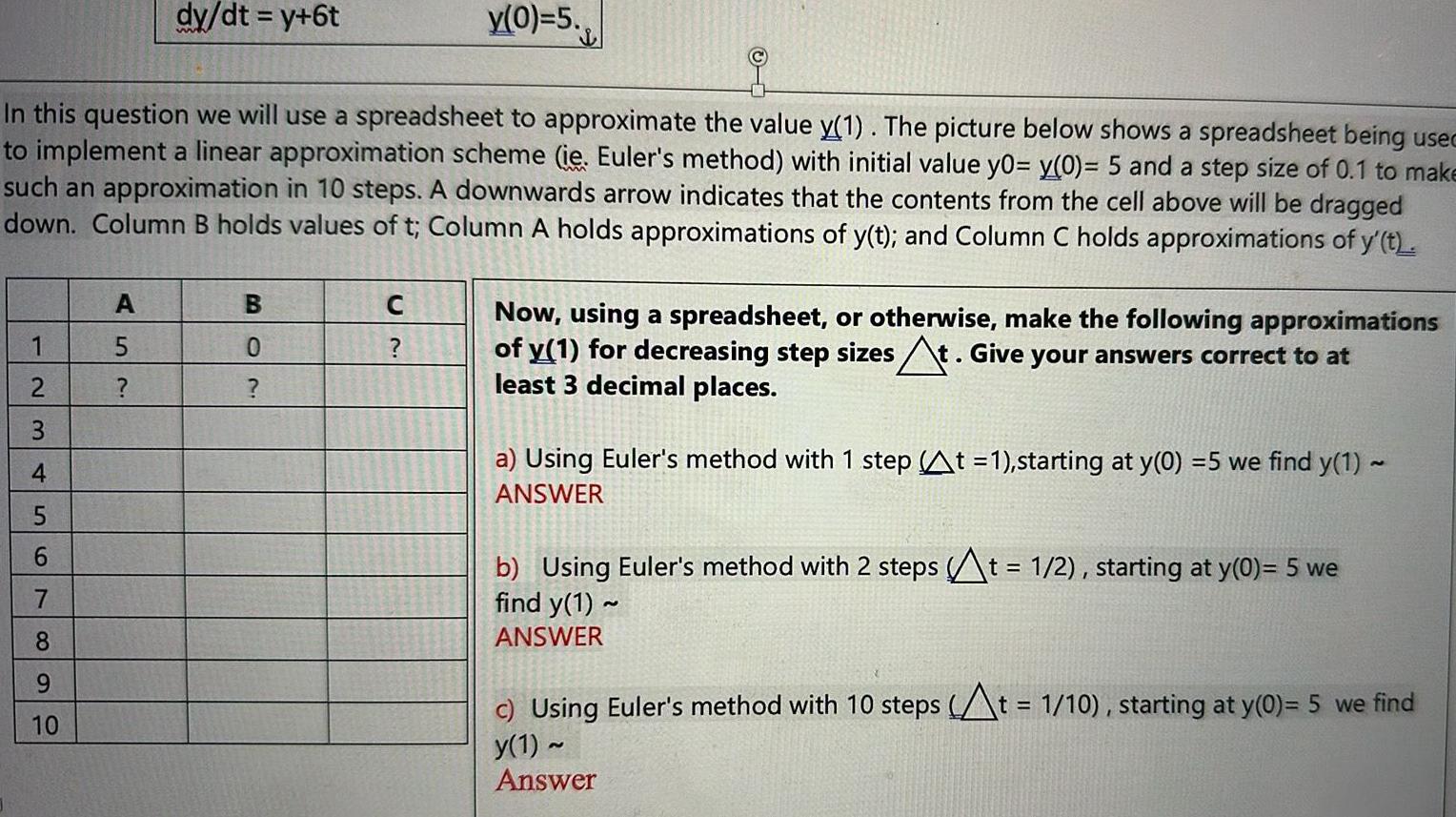
Differential equations1 In this question we will use a spreadsheet to approximate the value y 1 The picture below shows a spreadsheet being usec to implement a linear approximation scheme ie Euler s method with initial value y0 y 0 5 and a step size of 0 1 to make such an approximation in 10 steps A downwards arrow indicates that the contents from the cell above will be dragged down Column B holds values of t Column A holds approximations of y t and Column C holds approximations of y t 234 56 789 10 dy dt y 6t A 5 B 0 y 0 5 C Now using a spreadsheet or otherwise make the following approximations of y 1 for decreasing step sizes At Give your answers correct to at least 3 decimal places a Using Euler s method with 1 step t 1 starting at y 0 5 we find y 1 ANSWER b Using Euler s method with 2 steps t 1 2 starting at y 0 5 we find y 1 ANSWER c Using Euler s method with 10 steps t 1 10 starting at y 0 5 we find y 1 Answer

Calculus
DifferentiationCalculate the Reynolds number for human blood flowing through a 2mm radius vessel at average velocity of 0 2 m s Charactize the flow i e turbulent laminar or transitional

Calculus
Application of derivativesA publishing company sells 625 000 copies of certain books each year It costs the company 1 to store each book a year Each time it must print additional copies it costs the company 500 to set up the presses How many books should the company produce during each printing in order to minimize its total storage and setup costs The company should produce books each printing in order to minimize costs

Calculus
Differentiationet g x 3 1 5x and f x 3 1 5 Explore the rates of change constant average for th near function g and the exponential function f a Determine the value of the ratios i From x 0 to x 1 5 Ag x Ax Af x Ax ii From x Ag x Ax Af x Ax Ag x Ax iii From x Af x Ax 1 5 to x 3 3 to x 5 Ag x Ax and Af x Ax Preview Preview X Preview X Preview Preview Preview over the following intervals of x
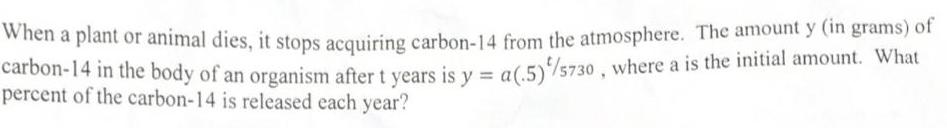
Calculus
Limits & ContinuityWhen a plant or animal dies it stops acquiring carbon 14 from the atmosphere The amount y in grams of carbon 14 in the body of an organism after t years is y a 5 75730 where a is the initial amount What percent of the carbon 14 is released each year
Calculus
Differential equationsA manufacturer of hospital supplies has a uniform annual demand for 500 000 boxes of bandages It costs 10 to one box of bandages for one year and 160 to set up the plant for production How many times a year should the company produce boxes of bandages in order to minimize the total storage and setup costs The company should produce boxes of bandages time s a year
Calculus
Limits & ContinuityDetermine the domain of each of the following functions Report the solution in interval form Also identify the equation s of the vertical asymptote s of each function f z log 32 6 The domain of is f The function f has a vertical asymptote at h z In 12 2x The domain of his The function h has a vertical asymptote at g x log r 1 The domain of g is The function g has a vertical asymptote at 9 and

Calculus
Application of derivativesStarting with a 160 foot long stone wall a farmer would like to construct a rectangular enclosure by adding 960 feet of fencing as shown in the figure to the right Find the values of x and w that result in the greatest possible area X W ft ft CCES 160 feet
Calculus
Application of derivativesLet R be the region bounded by y x x 1 and y 0 Use the shell method to find the volume of the solid generated when R is revolved about the line y 3 Set up the integral that gives the volume of the solid using the shell method Use increasing limits of integration Select the correct choice below and fill in the answer boxes to complete your choice Type exact answers 1 A OB 0 2x y 3 y dy Jo GEXER dx
Calculus
Vector CalculusFind the absolute maximum and minimum values of the function over the indicated interval and indicate the x values at which they occur f x 9x 1 A 0 4 B 5 6 A Find the first derivative of f f x 9 Simplify your answer The absolute maximum value is at x Use a comma to separate answers as needed


Calculus
Application of derivativesK Why do the values of cos x lie in the interval 0 1 Choose the correct answer below OA Cosine is undefined for negative values of x Cosine is only defined for values in the interval 0 B OC O D Cosine is only invertible for values outside the interval 0 Cosine is not one to one if any of the values outside the interval 0 are also included


Calculus
Application of derivativesSimplify the following expression 8 1 57 3 183 1 85k 17k1 13 1 8 Show your work here 8 Hint To add an exponent x type exponent or press A

Calculus
Application of derivativesA boat is towed toward a dock by a cable attached to a winch that stands 10 ft above the water level see figure Let 8 be the angle of elevation of the winch and let L be the length of the cable as the boat is towed toward the dock Complete parts a to c below a What is the rate of change of 0 with respect to L dL de 10 E OA dL L 10 de O C dL de 10L 100 de 10L OB dL 2 10 de 10 OD dL LL 100 10 ft
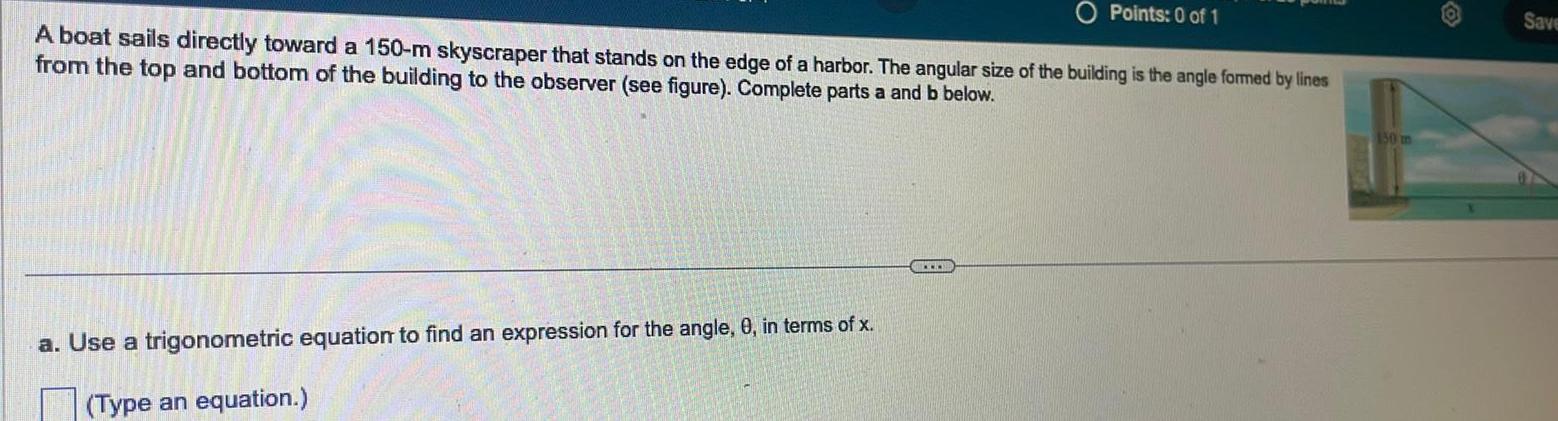
Calculus
Application of derivativesPoints 0 of 1 A boat sails directly toward a 150 m skyscraper that stands on the edge of a harbor The angular size of the building is the angle formed by lines from the top and bottom of the building to the observer see figure Complete parts a and b below a Use a trigonometric equation to find an expression for the angle 0 in terms of x Type an equation 150 m Save
Calculus
Application of derivativesFind the absolute maximum value on 0 co for f x 10x 5x In x Select the correct choice below and if necessary fill in the answer boxes to complete your choice OA The absolute maximum is at x Round to two decimal places as needed OB There is no absolute maximum
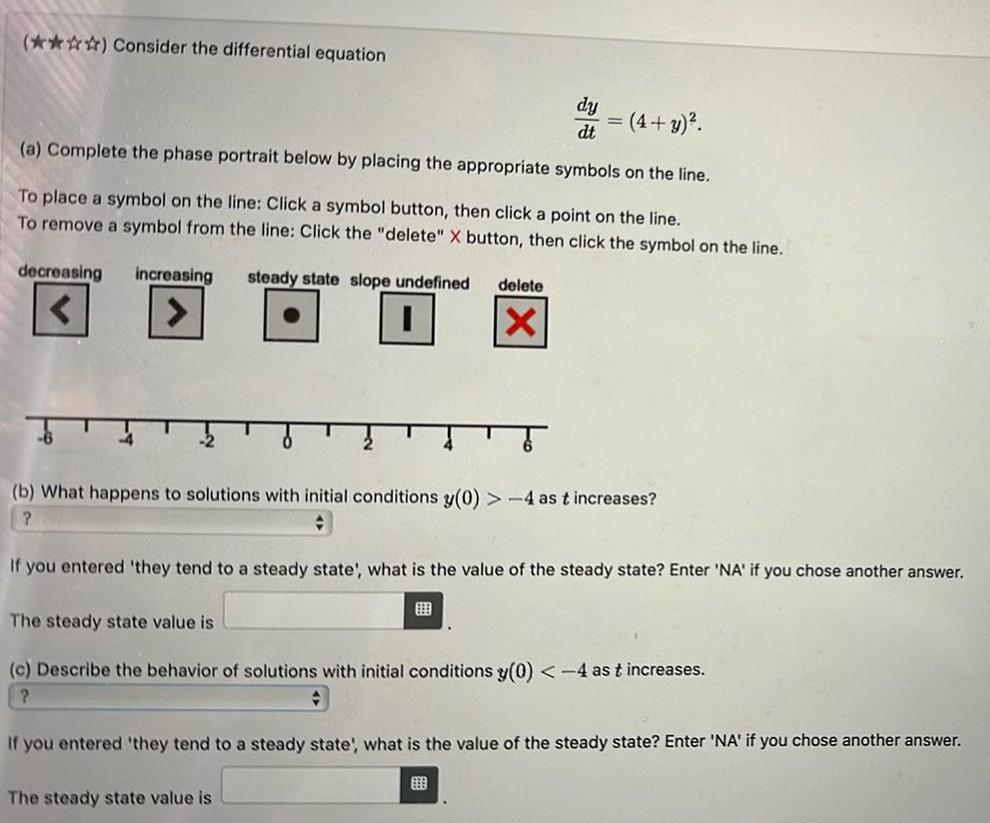
Calculus
Application of derivativesConsider the differential equation dy dt a Complete the phase portrait below by placing the appropriate symbols on the line To place a symbol on the line Click a symbol button then click a point on the line To remove a symbol from the line Click the delete X button then click the symbol on the line decreasing increasing steady state slope undefined 4 y delete X b What happens to solutions with initial conditions y 0 4 as t increases If you entered they tend to a steady state what is the value of the steady state Enter NA if you chose another answer The steady state value is c Describe the behavior of solutions with initial conditions y 0 4 as t increases The steady state value is If you entered they tend to a steady state what is the value of the steady state Enter NA if you chose another answer

Calculus
Indefinite IntegrationDetermine the indefinite integral S 6 16 x dx S 6 16 x dx Check the answer by differentiation
Calculus
Vector CalculusExpress in terms of x using the inverse sine inverse tangent and inverse secant functions 1 0 sin Simplify your answer including any radicals Use integers or fractions for any numbers in the expression Points 0 of 1
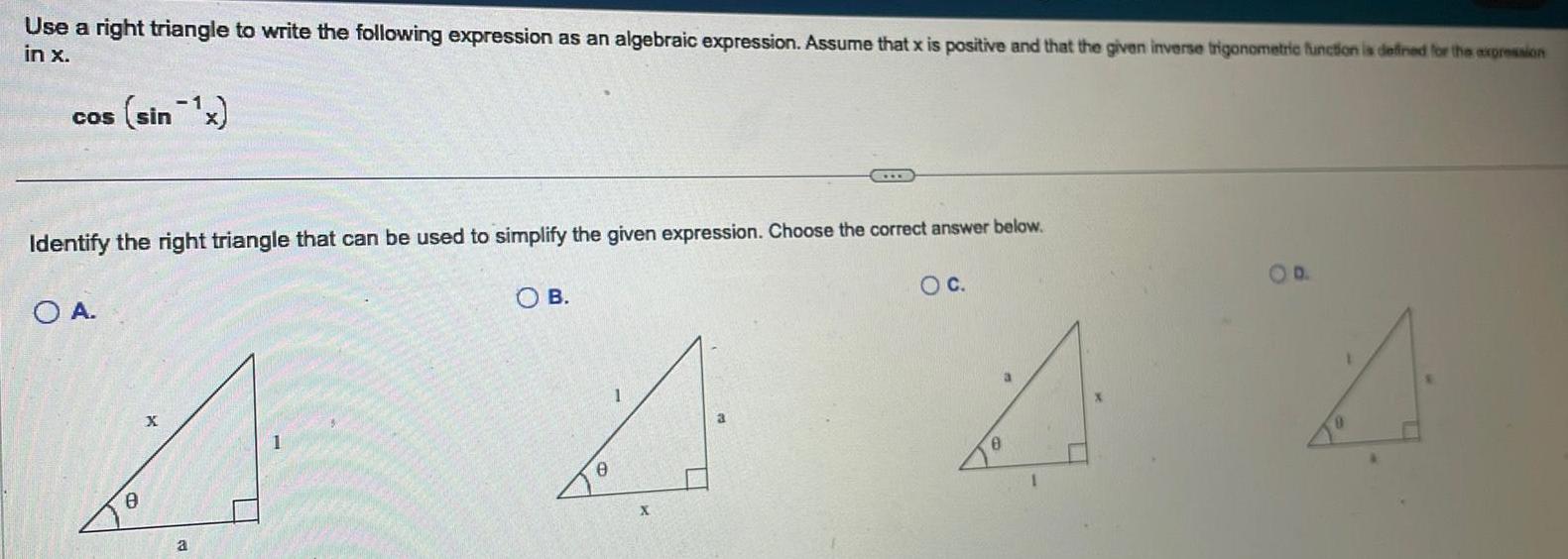
Calculus
Application of derivativesUse a right triangle to write the following expression as an algebraic expression Assume that x is positive and that the given inverse trigonometric function is defined for the expression in x sin x COS Identify the right triangle that can be used to simplify the given expression Choose the correct answer below OB O C O A 8 a 1 0 X A O D A
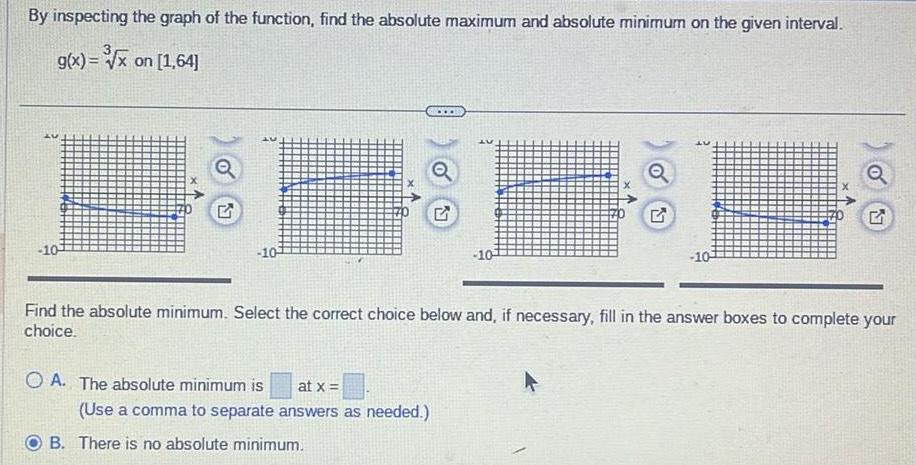
Calculus
DifferentiationBy inspecting the graph of the function find the absolute maximum and absolute minimum on the given interval g x x on 1 64 10 2 20 10 OA The absolute minimum is at x U Use a comma to separate answers as needed B There is no absolute minimum U 10 Find the absolute minimum Select the correct choice below and if necessary fill in the answer boxes to complete your choice 10

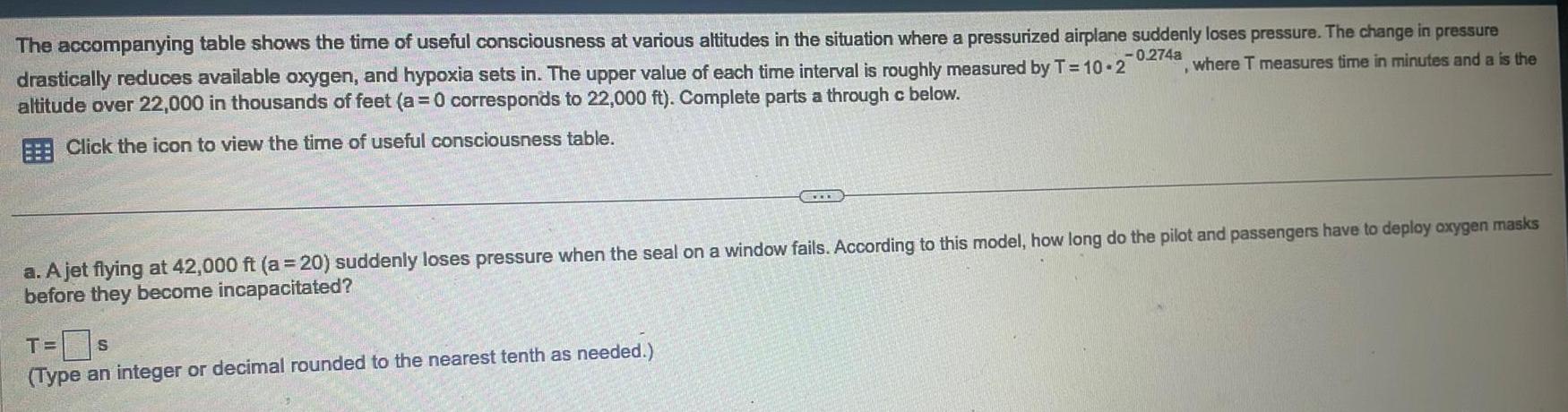
Calculus
Application of derivativesThe accompanying table shows the time of useful consciousness at various altitudes in the situation where a pressurized airplane suddenly loses pressure The change in pressure 0 274a where T measures time in minutes and a is the drastically reduces available oxygen and hypoxia sets in The upper value of each time interval is roughly measured by T 10 2 altitude over 22 000 in thousands of feet a 0 corresponds to 22 000 ft Complete parts a through c below Click the icon to view the time of useful consciousness table a A jet flying at 42 000 ft a 20 suddenly loses pressure when the seal on a window fails According to this model how long do the pilot and passengers have to deploy oxygen masks before they become incapacitated T S Type an integer or decimal rounded to the nearest tenth as needed
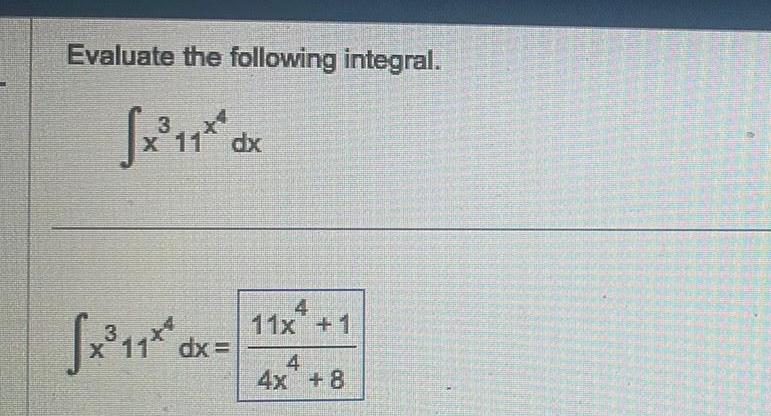
Calculus
Application of derivativesEvaluate the following integral x 11 3 x 11 dx fx 11 dx 3 11x 1 4 4x 8
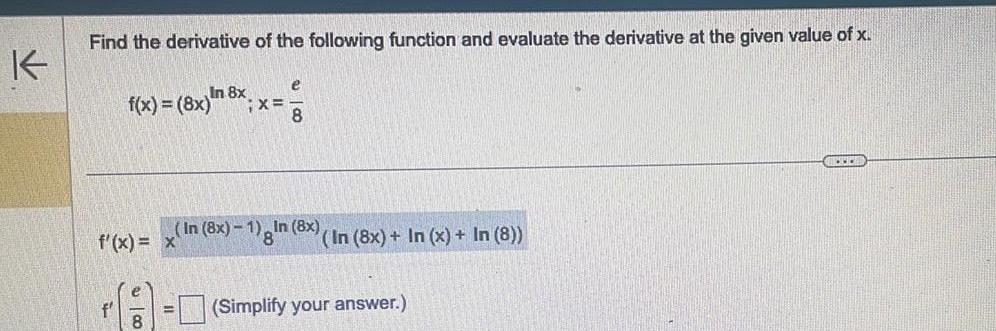
Calculus
Indefinite IntegrationK Find the derivative of the following function and evaluate the derivative at the given value of x f In 8x f x 8x f x x e 8 X In 8x 1 In 8x 8 In 8x In x In 8 Simplify your answer CED

Calculus
DifferentiationFind the derivative of the following function and evaluate the derivative at the given value of x In 8x f x 8x f x 16 X e 180
Calculus
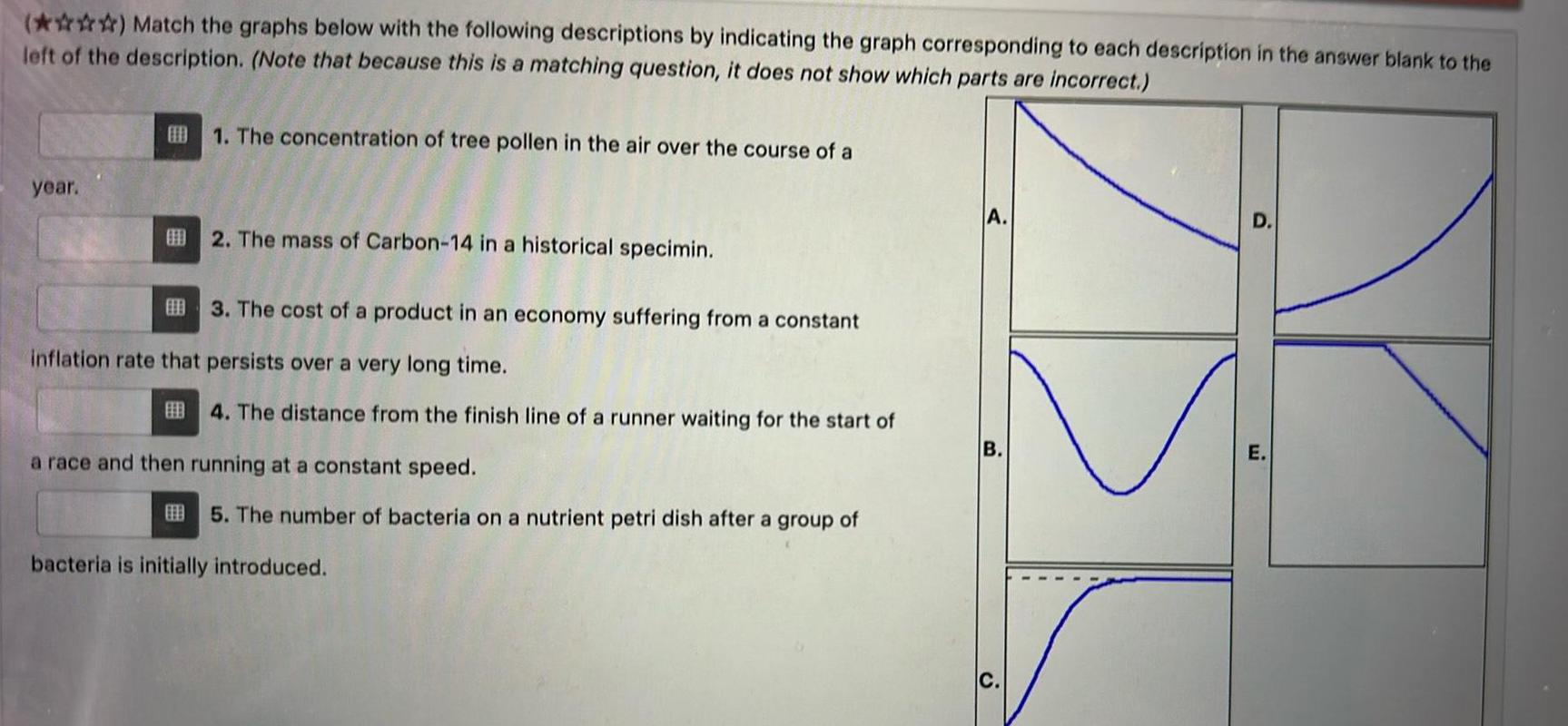
Vector CalculusMatch the graphs below with the following descriptions by indicating the graph corresponding to each description in the answer blank to the left of the description Note that because this is a matching question it does not show which parts are incorrect year 1 The concentration of tree pollen in the air over the course of a 2 The mass of Carbon 14 in a historical specimin 3 The cost of a product in an economy suffering from a constant inflation rate that persists over a very long time 4 The distance from the finish line of a ru a race and then running at a constant speed waiting for the start of 5 The number of bacteria on a nutrient petri dish after a group of bacteria is initially introduced A E
Calculus
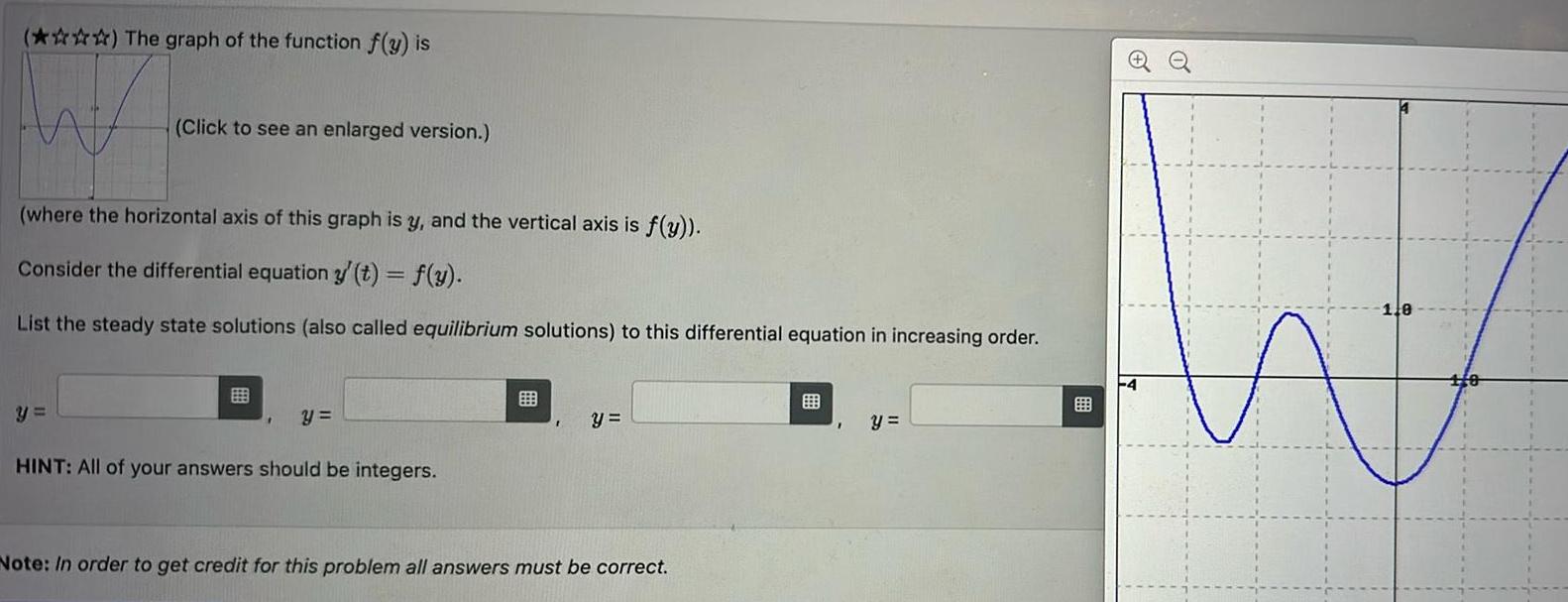
Differential equationsThe graph of the function f y is HAP Click to see an enlarged version where the horizontal axis of this graph is y and the vertical axis is f y Consider the differential equation y t f y List the steady state solutions also called equilibrium solutions to this differential equation in increasing order y HINT All of your answers should be integers y Note In order to get credit for this problem all answers must be correct y O
Calculus
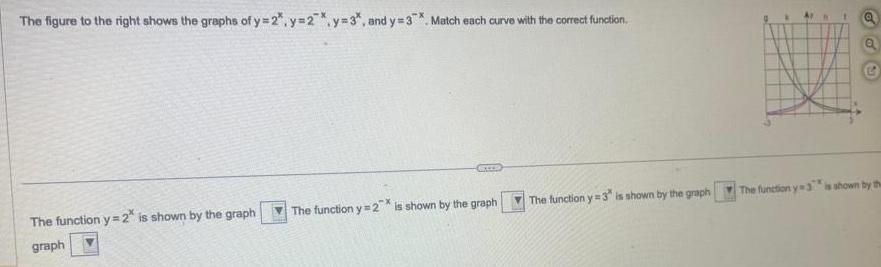
Application of derivativesThe figure to the right shows the graphs of y 2 y 2y 3 and y 3 Match each curve with the correct function The function y 2 is shown by the graph graph The function y 2 is shown by the graph The function y 3 is shown by the graph P The function y 3 is shown by the
Calculus
Vector CalculusO Points 0 of 1 a radioactive isotope used in medicine to test the function of the thyroid gland Its half life is 13 1 hours A 575 microaurie 0 dose of iodine 123 is admini Answer parts a through d patient The quantity Q left in the body after t hours is given by the equation Q 575 a Determine the time it takes for the level of iodine 123 to drop to 25 Ci It takes hr for the level of iodine 123 to drop to 25 Ci Type an integer or decimal rounded to two decimal places as needed 13 1 points
Calculus
Definite Integralsacceleration due to gravity a How much work is required to wind the entire chain onto the cylinder using the winch b How much work is required to wind the chain onto the cylinder if a 40 kg block is attached to the end of the chain orically from a cylinder attached to a winch Assume there is no friction in the system and that the chain has a density of 6 kg m Use 9 8 m s for the 8 9 8 60 y dy 60 a Set up the integral that gives the work required to wind the entire chain onto the cylinder using the winch Use increasing limits of integration 60 arri Type exact answers The amount of work required is 105840 Type an integer or a decimal b Set up the integral that gives the work required to wind the chain onto the cylinder if a 40 kg block is attached to the end of the chain Use increasing limits of integration 9 8 360 6y 40 9 8 dy 0 Type exact answers of 1 The amount of work required if a 40 kg block is attached to the end of the chain is 129384 J desimal Save
Calculus
DifferentiationFind the derivative of the following function and evaluate the derivative at the given value of x f x 8x 8x f x
Calculus
Limits & ContinuityUse the definition of the derivative to evaluate the limit lim h 0 lim h 0 3 h 7 h 343 h 3 h 7 h 343 h 147 343 log 7
Calculus
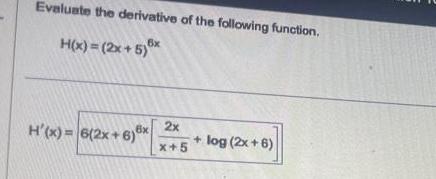
Application of derivativesEvaluate the derivative of the following function 6x H x 2x 5 x 6x 2x x 5 H x 6 2x 6 log 2x 6
Calculus
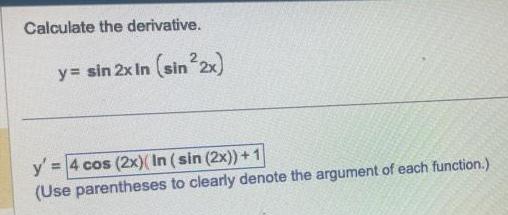
DifferentiationCalculate the derivative y sin 2x in sin 2x y 4 cos 2x In sin 2x 1 Use parentheses to clearly denote the argument of each function
Calculus
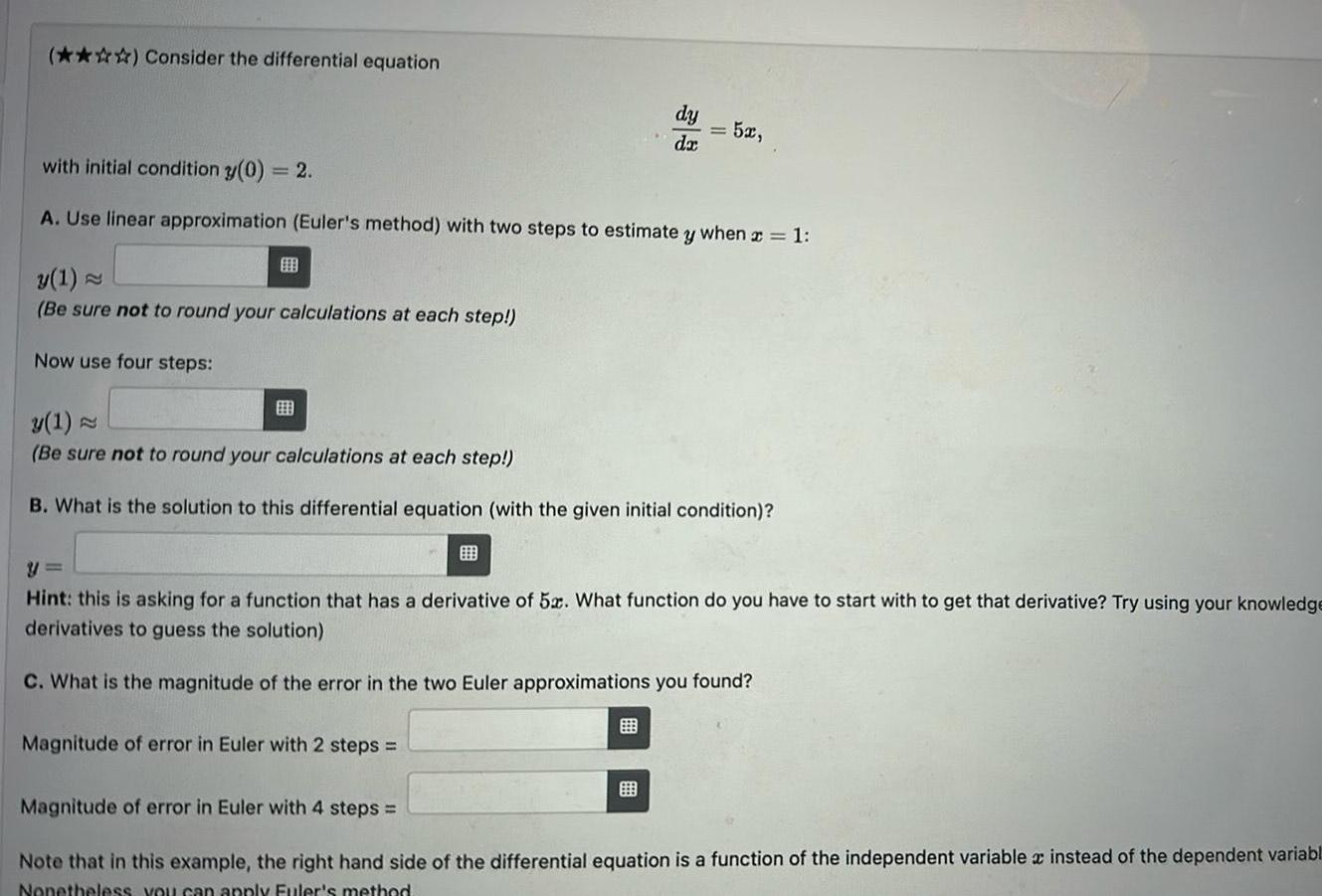
Vector CalculusConsider the differential equation B y 1 Be sure not to round your calculations at each step Now use four steps with initial condition y 0 2 A Use linear approximation Euler s method with two steps to estimate y when x 1 dy da B Magnitude of error in Euler with 2 steps 52 y 1 Be sure not to round your calculations at each step B What is the solution to this differential equation with the given initial condition Hint this is asking for a function that has a derivative of 5x What function do you have to start with to get that derivative Try using your knowledge derivatives to guess the solution C What is the magnitude of the error in the two Euler approximations you found Magnitude of error in Euler with 4 steps Note that in this example the right hand side of the differential equation is a function of the independent variable instead of the dependent variabl Nonetheless you can apply Euler s method

Calculus
Application of derivativesSuppose you have just poured a cup of freshly brewed coffee with temperature 90 C in a room where the temperature is 25 C Newton s Law of Cooling states that the rate of cooling of an object is proportional to the temperature difference between the object and its surroundings Therefore the temperature of the coffee T t satisfies the differential equation A What is the limiting value of the temperature of the coffee where Troom 25 is the room temperature and k is some constant Suppose it is known that the coffee cools at a rate of 1 C per minute when its temperature is 75 C lim T t tx B What is the limiting value of the rate of cooling dT lim t 00 dt C Find the constant k in the differential equation k EB dT dt CER k T Troom D Use Euler s method with step size Ax 3 minutes to estimate the temperature of the coffee after 15 minutes
Calculus
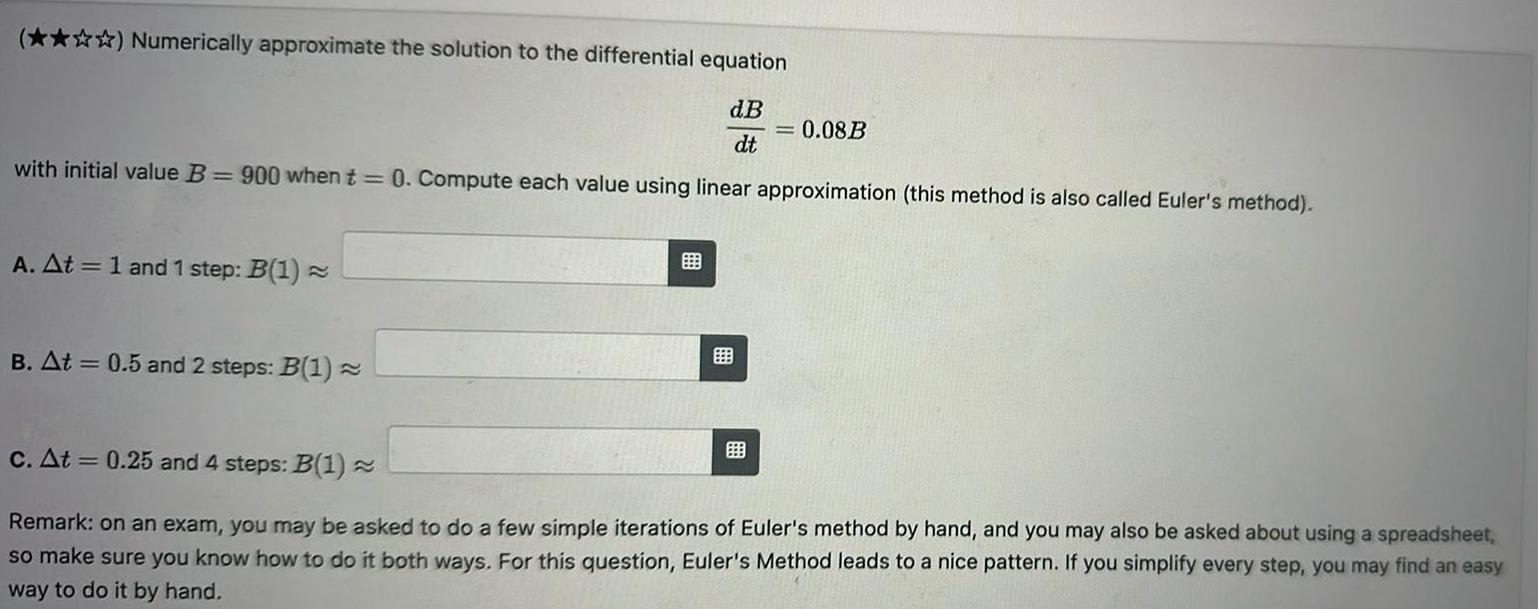
Differential equationsNumerically approximate the solution to the differential equation dB dt with initial value B 900 when t 0 Compute each value using linear approximation this method is also called Euler s method A At 1 and 1 step B 1 B At 0 5 and 2 steps B 1 0 08B c At 0 25 and 4 steps B 1 Remark on an exam you may be asked to do a few simple iterations of Euler s method by hand and you may also be asked about using a spreadsheet so make sure you know how to do it both ways For this question Euler s Method leads to a nice pattern If you simplify every step you may find an easy way to do it by hand

Calculus
Differential equationsTwo lakes have populations of fish but the conditions are quite different in these lakes In the first lake the fish population is growing and satisfies the differential equation dy dt Time where t is time in years At time t 0 there were 600 fish in this lake In the second lake the population is dying due to pollution Its population satisfies the differential equation years dy dt 0 7y 0 8y and initially there were 8000 fish in this lake At what time will the fish populations in the two lakes be identical
Calculus
Application of derivativesUse Euler s method with step size 0 2 to estimate y 1 where y x is the solution of the initial value problem y 5x y y 0 1

Calculus
Vector CalculusThe radioactive isotope carbon 14 is present in small quantities in all life forms and it is constantly replenished until the organism dies after which it decays to stable carbon 12 at a rate proportional to the amount of carbon 14 present with a half life of 5699 years Suppose C t is the amount of carbon 14 present at time t a Find the value of the constant k in the differential equation C kC k b In 1988 three teams of scientists found that the Shroud of Turin which was reputed to be the burial cloth of Jesus contained about 91 percent of the amount of carbon 14 contained in freshly made cloth of the same material 1 How old is the Shroud of Turin according to this data Age years 1 The New York Times October 18 1988