Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
Calculus
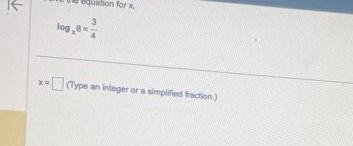
Application of derivativesX log 8 3 on for x Type an integer or a simplified fraction wwwwww
Calculus
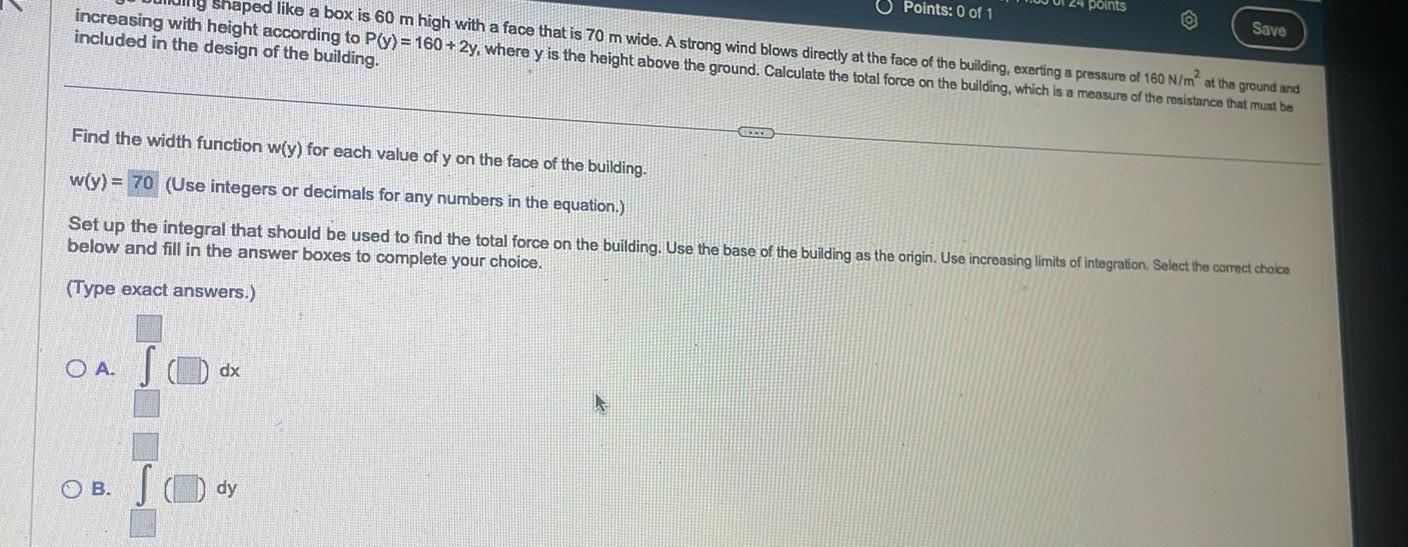
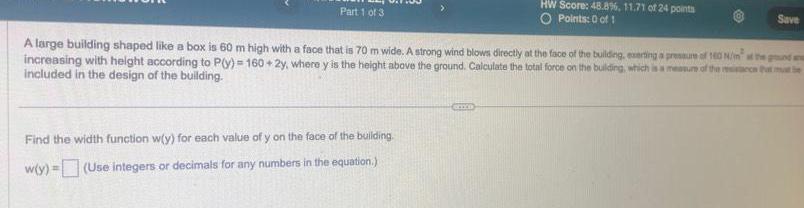
Definite Integralsshaped like a box is 60 m high with a face that is 70 m wide A strong wind blows directly at the face of the building exerting a pressure of 160 N m at the ground and increasing with height according to P y 160 2y where y is the height above the ground Calculate the total force on the building which is a measure of the resistance that must be included in the design of the building OA S OB SO Find the width function w y for each value of y on the face of the building w y 70 Use integers or decimals for any numbers in the equation Set up the integral that should be used to find the total force on the building Use the base of the building as the origin Use increasing limits of integration Select the correct choice below and fill in the answer boxes to complete your choice Type exact answers dx dy Points 0 of 1 STEED points Save
Calculus
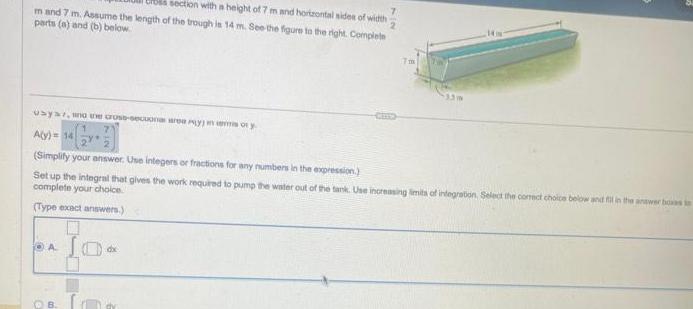
Definite Integralssection with a height of 7 m and horizontal sides of width m and 7 m Assume the length of the trough is 14 m See the figure to the right Complete parts a and b below usya who the cross secuona yoy A y 14 Simplify your answer Use integers or fractions for any numbers in the expression Set up the integral that gives the work required to pump the water out of the tank Use increasing limits of integration Select the correct choice below and fill in the answer boas in complete your choice Type exact answers A B dx
Calculus
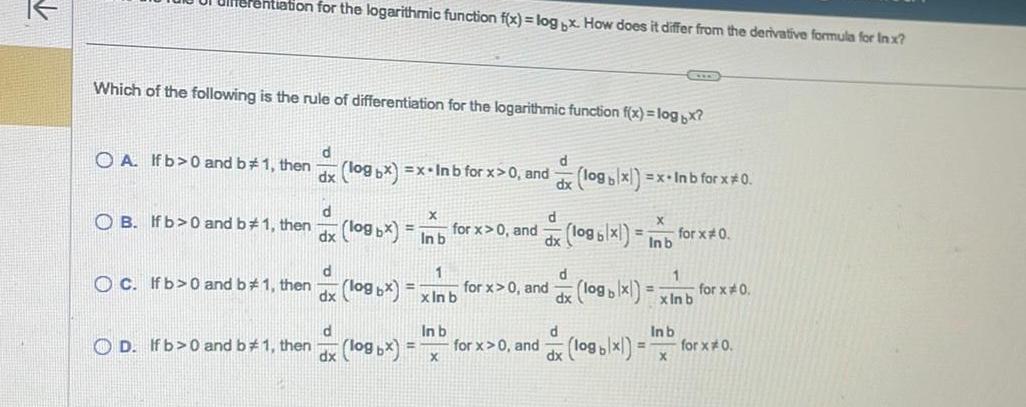
Differentiationrentiation for the logarithmic function f x log x How does it differ from the derivative formula for Inx Which of the following is the rule of differentiation for the logarithmic function f x log x OA If b 0 and b 1 then d dx log bx x In b for x 0 and d OB If b 0 and b 1 then dx C If b 0 and b 1 then d dx log bx In b for x 0 and 1 log bx x In b d In b OD If b 0 and b 1 then log x dx X for x 0 and for x 0 and d dx log blx x Inb for x 0 d logb x Inb d d dx logb x logx xInb for x 0 1 In b X for x 0 for x 0

Calculus
Differentiatione g The area between the curve y Part 5 of 7 Determine whether the following statements are true and give an explanation or counterexample Assume x 0 and 0 a In xy Inx Iny b In 0 1 c in x y Inx Iny 7 2 71 e Choose the comect answer below f 3 for any integer m2 1 1 and the x axis on the interval 1 is 1 UD Ine statement is true because the derivative of an exponentia sunction is defined asjae Cerra OA The statement is true because the derivative of an exponerial function is defined as OB The statement is false because the derivative of an exponential function is defined as 0 OC The statement is false because the derivative of an exponential function is defined as OD The statement is true because the derivative of an exponential function is defined as dx HW Score 79 27 19 Points 0 43 of 1 woo
Calculus
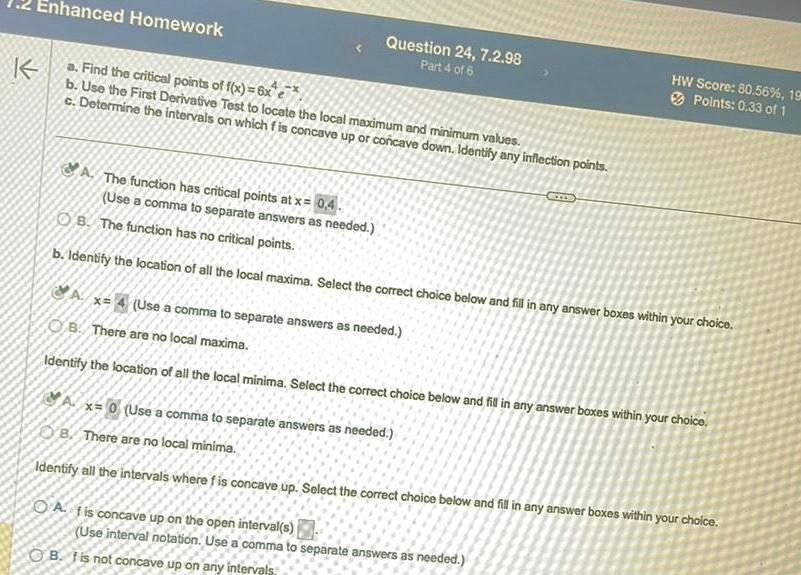
Application of derivativesK Enhanced Homework a Find the critical points of f x 6x e b Use the First Derivative Test to locate the local maximum and minimum values c Determine the intervals on which f is concave up or concave down Identify any inflection points A The function has critical points at x 0 4 Use a comma to separate answers as needed Question 24 7 2 98 Part 4 of 6 OB The function has no critical points b Identify the location of all the local maxima Select the correct choice below and fill in any answer boxes within your choice HW Score 80 56 198 Points 0 33 of 1 A x 4 Use a comma to separate answers as needed B There are no local maxima Identify the location of all the local minima Select the correct choice below and fill in any answer boxes within your choice Ax 0 Use a comma to separate answers as needed OB There are no local minima Identify all the intervals where f is concave up Select the correct choice below and fill in any answer boxes within your choice A fis concave up on the open interval s Use interval notation Use a comma to separate answers as needed OB I is not concave up on any intervals
Calculus
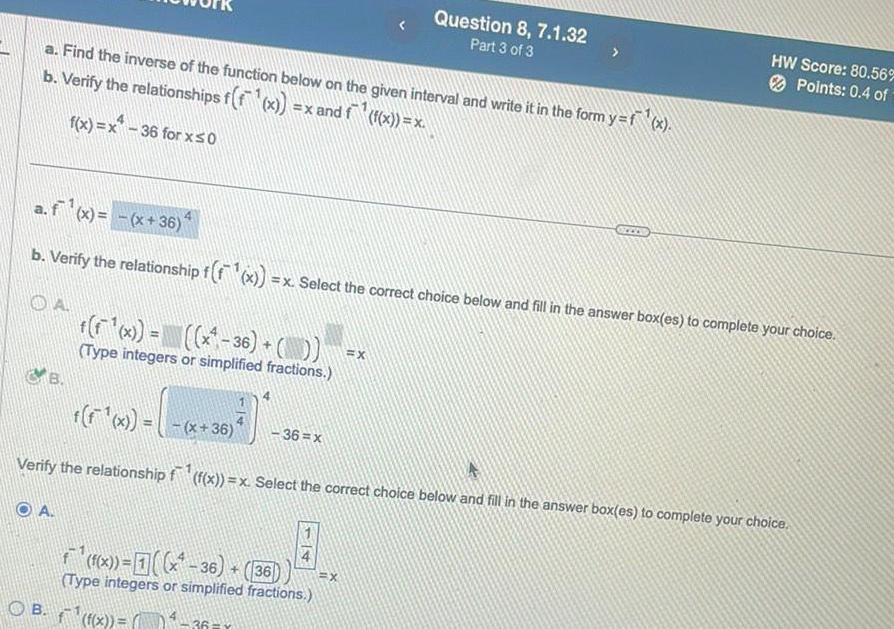
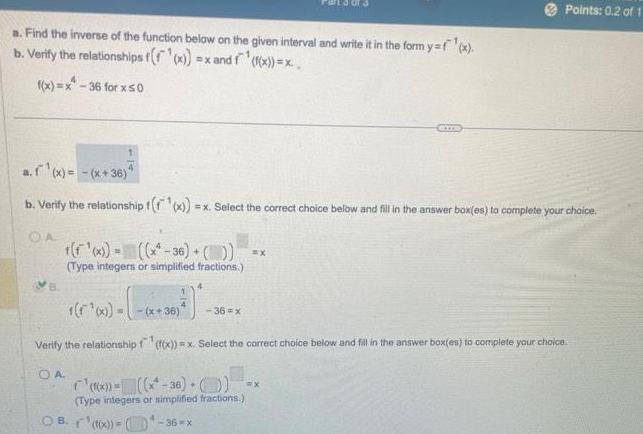
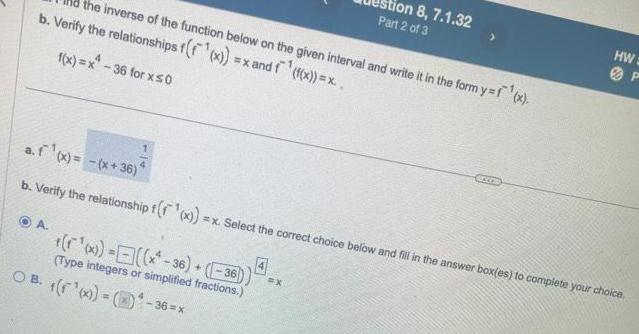
Application of derivativesa Find the inverse of the function below on the given interval and write it in the form y f x b Verify the relationships f f x x and f f x x f x x 36 for x 0 B a f x x 36 b Verify the relationship f f x x Select the correct choice below and fill in the answer box es to complete your choice f F x x 36 Type integers or simplified fractions OA f f x x 36 Verify the relationship f f x x Select the correct choice below and fill in the answer box es to complete your choice 36 x f f x 36 36 Type integers or simplified fractions OB x 36 Question 8 7 1 32 Part 3 of 3 X X HW Score 80 56 Points 0 4 of
Calculus
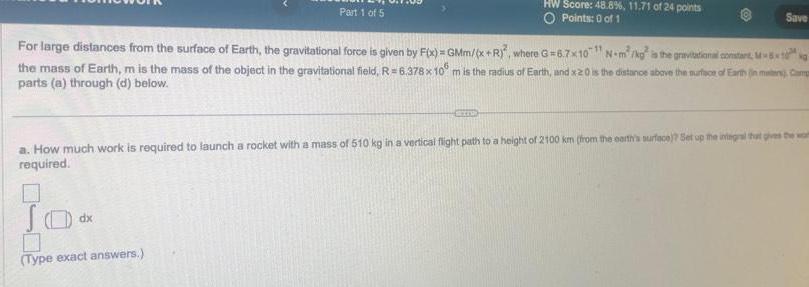
Definite IntegralsPart 1 of 5 JO 0 Type exact answers HW Score 48 8 11 71 of 24 points O Points 0 of 1 For large distances from the surface of Earth the gravitational force is given by F x GMm x R where G 6 7x10 N m kg is the gravitational constant M the mass of Earth m is the mass of the object in the gravitational field R 6 378 x 10 m is the radius of Earth and x20 is the distance above the surface of Earth in maten Cam parts a through d below dx Save 11 a How much work is required to launch a rocket with a mass of 510 kg in a vertical flight path to a height of 2100 km from the earth s surface Set up the integral that gives the wom required
Calculus
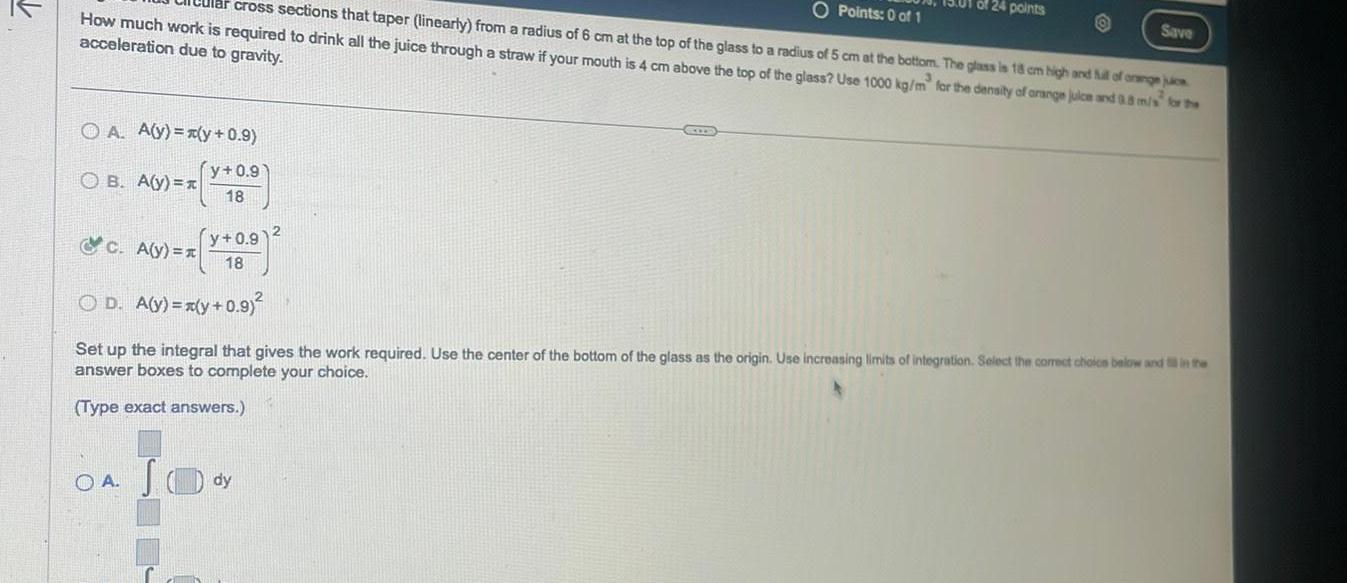
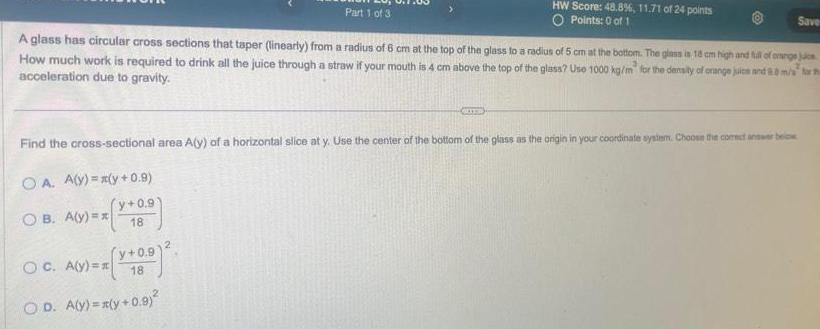
Definite IntegralsO Points 0 of 1 cross sections that taper linearly from a radius of 6 cm at the top of the glass to a radius of 5 cm at the bottom The glass is 18 cm high and full of orange juice How much work is required to drink all the juice through a straw if your mouth is 4 cm above the top of the glass Use 1000 kg m for the density of orange juice and 0 8 m s for the acceleration due to gravity OA A y x y 0 9 y 0 9 OB A y x 18 y 0 9 18 c A y x OD A y y 0 9 24 points OA S dy Save Set up the integral that gives the work required Use the center of the bottom of the glass as the origin Use increasing limits of integration Select the correct choice below and in the answer boxes to complete your choice Type exact answers
Calculus
Application of derivativesa Find the critical points of f x 6x e b Use the First Derivative Test to locate the local maximum and minimum values c Determine the intervals on which f is concave up or concave down Identify any inflection points Part 3 of 6 a Identify all the critical points Select the correct choice below and fill in any answer boxes within your choice A The function has critical points at x 0 4 Use a comma to separate answers as needed x 4 Use a comma to separate answers as needed OB The function has no critical points b Identify the location of all the local maxima Select the correct choice below and fill in any answer boxes within your choice HW Score 79 86 19 17 om Points 0 17 of 1 OA x Use a comma to separate answers as needed OB There are no local minima OB There are no local maxima Identify the location of all the local minima Select the correct choice below and fill in any answer boxes within your choice
Calculus
Definite IntegralsO Points 0 of 1 Use the shell method to find the volume of the solid formed when a hole of radius 1 is drilled symmetrically along the axis of a right circular cone of radius 6 and height OA S dy 6 B 3xx 6 x dx Part 2 of 2 Model the situation on a set of axes by placing the center of the base of the cone at the origin and the cone s axis along the positive y axis Set up the integral that gives the volume of the solid using the shell method Use nonnegative and increasing limits of integration Select the correct choice below and fill in the answer boxes to complete your choice Type exact answers The volume is Type an exact answer CETTE of 20 points Save
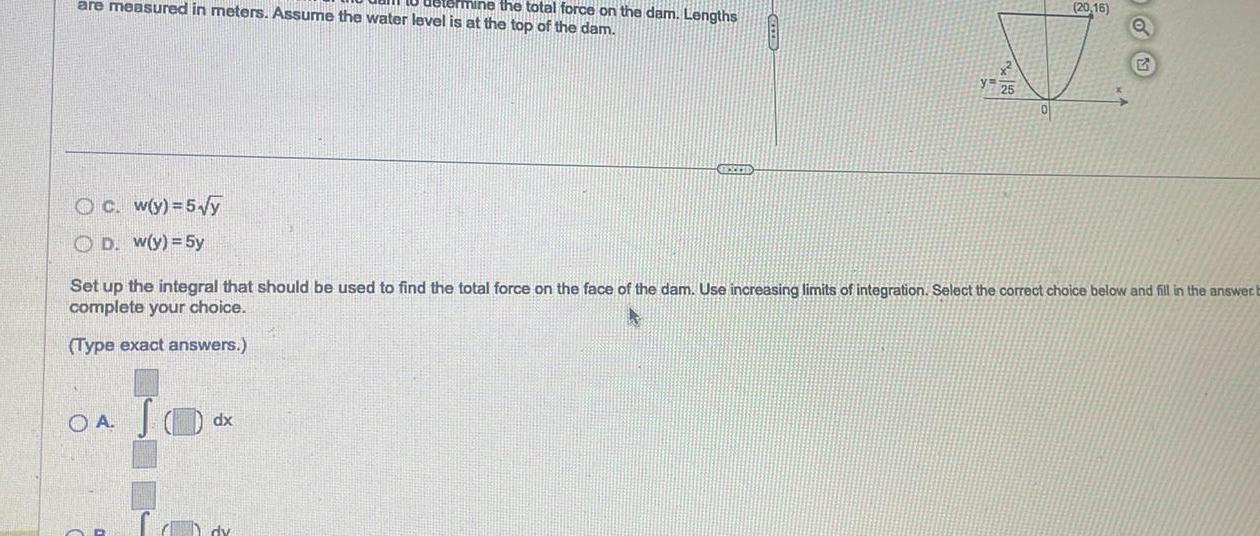
Calculus
Indefinite Integrationare measured in meters Assume the water level is at the top of the dam termine the total force on the dam Lengths Oc w y 5 y OD w y 5y OA JO Lo EEXEED Set up the integral that should be used to find the total force on the face of the dam Use increasing limits of integration Select the correct choice below and fill in the answer b complete your choice Type exact answers dx CO 20 16
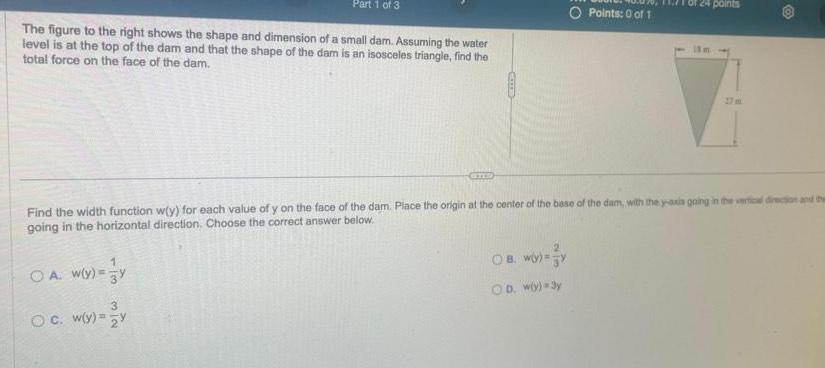
Calculus
Definite IntegralsThe figure to the right shows the shape and dimension of a small dam Assuming the water level is at the top of the dam and that the shape of the dam is an isosceles triangle find the total force on the face of the dam Part 1 of 3 OA W y y 3 O c w y y ams Find the width function w y for each value of y on the face of the dam Place the origin at the center of the base of the dam with the y axis going in the vertical direction and the going in the horizontal direction Choose the correct answer below O Points 0 of 1 OB W OD wly 3y 24 points
Calculus
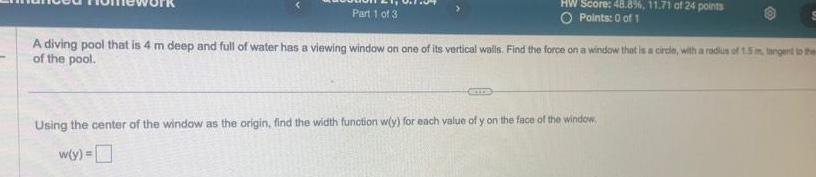
Definite IntegralsPart 1 of 3 HW Score 48 8 11 71 of 24 points O Points 0 of 1 A diving pool that is 4 m deep and full of water has a viewing window on one of its vertical walls Find the force on a window that is a circle with a radius of 1 5 m tangent to them of the pool Using the center of the window as the origin find the width function w y for each value of y on the face of the window w y
Calculus
DifferentiationPart 1 of 3 Find the width function w y for each value of y on the face of the building w y Use integers or decimals for any numbers in the equation HW Score 48 8 11 71 of 24 points O Points 0 of 1 A large building shaped like a box is 60 m high with a face that is 70 m wide A strong wind blows directly at the face of the building exerting a pressure of 160 N m at the ground a increasing with height according to P y 160 2y where y is the height above the ground Calculate the total force on the building which is a measure of the resistance that mat be included in the design of the building CHOCO Save
Calculus
Application of derivativesPart 1 of 3 A glass has circular cross sections that taper linearly from a radius of 6 cm at the top of the glass to a radius of 5 cm at the bottom The glass is 18 cm high and full of onenge jus How much work is required to drink all the juice through a straw if your mouth is 4 cm above the top of the glass Use 1000 kg m for the density of orange juice and 8 0 m s acceleration due to gravity Find the cross sectional area A y of a horizontal slice at y Use the center of the bottom of the glass as the origin in your coordinate system Choose the corect answer be OA A y y 0 9 OB A y x y 0 9 18 OC A y y 0 91 18 OD A y x y 0 9 HW Score 48 8 11 71 of 24 points O Points 0 of 1 2 Save
Calculus
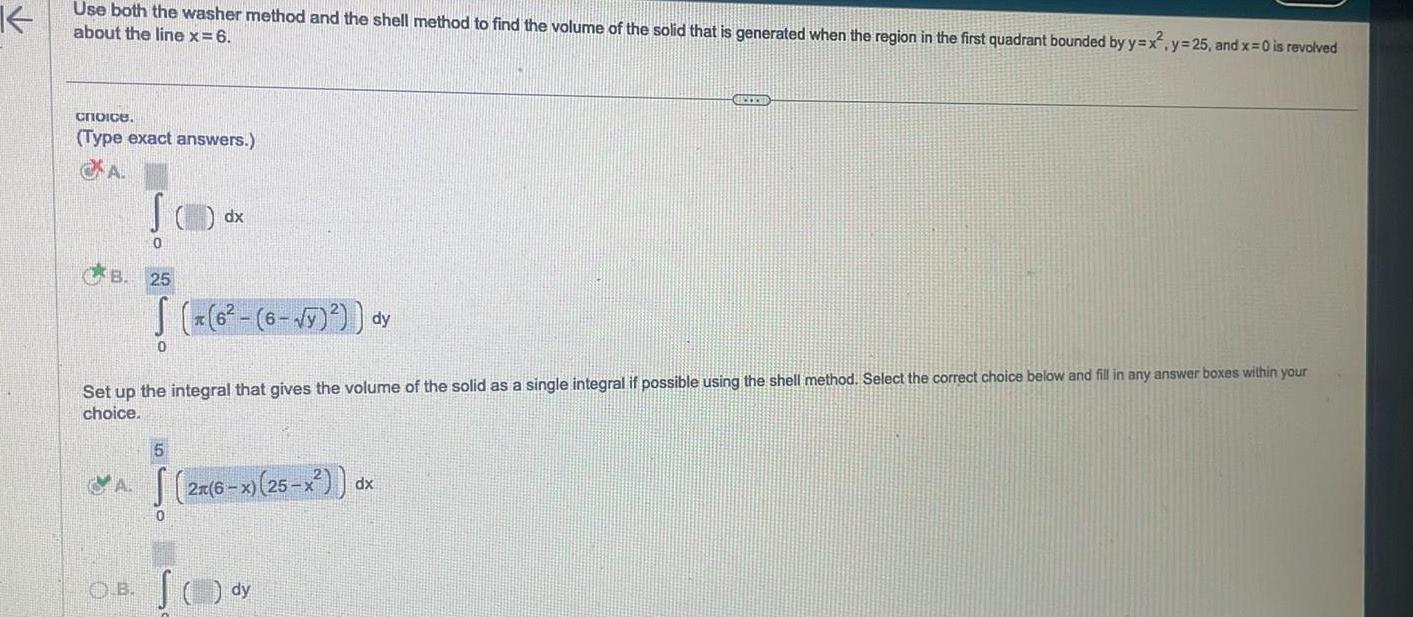
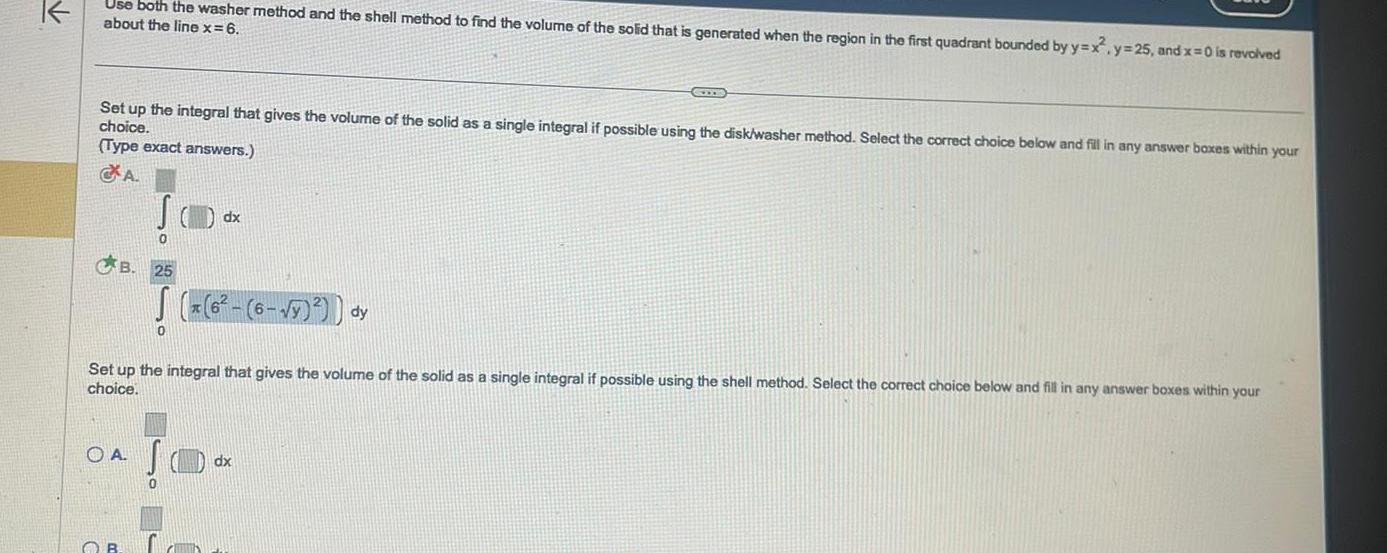
Definite IntegralsK Use both the washer method and the shell method to find the volume of the solid that is generated when the region in the first quadrant bounded by y x y 25 and x 0 is revolved about the line x 6 choice Type exact answers A B AB JO 0 O B 25 6 6 y dy Set up the integral that gives the volume of the solid as a single integral if possible using the shell method Select the correct choice below and fill in any answer boxes within your choice 0 dx 5 2n 6 x 25 x S dy BRECENT dx
Calculus
Indefinite IntegrationUse a change of variables to evaluate the following definite integral 2 9 27v 9 9 0 27v 9 S dv dv Type an exact answer using radicals as needed
Calculus
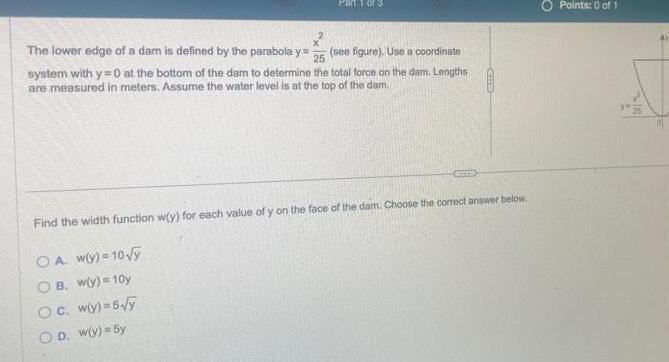
Application of derivatives25 The lower edge of a dam is defined by the parabola y see figure Use a coordinate system with y 0 at the bottom of the dam to determine the total force on the dam Lengths are measured in meters Assume the water level is at the top of the dam CHOCO Find the width function w y for each value of y on the face of the dam Choose the correct answer below OA w y 10 y OB w y 10y Oc wy 5 y OD w y 5y Points 0 of 1
Calculus
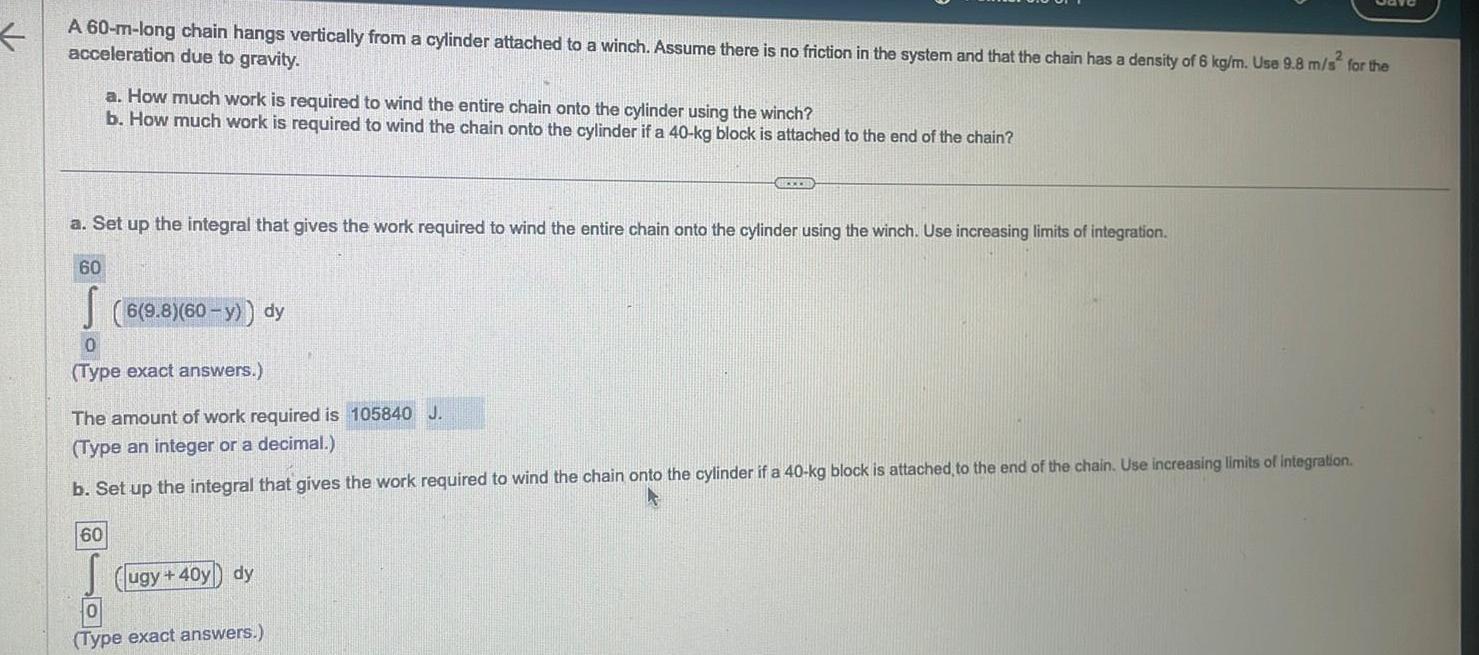
Definite IntegralsA 60 m long chain hangs vertically from a cylinder attached to a winch Assume there is no friction in the system and that the chain has a density of 6 kg m Use 9 8 m s2 for the acceleration due to gravity a Set up the integral that gives the work required to wind the entire chain onto the cylinder using the winch Use increasing limits of integration 60 a How much work is required to wind the entire chain onto the cylinder using the winch b How much work is required to wind the chain onto the cylinder if a 40 kg block is attached to the end of the chain 6 9 8 60 y dy 0 Type exact answers 60 The amount of work required is 105840 J Type an integer or a decimal b Set up the integral that gives the work required to wind the chain onto the cylinder if a 40 kg block is attached to the end of the chain Use increasing limits of integration ugy 40y dy 0 Type exact answers
Calculus
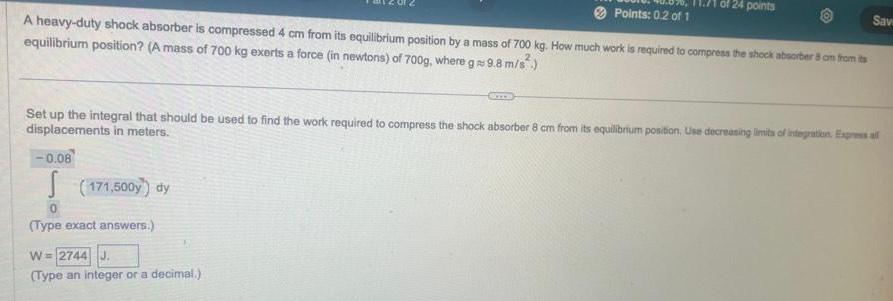
Definite IntegralsPoints 0 2 of 1 A heavy duty shock absorber is compressed 4 cm from its equilibrium position by a mass of 700 kg How much work is required to compress the shock absorber 8 om from its equilibrium position A mass of 700 kg exerts a force in newtons of 700g where g 9 8 m s 0 08 S 171 500y dy 0 Type exact answers of 24 points Set up the integral that should be used to find the work required to compress the shock absorber 8 cm from its equilibrium position Use decreasing limits of integration Express all displacements in meters W 2744 J Type an integer or a decimal Save
Calculus
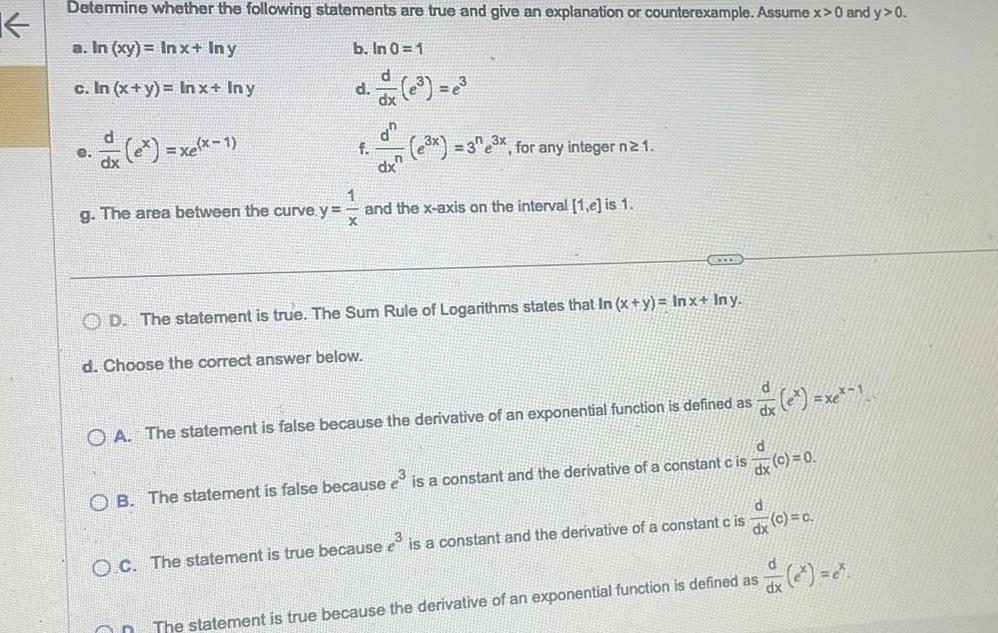
DifferentiationK Determine whether the following statements are true and give an explanation or counterexample Assume x 0 and y 0 a In xy Inx Iny b In 0 1 c In x y In x Iny e xelx 1 d f d On dx 3x 33x for any integer n 2 1 1 g The area between the curve y and the x axis on the interval 1 e is 1 X OCED OD The statement is true The Sum Rule of Logarithms states that In x y Inx Iny d Choose the correct answer below d dx A The statement is false because the derivative of an exponential function is defined as x 1 d OB The statement is false because e is a constant and the derivative of a constant cis O C The statement is true because e is a constant and the derivative of a constant c is dx c 0 dx d c c d e dx The statement is true because the derivative of an exponential function is defined as

Calculus
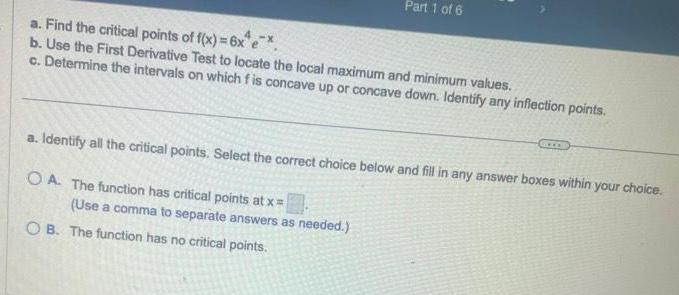
Application of derivativesPart 1 of 6 a Find the critical points of f x 6x e b Use the First Derivative Test to locate the local maximum and minimum values c Determine the intervals on which fis concave up or concave down Identify any inflection points a Identify all the critical points Select the correct choice below and fill in any answer boxes within your choice OA The function has critical points at x Use a comma to separate answers as needed OB The function has no critical points
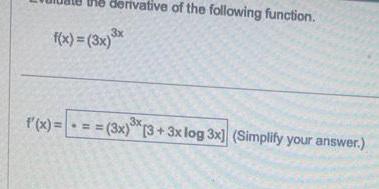
Calculus
DifferentiationCande derivative of the following function f x 3x x f x 3x 3x 3 3x log 3x Simplify your answer
Calculus
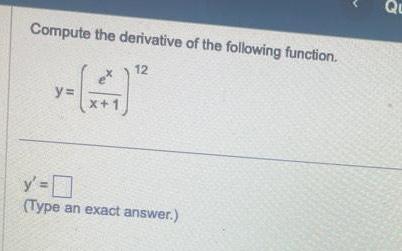
Application of derivativesCompute the derivative of the following function 12 x 1 y 0 Type an exact answer Qu

Calculus
Vector CalculusUse both the washer method and the shell method to find the volume of the solid that is generated when the region in the first quadrant bounded by y x y 25 and x 0 is revolved about the line x 6 Set up the integral that gives the volume of the solid as a single integral if possible using the disk washer method Select the correct choice below and fill in any answer boxes within your choice Type exact answers A B OA SO OB 0 25 6 y dy Set up the integral that gives the volume of the solid as a single integral if possible using the shell method Select the correct choice below and fill in any answer boxes within your choice GOODS 0 dx
Calculus
Differentiationa Find the inverse of the function below on the given interval and write it in the form y f x b Verify the relationships f f x x x and f f f x x 36 for x50 a f x x 36 4 b Verify the relationship t x x Select the correct choice below and fill in the answer box es to complete your choice OA t x x 36 Type integers or simplified fractions 5 00 x 36 F x 36 x Verify the relationship f f x x Select the correct choice below and fill in the answer box es to complete your choice OA x 36 Type integers or simplified fractions Points 0 2 of 1 B f x 36 x
Calculus
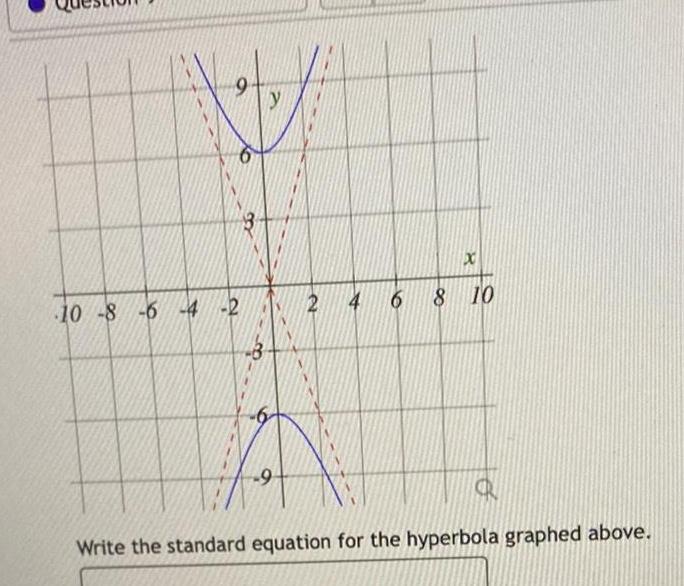
Application of derivativesW y 10 8 6 4 2 9 x 2 4 6 8 10 S Write the standard equation for the hyperbola graphed above
Calculus
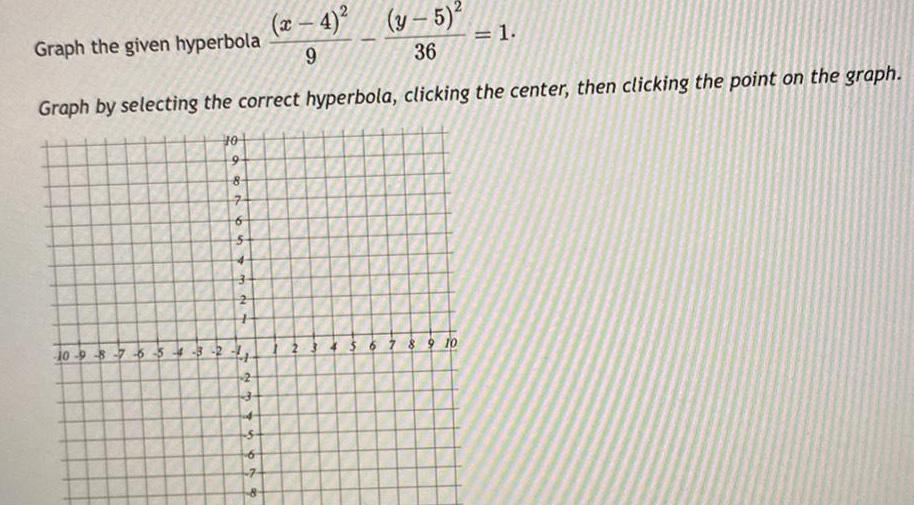
Vector Calculusx 4 y 5 Graph the given hyperbola 9 36 Graph by selecting the correct hyperbola clicking the center then clicking the point on the graph 10 9 8 7 654 3 to 10 9 8 7 65 5 732 2 3 6 8 2 6 7 8 9 10 1
Calculus
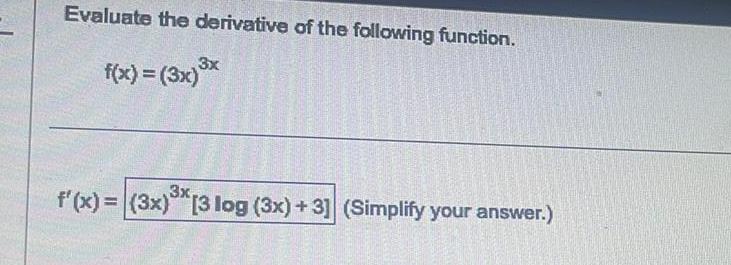
DifferentiationEvaluate the derivative of the following function f x 3x x 3x f x 3x 3 log 3x 3 Simplify your answer
Calculus
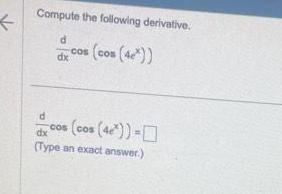
Application of derivativesCompute the following derivative d dx cos cos 4e d dx Type an exact answer cos cos 4e

Calculus
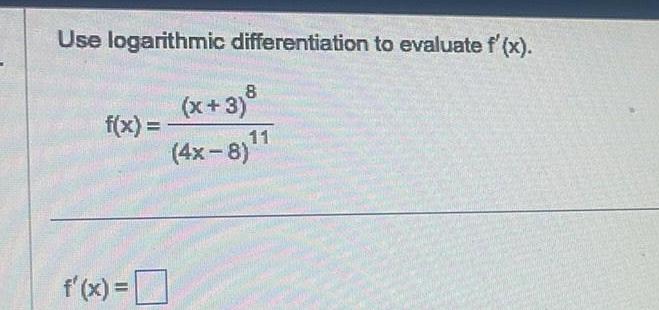
DifferentiationUse logarithmic differentiation to evaluate f x f x f x 5 2 3 5 x 6 x 8 5x 1 36
Calculus
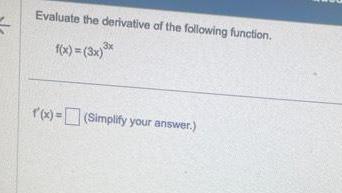
Differentiation5 Evaluate the derivative of the following function f x 3x x f x Simplify your answer
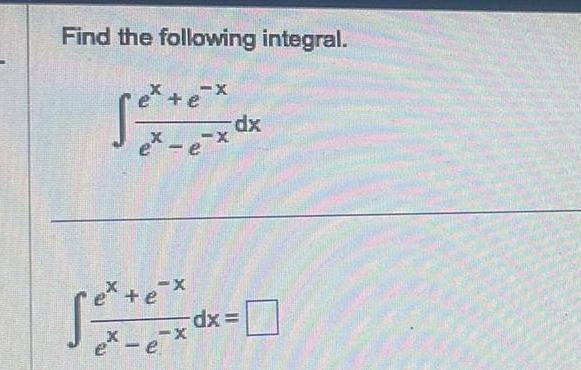
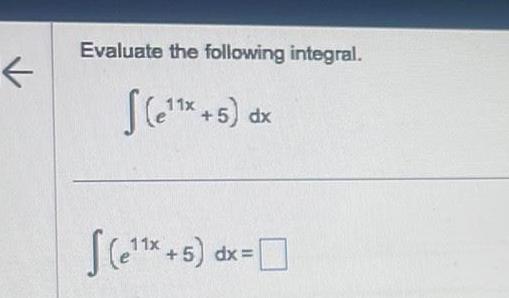

Calculus
Vector CalculusK Determine whether the following statements are true and give an explanation or counterexample a When using the shell method the axis of the cylindrical shells is parallel to the axis of revolution b If a region is revolved about the y axis then the shell method must be used c If a region is revolved about the x axis then in principle it is possible to use the disk washer method and integrate with respect to x or the shell method and integrate with respect to y GEXEND CC True The rotation of the function about the axis creates a cylindrical shape parallel to the axis OD False The rotation of the function about the axis creates a disk shape perpendicular to the axis b Choose the correct answer below A True Any time a function is revolved about an axis the shell method must be used OB False The shell method can only be used when a region is revolved about the x axis OC True Then the axis of the cylindrical shells is parallel to the y ixis D False The disk washer method may be used by integration with respect to y c Choose the correct answer below OA True If the disks washers are perpendicular to the axis of revolution x must be used and if the shells are parallel to the axis of revolution y must be used OB False Use the disk washer method and integrate with respect to y or the shell method and integrate with respect to x C True Integration must always to with respect to the parallel variable be used when revolved about the x axis
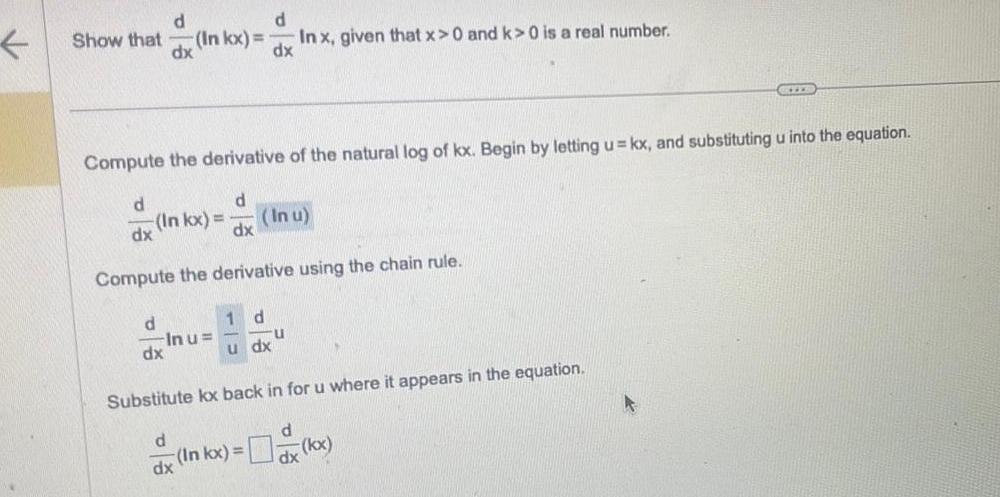
Calculus
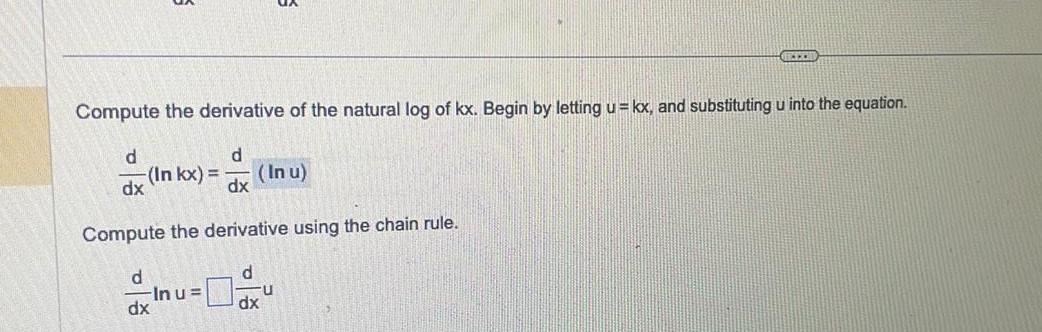
DifferentiationShow that d dx d d dx Inkx Compute the derivative of the natural log of kx Begin by letting u kx and substituting u into the equation d In kx In u dx Compute the derivative using the chain rule In u dx d 1 d u dx In x given that x 0 and k 0 is a real number dx u Substitute kx back in for u where it appears in the equation RILE x In kx x kx
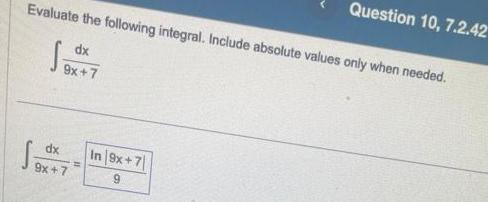
Calculus
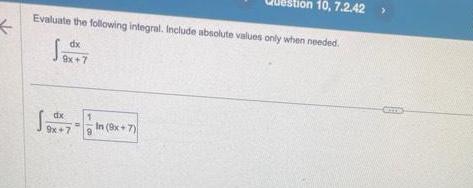
Definite IntegralsEvaluate the following integral Include absolute values only when needed dx 9x 7 dx 9x 7 Question 10 7 2 42 In 9x 7 9
Calculus
Limits & Continuitythe inverse of the function below on the given interval and write it in the form y f x b Verify the relationships f f x x and f f x x f x x 36 for x 0 A x x 36 36 Type integers or simplified fractions a f x x 36 b Verify the relationship f f x x Select the correct choice below and fill in the answer box es to complete your choice OB x 36 x tion 8 7 1 32 Part 2 of 3 X HW GOCOR P
Calculus
Indefinite IntegrationEvaluate the following integral Include absolute values only when needed dx 9x 7 Sa dx 9x 7 9 on 10 7 2 42 In 9x 7
Calculus
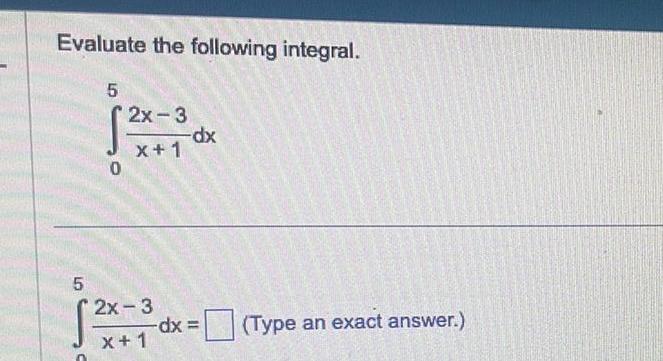
Definite IntegralsEvaluate the following integral 5 5 2x 3 X 1 2x 3 x 1 dx dx Type an exact answer
Calculus
Limits & ContinuityCompute the derivative of the natural log of kx Begin by letting u kx and substituting u into the equation d dx d In kx In u dx Compute the derivative using the chain rule d dx Inu U dx CH U
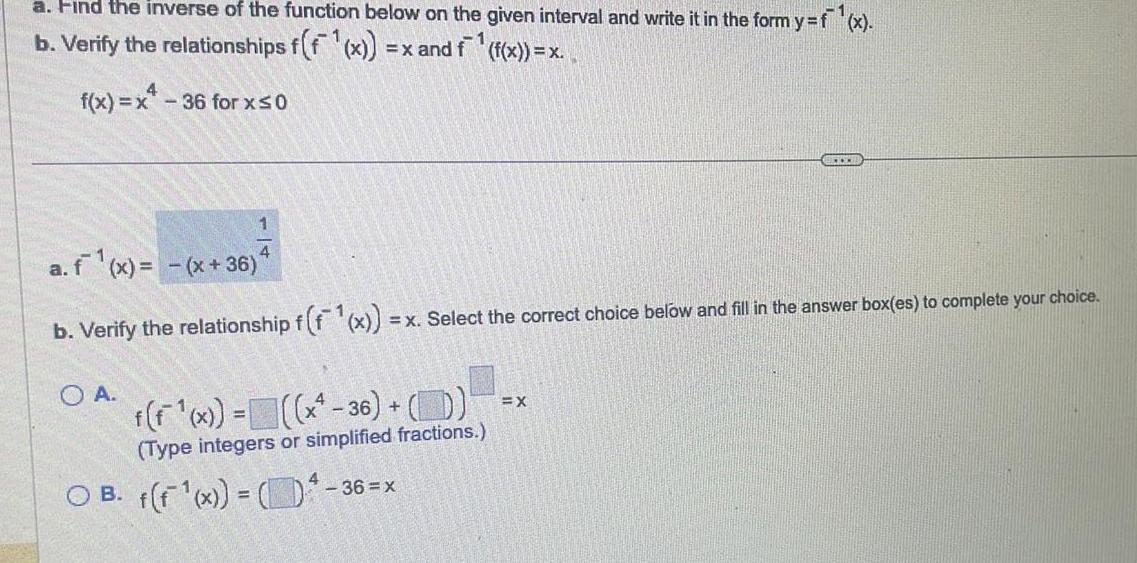
Calculus
Application of derivativesa Find the inverse of the function below on the given interval and write it in the form y f x b Verify the relationships f f x x and f f x x f x x 36 for x 0 1 4 a f x x 36 b Verify the relationship f f x O A f f x x 36 D Type integers or simplified fractions OB f f 1 x 3 x Select the correct choice below and fill in the answer box es to complete your choice 36 x BETER EX

Calculus
Application of derivativesEvaluate the following integral Include absolute values only when needed dx x 7 9x 7 dx 9x 7 www
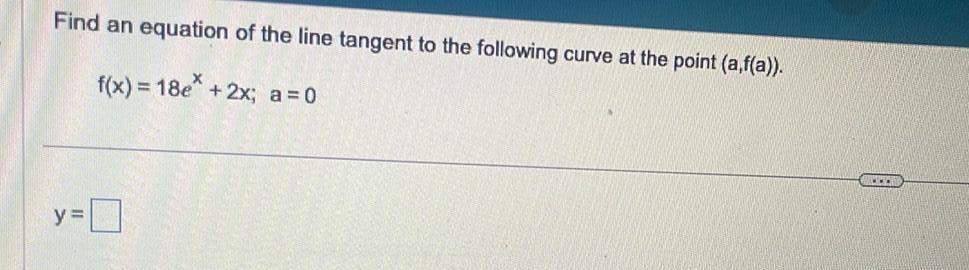
Calculus
Application of derivativesFind an equation of the line tangent to the following curve at the point a f a f x 18e 2x a 0 y BA
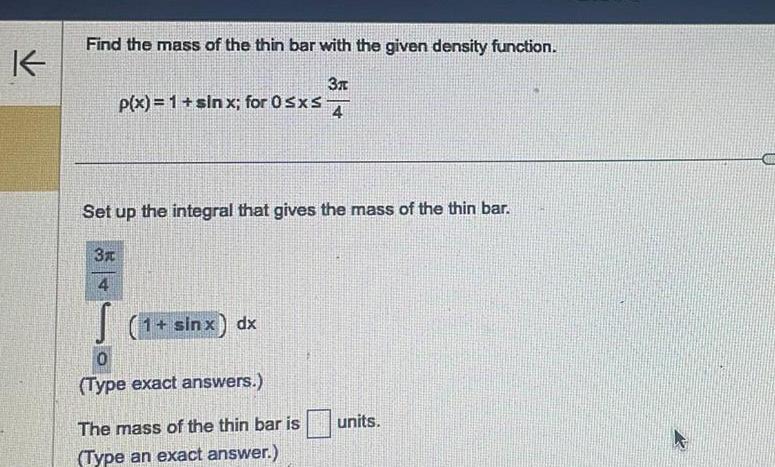
Calculus
Indefinite IntegrationK Find the mass of the thin bar with the given density function 3x 4 p x 1 sinx for 0 sxs Set up the integral that gives the mass of the thin bar 3x 4 S 1 sinx dx 0 Type exact answers The mass of the thin bar is Type an exact answer units
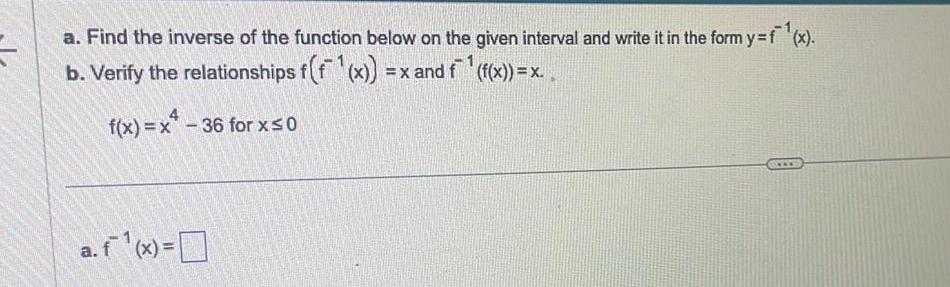
Calculus
Application of derivativesa Find the inverse of the function below on the given interval and write it in the form y f x b Verify the relationships f f x x and f f x x f x x 36 for x 0 a f x