Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
Calculus
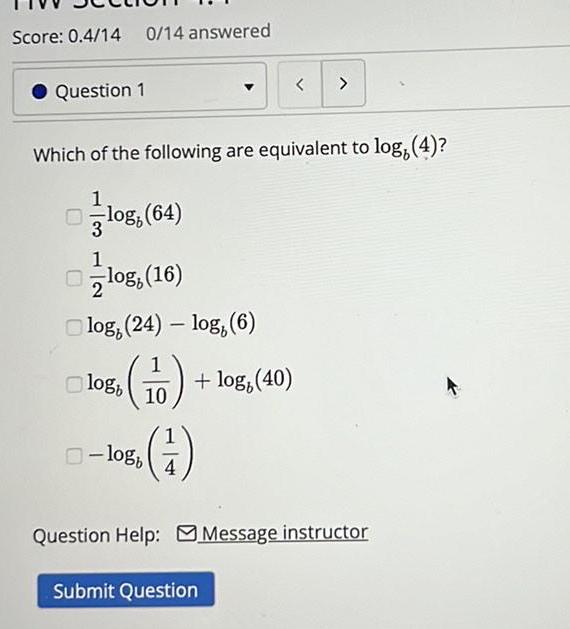
Limits & ContinuityScore 0 4 14 0 14 answered Question 1 3 Which of the following are equivalent to log 4 1 log 64 1 2 log 24 log 6 log 16 logb 10 log 40 1 logb Submit Question Question Help Message instructor
Calculus
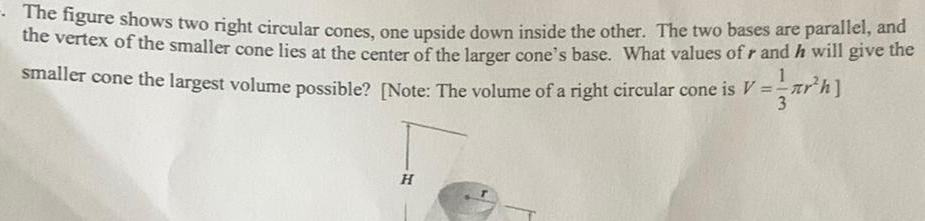
Vector CalculusThe figure shows two right circular cones one upside down inside the other The two bases are parallel and the vertex of the smaller cone lies at the center of the larger cone s base What values of r and he will give the smaller cone the largest volume possible Note The volume of a right circular cone is V th H
Calculus
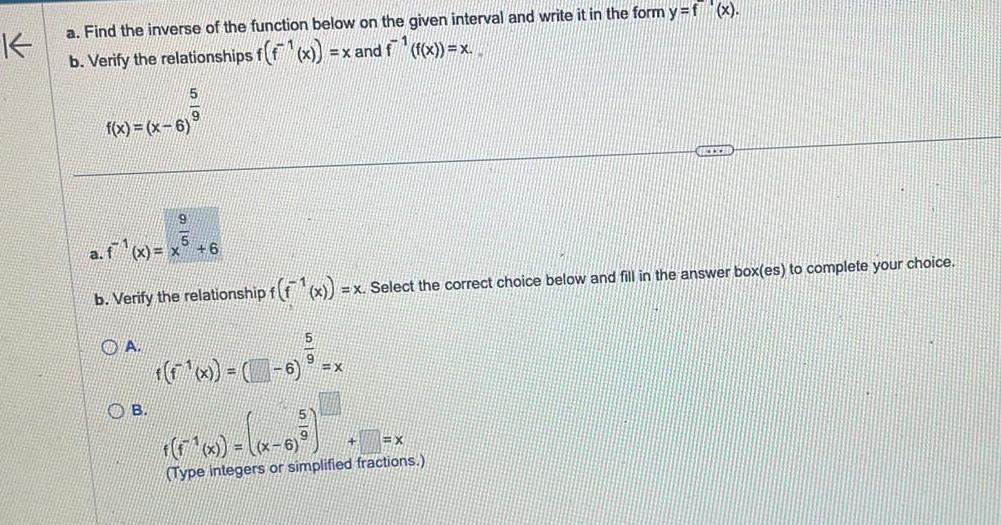
Application of derivativesK a Find the inverse of the function below on the given interval and write it in the form y f x x and f f x x b Verify the relationships f f x f x x 6 a f x x 5 9 A B 6 b Verify the relationship f f x x Select the correct choice below and fill in the answer box es to complete your choice x 6 x GEEXED x x 6 X Type integers or simplified fractions
Calculus
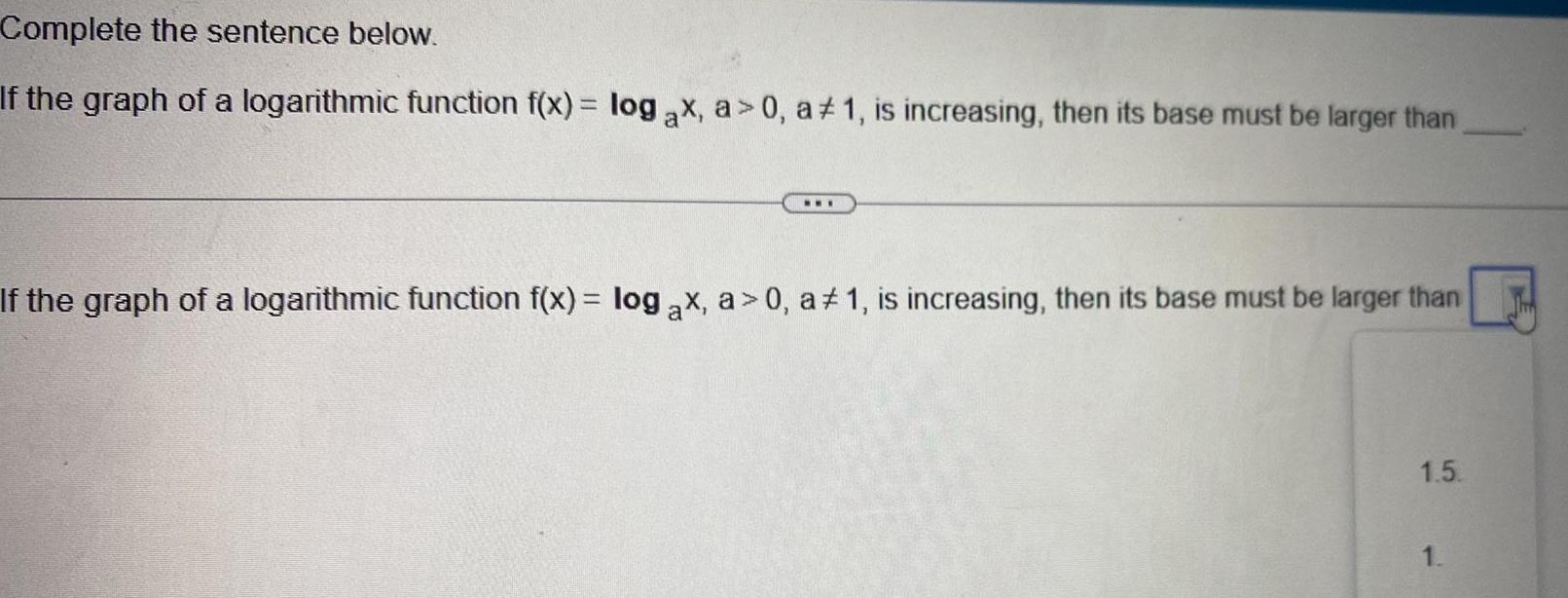
Application of derivativesComplete the sentence below If the graph of a logarithmic function f x log ax a 0 a 1 is increasing then its base must be larger than www If the graph of a logarithmic function f x log ax a 0 a 1 is increasing then its base must be larger than 1 5 1
Calculus
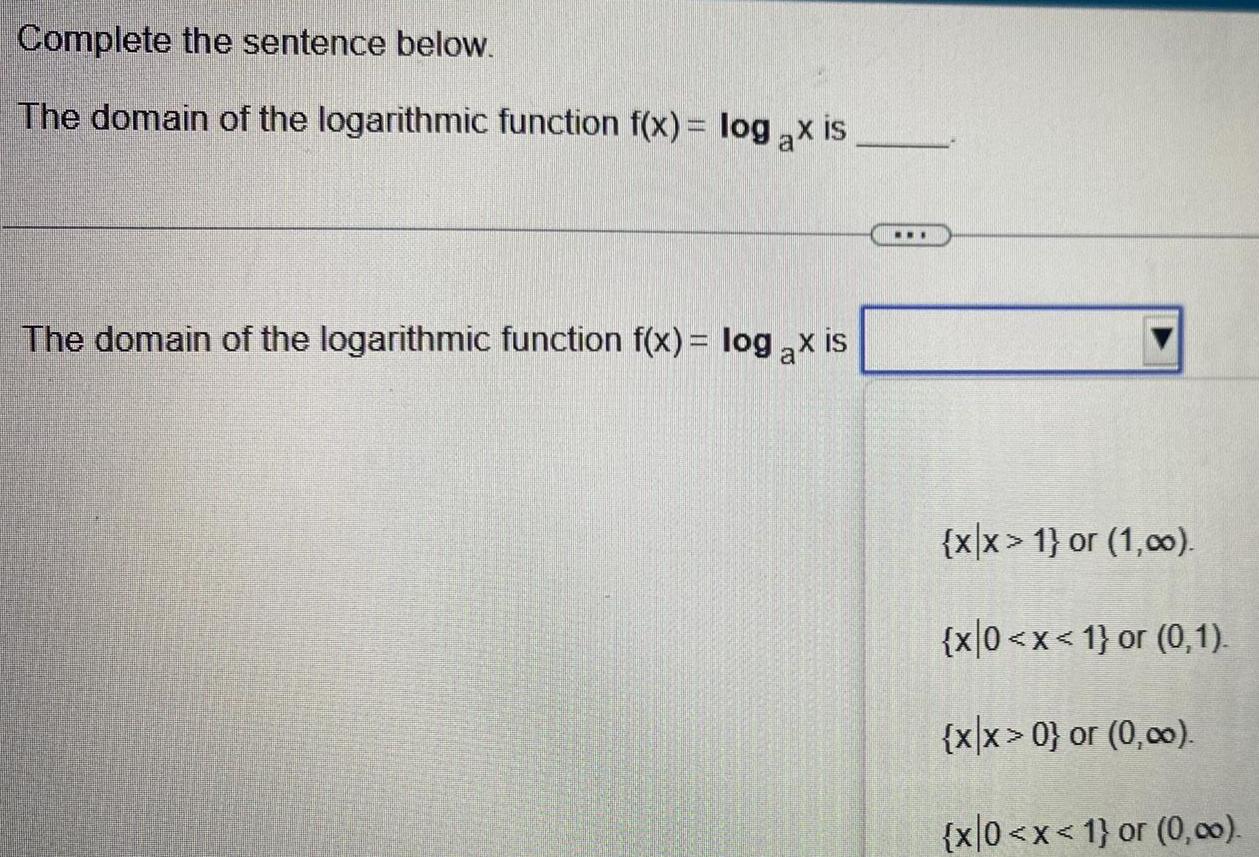
Application of derivativesComplete the sentence below The domain of the logarithmic function f x log ax is The domain of the logarithmic function f x log ax is xx 1 or 1 00 x 0 x 1 or 0 1 x x 0 or 0 00 x 0 x 1 or 0 00
Calculus
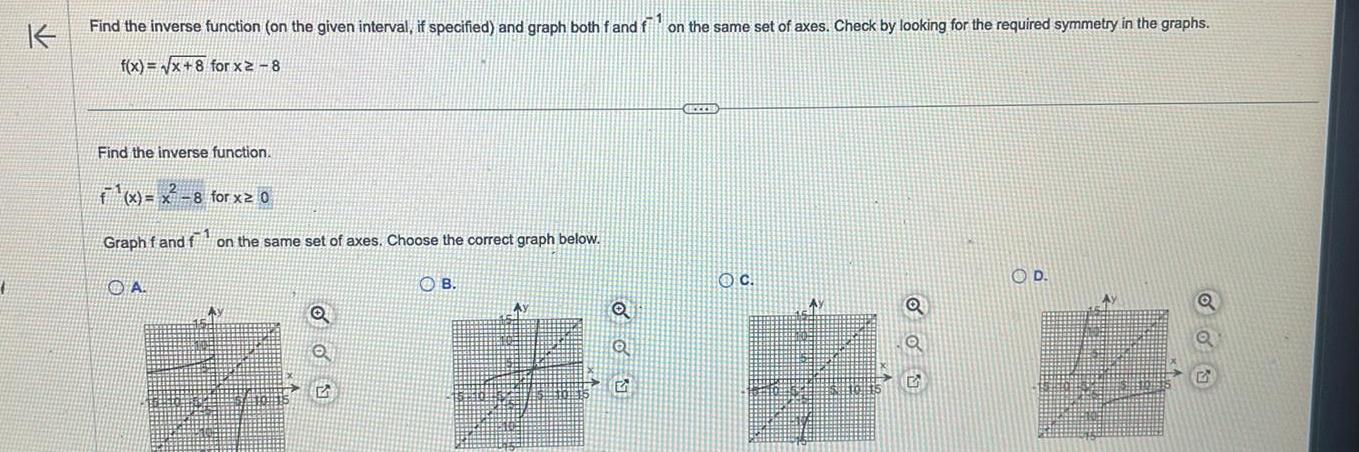
Vector CalculusK Find the inverse function on the given interval if specified and graph both f and f on the same set of axes Check by looking for the required symmetry in the graphs f x x 8 for x2 8 Find the inverse function f x x 8 for x 0 Graph f and f on the same set of axes Choose the correct graph below A OB HEZZES OC Ay

Calculus
Application of derivativesQuestion 1 A vehicle purchased for 27 500 depreciates at a constant rate of 5 Determine the approximate value of the vehicle 13 years after purchase Round to the nearest whole dollar Question Help Video Message instructor

Calculus
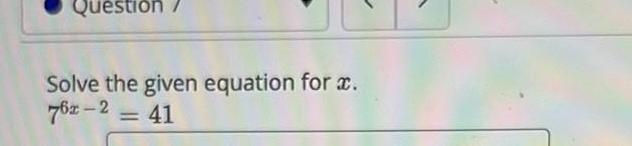
Application of derivativesQuestion 2 Which of the following are equivalent to 5 log u 1 3 Assume u 0 1 VTS log D log u 3 1 log u5 log 5 15 5 log u5 3 Question Help Message instructor

Calculus
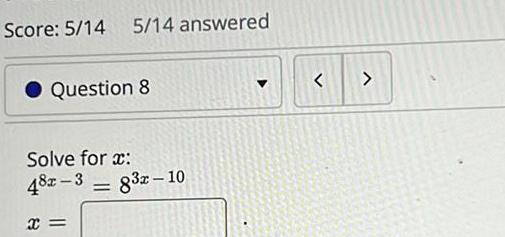
DifferentiationK Find the inverse of the following function and write it in the form f x 3 f x 2 X 1 for x 0 The inverse function is f x 3 xw 1 for 0 x 3 BOWWALI

Calculus
DifferentiationFind the derivative of the inverse of the following function at the specified point on the graph of the inverse function You do not need to find f f x 4x 2 14 4 The derivative is
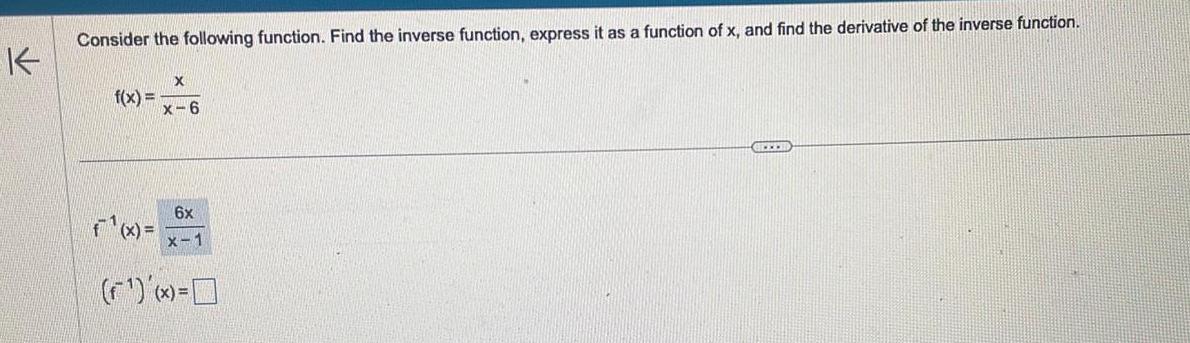
Calculus
Application of derivativesConsider the following function Find the inverse function express it as a function of x and find the derivative of the inverse function f x f x x x 6 6x x 1 GREE
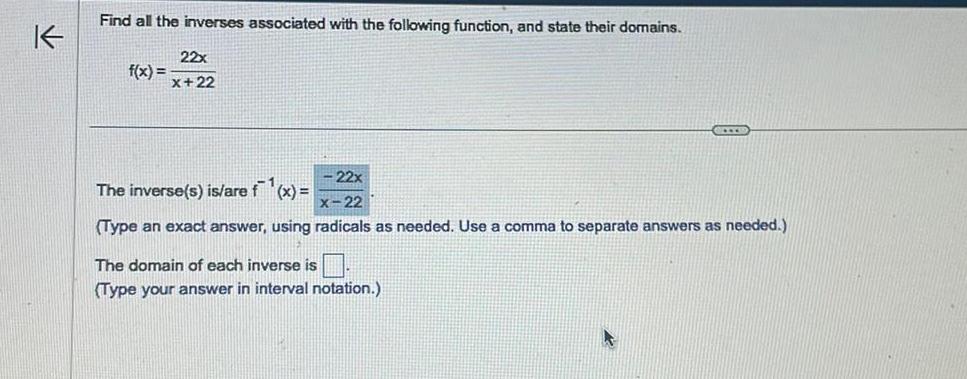
Calculus
DifferentiationK Find all the inverses associated with the following function and state their domains 22x x 22 f x 22x The inverse s is are f x 22 Type an exact answer using radicals as needed Use a comma to separate answers as needed The domain of each inverse is Type your answer in interval notation CITS K
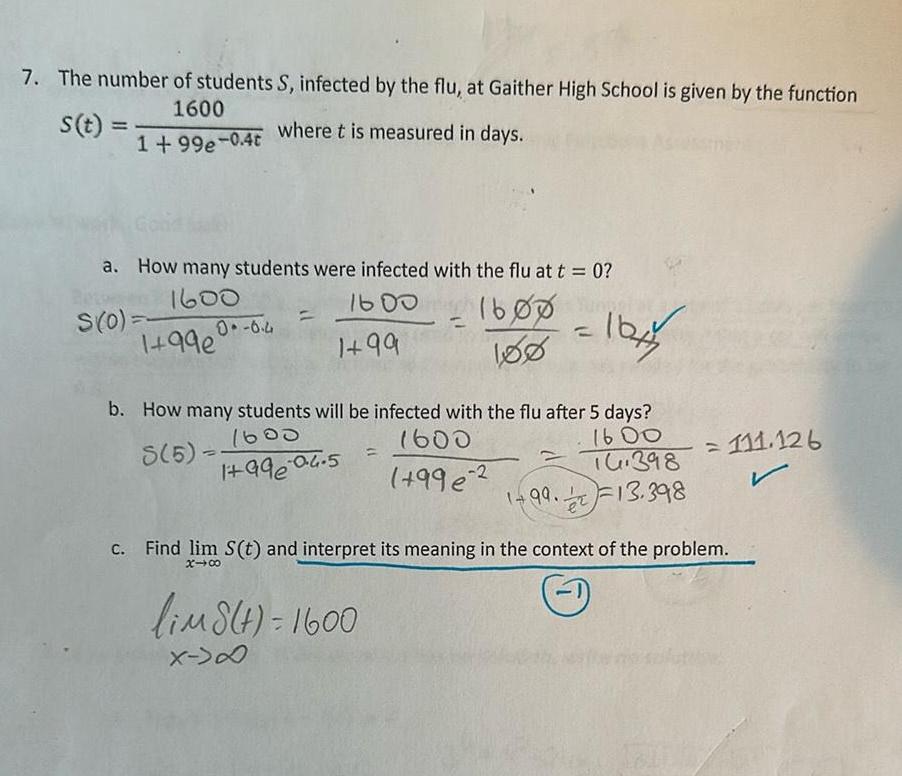
Calculus
Differentiation7 The number of students S infected by the flu at Gaither High School is given by the function 1600 where t is measured in days s t 1 99e 0 4t a How many students were infected with the flu at t 0 1600 1600 1600 1 99 180 S 0 1 99e 0 6 4 b How many students will be infected with the flu after 5 days 1600 8 5 1600 1600 1 99 04 5 16 398 996 2 1 99 13 398 1644 lim8 t 1600 X D Find lim S t and interpret its meaning in the context of the problem x 00 1 111 126 r
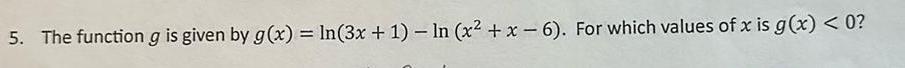
Calculus
Limits & Continuity5 The function g is given by g x ln 3x 1 ln x x 6 For which values of x is g x 0
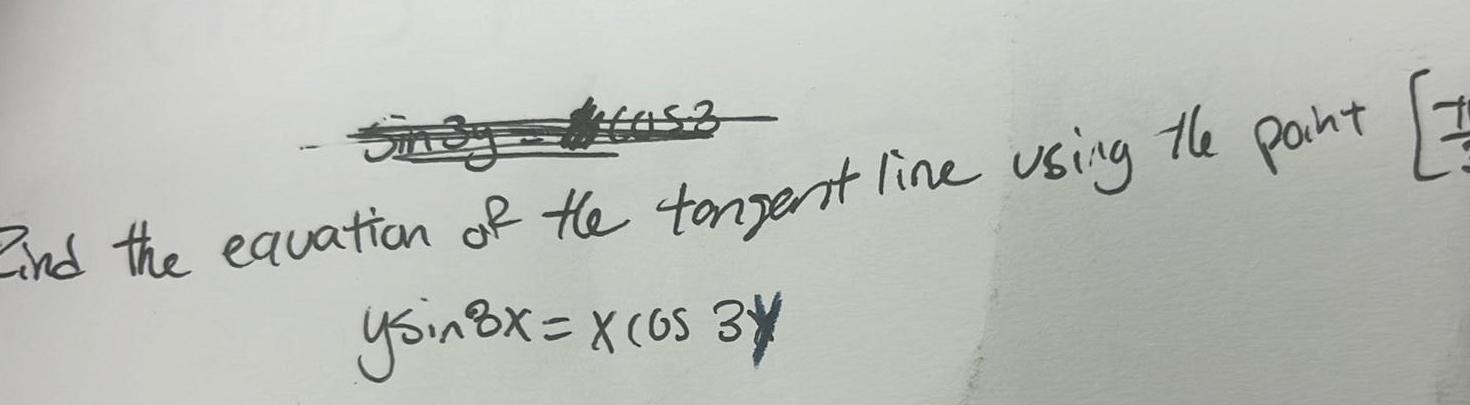
Calculus
DifferentiationSinay tas 7 Find the equation of the tangent line using the point ysin 8x x os 34

Calculus
DifferentiationA basebasll diamond is a square with side 90 ft A batter hits the ball and runs toward first base with a speed of 24 ft s 90 ft a At what rate is his distance from second base decreasing when he is halfway to first base Round your answer to one decimal place b At what rate is his distance from third base increasing at the same moment Round your answer to one decimal place ft s Enter an integer or decimal number more Question Help Message incr

Calculus
DifferentiationWhen air expands adiabatically without gaining or losing heat its pressure P and volume V are related by the equation PV 4 C where C is a constant Suppose that at a certain instant the volume is 300 cm and the pre is 80 kPa and is decreasing at a rate of 10 kPa min At what rate is the volume increasing at this instant Round your answer to the nearest whole number cm min Enter an integer or decimal number more Question Help Message instructor
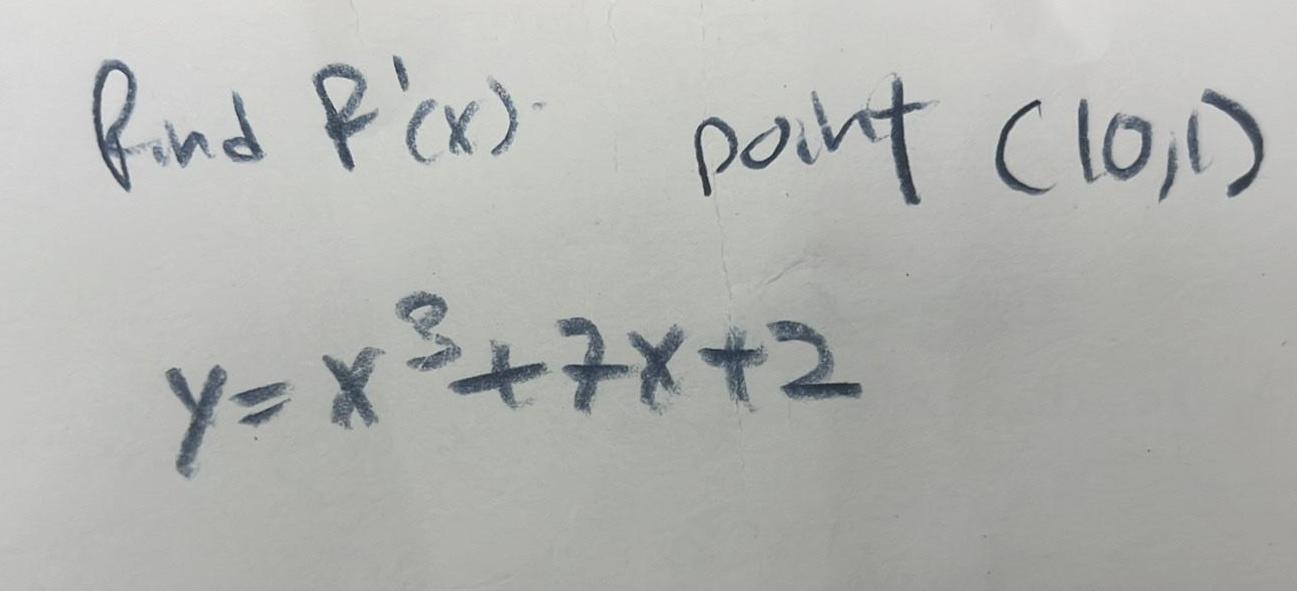

Calculus
DifferentiationA swimming pool is 20 ft wide 40 ft long 3 ft deep at the shallow end and 9 ft deep at its deepest point A cross section is shown in the figure If the pool is being filled at a rate of 1 ft min how fast the water level rising when the depth at the deepest point is 5 ft Round your answer to five decimal place ft min 6 12 16 6 Question Help Message instruct 3
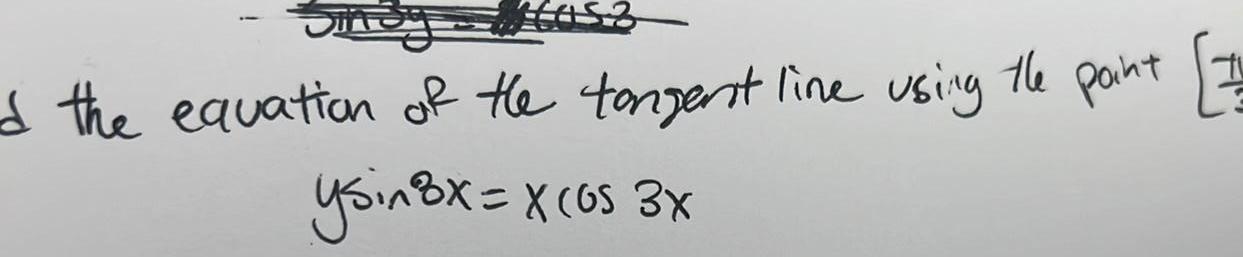
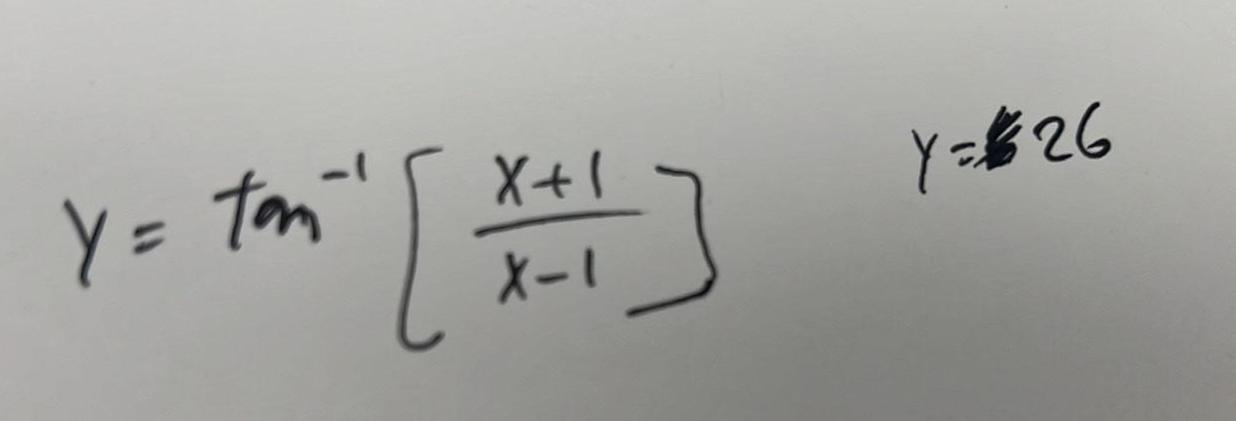

Calculus
DifferentiationA neutral hollow spherical conducting shell of inner radius 1 00 cm and outer radius 3 00 cm has a 2 00 C point charge placed at its center a Find the surface charge density on the inner surface of the shell b Find the surface charge density on the outer surface of the shell
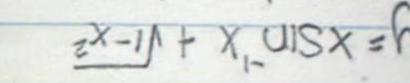
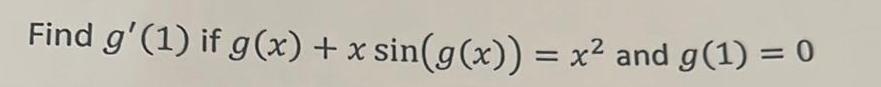

Calculus
Indefinite IntegrationLast month Kaitlin s average daily balance on her credit card was 1 340 71 The annual interest rate on that credit card is r charge 1 B 365 17 71 The minimum payment on that card is the interest n plus 2 of the ending balance or 25 which ever is larger If there were 30 days in that month and the ending balance was 1 946 54 what would be the minimum payment that Kaitlin could make Round your answer to the nearest penny Input the number Do not input the dollar sign Do not use a comma Example 89 65

Calculus
DifferentiationFor each problem find f x by using the formula 7 f x x x 3 dy 1 dx 9 where y f x dx dy 8 f x 3x 2x 5
Calculus
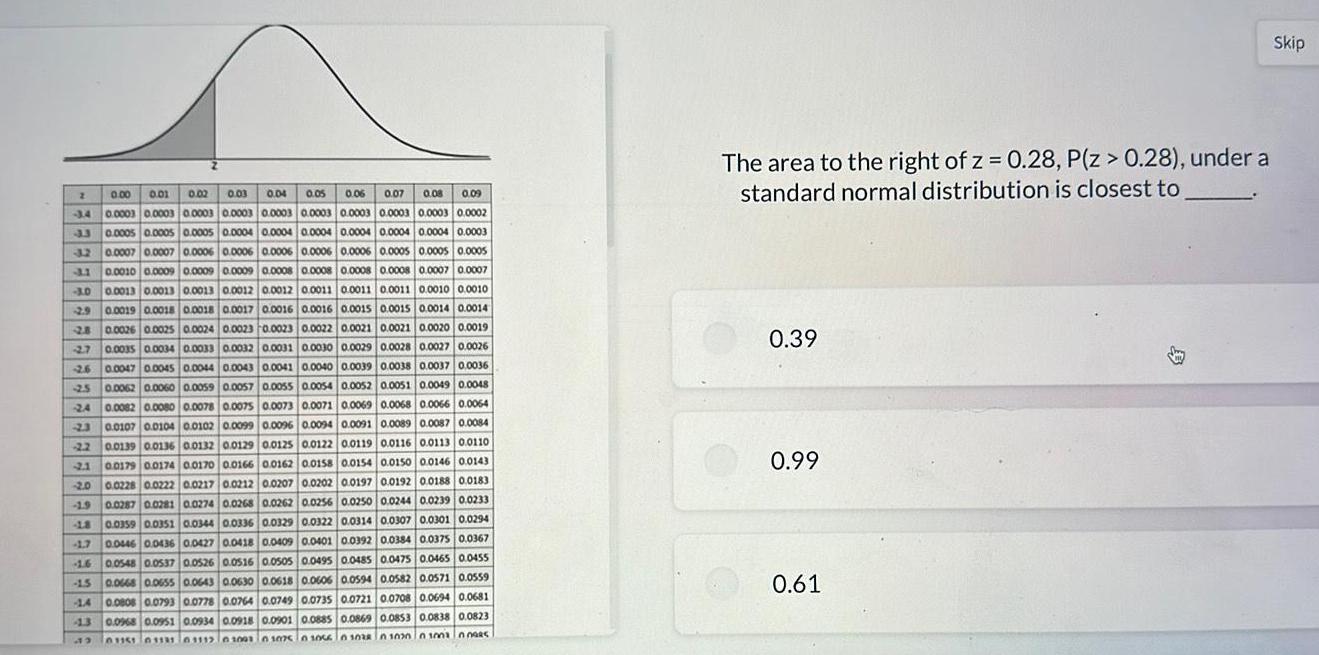
Differential equations2 0 00 0 01 0 02 0 03 0 04 0 05 0 06 0 07 0 08 0 09 3 4 0 0003 0 0003 0 0003 0 0003 0 0003 0 0003 0 0003 0 0003 0 0003 0 0002 33 0 0005 0 0005 0 0005 0 0004 0 0004 0 0004 0 0004 0 0004 0 0004 0 0003 32 0 0007 0 0007 0 0006 0 0006 0 0006 0 0006 0 0006 0 0005 0 0005 0 0005 31 0 0010 0 0009 0 0009 0 0009 0 0008 0 0008 0 0008 0 0008 0 0007 0 0007 3 0 0 0013 0 0013 0 0013 0 0012 0 0012 0 0011 0 0011 0 0011 0 0010 0 0010 2 9 0 0019 0 0018 0 0018 0 0017 0 0016 0 0016 0 0015 0 0015 0 0014 0 0014 2 8 0 0026 0 0025 0 0024 0 0023 0 0023 0 0022 0 0021 0 0021 0 0020 0 0019 27 0 0035 0 0034 0 0033 0 0032 0 0031 0 0030 0 0029 0 0028 0 0027 0 0026 26 0 0047 0 0045 0 0044 0 0043 0 0041 0 0040 0 0039 0 0038 0 0037 0 0036 2 5 0 0062 0 0060 0 0059 0 0057 0 0055 0 0054 0 0052 0 0051 0 0049 0 0048 24 0 0082 0 0080 0 0078 0 0075 0 0073 0 0071 0 0069 0 0068 0 0066 0 0064 2 3 0 0107 0 0104 0 0102 0 0099 0 0096 0 0094 0 0091 0 0089 0 0087 0 0084 2 2 0 0139 0 0136 0 0132 0 0129 0 0125 0 0122 0 0119 0 0116 0 0113 0 0110 2 1 0 0179 0 0174 0 0170 0 0166 0 0162 0 0158 0 0154 0 0150 0 0146 0 0143 2 0 0 0228 0 0222 0 0217 0 0212 0 0207 0 0202 0 0197 0 0192 0 0188 0 0183 0 0287 0 0281 0 0274 0 0268 0 0262 0 0256 0 0250 0 0244 0 0239 0 0233 0 0359 0 0351 0 0344 0 0336 0 0329 0 0322 0 0314 0 0307 0 0301 0 0294 0 0446 0 0436 0 0427 0 0418 0 0409 0 0401 0 0392 0 0384 0 0375 0 0367 1 6 0 0548 0 0537 0 0526 0 0516 0 0505 0 0495 0 0485 0 0475 0 0465 0 0455 1 5 0 0668 0 0655 0 0643 0 0630 0 0618 0 0606 0 0594 0 0582 0 0571 0 0559 1 4 0 0008 0 0793 0 0778 0 0764 0 0749 0 0735 0 0721 0 0708 0 0694 0 0681 19 4 8 1 7 13 0 0968 0 0951 0 0934 0 0918 0 0901 0 0885 0 0869 0 0853 0 0838 0 0823 61151 03331 01112 01001 01075 01066 0 1038 0 1030010010095 The area to the right of z 0 28 P Z 0 28 under a standard normal distribution is closest to 0 39 0 99 0 61 Skip

Calculus
DifferentiationFor each problem find x by using the theorem f x 1 x 3 f x 5x 1 5 f x 2x 3 4 f x 2x 2 6 f x 4x 4
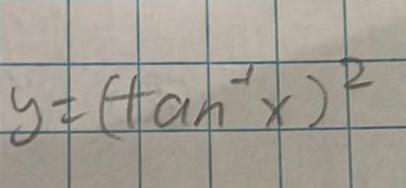

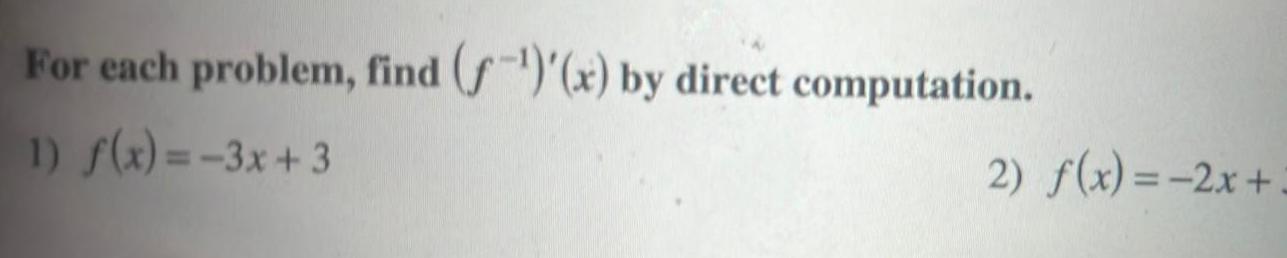
Calculus
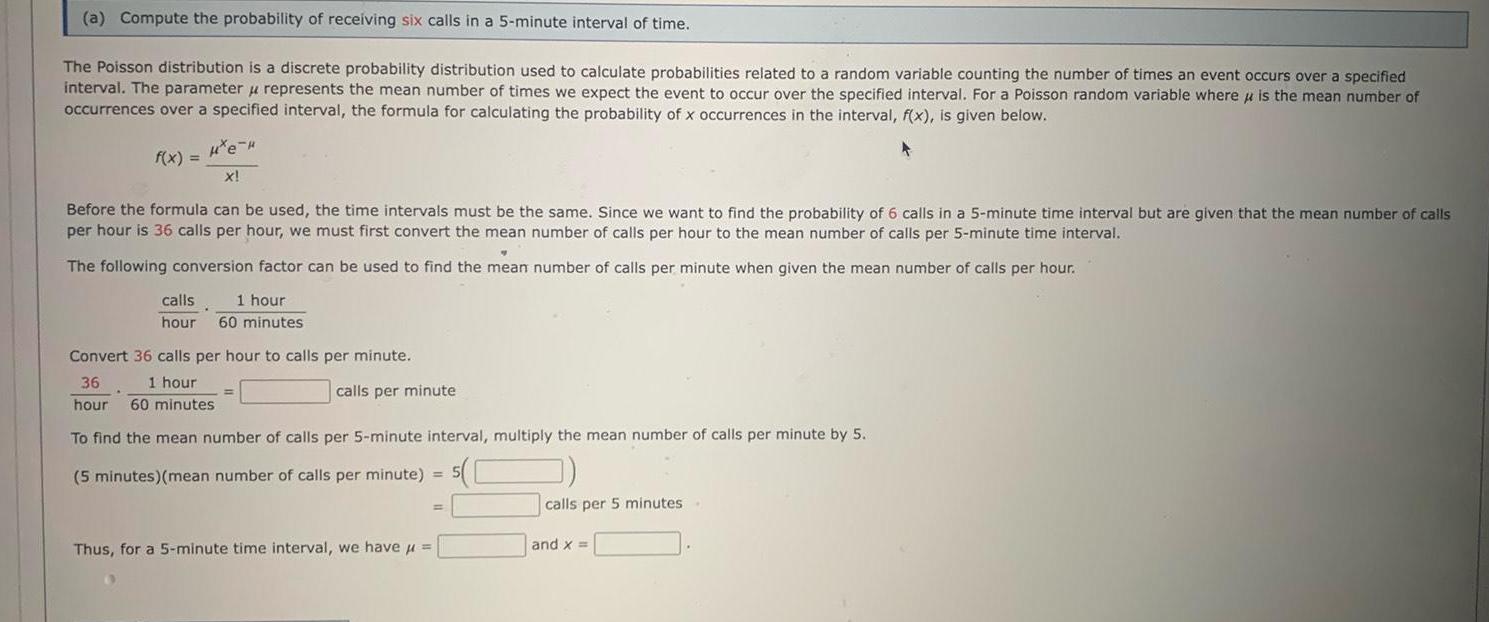
Limits & Continuitya Compute the probability of receiving six calls in a 5 minute interval of time The Poisson distribution is a discrete probability distribution used to calculate probabilities related to a random variable counting the number of times an event occurs over a specified interval The parameter u represents the mean number of times we expect the event to occur over the specified interval For a Poisson random variable where is the mean number of occurrences over a specified interval the formula for calculating the probability of x occurrences in the interval f x is given below He f x X Before the formula can be used the time intervals must be the same Since we want to find the probability of 6 calls in a 5 minute time interval but are given that the mean number of calls per hour is 36 calls per hour we must first convert the mean number of calls per hour to the mean number of calls per 5 minute time interval The following conversion factor can be used to find the mean number of calls per minute when given the mean number of calls per hour calls 1 hour hour 60 minutes Convert 36 calls per hour to calls per minute 36 1 hour hour 60 minutes calls per minute To find the mean number of calls per 5 minute interval multiply the mean number of calls per minute by 5 5 minutes mean number of calls per minute 5 Thus for a 5 minute time interval we have calls per 5 minutes and x
Calculus
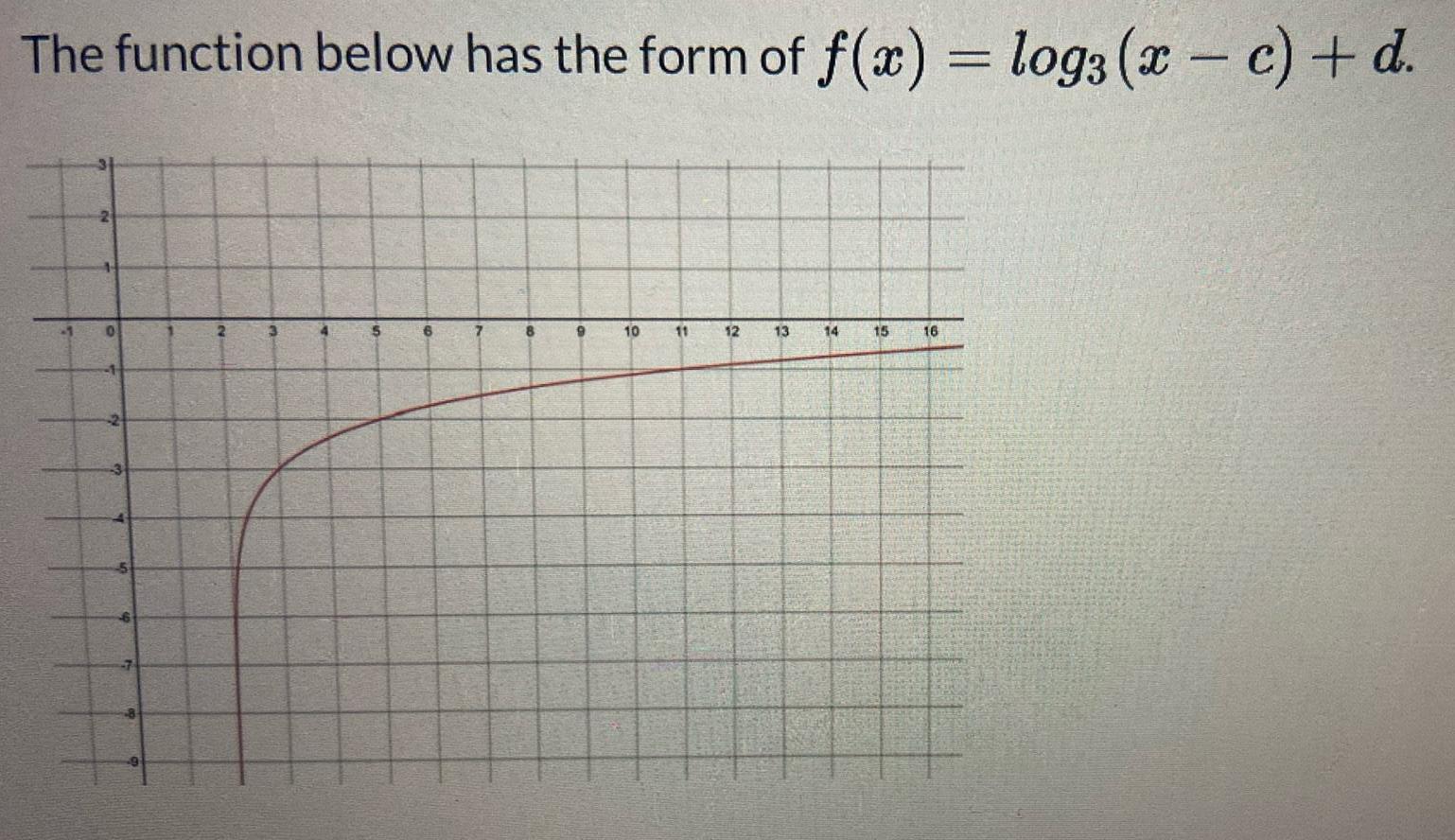
Vector CalculusThe function below has the form of f x log3 x c d 6 7 8 9 10 11 12 13 14 15 16
Calculus
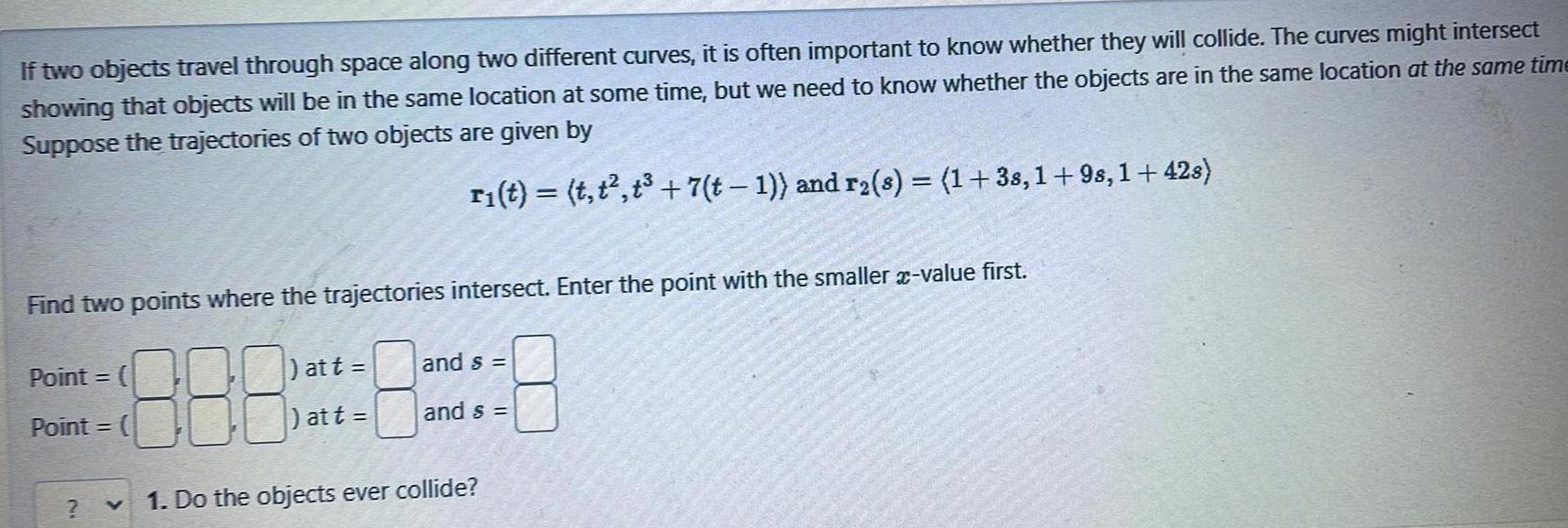
Vector CalculusIf two objects travel through space along two different curves it is often important to know whether they will collide The curves might intersect showing that objects will be in the same location at some time but we need to know whether the objects are in the same location at the same time Suppose the trajectories of two objects are given by r t t t t 7 t 1 and r s 1 38 1 9s 1 42s Find two points where the trajectories intersect Enter the point with the smaller x value first 888 1 Do the objects ever collide Point Point att at t and s and s

Calculus
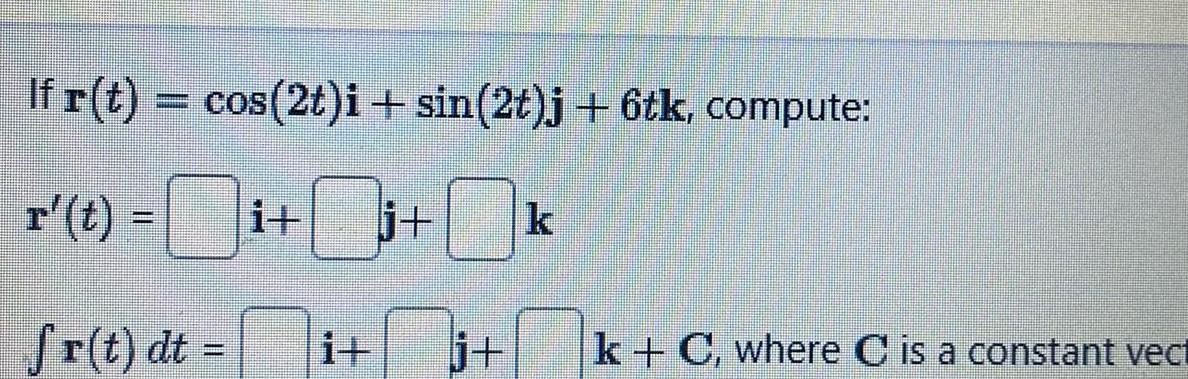
Definite IntegralsIf r t cos 2t i sin 2t j 6tk compute j k fr t dt it i j k C where C is a constant vect
Calculus
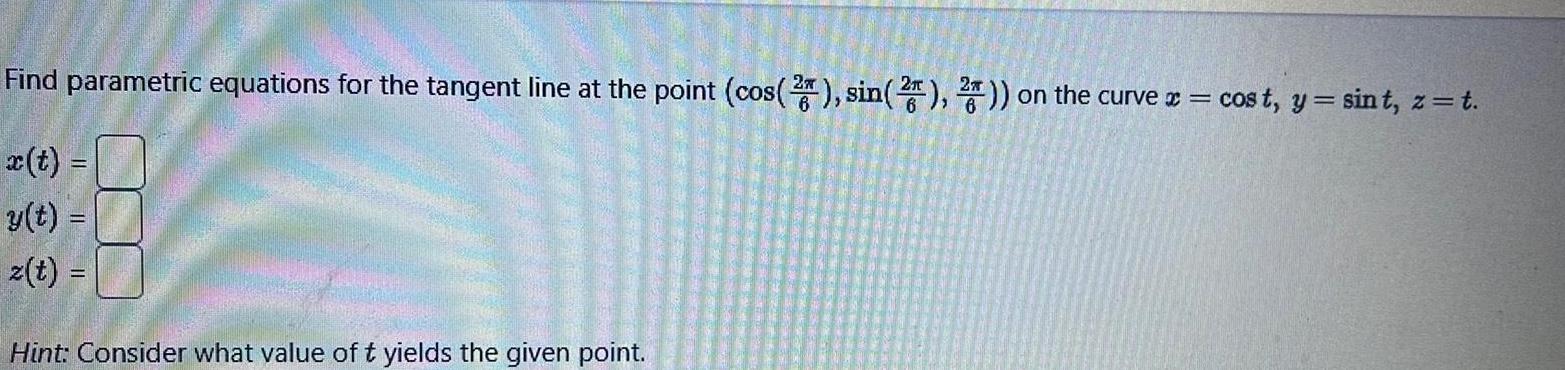
Vector CalculusFind parametric equations for the tangent line at the point cos 2 sin 2 2 on the curve x cost y sint z t y t z t Hint Consider what value of t yields the given point

Calculus
Vector CalculusFind a vector function that represents the curve of intersection of the paraboloid z 3x 5y2 and the cylinder y 6x Use the variable t for the parameter Hint The answer prompts you to use x t r t t 00



Calculus
Vector CalculusFor the given position vectors r t compute the tangent velocity vector r t for the given value of t A If r t cos 3t sin 3t Then I B If r t t t Then r 1 C If r t e ti e tj tk Then r 0 i j k

Calculus
Vector CalculusThe function below describes the volume V of a three dimensional sphere in terms of its radius Find the inverse of this function that gives the radius in terms of V Assume that rand V are nonnegative Express your answer in the form r f V 4 3 v r Type an expression using V as the variable
Calculus
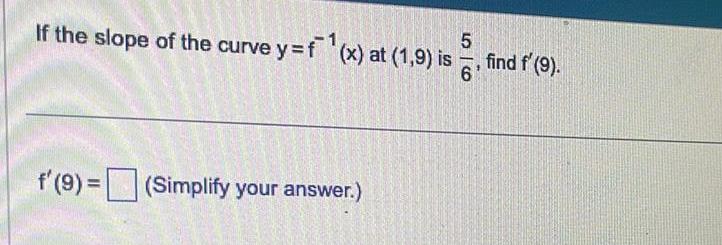
Limits & Continuity5 If the slope of the curve y f x at 1 9 is 6 f 9 Simplify your answer find f 9

Calculus
Limits & ContinuityFind the variation constant and an equation of variation where y varies inversely as x and y 7 when x 2 The variation constant is The equation of variation is y
Calculus
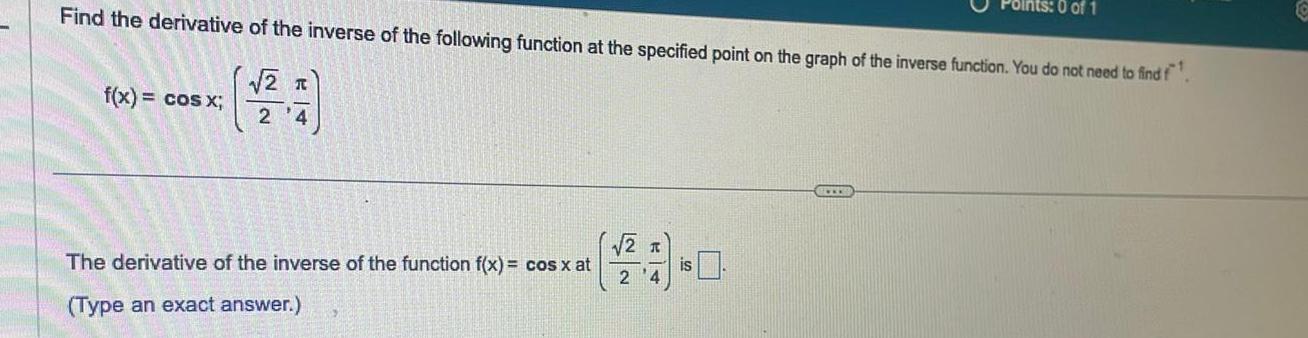
DifferentiationFind the derivative of the inverse of the following function at the specified point on the graph of the inverse function You do not need to find f 2 T 2 4 f x cos x The derivative of the inverse of the function f x cos x at Type an exact answer Points 0 of 1 2 T 24

Calculus
DifferentiationFind the derivative of the inverse of the following function at the specified point on the graph of the inverse function You do not need to find f f x 4x 2 14 4 The derivative is
Calculus
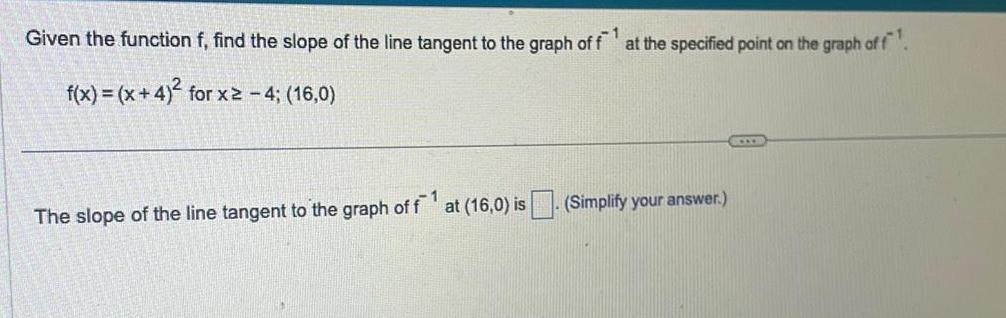
Indefinite IntegrationGiven the function f find the slope of the line tangent to the graph of f1 at the specified point on the graph of f f x x 4 for x2 4 16 0 The slope of the line tangent to the graph of f at 16 0 is Simplify your answer 1
Calculus
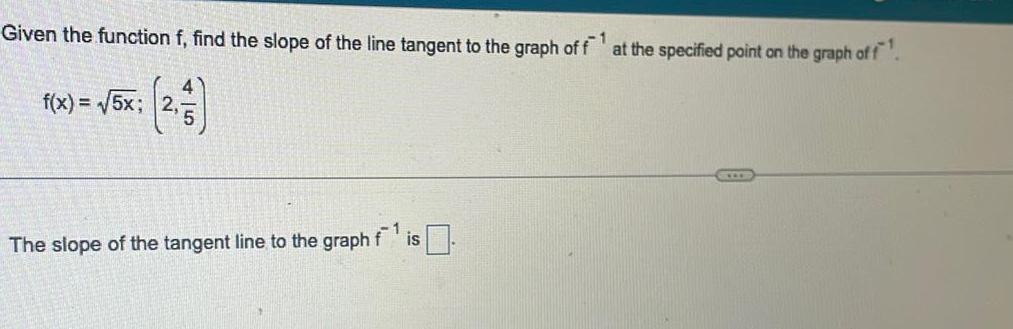
DifferentiationGiven the function f find the slope of the line tangent to the graph of f at the specified point on the graph of f f x 5x The slope of the tangent line to the graph f is