Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
Calculus
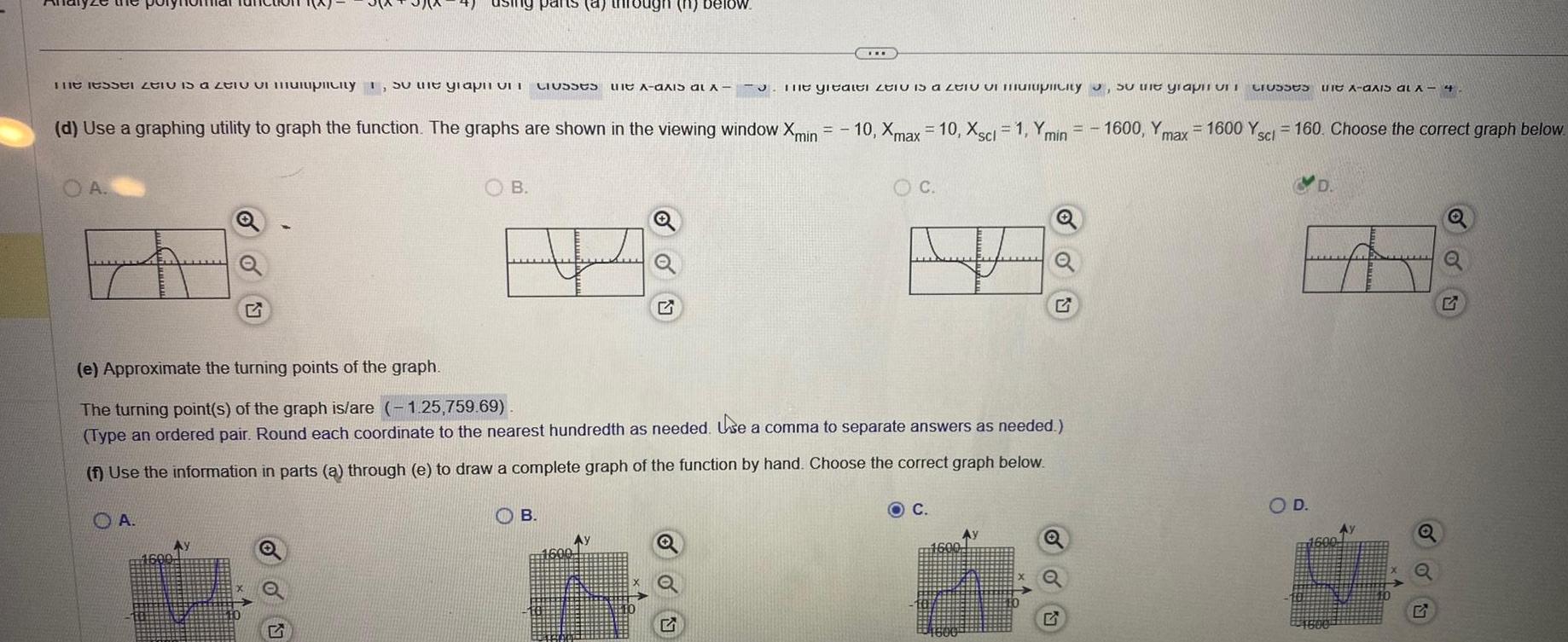
Application of derivativesThe lesser til is a zentiplicity so the graph on OA o OA d Use a graphing utility to graph the function The graphs are shown in the viewing window Xmin B pants a through n Classes B Ay 1600 IOW e Approximate the turning points of the graph The turning point s of the graph is are 1 25 759 69 Type an ordered pair Round each coordinate to the nearest hundredth as needed Use a comma to separate answers as needed f Use the information in parts a through e to draw a complete graph of the function by hand Choose the correct graph below S X The gitaiti i is a ti miplicity the graph in Crosses f A axis al x 4 10 Xmax 10 Xscl 1 Ymin 1600 Yn 1600 Y 160 Choose the correct graph below max O C C 1 1600 O D D 57 Q
Calculus
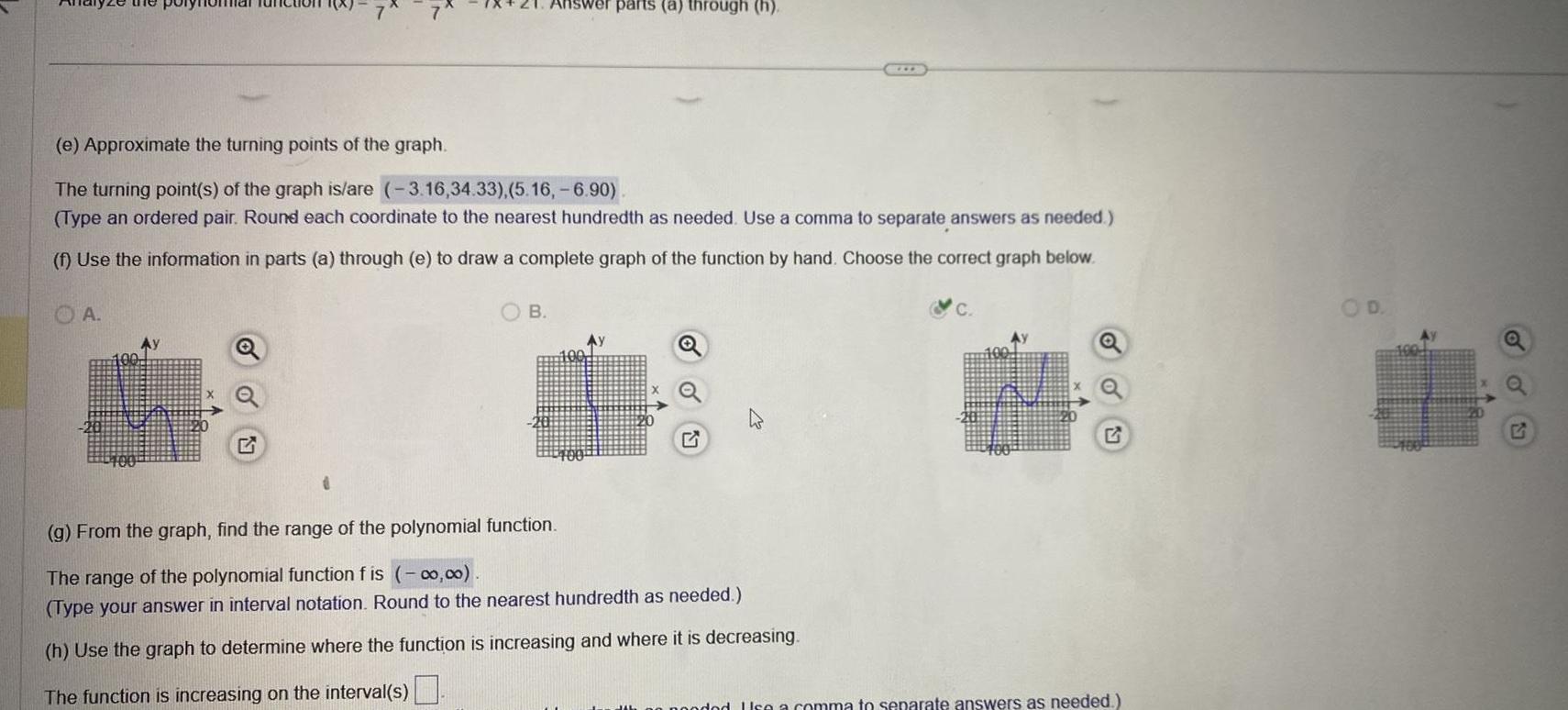
Application of derivativese Approximate the turning points of the graph The turning point s of the graph is are 3 16 34 33 5 16 6 90 Type an ordered pair Round each coordinate to the nearest hundredth as needed Use a comma to separate answers as needed f Use the information in parts a through e to draw a complete graph of the function by hand Choose the correct graph below OA wer parts a through h B Ay g From the graph find the range of the polynomial function The range of the polynomial function f is 0 00 Type your answer in interval notation Round to the nearest hundredth as needed h Use the graph to determine where the function is increasing and where it is decreasing The function is increasing on the interval s pooded Use a comma to separate answers as needed D
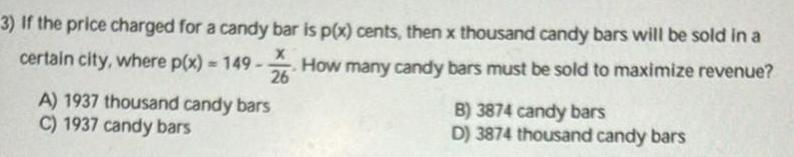
Calculus
Application of derivatives3 If the price charged for a candy bar is p x cents then x thousand candy bars will be sold in a certain city where p x 149 2 How many candy bars must be sold to maximize revenue A 1937 thousand candy bars C 1937 candy bars B 3874 candy bars D 3874 thousand candy bars
Calculus
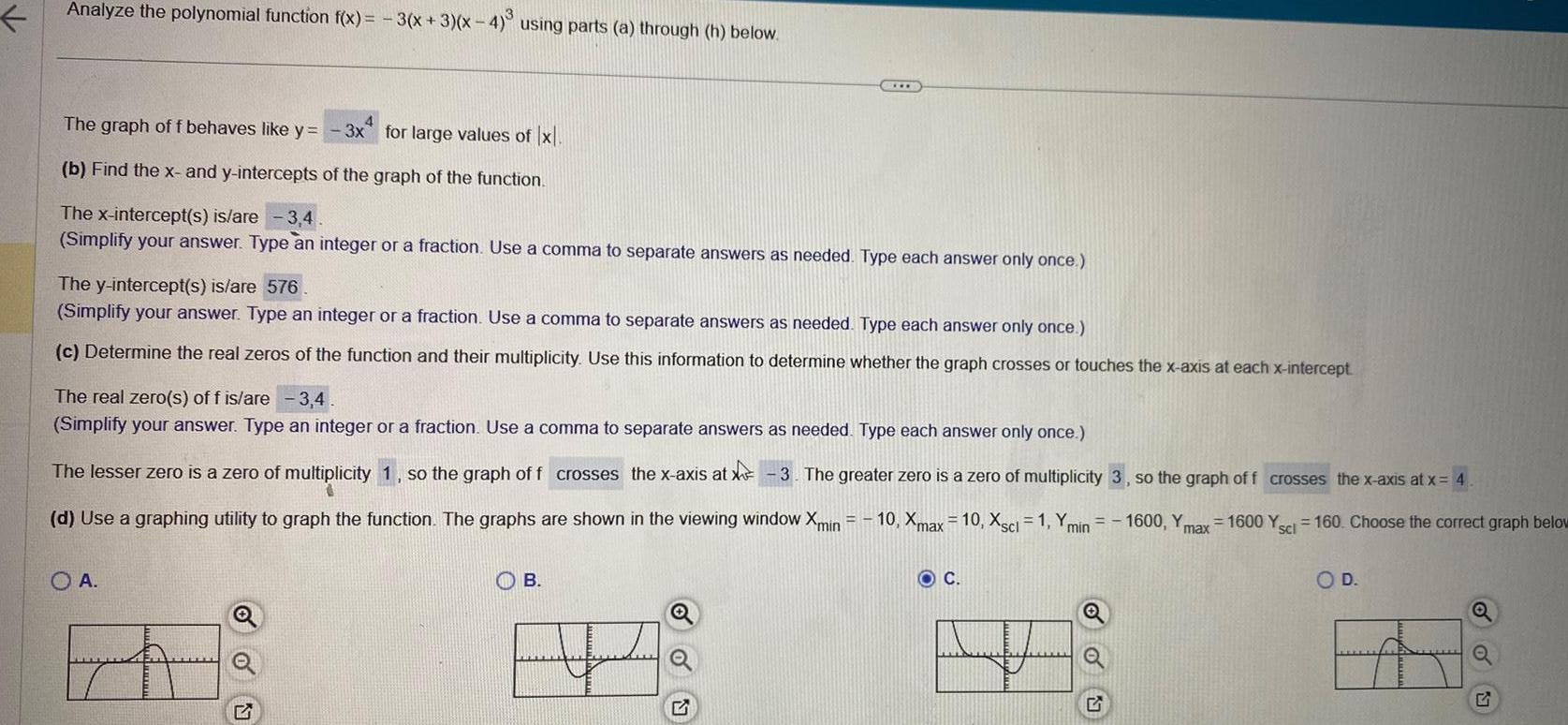
Application of derivativesAnalyze the polynomial function f x 3 x 3 x 4 using parts a through h below The graph of f behaves like y 3x for large values of x b Find the x and y intercepts of the graph of the function The x intercept s is are 3 4 Simplify your answer Type an integer or a fraction Use a comma to separate answers as needed Type each answer only once The y intercept s is are 576 Simplify your answer Type an integer or a fraction Use a comma to separate answers as needed Type each answer only once c Determine the real zeros of the function and their multiplicity Use this information to determine whether the graph crosses or touches the x axis at each x intercept The real zero s of f is are 3 4 Simplify your answer Type an integer or a fraction Use a comma to separate answers as needed Type each answer only once Y min 1600 Y max The lesser zero is a zero of multiplicity 1 so the graph of f crosses the x axis at X 3 The greater zero is a zero of multiplicity 3 so the graph of f crosses the x axis at x 4 d Use a graphing utility to graph the function The graphs are shown in the viewing window Xmin 10 Xmax 10 Xscl 1 1600 Yscl 160 Choose the correct graph below OA www C B O C OU O D

Calculus
DifferentiationFind the domain and range for the quadratic function with a vertex 10 0 if the graph opens down help intervals Domain M Range help intervals

Calculus
Definite IntegralsRewrite the quadratic function f x 5x 10x 9 in standard form f x a x h k and give the vertex help numbers f x Vertex help points
Calculus
Application of derivativesind the general form of the quadratic function with the vertex 3 2 and a point on the graph 5 6 f x help formulas

Calculus
Application of derivativesFind the general form of the quadratic function that has a vertex of 2 2 and a point on the graph 5 51 f x help formulas
Calculus
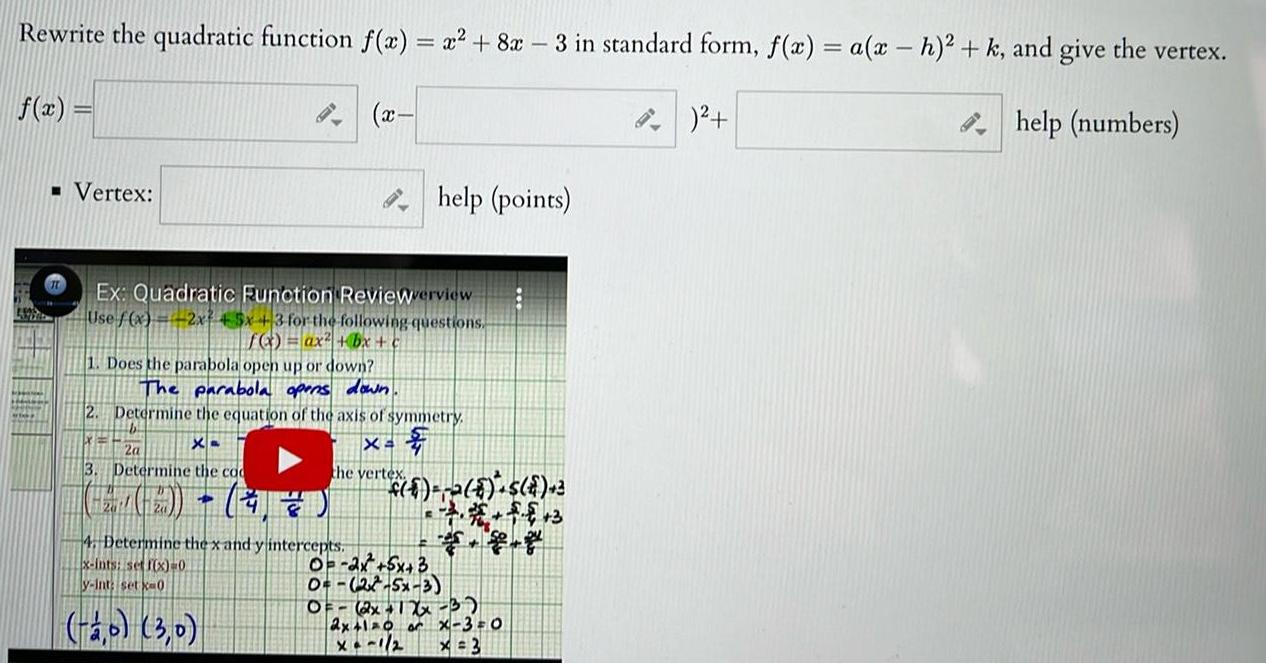
Application of derivativesRewrite the quadratic function f x x 8x 3 in standard form f x a x h k and give the vertex help numbers f x Vertex Ex Quadratic Function Reviewerview Use f x 2x 45x 3 for the following questions f x ax bx 1 Does the parabola open up or down The parabola opens down 2 Determine the equation of the axis of symmetry b X 2a the vertex Xa 3 Determine the co H Q x 4 Determine the x and y intercepts x ints set f x 0 y int set ka0 2 0 3 0 help points 6 2 8 S 2 0 2x 5x 3 0 27 5x 3 OF 2x 12x 3 2x 1 0 or X 3 0 x 3 G

Calculus
Application of derivativesFor the quadratic function f x x 4x 5 find the vertex the axis of symmetry and the x intercept s Express the vertex as a coordinate pair If there is more than one intercept enter as a comma separated list of points help points vertex axis of symmetry x intercept s help numbers help points

Calculus
Application of derivativesDetermine whether f x 4x 16x 4 has a minimum or maximum value and find the value of the minimum or maximum Also find the axis of symmetry The y value of the is The axis of symmetry for f x is given by help numbers help numbers

Calculus
Application of derivativesDetermine the domain and range of f x 7 x 5 3 Enter the solution in interval notation help intervals Domain Range help intervals
Calculus
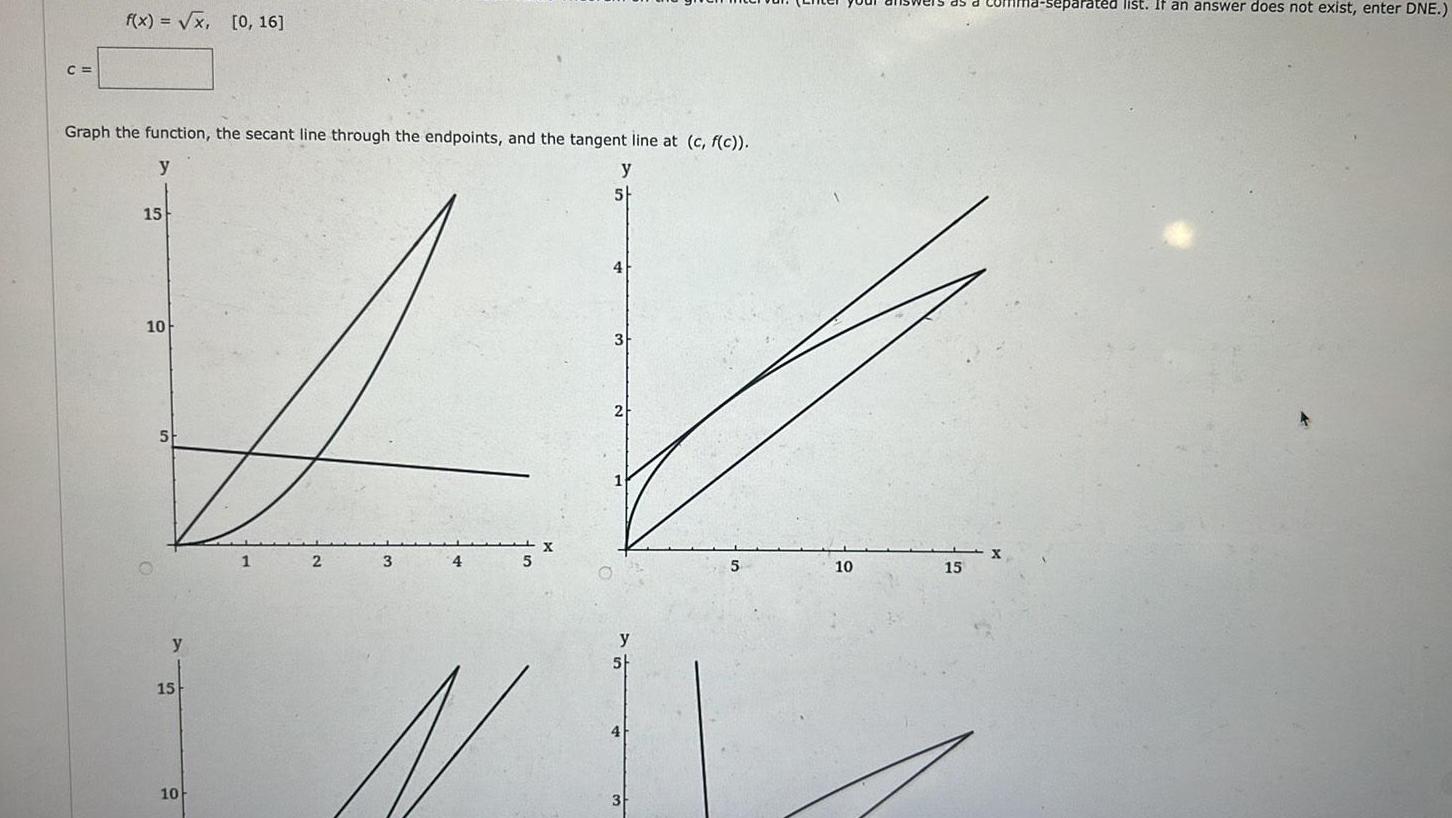
Application of derivativesC f x x 0 16 Graph the function the secant line through the endpoints and the tangent line at c f c y y 5 15 10 5 y 15 10 1 2 3 5 3 5 10 15 1 separated list If an answer does not exist enter DNE
Calculus
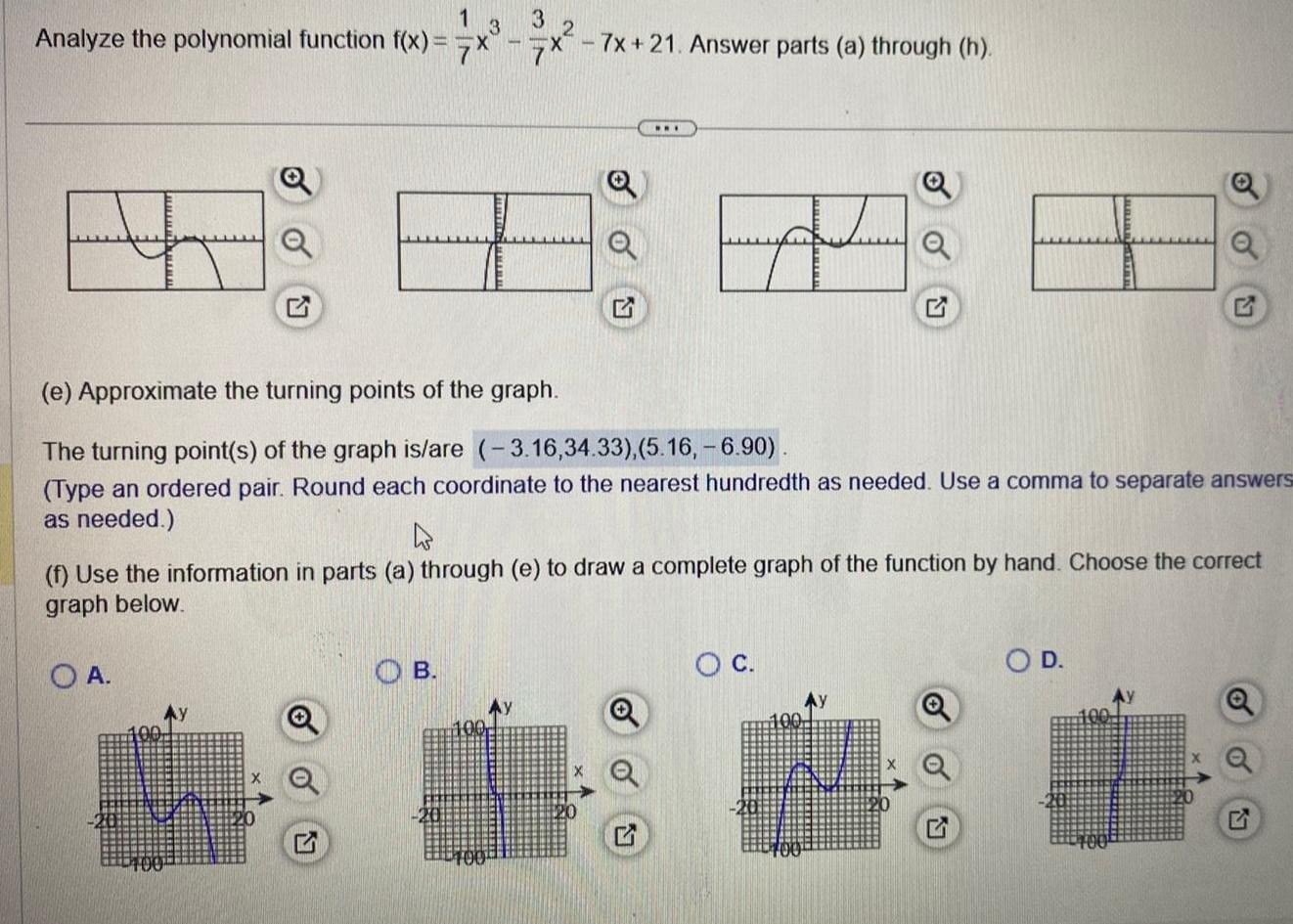
Application of derivatives13 3 Analyze the polynomial function f x x x 7x 21 Answer parts a through h 24 8 8 3 4 8 8 e Approximate the turning points of the graph The turning point s of the graph is are 3 16 34 33 5 16 6 90 Type an ordered pair Round each coordinate to the nearest hundredth as needed Use a comma to separate answers as needed f Use the information in parts a through e to draw a complete graph of the function by hand Choose the correct graph below OA www B 100 Ay O C O D

Calculus
DifferentiationLet f x x 3 2 Find all values of c in 1 4 such that f 4 f 1 f c 4 1 Enter your answers as a comma separated list If an answer does not exist enter DNE C Based off of this information what conclusions can be made about the Mean Value Theorem O This contradicts the Mean Value Theorem since f satisfies the hypotheses on the given interval but there does not exist any c on 1 4 such that f c This does not contradict the Mean Value Theorem since f is not continuous at x 3 f 4 f 1 This does not contradict the Mean Value Theorem since f is continuous on 1 4 and there exists a c on 1 4 such that f c This contradicts the Mean Value Theorem since there exists a c on 1 4 such that f c f 4 f 1 but f is not continuous at x 3 4 1 Nothing can be concluded f 4 f 1 4 1
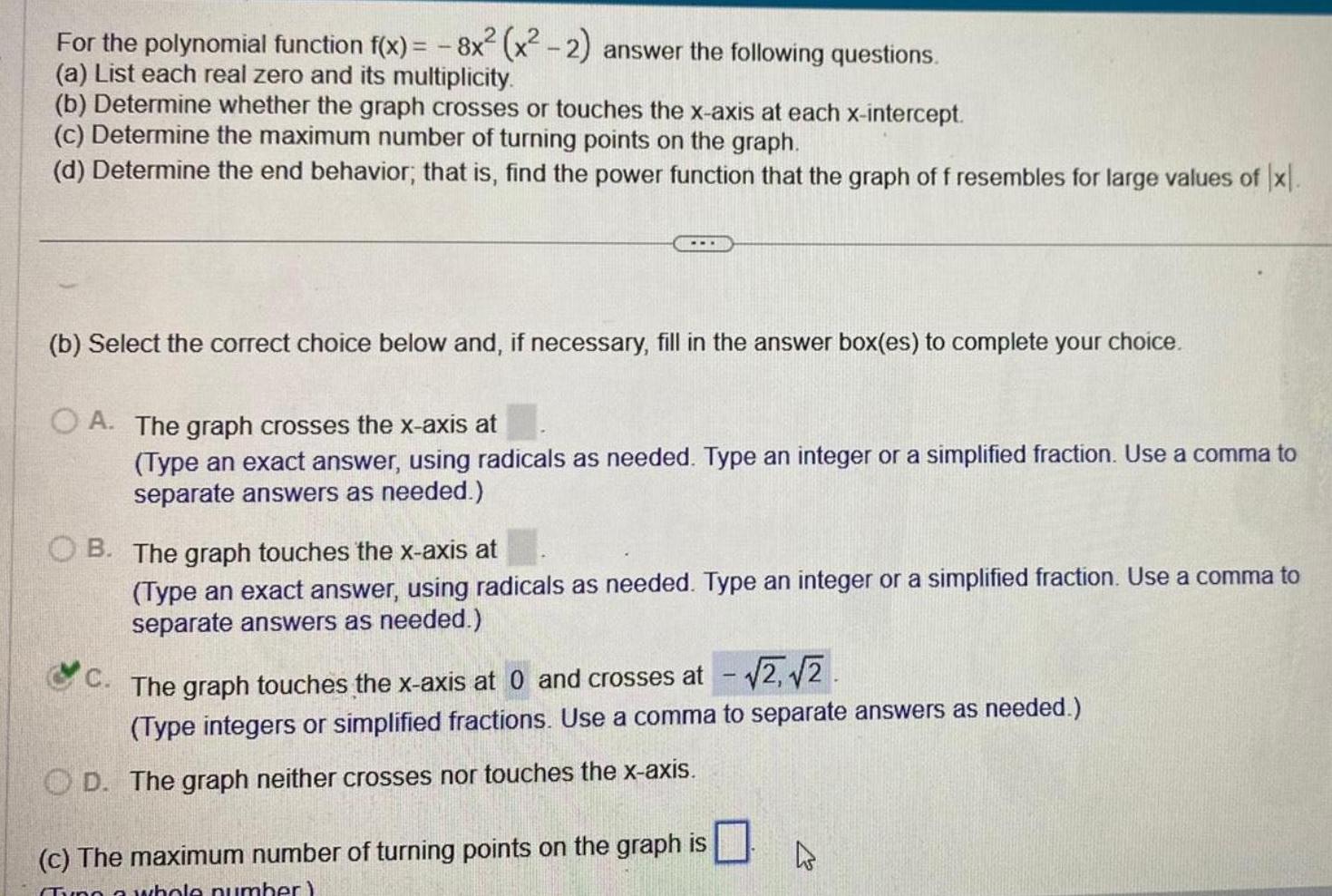
Calculus
Application of derivativesFor the polynomial function f x 8x x 2 answer the following questions a List each real zero and its multiplicity b Determine whether the graph crosses or touches the x axis at each x intercept c Determine the maximum number of turning points on the graph d Determine the end behavior that is find the power function that the graph of f resembles for large values of x b Select the correct choice below and if necessary fill in the answer box es to complete your choice OA The graph crosses the x axis at Type an exact answer using radicals as needed Type an integer or a simplified fraction Use a comma to separate answers as needed OB The graph touches the x axis at Type an exact answer using radicals as needed Type an integer or a simplified fraction Use a comma to separate answers as needed C The graph touches the x axis at 0 and crosses at 2 2 Type integers or simplified fractions Use a comma to separate answers as needed OD The graph neither crosses nor touches the x axis c The maximum number of turning points on the graph is Tyng a whole number

Calculus
Application of derivatives8 A town with a population of 100 people grows to a population of 200 in five years Assume the dP population P grows exponentially according to the equation kP Find the relative growth rate dt k
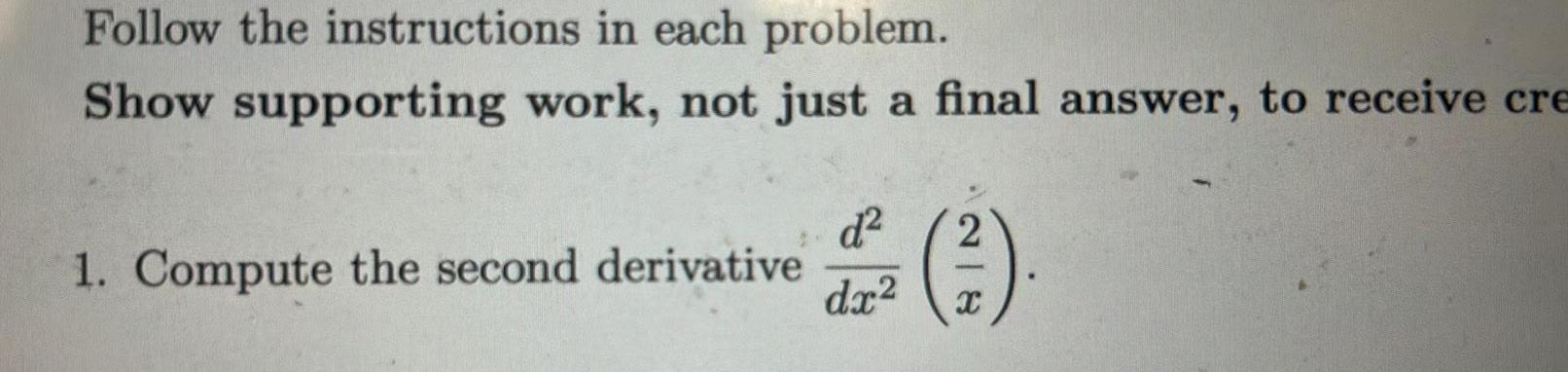
Calculus
DifferentiationFollow the instructions in each problem Show supporting work not just a final answer to receive cre 1 Compute the second derivative d dx2 218
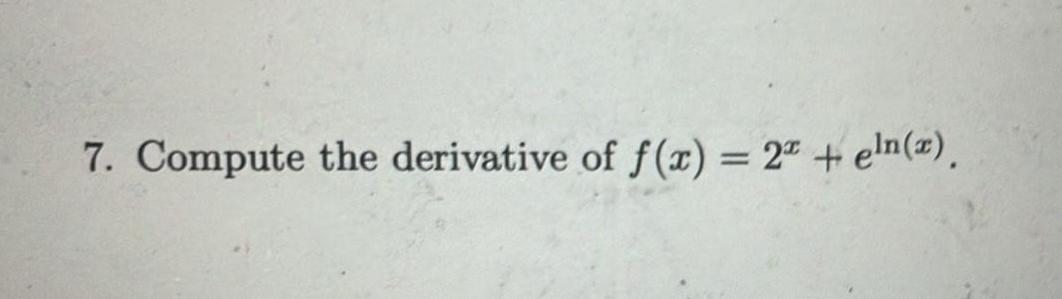
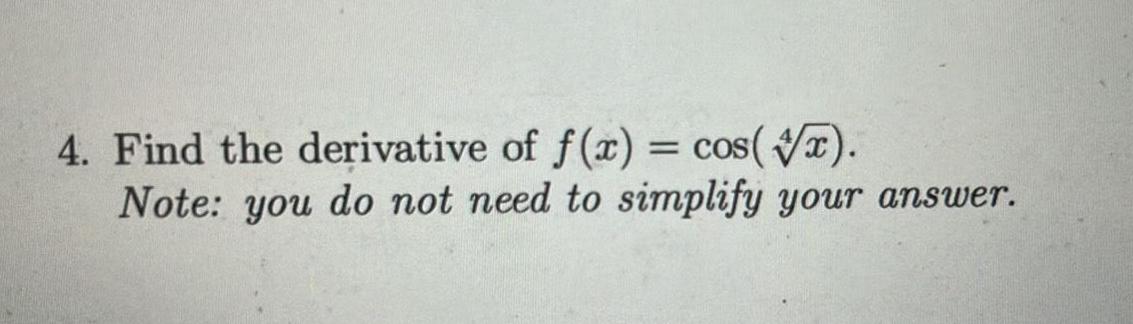
Calculus
Differentiation4 Find the derivative of f x cos x Note you do not need to simplify your answer
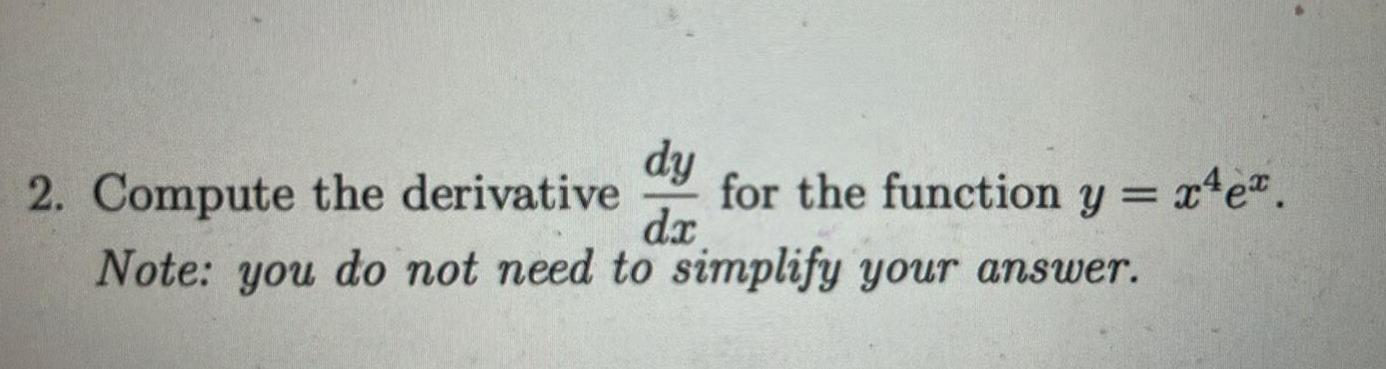
Calculus
Application of derivatives2 Compute the derivative for the function y x e dy dx Note you do not need to simplify your answer

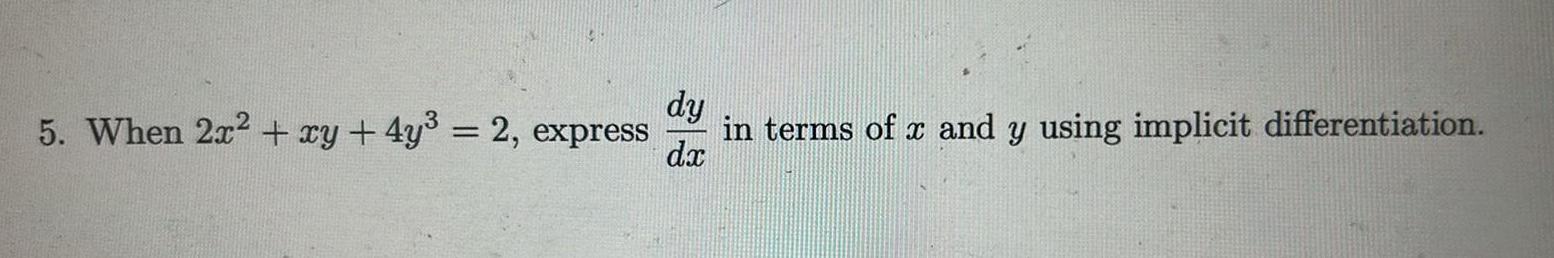
Calculus
Application of derivatives5 When 2x xy 4y 2 express dy in terms of x and y using implicit differentiation dx
Calculus
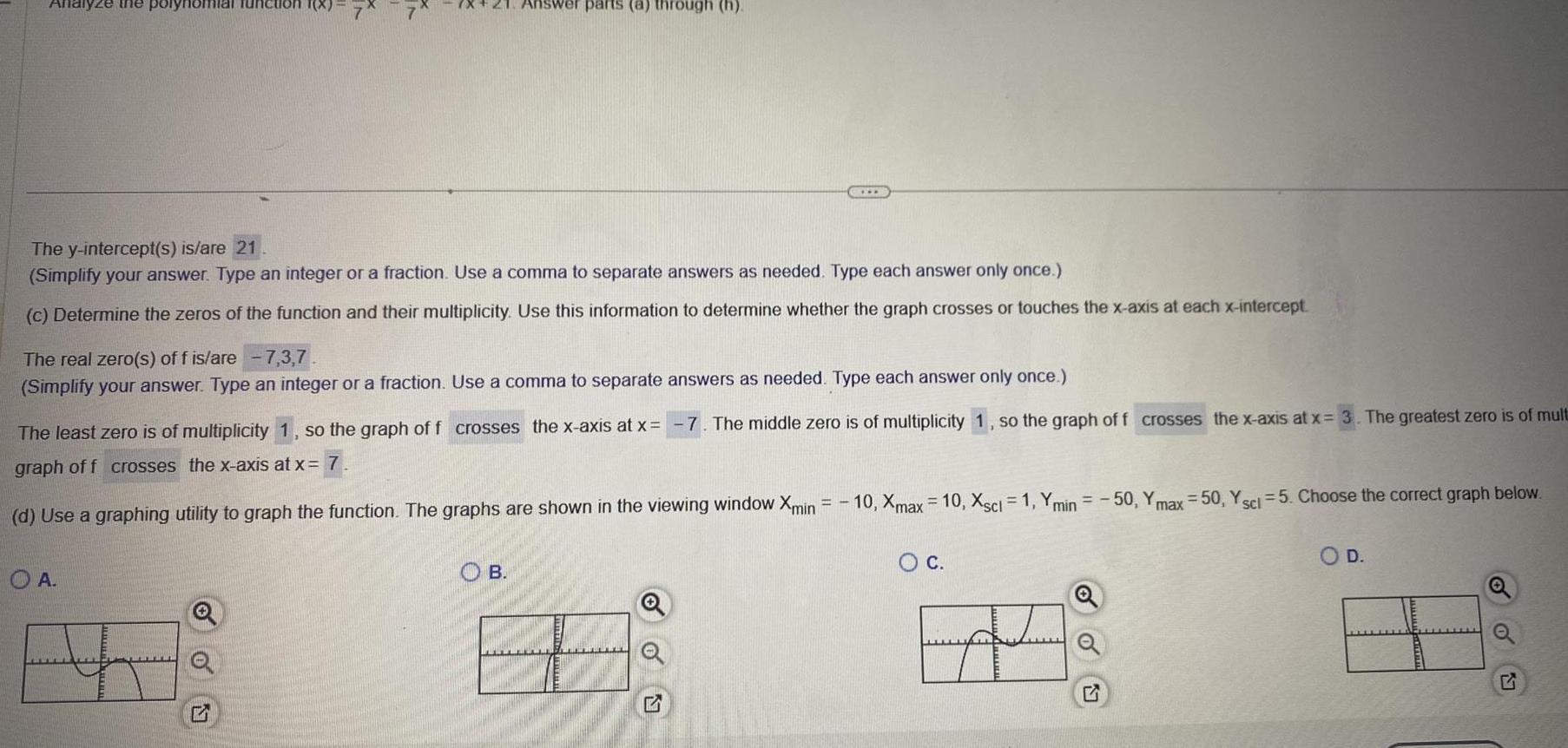
Application of derivativesAnalyze the polynomial function The y intercept s is are 21 Simplify your answer Type an integer or a fraction Use a comma to separate answers as needed Type each answer only once c Determine the zeros of the function and their multiplicity Use this information to determine whether the graph crosses or touches the x axis at each x intercept The real zero s of f is are 7 3 7 Simplify your answer Type an integer or a fraction Use a comma to separate answers as needed Type each answer only once A Answer parts a through h The least zero is of multiplicity 1 so the graph of f crosses the x axis at x graph off crosses the x axis at x 7 d Use a graphing utility to graph the function The graphs are shown in the viewing window Xmin 5 B 7 The middle zero is of multiplicity 1 so the graph of f crosses the x axis at x 3 The greatest zero is of mult 10 Xmax 10 Xscl 1 Ymin 50 Ymax 50 Y sci 5 Choose the correct graph below O C Q O D o O 5

Calculus
Application of derivativesThe radius of a sphere is increasing at a rate of 3 mm s How fast is the volume increasing when the diameter is 80 mm mm s
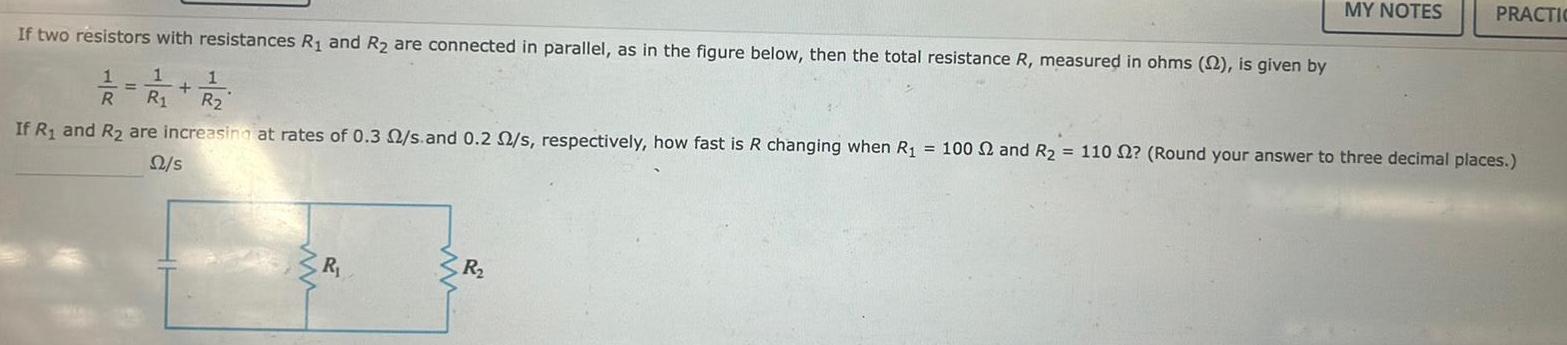
Calculus
Application of derivativesR If two resistors with resistances R and R are connected in parallel as in the figure below then the total resistance R measured in ohms 22 is given by 1 1 2 22 R If R and R are increasing at rates of 0 3 2 s and 0 2 2 s respectively how fast is R changing when R 100 2 and R 110 2 Round your answer to three decimal places 22 s www MY NOTES R PRACTIC

Calculus
DifferentiationEach side of a square is increasing at a rate of 2 cm s At what rate is the area of the square increasing when the area of the square is 81 cm cm s

Calculus
Application of derivativesh x 2x 15x 144x 1 Given the function above use the First Derivative Test to find the local extrema Select the correct answer below There is a local maximum at x 8 O There is a local maximum at x 3 O There is a local minimum at x 8 and a local maximum at x 3 There is a local maximum at x 8 and a local minimum at x 3 There is a local minimum at x 3
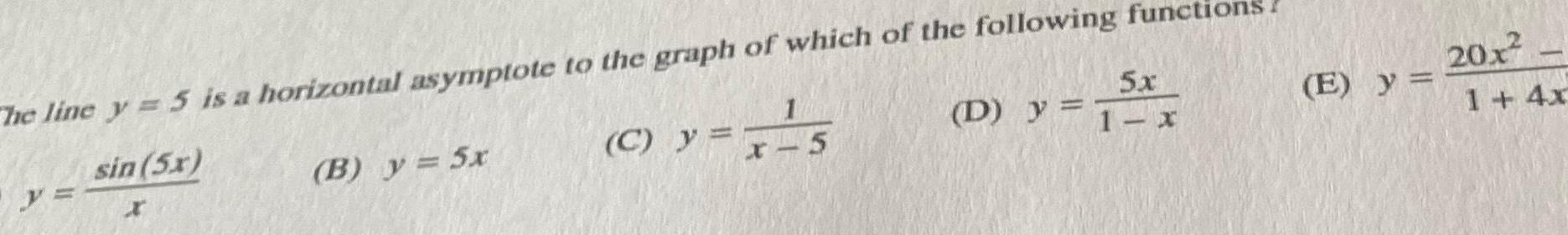
Calculus
Application of derivativesThe line y 5 is a horizontal asymptote to the graph of which of the following functi sin 5x y B y 5x C y 5x D 1 x 1 x 5 E y 20x 1 4x

Calculus
Differentiation31 02 03 04 1 5 25 Lt fbe the function given by f x 1 2 2 x 20 D nonexistent the line yb is a borineal asympaote to the graph Which of the following is true has a pimp discontinuity at 2 2 D has a discontinuity due to a vertical asymptote at x 2
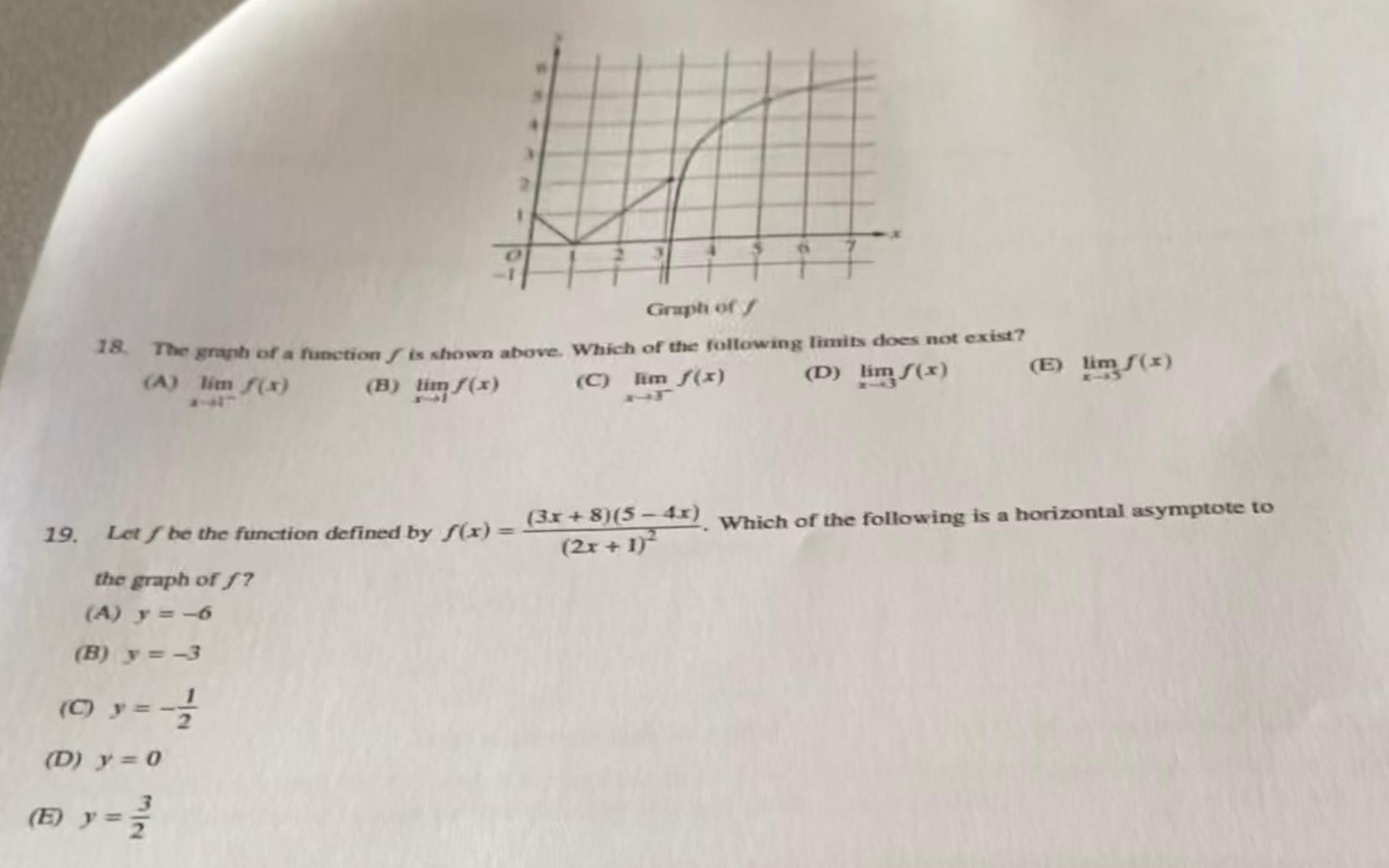
Calculus
Application of derivativesGraph of 18 The graph of a function is shown above Which of the following limits does not exist E lim f x A lim f x B im f x C lim f x D lim f x 19 Let be the function defined by f x 3x 8 5 4x Which of the following is a horizontal asymptote to 2x 1 2 the graph of f A y 6 B y 3 0 y 12 2 D y 0 E y 2
Calculus
Application of derivativesB 2 16 C 3 D nonexistent If f is a continuous function such that f 2 6 which of the following statements must be A lim 2x 3 B lim 2x 12 f x f 2 6 C lim D lim x 36 E lim f x 36 7 For which of the following pairs of functions f and g is lim 818 A f x x 2x and g x x ln x B f x 3x and g x x C f x 3 and g x x D f x 3e x and g x E f x In 3x and g x In 2x and g x 2e x f x infinite g x

Calculus
Application of derivatives1 Is the function f x continuous at x 27 Give a reason for your answer t hrs v t miy hr 1 2 4 5 7 3 8 6 10 3 2 A bug walks back and forth along a straight track The bug s velocity measured in miles per hour i ontinuous with selected values of the velocity shown in the table above time for 4 7 such that the velocity of the bug equals 0 Explain your reasoning

Calculus
DifferentiationA 2 19 2mx for x 2 i 11 Let be the function defined above where e is a constant If f is continuous at x 1 what is the value of 7 A 2 C S continuous A 3 and 1 only 3 1 and 2 1 only 1 and 2 only only B 3 12 Let f be the function defined above where e is a constant For what value of c if any is f continuous at x 2 E There is no such value of c B 7 D 9 C 9 2 sin x f x 1x cx 18 D 4 4 3 Let f be the function given by f x x 2 x 1 for x 2 for x 2 x 2 x 3 For which of the following values of x is f not

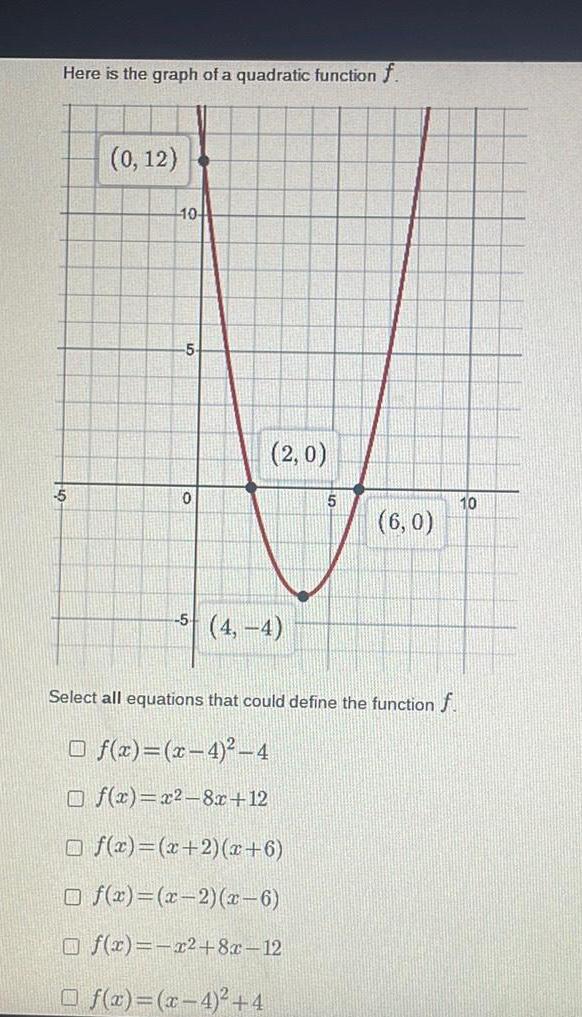
Calculus
Application of derivativesHere is the graph of a quadratic function f 5 0 12 10 5 0 2 0 5 4 4 Of x x 4 4 5 6 0 Select all equations that could define the function f Of x x 4 4 Of x x 8x 12 Of x x 2 x 6 Of x x 2 x 6 f x x 8x 12 10
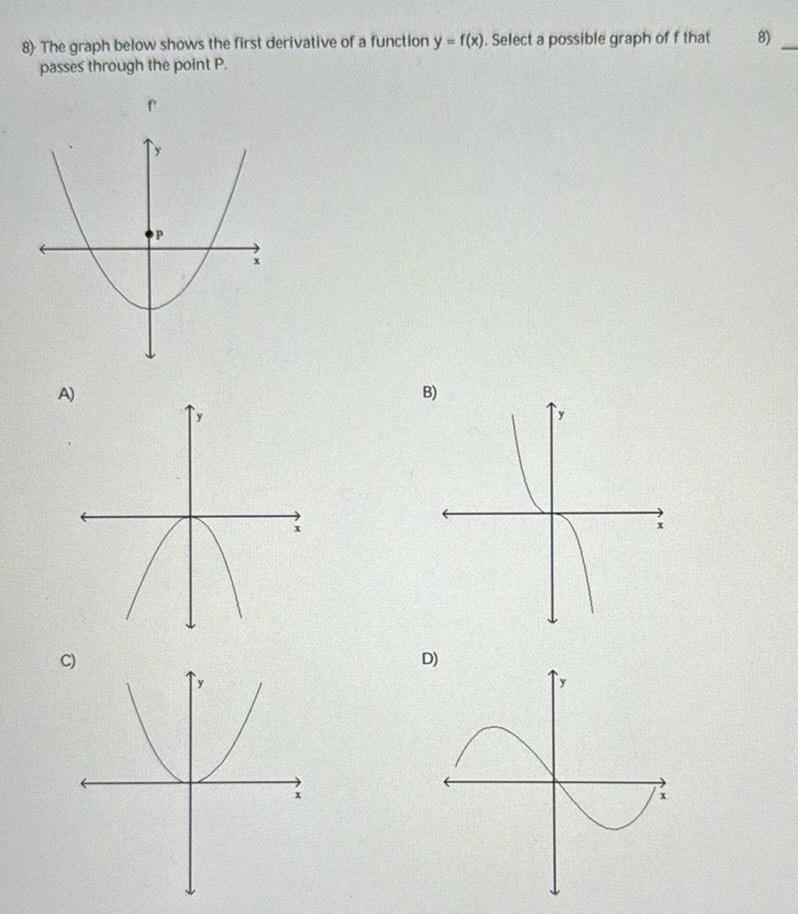
Calculus
Differentiation8 The graph below shows the first derivative of a function y f x Select a possible graph of f that passes through the point P A C f M B D 4 X 8

Calculus
Differentiation1 From a thin piece of cardboard 30 in by 30 in square corners are cut out so that the sides can be folded up to make a box What dimensions will yield a box of maximum volume What is the maximum volume Round to the nearest tenth if necessary A 20 in x 20 in x 10 in 4000 in 3 C 10 in x 10 in x 10 in 1000 in 3 B 20 in x 20 in x 5 in 2000 in3 D 15 in 15 in 7 5 in 1687 5 in3 M

Calculus
Differential equationsAn explanation of Rolle s Theorem How is it a special case of the MVT o What can it tell us about the location of critical point s o What continuity differentiability restrictions apply o Be sure to include a graph to help you explain Rolle s Theorem

Calculus
DifferentiationQuestion 3 20 points 3 Find the derivatives of the given functions a 2x 1 x y ln b In 2x In 1 x 3x y e x cos 4x
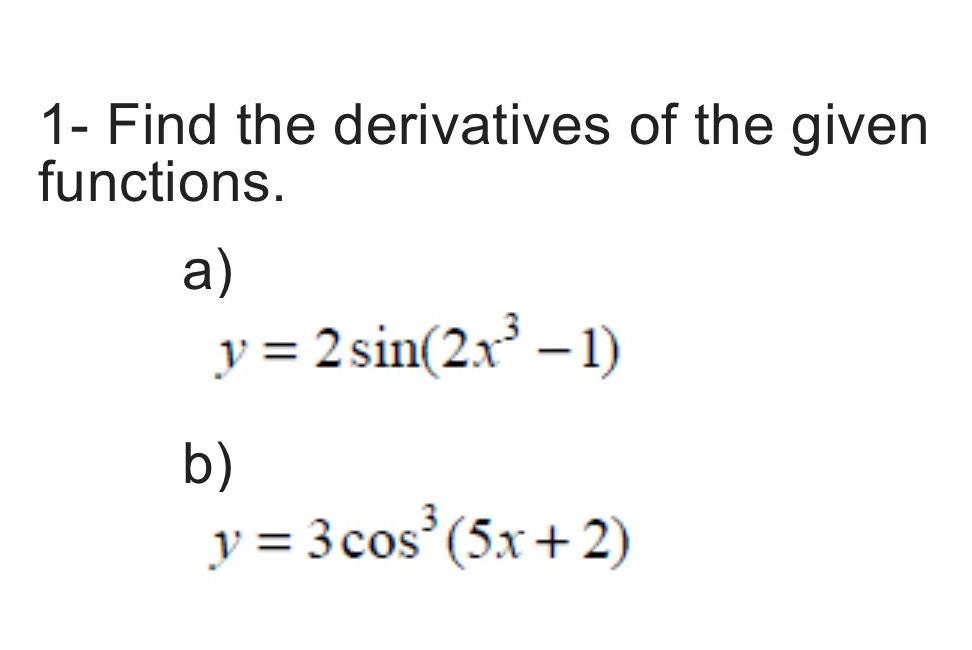
Calculus
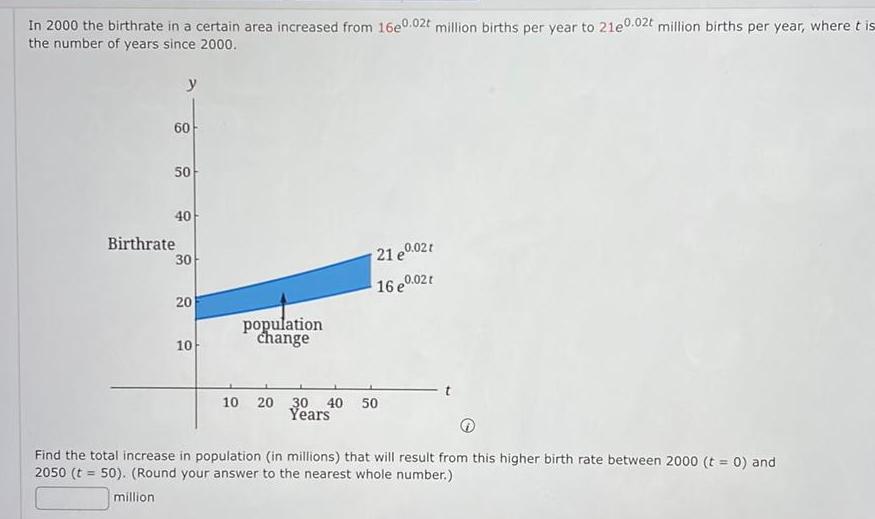
Definite IntegralsIn 2000 the birthrate in a certain area increased from 16e0 02t million births per year to 21e0 02t million births per year where it is the number of years since 2000 y 60 50 40 Birthrate 30 20 10 population change 21 e0 02t 16 e0 02t 10 20 30 40 50 Years Find the total increase in population in millions that will result from this higher birth rate between 2000 t 0 and 2050 t 50 Round your answer to the nearest whole number million

Calculus
DifferentiationVerify the identity tan u sin u tan u sin u sin u tan u sin u 11 E sin u cos u sin u cos u cos u sin u cos u 1 tan u sin u 1 cos u cos u

Calculus
Application of derivativesProve the identity tan x 1 tan x 3 1 3 tan x 1 3 tan x tan x tan F 3 tan x 3 1 3 tan x 3 tan x 1 3 tan x X
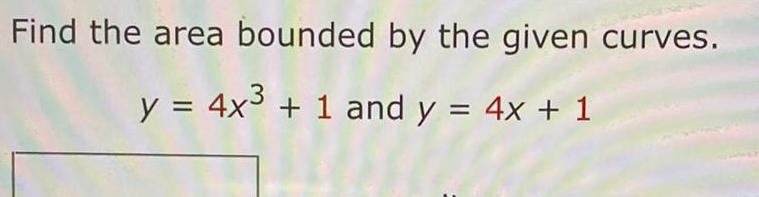

Calculus
Application of derivativesMath 126 Homework 15 2 12 pts Find all zeros real and non real Completely factor the polynomial into a polynomial with linear factors q x 4x 20xXx 4x 13
Calculus
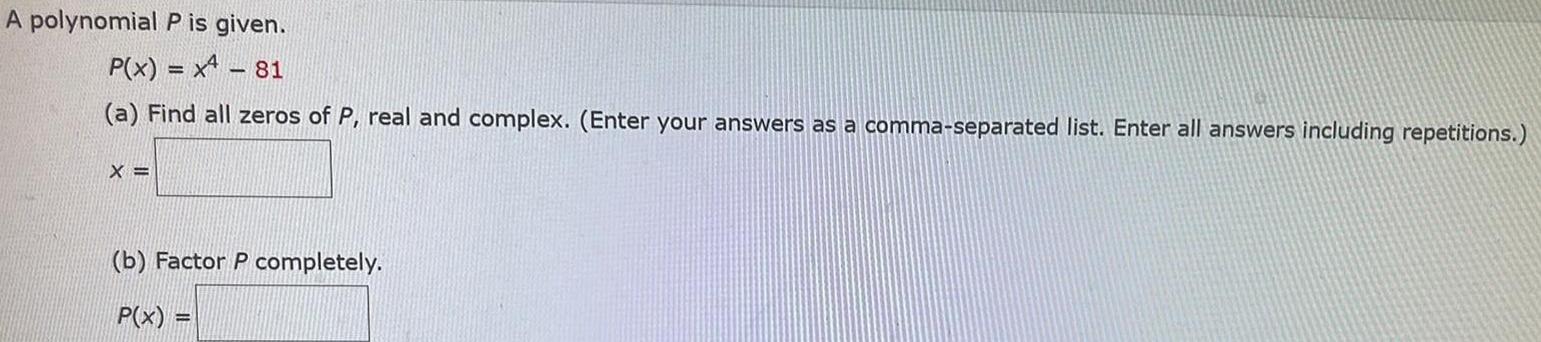
Application of derivativesA polynomial P is given P x x 81 a Find all zeros of P real and complex Enter your answers as a comma separated list Enter all answers including repetitions X b Factor P completely P x

Calculus
Differentiationa If a is a zero of the polynomial P x then b If a is a zero of multiplicity m of the polynomial P x then must be a factor of P x must be a factor of P x when we factor P completel

Calculus
Definite IntegralsProve the identity tan x tan x Use the Subtraction Formula for Tangent and then simplify tan x tan tan x 1 tan x x tan x 0 1 tan x

Calculus
Application of derivativesVerify the identity sin 8 tan 8 Use a Reciprocal Identity to rewrite the expression in terms of sine and cosine and then simplif sin 8 sin 8 tan 8 cos 8 sin 8 cos 8