Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
Differential equationsUse Newton s method with initial approximation x 1 to find x the second approximation to the root of the following equation x4 x 4 0 x x Enhanced Feedback Please try again and draw a diagram Keep in mind that Newton s method is x X f xn
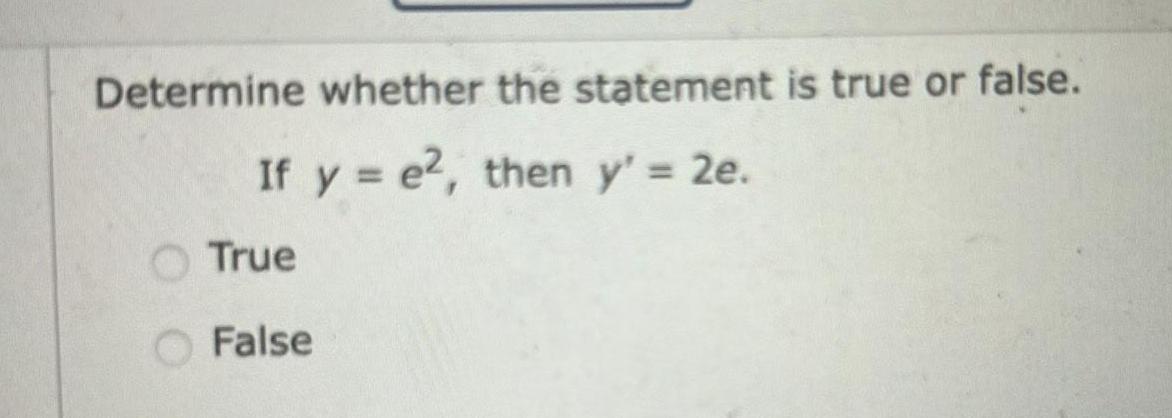
Calculus
Application of derivativesDetermine whether the statement is true or false If y e2 then y 2e True False

Calculus
Application of derivativesDetermine whether the statement is true or false d If f and g are differentiable then dx True False f g x f g x g x
Calculus
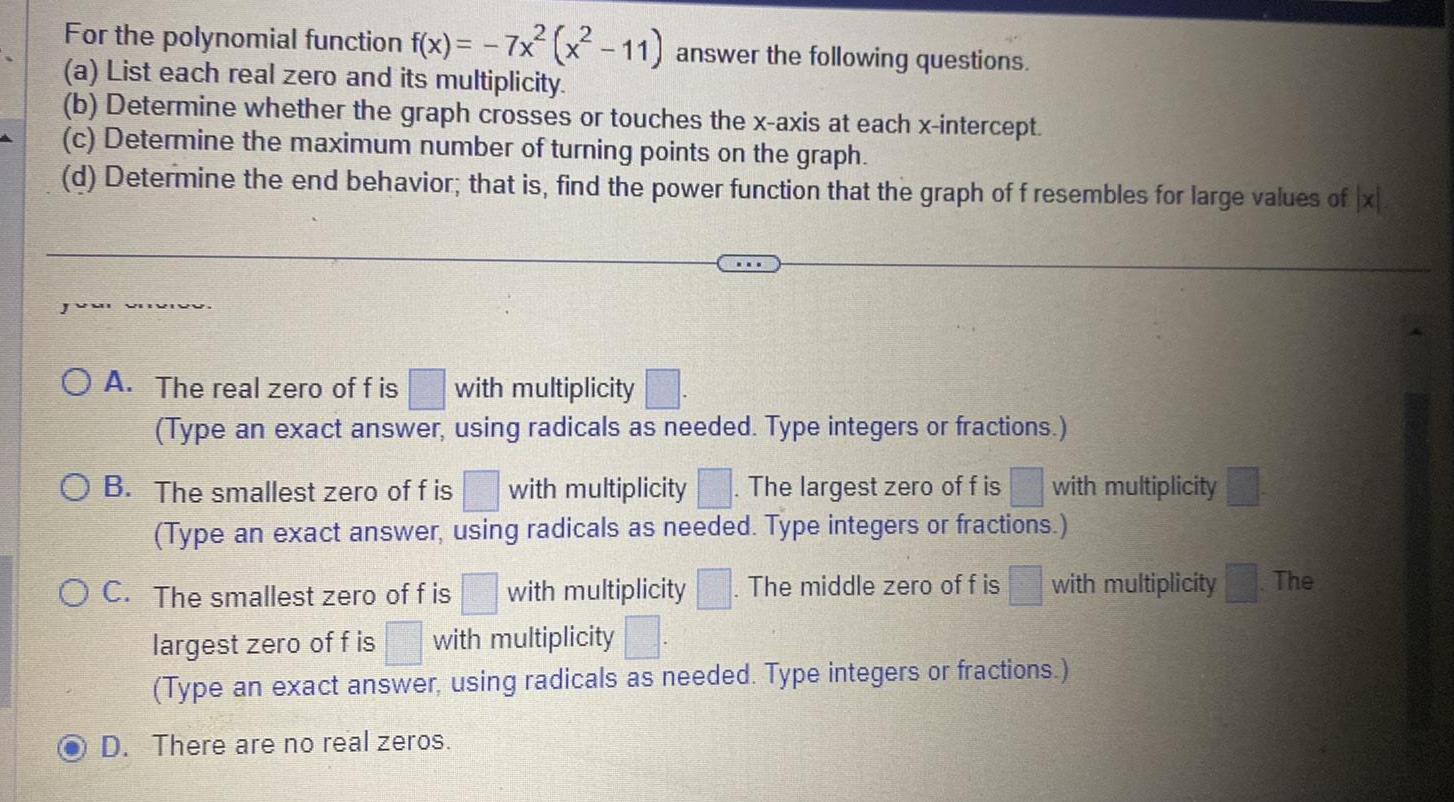
Application of derivativesFor the polynomial function f x 7x x 11 answer the following questions a List each real zero and its multiplicity b Determine whether the graph crosses or touches the x axis at each x intercept c Determine the maximum number of turning points on the graph d Determine the end behavior that is find the power function that the graph of f resembles for large values of x Juni VIIVIVU OA The real zero of f is with multiplicity Type an exact answer using radicals as needed Type integers or fractions OB The smallest zero of f is with multiplicity The largest zero of fis Type an exact answer using radicals as needed Type integers or fractions OC The smallest zero of f is with multiplicity The middle zero of f is largest zero of fis with multiplicity Type an exact answer using radicals as needed Type integers or fractions D There are no real zeros with multiplicity with multiplicity The
Calculus
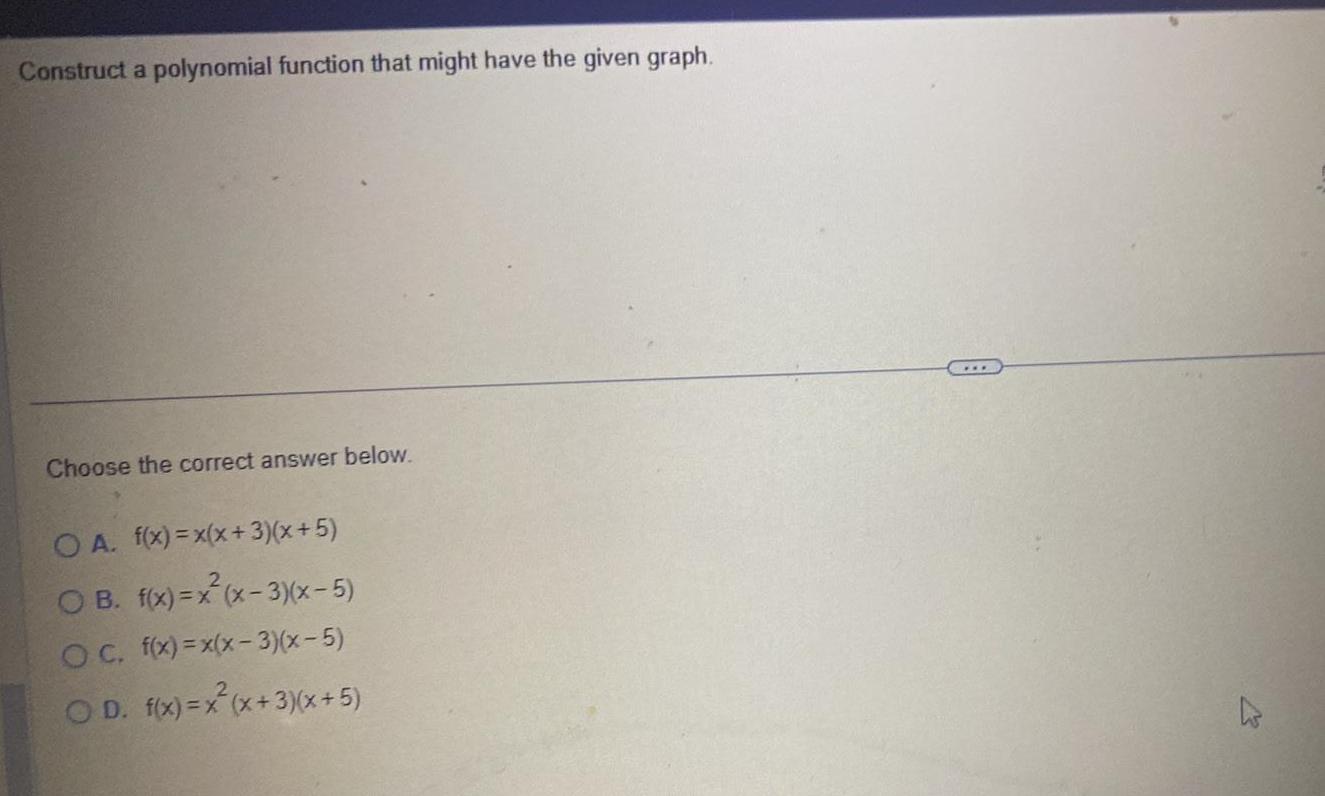
Application of derivativesConstruct a polynomial function that might have the given graph Choose the correct answer below OA f x x x 3 x 5 OB f x x x 3 x 5 OC f x x x 3 x 5 OD f x x x 3 x 5
Calculus
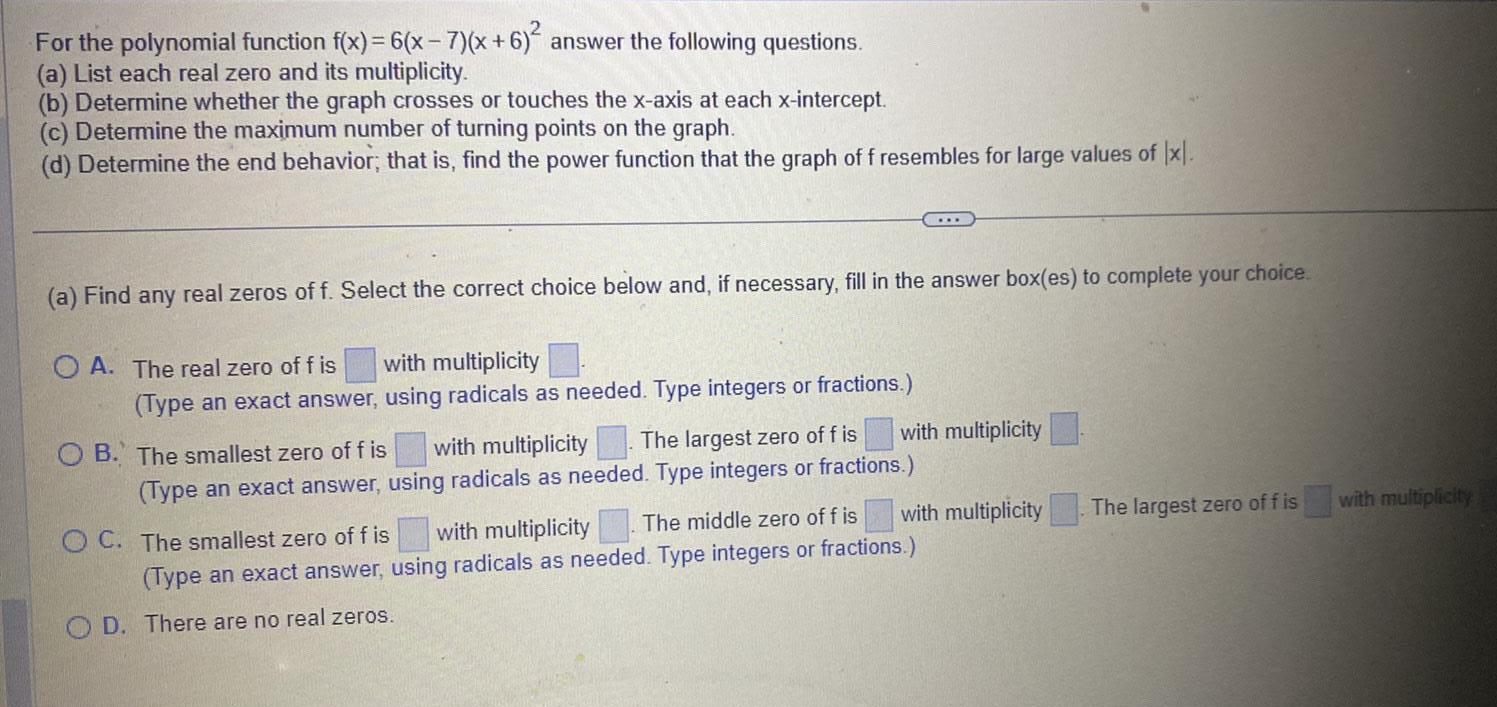
Application of derivativesFor the polynomial function f x 6 x 7 x 6 2 answer the following questions a List each real zero and its multiplicity b Determine whether the graph crosses or touches the x axis at each x intercept c Determine the maximum number of turning points on the graph d Determine the end behavior that is find the power function that the graph of f resembles for large values of x a Find any real zeros of f Select the correct choice below and if necessary fill in the answer box es to complete your choice OA The real zero of fis with multiplicity Type an exact answer using radicals as needed Type integers or fractions The largest zero of f is with multiplicity OB The smallest zero of f is with multiplicity Type an exact answer using radicals as needed Type integers or fractions with multiplicity The middle zero of f is OC The smallest zero of f is with multiplicity Type an exact answer using radicals as needed Type integers or fractions OD There are no real zeros The largest zero of f is with multiplicity
Calculus
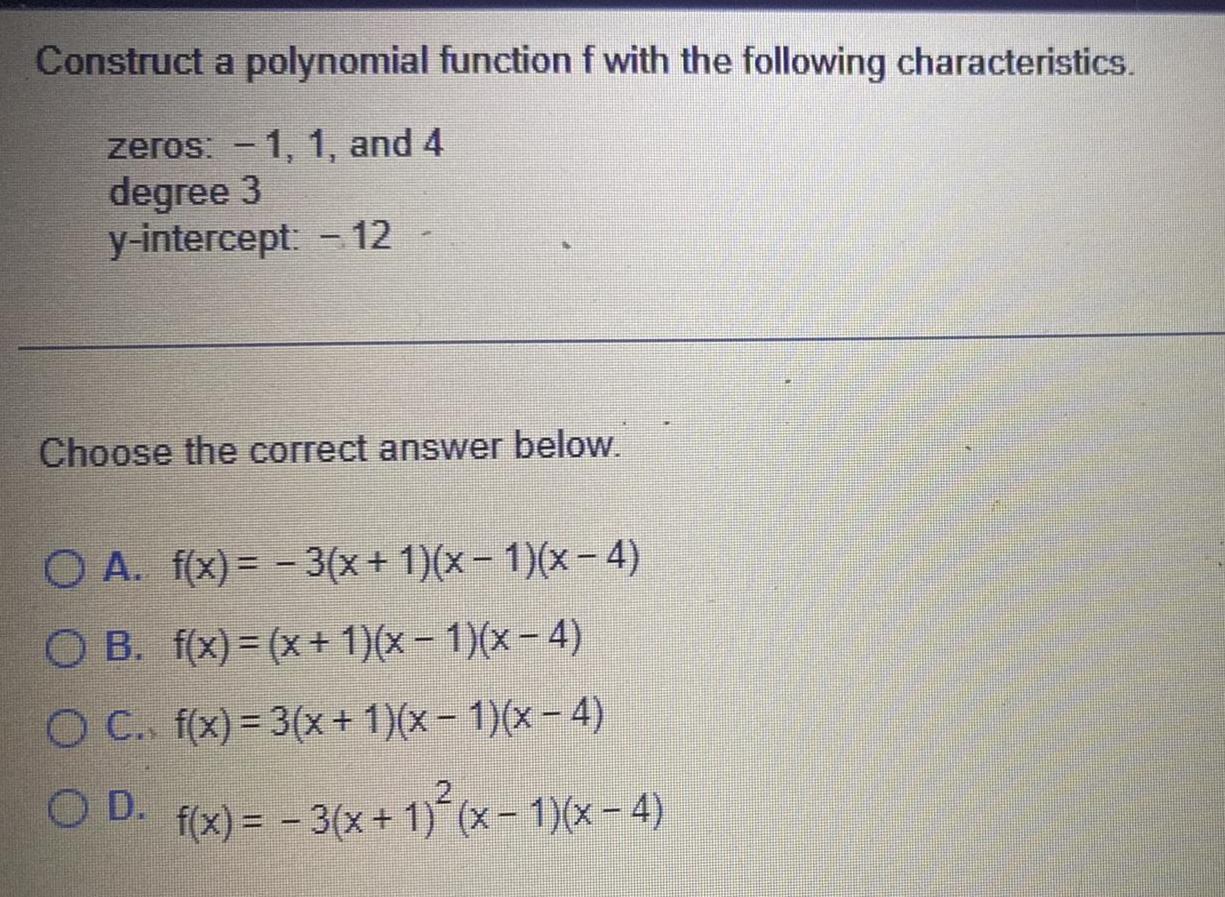
Application of derivativesConstruct a polynomial function f with the following characteristics zeros 1 1 and 4 degree 3 y intercept 12 Choose the correct answer below O A f x 3 x 1 x 1 x 4 O B f x x 1 x 1 x 4 O C f x 3 x 1 x 1 x 4 OD f x 3 x 1 x 1 x 4
Calculus
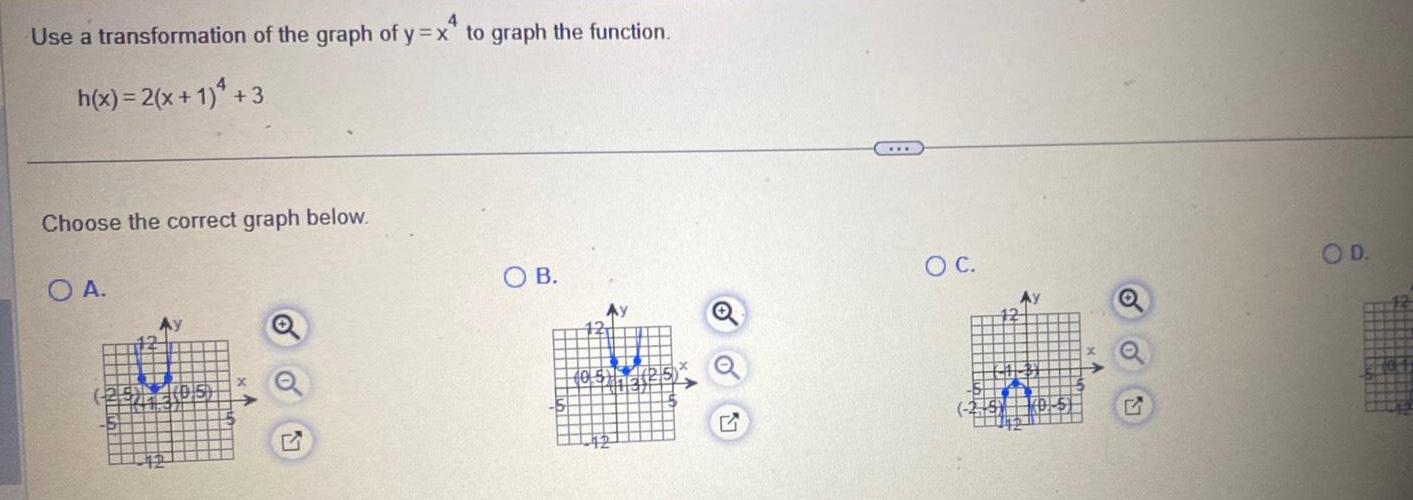
Application of derivatives4 Use a transformation of the graph of y x to graph the function 4 h x 2 x 1 3 Choose the correct graph below O A OB H hatt HOFF H OC Ay G OD
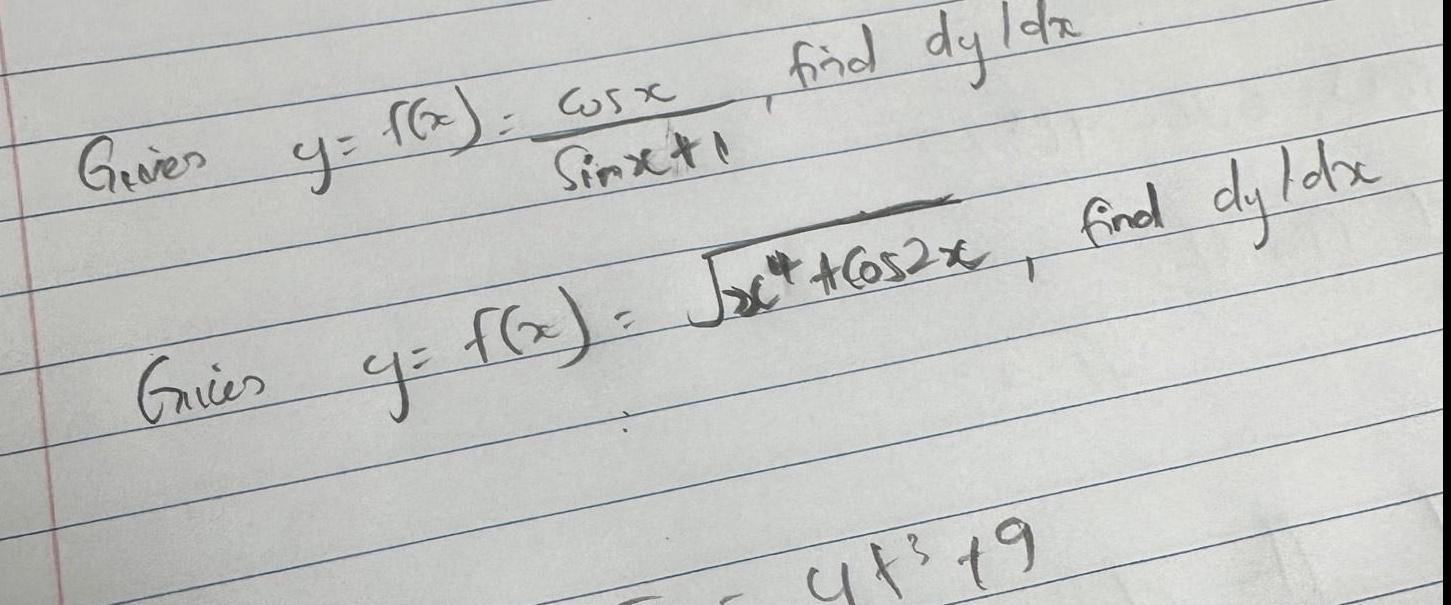
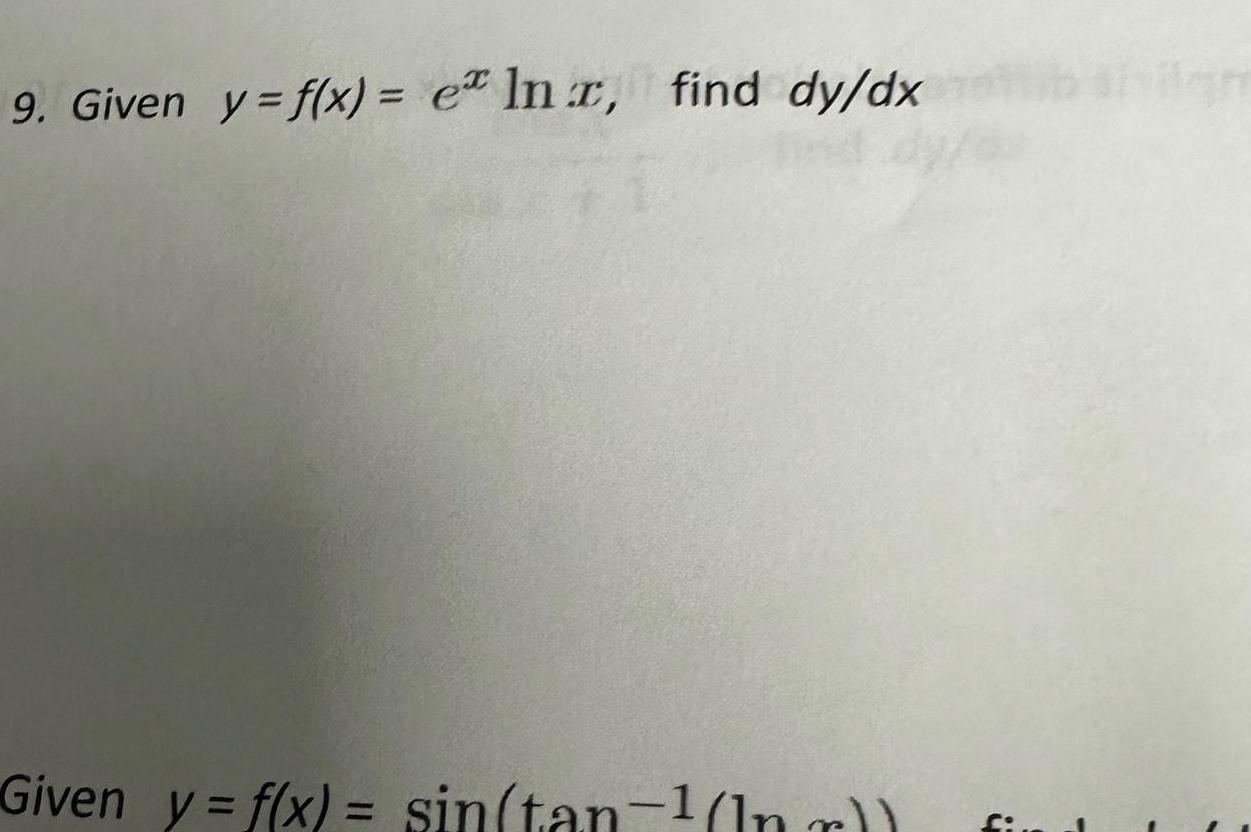
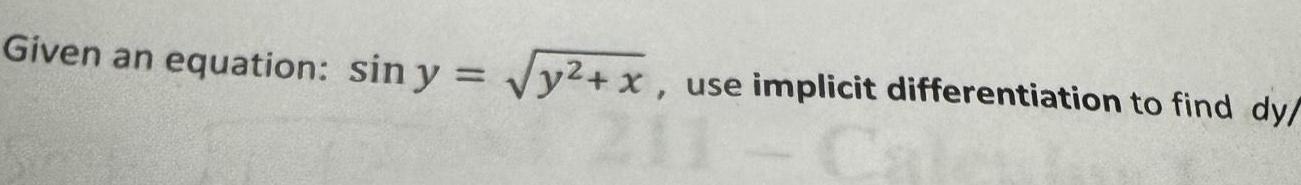
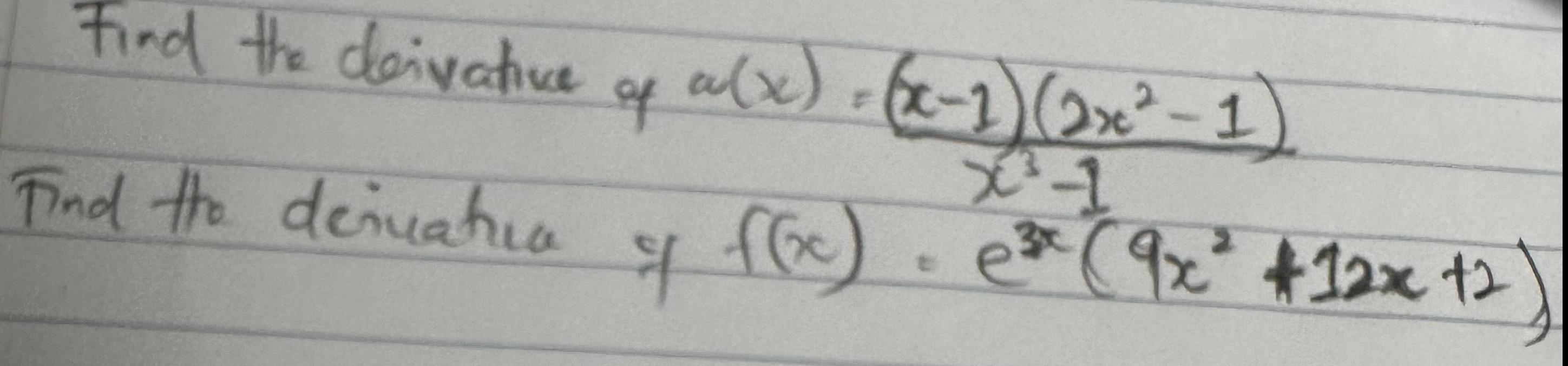
Calculus
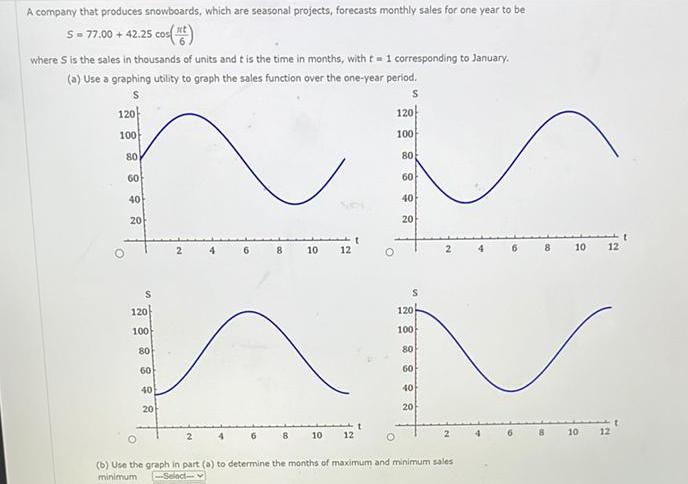
Limits & ContinuityA company that produces snowboards which are seasonal projects forecasts monthly sales for one year to be S 77 00 42 25 cos 6 where S is the sales in thousands of units and t is the time in months with t 1 corresponding to January a Use a graphing utility to graph the sales function over the one year period S 120 100 O 80 60 40 20 120 100 80 60 40 20 2 8 10 10 12 12 O 120 100 80 O 60 40 20 S 120 8 100 80 60 40 20 b Use the graph in part a to determine the months of maximum and minimum sales minimum Select 10 10

Calculus
Vector CalculusComplete the sentence below 5 If f x 3x x 2 6x 9 then f x 5 3 If f x 3x x 6x 9 then f x as as x and f x as x and f x as x as x
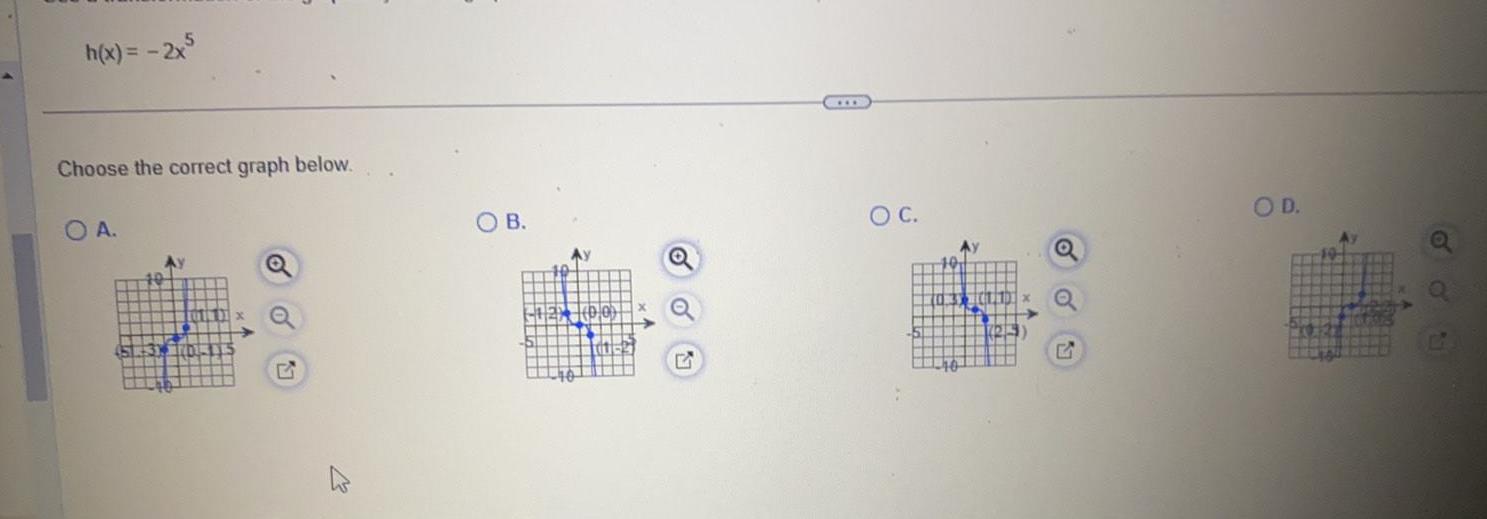
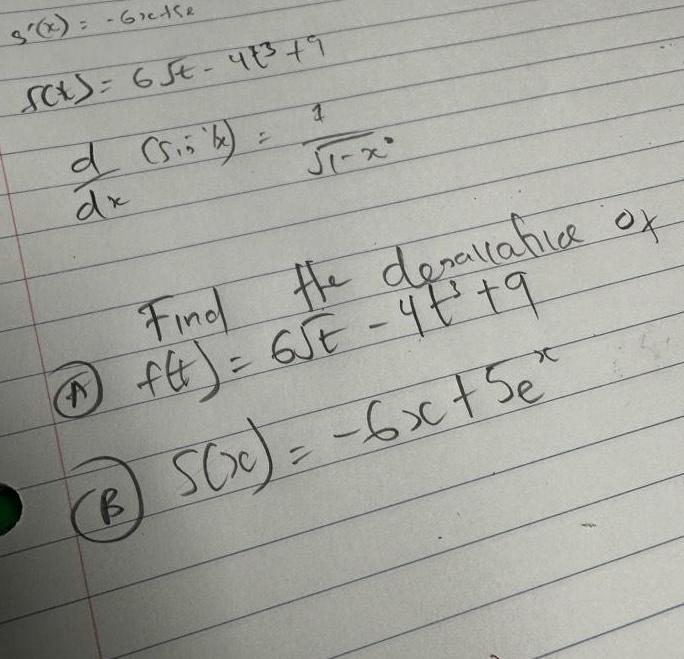
Calculus
Differentiation61158 s x SC 6 St 473 9 d 5 5 be dx 1 T x the desallative of Find ftt 65E 4 t t q A B S x 6x 5e
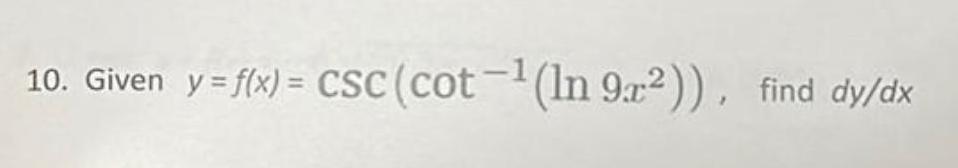
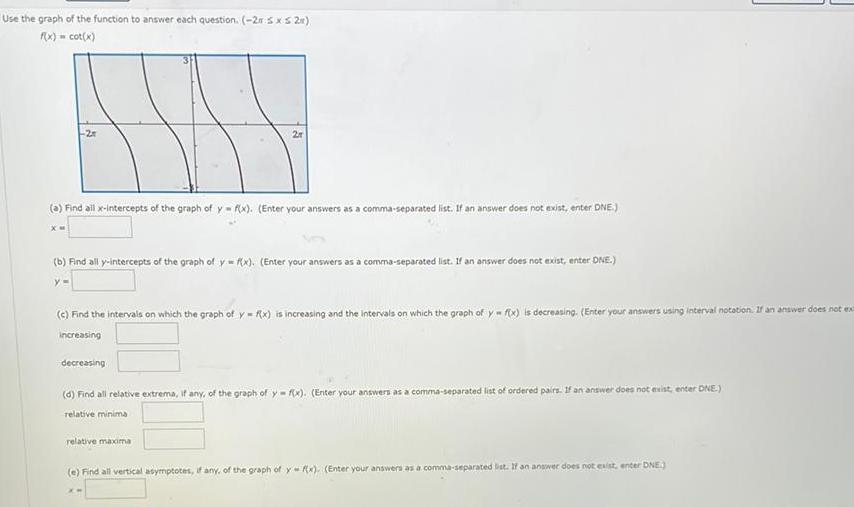
Calculus
Limits & ContinuityUse the graph of the function to answer each question 2r sxs 2x f x cot x a Find all x intercepts of the graph of y f x Enter your answers as a comma separated list If an answer does not exist enter DNE b Find all y intercepts of the graph of y f x Enter your answers as a comma separated list If an answer does not exist enter DNE c Find the intervals on which the graph of y f x is increasing and the intervals on which the graph of y f x is decreasing Enter your answers using interval notation If an answer does not ex increasing decreasing d Find all relative extrema if any of the graph of y f x Enter your answers as a comma separated list of ordered pairs If an answer does not exist enter DNE relative minima relative maxima e Find all vertical asymptotes if any of the graph of y f x Enter your answers as a comma separated list If an answer does not exist enter DNE

Calculus
Vector CalculusFind the point x y on the unit circle that corresponds to the real number t ST

Calculus
Application of derivativesThe circular blade on a saw has a diameter of 6 25 inches and rotates at 4600 revolutions per minute a Find the angular speed of the blade in radians per minute radians per minute b Find the linear speed of the saw teeth in inches per minute as they contact the wood being cut Round your answer to one decimal p inches per minute
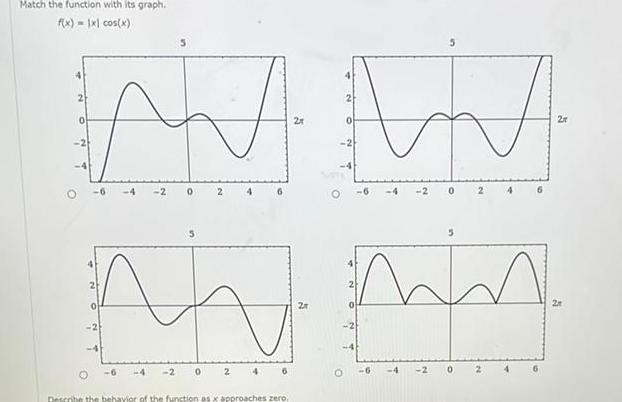
Calculus
Application of derivativesMatch the function with its graph f x x cos x 2 N M A mm 2 4 6 4 2 0 Describe the behavior of the function as x approaches zero 2r

Calculus
Definite IntegralsThe displacement from equilibrium of an oscillating weight suspended by a spring is given by Y t 1 cos 78 where y is the displacement in feet and it is the time in seconds see figure Find the displacement when tw0 t and t Round your answers to four decimal places 0 2 0 y Equilibrium 6 t 1 y Y O ft ft 0 ft At In 11 Maximum negative Maximum positive displacement displacement Simple Harmonic Motion Oft

Calculus
DifferentiationSketch the graph of the funciton Include two full periods Use a graphing utility to verify your result Choose the correct graph y csc J 10 20 10 20 UUU MENT 10 20

Calculus
Application of derivativesConstruct an appropriate triangle to complete the table 0 0s 90 050sn 2 Function e deg 0 rad Function Value sin

Calculus
Vector CalculusEvaluate if possible the sine cosine and tangent of the real number t If not possible enter IMPOSSIBLE 4 sin t cos t tan t
Calculus
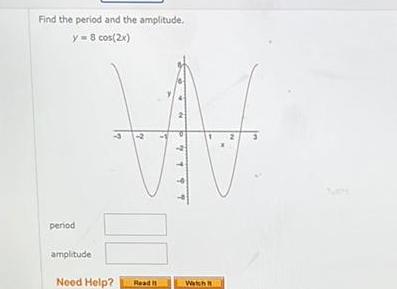
Application of derivativesFind the period and the amplitude y 8 cos 2x period amplitude 00 Need Help Read 2 Watch

Calculus
DifferentiationQuestion 1 15 points Find the general solution of the following differen equation on the indicated interval dy dt 2 cos t y tan t 0 t 2


Calculus
Application of derivativesFind the first partial derivatives of the following function 2u F u v w 3v 7w

Calculus
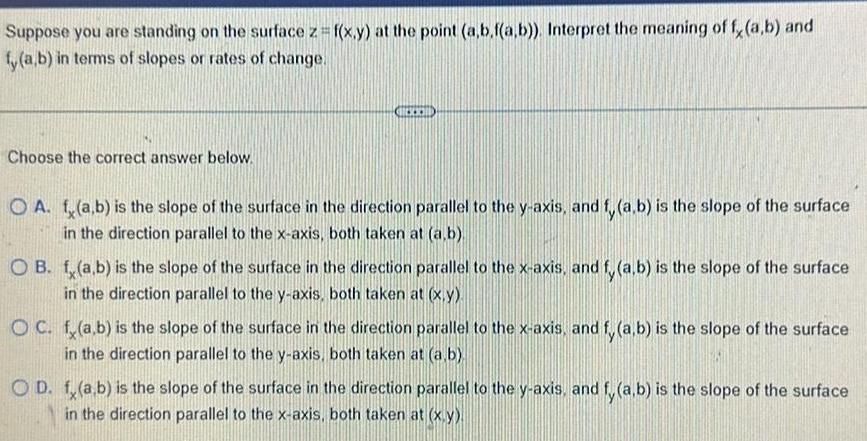
DifferentiationSuppose you are standing on the surface z f x y at the point a b f a b Interpret the meaning of f a b and fy a b in terms of slopes or rates of change Choose the correct answer below O A f a b is the slope of the surface in the direction parallel to the y axis and f a b is the slope of the surface in the direction parallel to the x axis both taken at a b OB f a b is the slope of the surface in the direction parallel to the x axis and fy a b is the slope of the surface in the direction parallel to the y axis both taken at x y OC f a b is the slope of the surface in the direction parallel to the x axis and fy a b is the slope of the surface in the direction parallel to the y axis both taken at a b OD f a b is the slope of the surface in the direction parallel to the y axis and fy a b is the slope of the surface in the direction parallel to the x axis both taken at x y

Calculus
Differential equations5 2 1 a 5 g x 9 7 C 7 b 145 y c 2 The continuous function g x is odd and increasing with selected values shown in the table above Find the values of a and b If the average rate of change of g x over the interval 1 5 is 2 find the value of c

Calculus
Application of derivativesQuestion 3 5 5 pts Find the absolute maximum and absolute minimum values of each of the following functions on the given intervals a f x 2x 3 5 on 3 4 b f x 2x 3x on 0 2

Calculus
Application of derivativestermine where the given function is concave up and where it is concave dc 7 f x x 9 x2 A Concave up on 3 0 concave down on 0 3 B Concave up on 0 concave down on 0 C Concave down on 3 0 concave up on 0 3 D Concave up on
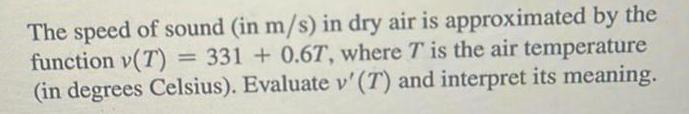
Calculus
DifferentiationThe speed of sound in m s in dry air is approximated by the function v T 331 0 67 where T is the air temperature in degrees Celsius Evaluate v T and interpret its meaning

Calculus
Application of derivativesd the absolute extreme values of the function on the interval 3 3 f x CSC X 75x5 37 2 A absolute maximum does not exist absolute minimum does not exist B absolute maximum is 0 at x 7 absolute minimum is 1 at x C absolute maximum is 1 at x t absolute minimum is 1 at x D absolute maximum is 1 at x t absolute minimum is 1 at x 0
Calculus
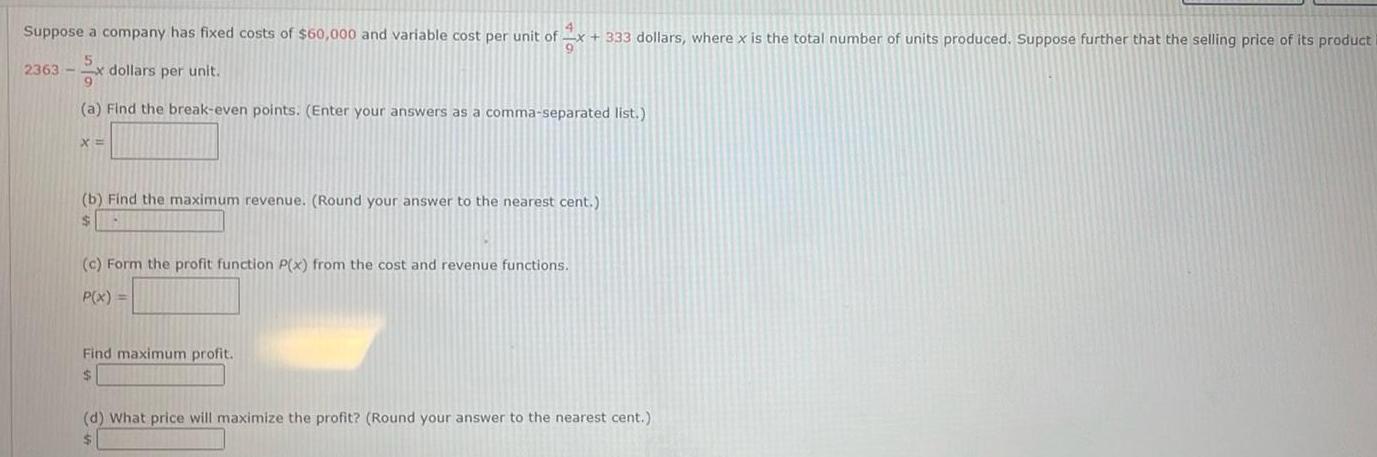
Application of derivatives4 Suppose a company has fixed costs of 60 000 and variable cost per unit of x 333 dollars where x is the total number of units produced Suppose further that the selling price 2363 dollars per unit a Find the break even points Enter your answers as a comma separated list X b Find the maximum revenue Round your answer to the nearest cent c Form the profit function P x from the cost and revenue functions P x Find maximum profit d What price will maximize the profit Round your answer to the nearest cent its product i
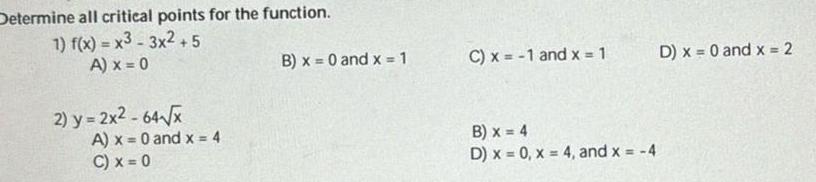
Calculus
Application of derivativesDetermine all critical points for the function 1 f x x3 3x2 5 A x 0 2 y 2x2 64 x A x 0 and x 4 C x 0 B x 0 and x 1 C x 1 and x 1 B x 4 D x 0 x 4 and x 4 D x 0 and x 2

Calculus
Limits & ContinuityLet f x arctan x The arctangent function and all of its derivatives are perfectly well behaved for every real value of x Use Maple to produce p x and p x when c 0 What is the interval of convergence Now repeat this problem using when c 4 What is the interval of convergence

Calculus
Application of derivatives3 Find an equation of the tangent line to the curve In a at the point 1 0
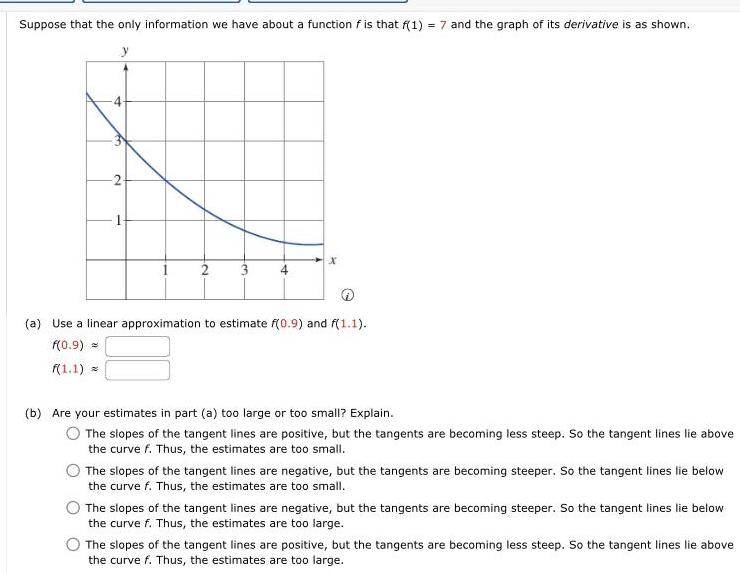
Calculus
Application of derivativesSuppose that the only information we have about a function f is that f 1 7 and the graph of its derivative is as shown fo 2 2 3 x a Use a linear approximation to estimate f 0 9 and f 1 1 f 0 9 f 1 1 b Are your estimates in part a too large or too small Explain The slopes of the tangent lines are positive but the tangents are becoming less steep So the tangent lines lie above the curve f Thus the estimates are too small The slopes of the tangent lines are negative but the tangents are becoming steeper So the tangent lines lie below the curve f Thus the estimates are too small The slopes of the tangent lines are negative but the tangents are becoming steeper So the tangent lines lie below the curve f Thus the estimates are too large The slopes of the tangent lines are positive but the tangents are becoming less steep So the tangent lines lie above the curve f Thus the estimates are too large
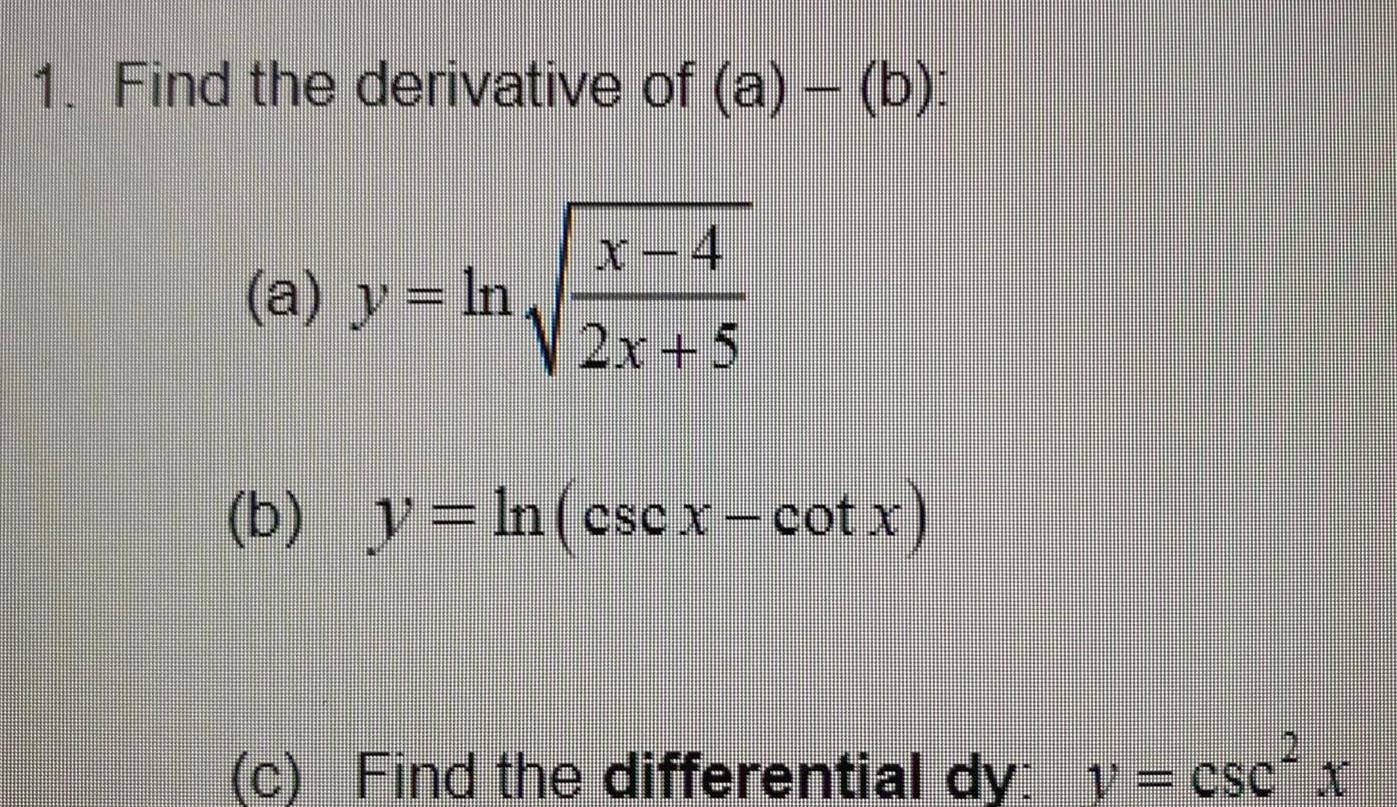
Calculus
Differentiation1 Find the derivative of a b a y ln x 4 2x 5 b y ln cscx cotx c Find the differential dy y csc x

Calculus
Limits & Continuity4 a It is well known that 1 converges to e Test a few values of k and assemble evidence to support this fact Submit this evidence with your lab report b Investigate the behavior of two related sequences 1 2 and 1 Discuss how the sequences differ in their behavior as n gets large n Vn
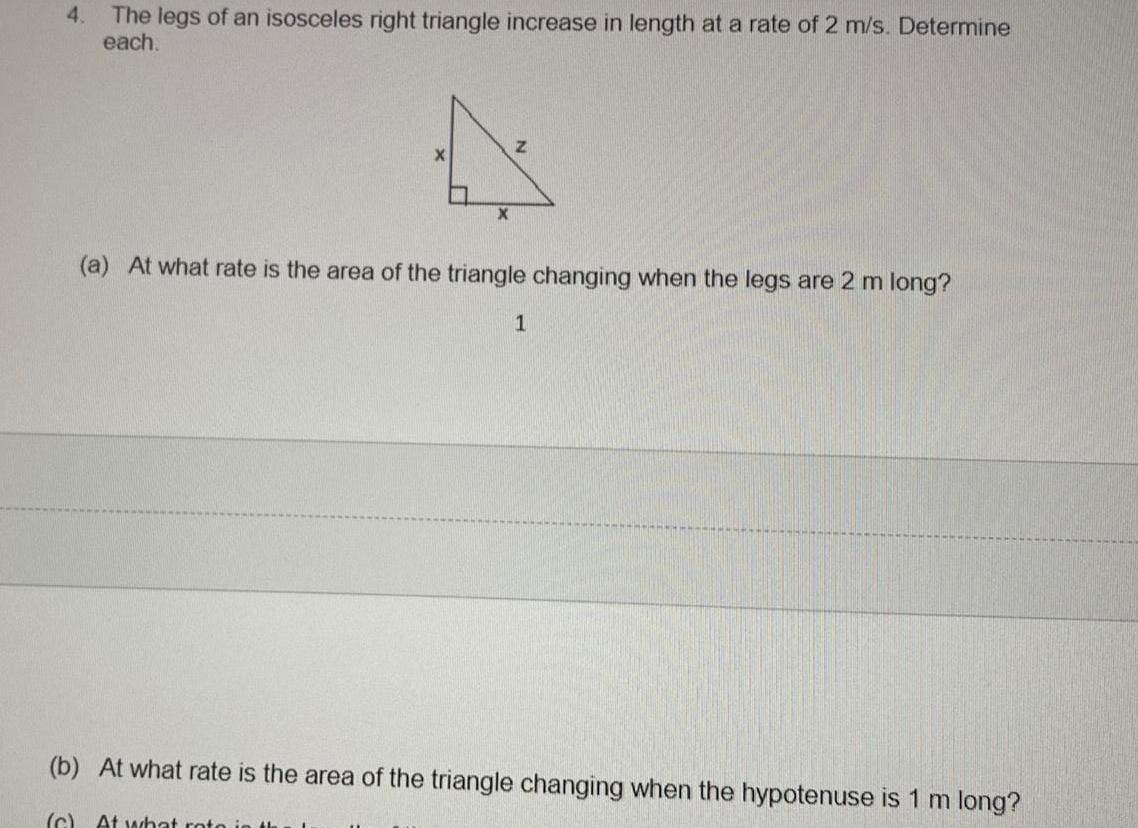
Calculus
Differentiation4 The legs of an isosceles right triangle increase in length at a rate of 2 m s Determine each X X Z a At what rate is the area of the triangle changing when the legs are 2 m long 1 b At what rate is the area of the triangle changing when the hypotenuse is 1 m long c At what rot

Calculus
Application of derivatives2 A ball is thrown vertically upward with a velocity of 80 ft s then its height after t seconds is s 80t 16t a What is the maximum height reached by the ball b What is the velocity of the ball when it is 96 ft above the ground on its way up On its way down

Calculus
Application of derivativesCompute Ay and dy for the given values of x and dx Ax y x 6x x 5 Ax 0 5 Ay dy Sketch a diagram showing the line segments with lengths dx dy and Av

Calculus
Application of derivativesThe circumference of a sphere was measured to be 74 cm with a possible error of 0 5 cm a Use differentials to estimate the maximum error in cm in the calculated surface area Round your answer to the nearest integer cm What is the relative error Round your answer to three decimal places b Use differentials to estimate the maximum error in cm in the calculated volume Round your answer to the nearest integer cm 3 What is the relative error Round your answer to three decimal places
Calculus
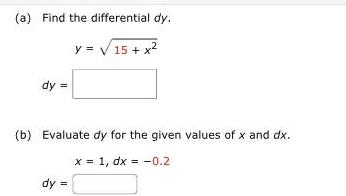
Application of derivativesa Find the differential dy y 15 x dy b Evaluate dy for the given values of x and dx x 1 dx 0 2 dy

Calculus
Application of derivativesThe radius of a circular disk is given as 28 cm with a maximum error in measurement of 0 2 cm a Use differentials to estimate the maximum error in cm in the calculated area of the disk Round your answer to tw decimal places cm b What is the relative error Round your answer to four decimal places What is the percentage error Round your answer to two decimal places
Calculus
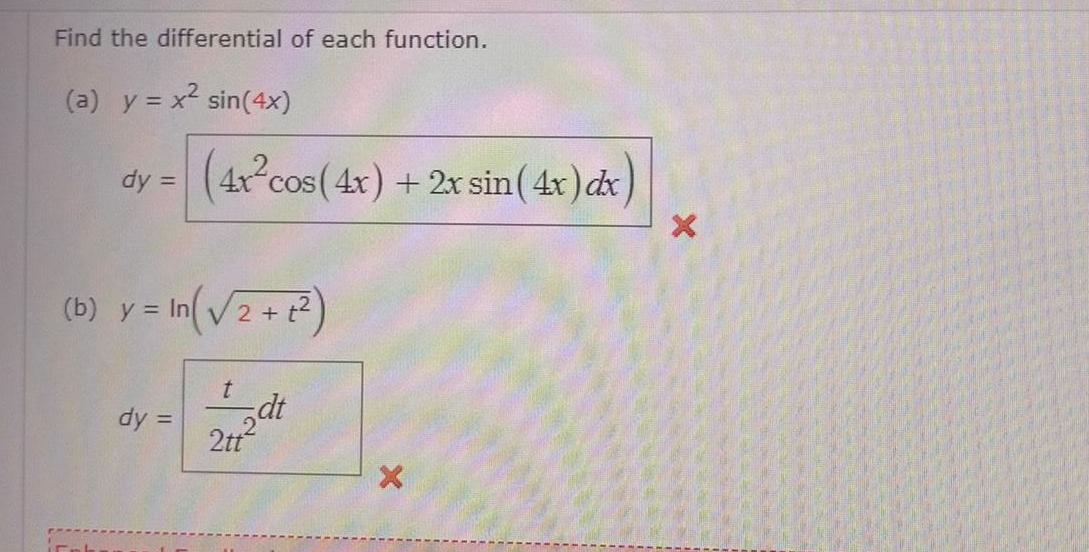
DifferentiationFind the differential of each function a y x sin 4x dy 4x cos 4x 2x sin 4x dx b y In 2 1 dy t 2dt 2tt X