Geometry Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.




Geometry
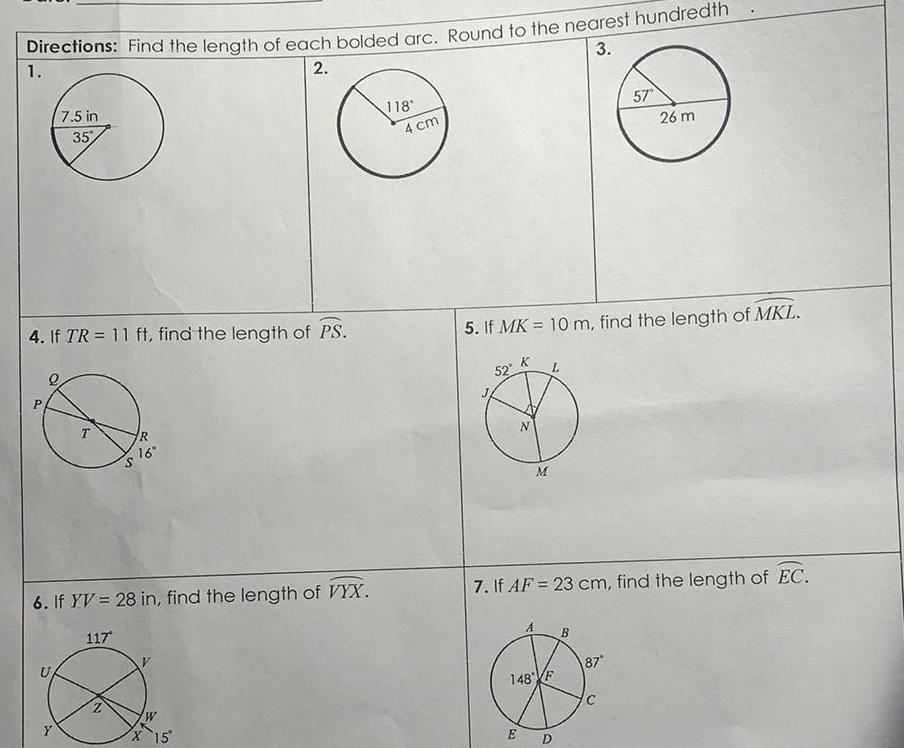
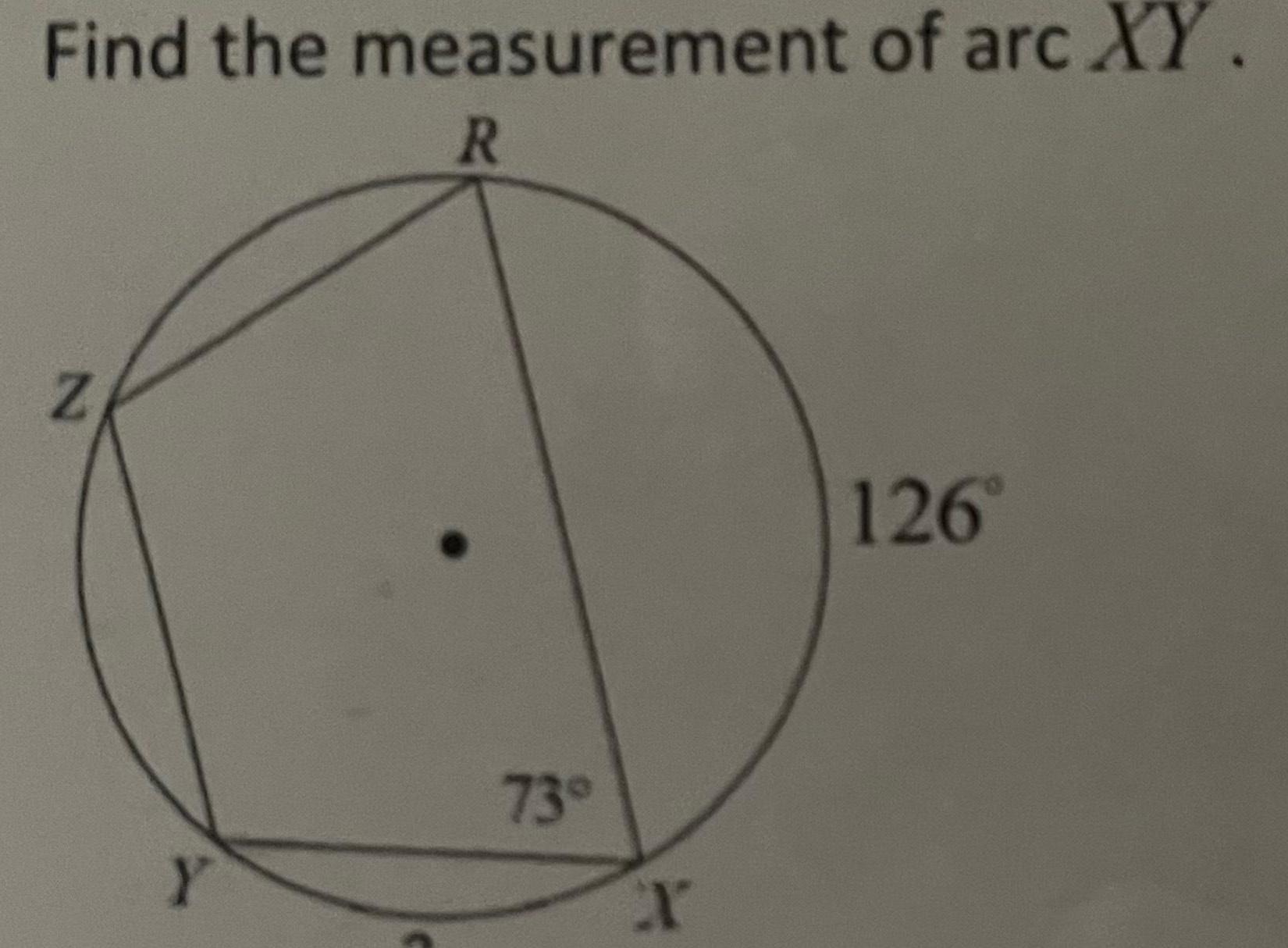
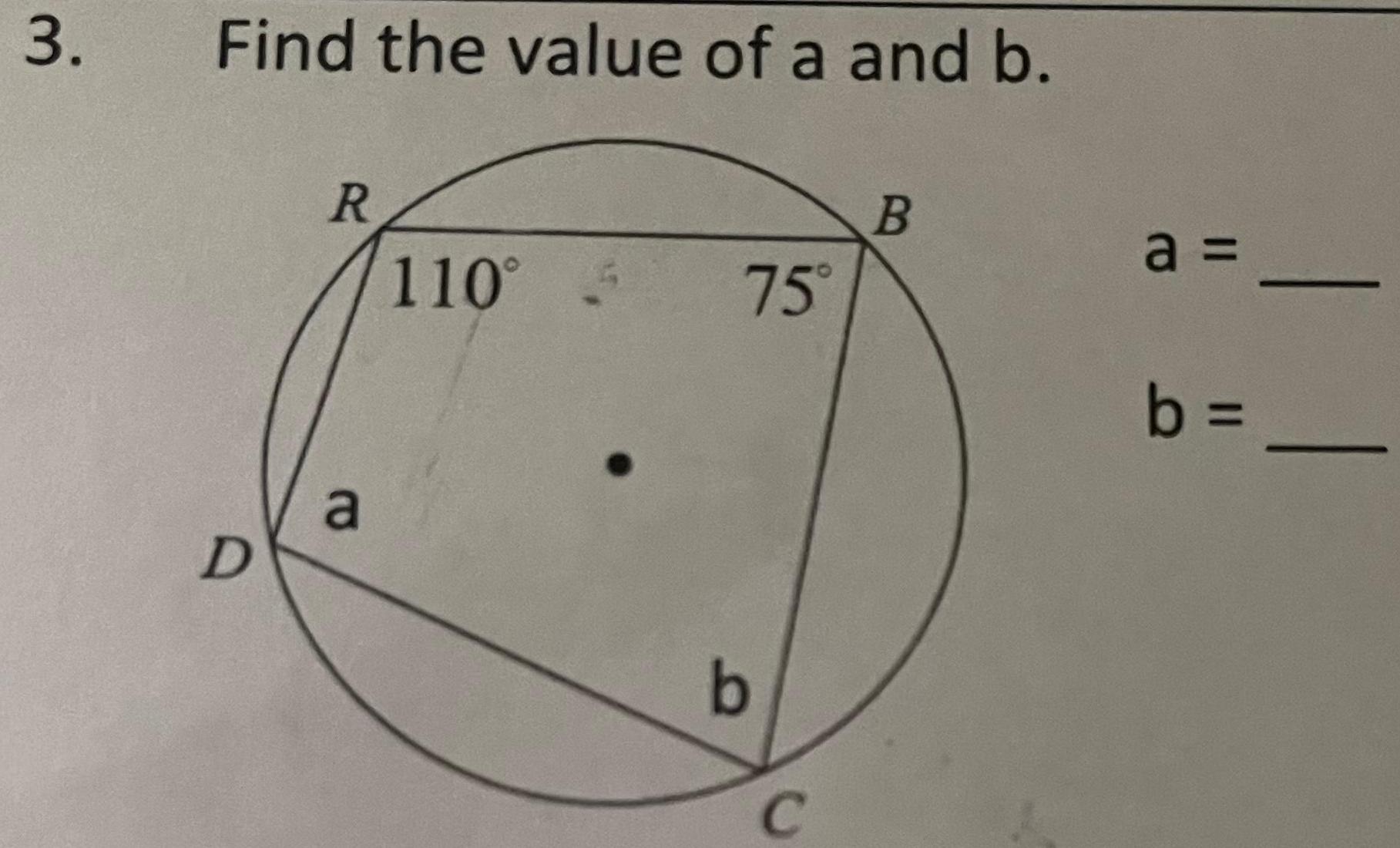
2D Geometry3 Directions Find the length of each bolded arc Round to the nearest hundredth 1 2 4 If TR 11 ft find the length of PS P 7 5 in 35 S T R 16 6 If YV 28 in find the length of VYX 117 12 W X 15 118 4 cm 52 5 If MK 10 m find the length of MKL M 148 F E 7 If AF 23 cm find the length of EC 57 D 26 m 87
Geometry
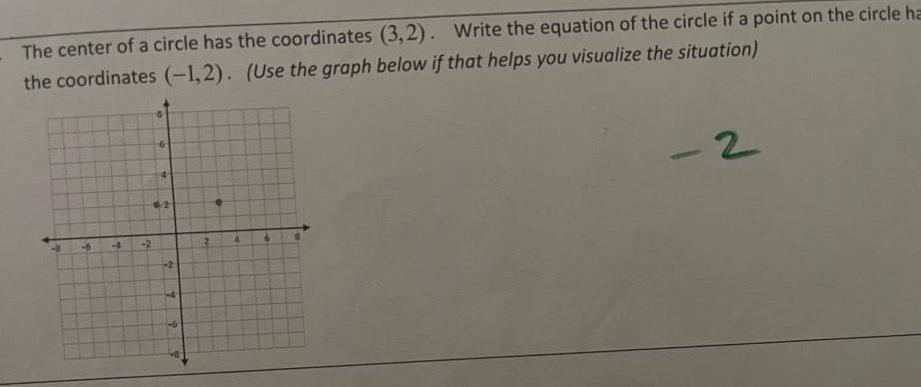
2D GeometryThe center of a circle has the coordinates 3 2 Write the equation of the circle if a point on the circle ha the coordinates 1 2 Use the graph below if that helps you visualize the situation 4 2 6 S B 2 4 P 6 2 4 6 2
Geometry
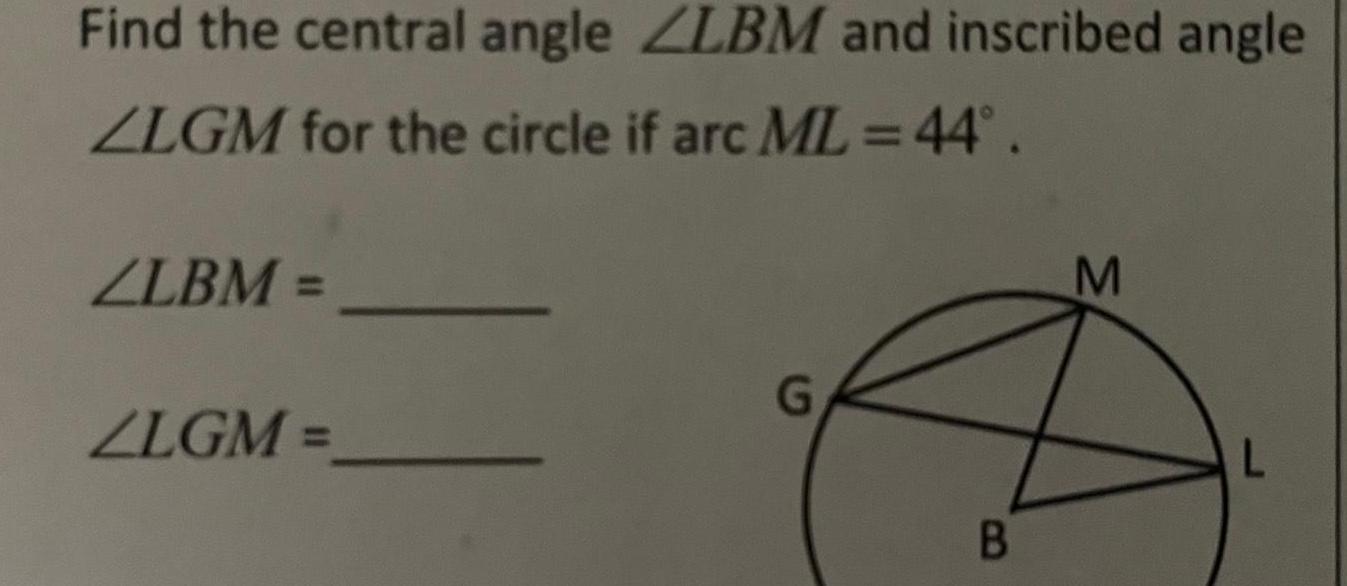
2D GeometryFind the central angle ZLBM and inscribed angle ZLGM for the circle if arc ML 44 ZLBM ZLGM G B M L

Geometry
AreaWhat is the approximate arc length in a circle with radius of 31 4 inches and arc measure of 82 Round both answers to 1 decimal place 1 31 40 82 7 S re Y 31 4 32 14 3 Approx 180 180
Geometry
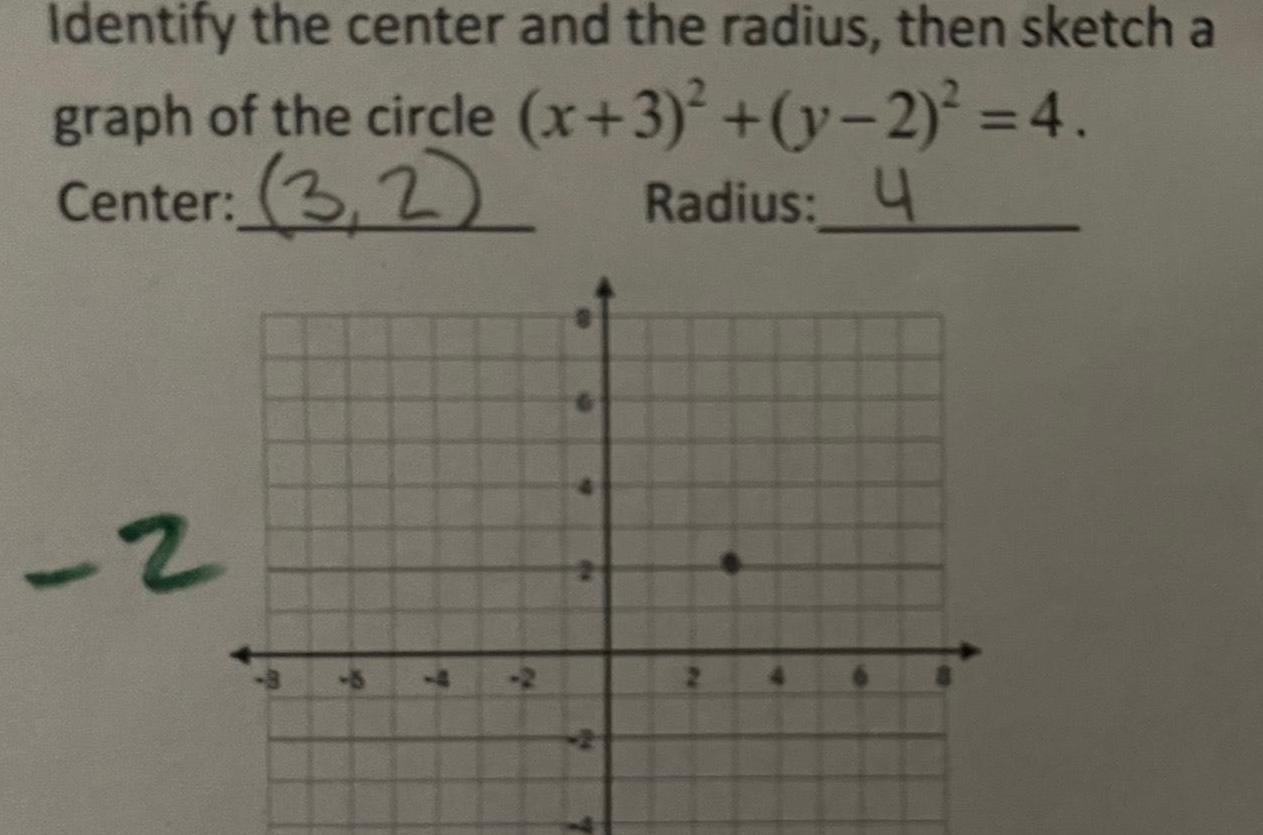
Heights & DistancesIdentify the center and the radius then sketch a graph of the circle Center 3 2 2 190 7 x 3 y 2 4 Radius 4 24
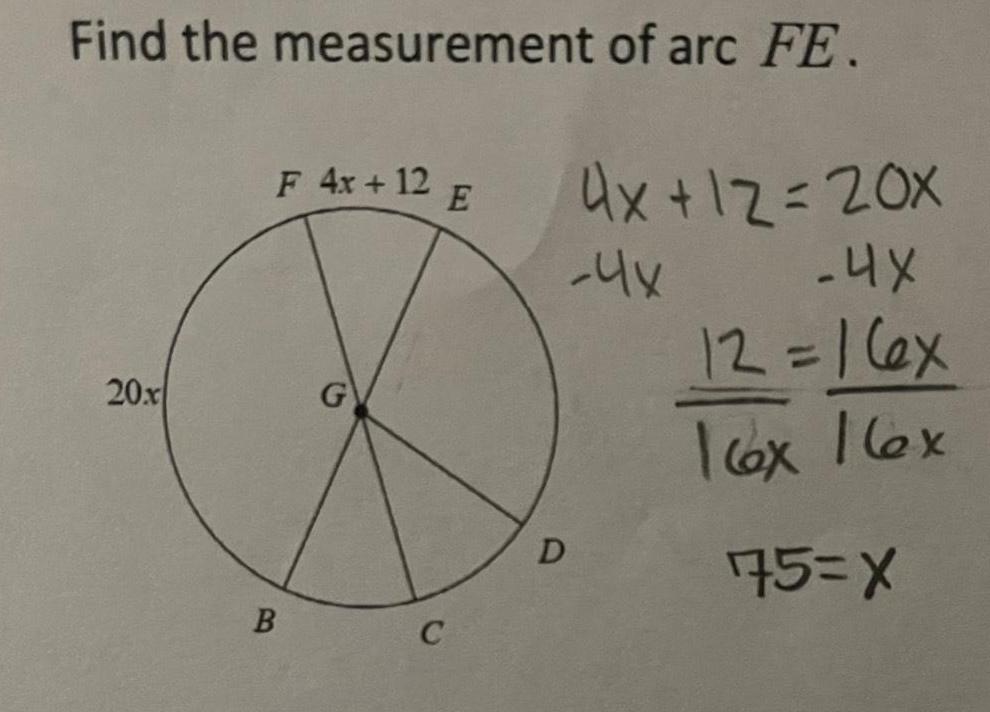
Geometry
AreaFind the measurement of arc FE 20x F 4x 12 E B G C 4x 12 20X 4X 12 16x 16x 16x 75 X 4x D
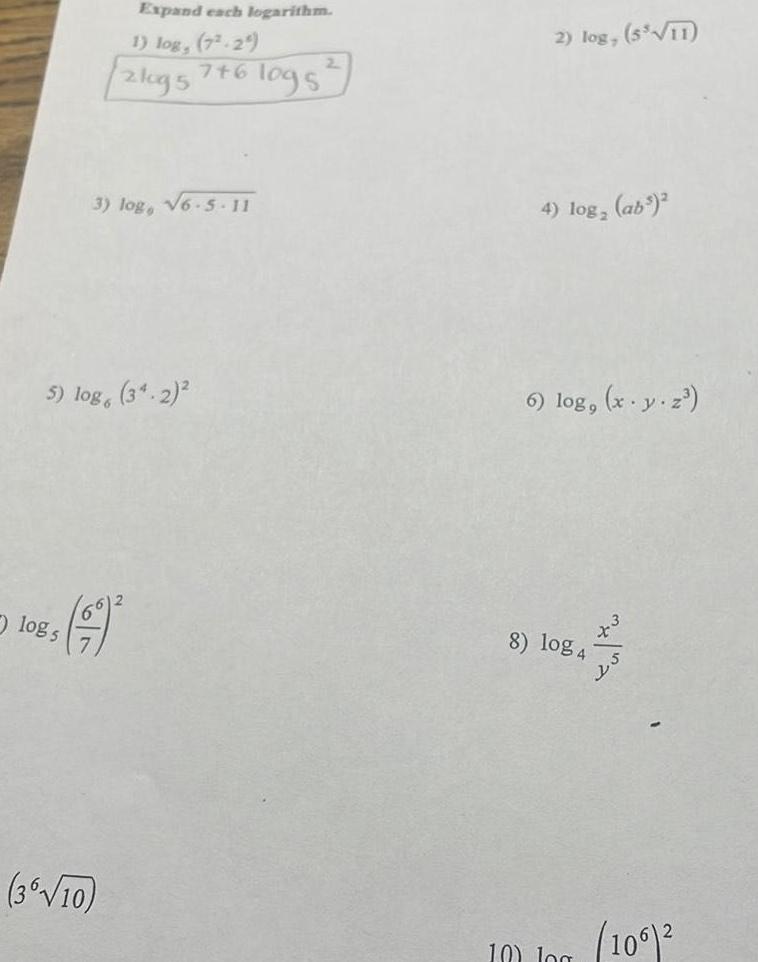
Geometry
Heights & Distanceslogs Expand each logarithm 1 log 7 2 2log 5 5 log 34 2 85 99 3 log 6 5 11 3 10 7 6 logs 2 2 log 5 11 4 log 3 ab 6 log x y z 8 log 4 10 Jog 106 2
Geometry
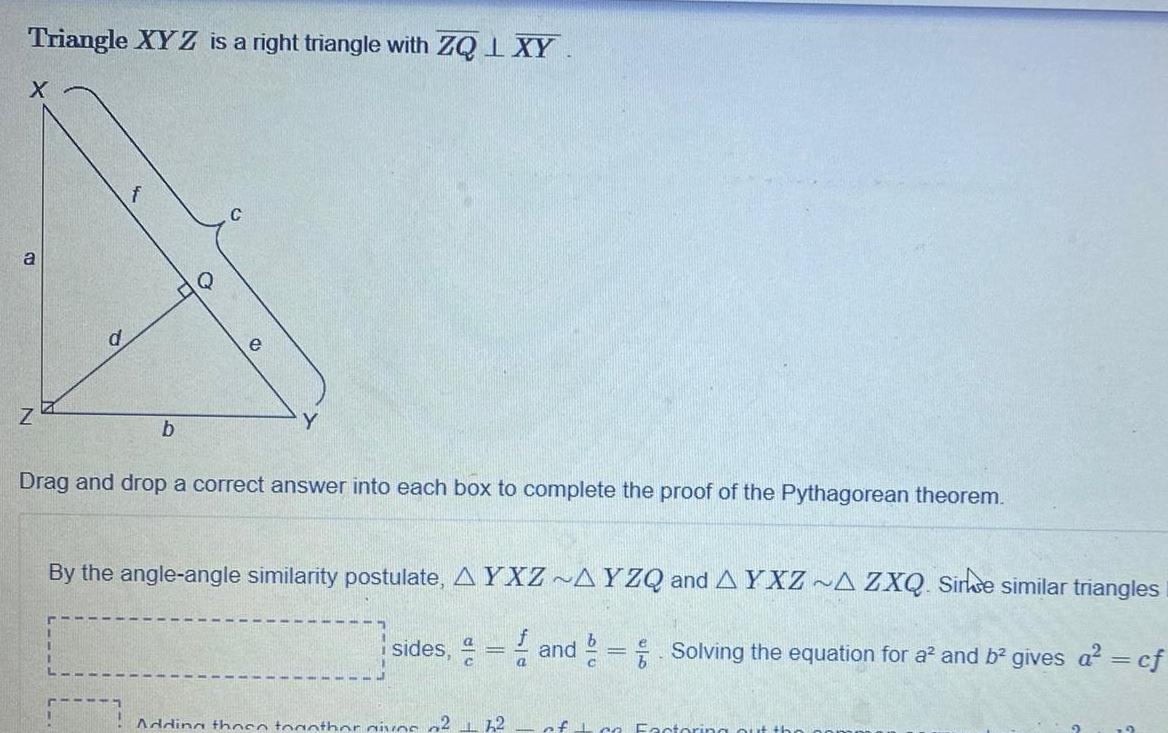
2D GeometryTriangle XYZ is a right triangle with ZQ L XY X a Z b Q Drag and drop a correct answer into each box to complete the proof of the Pythagorean theorem By the angle angle similarity postulate AYXZ AYZQ and AYXZ A ZXQ Sirke similar triangles b sides and Solving the equation for a and b gives a cf Adding those together gives of 2 12 a of co Factoring o
Geometry
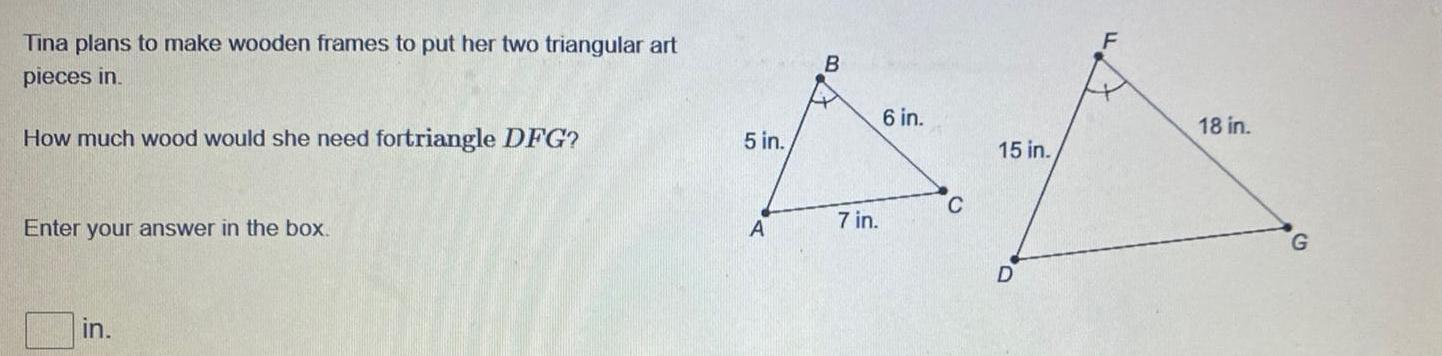
2D GeometryTina plans to make wooden frames to put her two triangular art pieces in How much wood would she need fortriangle DFG Enter your answer in the box in 5 in A B 7 in 6 in C 15 in D 427 F 18 in G
Geometry
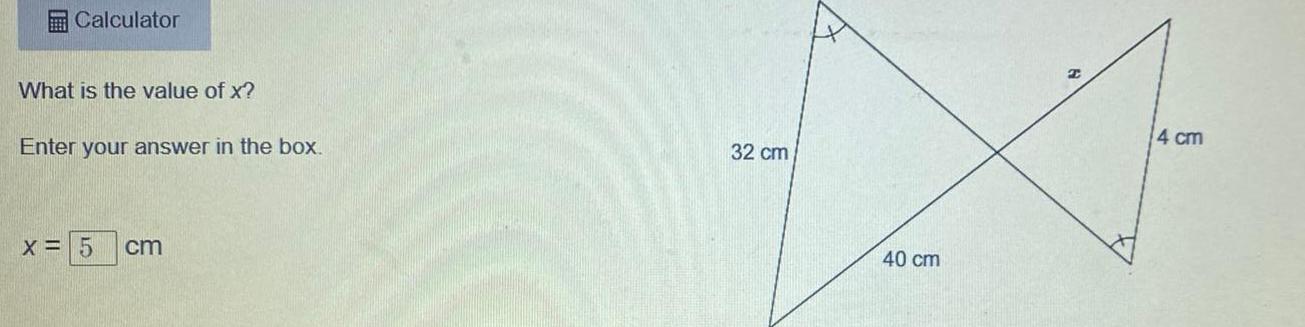
AreaCalculator What is the value of x Enter your answer in the box X 5 cm 32 cm 40 cm 2 4 cm
Geometry
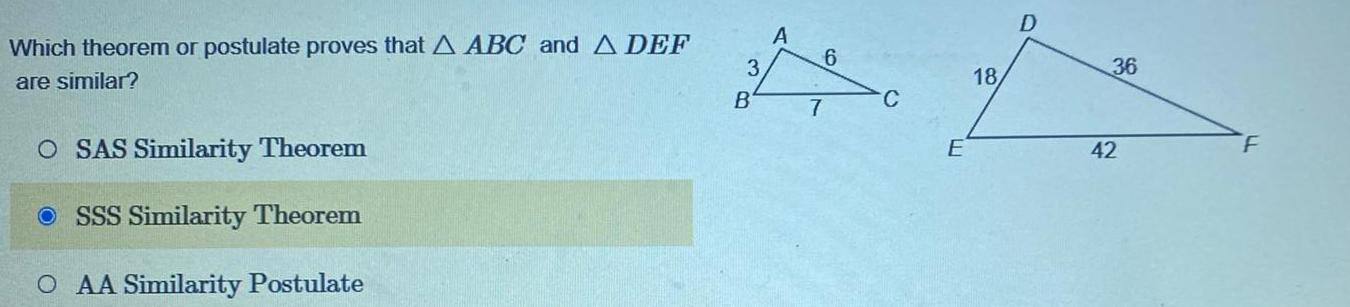
2D GeometryWhich theorem or postulate proves that A ABC and A DEF are similar O SAS Similarity Theorem SSS Similarity Theorem O AA Similarity Postulate 3 B A 7 6 C E 18 D 36 42

Geometry
2D GeometryUse the figure for Questions 3 and 4 3 What is m42 A 50 B 70 4 What is m24 F 10 G 60 C 110 H 100 D 120 J 120 70 40
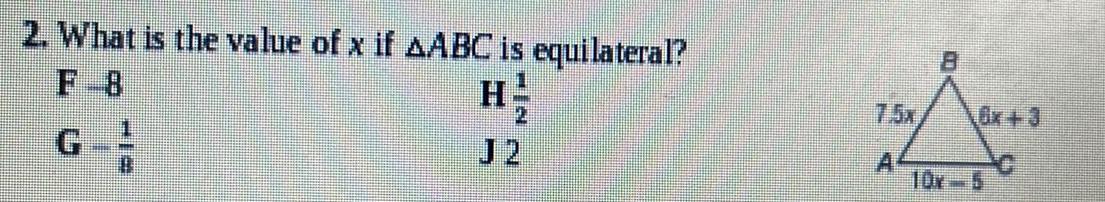
Geometry
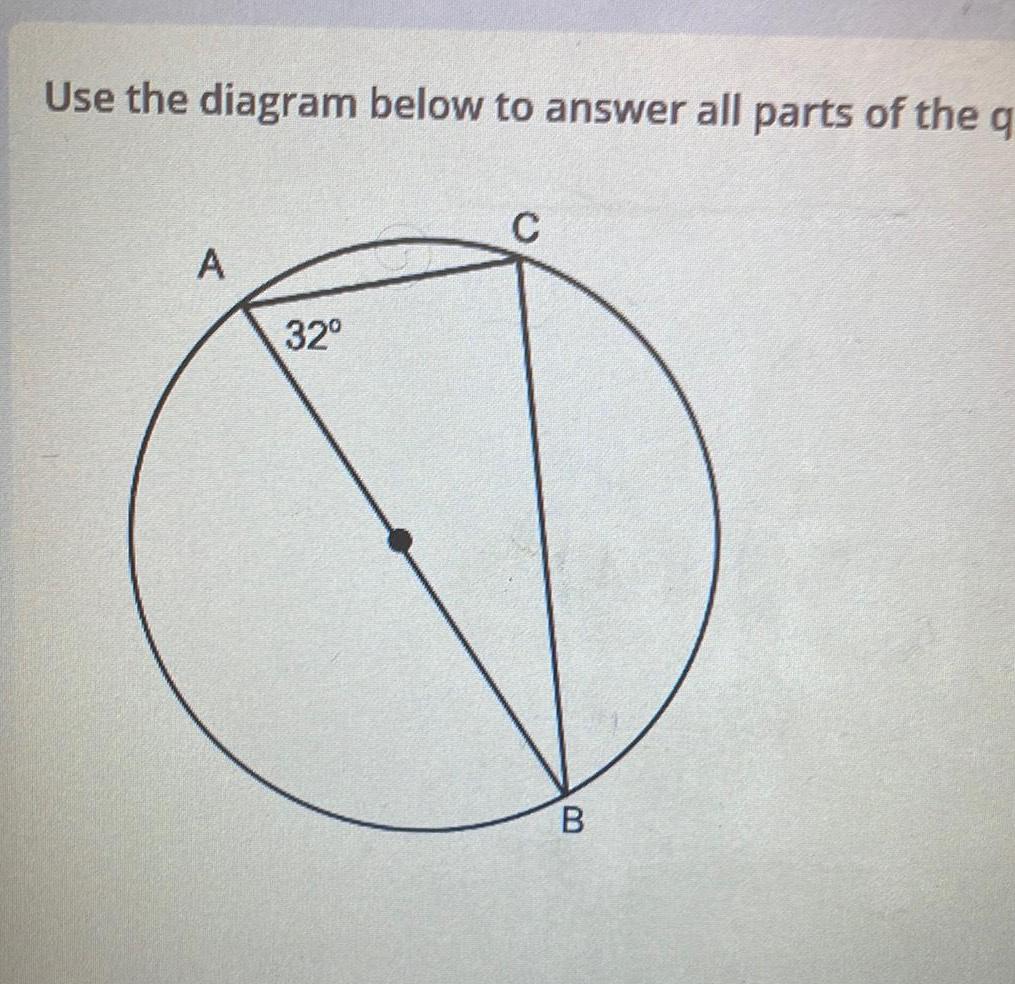
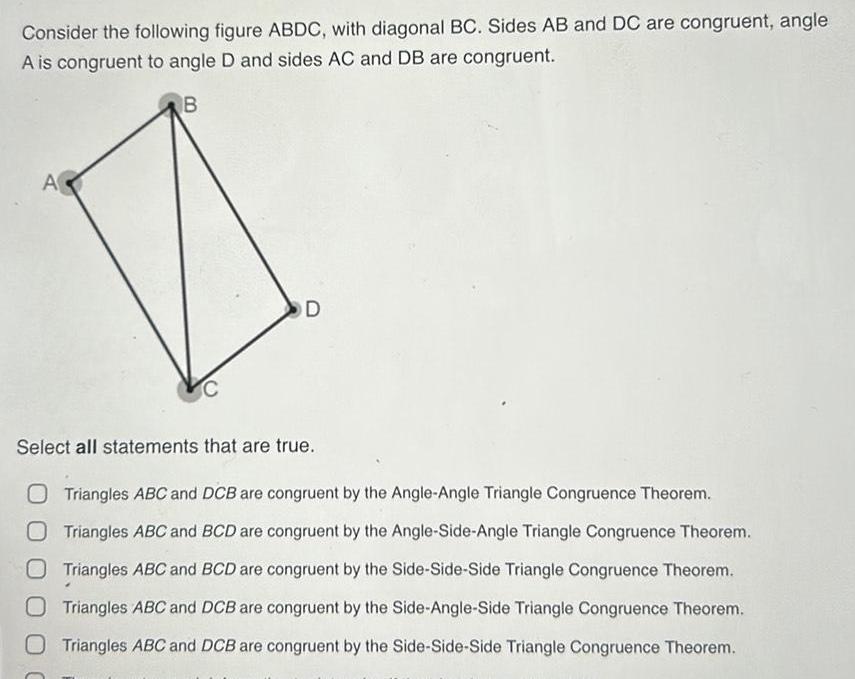
2D GeometryConsider the following figure ABDC with diagonal BC Sides AB and DC are congruent angle A is congruent to angle D and sides AC and DB are congruent B A C D Select all statements that are true O Triangles ABC and DCB are congruent by the Angle Angle Triangle Congruence Theorem O Triangles ABC and BCD are congruent by the Angle Side Angle Triangle Congruence Theorem Triangles ABC and BCD are congruent by the Side Side Side Triangle Congruence Theorem O Triangles ABC and DCB are congruent by the Side Angle Side Triangle Congruence Theorem O Triangles ABC and DCB are congruent by the Side Side Side Triangle Congruence Theorem
Geometry
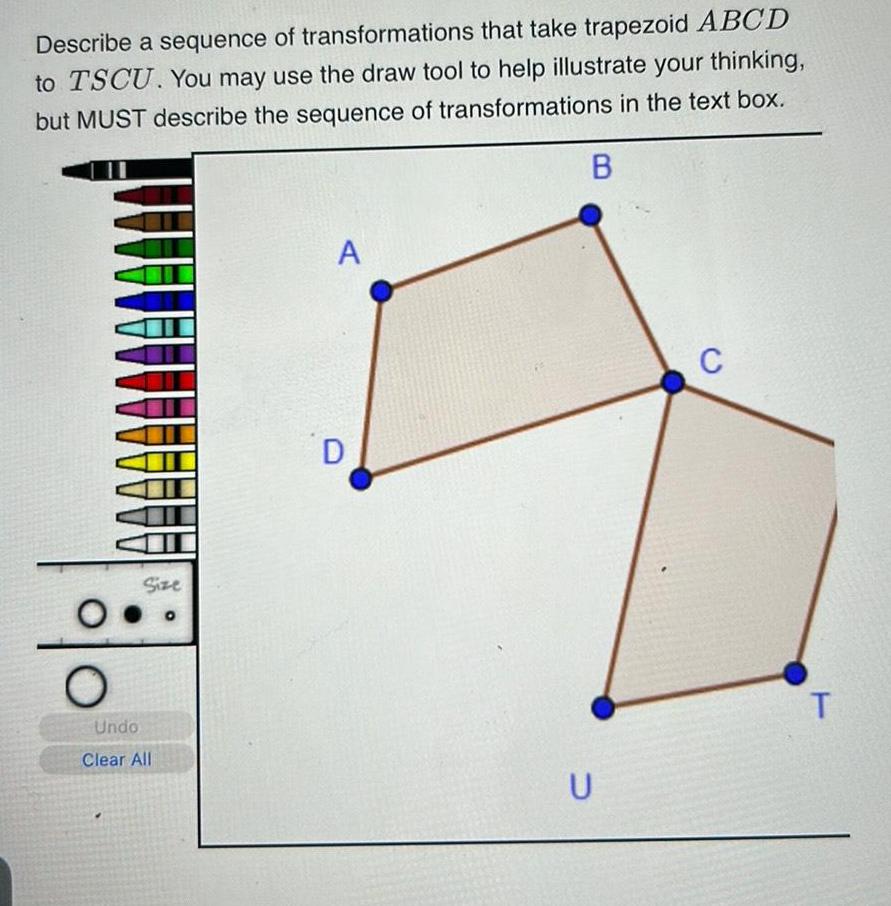
Coordinate systemDescribe a sequence of transformations that take trapezoid ABCD to TSCU You may use the draw tool to help illustrate your thinking but MUST describe the sequence of transformations in the text box B O Size Undo Clear All A D U C T

Geometry
2D GeometryLine m is represented by the equation y 1 represent lines perpendicular to line m 0 y 3x 1 3 O y 2 Oy 1 2 3 O y 1 x 5 2 3x 1 0 y 2 2 1 Oy y 3 3 2 x 1 Select all equations that 3
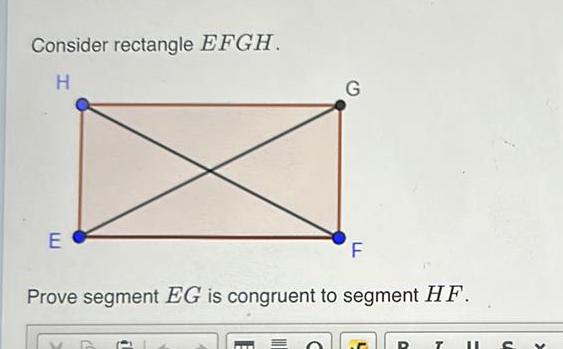
Geometry
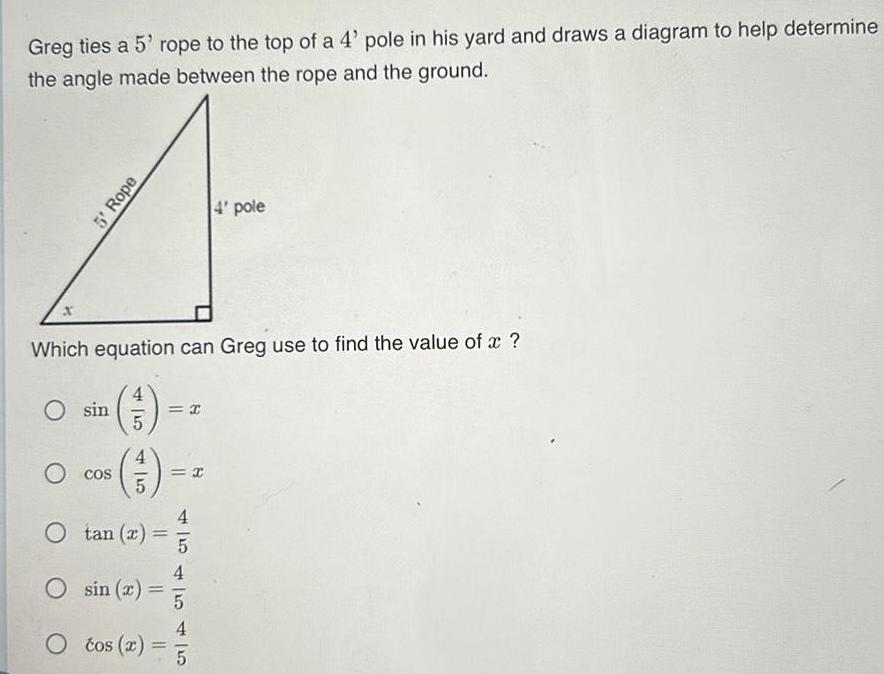
2D GeometryGreg ties a 5 rope to the top of a 4 pole in his yard and draws a diagram to help determine the angle made between the rope and the ground O sin 5 Rope Which equation can Greg use to find the value of x 3 5 O cos 45 4 5 x 4 pole O tan x 4 O sin r 5 4 O tos x 5
Geometry
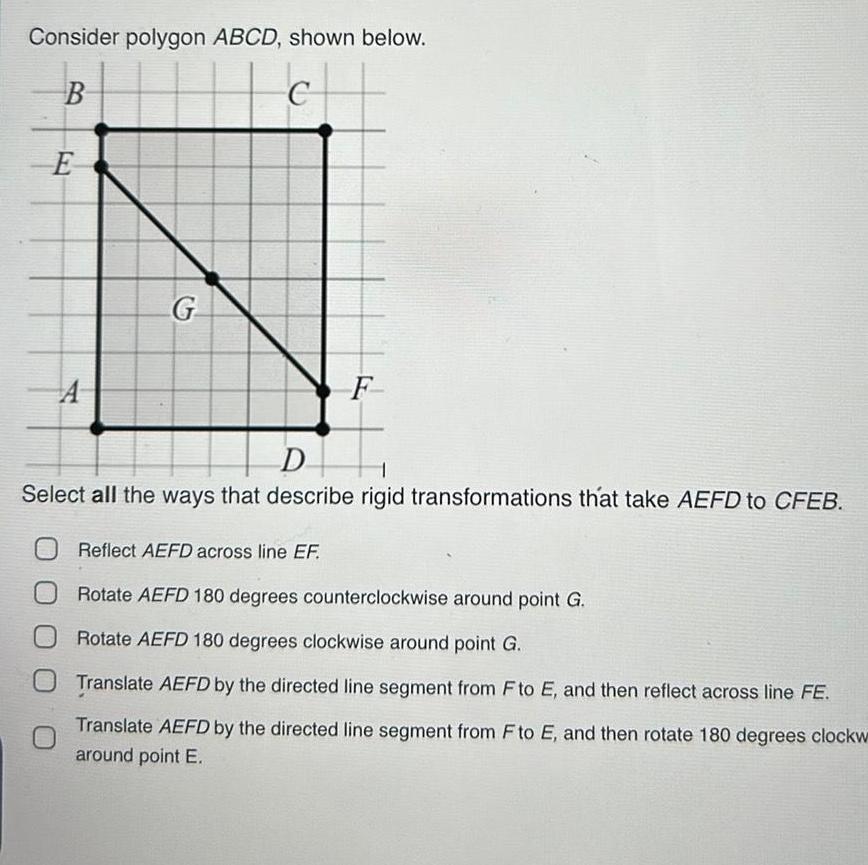
2D GeometryConsider polygon ABCD shown below B c E A G F D Select all the ways that describe rigid transformations that take AEFD to CFEB Reflect AEFD across line EF Rotate AEFD 180 degrees counterclockwise around point G Rotate AEFD 180 degrees clockwise around point G O Translate AEFD by the directed line segment from F to E and then reflect across line FE Translate AEFD by the directed line segment from F to E and then rotate 180 degrees clockw around point E

Geometry
2D Geometry10 The translation x y x 10 y 6 is applied to AABC to create a new image M B C Graph AA B C on the coordinate plane C 10 9 6 9 11 ARST is reflected across the line y x to form ARST Find the coordinates of the points R S and T
Geometry
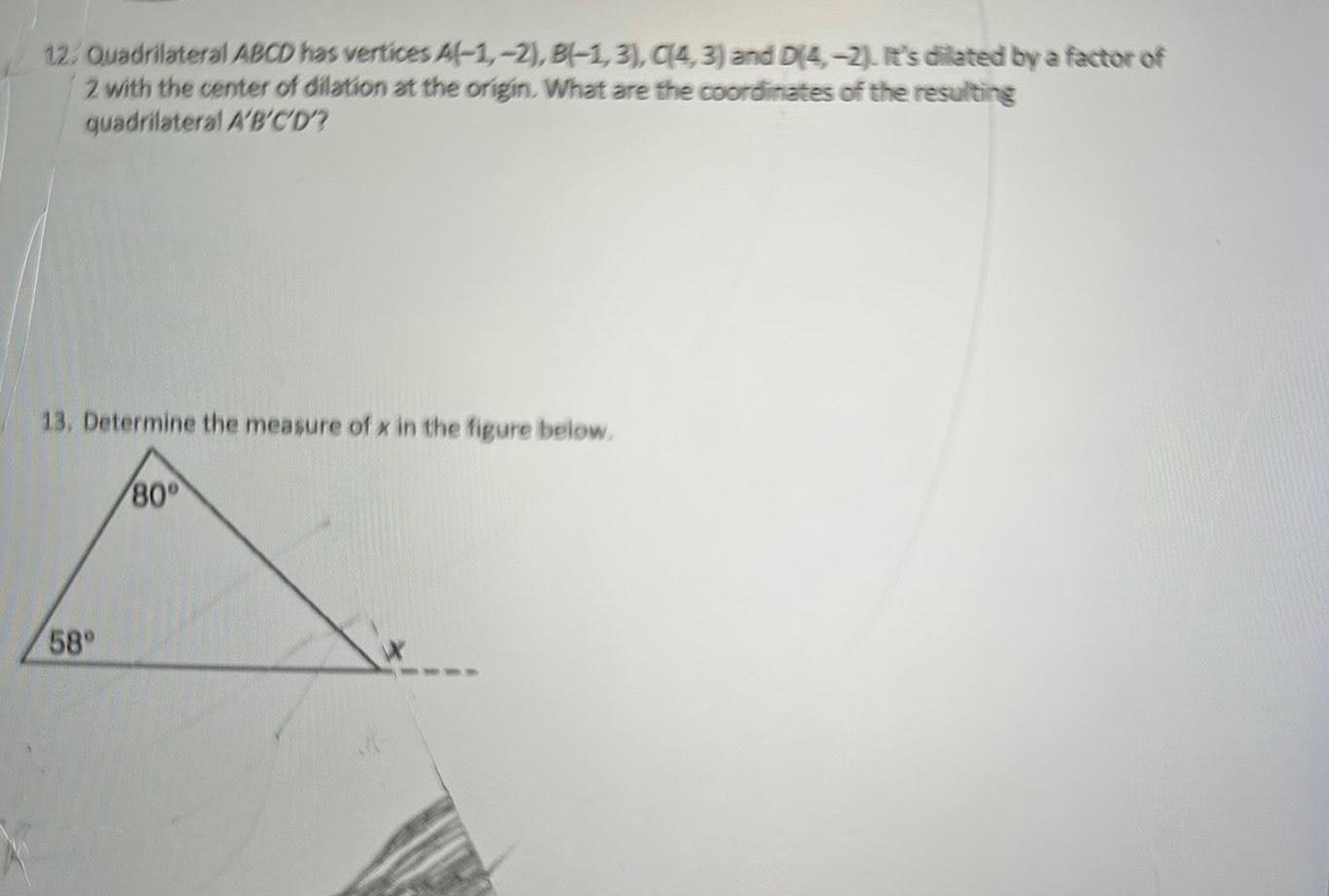
2D Geometry12 Quadrilateral ABCD has vertices A 1 2 B 1 3 C 4 3 and D 4 2 It s dilated by a factor of 2 with the center of dilation at the origin What are the coordinates of the resulting quadrilateral A B C D 13 Determine the measure of x in the figure below 58 80

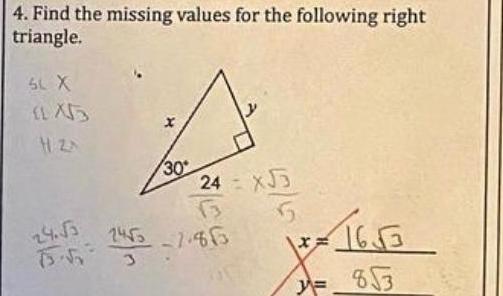
Geometry
Solution of triangles4 Find the missing values for the following right triangle SL X H ZA 24 3 30 24 x 3 63 5 1455 2453 7 853 16 3 853 x F

Geometry
AreaFind the volume V of the described solid S The base of S is the region enclosed by the parabola y 6 x and the x axis Cros perpendicular to the x axis are squares

Geometry
3D Geometry3 You work for a company that makes toy marbles The radius of the most popular marble is 0 3 inches The volume of a marble is given by the formula V where 3 14 ch out of every d a Rounded to the nearest tenth of a cubic inch what is the volume of glass needed to make one of the most popular marbles b What volume of glass is needed to make 105 marbles

Geometry
2D GeometrySolve problems involving the of a circle central angle circumference Solve problems involving Words to Know Write the letter of the definition next to the matching word as you work through the lesson You may use the glossary to help you arc length radian Define measure A a standard unit of measure for angles the measure of a central angle that subtends an arc that is equal in length to the radius of the circle B an angle whose vertex is at the center of a circle and whose sides are radii of that circle BOK C a portion of the circumference of a circle MAGNE AMOR ARRICANE D the distance around a circle

Geometry
2D GeometryCircumference of a Circle The circumference of any circle or the distance around the circle can be determined using either of these formulas 2 m r radius C md d Applying Circumference The London Eye is a Ferris wheel that at its highest point stands 135 meters tall The diameter of the London Eye is 120 meters A person rides the wheel two full revolutions How far has the person traveled Calculate the circumference Use the button on your calculator C nd C C 377 m Find the distance in two full revolutions 377 2 F O m
Geometry
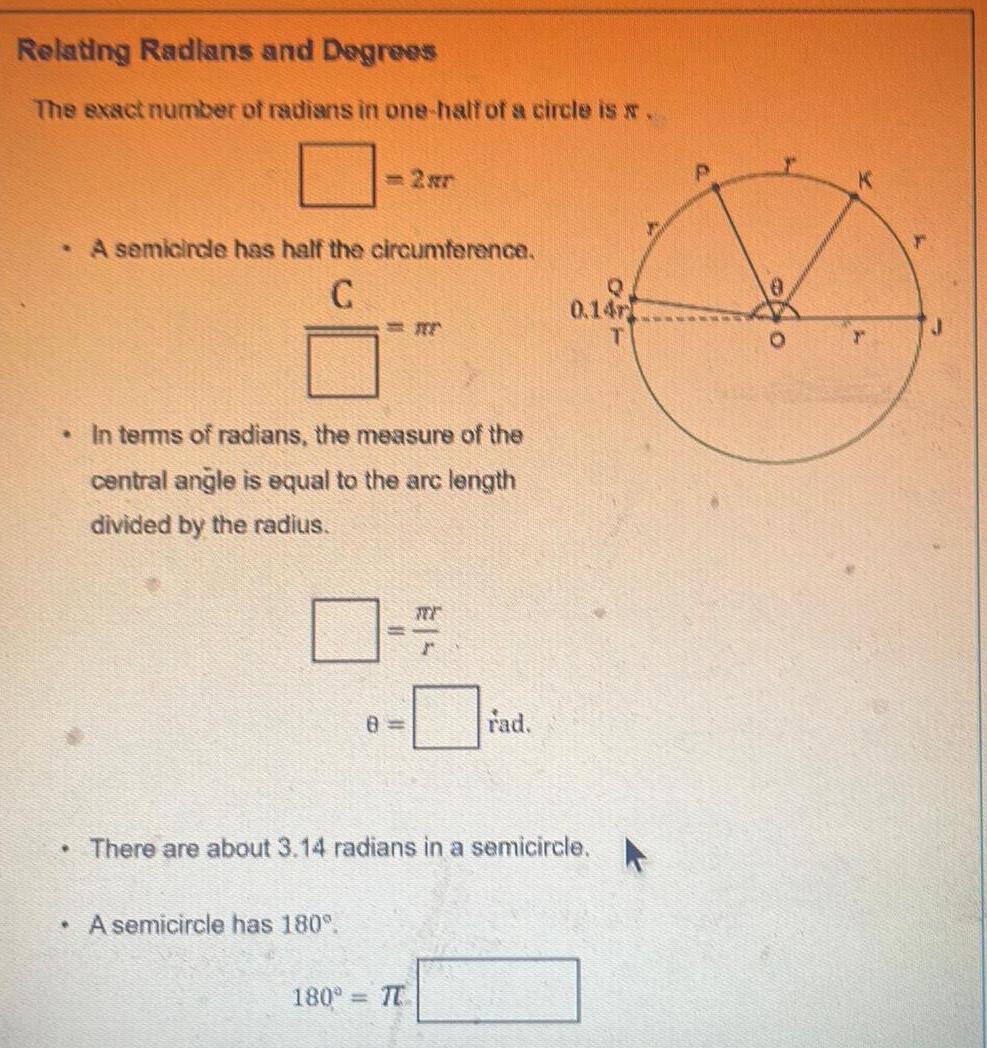
AreaRelating Radlans and Degrees The exact number of radians in one half of a circle is w A semicircle has half the circumference C In terms of radians the measure of the central angle is equal to the arc length divided by the radius 8 A semicircle has 180 E 180 T rad There are about 3 14 radians in a semicircle 0 14r
Geometry
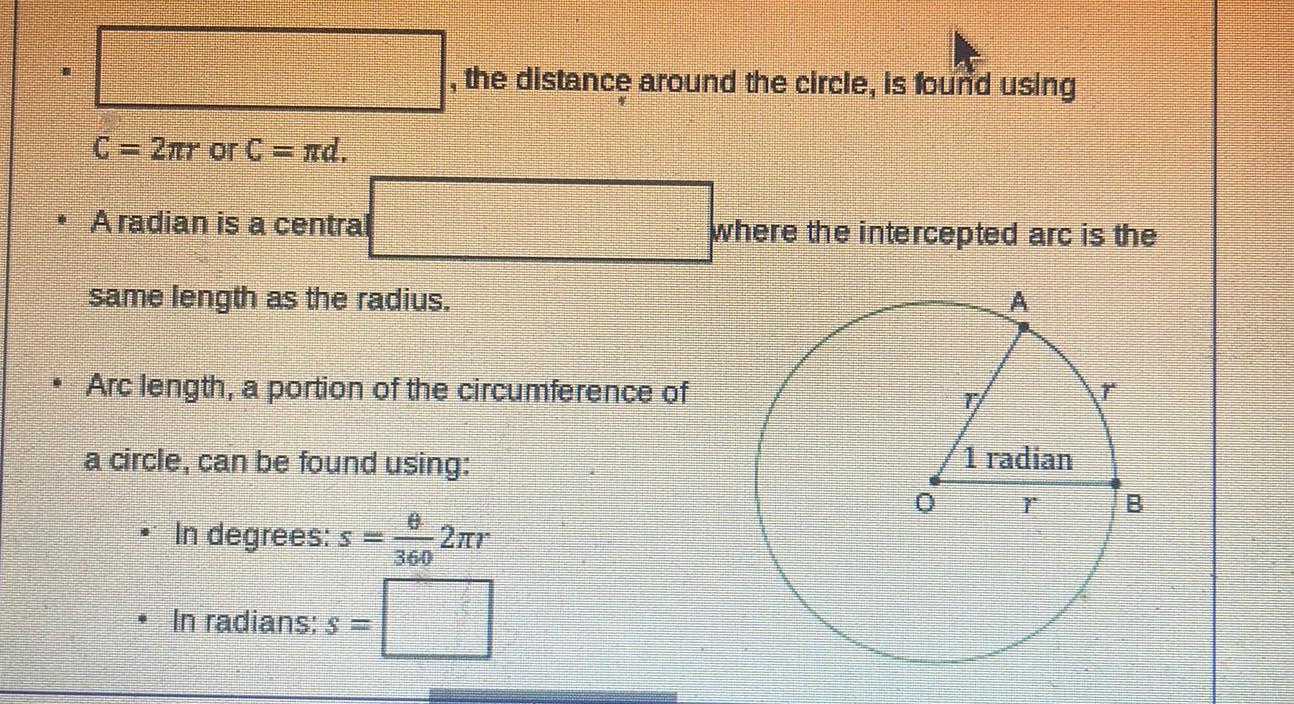
AreaC 2mr or C nd A radian is a central same length as the radius In degrees s Arc length a portion of the circumference of a circle can be found using In radians the distance around the circle is found using where the intercepted arc is the 1 radian r ww

Geometry
2D GeometryArc Length Arc length s is a c 2 C C 10m Use 3 14 as an approximation for this is of the whole circle 4 For any arc length s of the circumference of a circle S SA S A circle has 360 This arc has a central angle of 90 That means that 8 360 2 r 31 4 A where 8 is the central angle and r is the radius of the circle O 90 5 S B
Geometry
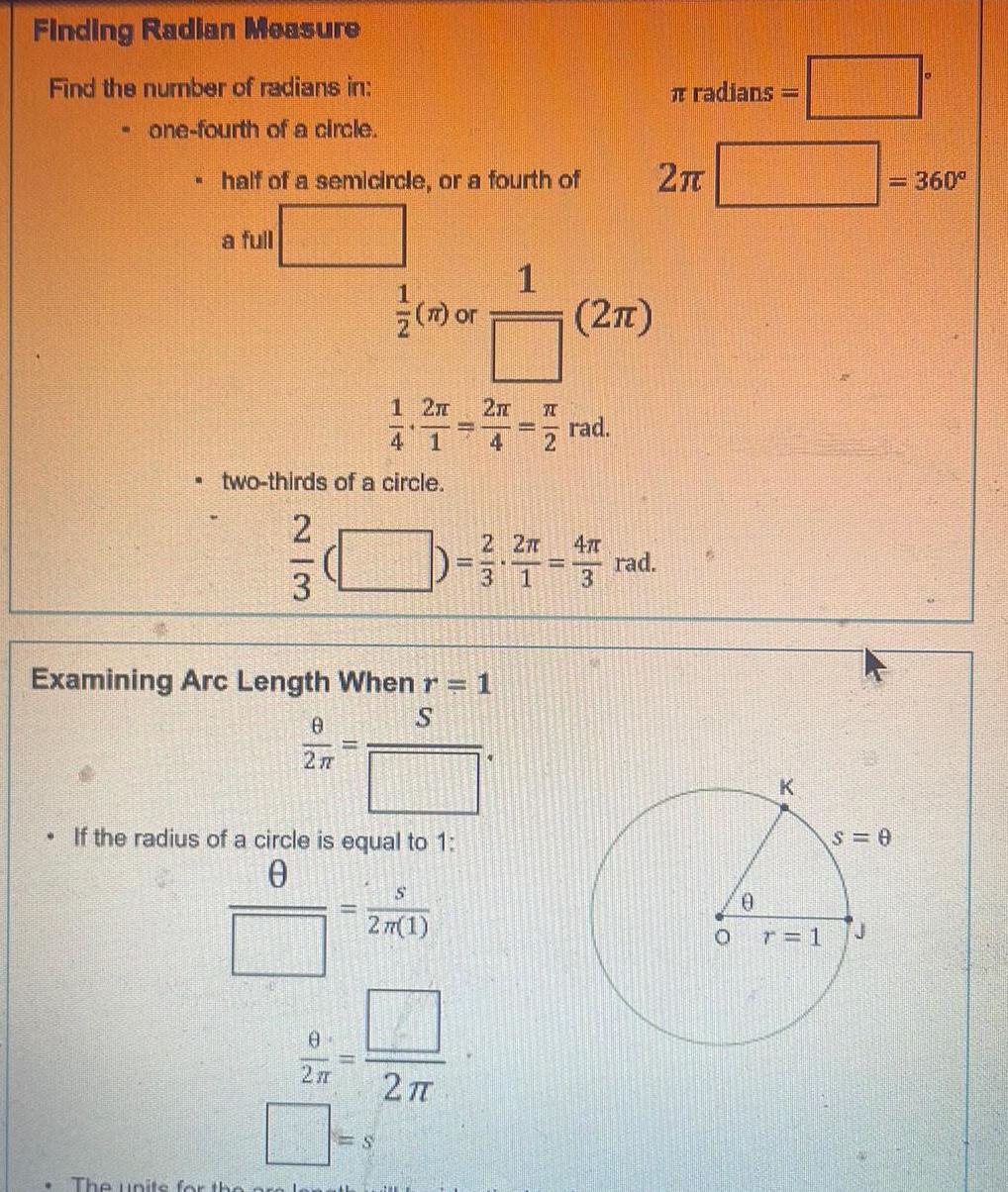
AreaFinding Radian Measure Find the number of radians in one fourth of a circle half of a semicircle or a fourth of 1 2 2 4 1 two thirds of a circle 2 3 Examining Arc Length When r 1 S 0 27 The units for the prel m or If the radius of a circle is equal to 1 0 0 2n S 277 1 S 2 1 H N 2TT 2 2 3 1 3 rad rad Tradians 2 0 0 K 360 S 0 L
Geometry
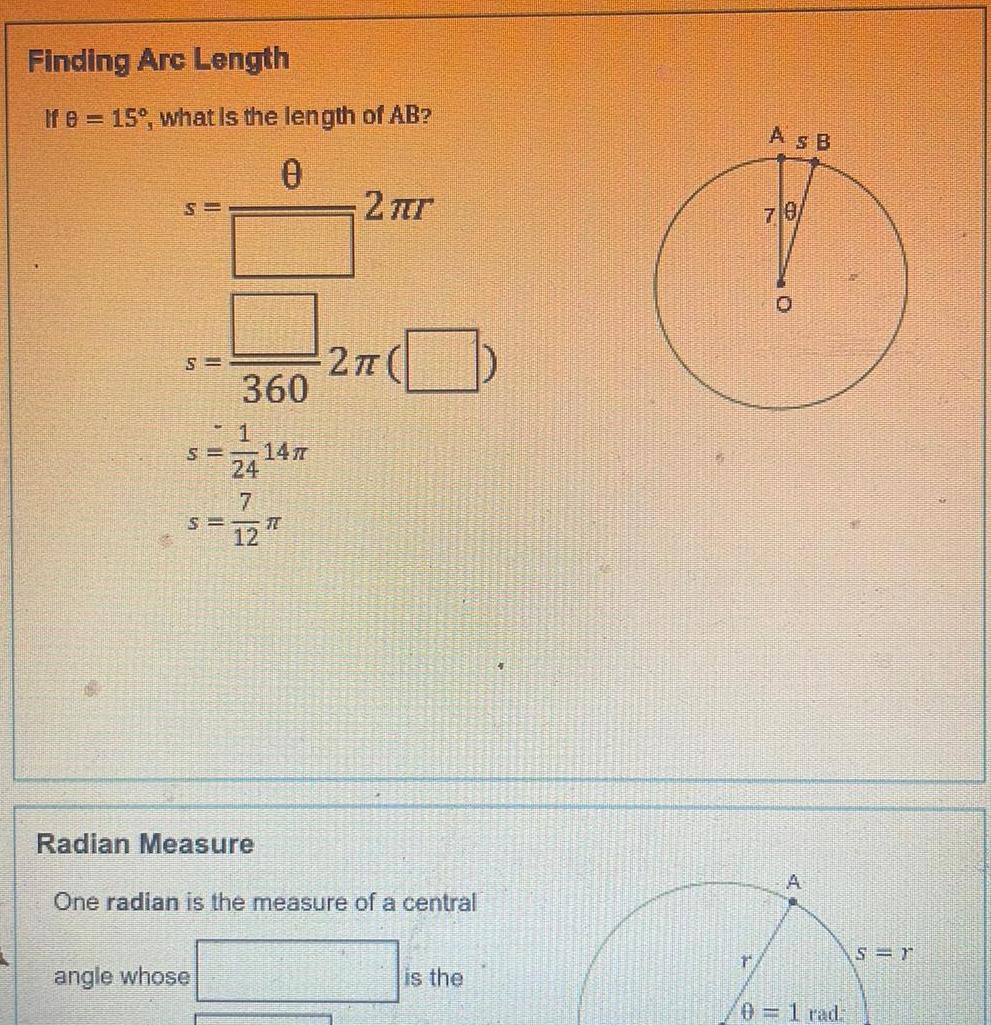
2D GeometryFinding Arc Length If e 15 what is the length of AB 0 S S S S 360 angle whose 24 7 12 147 T 2 r 2 Radian Measure One radian is the measure of a central is the t As B 70 A 0 1 rad S r
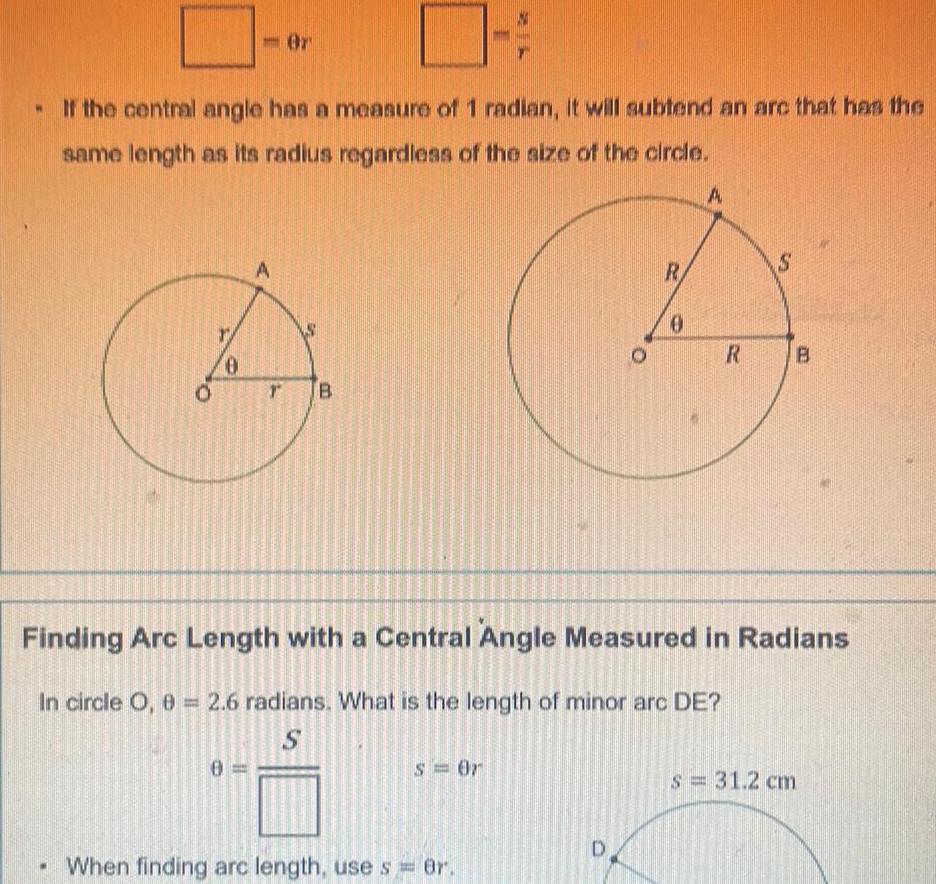
Geometry
2D GeometryIf the central angle has a measure of 1 radian it will subtend an arc that has the same length as its radius regardless of the size of the circle 0 Or 0 A 2 B s 0r When finding arc length use s 8r O D CE R 0 A R Finding Arc Length with a Central Angle Measured in Radians In circle O 0 2 6 radians What is the length of minor arc DE S S B S 31 2 cm
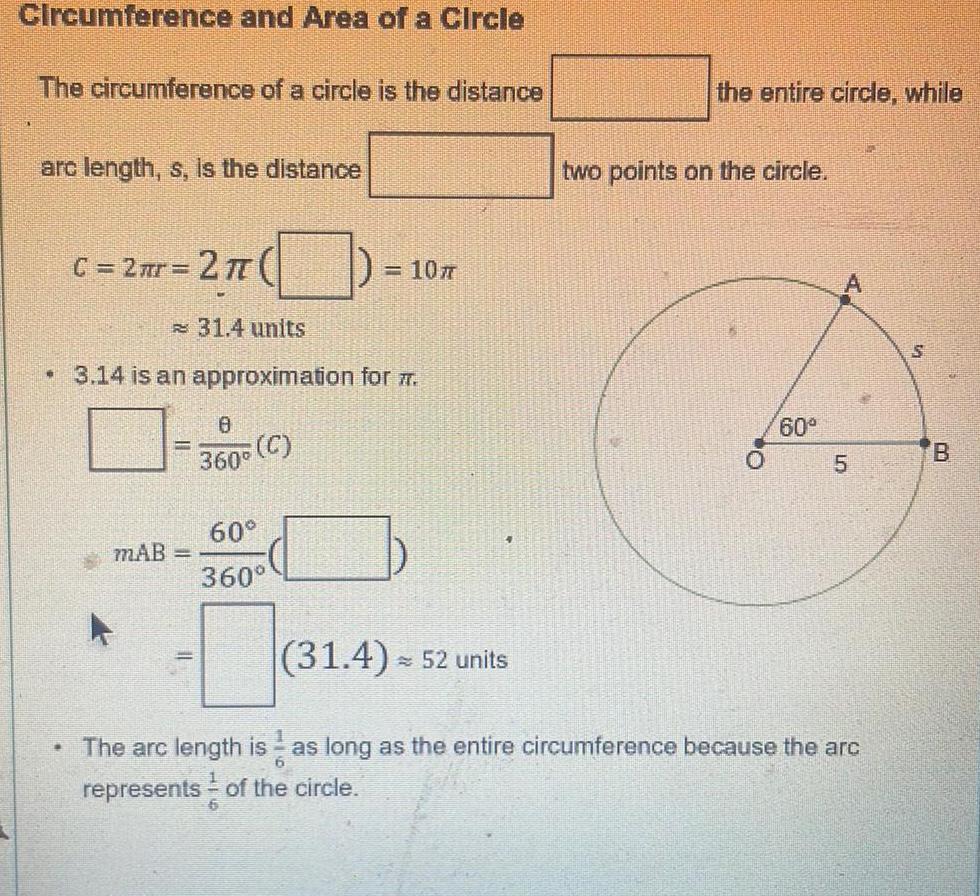
Geometry
2D GeometryCircumference and Area of a Circle The circumference of a circle is the distance arc length s is the distance C 2 r 2 TT 31 4 units 3 14 is an approximation for 7 B MAB C 360 107 60 360 31 4 52 units the entire circle while two points on the circle 60 5 The arc length is as long as the entire circumference because the arc 6 represents of the circle N S B

Geometry
2D GeometryThe area of a circle is determined by the radius of the circle with the formula The area of a creating the sector Area of sector Area of sector dimens 0 360 is determined by the size of the central angle 0 when the central angle is measured in when the central angle is measured in
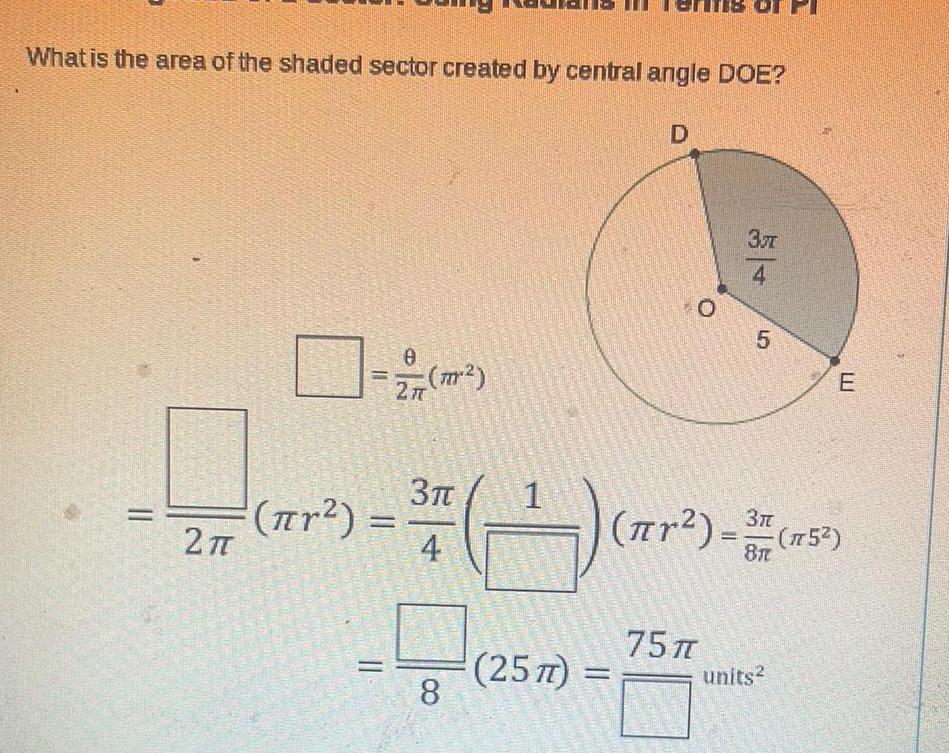
Geometry
Coordinate systemWhat is the area of the shaded sector created by central angle DOE 0 2 T 0 277 7 r 3 t 4 8 1 4 257 D 0 37 4 75 5 r 3 15 E units
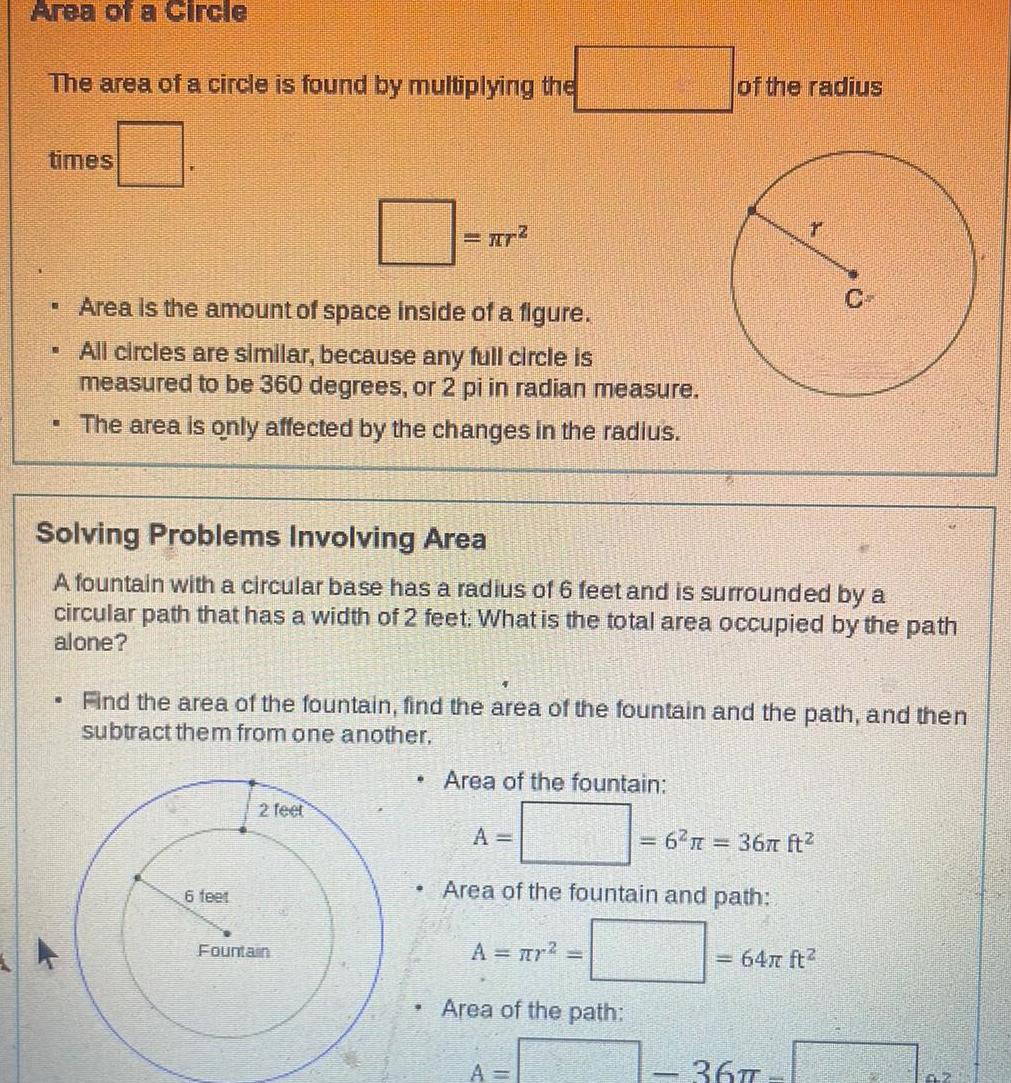
Geometry
AreaArea of a Circle The area of a circle is found by multiplying the times Area is the amount of space inside of a figure All circles are similar because any full circle is measured to be 360 degrees or 2 pi in radian measure The area is only affected by the changes in the radius KO 6 feet Solving Problems Involving Area A fountain with a circular base has a radius of 6 feet and is surrounded by a circular path that has a width of 2 feet What is the total area occupied by the path alone 2 feet r Fountain Find the area of the fountain find the area of the fountain and the path and then subtract them from one another Area of the fountain A A r Area of the path A 6 R of the radius Area of the fountain and path r 36 ft 9 64 ft 367
Geometry
AreaTULE DIUS 10 the area of the sector central DOS MONETANSARE Words to Know Write the letter of the definition next to the matching word as you work through the lesson You may use the glossary to help you CHERRIMON PERSO VARIND degree seco Minthem OPT S radian DASS AMOUR A Do for BOSTA MRISH SKECH SONG SONGS HAGE angle PHARETLY SATRZAS ELETT Pinces ARMELEG enrised Recor CARLMENTEER INSTAT me ke Analyze the sector of a circle D an angle whose vertex is at the center of a circle whose and sides are radii of that circle CHOLERNISS MARKE a circle veltestant A a standard unit of measure for angles the measure of a central angle that subtends an arc that is equal in length to the radius of the circle of B the region of a circle bounded by two radil and their intercepted arc C a unit of measure used in measuring angles and arcs there are 360 degrees in a circle P HONGE Sicht El de marque HAMAINEE Es Polaget TRAINE PLANT S Pes WANA AME AMPAST SA

Geometry
Coordinate systemWhen the measure of the sector is found by multiplying these two factors The ratio of the central angle over The area of the Area of a sector Ag nr 0 7 7 7 8 2 1 1 70 4 units is given in radians the area of a 2 2 Z Y 8
Geometry
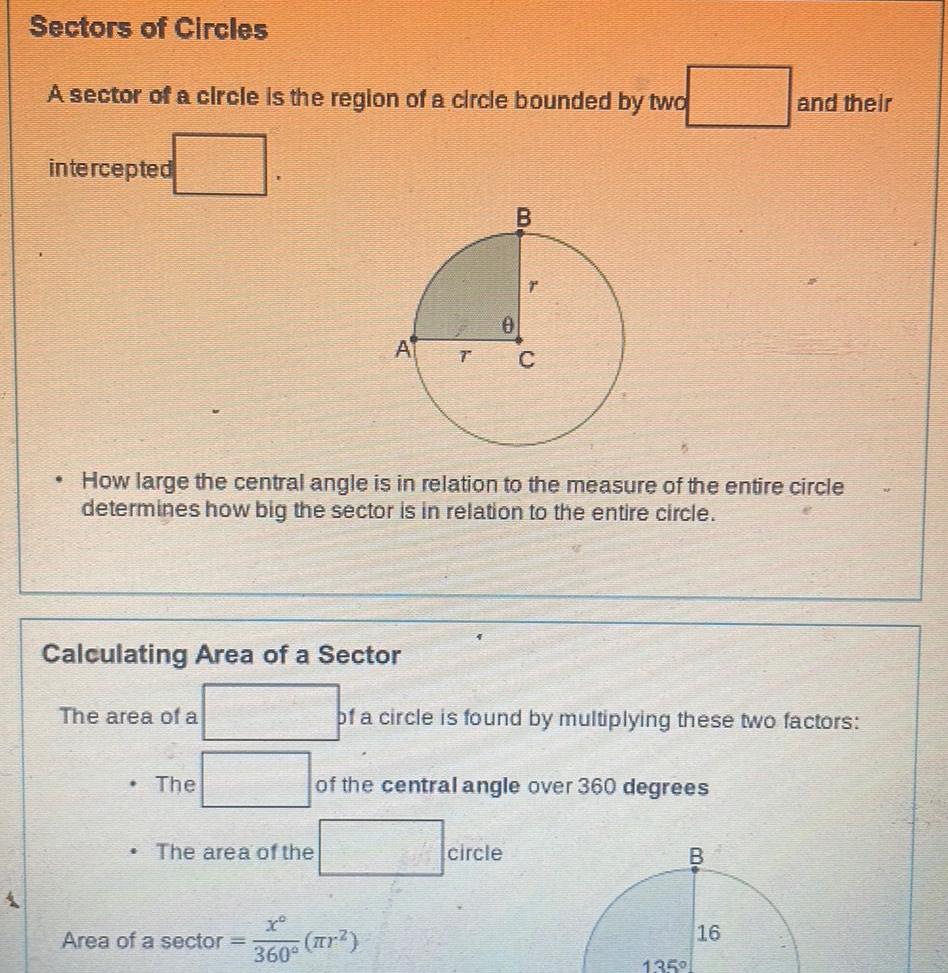
2D GeometrySectors of Circles A sector of a circle is the region of a circle bounded by two intercepted Calculating Area of a Sector The area of a How large the central angle is in relation to the measure of the entire circle determines how big the sector is in relation to the entire circle The A The area of the B T C x Area of a sector r 360 of a circle is found by multiplying these two factors of the central angle over 360 degrees circle B and their 135 16