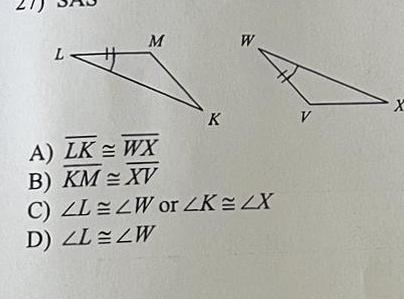
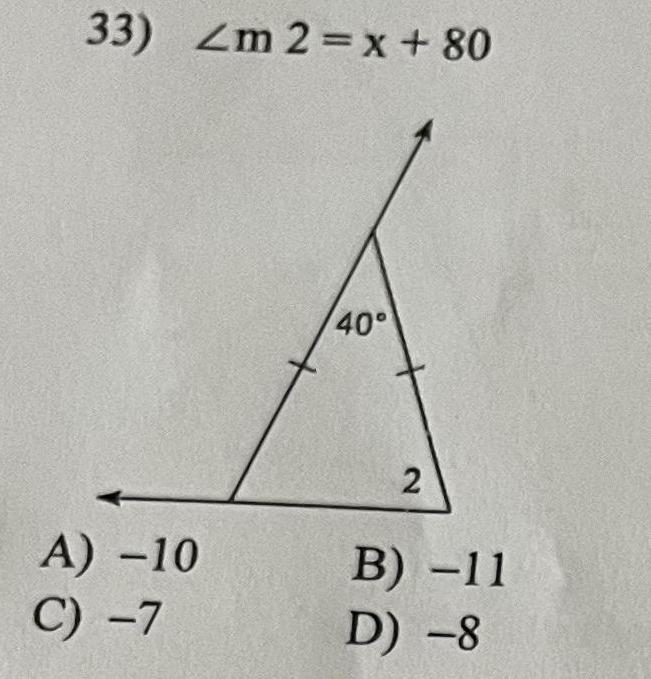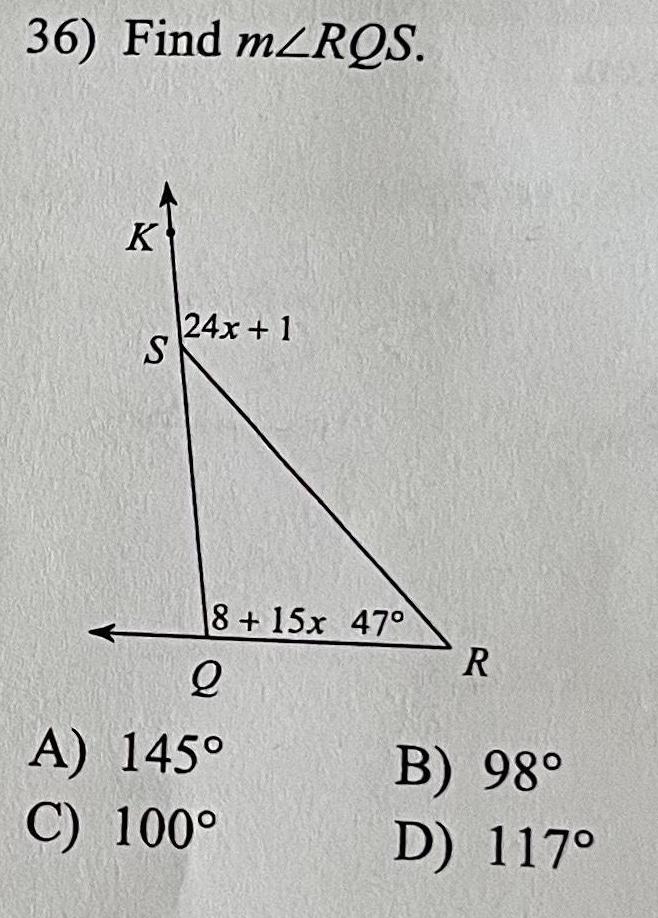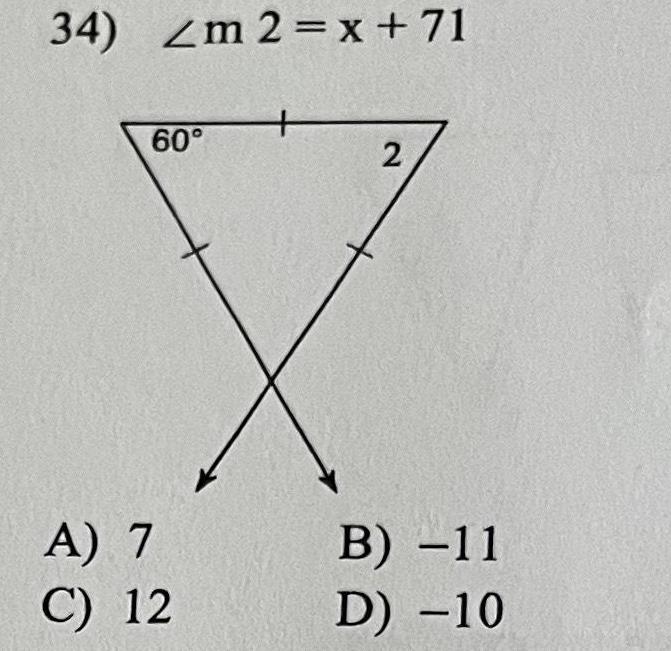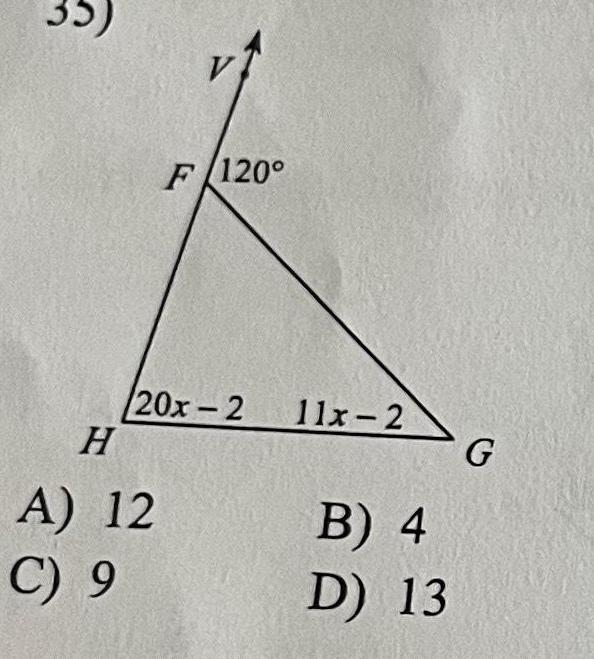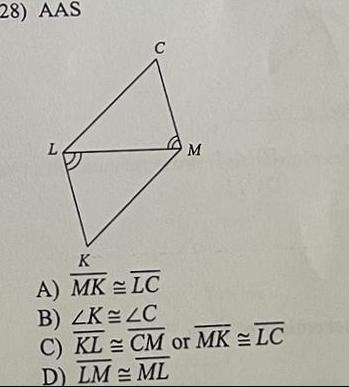Geometry Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
Geometry
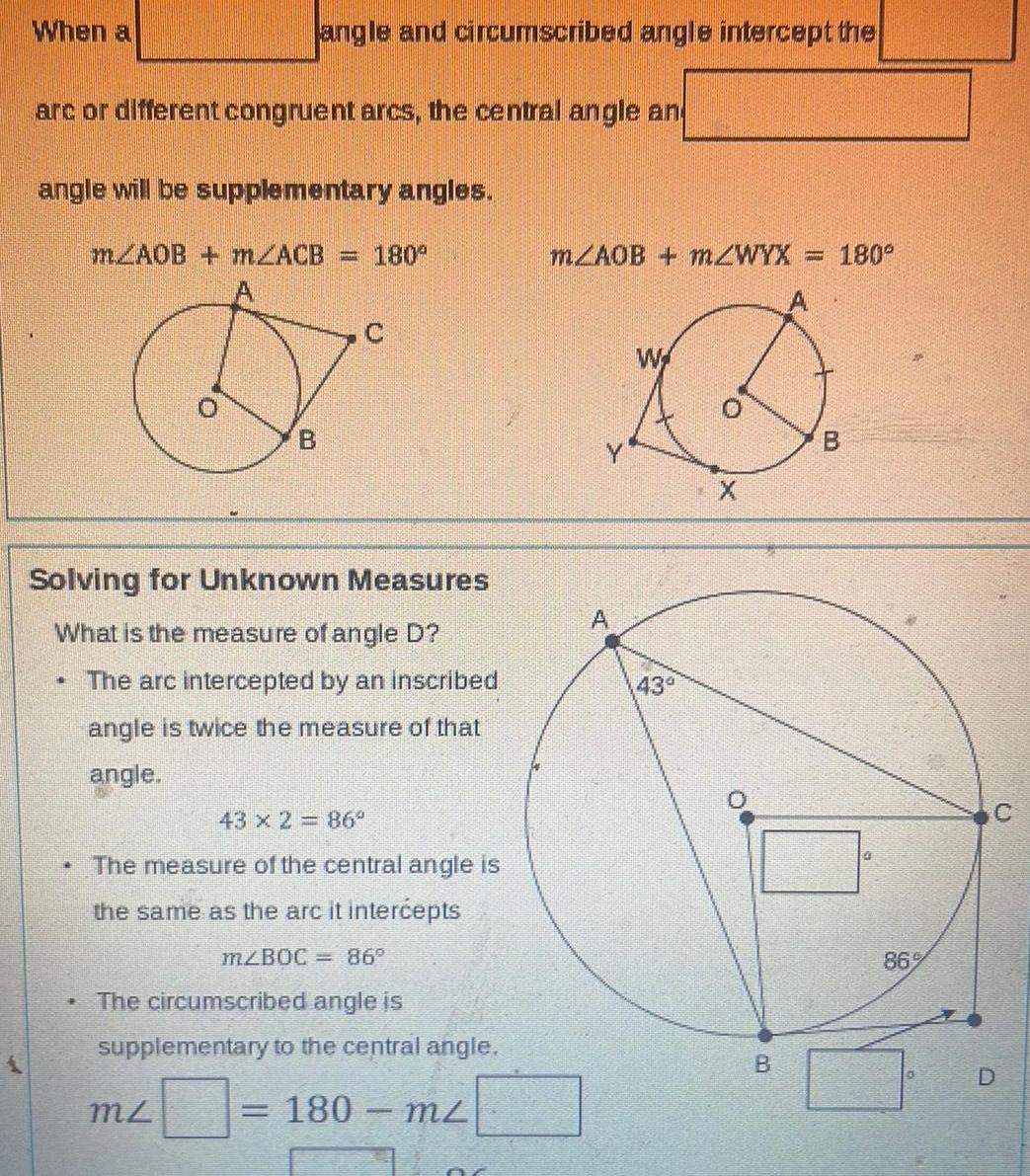
2D GeometryWhen a arc or different congruent arcs the central angle an angle will be supplementary angles mAOB m2ACB 180 1 angle and circumscribed angle intercept the Solving for Unknown Measures What is the measure of angle D The arc intercepted by an inscribed angle is twice the measure of that angle TR B 43 x 2 86 The measure of the central angle is the same as the arc it intercepts m BOC 86 mz The circumscribed angle is supplementary to the central angle 180 m m AOB mZWYX ST W 43 0 X B CO www 180 B 86 D O

Geometry
Coordinate systemFor central angles and inscribed angles that intercept the same arc W W M 1 the measure of the inscribed angle is the measure of the W angle when the intercepted arc is a semicircle a right triangle is created when the chords of the inscribed angle are congruent a For central angles and circumscribed angles that intercept the same arc created the central angle and the circumscribed angle are the angles form a kite angles is
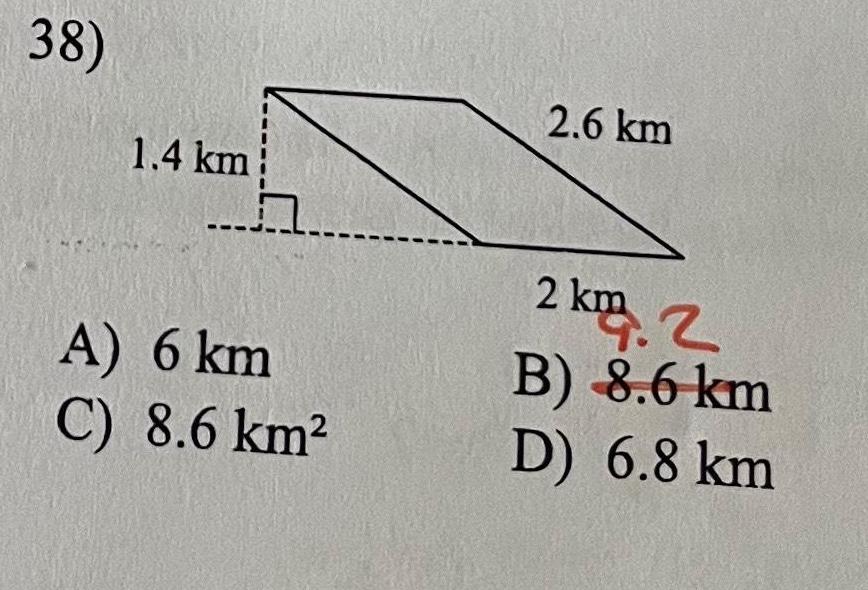

Geometry
2D Geometryand tangents to a Compare lengths of of a circle Compare of a circle Words to Know Fill in this table as you work through the lesson You may also use the glossary to help you an angle whose vertex is on a circle and whose sides are chords a segment with both endpoints on a circle an angle whose vertex is at the center of a circle and whose sides are radii of that circle a segment of a tangent that has an endpoint at the point of tangency an angle whose vertex is outside of a circle and whose sides are tangents to that circle two angles whose measures have a sum of 180

Geometry
AreaAn inscribed angle has two Intersecting chords with the vertex and the endpoints on the circle The sides are not necessarily A circumscribed angle is created by two intersecting segments The vertex is outside of the circle The sides are congruent 0

Geometry
2D GeometryWhen an inscribed angle intercepts a inscribed angle create a triangle The central angle is a straight angle so it has a measure of 180 The inscribed angle intercepts the same arc as the central angle so the measure of the inscribed angle is of 180 or 90 2 When the sides of the inscribed angle are congruent they create a 45 45 90 triangle the central angle and B Quadrilaterals Created by Central and Inscribed Angles GENERAL CASE What polygon is created when the inscribed angle does not intercept a diameter of the circle B Draw tick marks to show that the radil are congruent
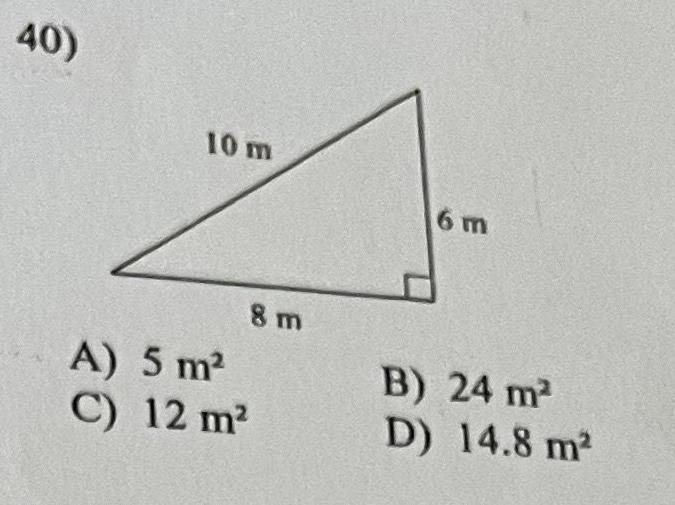
Geometry
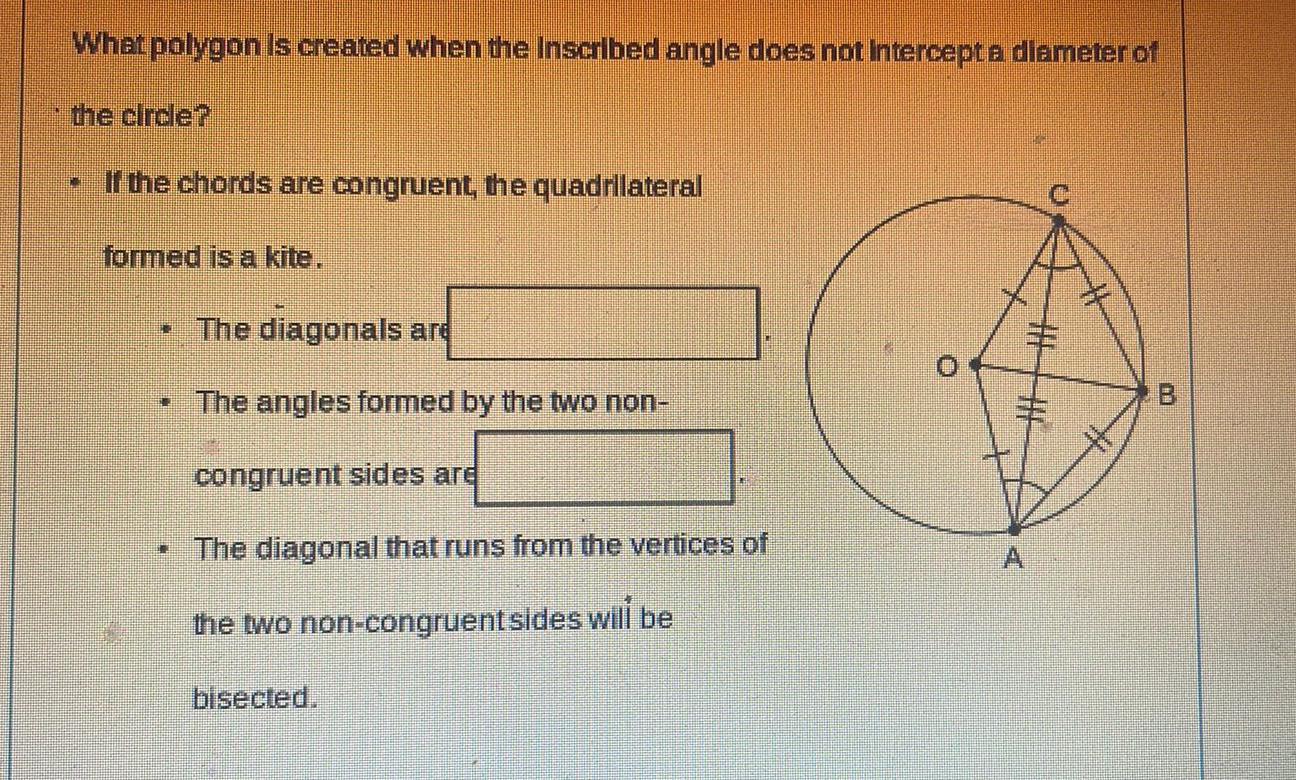
2D GeometryWhat polygon is created when the Inscribed angle does not intercept a diameter of the circle N If the chords are congruent the quadrilateral formed is a kite The diagonals are The angles formed by the two non congruent sides are The diagonal that runs from the vertices of the two non congruent sides will be bisected 1

Geometry
2D GeometryRelax How are the measures of inscribed angles and central angles related when they intercept the same arc or congruent arcs The Intercepted arc has the same measure as the central angle N The measure of the inscribed the intercepted arc will be half the measure of When a mzACB 1 of the 50 An inscribed angle that intercepts the same arc as a central angle will be of the measure of the central angle Determining Measures of Inscribed and Central Angles mAB mZAOB O congruent arcs the measure of the central angle will be angle 2 m AJB 0 angle and inscribed angle intercept the same arc or mZQOM 2 mZPRS O B P the measure
Geometry
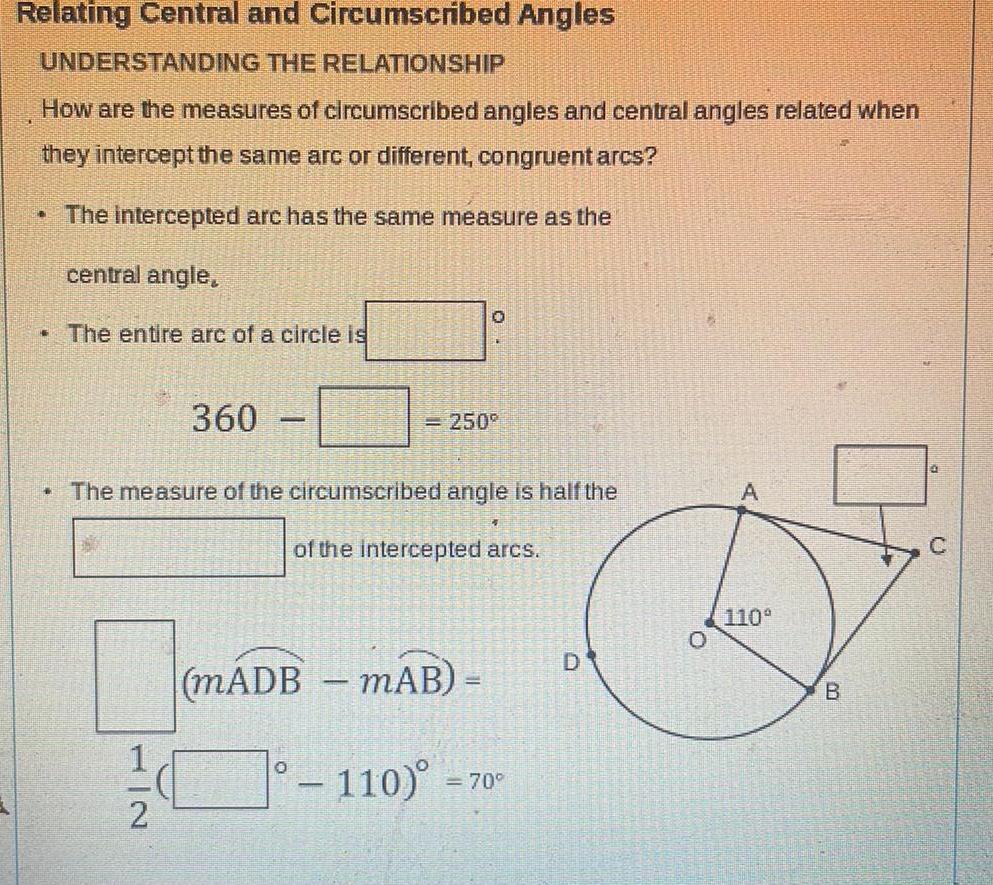
2D GeometryRelating Central and Circumscribed Angles UNDERSTANDING THE RELATIONSHIP How are the measures of circumscribed angles and central angles related when they intercept the same arc or different congruent arcs The intercepted arc has the same measure as the central angle THE The entire arc of a circle is 360 1 2 0 250 The measure of the circumscribed angle is half the of the intercepted arcs mADB mAB 110 70 D 0 110 B C
Geometry
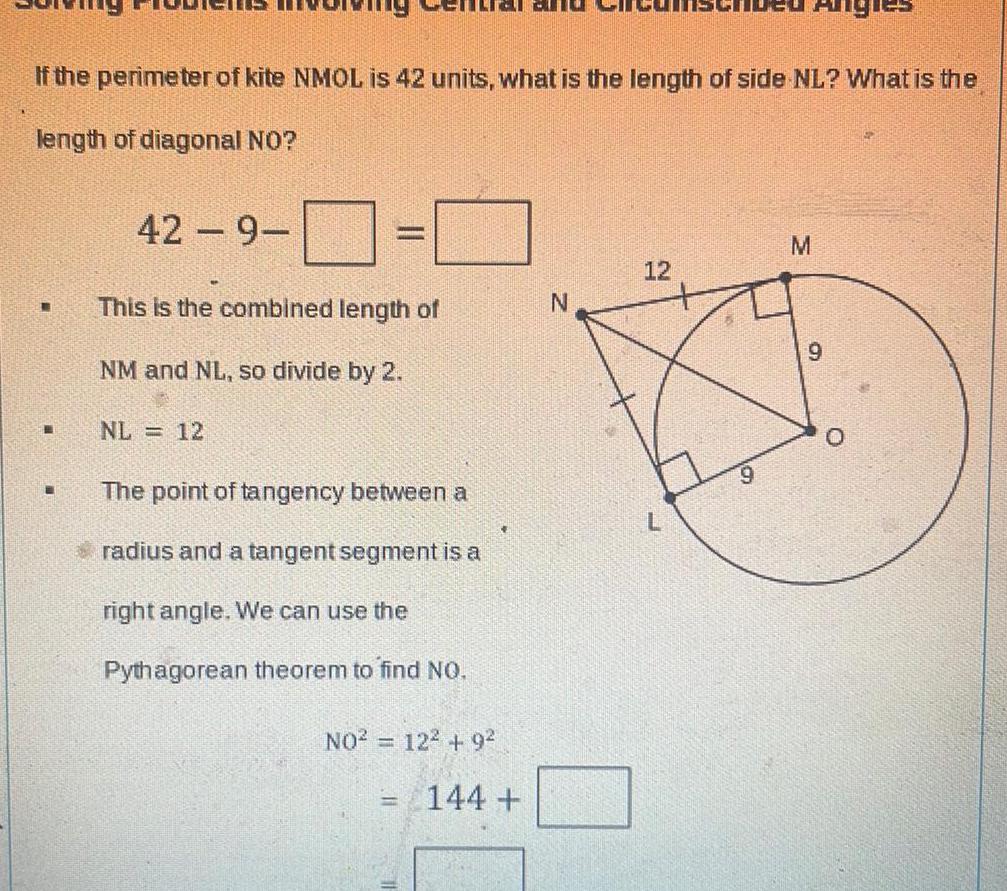
2D GeometryIf the perimeter of kite NMOL is 42 units what is the length of side NL What is the length of diagonal NO 42 9 This is the combined length of NM and NL so divide by 2 NL 12 The point of tangency between a radius and a tangent segment is a right angle We can use the Pythagorean theorem to find NO NO 12 9 144 N 12 Angit M 9 O
Geometry
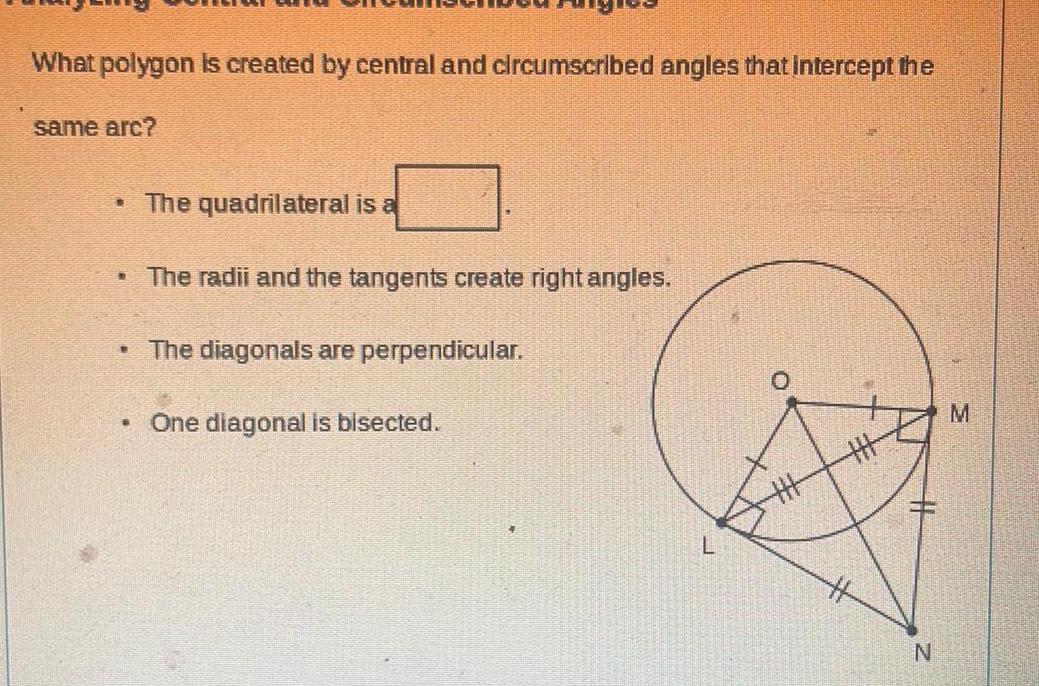
2D GeometryWhat polygon is created by central and circumscribed angles that intercept the same arc The quadrilateral is a The radii and the tangents create right angles 6 The diagonals are perpendicular One diagonal is bisected H N M

Geometry
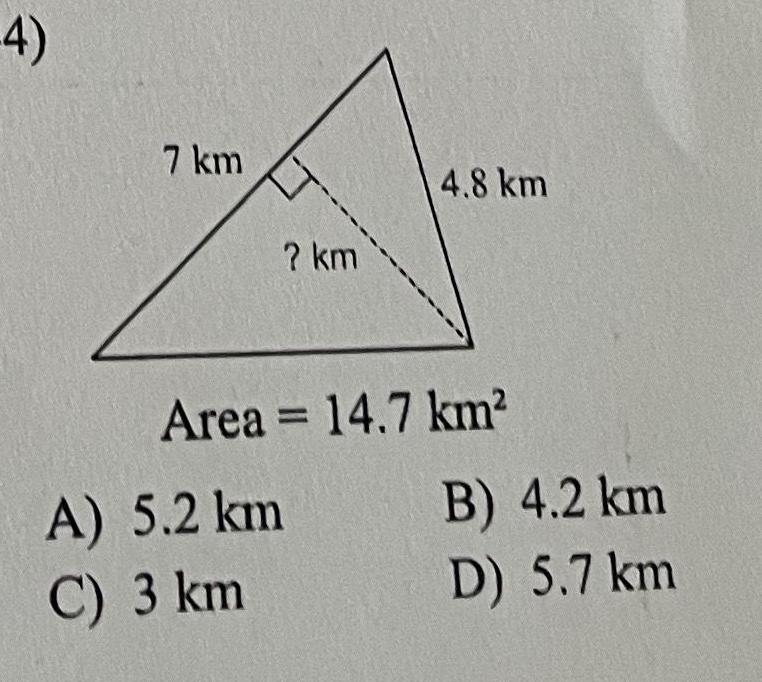
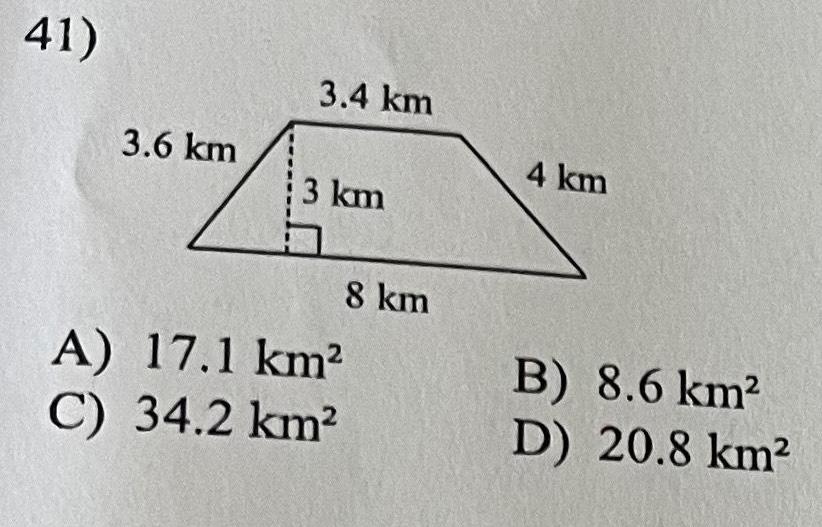
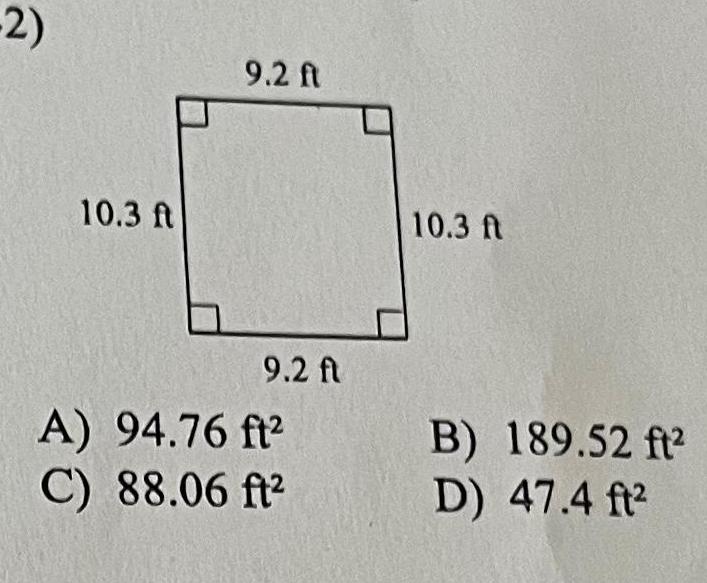
2D GeometryFind the area of each 39 2 8 mi 3 3 mi A 12 24 mi C 18 48 mi 6 4 mi 3 3 mi B 9 24 mi D 4 6 mi
Geometry
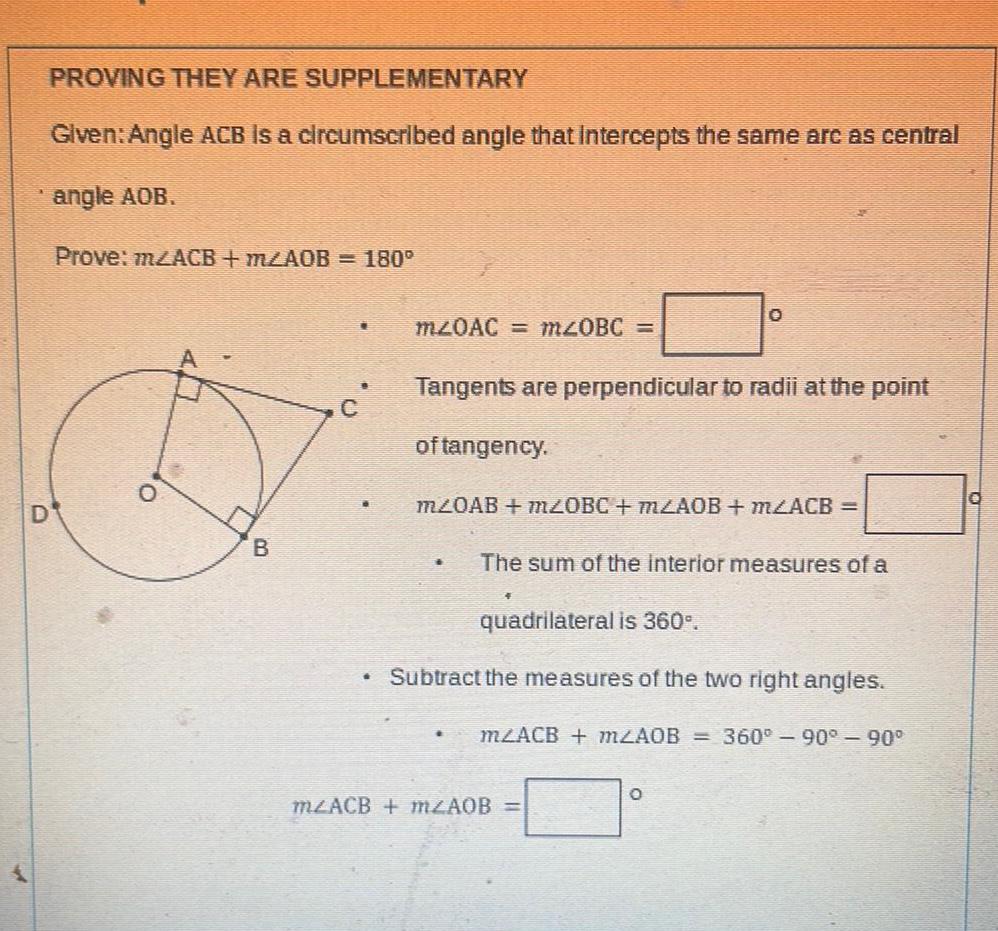
2D GeometryD PROVING THEY ARE Given Angle ACB is a circumscribed angle that intercepts the same arc as central angle AOB Prove m2ACB m2AOB 180 0 SUPPLEMENTARY B L m20AC m 0BC Tangents are perpendicular to radii at the point of tangency O m20AB mZ0BC m2AOB m2ACB The sum of the interior measures of a quadrilateral is 360 Subtract the measures of the two right angles m2ACB m2AOB 360 90 90 m2ACB m2AOB O
Geometry
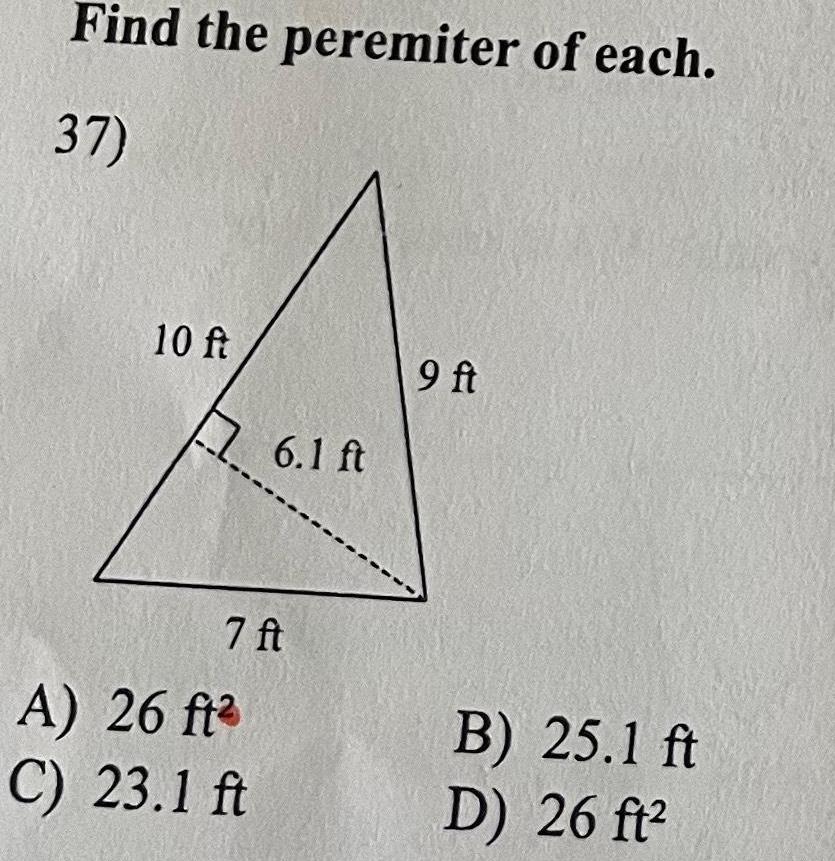
2D GeometryFind the peremiter of each 37 10 ft 6 1 ft 7 ft A 26 ft C 23 1 ft 9 ft B 25 1 ft D 26 ft

Geometry
2D GeometryCentral Inscribed and Circumscribed Angles Central angles circumscribed angles and inscribed angles are created tangent segments W W and outside of a circle by A chord is a segment that has two on the circle A tangent segment has an endpoint at the point of tangency that are Central angles are created by two radii They have a vertex at the of the circle The endpoints are on the circle and the sides are congruent radii chords and
Geometry
Heights & Distances11 4 points Mr Longo and Ms Johnson are celebrating the end of the year by getting ice cream Mr Long ordered 1 scoop of ice cream with a radius of 5 cm and Ms Johnson ordered 2 scoops both with a diame of 6 cm Given that each of their ice cream cones have a volume of 121 cm who has the most ice cream Explain your reasoning

Geometry
2D GeometryIdentify the and radius of a circle center Examine equations of circle hypotenuse radius given in standard form or general form Write the of a circle Words to Know Write the letter of the definition next to the matching word as you work through the lesson You may use the glossary to help you Determine if a given lles on a circle A the set of all points in a plane that are a given distance away from a given point called the center B a segment that extends from the center of a circle to any point on the circle C the fixed point that is equidistant from all points on a circle D the side of a right triangle that is opposite the right angle and is always the longest side of the triangle

Geometry
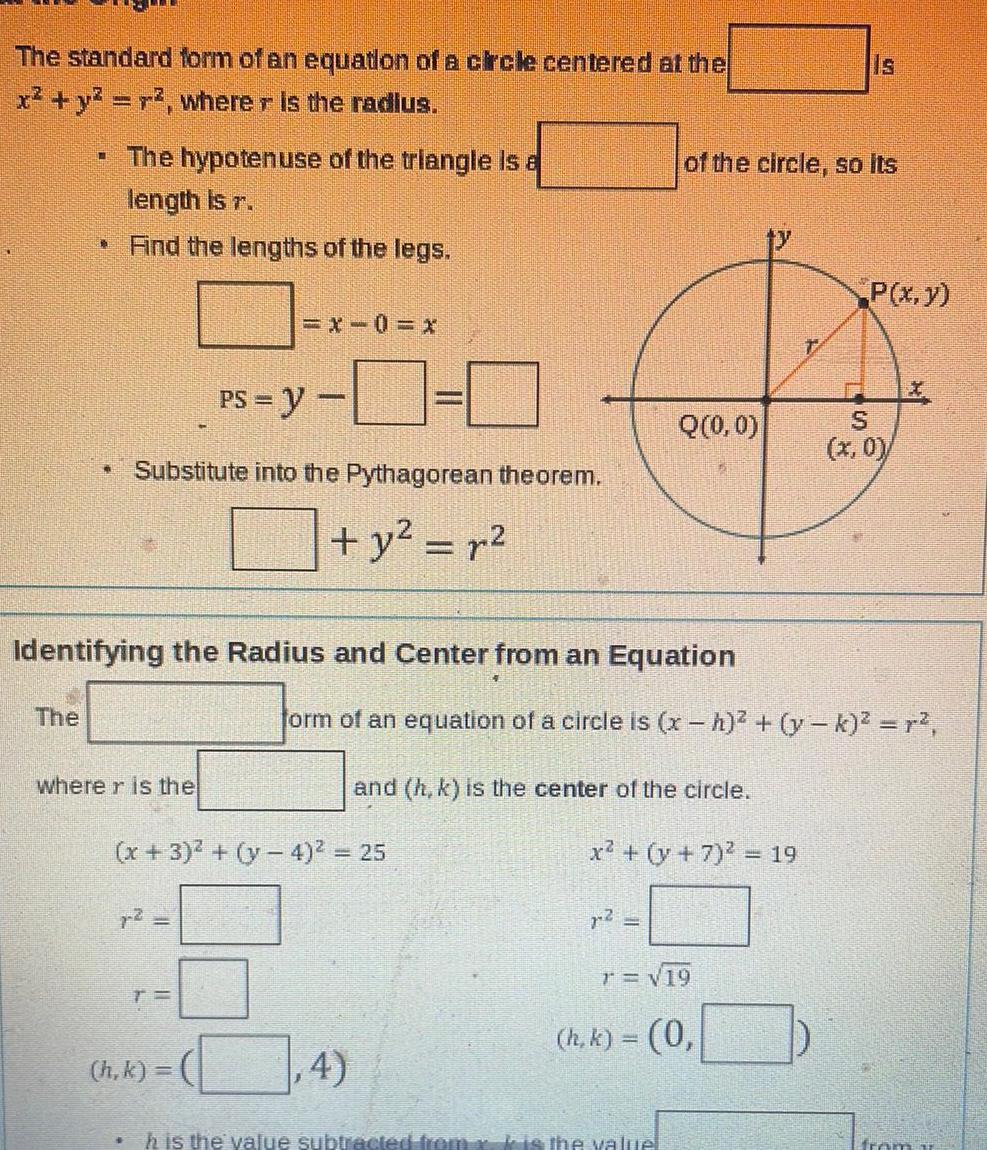
2D GeometryThe form of an equation of a circle is x h y k r The point h k is the center and is the The general form of an equation of a circle is x y Cx Dy E 0 1 Complete the form to convert from general form to standard

Geometry
Coordinate systemon the Circle the Equation Given the center and a Point Find the equation of the circle with a center at 1 5 that passes through the point 3 8 1 Use the d x x y y Let x y 1 5 and xz 3 8 formula to determine the radius T 13 3 1 8 5 4 8 5 V449 Substitute the known values into the standard form x h y k r x 1 y 5 13 x 1 y 5

Geometry
Area10 3 points A water cup in the shape of a cone has a diameter of 8 inches and a height cup is filled with water to half of its height determine the volume of water in the cup to the nearest hundredth of an inch Hint The height and radius are proportional in a cone so if the height is cut in half so is the radius
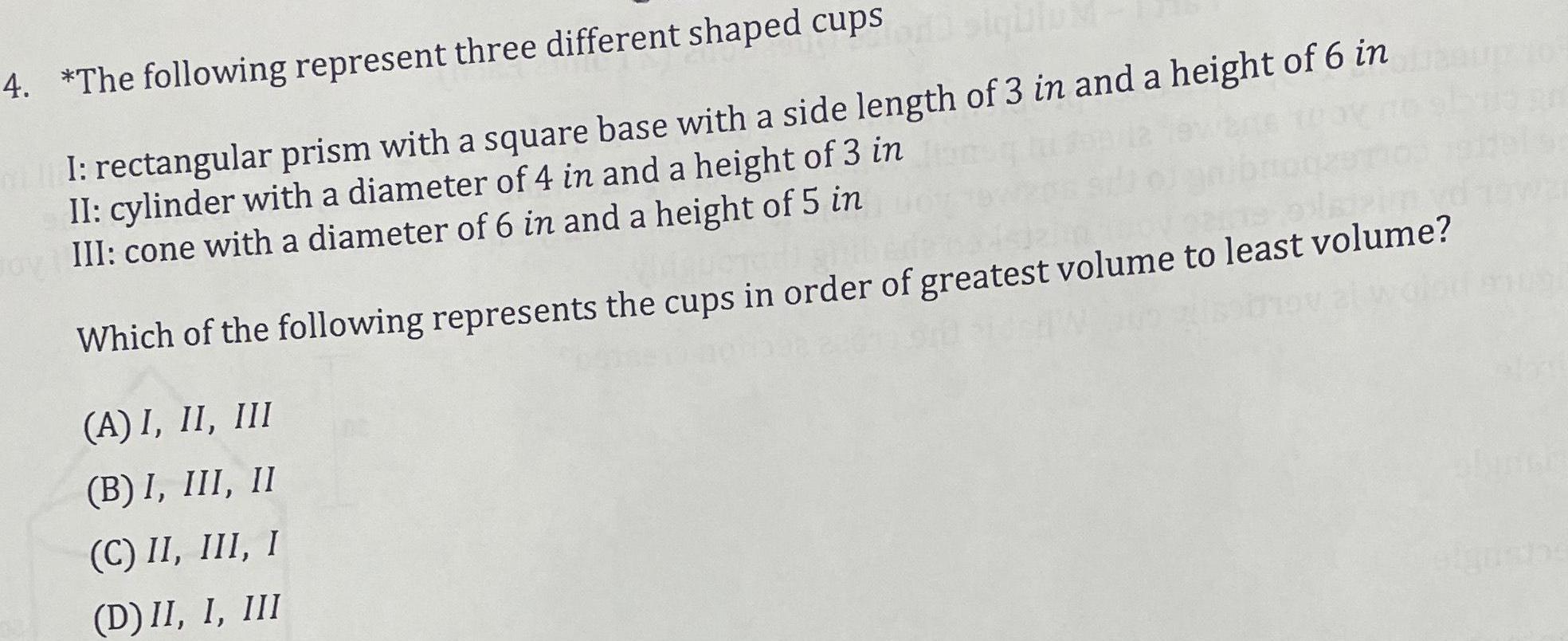
Geometry
Area4 The following represent three different shaped cups I rectangular prism with a square base with a side length of 3 in and a height of 6 in II cylinder with a diameter of 4 in and a height of 3 in III cone with a diameter of 6 in and a height of 5 in Which of the following represents the cups in order of greatest volume to least volume A I II III B I III II C II III I D II I III

Geometry
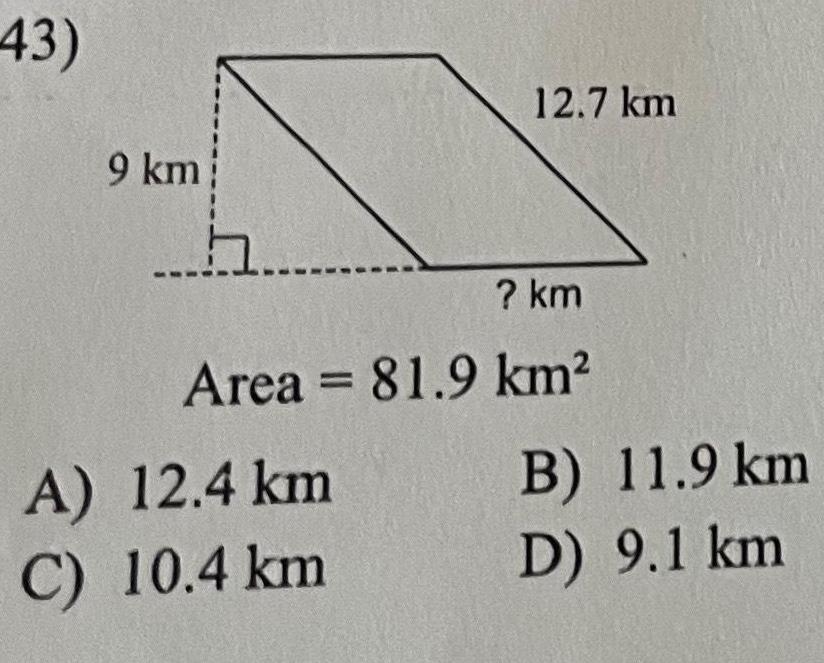
AreaUse the scenario below to answer 6 and 7 A rectangular prism fish tank has a base with a length of 40 inches a width of 35 inches and a height of 12 inches 6 If the tank is filled to 75 capacity what is the volume in the tank A 360 cubic inches B 480 cubic inches C 12 600 cubic inches D 16 800 cubic inches 7 Water is removed from the rectangular prism tank such that the water is at a height of 2 inches What is the volume in the tank now A 80 cubic inches B 840 cubic inches C 2 800 cubic inches D 16 800 cubic inches

Geometry
2D GeometryIdentifying the Center and Radius Given an Equation in General Form Identify the center and radius of a circle whose equation is x y 10x 14y 58 0 Complete the square for the x and y terms Group together the x terms x 10x y 14y Determine what value needs to be added to both sides of the equation to complete the square y 14y x 10x 58 25 49 16 Factor the polynomials Identify the center and radius x y ap 1 71 214 X 2 2 19 2 25 14 24 y 49

Geometry
Coordinate systemThe General Form of an Equation of a Circle The To convert an equation in general form to standard form square form of an equation of a circle is x y Cx Dy E 0 Complete the square for the x and y terms Group together the x terms x 4x y Determine what value needs to be added to both sides of the equation to complete the square x 4x 4 y 8y 16 10 4 16 10 Factor the polynomials x y 4x 8y 10 0 1 T 10 h k 2 10 2 41 the 2 4 2 2 20 y
Geometry
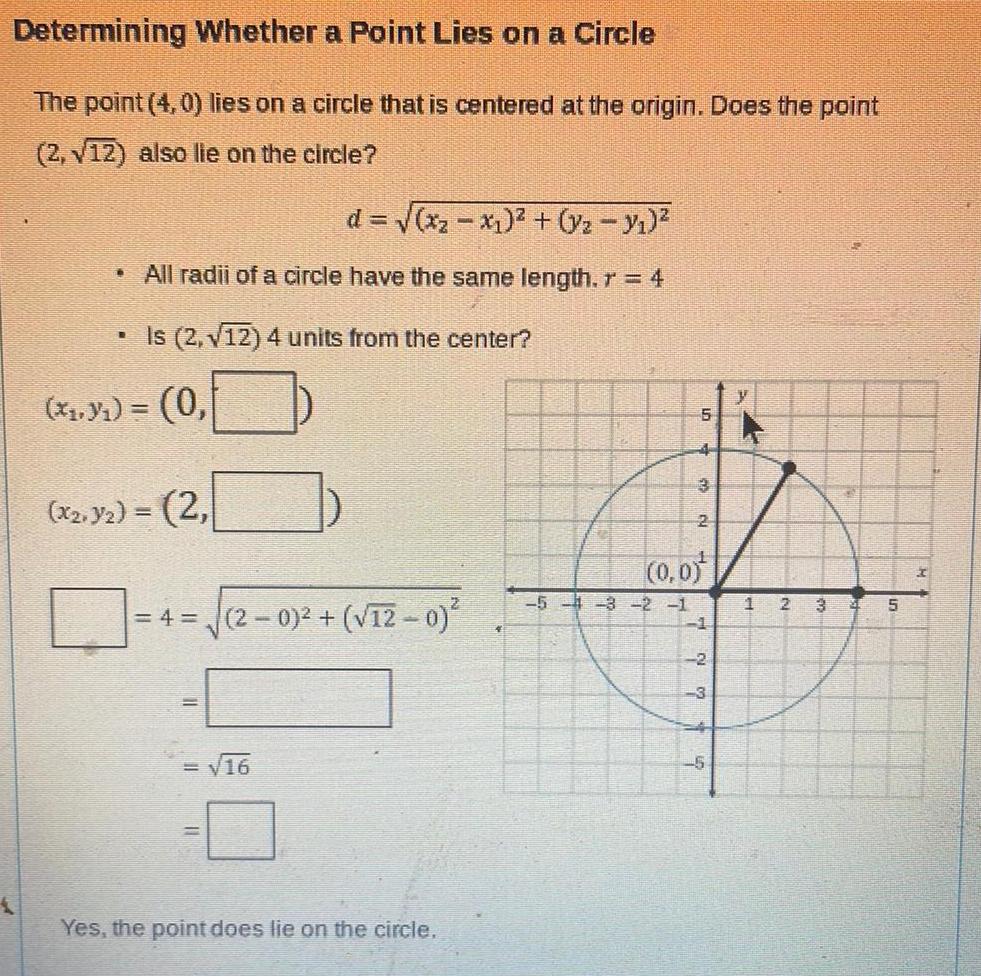
2D GeometryDetermining Whether a Point Lies on a Circle The point 4 0 lies on a circle that is centered at the origin Does the point 2 12 also lie on the circle d x x y y All radii of a circle have the same length r 4 R Is 2 12 4 units from the center x y 0 x2 y 2 4 2 0 12 0 16 Yes the point does lie on the circle 5 5 4 3 2 1 4 2 0 0 1 2 7 5 y 1 2 3 31 5

Geometry
Area5 A circular town with a maximum diameter of 4 miles The shaded region represents the water The land is in the shape of a rectangle There are currently 2 052 people living in the town below What is the population density in person per square mile of land A 128 3 B 163 3 C 213 2 D 698 0 4 miles OURIO 3 5 miles s dalwo003 A 2 75 miles

Geometry
2D Geometry10 29anoq o bobna squ 12 2 points On Saturday July 1st Yellowstone National Park had 25 000 visitors in the park at 1 00 PM The total area of the park is 8 983 13 km and the total area of water is 2 714 13 km Determine the density of people on land in Yellowstone National Park on Saturday July 1st at 1 00 PM to the nearest visitor
Geometry
2D GeometryThe standard form of an equation of a circle centered at the x y r where r is the radius The hypotenuse of the triangle is a length is r Find the lengths of the legs The 1 PS y Substitute into the Pythagorean theorem y r where r is the Identifying the Radius and Center from an Equation h k 1 0 x 3 y 4 25 4 of the circle so its Q 0 0 and h k is the center of the circle form of an equation of a circle is x h y k r 2 x y 7 19 h is the value subtracted from x is the value Is T 19 h k 0 P x y S x 0 from

Geometry
Solution of triangles2 AABC is continuously rotated around AB What 3D figure is formed A A cone with a diameter of 5 B A cone with a diameter of 10 C A cone with a diameter of 24 D A cylinder with a diameter of 10 A 12 8 B 5 C

Geometry
3D GeometryChristmas ornament in the shape of a sphere has a diameter of 5 5 inches If the mass of the ornament is opounds the density is 9 8 A 0 003 B 0 022 C 43 55 D 348 45 9 W to answer 8 and 9 8 A Inches per pound B Inches per pound C Pound per inch D Pound per inch

Geometry
2D Geometrybubble for the letter corresponding to the answer you think choose an answer by mistake erase your mistaken shading thoroughly i to bio of 1 The figure below is vertically cut What is the cross section created A Circle B Triangle C Rectangle D Pentagon bebola sat od srld mi sevil sigos 20 30 40 50
Geometry
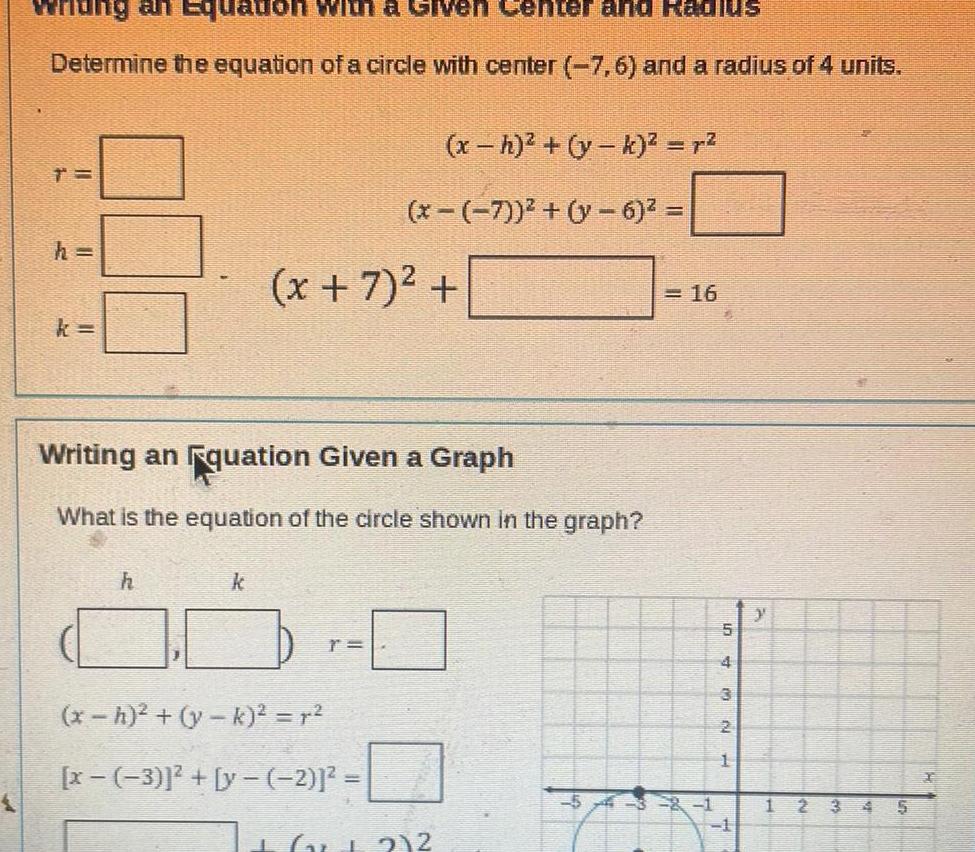
2D Geometryan Equation with a Givel Center and Radius Determine the equation of a circle with center 7 6 and a radius of 4 units h k h k Writing an quation Given a Graph What is the equation of the circle shown in the graph x h y k r x 7 6 x 7 x h y k x 3 y 2 x 2 2 16 5 3 2 1 NWU 4 2 1 1 A 1 2 S

Geometry
2D GeometryPythagorean theorem In a right triangle the square of the length of the hypotenuse is equal to the sum of the of the lengths of the A C a B The hypotenuse is the longest side in a right triangle c a b

Geometry
2D Geometry3 Jerome paints the box below in art class One can of paint covers 118 in How many cans of paint does Jerome need to buy A 1 B 2 C 3 D 4 simon 8 in 5 in 6 in

Geometry
2D GeometryLI SB Use relationships with length area and volume when an object is dild 3 SB 3 A superhero action figure has a volume 1500 cm The figure is dilated to create a store display The volume of the dilated figure is 45 000 cm What was the approximate scale factor of the dilation 5B 4 A pet supply company makes a small bag that holds 2 pounds of dog food They want to make a bag for large dogs that holds 40 pounds of dog food By approximately what factor will the surface area of the bag increase Round your answer to the nearest tenth