Geometry Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.


Geometry
2D Geometry26 Using the grid provided sketch the graph of the given function in the interval 5 5 and then determine the x intercepts if any y sin TCX 2 1 5 4 3 2 10 14 2 1 2 3 4 5 X

Geometry
2D Geometry1 Determine whether the Law of Sines or the Law of Cosines is needed to solve the triangle Then solve the triangle Round your answer to two decimal places A 42 B 35 c 1 4 O Law of Cosines No solution Law of Sines C 103 a 0 96 b 0 96 Law of Cosines C 103 a 0 82 b 0 96 Law of Sines No solution Law of Sines C 103 a 0 96 b 0 82

Geometry
2D Geometry28 Use the given values to evaluate if possible three trigonometric functions csc x tan x cot x 8 cos x 7 cos x 15 COS 17 17

Geometry
2D Geometry24 Evaluate the following expression 0 2an 6 where n is a whole number sec 30 1 1 cos 30 O cos 30 Osec 30 cos 30 O cos 30 O sec 30 sec 30

Geometry
Heights & DistancesA hot air balloon is floating above a straight road To estimate their height above the ground the balloonists simultaneously measure the angle of depression to two consecutive mileposts on the road on the same side of the balloon The angles of depression are for to be 22 and 24 How high is the balloon O 46 104 ft O 11 526 ft O 23 052 ft

Geometry
2D GeometryName Teacher Perpendicular Lines Find the equation of a line passing through the given point and perpendicular to the given equation Write your answer in slope intercept form 1 0 0 and y 3x 3 Answer 1 2 2 2 and y x 3 Answer 3 2 2 and y 1 X 2 Answer 4 1 1 and y x 2 Score Date 5 2 4 and y 6x 3 Answer 3 6 4 2 and y Answer X 4 Answer 7 3 2 and y 5x 3 8 1 2 and y 4x 10


Geometry
2D GeometryTo find the distance across a river a surveyor chooses points A and B which are 197 ft apart on one side of the river see the figure She then chooses a reference point C on the opposite side of the river and finds that LA 47 and LB 70 A distance from A to C OOOO 208 ft 207 ft 209 ft 206 ft A A cft 8 B

Geometry
Coordinate system1 The point P is on the unit circle The x coordinate of P is and P is in quadrant I Find the point P x y 7 0 1 48 7 48 0 7

Geometry
2D GeometryTwo tugboats that are 118 ft apart pull a barge as shown If the length of one cable is 206 ft and the length of the other is 227 ft find the angle formed by the two cable 37 38 28 03 31 15 DODDDDD000
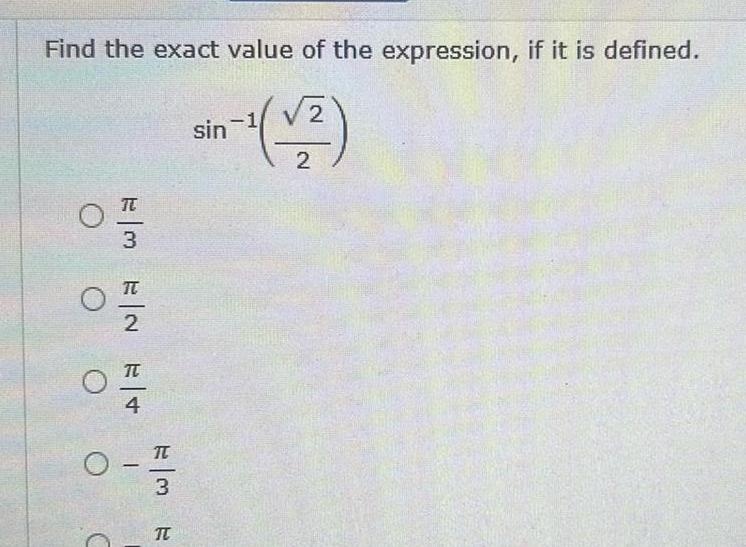
Geometry
2D GeometryFind the exact value of the expression if it is defined V2 sin 1 2 O EM EN E OOO E ME FR 3 N

Geometry
VectorsFind the exact values of the trigonometric functions sin O sinn 0 5 sin 1 0 5 sin 2 1 and sin 6 O sin x 0 5 sin x 0 5 sin 2 0 5 sin 0 5 1 6
Geometry
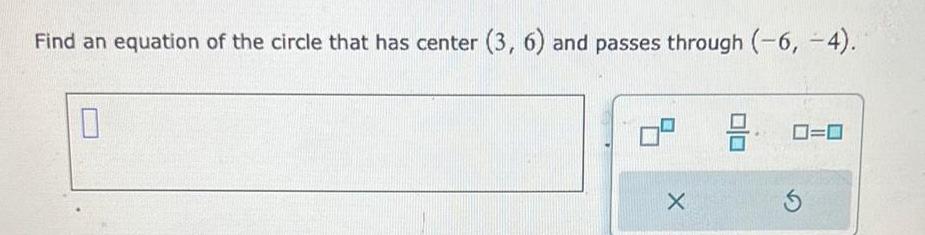
Coordinate systemFind an equation of the circle that has center 3 6 and passes through 6 4 0 X 8 0 0
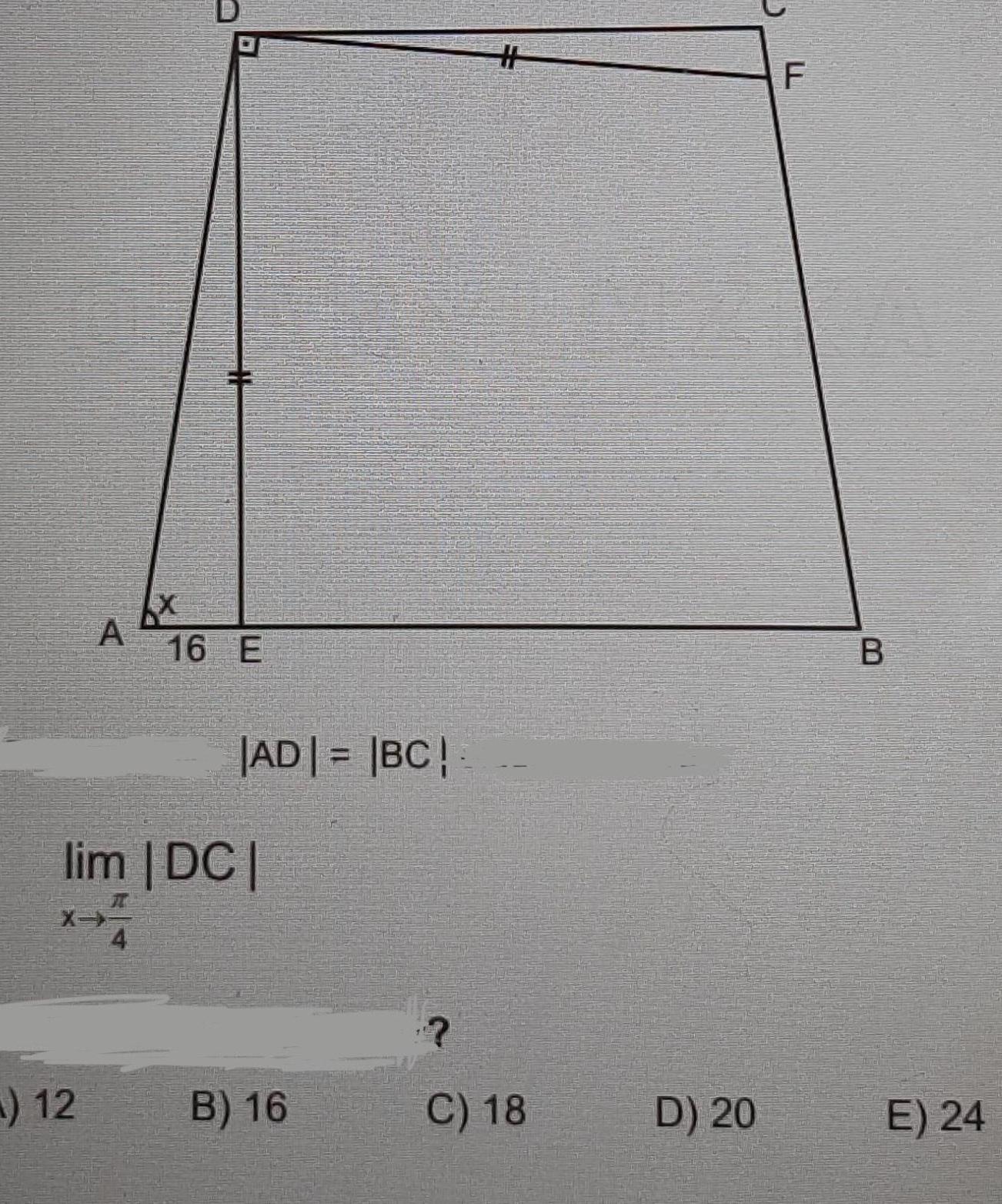
Geometry
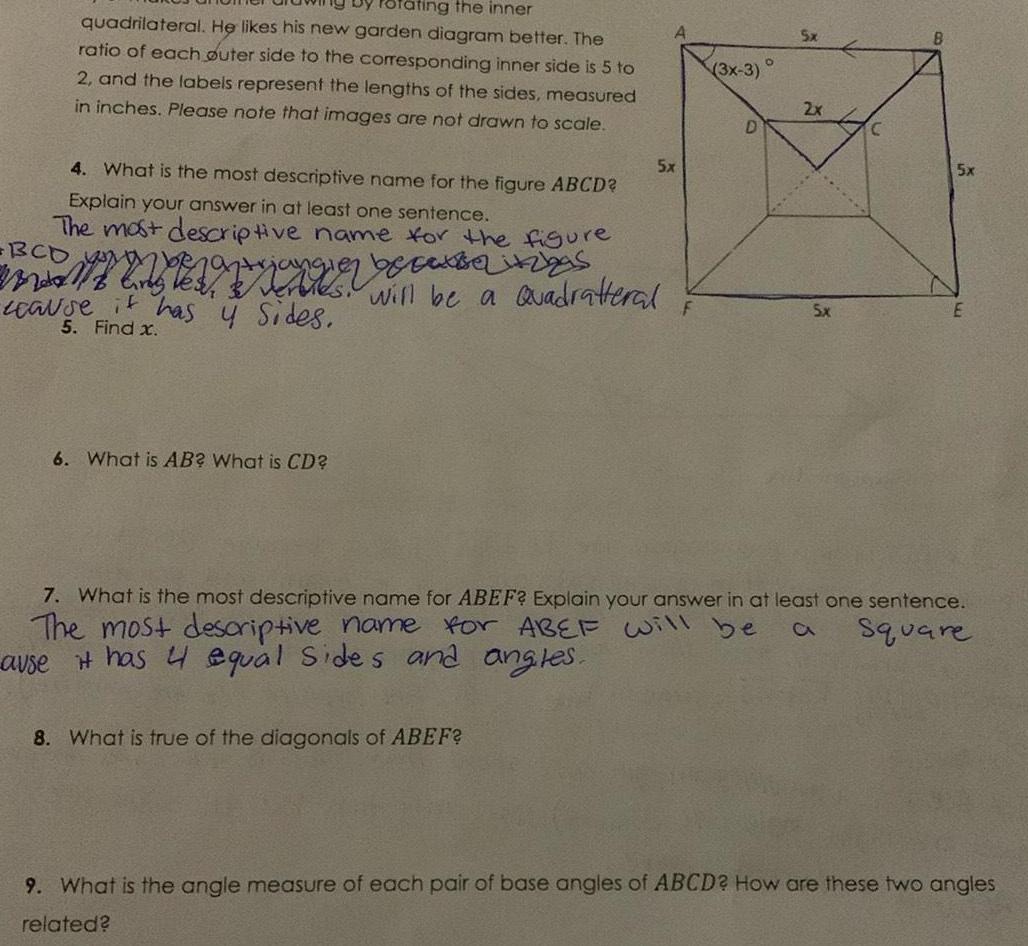
3D Geometryrating the inner quadrilateral He likes his new garden diagram better The ratio of each outer side to the corresponding inner side is 5 to 2 and the labels represent the lengths of the sides measured in inches Please note that images are not drawn to scale 4 What is the most descriptive name for the figure ABCD Explain your answer in at least one sentence The most descriptive name for the figure mangien e s cause it has y sides will be a Quadratteral 5 Find x 6 What is AB What is CD 5x 8 What is true of the diagonals of ABEF F 3x 3 D 5x 2x 5x E 7 What is the most descriptive name for ABEF Explain your answer in at least one sentence The most descriptive name for ABEF will be ause it has 4 equal sides and angles Square 9 What is the angle measure of each pair of base angles of ABCD How are these two angles related

Geometry
2D GeometrySimplify 1 cos 48cos 50 sin 40sin 50 A cos 8 B sin 0 C cos 90 D cos 30 2 sin 3ucos 3u cos 3usin 3u B cos 6u D sin 7u A sin 3u C sin 6u

Geometry
2D GeometryThe windshield wiper blade on Han s car is 25 inches long Each swipe of the wiper makes an angle of 125 degrees as pictured below To the nearest inch how far does the tip of the windshield wiper travel with each swipe of the blade 125 25

Geometry
Heights & DistancesA passenger in an airplane at an altitude of a 30 kilometers sees two towns directly to the east of the plane The angles of depression to the towns are 28 and 55 see figure How far apart are the towns How far apart are the ships Round your answer to one decimal place a km 55 28 88 Not drawn to sale
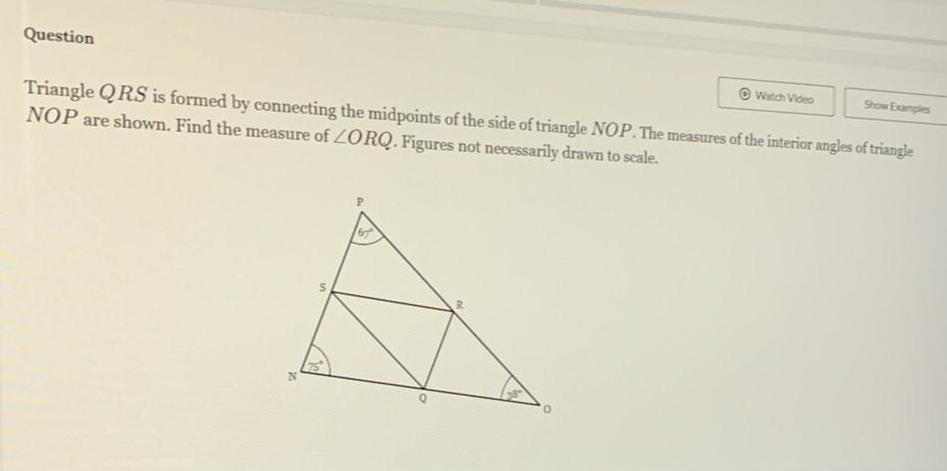
Geometry
Solution of trianglesQuestion Triangle QRS is formed by connecting the midpoints of the side of triangle NOP The measures of the interior angles of triangle NOP are shown Find the measure of ZORQ Figures not necessarily drawn to scale in R 0 Watch Video Show Examples
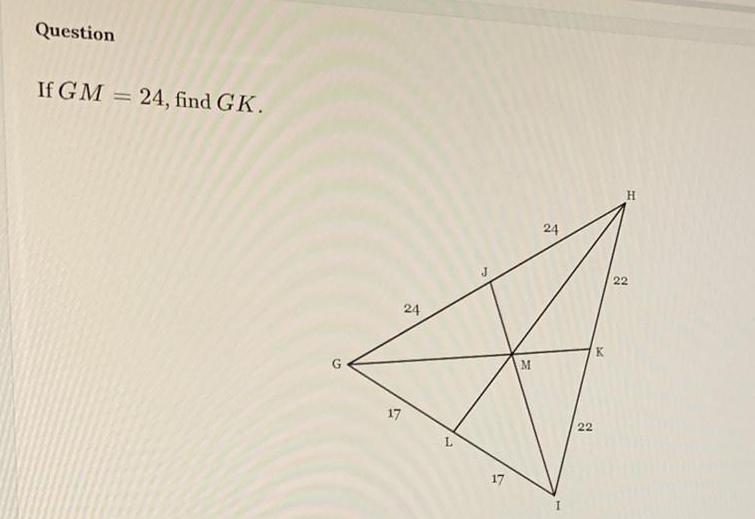

Geometry
2D GeometryQuestion In the diagram below of triangle TUV W is the midpoint of TV and X is the midpoint of UV If W X 53 6z and TU 46 7x what is the measure of W X U Watch Video Show Exa
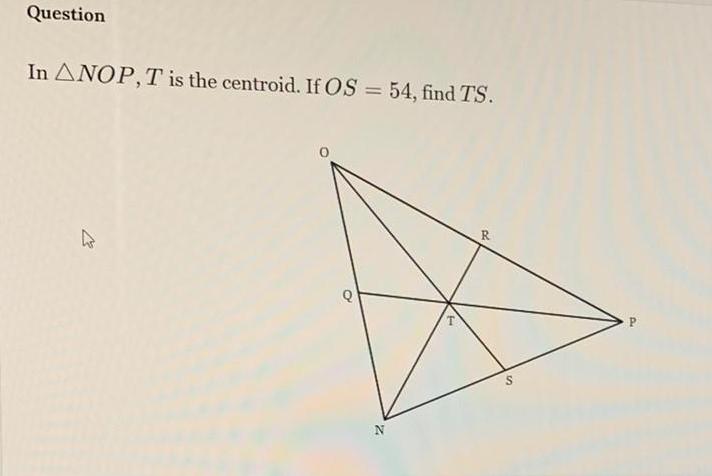

Geometry
2D Geometry9 15 Use the Laplace transform to solve the integral equation f t f sin t t f t dt sin t

Geometry
2D Geometry3 10 Use the Convolution theorem to evaluate the Laplace transform L cost cosh tt dt Do not evaluate the integral before transforming

Geometry
Vectors10 15 Use the Laplace transform to solve the initial value problem y y 8 t 2n y 0 1 y 0 0 No credit for any other method

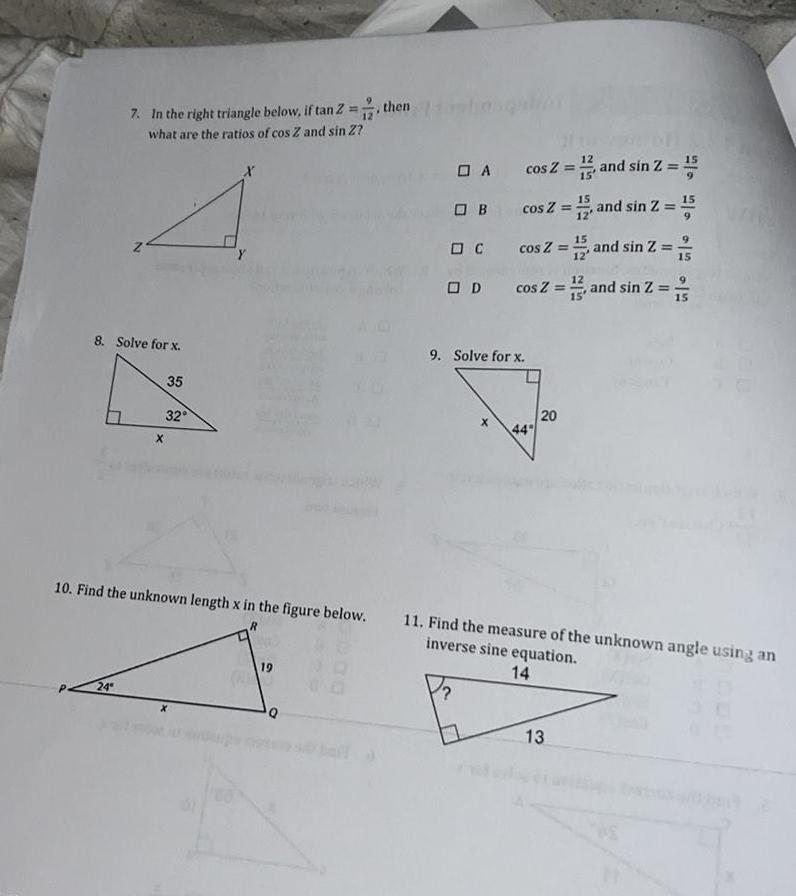
Geometry
Solution of triangles7 In the right triangle below if tan Z what are the ratios of cos Z and sin Z N 8 Solve for x 24 X 35 32 X 19 then Q 15 A cos Z and sin Z OB cos Z 1 and sin 2 15 cos Z 15 and sin Z 2 12 15 cos Z C OD 9 Solve for x 44 20 10 Find the unknown length x in the figure below 11 Find the measure of the unknown angle using an inverse sine equation 14 12 13 15 and sin Z 2

Geometry
Solution of trianglesEXPLAIN 1 Applying Relationships in Special Right Triangles Read Explain 1 and complete Your Turn 1 4 adapted from Lesson 13 3 Show all your work Side length Relationships in a 45 45 90 Right Triangle The hypotenuse is 2 time as long as each leg for any sized right triangle with 45 45 90 interior angles 60 45 2x x 2 Side length Relationships in a 30 60 90 Right Triangle The hypotenuse is twice as long as the shorter leg and the longer leg is 3 times as long as the shorter leg for any sized right triangle with 30 60 90 interior angles 30 45 x 3 Example If the hypotenuse has a length of 3 2 ft then x 3 The height and width are 3 ft long Example If the hypotenuse has a length of 6 ft then x 3 The height is 3 3 ft and the width is 3 ft If the hypotenuse is 6 feet then by rule 2x 6 Divide 2 on both sides makes x 3

Geometry
Vectorsangle Your Turn Apply the tangent ratio to find unknown lengths 1 A ladder needs to reach the second story window which is 10 feet above the ground and make an angle with the ground at 70 How far out from the building does the base of the ladder need to be positioned Round your answer to the nearest tenth EXPLAIN 3 Finding an Angle Measure Using Tangent Read Explain 3 and complete Your Turn 1 2 adapted from Lesson 13 1 Show all your work The inverse tangent function tan x takes a tangent ratio x and returns the angle If ratio the length of the two legs of a right triangle are nown then the inverse tangent function can be used to find the unknown measure of an angle of that right triangle You can use a scientific calculator to determine the value of this angle for any given ratio Again when using a calculator to evaluate an inverse trigonometric function you will need to make sure it is in degree mode not radian mode see explain 2 above Inverse of the Tangent Function Words Symbols Let ZA be an acute angle of right triangle A ABC and let x be the tangent ratio of ZA The inverse tangent of x is the measure of ZA tan 1 If tan A x then tan x mLA Y CA m A 70 X 10 ft Z tan x angle

Geometry
VectorsENGAGE Simplifying Radical Expressions Complete the following activity with your teacher in order to start your learning on trigonometry Simplifying Radicals a 49 c 175 Multiplying Radicals e 5 10 Ge B 3 12 6 b 18 d 5 45 f 6 6 h 4 20 5 80 A 8 10 4 Matic factor free Circle pairs Pull one number from each pair and marply 2 x 2 455 4 The number the branch at the end ot circled is left inside the radical Answer 455 5 2 5 10 Combine into one radical Then simplify what s inside 2 5 73 2 7 5 3 14 15 Multiply the regular numbers together and multipy the radicals together


Geometry
Solution of trianglesLesson 13 1 Homework 1 Z EVALUATE HW 3 3 Find the ratio for tan X X Find the numerical value of the following trigonometric function tan 37 0 15 12 A tan 0 B 5 Which equation can be used in solving for 07 A B tan 8 C tan 0 D tan 0 11 Complete problems 1 10 below for independent practice All angles below are in terms of degrees NOT radians Use a separate piece of paper if you need more space When you are finished check the solutions with your teacher 1W E Independent Practice 9 8 2 Find the numerical value of the following trigonometric function tan 73 4 Find the ratio for tan X 30 X Z 24 A 7 L 6 Which equation can be used in solving for 8 0 Y 18 A tan 0 B tan 0 0 tan 8 D tan 0 11 E B
Geometry
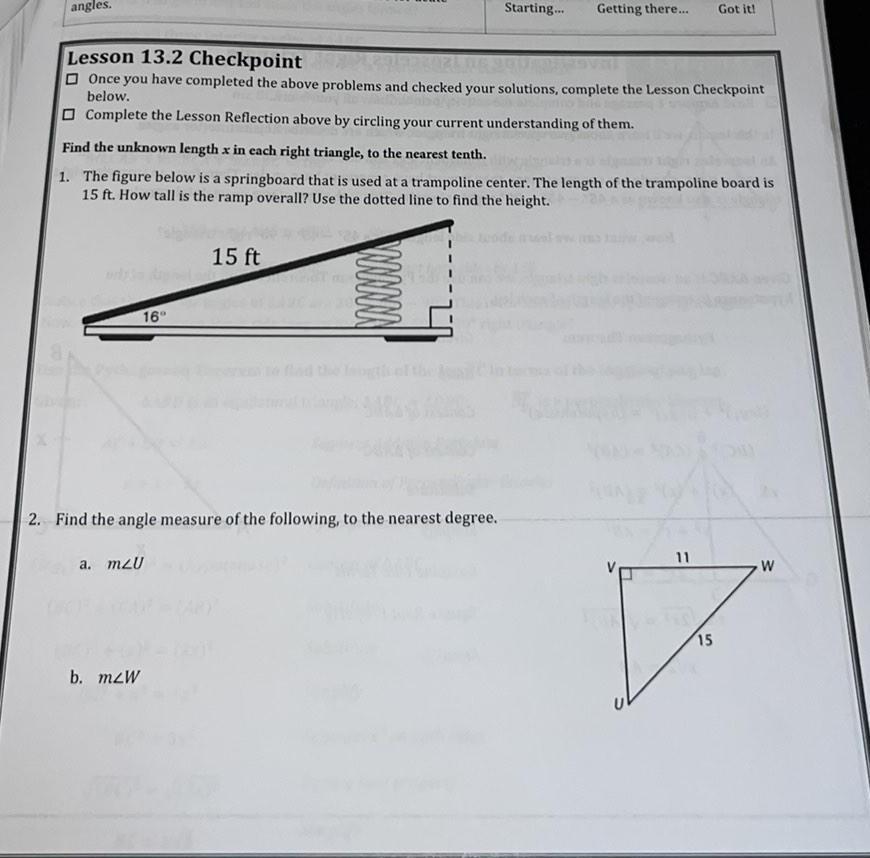
Coordinate systemangles Lesson 13 2 Checkpoint Once you have completed the above problems and checked your solutions complete the Lesson Checkpoint below Complete the Lesson Reflection above by circling your current understanding of them Find the unknown length x in each right triangle to the nearest tenth 1 The figure below is a springboard that is used at a trampoline center The length of the trampoline board is 15 ft How tall is the ramp overall Use the dotted line to find the height 16 a m2U b mzW 15 ft NNNNNN 2 Find the angle measure of the following to the nearest degree Starting Getting there S Got it 11 7 15 W

Geometry
Solution of trianglesopposite adjacent and hypotenuse At the same time the new vocabulary words cross reference How do you w it all organized in your head With memory techniques Below is an example of how acronyms are used to help Within two lessons you have learned a lot of new vocabulary words such as sine cosine tangent inverse remember and organize new knowledge Memory Technique Acronyms Acronyms are words formed from the first letters from a list of words Use an acronym to remember trigonometric ratios Memory Technique for Trigonometric Ratios SOHCAHTOA The acronym SOHCAHTOA pronounced soh cah toa comes from the first letters from the list of words sine opposite hypotenuse cosine adjacent hypotenuse tangent opposite adjacent Get it It is to help you remember the three trig ratios and how to set up the fraction such as what side belongs in the numerator or denominator Fill in the blank 0 O A S C T H H CH Graphic Organizer Use this graphic being asked to angle Examp Fir This is to help you remember Sine is opposite over hypotenuse Cosine is adjacent over hypotenuse Tangent is opposite over adjacent Imagine if you didn t know the acronym SOHCAHTOA You would be saying Sine is opposite over potenuse Cosine is adjacent over hypotenuse Tangent is opposite over adjacent over and over and over until you remembered it Optional It may even help if you color it in to remember the acronym Trigonometric cha SOUCA IO 1
Geometry
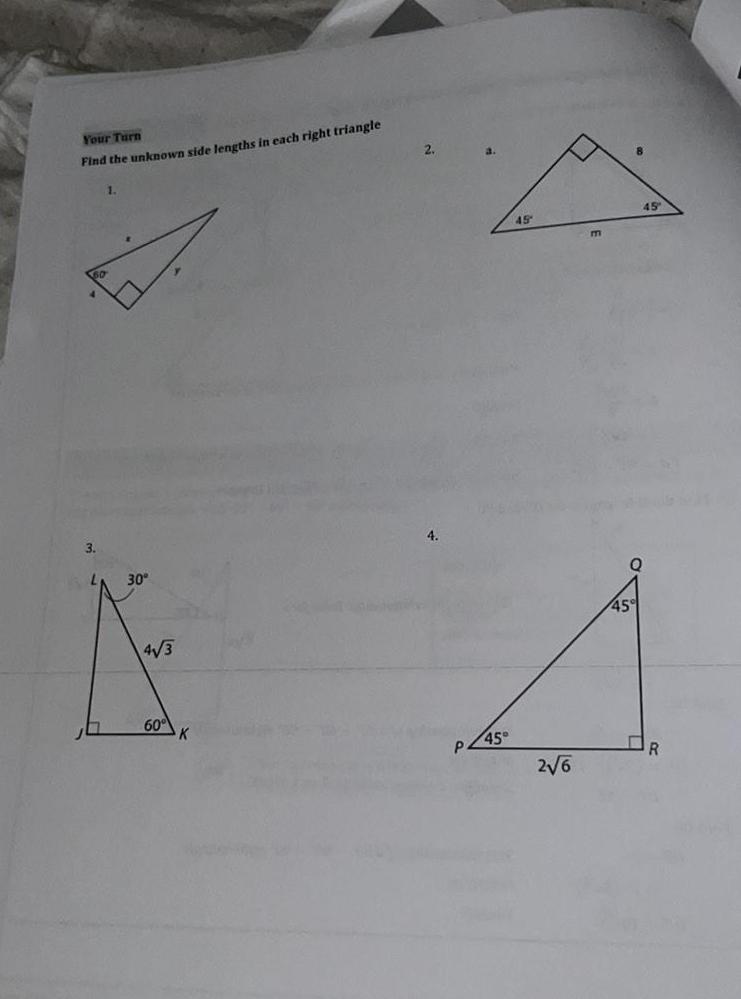
AreaYour Turn Find the unknown side lengths in each right triangle 3 1 30 4 3 60 2 4 P a 45 45 2 6 m 45

Geometry
2D GeometryLesson HW 1 Which trigonometric function is represented by 2 Which trigonometric ratio best represents the ratio opposite leg solving a cosine function hypotenuse X DA OB C B 3 Which trigonometric ratios are equivalent to 12 Choose two 37 OA B C OD work Complete problems 1 11 below for independent practice Sine Cosine Tangent A OB C OD Y 12 11 FROHEAT Sin X Cos X Sin Z Cos Z 24 X 5 Find the correct equation to solve for x sin x cos 24 When you are finished check the solutions with your teacher 11 cos x 1 24 sin 24 11 35 37 Z A OB C OD A B C D 4 Which trigonometric ratios are equivalent to Choose two opposite leg adjacent leg hypotenuse DA B adjacent leg adjacent leg hypotenuse opposite leg hypotenuse D Z X Sin X Cos Z Sin Z Cos X 21 6 Find the correct equation to solve for x Q 55 10 R sin 55 cas 55 15 1551 51 cos 55 sin 55 10 35 28 X

Geometry
2D GeometryEVALUATE Independent Practice bas sale S Ele Learning Goal Lesson Reflection Circle I can explain how to derive the trigonometric ratios for acute angles Starting Getting there Lesson 13 1 Checkpoint Once you have completed the above problems and checked your solutions complete the Lesson Checkpoint below Complete the Lesson Reflection above by circling your current understanding of them 1 Find DE Round your answer to the nearest tenth D 13 9 210 F the 2 Find ZR Round your answer to the degree 24 R 3 Find LP Round your answer to the degree
Geometry
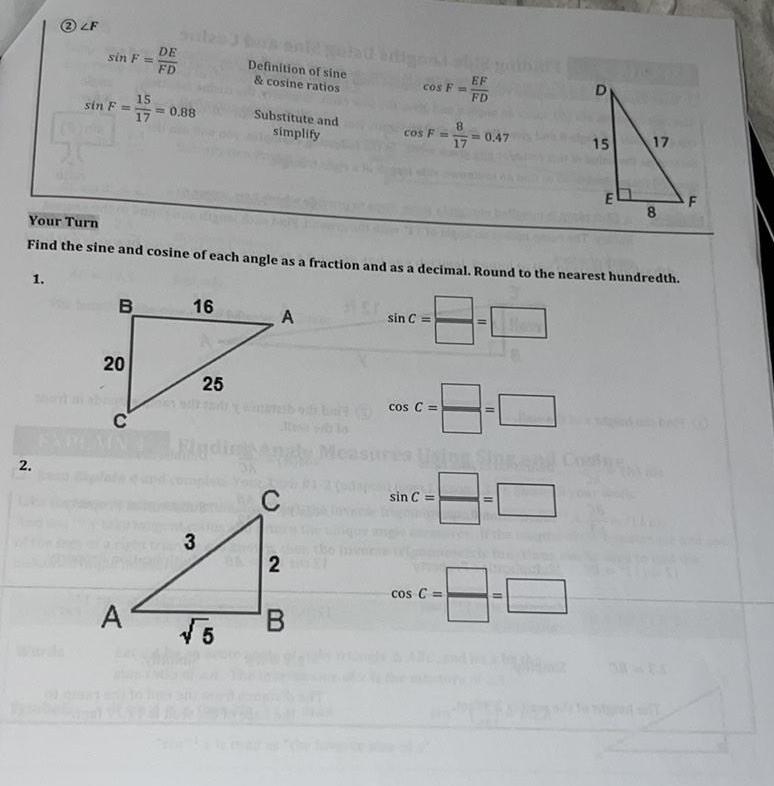
Solution of triangles1 2LF 2 sin F sin F B 20 C DE FD 15 17 0 88 A 16 3 25 Definition of sine cosine ratios 5 Substitute and simplify Your Turn Find the sine and cosine of each angle as a fraction and as a decimal Round to the nearest hundredth A C 2 cos F B cos F sin C cos C sin C 17 cos C EF FD 0 47 11 11 11 D 15 Cos E 17 8 F
Geometry
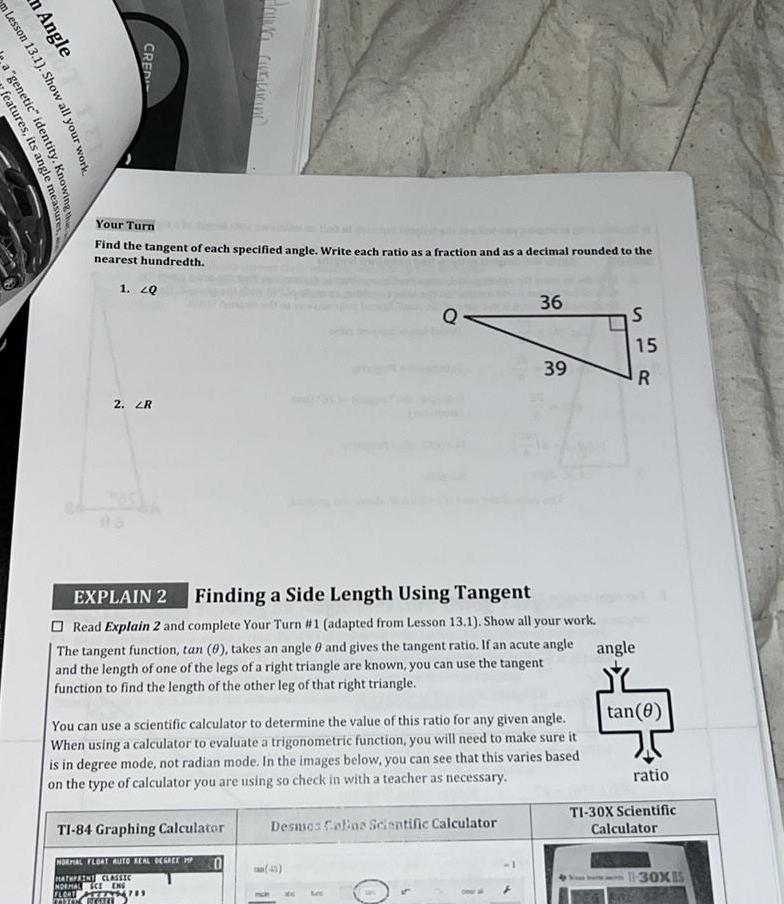
2D Geometryn Lesson 13 1 Show m Angle features its angle measures a genetic identity Knowing the CREDI Your Turn Find the tangent of each specified angle Write each ratio as a fraction and as a decimal rounded to the nearest hundredth 1 20 2 ZR EXPLAIN 2 Finding a Side Length Using Tangent Read Explain 2 and complete Your Turn 1 adapted from Lesson 13 1 Show all your work The tangent function tan 0 takes an angle 8 and gives the tangent ratio If an acute angle and the length of one of the legs of a right triangle are known you can use the tangent function to find the length of the other leg of that right triangle TI 84 Graphing Calculator You can use a scientific calculator to determine the value of this ratio for any given angle When using a calculator to evaluate a trigonometric function you will need to make sure it is in degree mode not radian mode In the images below you can see that this varies based on the type of calculator you are using so check in with a teacher as necessary NORMAL FLOAT AUTO REAL DEGREE MP MATHPAINT CLASSIC NORMAL CE ENG FLOOT YRITYS479 THE RESELL 0 36 Desmas Colias Scientific Calculator 39 45 S 15 R angle tan 0 ratio TI 30X Scientific Calculator 11 30XIS

Geometry
3D GeometryYour Turn 1 Suppose a new regulation states that the maximum angle of a wheelchair ramp is 8 At least how long must the new ramp be Round to the nearest tenth of a foot Definition of sine ratio sin A sin 8 AC BC AC 2 3 AC AC sin 8 2 3 2 3 sin 8 AC 16 5 Substitution Property Multiplication Property Division Property Simplify C wall B 2 3 ft An A

Geometry
Solution of trianglesIn the following example you will learn how to apply the inverse tangent function to find an unknown a Example Apply the tangent ratio to find unknown angles Find the measure of the indicated angle Round your answer to the nearest tenth of a degree What is mLA BC tan A CA tan A A tan mzA What is m2B A 27 8 tan B tan B B tan 19 2 Find m2K 36 H 1 CA BC 36 19 36 m2B 62 2 Definition of tangent ratio Substitution Property Definition of an Inverse Tangent 1 use calculator Calculate tan Definition of tangent ratio Substitution Property Definition of an Inverse Tangent Calculate tan use calculator 36 in Your Turn Find the measure of the indicated angle Round your answer to the nearest tenth of a degree 1 Find m2 K 19 in Dc 93 Graphic Organize Use this graphic org you are being aske side or angl

Geometry
Coordinate systemWhat is P factor of 18 Simplify your answer and write it as a fraction or whole number

Geometry
2D GeometryDividing Radicals 6 V100 1 5 5 3 NSSSSS 3 3 2 2 2 2 Multiply by Simplify Rational denom

Geometry
Coordinate systemFind the equation of a line passing through the given point and parallel to the given equation Write your answer in slope intercept form 1 4 4 and y Answer 2 4 4 and y x 1 Answer x 3 9 3 0 4 and y Answer 5 x 1 2X 4 0 4 and y 3x 3 5 1 1 and y 4x 4 Answer 6 1 3 and y x 4 Answer 7 3 1 and y 4x 10 Answer 8 4 4 and y x 2
Geometry
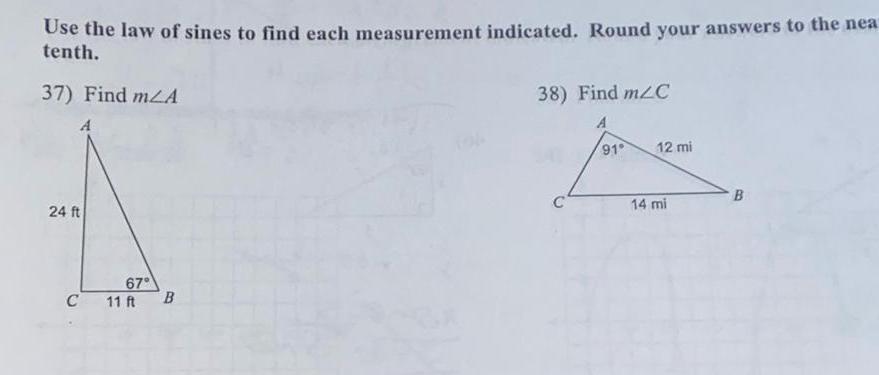
2D GeometryUse the law of sines to find each measurement indicated Round your answers to the nea tenth 37 Find mA 24 ft 67 C 11 ft B 38 Find m C 91 12 mi 14 mi B
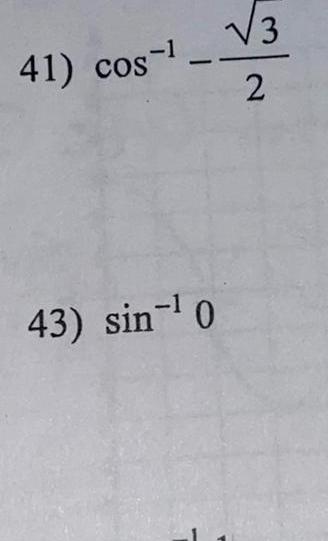
Geometry
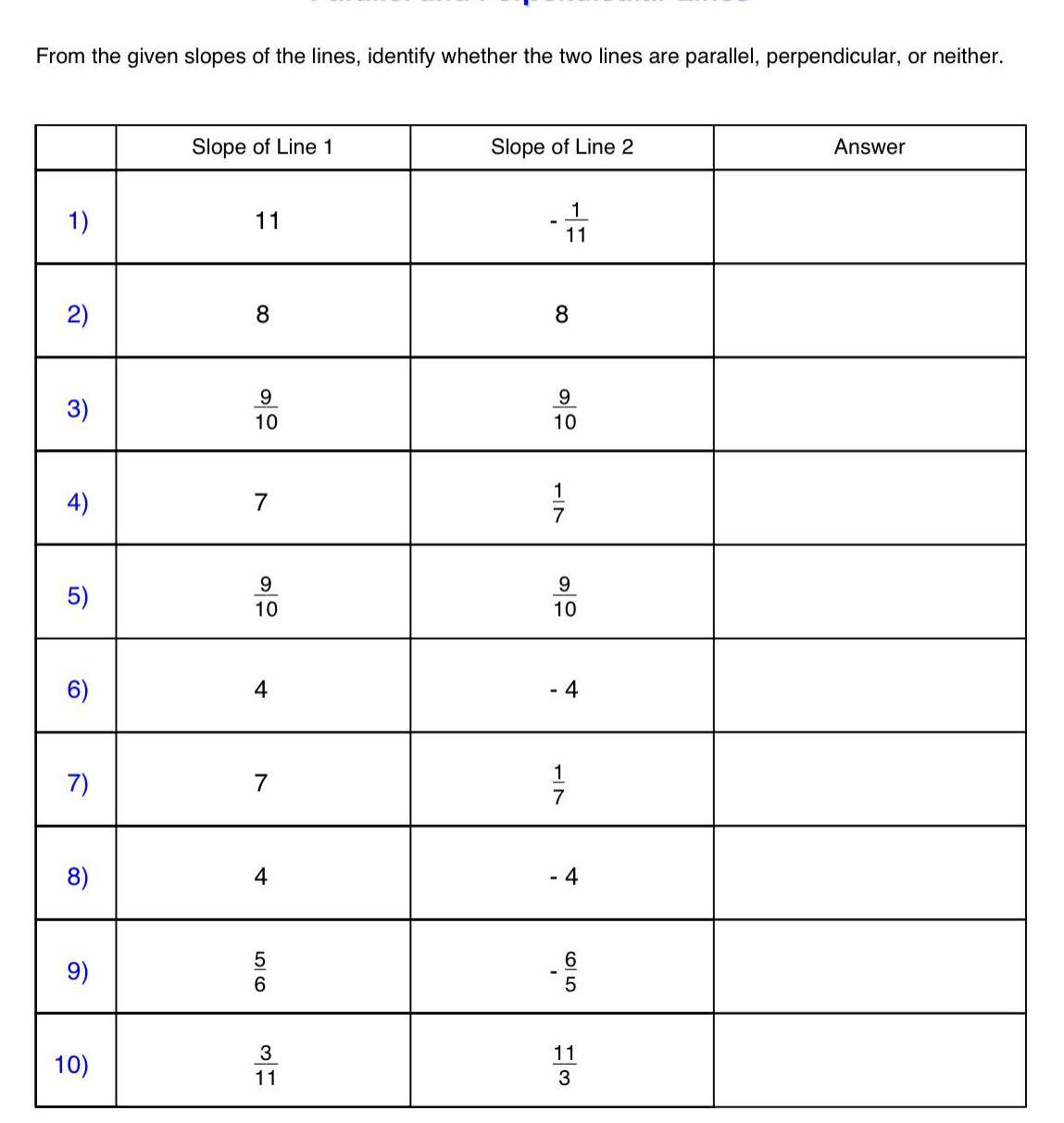
2D GeometryFrom the given slopes of the lines identify whether the two lines are parallel perpendicular or neither 1 2 3 4 5 6 7 8 9 10 Slope of Line 1 11 8 9 10 7 9 10 4 7 4 5 6 3 11 Slope of Line 2 8 1 11 9 10 TIN 1 9 10 1 7 4 2015 6 11 3 Answer

Geometry
2D GeometryFor the given slope find the slope of any parallel and perpendicular line to it 1 2 3 4 5 6 7 8 9 10 Slope of a Line 3 8 11 2 8 N 12 11 12 4 2 4 7 611 9 Slope of Any Parallel Line Slope of Any Perpendicular Line

Geometry
2D Geometry6 An obtuse angle has the point B x y on its terminal arm a Express the length of line segment OB in terms of x and y ometric ratios for the angle