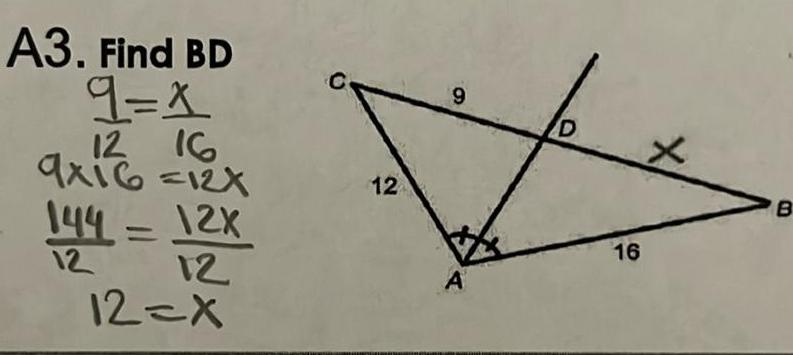
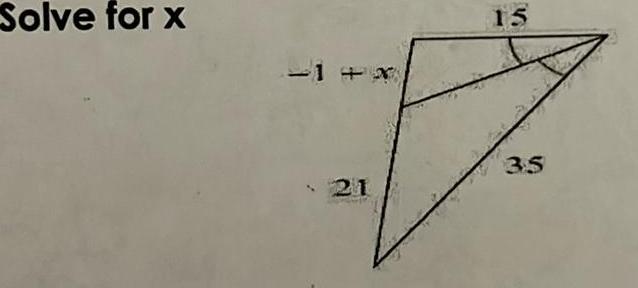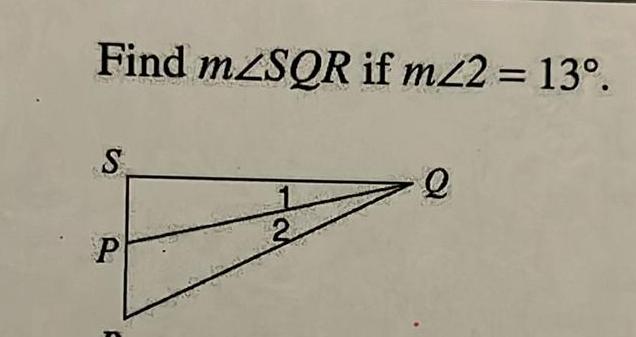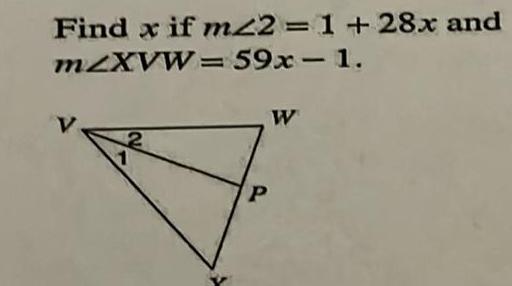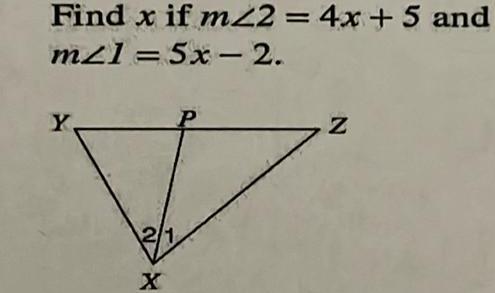Geometry Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Geometry
Solution of trianglesMP and NP are midsegments of AJKL Your Turn 1 Find mzJLK MP LK LJMP LJLK mzJMP mzJLK 105 mzJLK 2 Find JL 2PN JL 2 39 JL 78 JL 2QR MN 2 4n 9 14n 8n 18 14n 18 6n 3 n MN 14n Triangle Midsegment Theorem Corresponding Angles Theorem Definition of Congruent Angles Substitution Property MN 14 3 MN 42 Triangle Midsegment Theorem Substitution Property EXPLAIN 2B Using the Triangle Midsegment Theorem Read Explain 2B and complete Your Turn 3 4 Adapted from Lesson 8 4 Show all your work Example M 1 Find MN Simplify Triangle Midsegment Theorem Substitution Property Distributive Property Subtraction Property of Equality Division Property of Equality Given 105 M H Substitution Property Simplify Q P P 39 N 4n 9 9 14n R N

Geometry
Coordinate systemCalculate the exact value of cos a given cos 2x 12 and Do not use a calculator
Geometry
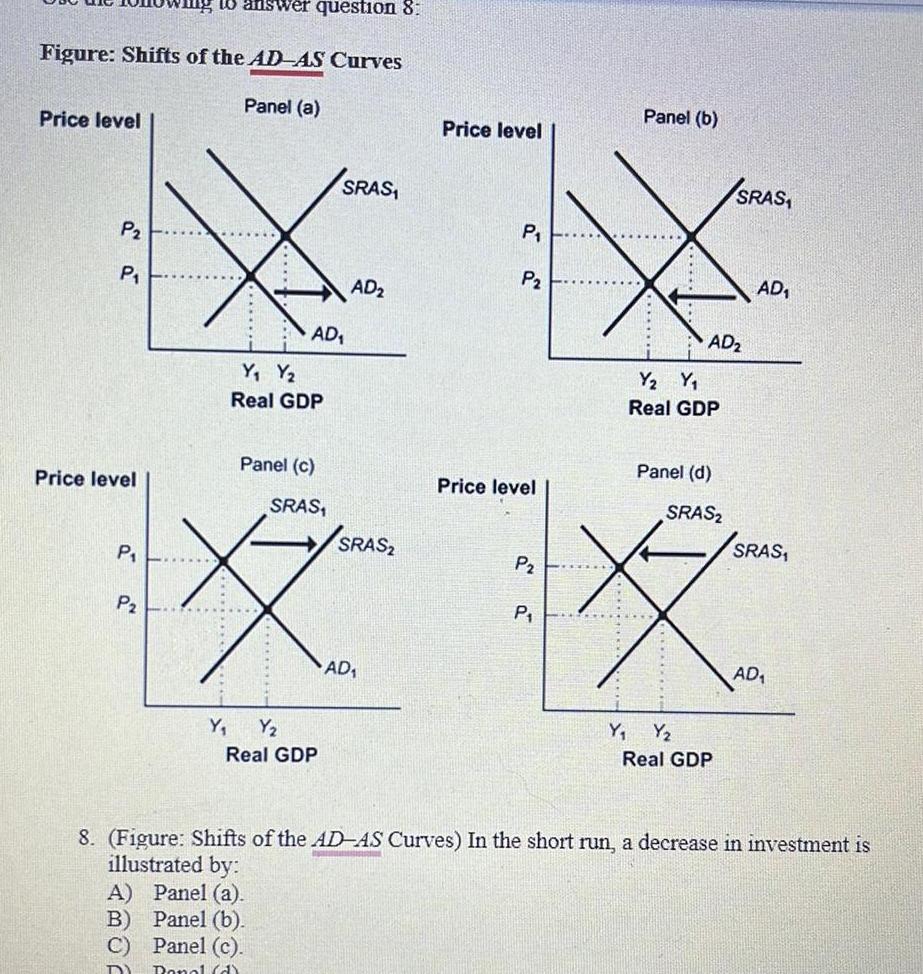
Area10 answer question 8 Figure Shifts of the ADAS Curves Panel a Price level P2 P Price level P P Y Y Real GDP AD SRAS Y Y Real GDP Panel c SRAS SRAS AD A Panel a B Panel b C Panel c DY Ronal d AD Price level P P Price level P P Y Panel b AD Y Y Real GDP Panel d SRAS SRAS Y Real GDP AD SRAS AD 8 Figure Shifts of the AD AS Curves In the short run a decrease in investment is illustrated by

Geometry
Area18 Using monetary policy to address a recessionary gap created by a supply shock involves to A decreasing the amount of money in circulation lower the aggregate price level B increasing interest rates decrease investment spending C decreasing interest rates lower the aggregate price level D increasing the amount of money in circulation lower the unemployment rate

Geometry
Solution of trianglesLines Angles and Triangles Part 2 ASSESSMENT Credit Checkpoint Complete the following problems Show all your work Learning Goal from Lesson 6 2 6 3 and 7 3 I can prove theorems about geometric figures using triangle congruence and similarity a 1 Identify the sides or angles that need to be congruent in order to make the given triangles congruent by AAS Lesson 6 2 1 point a D AV B DA OB C B C F D 2 Which of the following properties prove that the triangles are congruent Lesson 6 2 and 6 3 1 point b Which statement would prove AAMC ABMC by HL Congruence Theorem M E E ASA Congruence Theorem AAS Congruence Theorem SAS Congruence Theorem b How I Did Circle one I got it I m still learning it A4 E A D A LA LB B ZMCA LMCB C 4C C B

Geometry
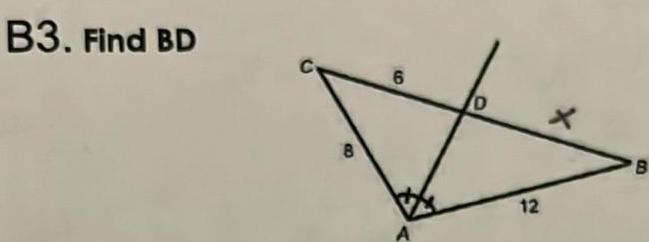
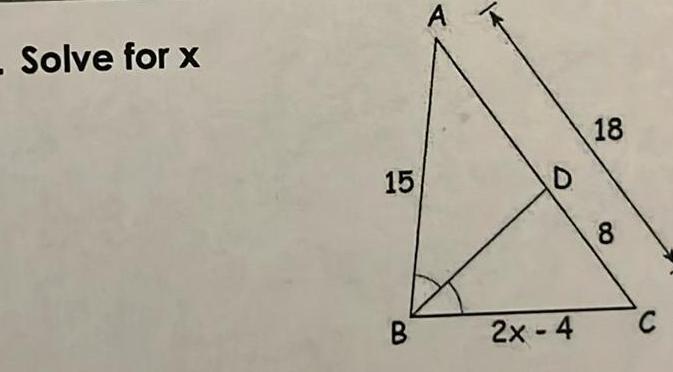
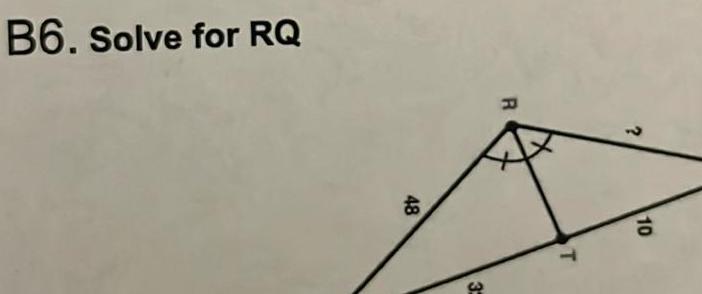
Solution of trianglesour Turn 1 12 unit Use the Triangle Inequality Theorem to fell with the given lengths Fynl
Geometry
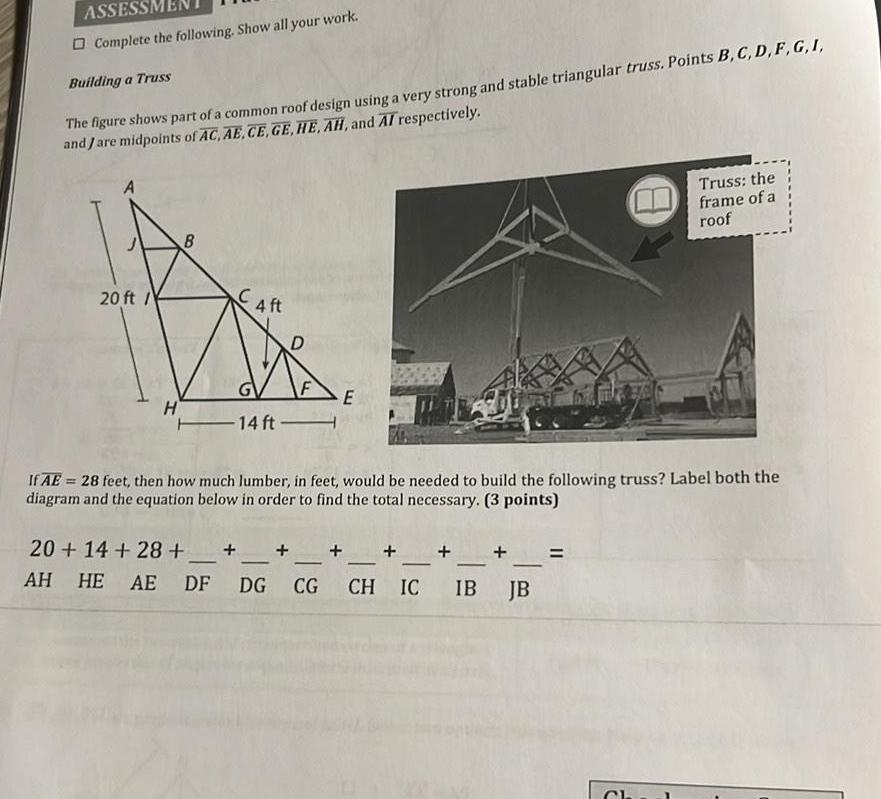
2D GeometryASSESSM Complete the following Show all your work Building a Truss The figure shows part of a common roof design using a very strong and stable triangular truss Points B C D F G I and Jare midpoints of AC AE CE GE HE AH and AI respectively 20 ft H B 4 ft F 14 ft E If AE 28 feet then how much lumber in feet would be needed to build the following truss Label both the diagram and the equation below in order to find the total necessary 3 points 20 14 28 AH HE AE DF DG CG CH IC IB Truss the frame of a roof JB
Geometry
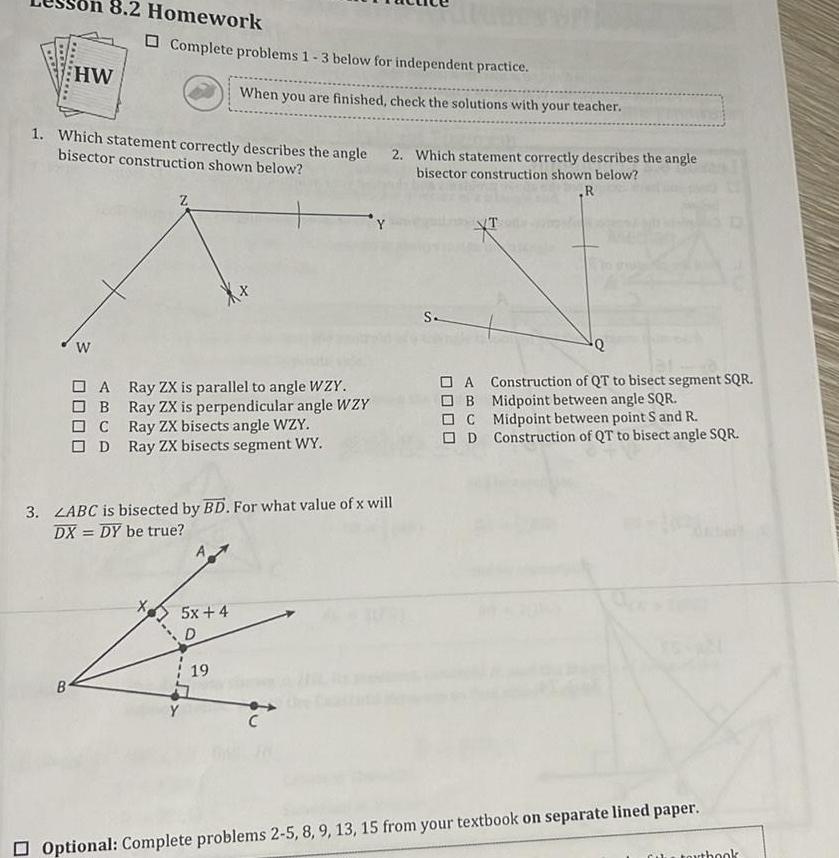
2D Geometry8 2 Homework HW B W 1 Which statement correctly describes the angle bisector construction shown below Complete problems 1 3 below for independent practice A B C OD Z When you are finished check the solutions with your teacher Ray ZX is parallel to angle WZY Ray ZX is perpendicular angle WZY Ray ZX bisects angle WZY Ray ZX bisects segment WY 3 LABC is bisected by BD For what value of x will DX DY be true 5x 4 D 19 2 Which statement correctly describes the angle bisector construction shown below R C S A Construction of QT to bisect segment SQR OB Midpoint between angle SQR C Midpoint between point S and R D Construction of QT to bisect angle SQR Optional Complete problems 2 5 8 9 13 15 from your textbook on separate lined paper book

Geometry
2D Geometry3 Consider ZF such that cos F 37 a Which quadrants can ZF be in b Find the coordinates of a point on the terminal arm of the angle in each quadrant c If you are also told that the sine of the angle is negative in which quadrant is F other primary trigonometric ratios for ZF in the quadrant identified in part c
Geometry
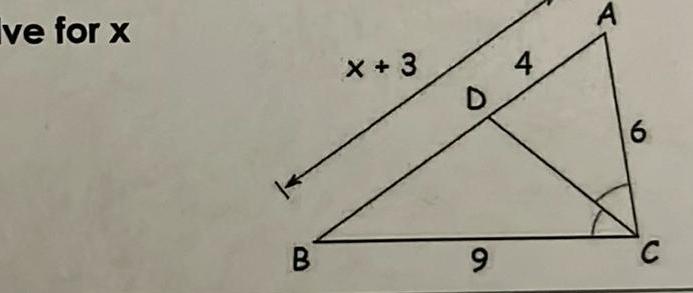
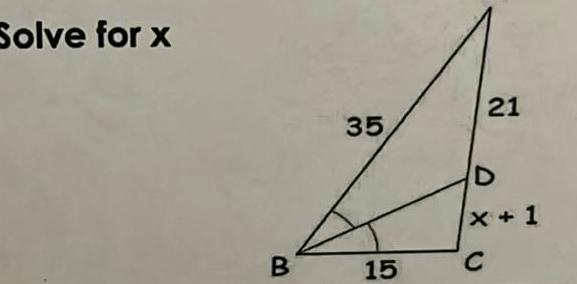
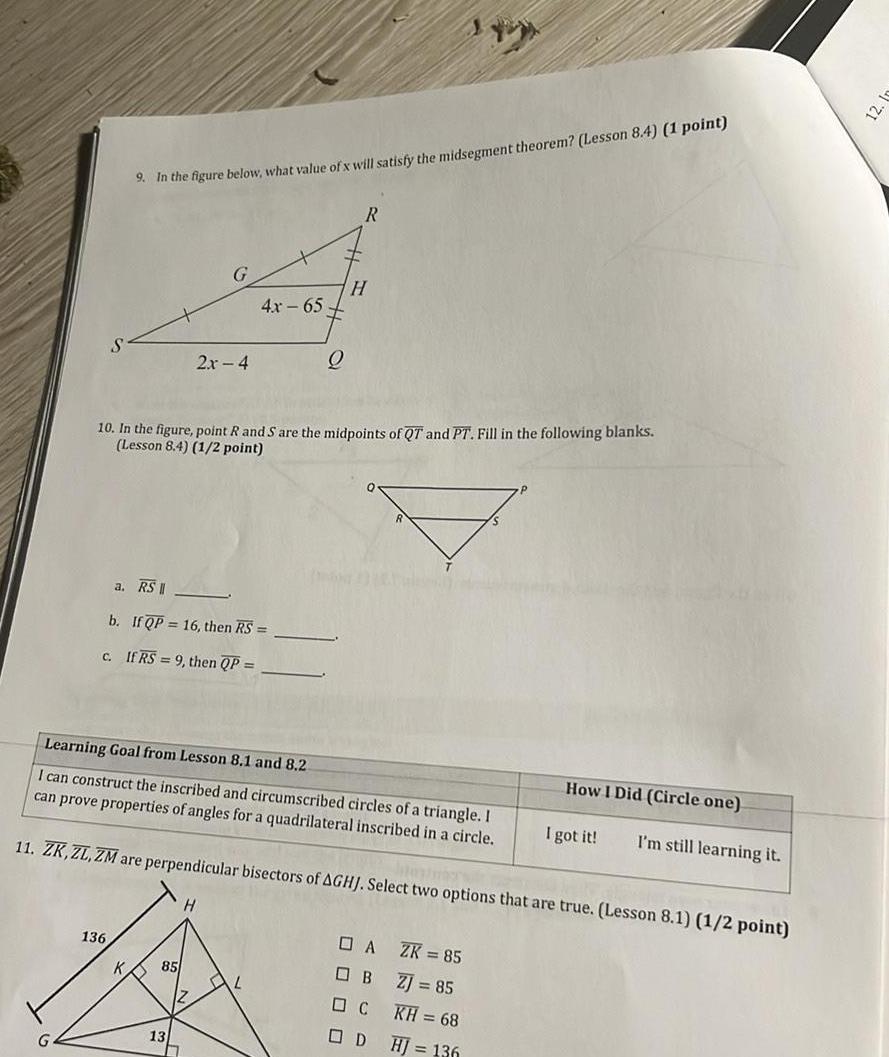
Vectors9 In the figure below what value of x will satisfy the midsegment theorem Lesson 8 4 1 point 136 G a RS II b If QP 16 then RS C If RS 9 then QP 2x 4 85 10 In the figure point R and S are the midpoints of QT and PT Fill in the following blanks Lesson 8 4 1 2 point 13 4x 65 Learning Goal from Lesson 8 1 and 8 2 I can construct the inscribed and circumscribed circles of a triangle I can prove properties of angles for a quadrilateral inscribed in a circle 11 ZK ZL ZM are perpendicular bisectors of AGHJ Select two options that are true Lesson 8 1 1 2 point Q AL R H A OB C D ZK 85 ZJ 85 KH 68 HJ 136 How I Did Circle one I got it I m still learning it 12 1
Geometry
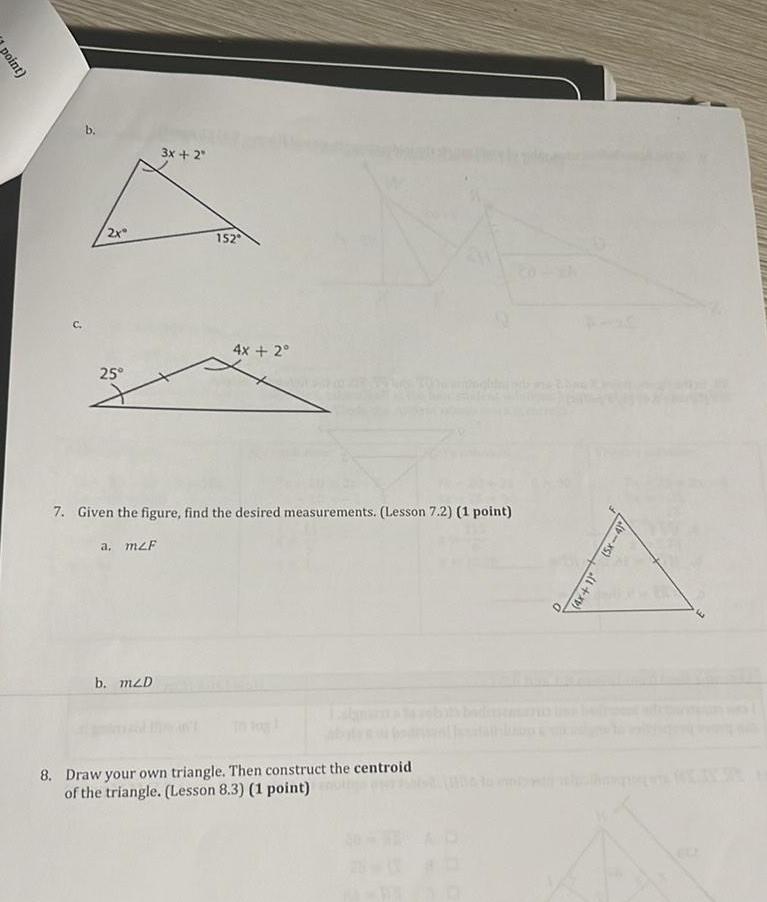
2D Geometrypoint 2x 25 3x 2 b mzD 152 4x 2 7 Given the figure find the desired measurements Lesson 7 2 1 point a mzF 8 Draw your own triangle Then construct the centroid of the triangle Lesson 8 3 1 point 4x 1 5x 4

Geometry
Coordinate systemEVALUATE Independent Practice Lesson 8 4 Homework HW DE II 2DE 1 Fill in the following statements 14 3 Find the measurement of ED H 5 Solve for x W Complete problems 1 6 below for independent practice x 6 When you are finished check the solutions with your teacher X 2 Fill in the following statements R 4 QP 11 2RS 4 Find the measurement of NL 6 Solve for x M x 14 11 x 011 15 19 from your textbook on separate lined paper
Geometry
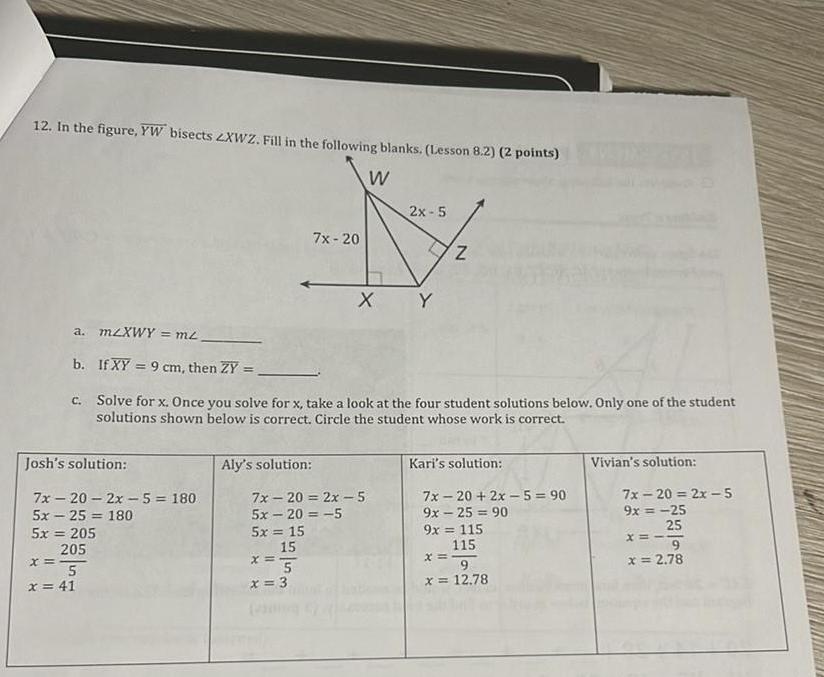
2D Geometry12 In the figure YW bisects ZXWZ Fill in the following blanks Lesson 8 2 2 points W 2x 5 7x 20 N X Y Josh s solution a m XWY m b If XY 9 cm then ZY c Solve for x Once you solve for x take a look at the four student solutions below Only one of the student solutions shown below is correct Circle the student whose work is correct 7x 20 2x 5 180 5x25 180 5x 205 205 x 5 x 41 Aly s solution 7x 20 2x 5 5x 20 5 5x 15 15 x 5 N x 3 Kari s solution 7x 20 2x 5 90 9x 25 90 9x 115 115 x 9 x 12 78 Vivian s solution 7x 20 2x 5 9x 25 25 x 9 x 2 78

Geometry
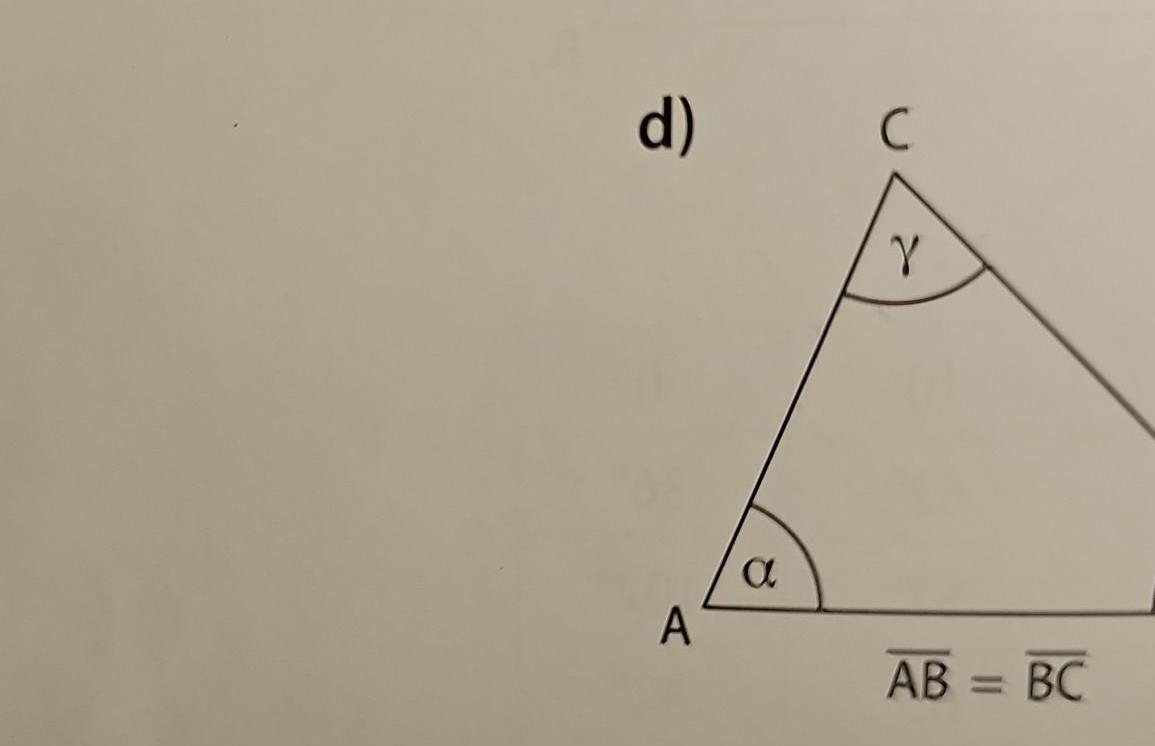
2D Geometry3 Determine whether a triangle can have the following sides with the given lengths Lesson 7 3 1 point a 5 mi 19 mi 15 mi b 4 ft 3 ft 10 ft 4 Write the angles of ADEF in order from smallest to largest Lesson 7 3 0 5 points Learning Goal from Lesson 7 1 7 2 8 3 and 8 4 I can prove the following theorems about triangles 2 25 E 1 105 D The measures of interior angles of a triangle sum to 180 The base angles of isosceles triangles are congruent The medians of a triangle meet at a point The segment joining midpoints of two sides of a triangle is parallel to the third side and half the length 5 Write the sides of AGHI in order from smallest to largest Lesson 7 3 0 5 points 6 Find the value of x in each of the given figures Lesson 7 1 and 7 2 2 points a How I Did Circle one I got it 59 61 H I m still learning it

Geometry
2D Geometryn Your Turn Use the Triangle Inequality Theorem to tell whether a triangle can have the following sides with the given lengths Explain 1 12 units 4 units 17 units EXPLAIN 3 largest angle Read Explain 3 and complete Your Turn 1 2 adapted from Lesson 7 3 Show all your work In relation to each other the relative size of the side lengths of a triangle can be used to determine the relative size of the angles This means that if you are given the side lengths in order you can use them to order the angle by size largest side Ordering a Triangle s Angle Measures Given Its Side Lengths Side Angle Relationships in Triangles 2 24 cm 8 cm 30 cm Embr medium side medium angle In any triangle the larger angle is opposite the longer side AB AC BC SO mzC m2B mzA B Example For each triangle order its angle measures from least to greatest In the figure we see that the sides from shortest to longest are AB BC and AC The angles opposite these sides are LC LA and LB respectively So the order of angles from least to greatest is LC LA and LB shortest angle shortest side 2 4 15 3 A C 12

Geometry
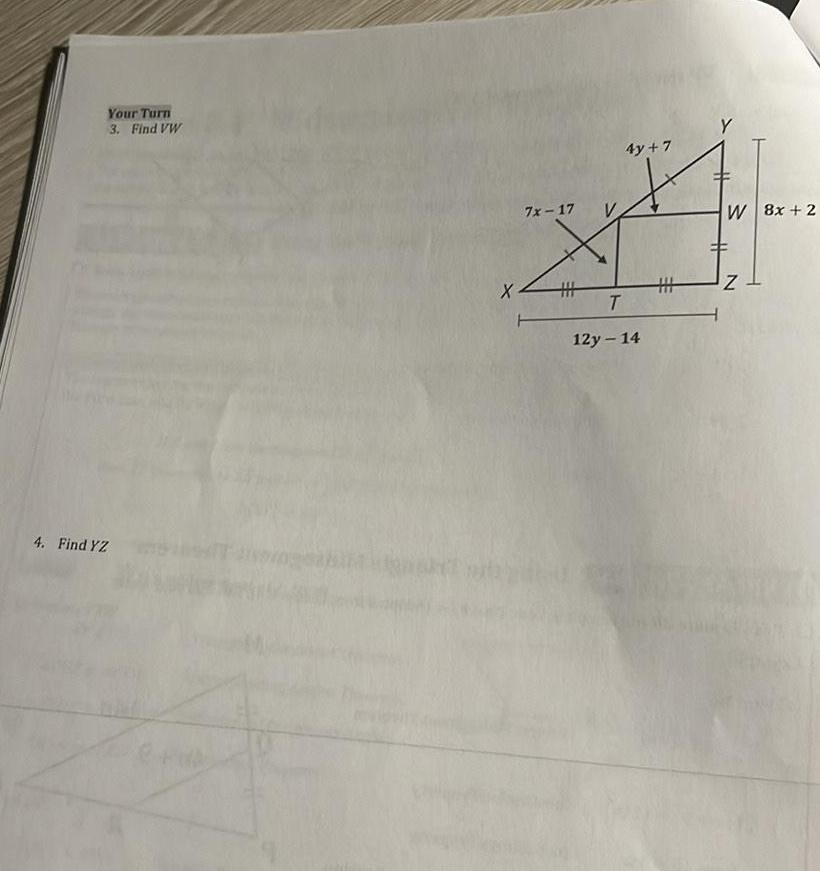
2D GeometryLearning Goal I can prove the following theorems about triangles The segment joining midpoints of two sides of a triangle is parallel to the third side and half the length X Q Lesson 8 4 Checkpoint Once you have completed the above problems and checked your solutions complete the Lesson Che below Complete the Lesson Reflection above by circling your current understanding of the Learning Goal 1 Given the figure below solve for x Then find the value of QP H x 3 x 3 3x 3 P 2 Given the figure below solve for x Then find the value of XV x 2 I V G P Starting Getting there
Geometry
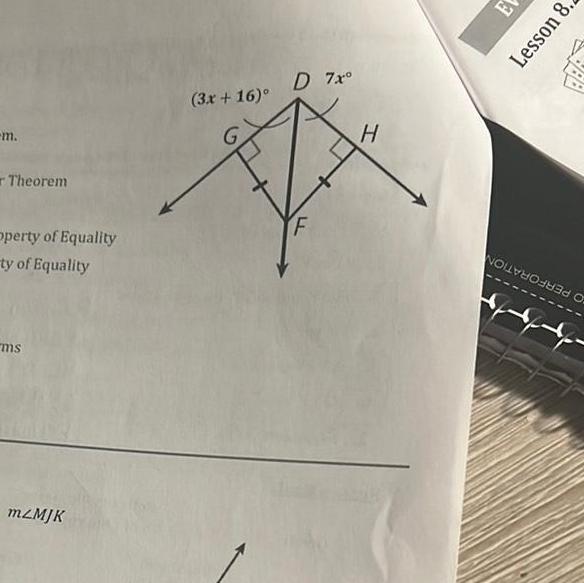
2D Geometrym Theorem Operty of Equality ty of Equality ms mzMJK 3x 16 D 7x F H E Lesson 8 NOREER O

Geometry
2D GeometryCool Down Make Your Own Invent measurements that would show triangle XYZ is similar to triangle NLM using the Side Angle Side Triangle Similarity Theorem Z N M

Geometry
VectorsFind the area of the triangle having the indicated angle and sides Round your answer to one decimal place C 128 a 3 b 5

Geometry
2D Geometryangle DBC angle ABE angle ABC A In the diagram which angles are vertical angles Choose 2 pairs angle EBD E B C angle DBC O O O O angle ABE O O O angle ABC O OOO angle EBD O O O

Geometry
2D GeometryIn the triangle below x 8 Use the Law of Cosines to solve the triangle Round your answers to two decimal places A B 12 cm O B 0 O 18 cm x cm C
Geometry
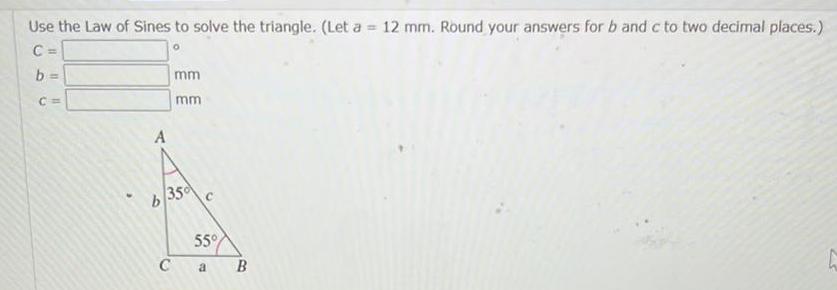
Coordinate systemUse the Law of Sines to solve the triangle Let a 12 mm Round your answers for b and c to two decimal places 0 C b A mm C mm b 350 C 55 a B 25

Geometry
3D GeometryUse a graphing utility to complete the table and graph the functions in the same viewing window Use both the table and the graph as evidence that yyz Round your answers to four decimal places Y cos x sin x tan x y2 sec x X 4 3 Y Y2 Verify the identity algebraically 4 8 Y cos x sin x tan x cos x cos x 1 cos x cos x X 5 3 X 5 8 6 3 6 8 7 3
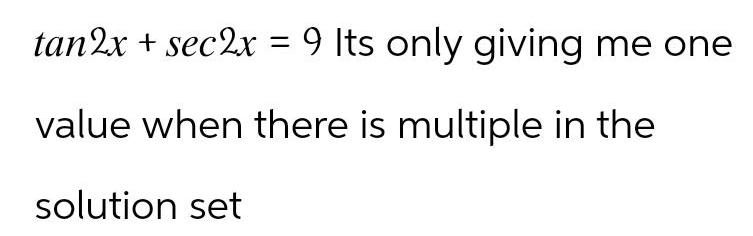
Geometry
2D Geometrytan2x sec2x 9 Its only giving me one value when there is multiple in the solution set

Geometry
Heights & DistancesFind the exact values of sin u 2 cos u 2 and tan u 2 using the half angle formulas cot u 3 u 3 2 sin u 2 cos u 2 tan u 2

Geometry
Coordinate systemWhat single theorem can take the given directly to the prove statement Given 41 and 42 are complementary 43 and 42 are complemtary Prove m41 m43 BI 3 D

Geometry
Coordinate system5 2 Points Give the reason for the last statement in the proof Statement 1 41 and 42 are a linear pair 2 41 42 180 BAUMLIEK Enter your answer Reason 1 Given 2

Geometry
2D Geometry10 Suppose that you decide to buy a car for 36 635 You saved 9000 for dow payment and you can get a 5 year car loan at 7 88 Use the formula PMT P 5 8 pts 1 1 nt
Geometry
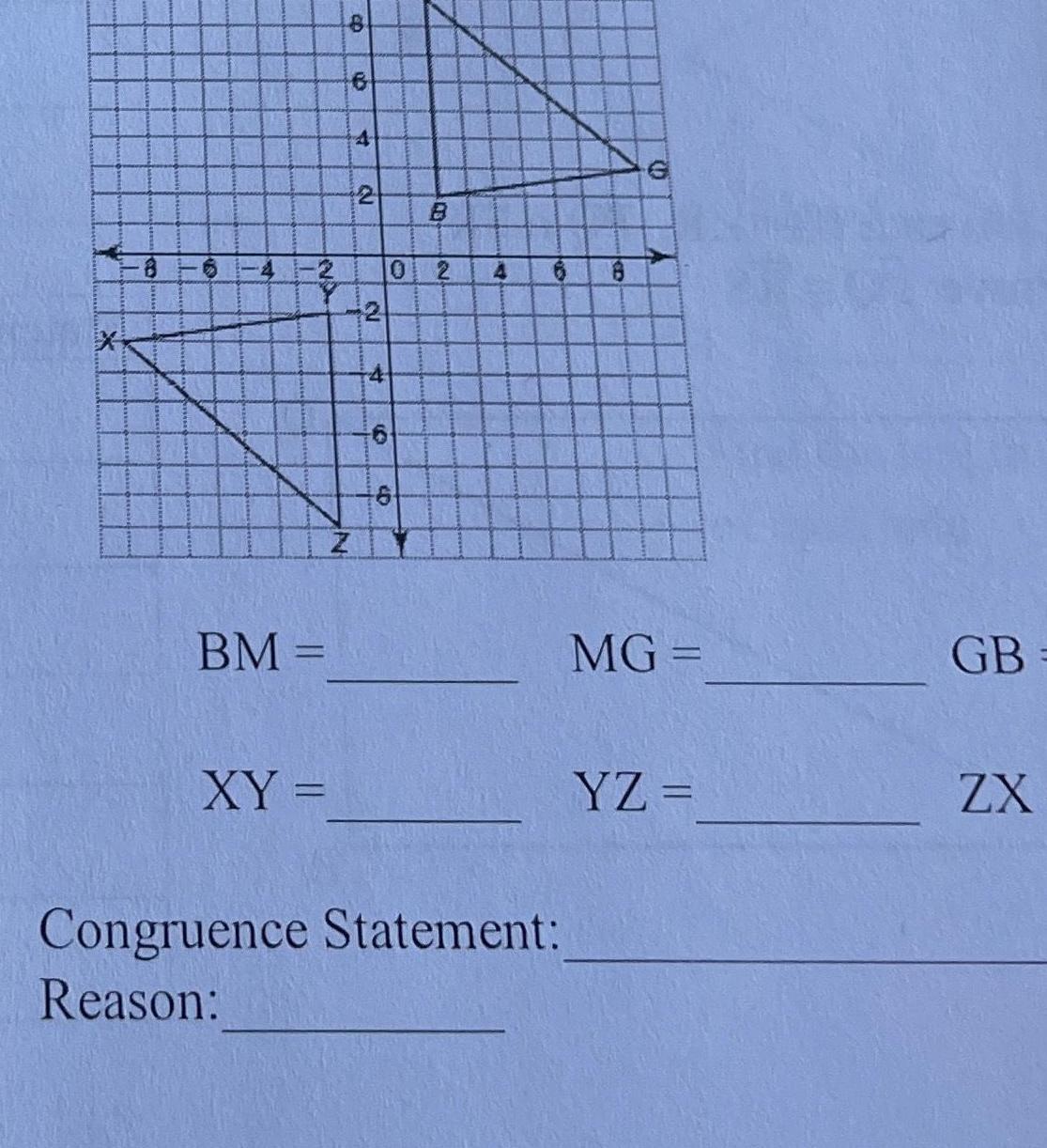
Coordinate system8 6 1 4 NA BM XY ARKKING B Z 6 4 2 2 4 O 6 2 4 Congruence Statement Reason 8 1 MG YZ GB ZX

Geometry
Solution of trianglesUse the congruency statement to state corresponding congruent parts 16 AKIT AEAS 17 ALMO ANOM ZK ZS Z1 KT AS IK ZOMLE ZOMN ZN ON OL MO
Geometry
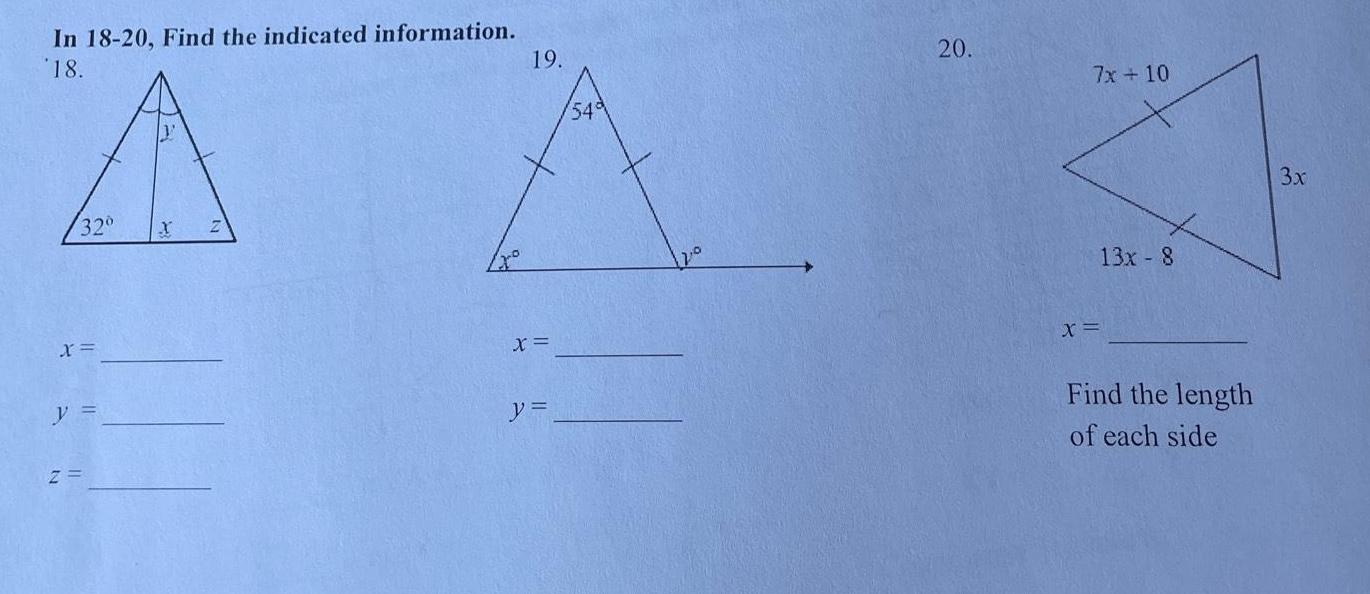
Solution of trianglesIn 18 20 Find the indicated information 18 A 32 X y Z 19 X y 54 20 7x 10 X 13x 8 Find the length of each side 3x


Geometry
Heights & DistancesA Given AAEF is isosceles D is midpoint AF Prove ZAED FED E D F Statement Reason
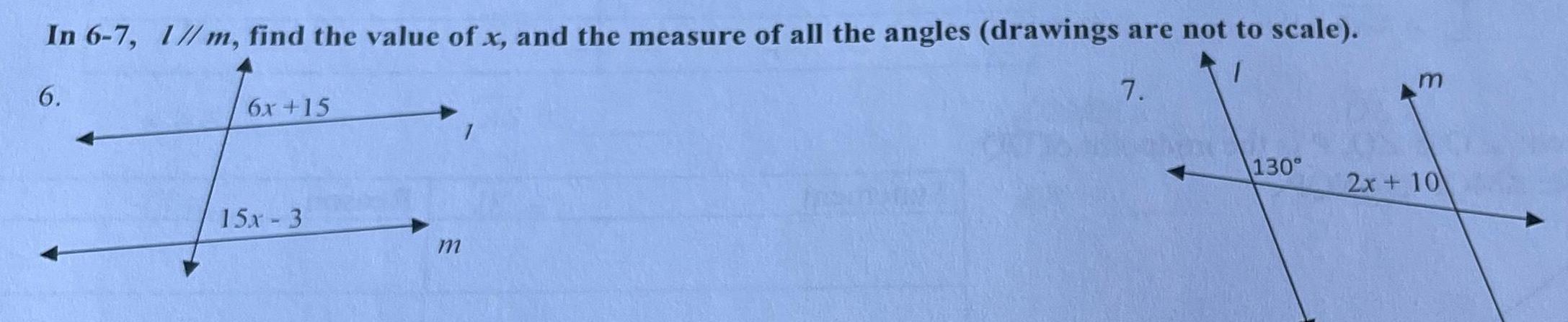
Geometry
Solution of trianglesIn 6 7 6 1 m find the value of x and the measure of all the angles drawings are not to scale 7 6x 15 15x 3 m 130 2x 10

Geometry
Solution of trianglesIn 10 11 If possible write a congruency statement and state the theorem SSS use to prove the triangles congruent 10 R A U Congruence Statement Reason T 11 E Reason D Congruence Statement C
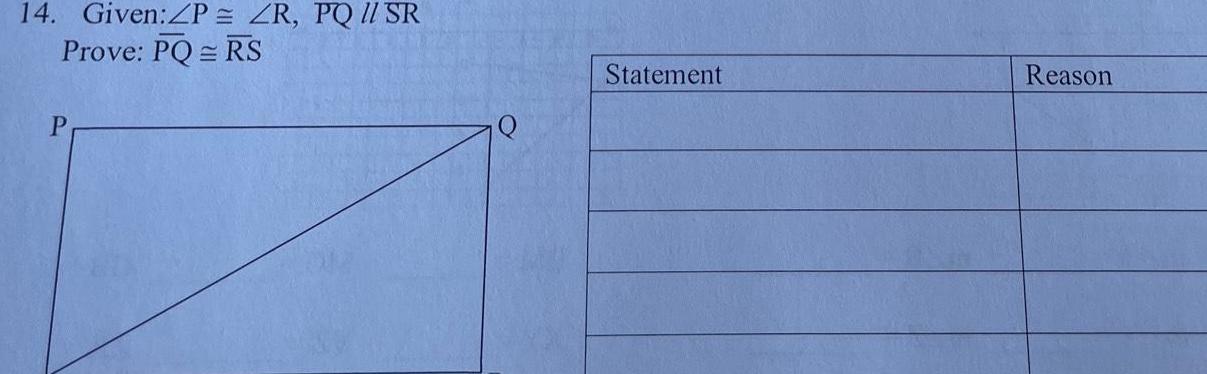

Geometry
Solution of triangles13 Given 20 ZQ P is the midpoint of OQ Prove AMOP ANQP M O P N Statement Reason

Geometry
2D GeometryIn I Identify the following angle pairs as Corresponding Angles Alternate Interior Angles Same Side Interior Angles Vertical Angles or Linear Pairs a 41 and 27 c 43 and 26 b 22 and 4 d 45 and 48 m 4 3 1 2 76 b