Geometry Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Geometry
Solution of trianglesStep 1 Given Information Two official languages in Canada are English and French When a Canadian is chosen randomly and asked about their mother tongue the distribution of responses combining the majority of separate languages from the broad Asia Pacific region is as follows Probability of English is P E 0 63 Probability of French is P F Probability of Other languages from Asia Pacific region is P A p 0 06 Step 2 Probability Distribution In a probability distribution The probabilities must be non negative The sum of probabilities of all events should add up to 1 Using the second condition we can calculate the probability of Other languages from Asia Pacific region as P Other 1 P E P F P A p 10 91 0 09 0 22 Therefore the probability that should replace is 0 09 0 37 Step 3 Probability of not English The probability that a Canadian s mother tongue is not English can be calculated by using the complementary probability formula P notEnglish 1 P English 1 0 63 Therefore the probability that a Canadian s mother tongue is not English is 0 37 0 15 Step 4 Probability of Other languages The probability that a Canadian s mother tongue is a language other than English or French can be calculated by adding the probabilities of Other languages from Asia Pacific region and languages other than Official Languages i e P Asian Pacificor Other P Asian Pacific P Other 0 06 0 09 Therefore the probability that a Canadian s mother tongue is a language other than English or French is 0 15

Geometry
Heights & DistancesStep 1 Given information Player 1 and Player 2 are both equally likely to choose rock paper or scissors in a rock paper scissor game Step 2 a Let a b represent the outcome of the game where a and b are the choices of player 1 and player 2 respectively Let R represent the rock S represents the scissor and P represent the paper The total of 9 possible outcomes of the game will be PossibleA outcomes R R R P R S P R P P P S S R S P S S Each outcome is equally likely to happen with a probability of The probability model will be a b P a b Step 3 b From the above table there are only 3 outcomes player 1 is winning that are R S P R and S P The probability that Player 1 wins the game on the first throw will be computed as Winning outcomes Total outcomes R R 1 9 P Player 1 R P 1 9 R S 19 P R 1 9 P P 1 9 3 0 33 So the probability that Player 1 wins the game on the first throw is 0 33 P S 9 S R 1 9 S P 19 S S 10 9

Geometry
2D GeometryProvide a trigonometric equation Considering only the space between x 0 and 2 pie the equation must only have solutions at x 1 and x 2 explain your thought process and the work you did to create the equation You may round decimal values to 3 places

Geometry
Coordinate systemCreate a single BPMN diagram using the Camunda Modeler of the below process narrative Feature appropriate pools and lanes to represent the different entities participants and the message flows between these entities participants Please label all flows sequences messages Do not use sub processes Canvas is a leading provider of LMS Learning Management Software software Canvas is used by many colleges as a teaching course portal

Geometry
Heights & Distancesn 6 S 1 1 n 2 S 13 80 e Refer to the diagram for question 12 22 Plot a graph of the values of energy y axis against the square of the number of the level i e n on the x axis C

Geometry
VectorsThe distance D between a point Q and a line in space is given by PQ x u D X where u is a direction vector for the line and P is a point on the line a Find the shortest distance between the point Q 9 0 0 and the line passing through the points P 0 0 8 and P 0 1 9 b Find the shortest distance between the point Q 9 0 0 and the line segment from P 0 0 8 to P 0 1 9
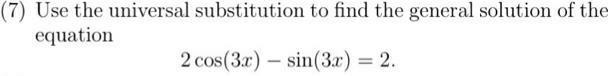
Geometry
Solution of triangles7 Use the universal substitution to find the general solution of the equation 2 cos 3x sin 3x 2
Geometry
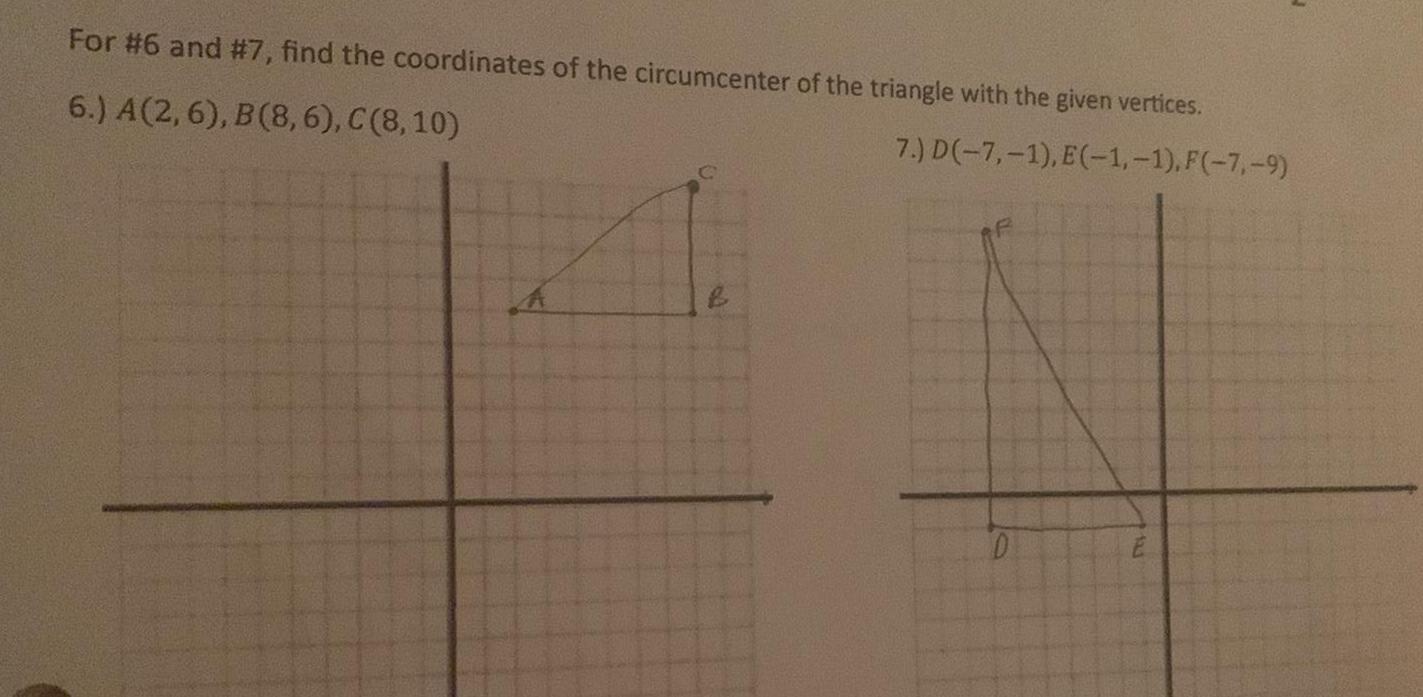
2D GeometryFor 6 and 7 find the coordinates of the circumcenter of the triangle with the given vertices 6 A 2 6 B 8 6 C 8 10 7 D 7 1 E 1 1 F 7 9 D
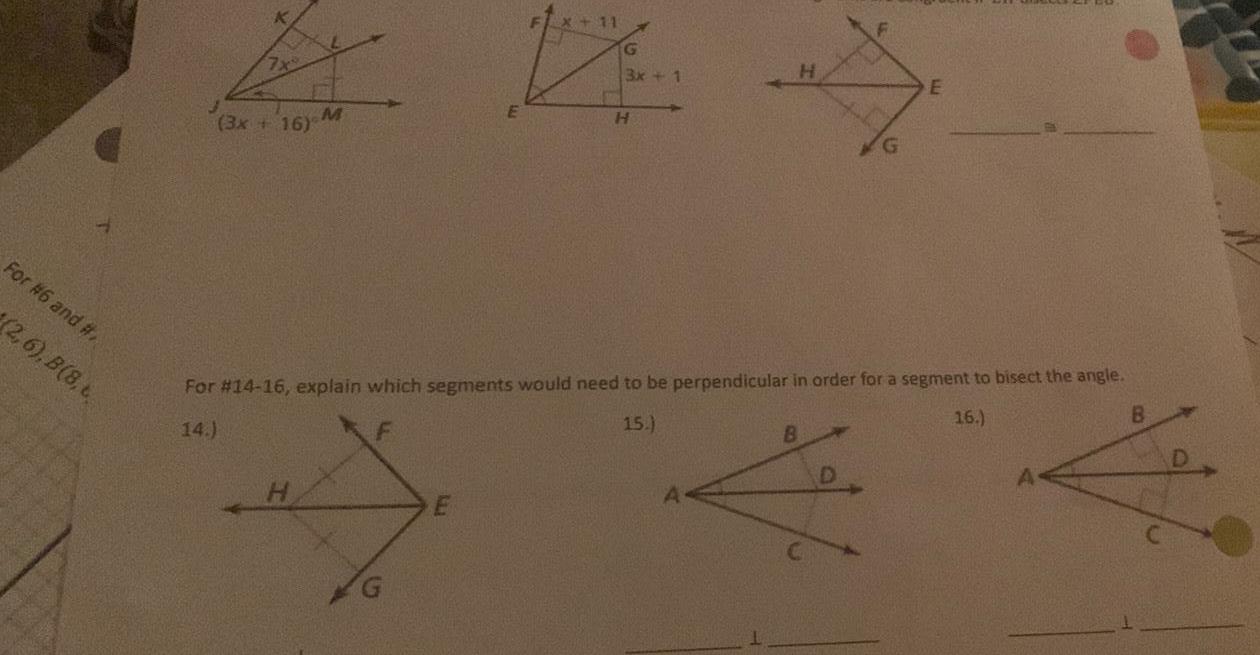
Geometry
2D GeometryFor 6 and 2 6 B 8 t EX 3x 16 FX 11 K H 3x 1 E For 14 16 explain which segments would need to be perpendicular in order for a segment to bisect the angle 14 16 15 B
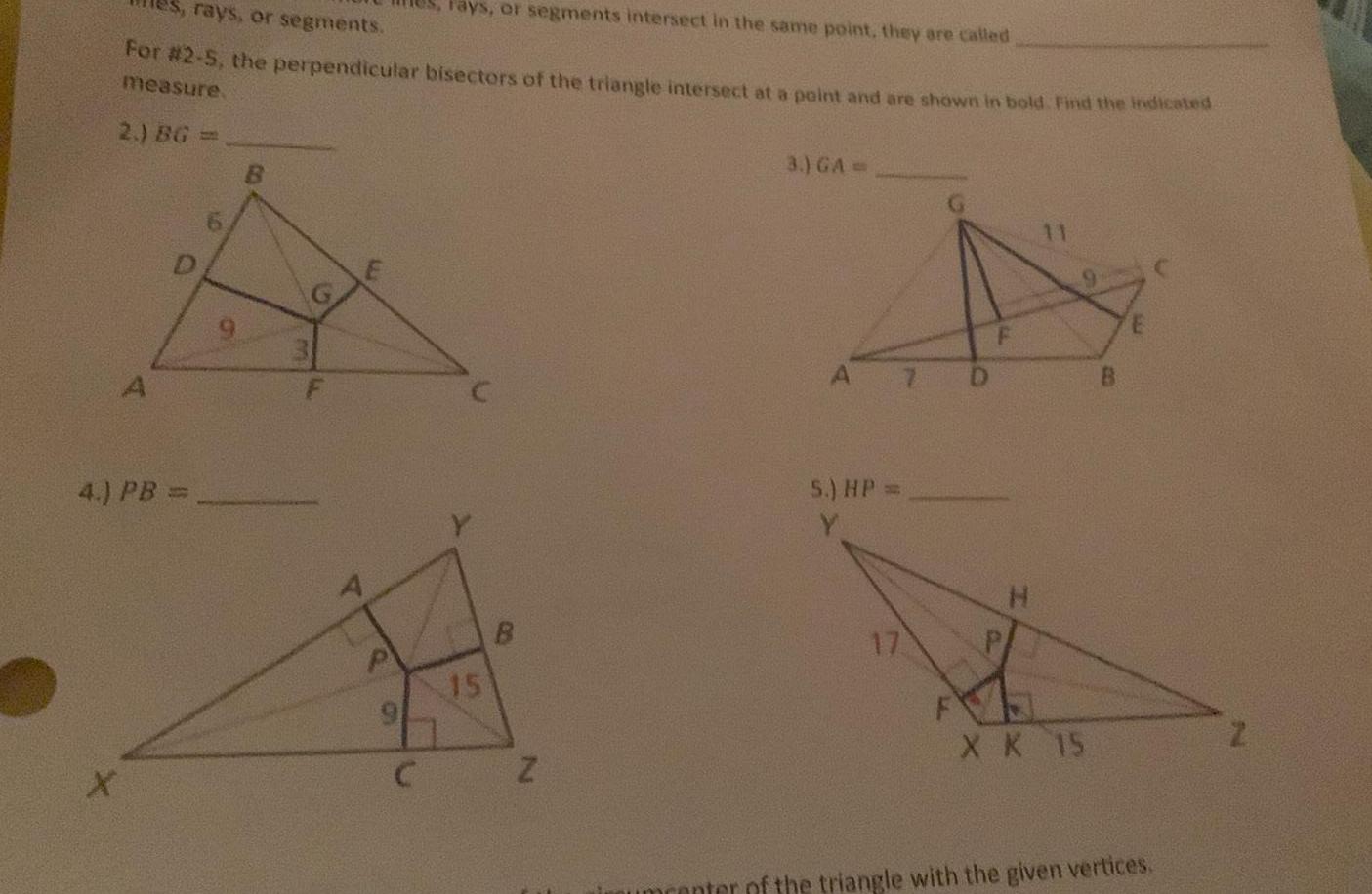
Geometry
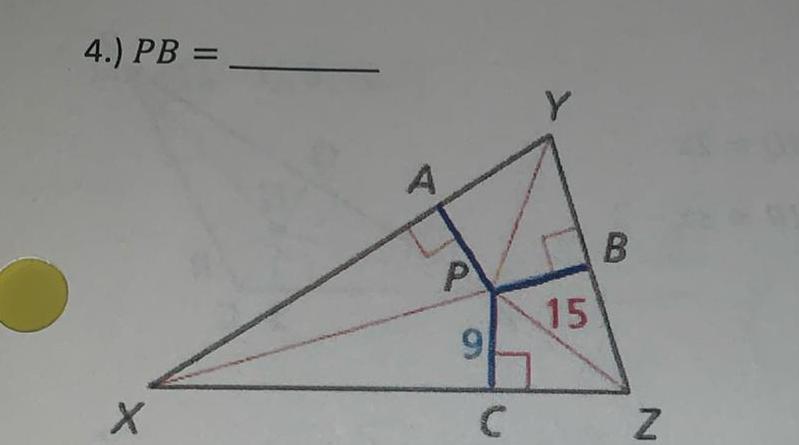
2D GeometryFays or segments intersect in the same point they are called rays or segments For 2 5 the perpendicular bisectors of the triangle intersect at a point and are shown in bold Find the indicated measure 2 BG X A 4 PB B G C 15 N 3 GA 5 HP 17 D 11 X X 15 nter of the triangle with the given vertices
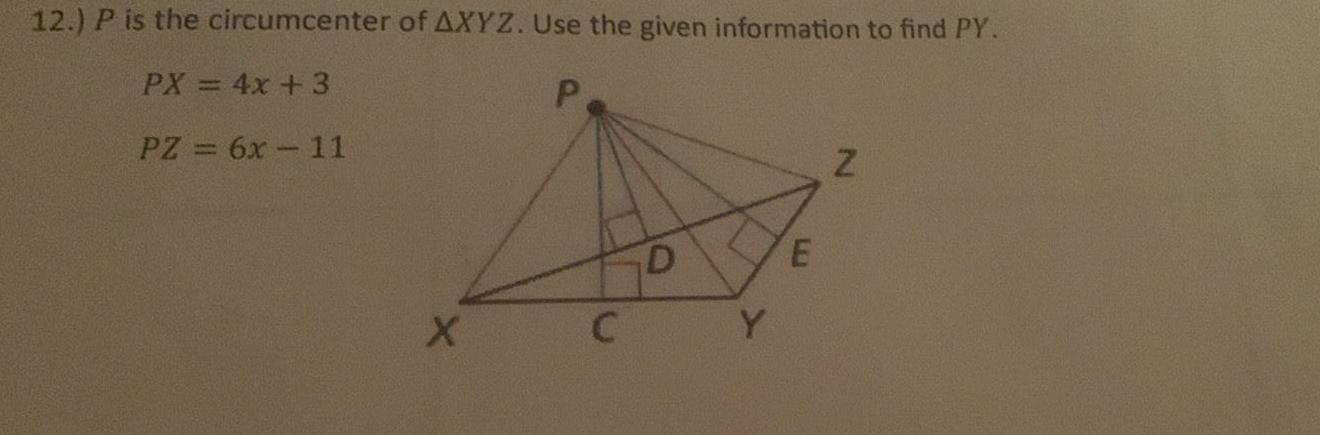
Geometry
2D Geometry12 P is the circumcenter of AXYZ Use the given information to find PY PX 4x 3 P PZ 6x 11 X D CY E Z
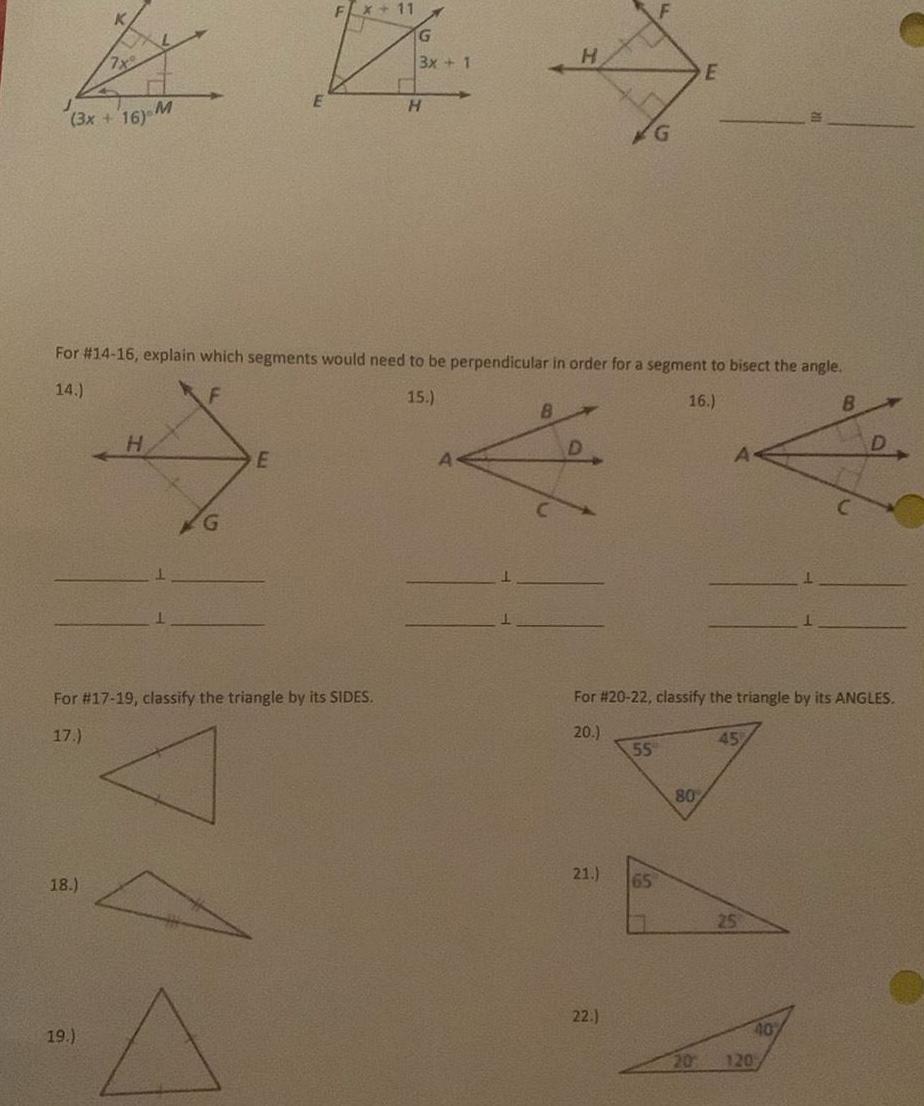
Geometry
2D Geometry3x 16 M 18 H 19 G N E FX 11 For 17 19 classify the triangle by its SIDES 17 G For 14 16 explain which segments would need to be perpendicular in order for a segment to bisect the angle 14 F 15 16 3x 1 H H 8 D 21 22 F For 20 22 classify the triangle by its ANGLES 20 55 65 M E 80 A 45 25 40 20 120
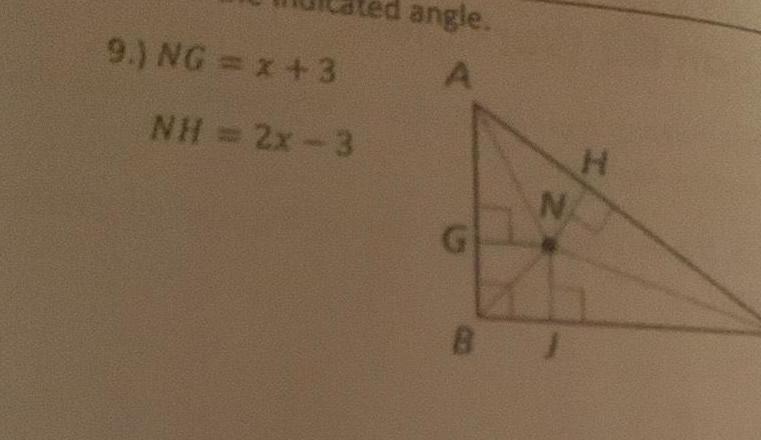
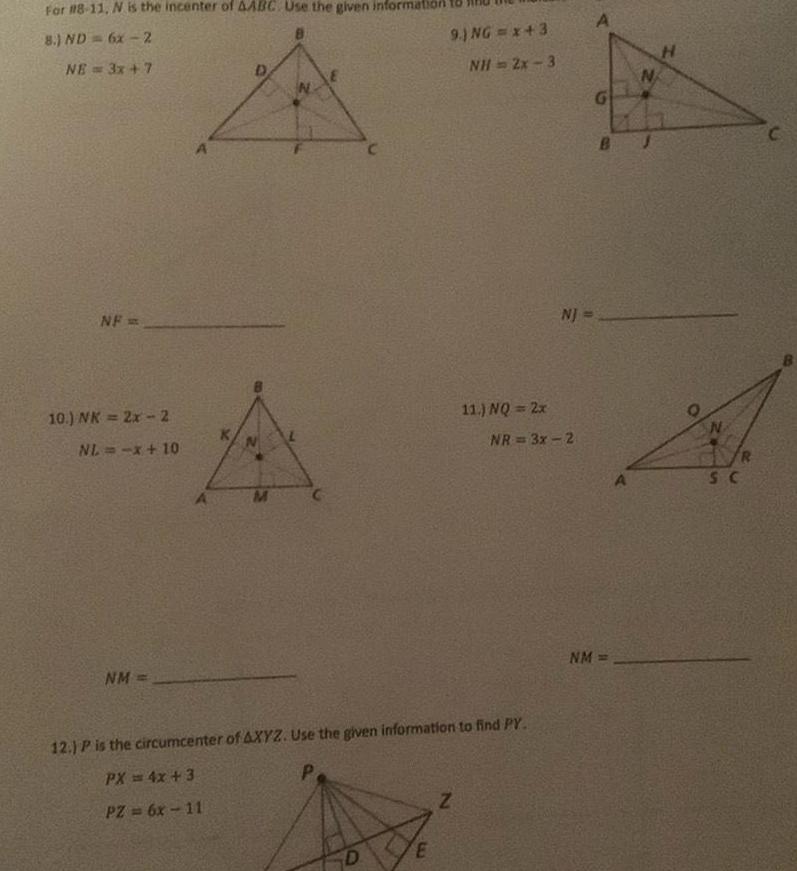
Geometry
2D GeometryFor 8 11 N is the incenter of AABC Use the given inform 8 ND 6x 2 NE 3x 7 NF 10 NK 2x 2 NL x 10 NM M ING 143 NH 2x 3 D 12 P is the circumcenter of AXYZ Use the given information to find PY P PX 4x 3 PZ 6x 11 Z 11 NQ 2x NR 3x 2 G NJ N BJ NM H N SC
Geometry
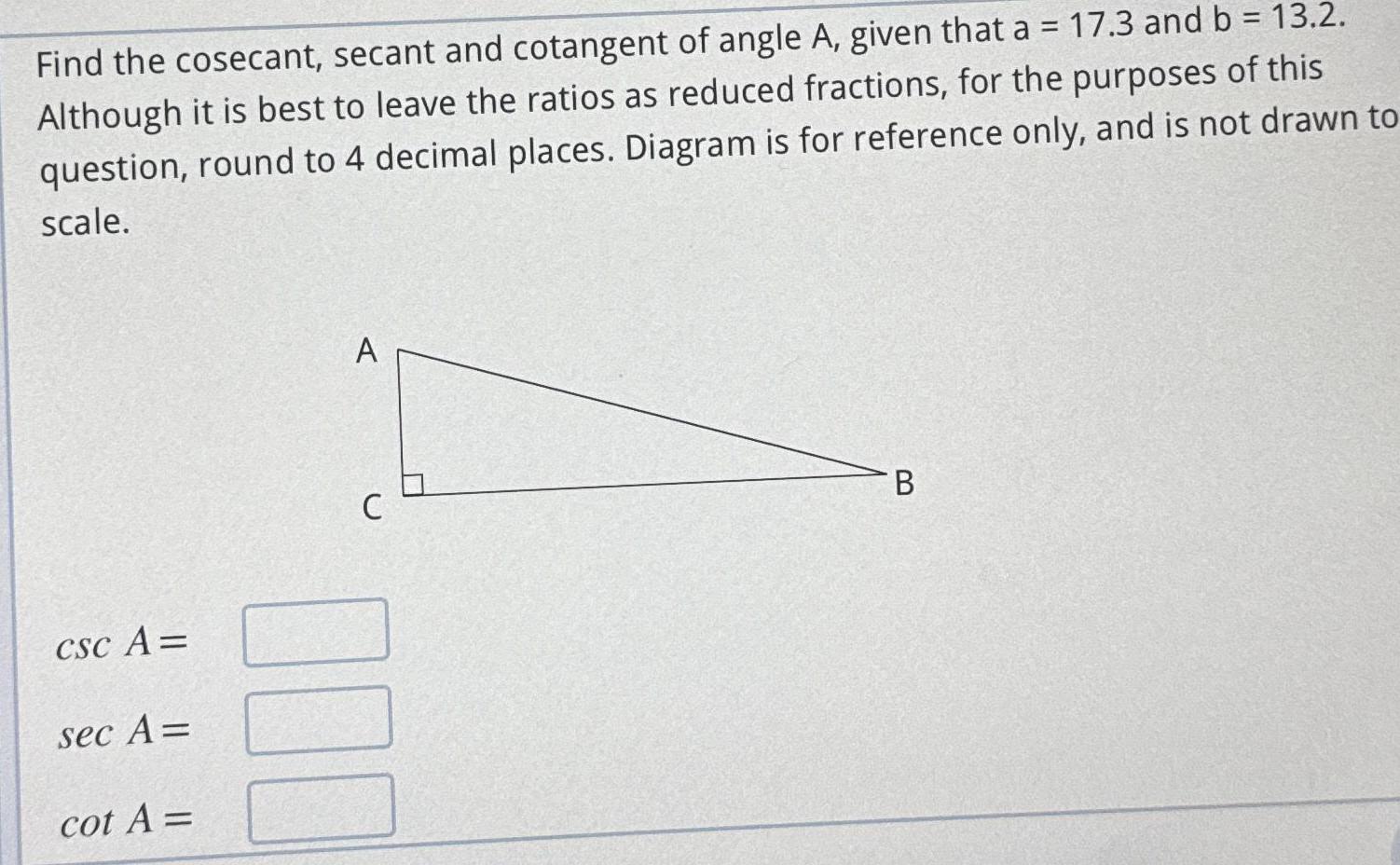
Heights & DistancesFind the cosecant secant and cotangent of angle A given that a 17 3 and b 13 2 Although it is best to leave the ratios as reduced fractions for the purposes of this question round to 4 decimal places Diagram is for reference only and is not drawn to scale CSC A sec A cot A A C 000 B


Geometry
Coordinate systemWrite a function based on the given parent function and transformations in the given order Parent function y H 1 Shift 2 5 units to the right 2 Shrink horizontally by a factor of 3 Reflect across the y axis The function based on the given parent function and transformations in the given order is y 23
Geometry
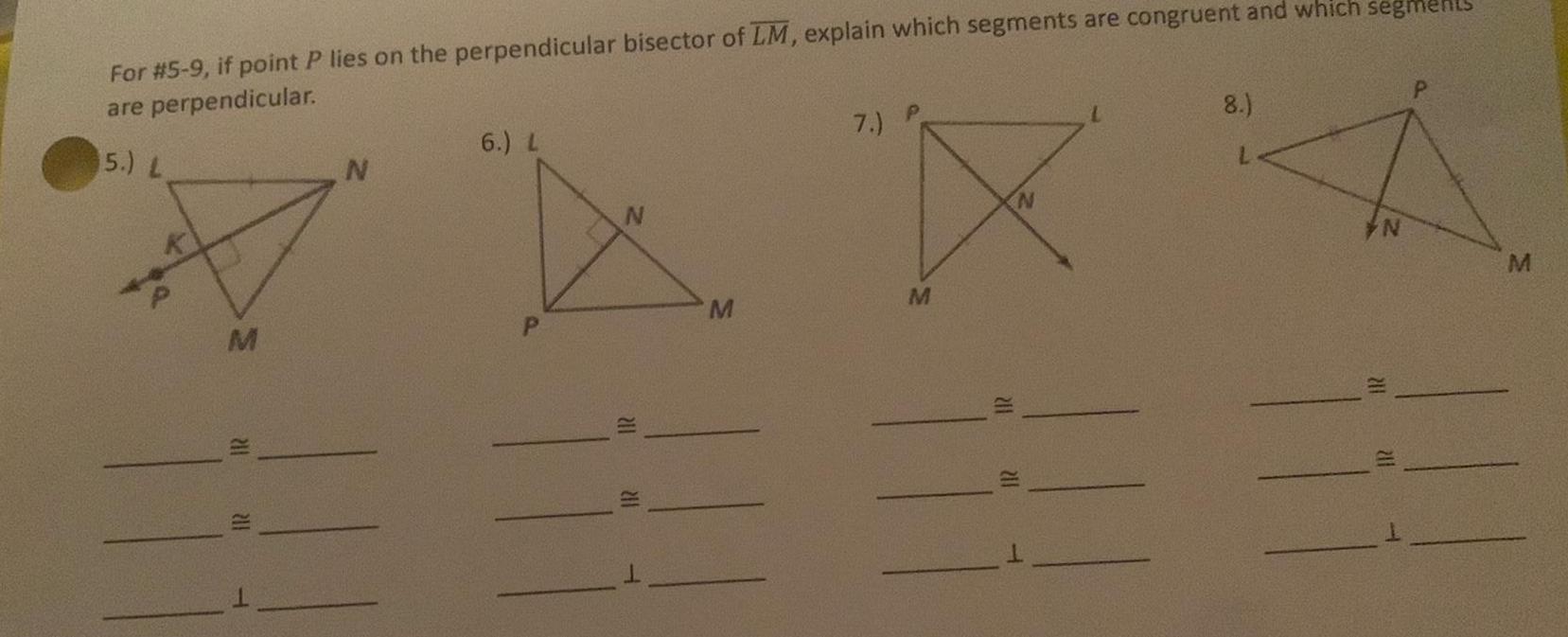
Coordinate systemFor 5 9 if point P lies on the perpendicular bisector of LM explain which segments are congruent and which segmen are perpendicular 5 L M 201 211 N 6 L 211 211 M 7 P M 211 N 211 T 8 L N 211 211 P M
Geometry
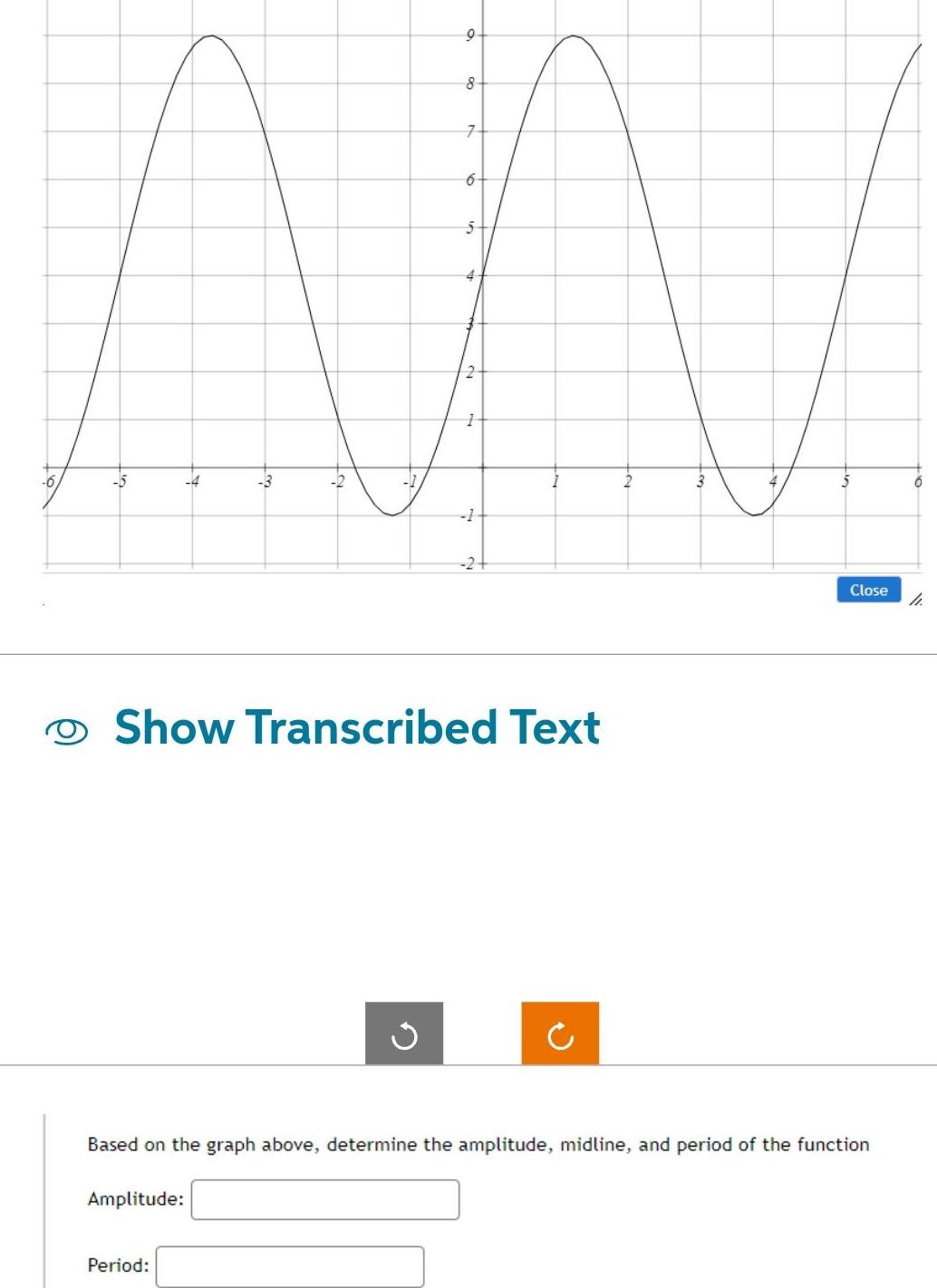
2D GeometryAmplitude 9 3 Period 8 7 6 5 4 Show Transcribed Text 1 24 4 Based on the graph above determine the amplitude midline and period of the function Close 4
Geometry
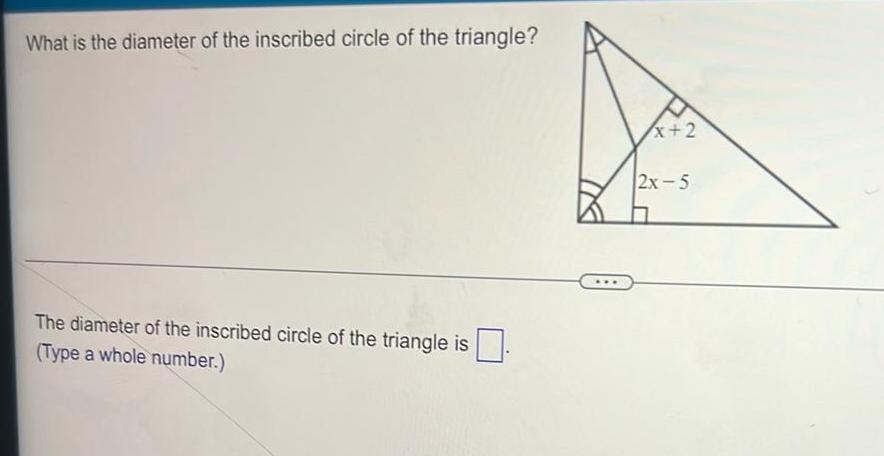
Coordinate systemWhat is the diameter of the inscribed circle of the triangle The diameter of the inscribed circle of the triangle is Type a whole number x 2 2x 5

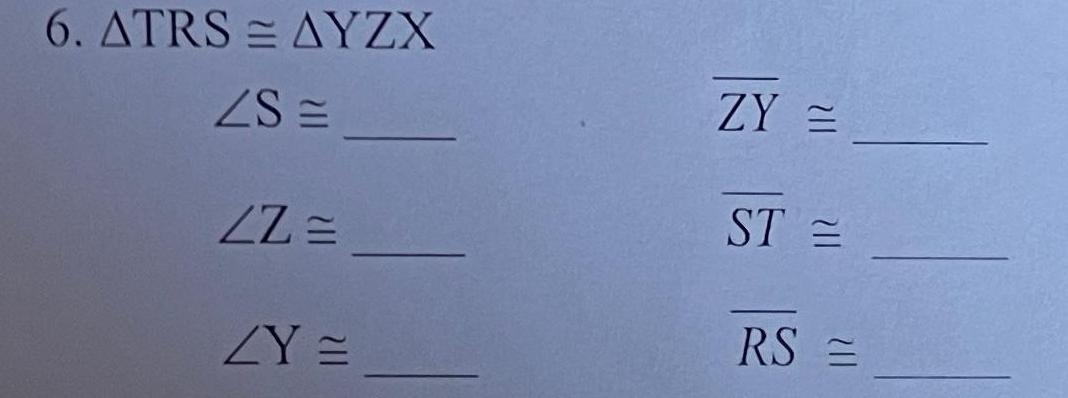


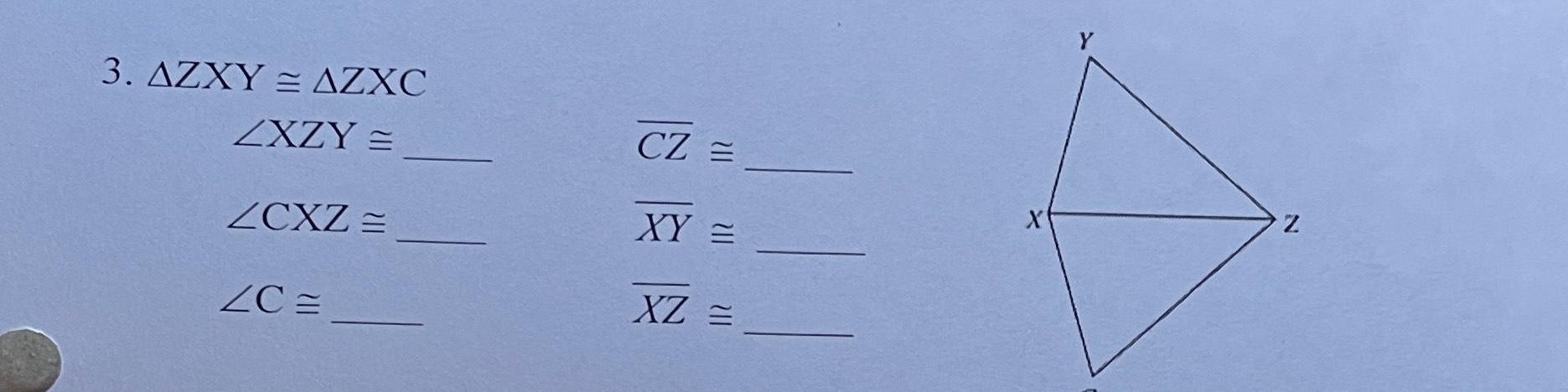

Geometry
Solution of triangles1 ATUV AGFE ZT ZU ZV 2 AWVU AGHI ZHE ZW 21 3 AZXY AZXC ZXZY ZCXZ ZC 4 ADEF ADSR ZF ZS ZFDE and Mark corresponding congruent parts for the given congruent triangles U UV E EG UT VW VU E GI CZ XY XZ EF RD SD W R U G H
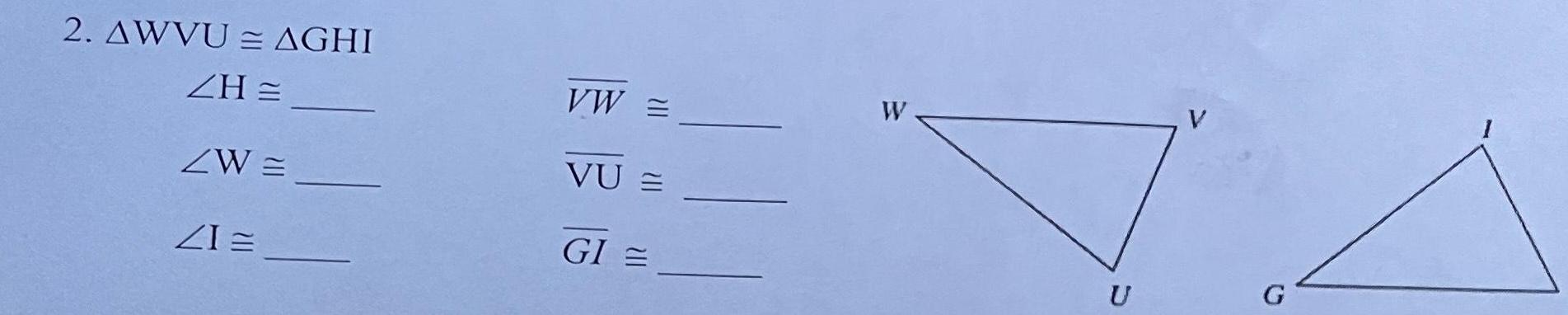
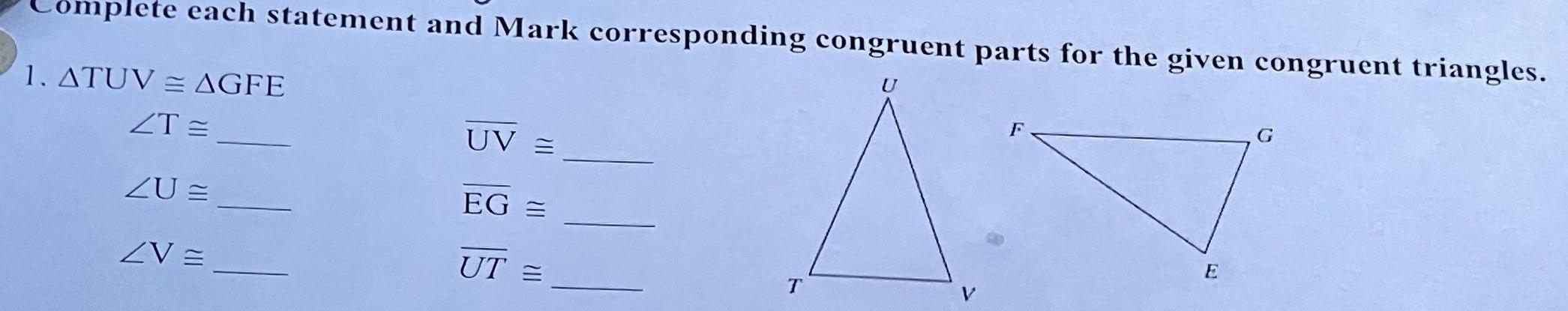
Geometry
Coordinate systemomplete each statement and Mark corresponding congruent parts for the given congruent triangles 1 ATUV AGFE ZT ZU ZV UV EG UT T F E
Geometry
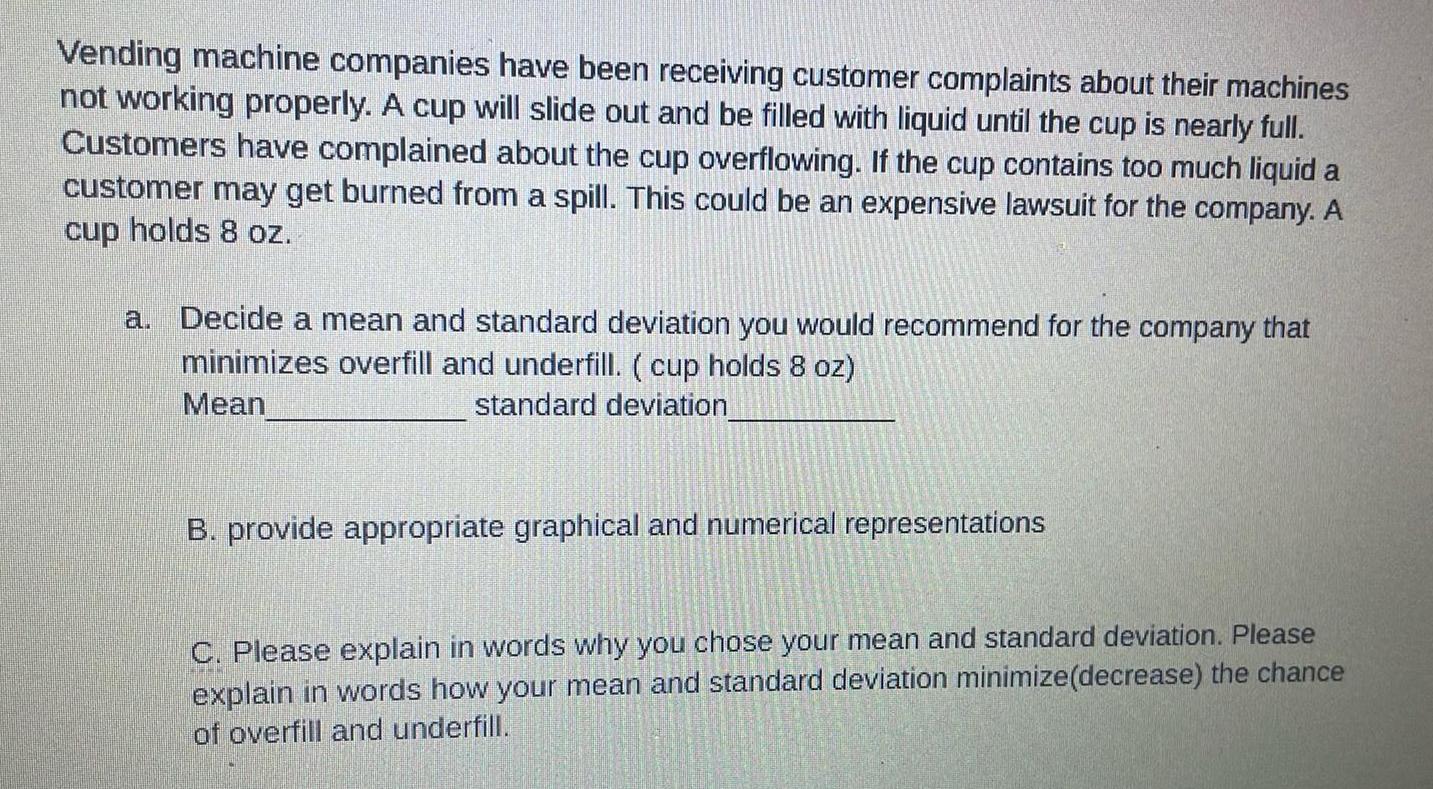
2D GeometryVending machine companies have been receiving customer complaints about their machines not working properly A cup will slide out and be filled with liquid until the cup is nearly full Customers have complained about the cup overflowing If the cup contains too much liquid a customer may get burned from a spill This could be an expensive lawsuit for the company A cup holds 8 oz a Decide a mean and standard deviation you would recommend for the company that minimizes overfill and underfill cup holds 8 oz Mean standard deviation B provide appropriate graphical and numerical representations C Please explain in words why you chose your mean and standard deviation Please explain in words how your mean and standard deviation minimize decrease the chance of overfill and underfill
Geometry
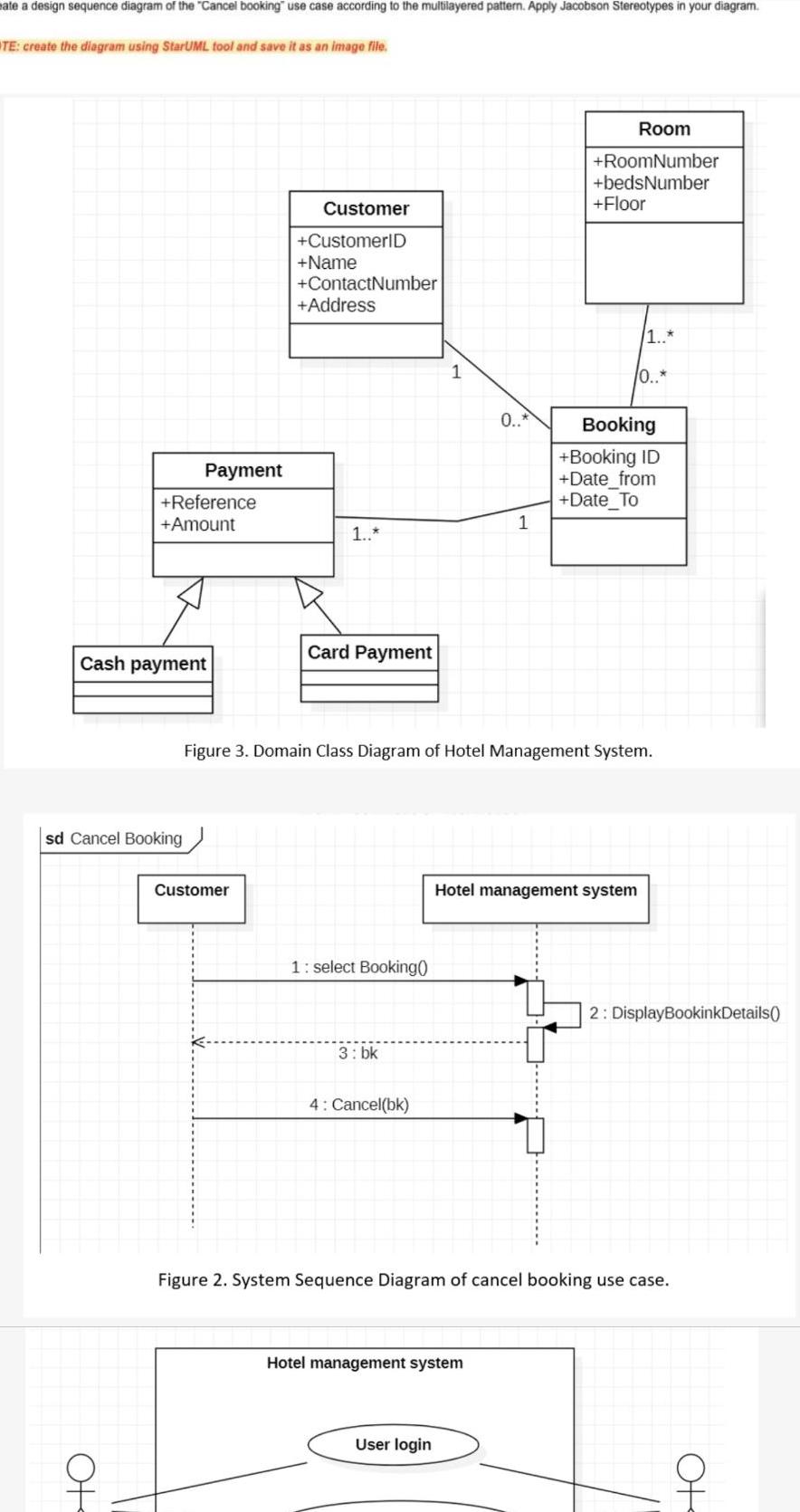
Heights & Distancesate a design sequence diagram of the Cancel booking use case according to the multilayered pattern Apply Jacobson Stereotypes in your diagram TE create the diagram using StarUML tool and save it as an image file Payment Reference Amount Cash payment sd Cancel Booking Ot Customer CustomerID Name Customer ContactNumber Address 1 Card Payment 1 select Booking 3 bk 4 Cancel bk 1 0 Figure 3 Domain Class Diagram of Hotel Management System User login 1 Hotel management system Room RoomNumber bedsNumber Floor 1 Hotel management system 0 Booking Booking ID Date from Date To Figure 2 System Sequence Diagram of cancel booking use case 2 DisplayBookinkDetails Ot

Geometry
Coordinate systemUse the power spectral density P n4f generate stochastic processes s mT having this energy distribution where T is the sampling period and M the desired number of signal samples in time This is easily done through the following equation s m 7 2 df P n cos 2 n df m T p n 0 Where s m T The stochastic process df frequency resolution fs N P n the PSD mT the amount of time covered for m samples Random phase from U 0 2 where each is drawn from U 0 2 The square root is necessary to transform from power to voltage The factor of one half takes into consideration that power spectra of real signals are symmetric in frequency and only positive frequencies are used in this formulation Multiplication by the sampling period Tscales the power to the correct level Keep in mind that computers don t know absolute time and frequency Therefore example P naf is the nth PSD value in a vector Like the cosine about is the mth element of a vector of length M Labeling frequency axes and time axes requires your consideration and DSP expertise The amplitude of synthesized signals may differ from original ones provided but their characteristics should look the same Provide plots of the signals that you synthesize Comment on their similarity or difference from the provided signals Provide your source code

Geometry
2D Geometry1 Plot each point then use A 4 3 B 1 3 C 3 1 D 0 2 E 3 2 and F 2 4 to prove ZABC ZEDF

Geometry
Solution of trianglesThis application will assess the haze severity for Perak Malaysia Please enter the API Safety Level District 2 Genk Kuala Kangsar Ipoh Tronoh Taiping Calculate Average Level API Level Clear Level Exit Requirements 1 Name the frame labels textboxes and buttons accordingly 2 This application will assess the API Level for state of Perak It allows the user to enter the API Level for different districts in Perak Whenever the year leaves the API Laval taxthox of agah district laval for that specific API
Geometry
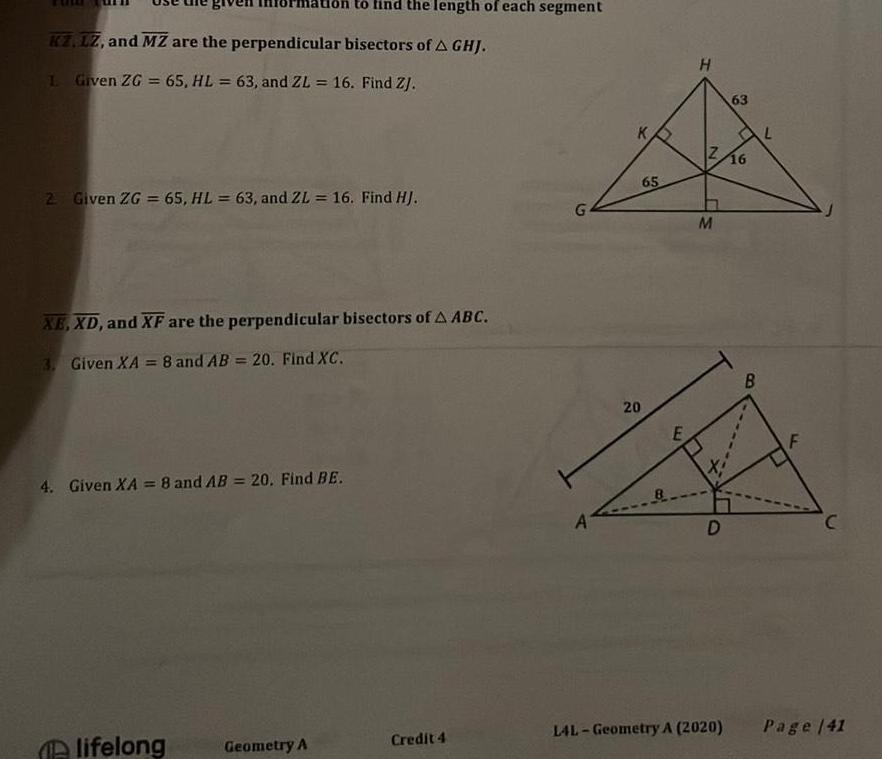
2D Geometryon to find the length of each segment KZ LZ and MZ are the perpendicular bisectors of A GHJ 1 Given ZG 65 HL 63 and ZL 16 Find ZJ 2 Given ZG 65 HL 63 and ZL 16 Find HJ XE XD and XF are the perpendicular bisectors of A ABC 3 Given XA 8 and AB 20 Find XC 4 Given XA 8 and AB 20 Find BE lifelong Geometry A Credit 4 G A 20 65 E H Z 16 M D 63 L4L Geometry A 2020 B L F C Page 141

Geometry
VectorsThe lines represented by the equations 2y 3x Answer Attempt 1 out of 5 O parallel neither parallel nor perpendicular O the same line O perpendicular 18 and y x 4 are Submit Answer

Geometry
Solution of triangles57 Then use 3 Let s consider the unit circle for 0 900 180 270 and 360 Angles 0 90 180 270 4 360 1 X Now complete the chart for 0 900 1800 270 and 360 x y Sin YO 1 SOH CaH TOA Cos Consider the rt triangle in the unit circle y I zy Sin 0 Cos 0 Tan 0 Tan x y C 2x A

Geometry
2D GeometryThe lines represented by the equations y 2x 2 and 4y 2x 12 are Answer Attempt 1 out of 5 O the same line O neither parallel nor perpendicular O parallel O perpendicular Submit Answer
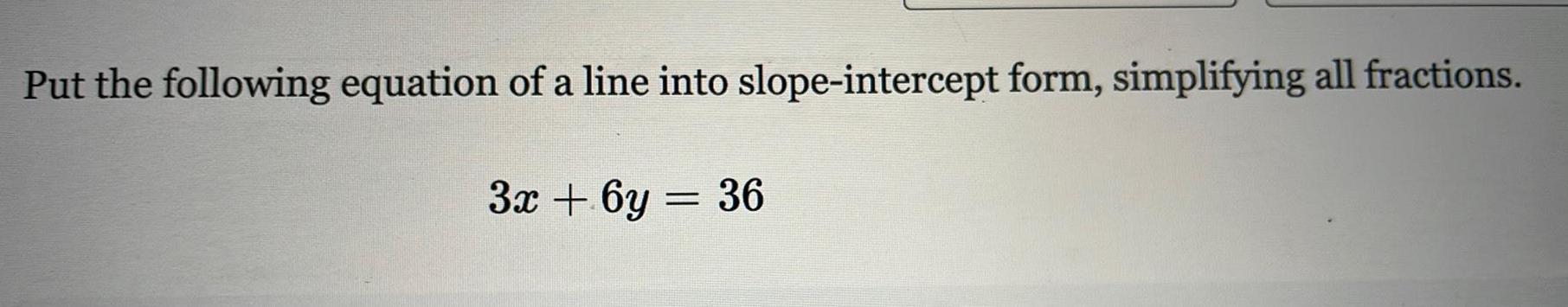
Geometry
Solution of trianglesPut the following equation of a line into slope intercept form simplifying all fractions 3x 6y 36

Geometry
2D GeometryPut the following equation of a line into slope intercept form simplifying all fractions 4x 3y 21

Geometry
Coordinate systemWhat is the slope of the line that passes through the points 8 6 and 11 12 Write your answer in simplest form Answer Attempt 1 out of 5 ubmit Answer

Geometry
2D GeometryWhat is the slope of the line that passes through the points 3 8 and 2 13 Write your answer in simplest form Answer Attempt 1 out of 5

Geometry
2D Geometry4 Draw 2 lines that could be the image of line m by a dilation Label the lines n and P 0 MATH m

Geometry
2D Geometryram shores A BDF its medians centroid H and the lengths of of the subsegments Apply the Centroid theorem to find other lengths Given Bl 18 find EH 2 Given BH 18 find BE 3 Given CH 4 find CF 4 Given BD 30 find BC 4 is done for you BD BC CD Segment Addition Postulate 30 BC BC Definition of Midpoint 30 2BC 15 BC Simplify Division Property of Equality 5 Given BG 11 find BF B 18 H E D

Geometry
2D GeometryComplete the Two Column Proof of the Converse of the Angle Bisector Theorem Given VX1YX and VZ 1 YZ and VX VZ Prove YV bisects ZXYZ Two Column Proof of the Converse of the Angle Bisector Theorem Statements 1 VX 1 YX and VZ 1 YZ 2 VX VZ 3 ZVXY and ZVZY are right angles 4 YV YV 5 AVXY A VZY 6 LXYV LZYV 7 YV bisects ZXYZ Reason Bank Given Reasons Reflexive Property of Congruence Definition of Perpendicular Lines
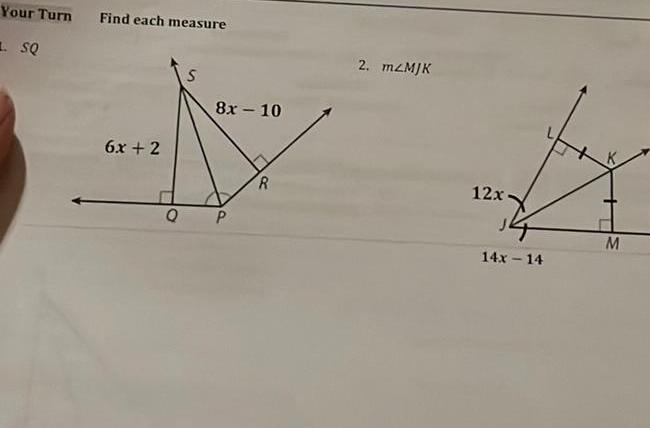
Geometry
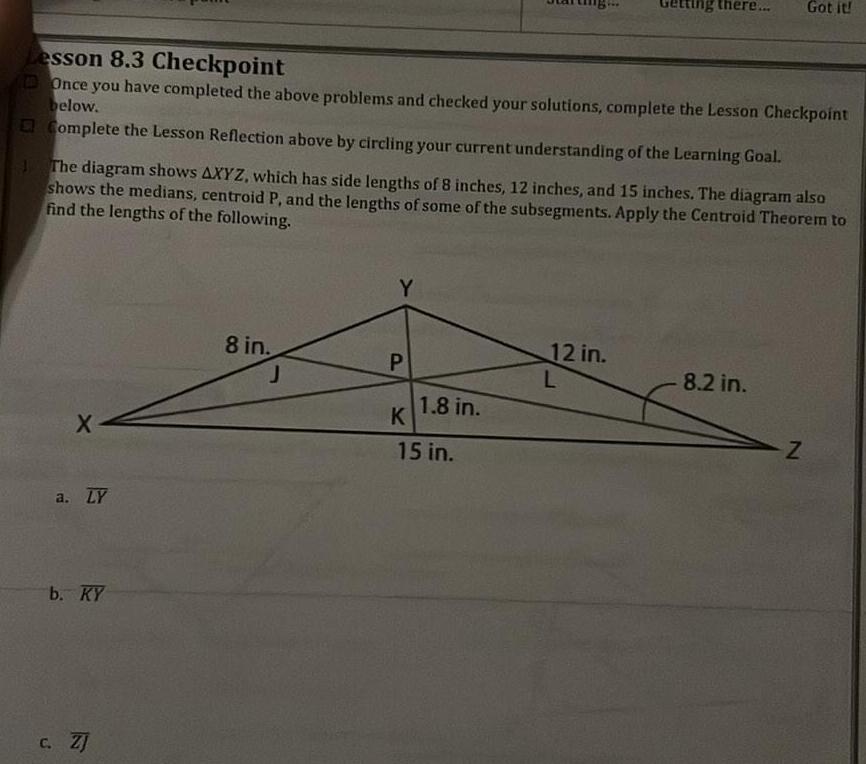
2D GeometryLesson 8 3 Checkpoint Once you have completed the above problems and checked your solutions complete the Lesson Checkpoint below Complete the Lesson Reflection above by circling your current understanding of the Learning Goal X The diagram shows AXYZ which has side lengths of 8 inches 12 inches and 15 inches The diagram also shows the medians centroid P and the lengths of some of the subsegments Apply the Centroid Theorem to find the lengths of the following a LY b KY c ZJ 8 in J Y P K 1 8 in 15 in ng there 12 in L Got it 8 2 in Z

Geometry
Coordinate systemYour Turn Given Lines l m and n are the perpendicular bisectors of AB AC and BC respectively P is the intersection of lines l m and n From the previous page use the Paragraph Proof of the Circumcenter Theorem to write two column proof of the Circumcenter Theorem Refer to the reason bank below Prove PA PB PC Two Column Proof of the Circumcenter Theorem Statements 1 Lines l m and n are the perpendicular bisectors of AB AC and BC respectively P is the intersection of lines l m and n 2 3 PA PB 4 PB PC 5 PA PB PC Reason Bank Reasons 1 2 3 4 5 E

Geometry
2D GeometryLesson 7 3 Homework HW Independent Practice 100 6 1 Order the sides from shortest to longest Complete problems 1 8 below for independent practice 12 When you are finished check the solutions with your teacher 3 Order the angles from least to greatest M e 2 Order the sides from shortest to longest L K 97 55 4 Order the angles from least to greatest 17 16 R 5 State if the following measures can be the sides 6 State if the following measures can be the sides of a triangle of a triangle 12 6 13 9 18 9 7 State if the following measures can be the sides 8 State if the following measures can be the sides of a triangle of a triangle 8 3 6 11 7 20 Optional Complete problems 5 7 13 14 17 19 21 23 from your textbook on separate lined paper When you are finished check the odd problems for solutions at the back of the textbook

Geometry
2D GeometryLesson 7 2 Homework A HW 12 Complete problems 1 6 below for independent practice 1 Find the value of x in the figure below 45 When you are finished check the solutions with your teacher 3 Find the value of x in the figure below 5 Find the value of x in the isosceles triangle shown below Then find the measure of Z A B 2r 4 3r Optional Complete problems 4 5 7 9 16 2 Find the value of x in the figure below x 4 Find the value of x in the figure below 2x 8 X 10 55 6 In the figure below 2WXZ and ZWYZ are bisected forming isosceles triangle WXY and ZXY What is the value of W W 25