Geometry Questions

3 Determine if the triangles can be proven to be congruent If so complete the congruence statement and provide reasoning SAS SSS or HL If they can t be proven congruent write CBD Cannot Be Determined b X AARC BA Reasoning W AYZW A Reasoning APSQ A Reasoning

The circle with center C 2 5 and containing the point P 2 1

5 The function g has a zero at 4 with multiplicity 2 a zero at x 1 with a multiplicity 3 and a zero at x 4 with multiplicity 1 Sketch a possible graph of g x 3 2 5A 4 3 2 1 0 1 3 6 3 4 5 x

2 Write a proof Given CA a CD B is the midpoint of AD Prove ACAB ACDB B Statements Reaso

D A 2 1 6 4 2 2 4 6 8 0 O B G CO

Consider the following y 4 cot Find the period Give the equations for two consecutive vertical asymptotes for the graph of the function Enter your answers as a comma separated I X TX 5 Consider the following y 3 tan 2x Find the period Give the equations for two consecutive vertical asymptotes for the graph of the function Enter you

Use the parent function f x b and transformation techniques to graph g x e 1 Also indicate which transformation s is are applied Determine the domain range and horizontal asymptote of 9 Select all transformations that apply Vertically compress the graph of f by a factor of 6 Shift the graph of f 1 unit up Shift the graph of f 1 unit down Reflect the graph of f about the z axis Reflect the graph of f about the y axis Horizontally stretch the graph of f by a factor of 1 Vertically stretch the graph of f by a factor of 1 Shift the graph of f 6 units to the right Horizontally compress the graph of f by a factor of 6 Shift the graph of f 6 units to the left

Use the parent function f x b and transformation techniques to graph h z 2 1 Also indicate which transformation s is are applied Determine the domain range and horizontal asymptote of h Select all transformations that apply Reflect the graph of f about the z axis Shift the graph of f 1 unit down Reflect the graph of f about the y axis Shift the graph of f 1 unit up Vertically compress the graph of f by a factor of 1 Horizontally compress the graph of f by a factor of 1 Vertically stretch the graph of f by a factor of 1 Shift the graph of f 1 unit to the right Shift the graph of f 1 unit to the left Horizontally stretch the graph of f by a factor of 1

14 too 22

Consider ATUV in the figure below The perpendicular bisectors of its sides are AD BD and CD They meet at a single point D In other words D is the circumcenter of A TUV Suppose CD 30 UV 142 and UD 78 Find BV VD and TC Note that the figure is not drawn to scale T D A B V BV 0 0 VD TC X

AB FE In 3 4 find the length of indicated sides d x x y y and use a protractor to measure the indicated angle Mark congruent angles and sides If the triangles are congruent write a triangle congruency statement by SAS 3 E 8 F 6 4 D 2 8 DE 4 6 2 BC ongruence Statement 81 2 6 4 A B 02 4 6 8 m B m E 4 8 6 4 2 D BR AD 8 6 4 2 2 10 4 R 6 8 2 BG 4 AM B 6 Congruence Statement G 8 m B m A

SIDE SIDE SIDE In 1 2 find the indicated lengths d x x y y Mark congruent sides If all three sides are congruent write a triangle congruency statement by SSS 1 2 JH LK G 6 H HG KM Congruence Statement 6 8 GJ ML PN XY M NM YZ Congruence Statement MP ZX

2 Direct labour per unit Variable overhead perunit 16 3 lost per unit of finished goods Total cont product lost per unit Number of units in fineshed Total cost of finished goods invertory Total product cost per unit Number of units in sold goods Total cost of sold goods 31 31 4 350 134 850 16000 496 000

C Graph y x 3 4 x y x ay d Graph y x 5 x y x ay x hy k x hy k 10 HHH O

Barnes Company reports the following for its product for its first year of operations 36 per unit 26 per unit 12 per unit 54 000 per year 2 per unit 21 000 per year Direct materials Direct labor Variable overhead Fixed overhead Variable selling and administrative expenses Fixed selling and administrative expenses The company sells its product for 160 per unit Compute contribution margin using variable costin company a produces and sells 2 000 units and b produces 2 700 units and sells 2 000 units Contribution margin using variable costing Variable expenses Contribution margin a 2 000 Units Produced and b 2 700 Units Produced 2 000 Units Sold and 2 000 Units Sold

Complete the process of solving the equation Fill in the missing term and select the missing description Simplify any fractions 8 x 5 16 X 5 2 X Add 8 to both sides Subtract 8 from both sides Multiply both sides by 8 Divide both sides by 8 Combine like terms

is divided into smaller chunks that can fit into memory In this phase we read the input data sequentially and write the chunks to temporary files 1 7 Merging Phase The sorted temporary files are merged together in a way that minimizes the number of passes In this phase data is read from the temporary files and written into a final output file To calculate the cost of performing this modified external merge sort you can break down the costs into these phases Intermediate Sorting Phase Each of the temporary files created in the initial splitting phase is sorted in memory For each file you read its content into memory sort it and write the sorted data back to a new temporary file Sequential Reads You mentioned that 8 sequential reads are free and that the cost of 8 sequential reads is 1 You ll want to count how many sets of 8 sequential reads are needed in each phase initial splitting intermediate sorting and merging For any leftover reads you can apply the cost of single reads Sequential Writes Sequential writes are never free You mentioned that the cost of N writes is always 2N So count the total number of writes in each phase and calculate the cost accordingly Here s a simplified example to illustrate how to calculate the cost Suppose you have an external merge sort with Input size 80 pages Memory can hold 10 pages Number of temporary files created in the initial splitting phase 8 Number of temporary files created in the merging phase 2 1 Initial Splitting Phase D Sequential Reads 10 reads per file x 8 files 80 reads D Sequential Writes 10 writes per file x 8 files 80 writes 2 Intermediate Sorting Phase Assuming each sorted file fits in memory Sequential Reads 1 read per file x 8 files 8 reads Sequential Writes 2 writes per file x 8 files 16 writes 4 Merging Phase

Ruby is visiting San Francisco From her hotel she walks 1 block east and 2 blocks north to a coffee shop Then she walks blocks west and 3 blocks north to a museum Where is the museum in relation to her hotel The museum is block s and block s of her hotel

The mov How would the following triangle be classified 4 O isosceles right O scalene acute O scalene right isosceles acute

9 1 Find the measure of x 9 pts for a non trig solution 2 pts for a trig solution A 20 60 to E 30 50 B

Role I Service Fact service line id service id I service type id employee id I labor cost I service start date service end date I I total service price I Part Fact I service line id I part id I I part vendor I I unit cost I I part count I I part cost at service Explanations Bike Type and Bike Brand Type 1 SCD is chosen because bike types and brands are unlikely to change If they do change a new record can be inserted

Females 7 1 inches 5th percentile 10 1 inches 95th percentile Conclusion Males The 10th to 90th percentile of males will fit this workstation Females The 5th to 95th percentile of females will fit this workstation Additional Notes The above assumes that the J key is 0 5 inches above the desk If the J key is at a different height then the percentile range will need to be adjusted accordingly The above also assumes that a footrest is provided for workers with shorter legs If a footrest is not provided then the percentile range will need to be adjusted to exclude workers whose seated elbow position is below 7 5 inches

Measurement Seated elbow position Calculations Percentile 9 5 inches Males Males 50th percentile 0 3 inches 7 5 inches 10th percentile Standard Deviation 9 1 inches Females 50th percentile 0 2 inches Males Minimum resting elbow height 9 5 inches 2 inches 7 5 inches Maximum resting elbow height 9 5 inches 1 inch 10 5 inches Females Export t Minimum resting elbow height 9 1 inches 2 inches 7 1 inches Maximum resting elbow height 9 1 inches 1 inch 10 1 inches Percentile range

Prove that for every x cos 3 x cos x 2 sin 2x sin 3x sin x

Ecologists surveying a location often need to calculate the area of irregular regions For example they may need to find the area of the home range of a marked animal with known multiple locations This calculation is done by recording certain lengths and angles associated with the region An example of such a region is shown in the figure The lengths are measured in meters b 110 az 40 A 20 a 200 F 70 C Macmillan Learning ration for Calculus 102022 Find the unknown sides and angles in the figure Use decimal notation Give your answers to one decimal place where needed Include the degree symbol in your answers where needed m C m

One of the two sets of functions f1 fa f3 or g1 92 93 is graphed in the figure to the left below the other set is graphed in the right figure Points A and B each have x 0 Taylor polynomials of degree 2 approximating these functions near x 0 are as follows fi x 4 x 2x 91 x 2 x x f2 x 4 x 2x 92 x 2 x x f3 x 4 x x 93 x 2 x 2x 11 a Match the functions to the appropriate figure f matches C g matches C b What are the coordinates of the points A and B A B 2 O B c Match each function with the graphs a c in the appropriate figure f f fs O 91 O 92

Given T R 2 1 2 1 15 4 t and sin t 1 15 4 00 1 15 4 None of the above 1 4 find the value of sin t 28 cos t 28

2 a Sketch the polar graph of r 0 the interval 0 2 How many petals do you see sin 20 in b Which values of 0 correspond to the petal in the first quadrant c Experiment with the polar graphs for r 0 sin k0for other integer values of k Make a conjecture about the connection between the integer k and the number of petals in the polar graph for values of 0 in the interval 0 2 Fill in the blanks When k is odd the number of petals equals When k is even the number of petals is

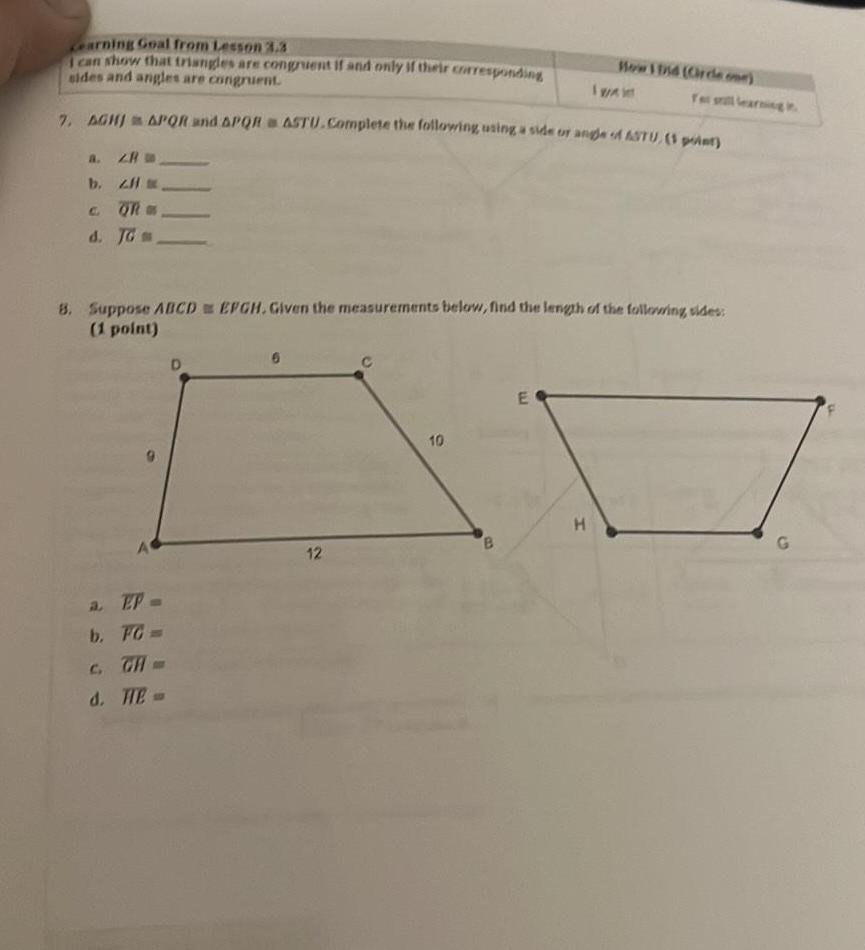
earning Goal from Lesson 3 3 I can show that triangles are congruent if and only if their corresponding sides and angles are congruent 7 AGHJ APQR and APQR a ASTU Complete the following using a side or angle of ASTU 1 point a ZR b z H C QR d JG a EP b FG C GA d HE 8 Suppose ABCDEFGH Given the measurements below find the length of the following sides 1 point D 6 12 10 B E How I Did Circle Te still learning H I wai

Learning Goal from Lesson 3 1 When given a geometric figure and a specific transformation I can draw the transformed figure by using graph paper tracing paper or geometry software Given two figures I can specify a sequence of transformations that will carry one figure onto another 4 ty 5 Reflect AABC over the y axis translate by 2 1 and rotate the result 180 about the origin Plot AA B C on the grid below 2 points 2 4 2 0 A 2 B Transformation rule Preimage ABC How I Did Circle one Image A B C I got it I m still learning it Image A B C Image A B C

9 Use the following triangles to answer the following Assume AABC ADEF 2 points B 3x 6 ft A a 6y 12 a What is the length of AB 3x 20 25 ft B y 7 C 10 AABC AEFG Solve the following problems below 2 points A F 14 ZD 18 C By 2 4x ft E b What is mLEDF 3y 7 E 5x 80 Solve for x Then using that information find the measure b Solve for y Then using that information find the measure of FE and AB of LA Checkpoint Score Total

da 2 3 8 7 6 5 4 3 2 2 3 4 O 5 3 q The graph of a function y f x is shown Make a sketch of the antiderivative F given that F is continuous and F 0 1 OS 6 7 6

Learning Goal from Lesson 3 2 Given two figures I can determine if they are congruent using properties of rigid motion a 6 In each graph determine which type of transformation was used to make AABC and AMNP congruent 1 2 point each O C A Rotation OB Reflection DC Translation OD The two shapes are NOT congruent N 43 A Rotation by 180 about the origin B Reflection across the y axis OC Translation of x y x 4 y OD The two shapes are NOT congruent b d How I Did Circle one I m still learning it B I got it N e A Rotation B Reflection OC Translation OD The two shapes are NOT congruent 43 R r A 90 rotation clockwise around the origin B Reflection across the y axis C 90 rotation counterclockwise around the origin OD The two shapes are NOT congruent

EXPLAIN 1 Determining if Figures are congruent Read Explain 1 and complete Your Turn 1 2 adapted from Lesson 3 2 and complete the following A way to determine if two geometric figures are congruent is to show that one figure maps onto the other by a sequence of rigid motions such as a sequence of reflections translations and or rotations This was practiced in Lesson 3 1 Sequences of Transformations First practice with just one transformation Example The figures shown are congruent Find a rigid motion that maps one figure to the other Give coordinate notation for the transformations you use 2 AABC AXYZ CDEF JKLM The answer is B D 8 4 8 E L 0 4 y M 8 4 8 Part 1 Figure CDEF can be mapped onto JKLM by A Rotation B Reflection C Translation OD The figures are not congruent Part 2 The coordinate notation is x y x y a reflection across the y axis 8 Y 0 4 ty X 8 N C B A Part 1 Figure ABC can be mapped onto XYZ by A Rotation The answer is A Part 2 The coordinate notation is x y y x a rotation of 90 B Reflection DC Translation OD The figures are not congruent

6 for independent practice inished check the solutions with your teacher ven rotation Create a table to find the coordinates of the image 2 rotation 180 about the origin C D

6 rotation 180 about the origin G H F

5 rotation 90 about the origin H A G U x

Suppose f x 12x Determine and graph four distinct antiderivatives of f 10 10 8 6 4 2 8 6 4 2 2 4 6 8 10 2 4 6 8 16 Clear All Draw IEE

4 rotation 270 about the origin E A

3 rotation 90 clockwise about the origin A B X

ASSESSMENT Credit Checkpoint Complete the following Show all your work Learning Goal from Lesson 2 1 2 3 I can develop definitions of translations reflections and rotations in terms of angles perpendicular lines parallel lines and line segments A x y x 5 y 2 B x y x 2 y 5 C x y x 5 y 2 D x y x 2 y 5 1 Which of the following rules correctly represents the translation from ABC to MNP 1 point A R 2 N T 9 2 the 1 og 2 Reflect the shape below across the line x 2 Label the new coordinates 1 point 9 When no direction is specified you can assume the rotation is counterclockwise Transformation Rule x y B How I Did Circle one C I got it 2 4 2 ON 2 N 4 P I m still learning it M Image

ane Translate a units to the right Translate a units to the left Translate b units up Translate b units down Rules for Reflection on a Coordinate Plane Reflection across the x axis Reflection across the y axis Reflection across line y x Reflection across line y x Rules for Rotation on a Coordinate Plane 90 rotation counterclockwise 180 rotation 270 rotation counterclockwise 360 rotation Transformation Rule x y Figure 1 x y x a y x y x a y x y x y b x y x y b Coordinate Notation 1st Transformation x y x y x y x y x y y x x y y x Coordinate Notation x y y x x y x y x y y x x y x y 2nd Transformation 2 Figure 2 P 11 2 B 0 2 2 8 NYN 2 0 2 0 2 41YB N 4 4 M O 2 AD 2 P 4 X X 4

3 AABC and AA B C are shown on the coordinate plane Devon claims that a sequence of rigid motions carries AABC onto AA B C Which actions could he take to prove his claim 8 6 4 B B Sot C 6 4 N 0 A 2

P I can show that triangles are congruent if and only corresponding sides and angles are congruent Lesson 3 3 Checkpoint below Once you have completed the above problems and checked your solutions complete the Lesson Checkpoint Complete the Lesson Reflection above by circling your current understanding of the Learning Goal 1 AABC ATUV Find the following side length and angle measure a Find the mzU b Find the length of BC M Z 3y 2 6x 2 cm 2 Given that AYMZ and AQMP are identical and YZ 13 QM 15 and PM below to determine the remaining measurements Q B Side QP YM ZM 6x 1 cm 5x 7 cm Chry T Measure Kasay 4y 4y 18 15 complete the table MUC

1 ADEF AWVU D W 3 Which of the following is NOT true about congruent triangles AABC and ADEF A AB DE B BC FD C ZABC ZDEF D ZCAB LFDE Given the information above the following sides are are equal equal DE 5 Which of the following is NOT true about congruent quadrilaterals QRST and WXYZ A RS XY B ZSTQZYZW C ZRQTZXWZ D ST XW 2 LABC LLMN Cou M Given the information above the following angles LACB L 4 Which of the following is NOT true about congruent triangles AAGK and AQVZ A ZKGA LZVQ B KG ZV C AG VZ D ZGKA ZVZQ 6 Which of the following is NOT true about congruent polygons JKLMN and TUVWX A LMN LUVW B MN WX C LK VU D ZMNJ WXT Optional Complete problems 1 5 8 13 17 18 from your textbook on separate lined paper When you are finished check the odd problems for solutions at the back of the textbook

Draw and 1 Rotate AABC 270 about the origin and then reflect over the x axis B T C Preimage ABC A 1 2 B 3 4 C 2 5 6 2 A 0 TY 6 Transformation rule y B 2 8 6 4 2 image of AABC after the given sequence of transformations 2 Translate AABC by 4 4 and rotate 90 about the origin 4 6 A 8 6 2 0 Transformation rule Image A B C Preimage ABC A 1 1 B 3 3 C 2 4 2 4 6 8 Image A B C X Image A B C Image A B C

Your Turn 1 AABC DEF Find the length of CA DE EF Find the angle measure of 2A 2B 2C re 2 6 cm B 3 7 cm 3 5 cm 42 The side lengths are follows CA 3 5 cm DE 2 6 cm EF 3 7 cm a LV b OP C ST D 73 Since AABC ADEF these six facts are always true Corresponding sides are congruent 65 Corresponding angles are congruent The angle measures are as follows mLA 73 m2B 65 m2C 42 2 The following figures are congruent Find the measure of the following 0 112 43 51 km 69 N 21 km M bigmund V 39 km 16 km 43 MATRASONE S ilmoge 136 D ogla 69 hogestio Need help Visit the L4L Math Resources Website http Bit ly L4Lmath to find videos and other resources for this lesson

Your Turn Quadrilateral GHJK quadrilateral LMNP Find the given side length or angle measure 18 cm 10y 1 Find LM 4x 3 cm 9y 17 Your friend s work H m2H mzL 9y 17 10y 6x13 cm 3 Your friend tries to solve mZH Your friend did not set up to solve for mzH correctly Explain to your friend their misunderstanding and how to set it up correctly Explain to your friend their misunderstanding and how to set it up correctly 11y 1 M 2 Find m2H

Read Explore and complete the following adapted from Lesson 3 2 Show all your work Two geometric figures are congruent if and only if they have the same size shape and angle measures In geometry the symbol can be used two indicate the two figures are congruent A landscape architect uses a grid to design the landscape around a mall Use tracing paper to confirm that the landscape elements are congruent A Trace planter ABCD Describe a transformation you can use to move the tracing paper so that planter ABCD is mapped onto planter EFGH What does this confirm about the planters B Trace pools JKLM and NPQR Fold the paper so that pool JKLM is mapped onto pool NPQR Describe the transformation What does this confirm about the pools CDetermine whether the lawns are congruent Is there a rigid transformation that maps ALMN to ADEF What does this confirm about the lawns Reflect 1 How do the sizes of the pairs of figures help determine if they are congruent D C M M N A B H G K Q E E R L N D

Por 1 2 draw the image after the given transformations You can create a table to organize your work Don t forget to label the points for the first and second image 10 1 Reflect Rectangle ABCD across the y axis then translate it using the following rule x y x 4 y 3 B D C N 0 A B 10 C D 3 x y x 2 y x y A B C D Describe the type of transformations of 2 Rotate Rectangle ABCD 90 counterclockwise Then translate it along the vector 3 4 B D C 2nd 2 O 2 2 A N B C D A B C D 4 x y x y 8 x y Describe the type of transformations 1st J