Geometry Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
Geometry
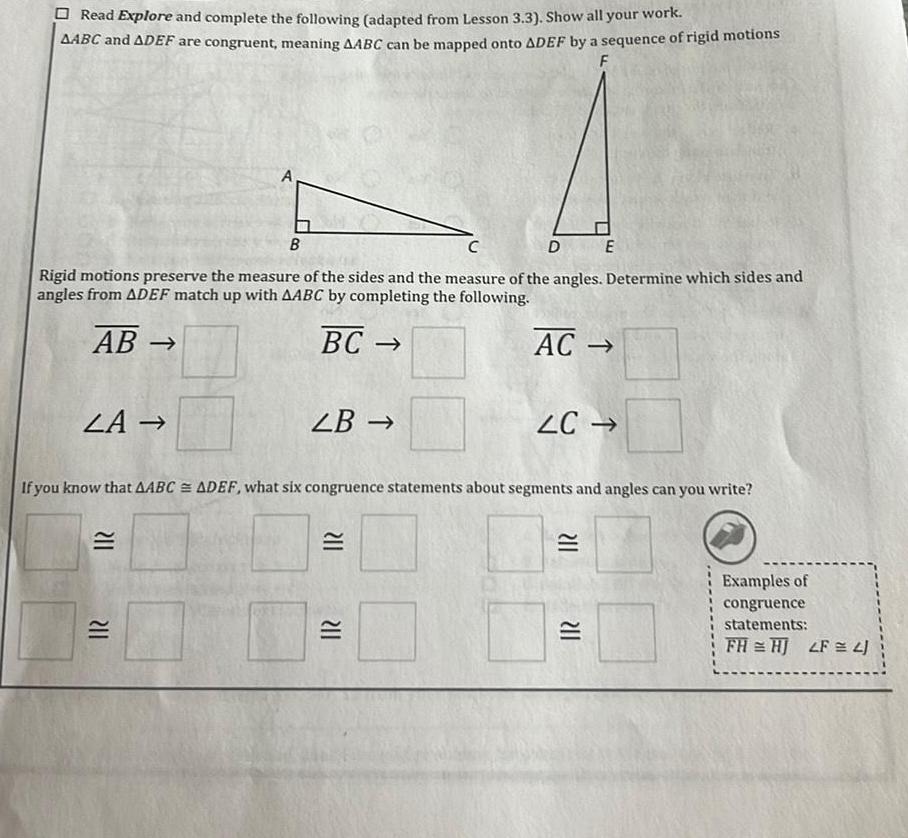
2D GeometryRead Explore and complete the following adapted from Lesson 3 3 Show all your work AABC and ADEF are congruent meaning AABC can be mapped onto ADEF by a sequence of rigid motions F C DE Rigid motions preserve the measure of the sides and the measure of the angles Determine which sides and angles from ADEF match up with AABC by completing the following AB BC LA 211 B 211 LB If you know that AABC ADEF what six congruence statements about segments and angles can you write 211 AC 211 LC 211 211 Examples of congruence statements FH HJ LF 4
Geometry
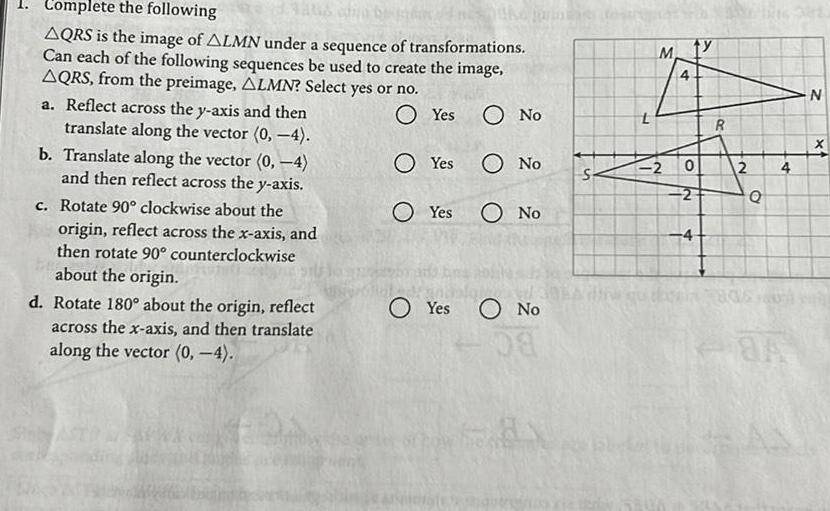
2D Geometry1 Complete the following to co O Yes O No AQRS is the image of ALMN under a sequence of transformations Can each of the following sequences be used to create the image AQRS from the preimage ALMN Select yes or no a Reflect across the y axis and then translate along the vector 0 4 b Translate along the vector 0 4 and then reflect across the y axis c Rotate 90 clockwise about the origin reflect across the x axis and then rotate 90 counterclockwise about the origin O No Yes O No d Rotate 180 about the origin reflect across the x axis and then translate along the vector 0 4 Yes Yes O No S 7 M 4 2 0 2 4 4 R 2 Q HOS 4 84 N X
Geometry
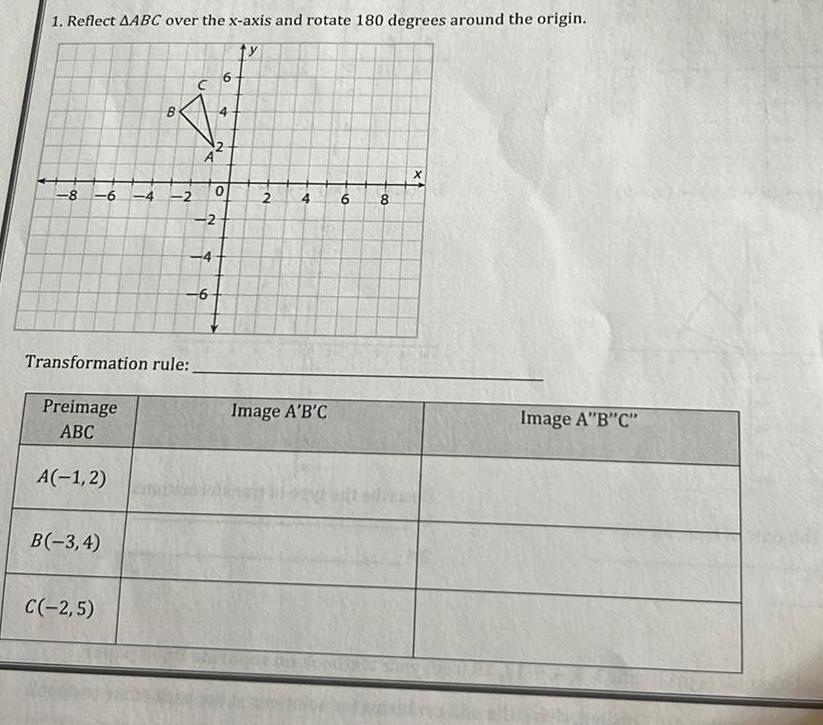
2D Geometry1 Reflect AABC over the x axis and rotate 180 degrees around the origin ty 8 6 4 2 Transformation rule Preimage ABC A 1 2 B B 3 4 C 2 5 N 4 6 6 4 2 0 O VAL 2 4 Image A B C 6 8 x1 X Image A B C
Geometry
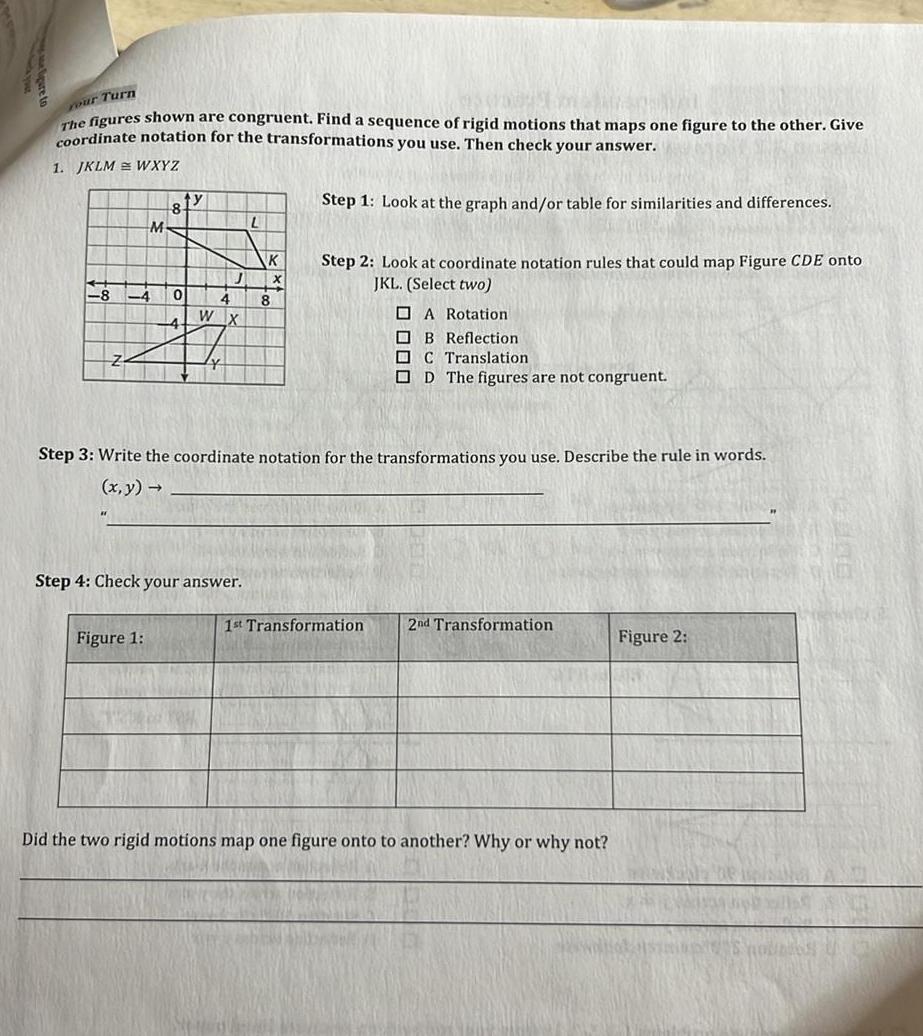
Heights & DistancesYour Turn The figures shown are congruent Find a sequence of rigid motions that maps one figure to the other Give coordinate notation for the transformations you use Then check your answer 1 JKLM WXYZ Step 1 Look at the graph and or table for similarities and differences 8 M 81y Figure 1 0 W 4 X Step 4 Check your answer L K 8 Step 2 Look at coordinate notation rules that could map Figure CDE onto JKL Select two Step 3 Write the coordinate notation for the transformations you use Describe the rule in words x y A Rotation B Reflection C Translation OD The figures are not congruent 1st Transformation 2nd Transformation Did the two rigid motions map one figure onto to another Why or why not Figure 2
Geometry
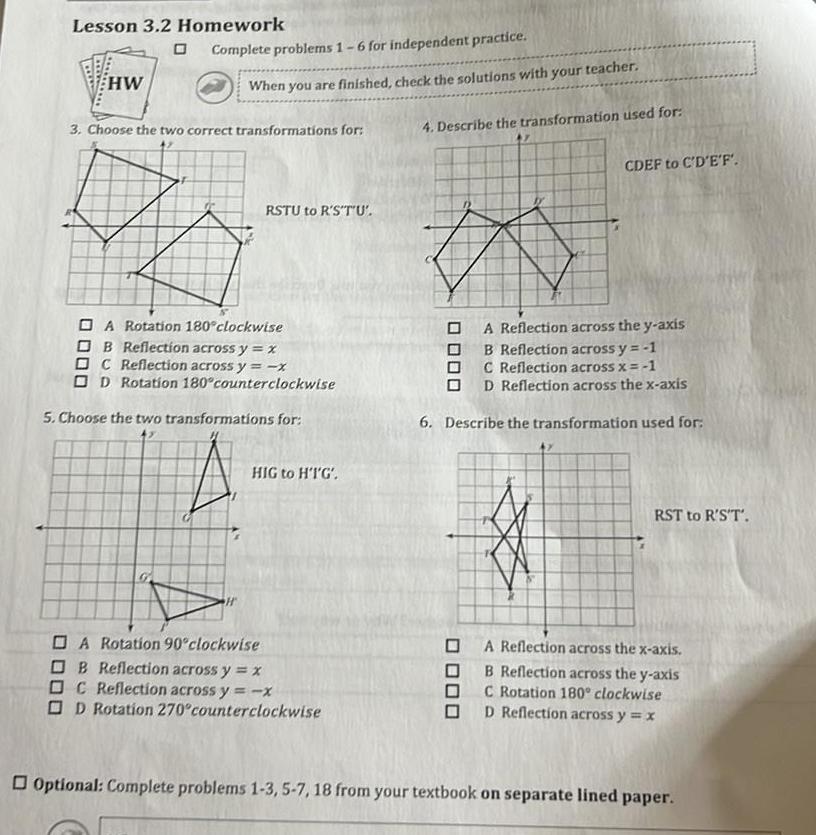
2D GeometryLesson 3 2 Homework HW Complete problems 1 6 for independent practice When you are finished check the solutions with your teacher 3 Choose the two correct transformations for RSTU to R S T U A Rotation 180 clockwise OB Reflection across y x DC Reflection across y x OD Rotation 180 counterclockwise 5 Choose the two transformations for HIG to HT G A Rotation 90 clockwise OB Reflection across y x OC Reflection across y x OD Rotation 270 counterclockwise 4 Describe the transformation used for 47 a CDEF to C D E F A Reflection across the y axis B Reflection across y 1 C Reflection across x 1 OD Reflection across the x axis 6 Describe the transformation used for RST to R S T A Reflection across the x axis B Reflection across the y axis C Rotation 180 clockwise D Reflection across y x Optional Complete problems 1 3 5 7 18 from your textbook on separate lined paper
Geometry
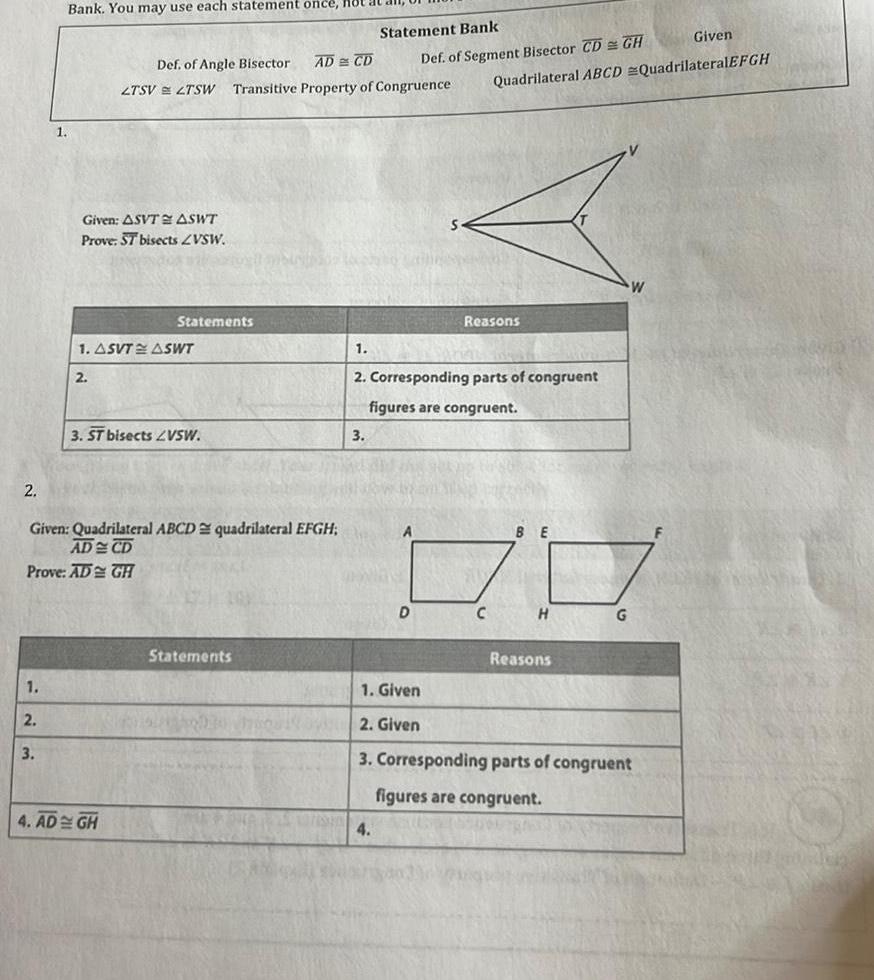
2D Geometry2 1 2 1 3 Bank You may use each statement once Hot Given ASVT ASWT Prove ST bisects ZVSW 2 1 ASVT ASWT Given Quadrilateral ABCD quadrilateral EFGH AD CD Prove AD GH Def of Angle Bisector AD CD LTSV LTSW Transitive Property of Congruence Statements 3 ST bisects VSW 4 AD GH Statements Statement Bank 3 Given Def of Segment Bisector CD GH Quadrilateral ABCD QuadrilateralEFGH 1 2 Corresponding parts of congruent figures are congruent 4 D Reasons BE H Reasons G 1 Given 2 Given 3 Corresponding parts of congruent figures are congruent

Geometry
2D GeometryYour Turn Formos The figures shown are congruent Find a rigid motion that maps one figure to the other Give coordinate notation for the transformations you use 1 ABCD WXYZ Part 1 Figure ABCD can be mapped onto WXYZ by A Rotation B Reflection DC Translation OD The figures are not congruent Part 2 The coordinate notation is 2 ABCDE PQRST Part 1 ABCDE can be mapped onto PQRST by A Rotation B Reflection DC Translation D The figures are not congruent Part 2 The coordinate notation is 20 000 8 8 Y 4 X B 80 4 R ty A 0 Z4 4 A ty E 0 2N 4 D 8 W 8 S DX 4 8

Geometry
2D Geometry7 8 Identify the surface whose equation is given p cos 1 Answer Horizontal plane ha

Geometry
Solution of triangles11 Using coordinate geometry and algebra find the coordinates of the vertices of AABC a A 5 3 H 1 4 H 3 1 b A 4 5 H 2 3 H 1 2
Geometry
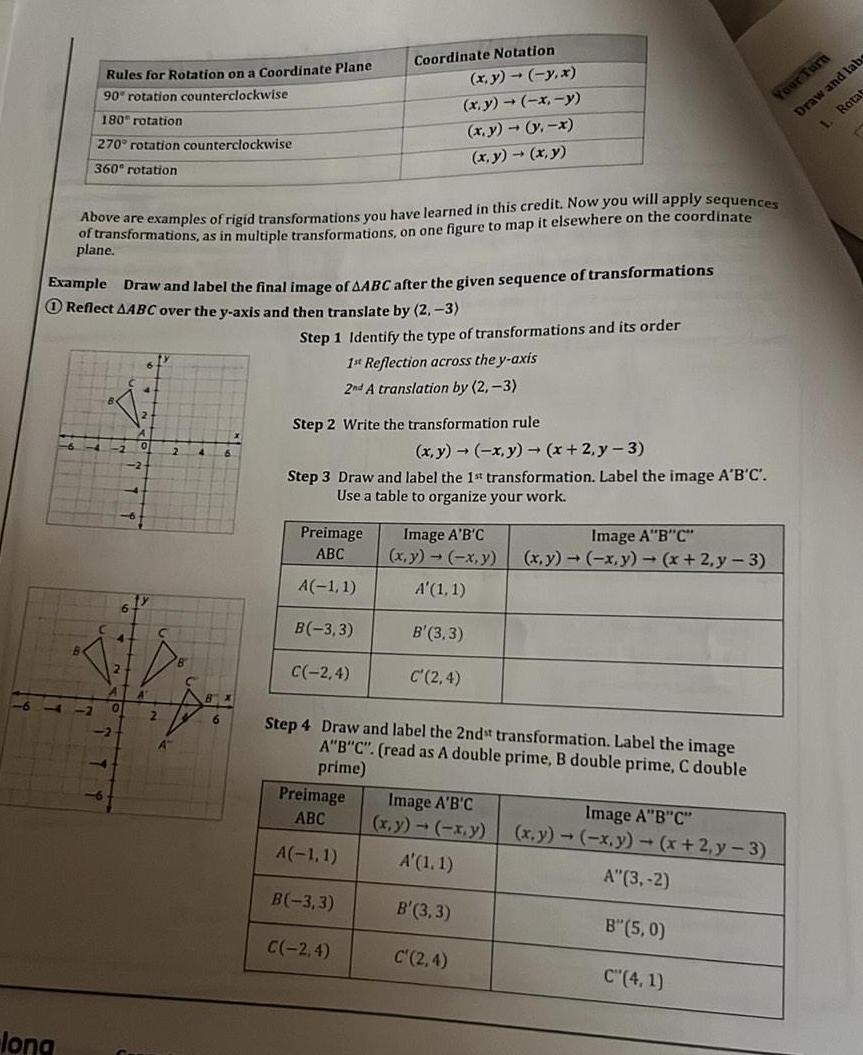
Coordinate systemRules for Rotation on a Coordinate Plane 90 rotation counterclockwise 180 rotation 270 rotation counterclockwise 360 rotation long Example Draw and label the final image of AABC after the given sequence of transformations Reflect AABC over the y axis and then translate by 2 3 Above are examples of rigid transformations you have learned in this credit Now you will apply sequences of transformations as in multiple transformations on one figure to map it elsewhere on the coordinate plane Coordinate Notation Step 1 Identify the type of transformations and its order x y y x x y x y x y y x x y x y 1st Reflection across the y axis 2nd A translation by 2 3 Step 2 Write the transformation rule Preimage ABC A 1 1 B 3 3 x y x y x 2y 3 Step 3 Draw and label the 1st transformation Label the image A B C Use a table to organize your work C 2 4 Preimage ABC A 1 1 B 3 3 C 2 4 Image A B C x y x y A 1 1 B 3 3 C 2 4 Step 4 Draw and label the 2ndst transformation Label the image A B C read as A double prime B double prime C double prime Image A B C x y x y x 2 y 3 Image A B C x y x y A 1 1 B 3 3 C 2 4 Image A B C x y x y x 2 y 3 A 3 2 B 5 0 Your Turn Draw and labs 1 Rotat C 4 1 r
Geometry
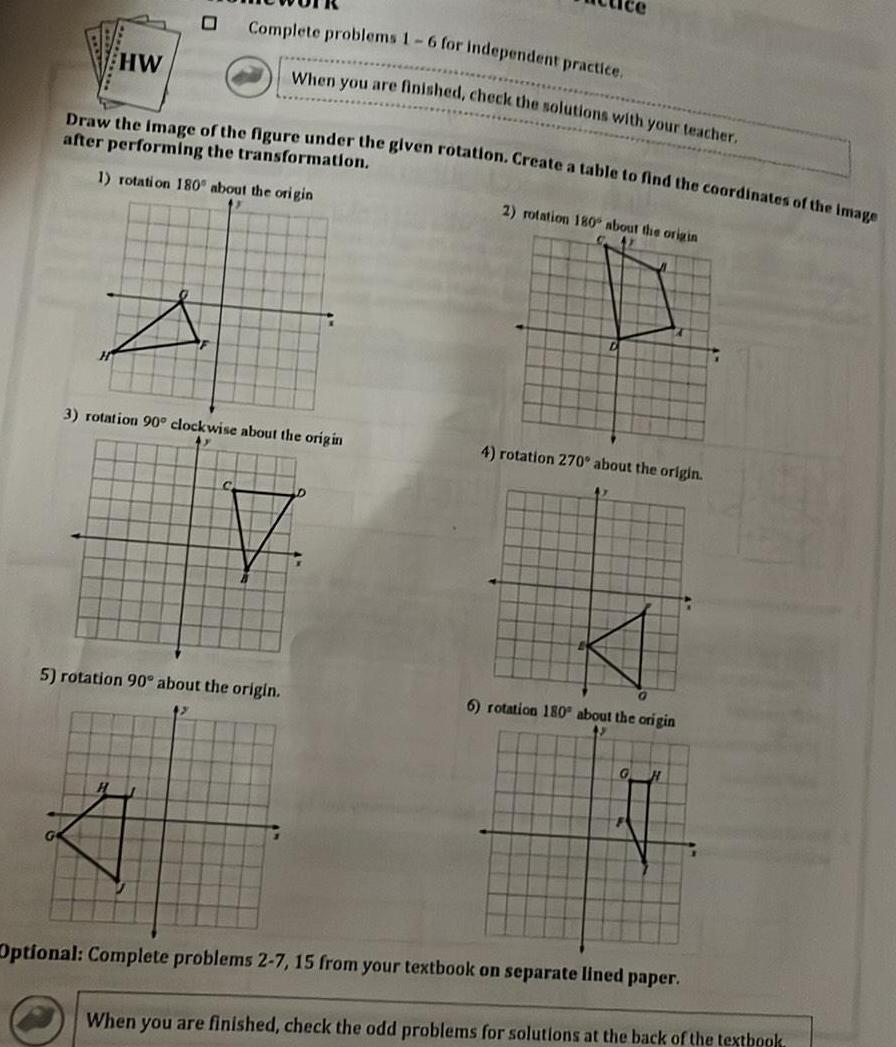
2D GeometryHW 0 Complete problems 1 6 for independent practice When you are finished check the solutions with your teacher Draw the image of the figure under the given rotation Create a table to find the coordinates of the image after performing the transformation 1 rotation 180 about the origin 3 rotation 90 clockwise about the origin 5 rotation 90 about the origin 2 rotation 180 about the origin 4 rotation 270 about the origin 6 rotation 180 about the origin G H Optional Complete problems 2 7 15 from your textbook on separate lined paper D When you are finished check the odd problems for solutions at the back of the textbook
Geometry
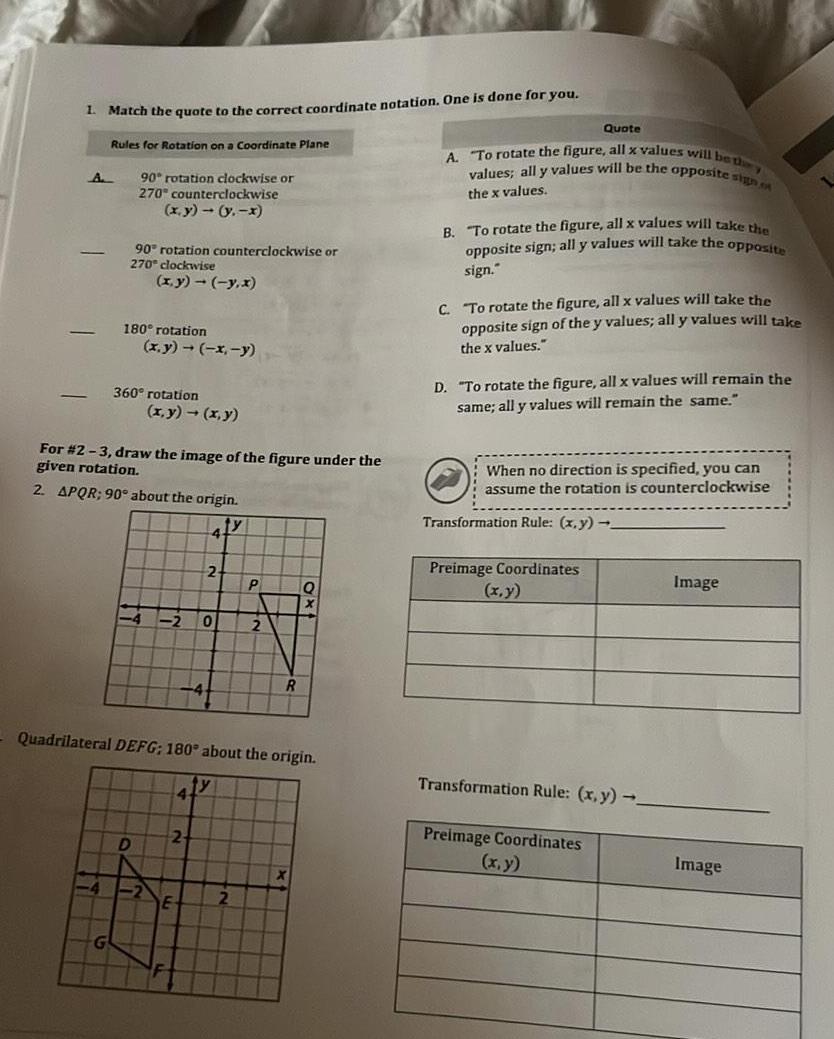
2D Geometry1 Match the quote to the correct coordinate notation One is done for you A Rules for Rotation on a Coordinate Plane 90 rotation clockwise or 270 counterclockwise x y y x 90 rotation counterclockwise or 270 clockwise x y y x 180 rotation G 360 rotation x y x y For 2 3 draw the image of the figure under the given rotation 2 APQR 90 about the origin ty 4 D x y x y 4 2 4 2 E 2 Quadrilateral DEFG 180 about the origin 0 P 2 R Q X Quote A To rotate the figure all x values will be they values all y values will be the opposite sign the x values B To rotate the figure all x values will take the opposite sign all y values will take the opposite sign C To rotate the figure all x values will take the opposite sign of the y values all y values will take the x values D To rotate the figure all x values will remain the same all y values will remain the same When no direction is specified you can assume the rotation is counterclockwise Transformation Rule x y Preimage Coordinates x y Transformation Rule x y Preimage Coordinates x y Image Image
Geometry
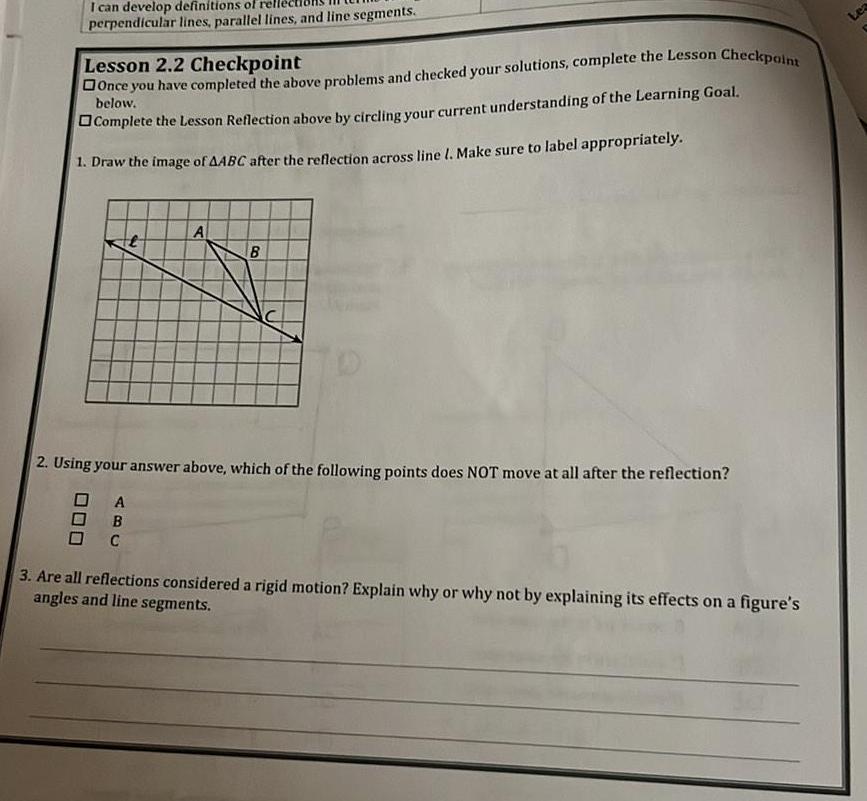
2D GeometryI can develop definitions of rel perpendicular lines parallel lines and line segments Lesson 2 2 Checkpoint Once you have completed the above problems and checked your solutions complete the Lesson Checkpoint below Complete the Lesson Reflection above by circling your current understanding of the Learning Goal 1 Draw the image of AABC after the reflection across line 1 Make sure to label appropriately A A OB C B 2 Using your answer above which of the following points does NOT move at all after the reflection 3 Are all reflections considered a rigid motion Explain why or why not by explaining its effects on a figure s angles and line segments
Geometry
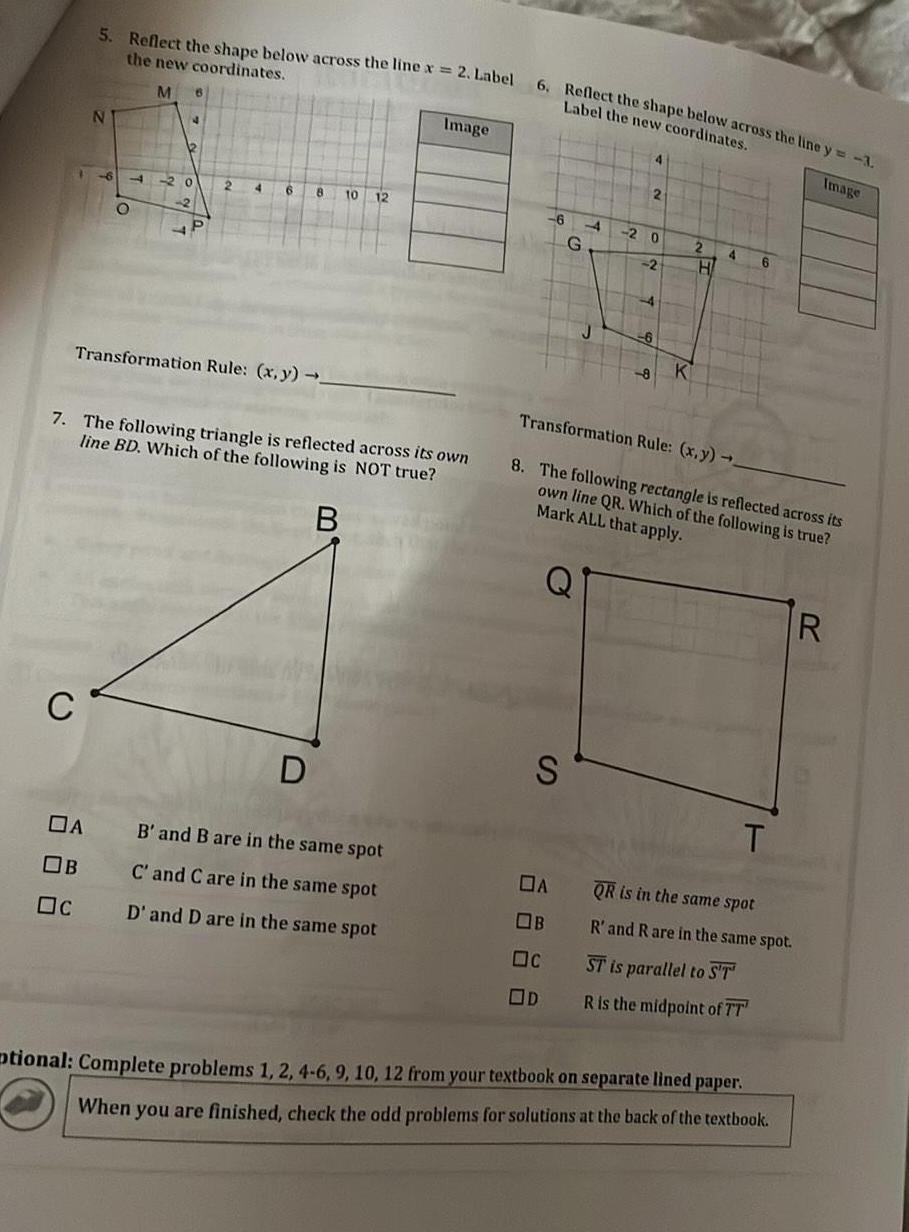
2D Geometry5 Reflect the shape below across the line x 2 Label the new coordinates M C N DA OB Oc 6 O 20 2 2 4 Transformation Rule x y 6 10 7 The following triangle is reflected across its own line BD Which of the following is NOT true B D 12 Image B and B are in the same spot C and C are in the same spot D and D are in the same spot 6 Reflect the shape below across the line y 3 Label the new coordinates Image 6 S G A OB c OD J 2 2 0 2 4 K 2 H 4 Transformation Rule x y 8 The following rectangle is reflected across its own line QR Which of the following is true Mark ALL that apply 6 T QR is in the same spot R and R are in the same spot ST is parallel to ST R is the midpoint of TT ptional Complete problems 1 2 4 6 9 10 12 from your textbook on separate lined paper When you are finished check the odd problems for solutions at the back of the textbook R
Geometry
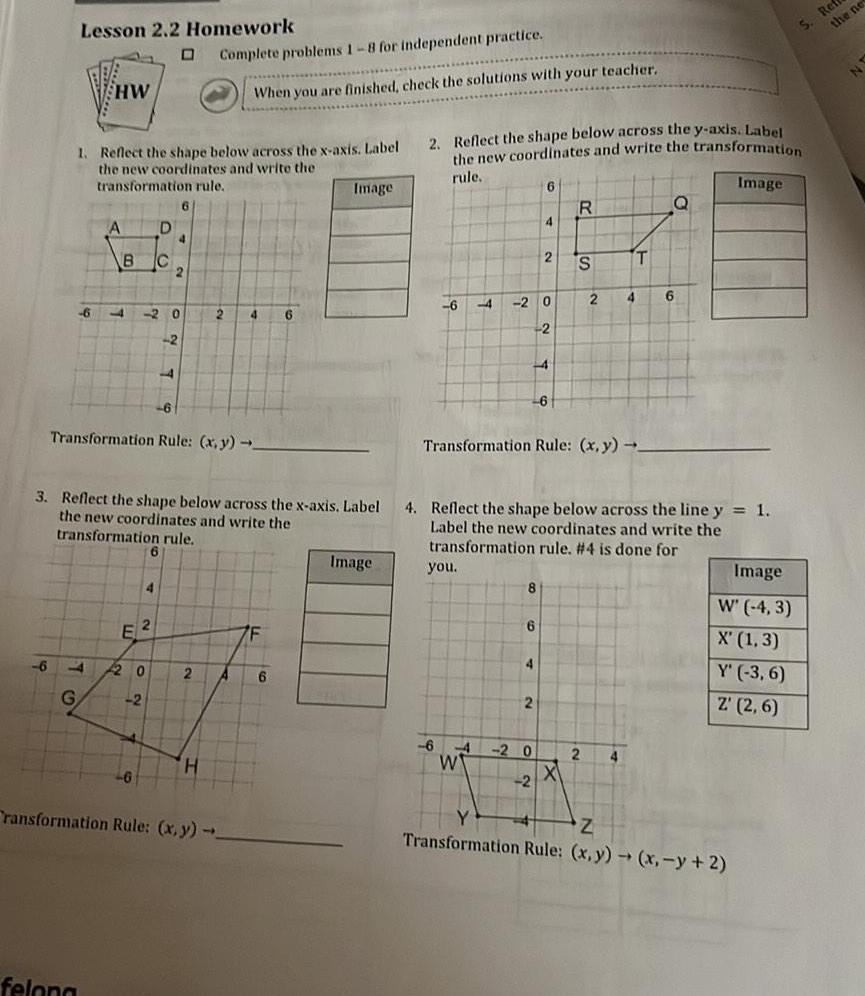
2D GeometryLesson 2 2 Homework D 6 HW 1 Reflect the shape below across the x axis Label the new coordinates and write the transformation rule felona 6 4 G A B C y E D 46 20 4 2 20 2 4 Transformation Rule x y 6 2 2 3 Reflect the shape below across the x axis Label the new coordinates and write the transformation rule Complete problems 1 8 for independent practice When you are finished check the solutions with your teacher 2 H 2 A 4 6 ransformation Rule x y F Image 6 Image 2 Reflect the shape below across the y axis Label the new coordinates and write the transformation rule Image 6 4 2 you 8 6 6 4 6 4 2 0 W 4 14 2 2 2 6 0 2 Transformation Rule x y R 4 Reflect the shape below across the line y 1 Label the new coordinates and write the transformation rule 4 is done for S X 2 2 4 T 4 Q 6 Image W 4 3 X 1 3 Y 3 6 Z 2 6 Z Transformation Rule x y x y 2 S Refr the ne N

Geometry
2D Geometryangles perpendicular lines parallel lines and line segments can develop definitions of reflections in terms of Standard G CO A 4 EXPLORE Exploring Reflections Read Explore in your textbook Lesson 2 2 and complete the following Show all your work Using tracing paper complete steps Instead of using quadrilateral ABCD from your book use quadrilateral and B FGHI to the right Label appropriately from your textbook attach tracing paper here LAL Math Resources http Bit ly L4LMath H C Draw segments to connect each vertex of quadrilateral FGHI with its image Use a protractor to measure the angle formed by each comment and ling What do you notice
Geometry
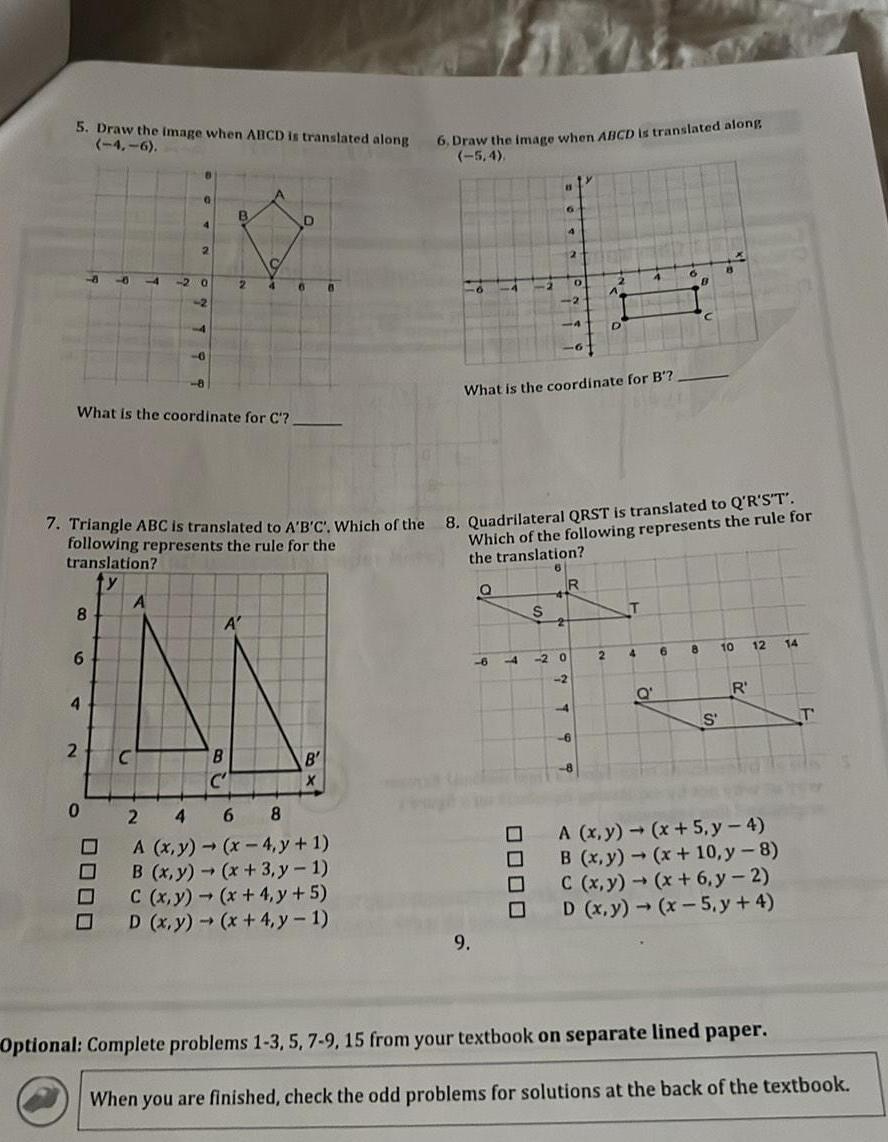
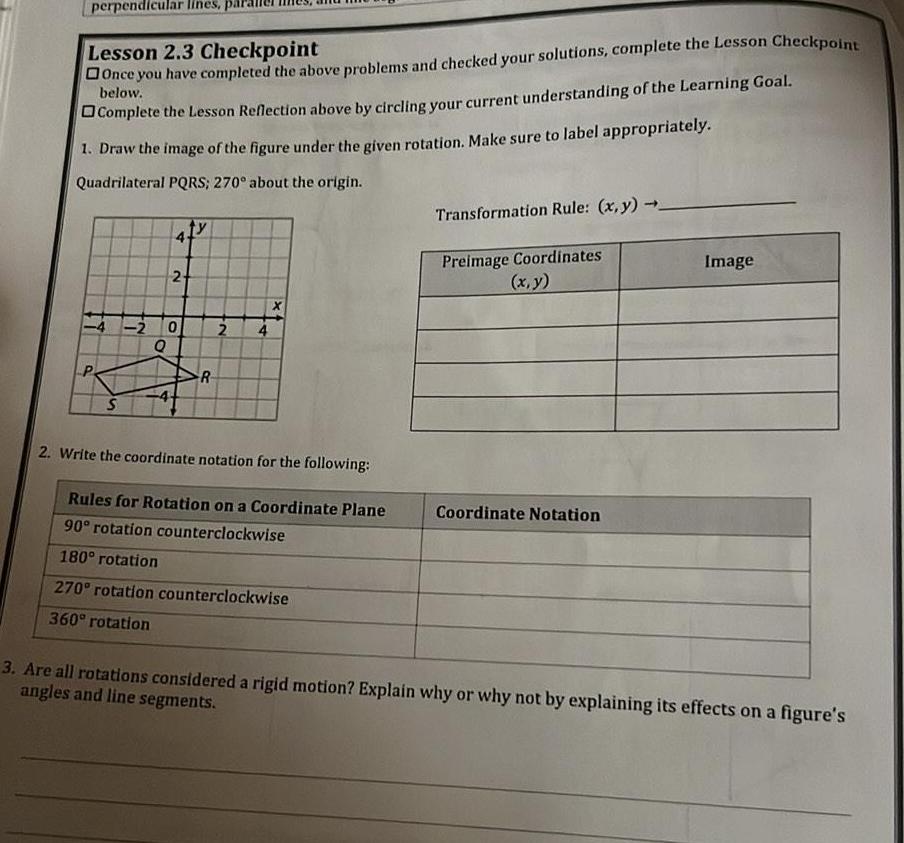
2D Geometry5 Draw the image when ABCD is translated along 4 6 8 6 4 4 2 What is the coordinate for C 0000 C 2 2 0 A 0 2 4 B 2 B C 4 A 7 Triangle ABC is translated to A B C Which of the 8 Quadrilateral QRST is translated to Q R S T following represents the rule for the translation D 6 B X 6 Draw the image when ABCD is translated along 6 8 A x y x 4 y 1 B x y x 3 y 1 C x y x 4 y 5 D x y x 4 y 1 What is the coordinate for B 9 6 11 7 0000 Which of the following represents the rule for the translation S D 20 2 R 2 4 T 4 B Q 6 13 8 10 S R 12 A x y x 5 y 4 B x y x 10 y 8 C x y x 6 y 2 D x y x 5 y 4 Optional Complete problems 1 3 5 7 9 15 from your textbook on separate lined paper 14 T When you are finished check the odd problems for solutions at the back of the textbook
Geometry
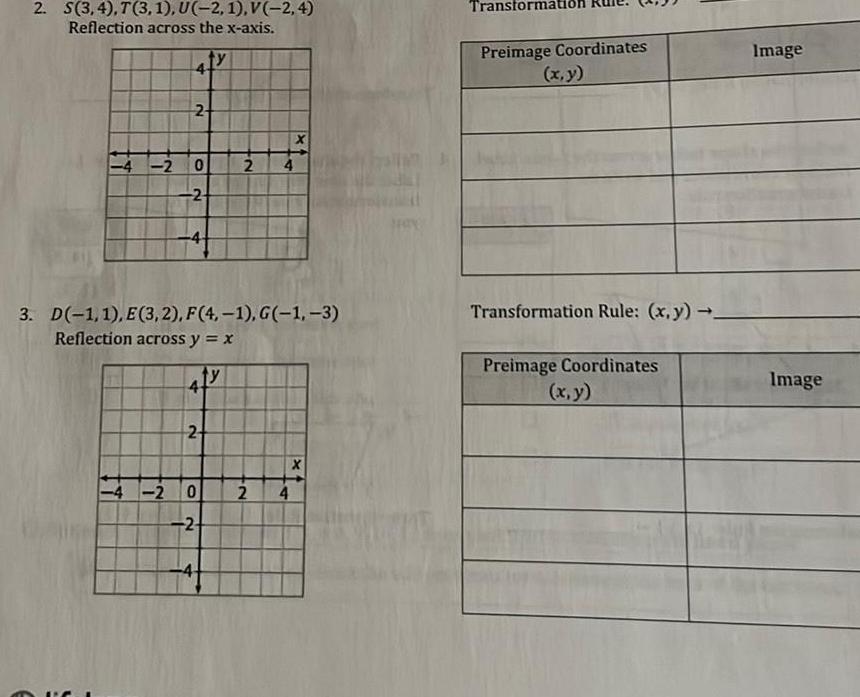
Areaperpendicular lines Lesson 2 3 Checkpoint Once you have completed the above problems and checked your solutions complete the Lesson Checkpoint below Complete the Lesson Reflection above by circling your current understanding of the Learning Goal 1 Draw the image of the figure under the given rotation Make sure to label appropriately Quadrilateral PQRS 270 about the origin S 2 2 0 R 2 4 2 Write the coordinate notation for the following Rules for Rotation on a Coordinate Plane 90 rotation counterclockwise 180 rotation 270 rotation counterclockwise 360 rotation Transformation Rule x y Preimage Coordinates x y Coordinate Notation Image 3 Are all rotations considered a rigid motion Explain why or why not by explaining its effects on a figure s angles and line segments

Geometry
Coordinate systemYour Turn Draw the image of the triangle after the given rotation You will need a protractor 1 Counterclockwise rotation 40 about point P 2 Clockwise rotation of 125 around point Q S P L

Geometry
Coordinate systemA B C B Line I has a slope of 2 the segments must have an opposite reciprocal slope of Line I has a slope of the segments must have an opposite reciprocal of

Geometry
2D GeometryLesson 2 1 Checkpoint Once you have completed the above problems and checked your solutions complete the Lesson Checkpoint Complete the Lesson Reflection above by circling your current understanding of the Learning Goal below 1 Draw the preimage and image of the triangle under a translation along 1 3 Make sure to label appropriately Triangle P 1 3 Q 3 1 R 4 3 2 2 0 2 y 2 Are all translations considered a rigid motion Explain why or why not by explaining its effects on a figure s angles and line segments 2 4 X Forgot what rigid motion is Look at your Credit 1 notes
Geometry
Coordinate system2 S 3 4 T 3 1 U 2 1 V 2 4 Reflection across the x axis ty 4 2 2 0 2 3 D 1 1 E 3 2 F 4 1 G 1 3 Reflection across y x 2 2 4 4 2 0 2 2 4 X Transformati Preimage Coordinates Transformation Rule x y Preimage Coordinates x y Image Image

Geometry
Coordinate systemYour Turn 1 Match the quote to the correct coordinate notation One is done for you Rules for Reflection on a Coordinate Plane D Reflection across the x axis x y x y Reflection across the y axis x y x y Reflection across line y x x y y x Quote A To reflect the figure all x values will take the opposite sign all y values will remain the same B To reflect the figure all x values will be the opposite sign of the y values all y values will be the opposite sign of the x values C To reflect the figure all x values will be the y values all y values will be the x values
Geometry
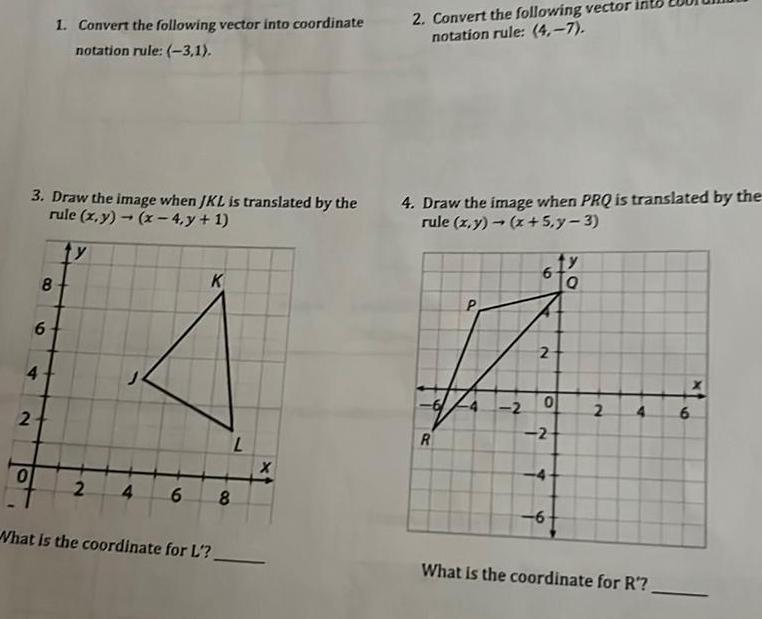
Area3 Draw the image when JKL is translated by the rule x y x 4 y 1 y 4 2 0 8 6 1 Convert the following vector into coordinate notation rule 3 1 2 K 4 6 8 What is the coordinate for L 2 Convert the following vector into notation rule 4 7 4 Draw the image when PRQ is translated by the rule x y x 5 y 3 R P 2 6 2 0 2 4 6 y Q 2 4 6 What is the coordinate for R

Geometry
2D GeometryDraw the preimage and image of each triangle under a translation along 4 1 2 Triangle with coordinates P 2 1 Q 2 3 R 4 3 ty 2 2 0 2 2 Transformation Rule x y Preimage Coordinates Image

Geometry
Coordinate systemDraw the preimage and image of each triangle under a translation along 4 1 1 Triangle with coordinates A 2 4 B 1 2 C 4 2 y 4 2 0 2 Transformation Rule x y Preimage Coordinates x y Image

Geometry
Area1 Draw the image of AABC after a translation along A B 12 C Describe how the direction of the above vector is moving AABC 2 In your own words explain what a translation of a figure is
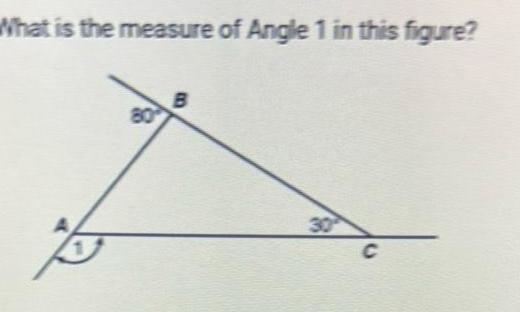
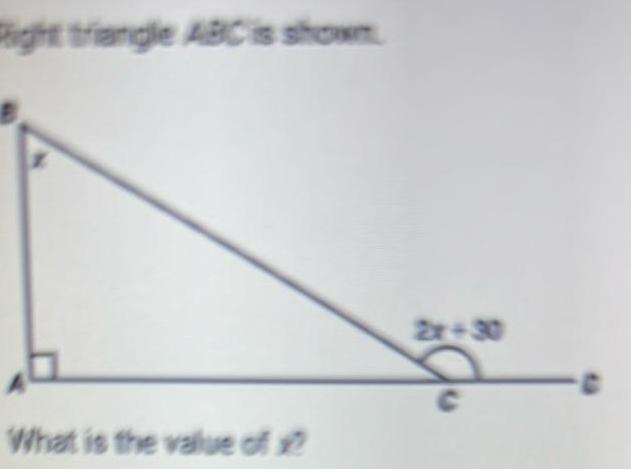

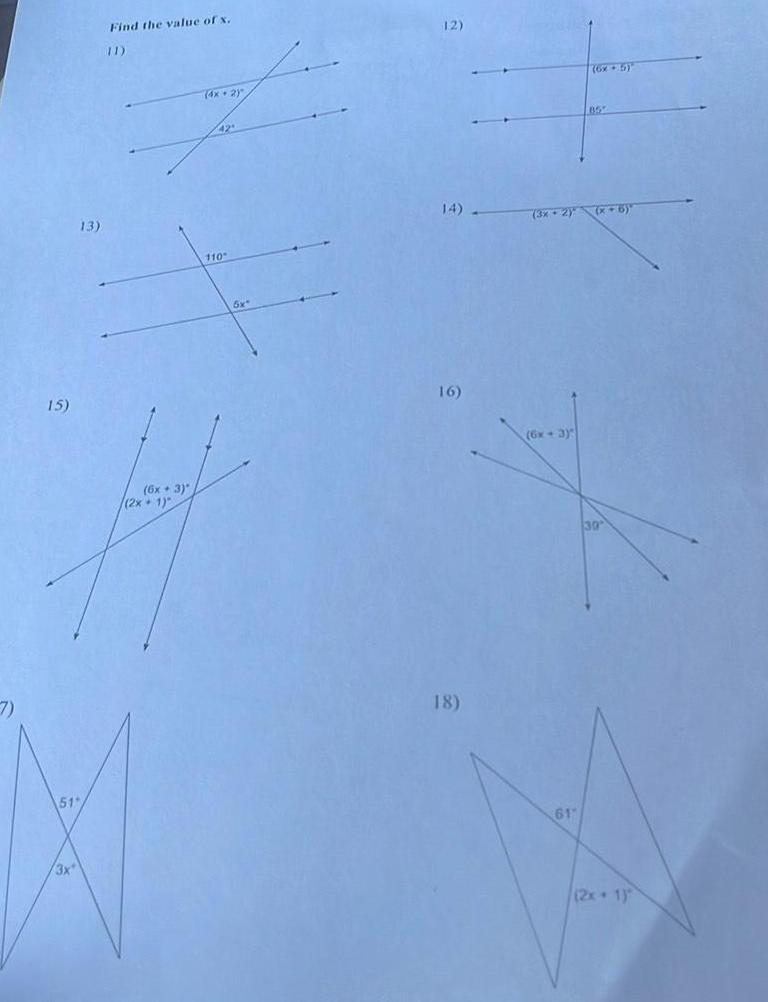
Geometry
Coordinate system15 13 51 Find the value of x 6x 3 4x2 2x 1 110 6x 12 16 18 6x 5 3x 2 x 6 6x 3 85 f 61 30 2x 1
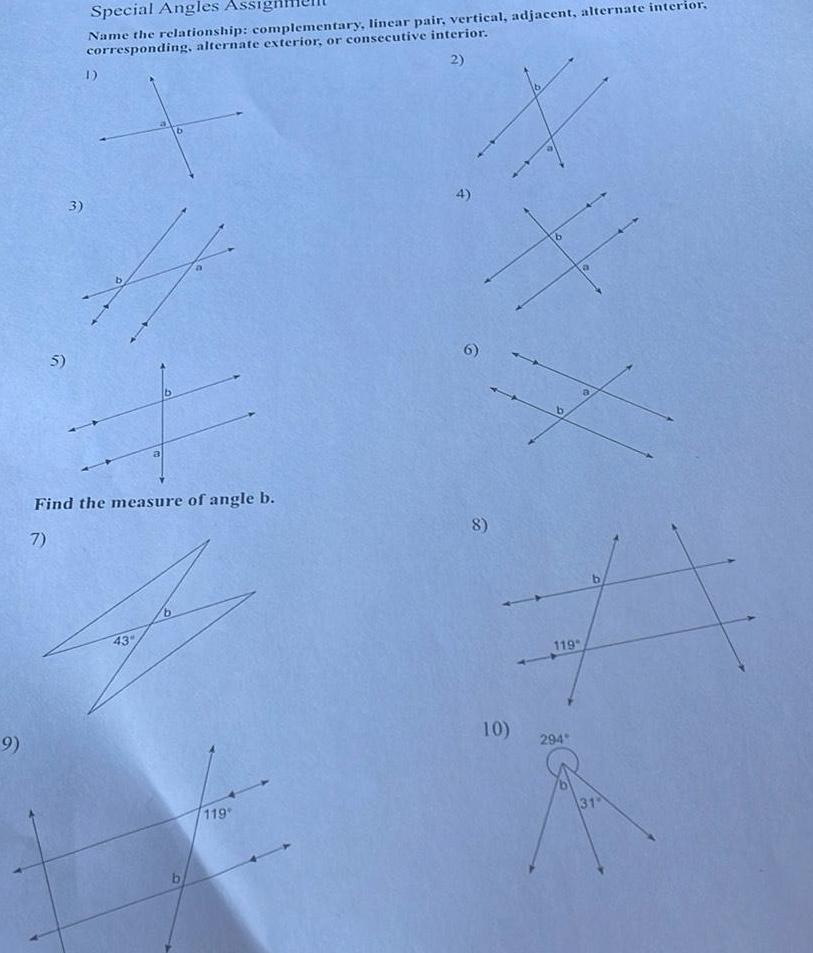
Geometry
Area9 5 3 Special Angles Assign Name the relationship complementary linear pair vertical adjacent alternate interior corresponding alternate exterior or consecutive interior 2 1 b Find the measure of angle b 7 43 119 4 6 8 10 119 294 31

Geometry
VectorsA cricket striker hits the ball with an angle of 0 46 and an initial speed of Vo 105 feet per second There is a helping wind blowing with an angle of elevation of a 9 and a speed of w 8 feet per second The speed represents the length of the wind vector 0 y y t b Determine the time for the ball to hit the ground Ground time a Determine the parametric representations for x and y as functions of time where t is in seconds Note If entering exact values your angles must be in radians not degrees x x t seconds c Determine the downrange distance Downrange Distance W foot a Wx W
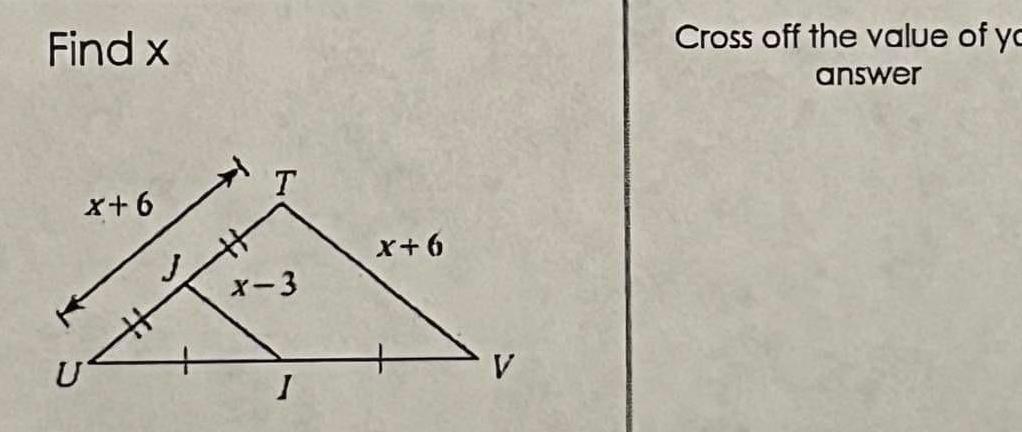

Geometry
Coordinate systemThe blue figure is a dilation image of the black figure The labeled point is the center of dilation Tell whether the dilation is an enlargement or a reduction Then find the scale factor of the dilation Is the dilation an enlargement or a reduction Enlargement Reduction Find the scale factor n n Simplify your answer E 0
Geometry
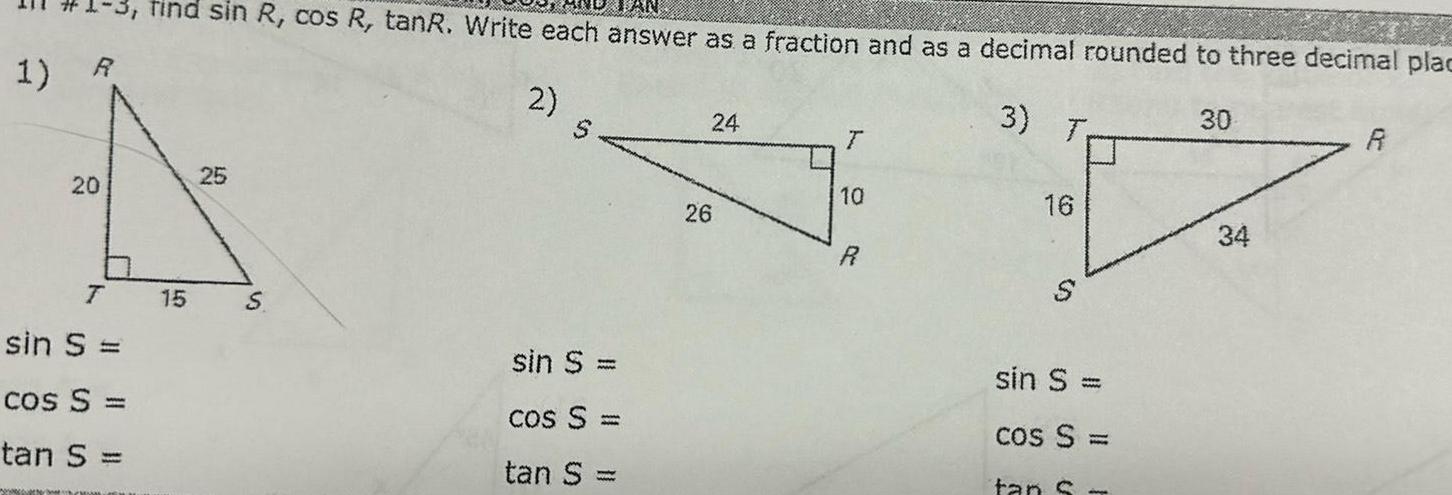
Coordinate system1 R 20 7 J sin S cos S tan S find sin R cos R tanR Write each answer as a fraction and as a decimal rounded to three decimal plac 3 T 2 15 25 S sin S cos S tan S 24 26 T 10 8 16 S sin S cos S tan S 30 34 R
Geometry
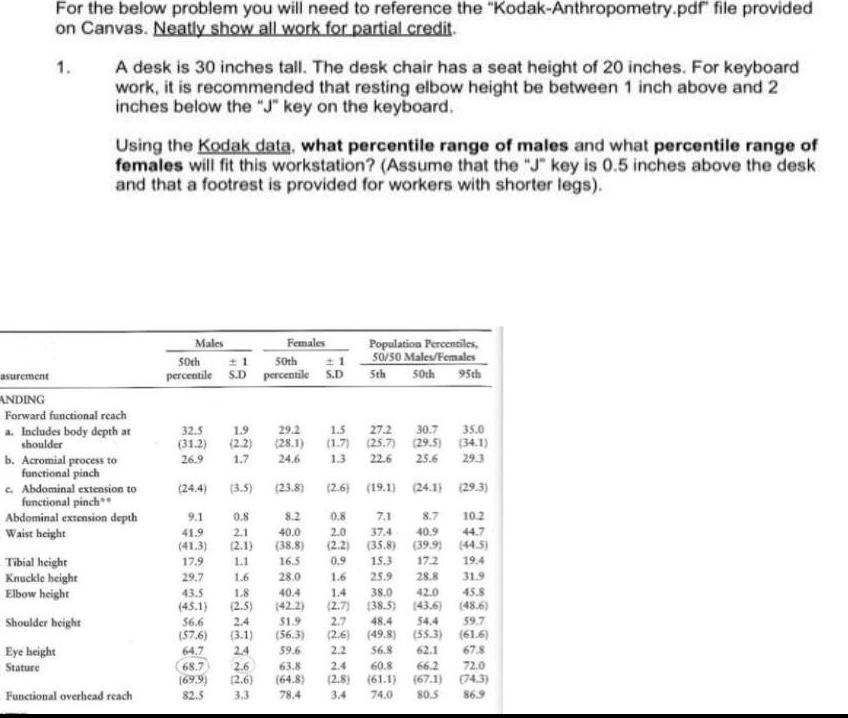
Coordinate systemasurement For the below problem you will need to reference the Kodak Anthropometry pdf file provided on Canvas Neatly show all work for partial credit 1 A desk is 30 inches tall The desk chair has a seat height of 20 inches For keyboard work it is recommended that resting elbow height be between 1 inch above and 2 inches below the J key on the keyboard Using the Kodak data what percentile range of males and what percentile range of females will fit this workstation Assume that the J key is 0 5 inches above the desk and that a footrest is provided for workers with shorter legs ANDING Forward functional reach a Includes body depth at shoulder Tibial height Knuckle height Elbow height Shoulder height Eye height Stature b Acromial process to functional pinch c Abdominal extension to functional pinch Abdominal extension depth Waist height Functional overhead reach Males Females 1 50th 50th 1 percentile S D percentile S D 32 5 31 2 26 9 24 4 9 1 41 9 41 3 17 9 29 7 43 5 45 1 56 6 57 6 64 7 68 7 699 82 5 1 9 2 2 1 7 3 5 29 2 28 1 24 6 23 8 0 8 8 2 2 1 40 0 2 1 38 8 1 1 16 5 1 6 28 0 1 8 40 4 2 5 42 2 2 4 1 9 3 1 56 3 2 4 59 6 2 6 63 8 2 6 64 8 3 3 78 4 Population Percentiles 50 50 Males Females 5th 50th 95th 1 5 27 2 30 7 1 7 25 7 29 5 1 3 22 6 25 6 2 6 19 1 24 1 29 3 0 8 7 1 8 7 2 0 37 4 40 9 35 8 39 9 2 2 0 9 15 3 17 2 2 4 2 8 3 4 35 0 34 1 29 3 1 6 25 9 28 8 31 9 45 8 48 6 1 4 38 0 42 0 2 7 38 5 43 6 2 7 48 4 54 4 2 6 49 8 55 3 2 2 56 8 62 1 60 8 66 2 61 1 67 1 74 0 80 5 10 2 44 7 44 5 19 4 59 7 61 6 67 8 72 0 74 3 86 9
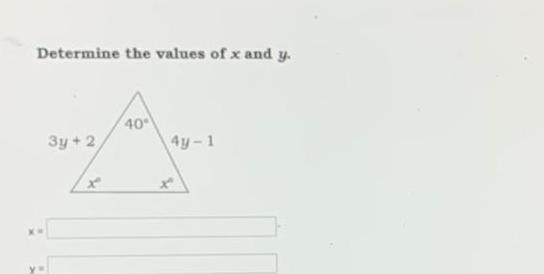
Geometry
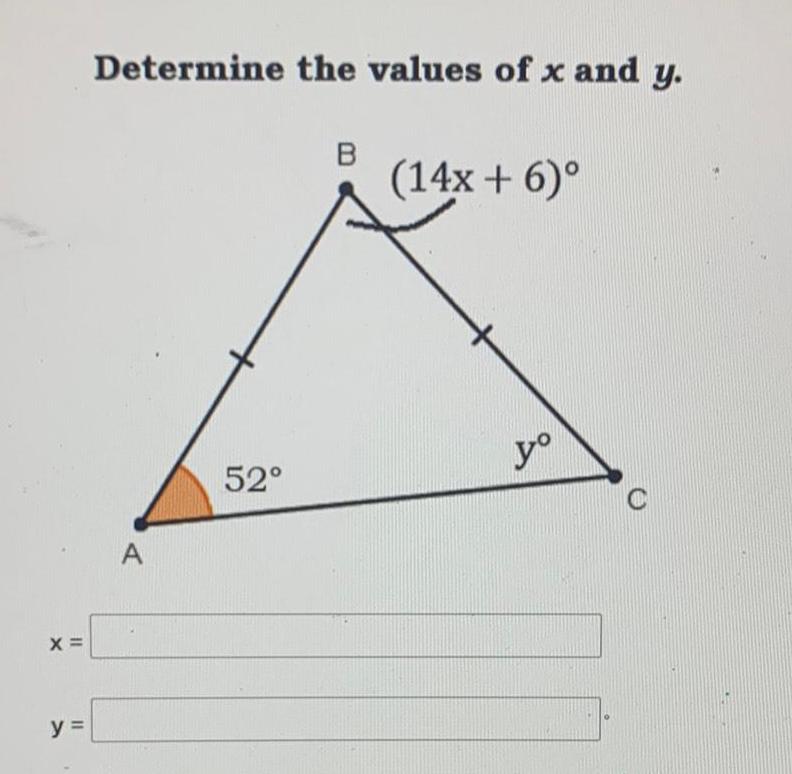
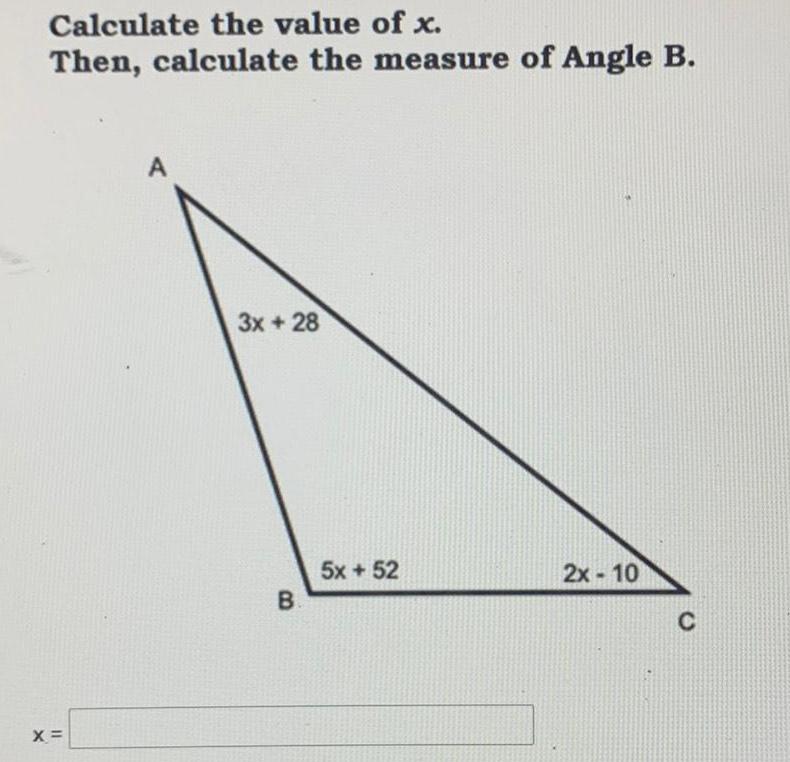
2D GeometryCalculate the value of x Then calculate the measure of Angle B X A 3x 28 B 5x 52 2x 10 C
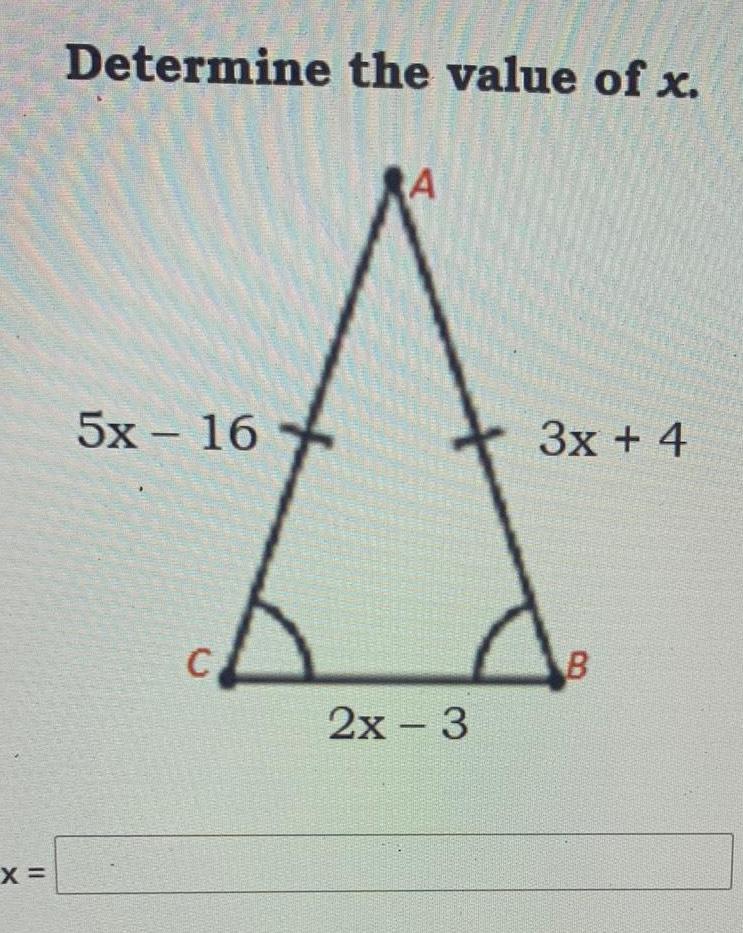
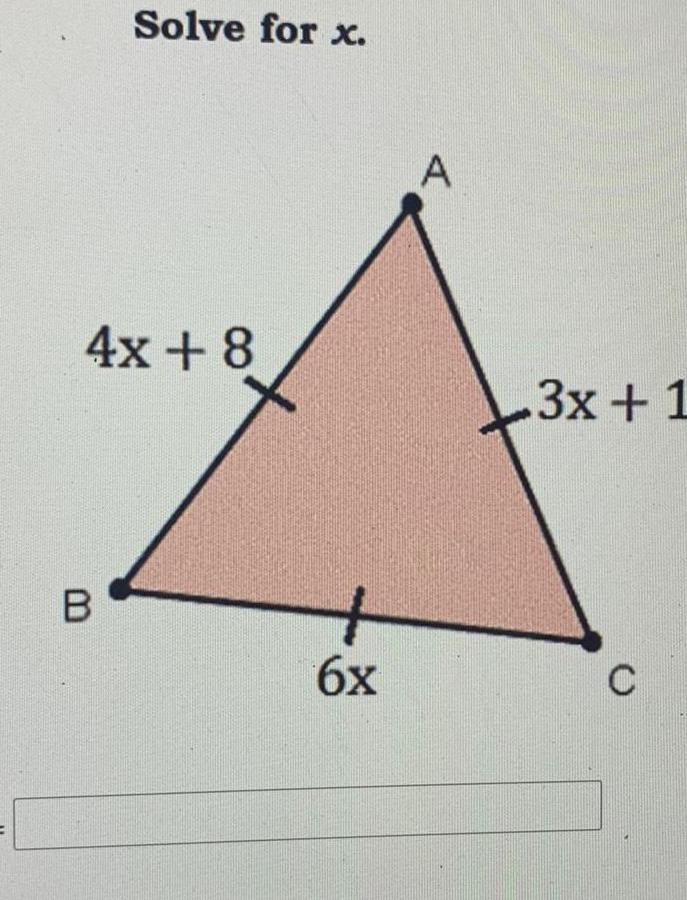

Geometry
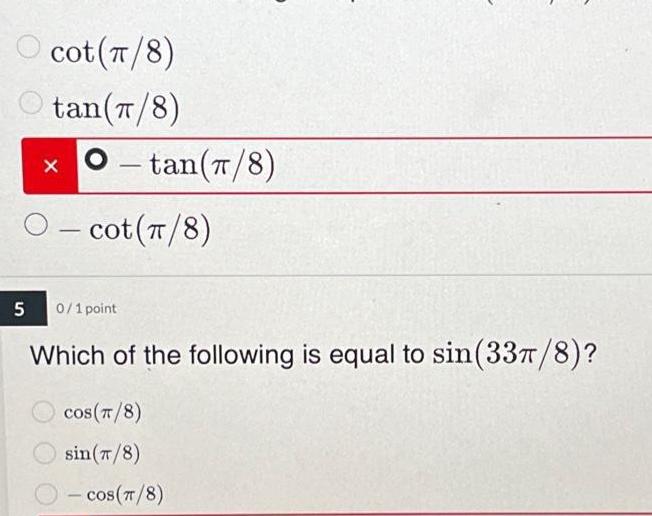
Coordinate systemcot 8 tan 8 X O tan 8 Ocot 8 5 0 1 point Which of the following is equal to sin 337 8 cos 8 sin 7 8 cos 8
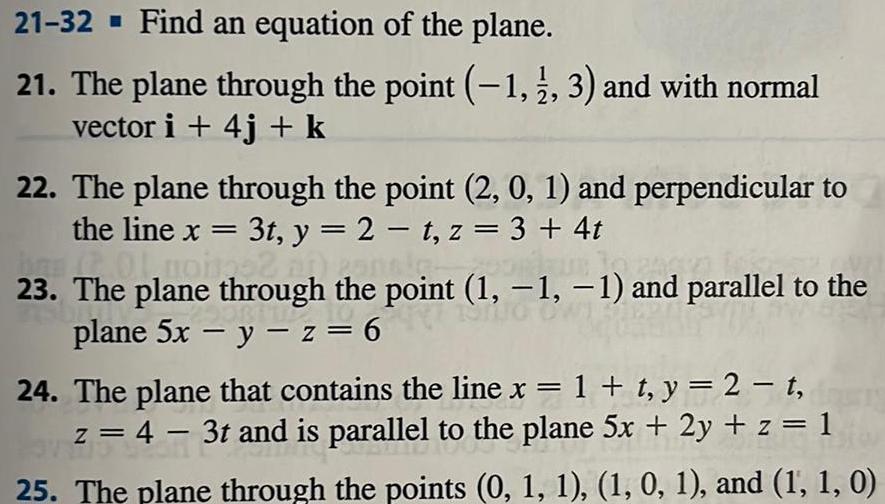
Geometry
2D Geometry21 32 Find an equation of the plane 21 The plane through the point 1 3 and with normal vector i 4j k 22 The plane through the point 2 0 1 and perpendicular to the line x 3t y 2 t z 3 4t on panola 01 mongs 23 The plane through the point 1 1 1 and parallel to the plane 5x y z 6 24 The plane that contains the line x 1 t y 2 t z 4 3t and is parallel to the plane 5x 2y z 1 25 The plane through the points 0 1 1 1 0 1 and 1 1 0 31
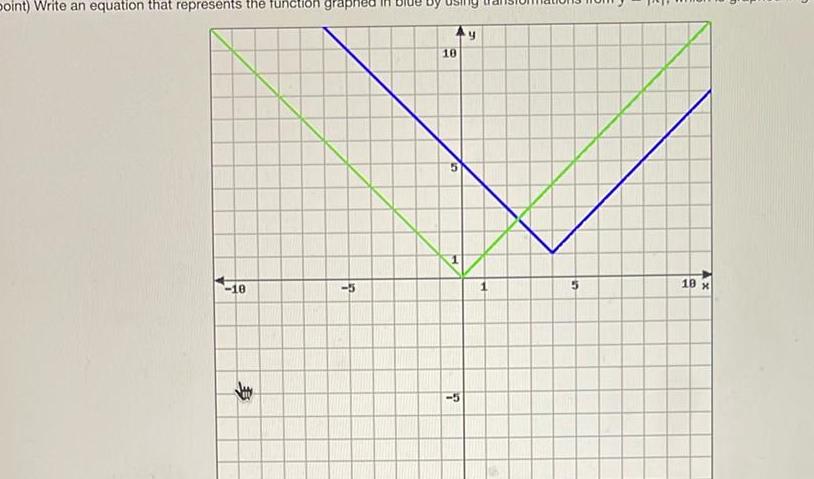
Geometry
2D Geometry39 a Find parametric equations for the line of intersection of the planes x y z 1 and x 2y 2z 1 Q b Find the angle between these planes
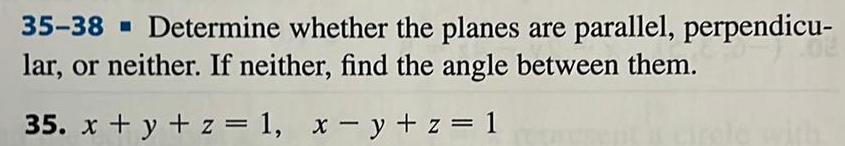
Geometry
Vectors35 38 Determine whether the planes are parallel perpendicu lar or neither If neither find the angle between them 35 x y z 1 x y z 1

Geometry
Vectors21 32 Find an equation of the plane 21 The plane through the point 1 1 3 and with normal vector i 4j k
Geometry
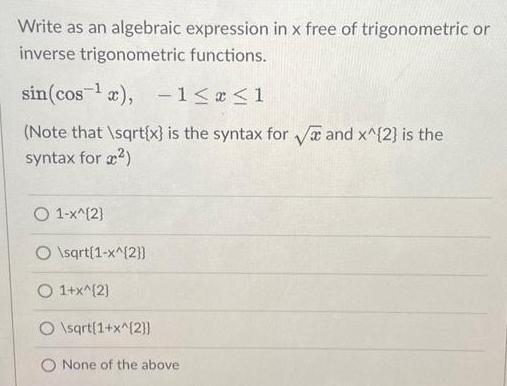
Coordinate systemWrite as an algebraic expression in x free of trigonometric or inverse trigonometric functions sin cos x 1 x 1 Note that sqrt x is the syntax for and x 2 is the syntax for 1 x 2 O sqrt 1 x 2 O 1 x 2 O sqrt 1 x 2 O None of the above