Geometry Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Geometry
Solution of trianglesWhich of the diagrams below represents the statement If it is an equilatera triangle then it is isosceles equilateral triangle isosceles triangle Figure A O A Figure A B Figure B isosceles triangle equilateral triangle Figure B

Geometry
2D GeometryFor the equations below determine A If the parabola opens up down left or right B The vertex of the parabola C The location of the focus D The equation of the directrix E The equation of the axis of symmetry 1 x 5 1 40 y 5 2 x 8 1 44 y 1 3 x 8 1 28 y 9 4 x 3 1 16 y 4 5 y 9 1 12 x 7 6 y 1 1 4 x 2 7 x 4 1 4 y 3 8 y 2 1 8 x 4 9 y 5 1 12 x 4
Geometry
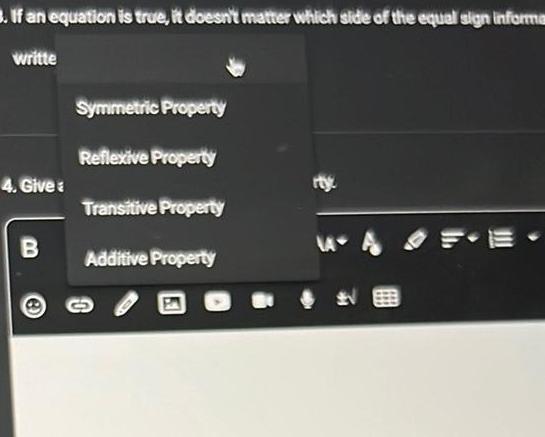
VectorsIf an equation is true it doesn t matter which side of the equal sign informa writte 4 Give B Symmetric Property Reflexive Property Transitive Property Additive Property rty
Geometry
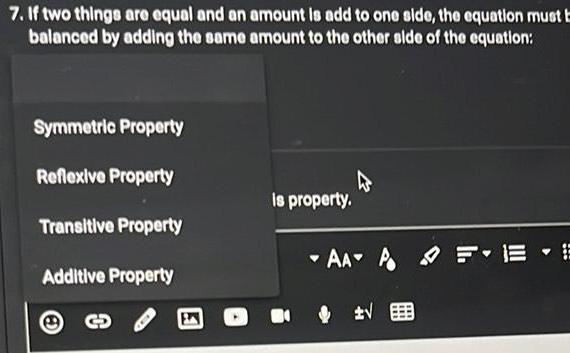
2D Geometry7 If two things are equal and an amount is add to one side the equation must E balanced by adding the same amount to the other side of the equation Symmetric Property Reflexive Property Transitive Property Additive Property is property W AAA FE E
Geometry
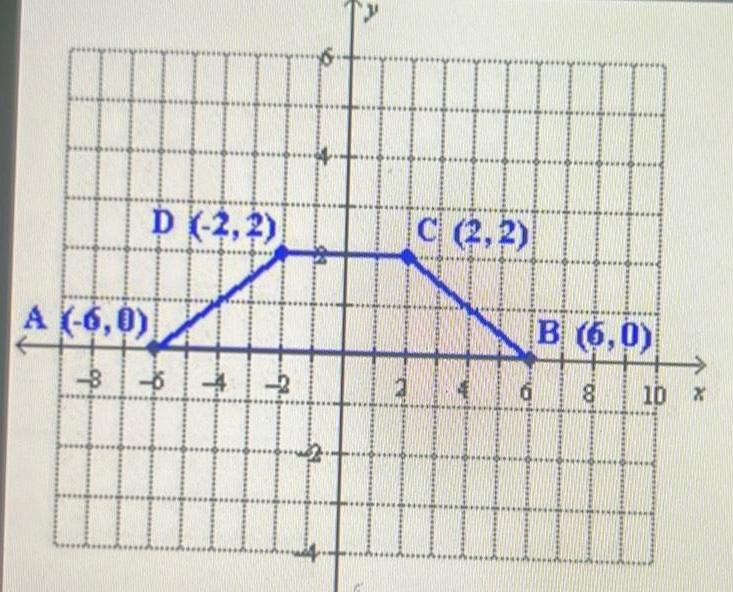
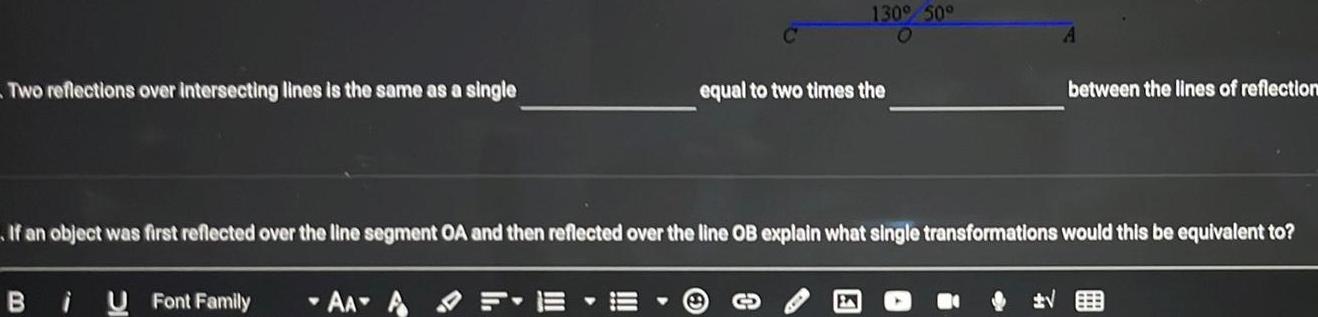
Coordinate systemTwo reflections over intersecting lines is the same as a single B i U Font Family Y 130 50 AAAF equal to two times the If an object was first reflected over the line segment OA and then reflected over the line OB explain what single transformations would this be equivalent to A between the lines of reflection
Geometry
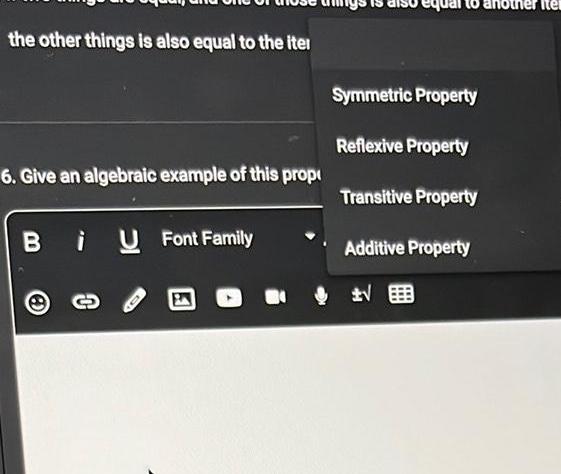
Heights & Distancesthe other things is also equal to the iter 6 Give an algebraic example of this prop Bi Font Family S Symmetric Property Reflexive Property Transitive Property Additive Property er ite
Geometry
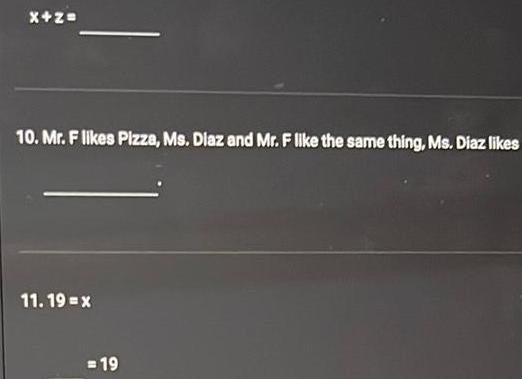
2D GeometryX z 10 Mr F likes Pizza Ms Diaz and Mr F like the same thing Ms Diaz likes 11 19 x 19
Geometry
2D Geometrye an algebraic example i Font Far Symmetric E Reflexive Pr Transitive P Additive Pro

Geometry
Coordinate system5 Determine if the following is a reflection a rotation or a translation O Reflection about the y axis O Rotation O Translation O Reflection about the x axis

Geometry
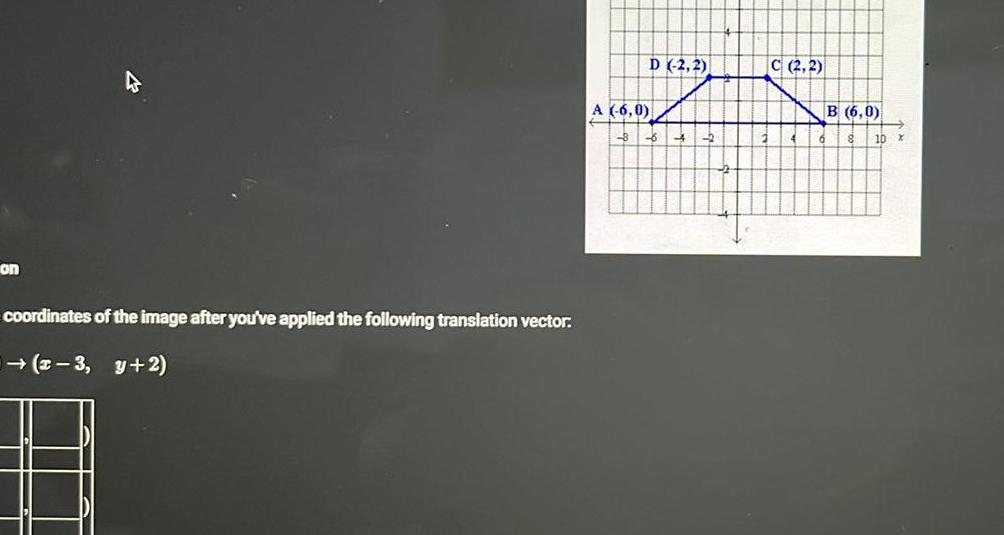
Coordinate systemon coordinates of the image after you ve applied the following translation vector 3 y 2 A 6 0 D 2 2 4 C 2 2 B 6 0 10 X

Geometry
Solution of triangles5 In ARST M and N are the midpoints of RT and RS respectively Given MN 2x 3 ST 3x Find x MN 2 points R M S N T

Geometry
Area1 Determine whether the statement is true or false 1 point each a The median of a trapezoid is parallel to each base b The diagonals of a kite bisect each other c The consecutive angles of a parallelogram are supplementary

Geometry
2D Geometry10 In AABC M and N are the midpoints of AB and BC respectively MN x 5 AC x 2x 5 Find x MN AC 2 points C A M N B

Geometry
Area2 Given ABCD with diagonal AC Prove AABC ACDA I 1 Statements 2 ABCD and BC AD 3 ZCABZACD and ZACBZCAD 4 AC AC 4 points Proof 1 2 3 4 5 A D Reasons B C

Geometry
Solution of triangles8 Given AC BC and D is the midpoint of BC AB 2x 1 AC 3x 4 BD x 1 Find x AB BC X 2 points B A AB D BC C


Geometry
2D Geometry11 In trapezoid ABCD with AB DC M and N are the midpoints of AD and BC 2 points respectively AB 4x 9 DC 6x 3 and MN 3x 4 Find x MN AB DC A B D M X N MN C
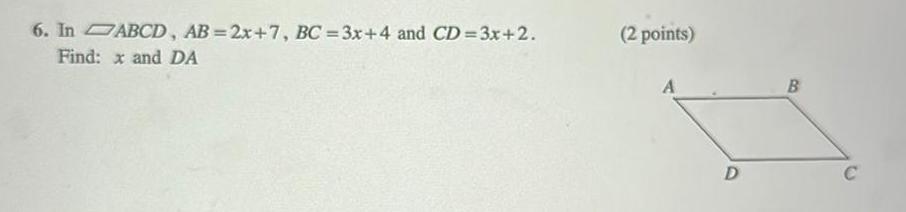

Geometry
Solution of triangles7 The perimeter of AABC is 68 AB 2x 3 Find x AB AC AC 3x 2 and BC 4x 5 2 points B X A AB C
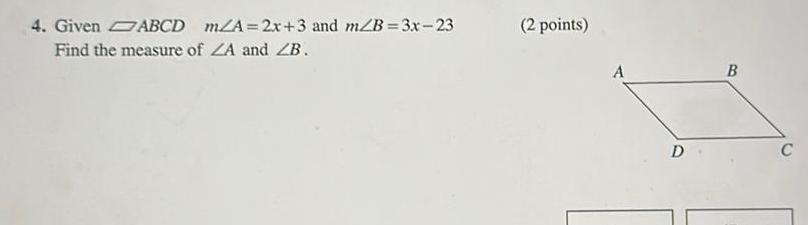
Geometry
2D Geometry4 Given ABCD m A 2x 3 and m B 3x 23 Find the measure of ZA and ZB 2 points A D B C
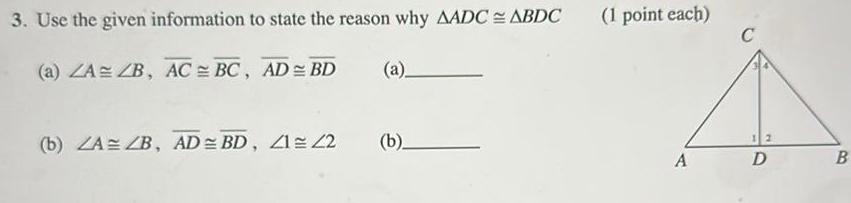
Geometry
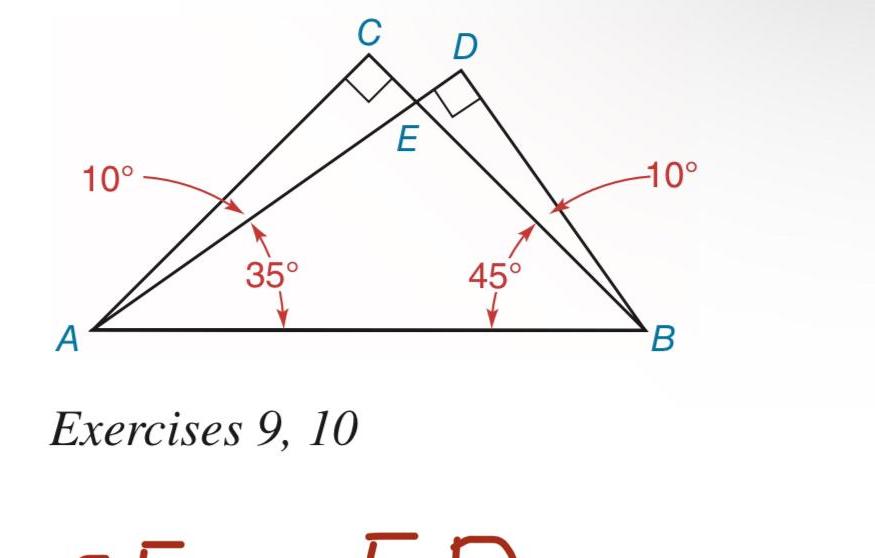
2D Geometry3 Use the given information to state the reason why AADC ABDC a ZA ZB AC BC AD BD b ZA ZB AD BD 41 42 a b 1 point each A 12 D B
Geometry
2D Geometrya Similarity Question 1 Select one BE In the figure above which of the following would allow you to prove A CBA similar to A EDA O DA CB ZDEA ZA A ZC LA

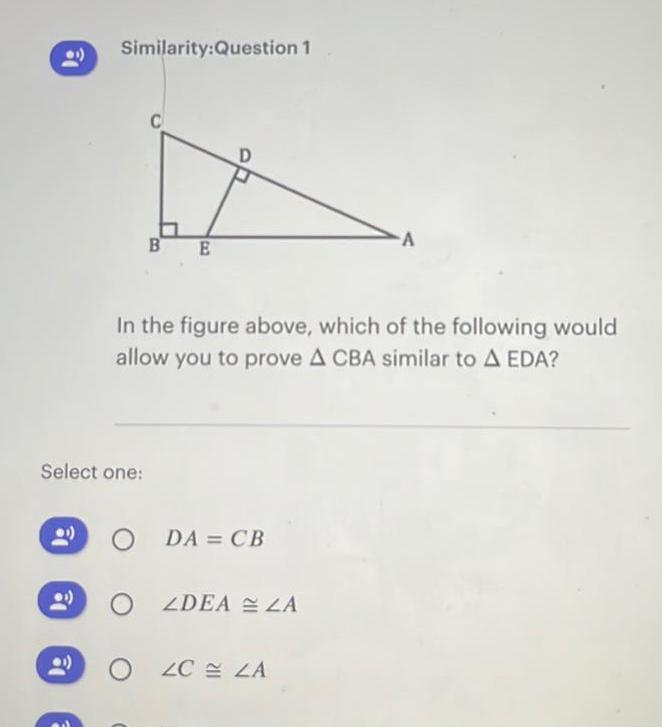
Geometry
Area8 Find the sum of the measures of the interior angles of a poly gon of n sides if a n 6 b n 8

Geometry
3D Geometry20 Find the number of sides for a regular polygon whose exterior angles each measure a 45 b 9 STO

Geometry
2D Geometry11 Find the sum of the measures of the exterior angles of a an equilateral triangle b a rectangle each interior angle is a right angle

Geometry
2D Geometry3 Find the measure of each exterior angle of a regular polygon of n sides if a n 4 b n 12
Geometry
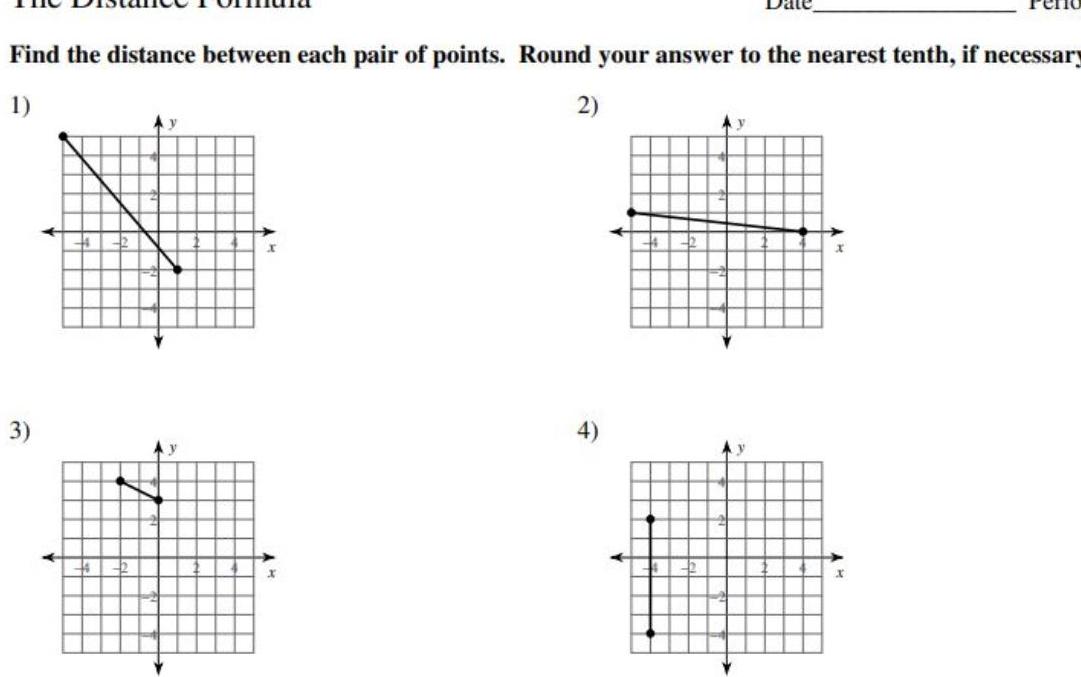
Coordinate systemFind the distance between each pair of points Round your answer to the nearest tenth if necessary 1 2 3

Geometry
2D Geometry29 Given Prove Plan R Parallelogram RSTV also XY VT 21 LS First show that RSYX is a parallelogram S

Geometry
2D GeometryIn Exercises 19 to 22 classify each statement as true or false In Exercises 19 and 20 recall that the symbol C means is a subset of 19 Where Q quadrilaterals and P polygons QCP 20 Where Q OCP quadrilaterals and P parallelograms

Geometry
2D Geometry3 MNPQ is a and m M 110 Find a QP b NP parallelogram Suppose that MQ M P N c mZQ d m P 5 MN
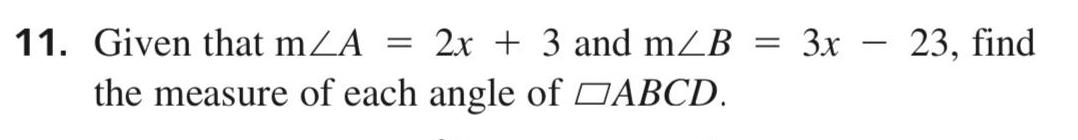

Geometry
2D GeometryIn Exercises 27 to 30 use the definition of a parallelogram to complete each proof 27 Given Prove R V 1 RS VT 2 3 4 RS VT RV 1 VT and ST VT RSTV is a parallelogram Statements S PROOF Reasons 1 2 Given 3 If two lines are to the same line they are to each other 4 If both pairs of opposite sides of a quadrilateral are II the quadrilateral is a
Geometry
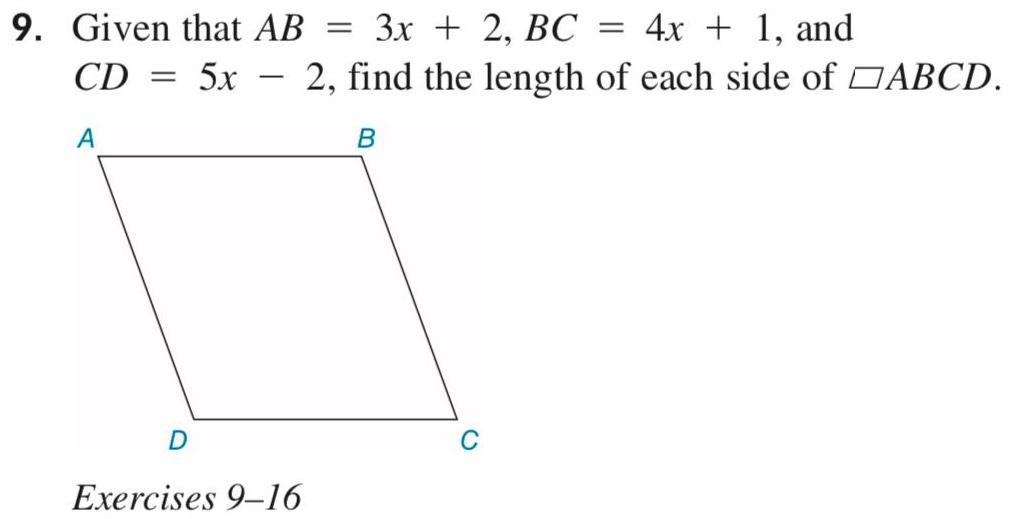
2D Geometry9 Given that AB 3x 2 BC CD 5x A D 4x 1 and 2 find the length of each side of ABCD B Exercises 9 16 C
Geometry
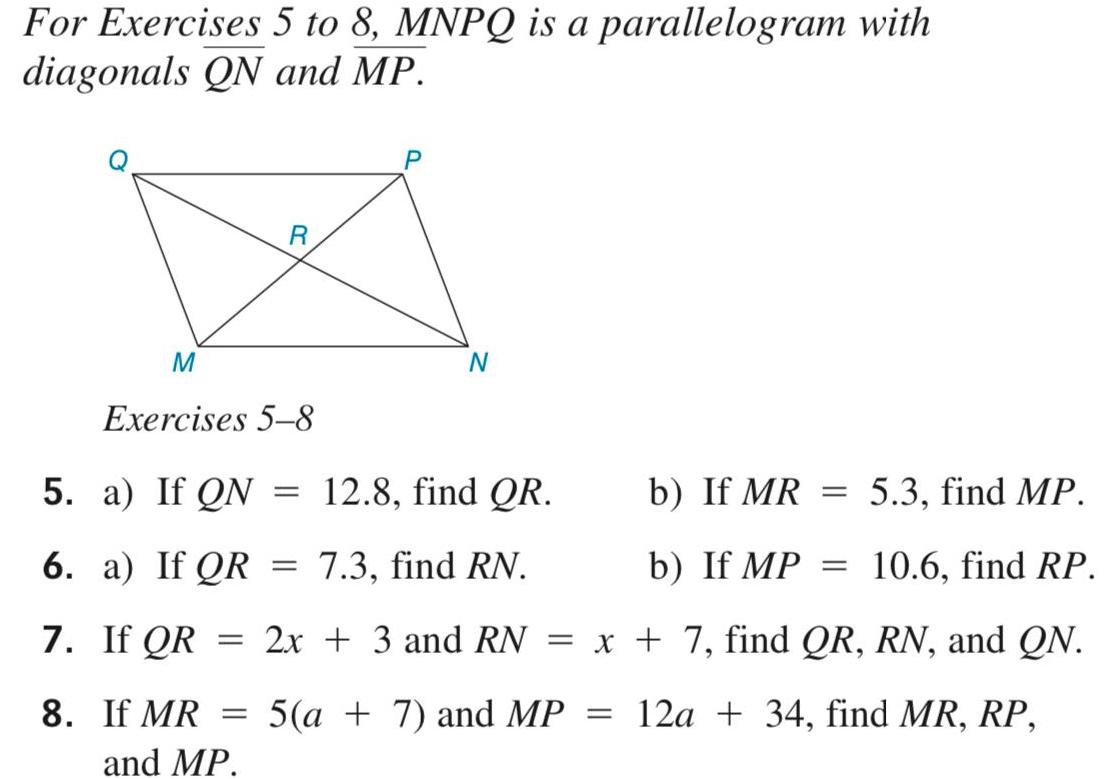
2D GeometryFor Exercises 5 to 8 MNPQ is a parallelogram with diagonals QN and MP 7 8 M Exercises 5 8 5 a If QN 12 8 find QR a If QR 7 3 find RN If QR R If MR and MP N b If MR 5 3 find MP b If MP 10 6 find RP 2x 3 and RN x 7 find QR RN and QN 5 a 7 and MP 12a 34 find MR RP

Geometry
2D GeometryIn Exercises 17 and 18 consider RSTV with VX 1 RS and VY I ST 17 a Which line segment is the altitude of RSTV with respect to base ST b Which number is the height of RSTV with respect to base ST 18 a Which line segment is the altitude of RSTV with respect to base RS R 12 20 b Which number is the Exercises 17 18 height of RSTV with respect to base RS 16 15
Geometry
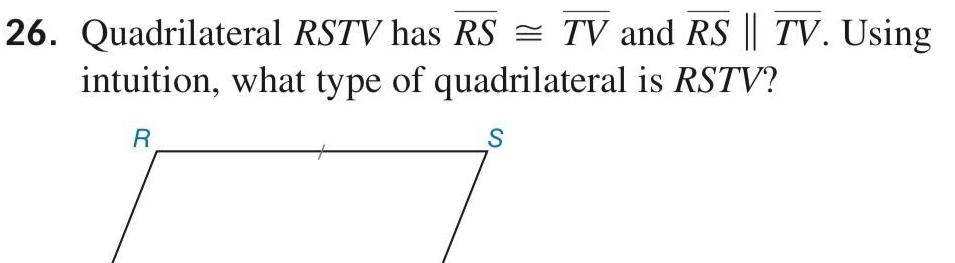
2D Geometry26 Quadrilateral RSTV has RS TV and RS TV Using intuition what type of quadrilateral is RSTV R S

Geometry
2D Geometry5 Fill in each blank with always sometimes or never a The corresponding angles of two parallel lines have measures that are equal b A closed figure is c The diameter of a circle is bigger than a radius of that circumference d Isosceles triangles are right triangles 6 a Determine each angle measure in the triangle b Then state whether the triangle is acute right or obtuse AND c also state whether the triangle is scalene isosceles or equilateral x 30 2x 120 C simple 4x 15

Geometry
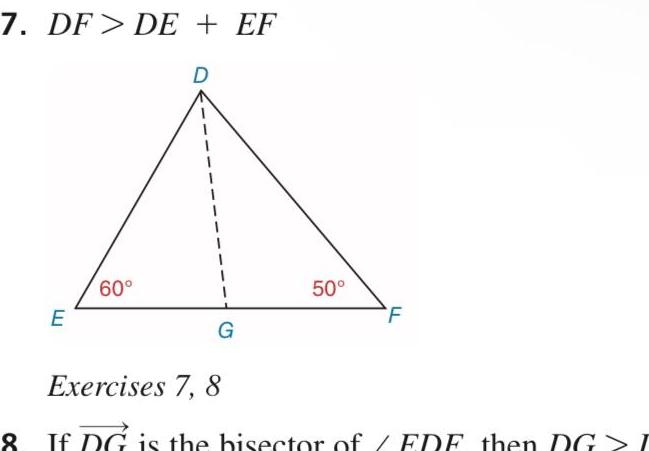
2D GeometryIn Exercises 15 to 18 describe the triangle AXYZ not shown as scalene isosceles or equilateral Also is the triangle acute right or obtuse 15 m X 43 and m Y 47 16 m X 60 and LY LZ 17 m X mZY 40 18 m X 70 and m Y 40 19 Two of the sides of an isosceles triangle have lengths of 10 cm and 4 cm Which length must be the length of the base
Geometry
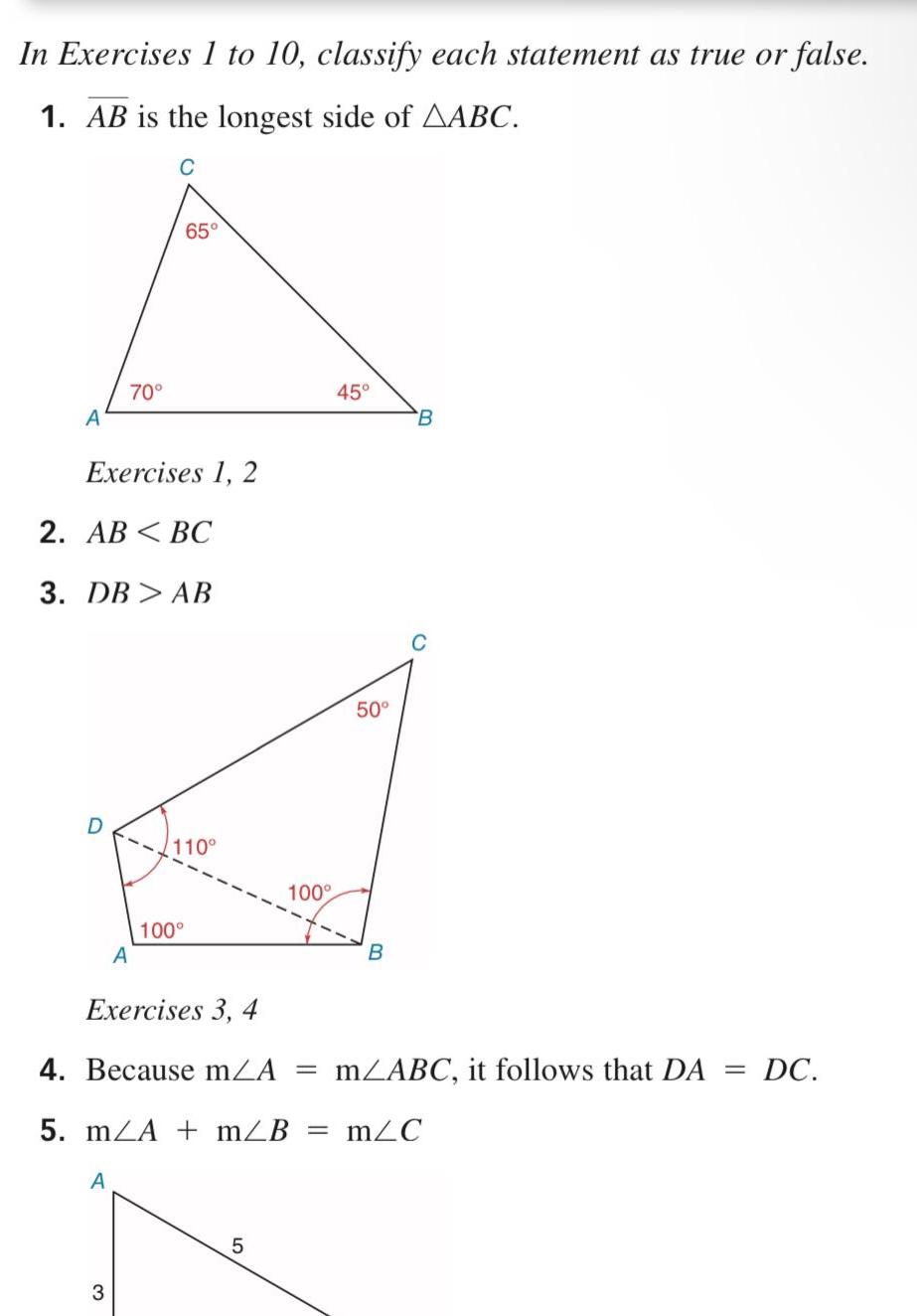
Coordinate systemIn Exercises 1 to 10 classify each statement as true or false 1 AB is the longest side of AABC A Exercises 1 2 70 2 AB BC 3 DB AB A 65 A 32 110 100 100 5 45 50 B Exercises 3 4 4 Because mA m ABC it follows that DA DC 5 m A m B m C B C
Geometry
2D Geometry14 Is it possible to draw a triangle whose sides measur a 7 7 and 14 9 b 6 7 and 14 c 6 7 and 8 9
Geometry
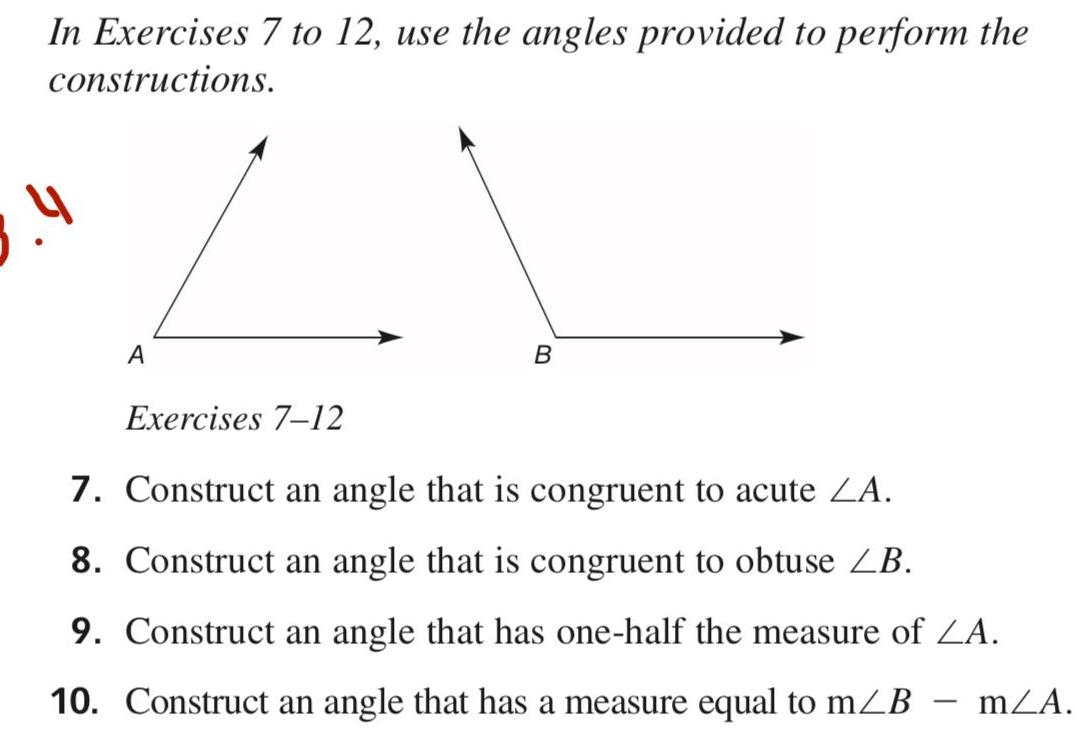
VectorsIn Exercises 7 to 12 use the angles provided to perform the constructions 1 4 A B Exercises 7 12 7 Construct an angle that is congruent to acute ZA 8 Construct an angle that is congruent to obtuse ZB 9 Construct an angle that has one half the measure of ZA 10 Construct an angle that has a measure equal to m B MZA

Geometry
2D GeometryIn Exercises 15 to 18 construct angles having the given measures 15 90 and then 45


Geometry
AreaIn Exercises 23 to 26 use line segments of lengths a and c as shown 23 Construct the right triangle with hypotenuse of length c and a leg of length a C

Geometry
2D Geometry20 Describe how you would construct an angle measuring 75 21 Construct the complement of the acute angle Q shown Q
