Geometry Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Geometry
2D Geometry7 In Exercises relationship sets intersect 11 to 14 determine whether the sets have a subset Are the two sets disjoint or equivalent Do the 11 L equilateral triangles E equiangular triangles 12 S triangles with two sides A triangles with two Ls 13 R right triangles O obtuse triangles

Geometry
2D Geometry23 A surveyor knows that a lot has the shape of an isosceles triangle If the vertex angle measures 70 and each equal 23 side is 160 feet long what measure does each of the base

Geometry
2D Geometry22 Is it possible for a triangle to be a an acute isosceles triangle b an obtuse isosceles triangle c an equiangular isosceles triangle

Geometry
2D GeometryIn Exercises 31 to 34 suppose that BC is the base of isosceles AABC not shown 3 3 31 Find the perimeter of AABC if AB 8 and BC 10 32 Find AB if the perimeter of AABC is 36 4 and BC 14 6 33 Find x if the perimeter of AABC is 40 AB x and BC x 4

Geometry
2D Geometry38 Because of construction along the road from A to B Alinna drives 5 miles from A to C and then 12 miles from C to B How much farther did Alinna travel by using the alternative route from A to B A B


Geometry
2D GeometryB D 1 2 Exercises 5 6 6 Given Prove 7 Given Prove 8 Given Prove 9 Given Prove 10 Given Prove 21 and 22 are right s AB bisects CAD AABC AABD P is the midpoint of both MR and NQ AMNP AROP MN OR MN QR AMNP AROP LR and LV are right s 21 42 ARST AVST 21 42 23 24 ARST AVST Exercises 7 8 S M 1 2 R R 3 4

Geometry
Coordinate systemIn Exercises 21 to 26 AABC is a right triangle Use the given to find the length of the third side of the triangle information 3 2 21 a 4 and b 22 a 3 12 and b 5 23 a 15 and c 17 24 b 6 and c 10 A a B

Geometry
2D GeometryIn Exercises 1 to 4 state the reason SSS SAS ASA AAS or HL why the triangles are congruent 1 Given Prove 2 Given Prove 3 Given Prove 4 Given Prove 21 42 LCAB LDAB ACABADAB LCAB LDAB AC AD ACABADAB LM and LR are right angles MN QR MP RP AMNP AQRP P is the midpoint of MR and LN 40 AMNP AQRP C B D 1 2 Exercises 1 2 M Exercises 3 4 P R A N

Geometry
2D GeometryFind the equation of the graph given below Notice that the cosine function is used in the answer template representing a cosine function that is shifted and or reflected Use the variable x in your equation rather than the multiplication x symbol Provide your answer below 2 0 5 3 6 TT 2 1 0 0 5 TT

Geometry
2D GeometryWrite a system of equations associated with the augmented matrix Do not try to solve 11 5 5 O 9x y z 7 x 5y 3 9x y 7 x 3y 3 5x 5y 9 9x 7 x y 3 5x 5y 9

Geometry
2D Geometryy 4 csc x 7 1 Drag the movable red point to shift the function the black point to set the vertical asymptotes and the blue point at the correct set of coordinates You may click on a point to verify its coordinates Note Make sure to move the points in the direction of the phase shift represented in the function Provide your answer below 2TT 31 2 8 71 g 2 6 5 4 3 2 0 0 10 2 2 1 TT 2 0 3m 2 211

Geometry
2D GeometryFor the function f x csc x set the moving point to a possible values of f x Provide your answer below 1 1 T 2TT 4 2 0 0 23 0 1 1 1 1 2TT 1 1


Geometry
2D GeometryMake a table of values using multiples of 4 for x If an answer is undefined enter UNDEFINED y sec x X 0 Ala 3x K 5x 4 3x 2 7 4 2x 5 Use the entries in the table to sketch the graph of the function for x between 0 and 2x

Geometry
AreaUse the unit circle to find the value of tan 2x and periodic properties of trigonometric functions to find the value of tan 7 2 2 1 0 2 4 0 1 0 1 40 1 0 5 Q 27
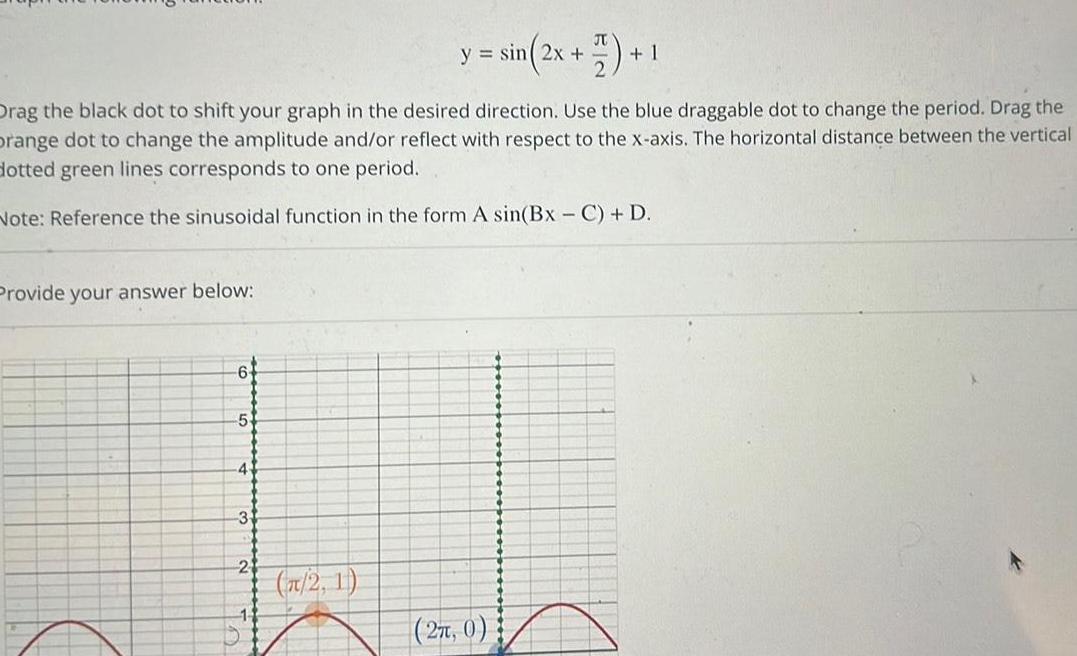
Geometry
2D GeometryProvide your answer below Drag the black dot to shift your graph in the desired direction Use the blue draggable dot to change the period Drag the orange dot to change the amplitude and or reflect with respect to the x axis The horizontal distance between the vertical dotted green lines corresponds to one period Note Reference the sinusoidal function in the form A sin Bx C D 6 5 4 3 2 t y sin 2x 1 2 1 27 0 6 9 1

Geometry
2D GeometryA If the parabola opens up down left or right B The location of the focus C The equation of the directrix 1 y 1 48 x 2 y 1 8 x 3 x 1 40 y 4 x 1 8 y 5 y 1 28 x 6 x 1 36 y 7 x 1 12 y 8 y 1 36 x

Geometry
2D Geometry1 Center 5 1 passing through 8 2 2 Center 0 0 passing through 4 3 3 Center 2 3 passing through 1 3 4 Center 1 2 passing through 1 0 5 Center 5 9 passing through 2 9 6 Center 4 3 passing through 2 2 7 Center 7 2 passing through 1 6 8 Center 3 3 passing through 3 2 9 Center 3 2 passing through 5 2

Geometry
Coordinate system29 Which of the following can you not conclude from this diagram K A B C D X 15 G 5 ALKG AMLG AKGLAMGL AKGL ALGM LG LG M


Geometry
2D GeometryDeandre wants to paint a rectangular region of a wall with one layer of paint He has 12 ft of tape to tape around the border of the region he paints He is considering three regions with lengths of 1 ft 3 ft and 4 ft Answer the questions below to find which of these regions would require the most paint a Fill in the table to find the width and the area for each region Region 11 Region 2 Region 31 Length 1 ft 3 ft 4 ft Width 0ft b Which of these regions would require the most paint Region 1 O Region 2 Region 3 Area 0

Geometry
2D GeometryN In Exercises 21 to 24 the triangles named can be proved congruent Considering the congruent pairs marked name the additional pair of parts that must be congruent in order to use the method named 3 1 21 SAS 22 ASA W 23 SSS M 24 AAS E D E AABD ACBE X AWVY AZVX N AMNO AOPM G Y QN P C Z H

Geometry
2D Geometry5 N A Exercises 25 26 26 Given Prove DC AB and AD BC AABC ACDA Statements 1 DC AB 2 LDCA LBAC 3 4 B 5 AC AC 6 PROOF Reasons 1 2 3 Given 4 If two lines are cut by a transversal alternate interior Ls are 5 6 ASA

Geometry
2D GeometryIn Exercises 13 to 18 use only the given information to state the reason why AABC ADBC Redraw the figure and use marks like those used in Exercises 9 to 12 3 A 3 4 12 B Exercises 13 18 D

Geometry
2D GeometryIn Exercises 9 to 12 congruent parts are indicated by like dashes sides or arcs angles State which method SSS SAS ASA or AAS would be used to prove the two triangles congruent 3 1 9 10 11 12 A C M AA R B N E S D

Geometry
2D Geometry6 In a right triangle the sides that form the right angle are the legs the longest side opposite the right angle is the hypotenuse Some textbooks say that when two right triangles have congruent pairs of legs the right triangles are congruent by the reason LL In our work LL is just a spe cial case of one of the postulates in this section Which postu late is that

Geometry
AreaIn Exercises 1 to 4 consider the congruent triangles shown 1 For the triangles shown we can express their congruence with the statement AABC AFED By reordering the vertices express this congruence with a different statement 8 11 10 B E a b F Exercises 1 4 2 With corresponding angles indicated the triangles shown are congruent Find the lengths of sides indicated by a b and c

Geometry
2D Geometry6 Find x Degrees 7 Explain how you got your answer A What properties did you use B What formula did you use

Geometry
2D Geometryand h x z 19 Then what MUST be true 20 Explain how you arrived at your answer A What Algebra Property did you use to come to your solution B What was the logic process you went through to determine the ans a

Geometry
2D GeometryCenter 2 4 4 Radius is 4 2 6 What is the equation of this circle y Input the correct sign or along with the appropriate value WITHOUT space

Geometry
2D GeometryIf 4XYZ 130 find a and Ab b Z 16 The relationship between a and b is that they are 17 Set up an equation to model this information Use a for the measure of a and b for the measure of b Write your answer WITHOUT spaces

Geometry
Vectors9 Find the equation of the circle whose center is 2 1 and radius 5 units O x 2 y 1 25 O 2 y 1 25 O x 2 y 1 25 O x 2 y 1 25

Geometry
2D GeometryB C A is a right angle and C 30 13 Set up an equation to model this information use B for the m Use the button to input the equation Write your answer WITHOUT spaces 14 Solve the equation for B

Geometry
2D GeometryUsing the equation to determine the following for the next two questions 3 y 9 81 10 Find the Center of the circle 11 Find the Radius of the circle units

Geometry
2D Geometry15 Name the property AB CD then AB EF CD EF O Reflexive Property O Symmetric Property O Transitive Property O Additive Property



Geometry
2D GeometryUsing the figure below to determine the following for the next three questions 1 Name a Secant line O AF GH EB DC 2 Name a Central Angle

Geometry
3D Geometry4 If AB is 30 feet find the diameter of the circle feet 5 Explain how you got your answer A What properties did you use B What formula did you use

Geometry
2D Geometry23 Consider any triangle and one exterior angle at each vertex What is the sum of the measures of the three exterior angles of the triangle

Geometry
2D Geometry1 3 18 Given Prove Statements 1 e m 2 1 2 3 42 43 e m 23 44 e n 4 5 L1 24 6 PROOF n l m 4 2 1 3 Reasons t 1 2 3 If two lines intersect the vertical Zs formed are 4 Given 5 Transitive Property of 6



Geometry
2D Geometry3 In Exercises 7 to 16 name the lines if any that must be parallel under the given conditions Al p q 1 2 78 13 14 19 20 Exercises 7 16 7 21Z20 8 3 210 9 19 214 10 47 211 11 Ip and n I n 3 3 4 9 10 15 16 21 22 An 5 6 11 12 17 18 23 24

Geometry
3D GeometryIn Exercises 1 to 6 and m are cut by transversal v On the basis of the information given determine whether must be parallel to m 1 m1 107 and m25 107 2 m2 65 and m 7 65 3 m 1 106 and m 7 76 4 m 1 106 and m24 106 m 1 2 3 4 5 6 7 8

Geometry
2D GeometryIn Exercises 1 and 2 which sentences are statements If a entence is a statement classify it as true or false 1 a Where do you live b 4 7 5 c Washington was the first U S president

Geometry
2D GeometryA way of describing points that lie on the same plane A way of describing a set of lines or curves that never meet or intersect A way of describing a line which crosses another line forming a right angle Choose Choose Choose

Geometry
Coordinate systemInstructions Your job is to add each of the four bases to the simulated spill to determine exactly how much of each is required to neutralize the acid Remember that neutralizing means to make the pH 7 This process of determining the amount of a chemical needed for a certain reaction is called a titration Chemical Magnesium Hydroxide Mg OH 2 Laboratory Acid Base Neutralizaton keachokd Reactions The Perfect Storm Spill Drill Sodium Hydroxide NaOH Sodium Carbonate Na CO Calcium Hydroxide Ca OH 1 Shovels required to neutralize acid Amount required to neutralize the acid 500 kg per shovel kg 500 kg cost per 1000kg 3085 Cost per 1000 kg kg 330 308 88 88 Total Cost I

Geometry
2D GeometryFor each of the following right triangles set up a trigonometric ratio involving ZA and then find the measure of ZA by using the appropriate inverse trigonometric ratio Round to the nearest whole degree b a c A B 18 6 10 A 7 B d B 14 CO A 28 A 12 B T 20 22