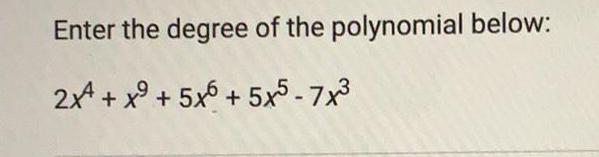Math Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Math
Application of derivativesConsider the following vector function.
r(t) = (7t2, sin(t)- t cos(t), cos(t) + t sin(t)), t> 0
(a) Find the unit tangent and unit normal vectors T(t) and N(t).
T(t) =
N(t) =
(b) Use this formula to find the curvature.
k(t) =

Math
FunctionsFill out the table of values and select whether each function is odd, even or neither.
For the trig functions, make sure your calculator is in radian mode. You may only
submit once the tables of values have been filled out correctly.
Note: An expression like sinx+ 5 should be typed as sin (x) + 5.

Math
Application of derivativesA cylinder shaped can needs to be constructed to hold 450 cubic centimeters of soup. The material for the sides of the can costs 0.02 cents per square centimeter. The material for the top and bottom of the can need to be thicker, and costs 0.06 cents per square centimeter. Find the dimensions for the can that will minimize production cost.
Helpful information:
h: height of can, r: radius of can
Volume of a cylinder: V = π²h
Area of the sides: A=2πrh
Area of the top/bottom: A=πr²
To minimize the cost of the can:
Radius of the can:
Height of the can:
Minimum cost: cents

Math
Permutations and CombinationsWhich of the following describes a permutation?
A. The boss selected 5 workers to be on a planning committee.
B. A teacher arranged 5 students in a row from shortest to tallest.
C. George ordered 5 toppings to put on a supreme pizza.
D. Anna chose 5 sweaters from her closet to donate to charity.

Math
Quadratic equationsWhat number would you add to complete the square for the equation below?
x² + 6x = 0

Math
Basic MathWhich of the following shows the polynomial below written in descending
order?
3x³ +9x7-x+ 4x12
A. -x+3x³ +9x7 + 4x¹2
B. 4x12 + 9x + 3x³ - x
C. 9x7 + 4x¹2 + 3x³ - x
D. 3x³ + 4x¹2 + 9x²-x
Math
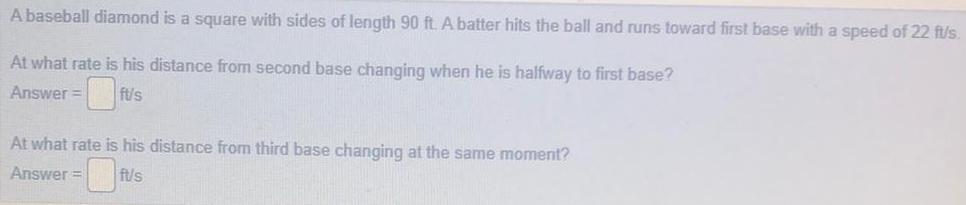
Application of derivativesA baseball diamond is a square with sides of length 90 ft. A batter hits the ball and runs toward first base with a speed of 22 ft/s.
At what rate is his distance from second base changing when he is halfway to first base?
Answer= ft/s
At what rate is his distance from third base changing at the same moment?
Answer=ft/s

Math
Application of derivativesIf an arrow is shot straight upward on the moon with a velocity of 72 m/s, its height (in meters) after t seconds is given by s(t) = 72t - 0.83t²
What is the velocity of the arrow (include units) after 8 seconds?
How long will it take for the arrow to return and hit the moon (include units)?
With what velocity (include units) will the arrow hit the moon?
Math
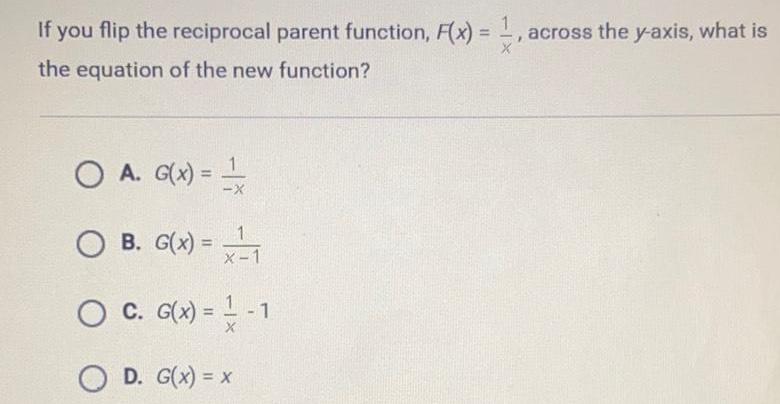
Coordinate systemIf you flip the reciprocal parent function, F(x) = 1/x, across the y-axis, what is
the equation of the new function?
A. G(x) = -¹/-x
B. G(x) = 1/x-1
C. G(x) = 1/x - 1
D. G(x) = x
Math
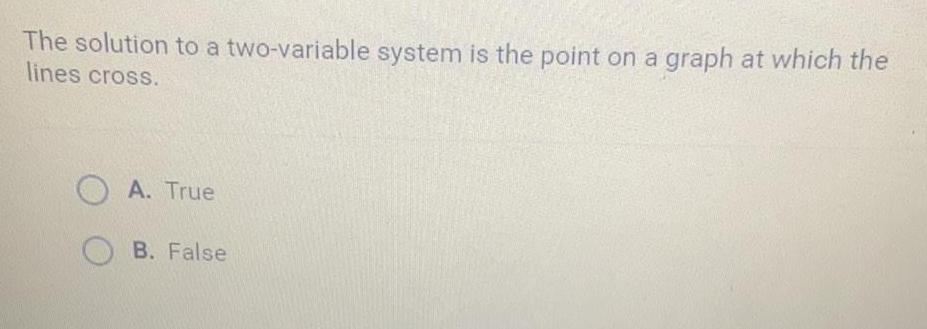
Basic MathThe solution to a two-variable system is the point on a graph at which the
lines cross.
A. True
B. False
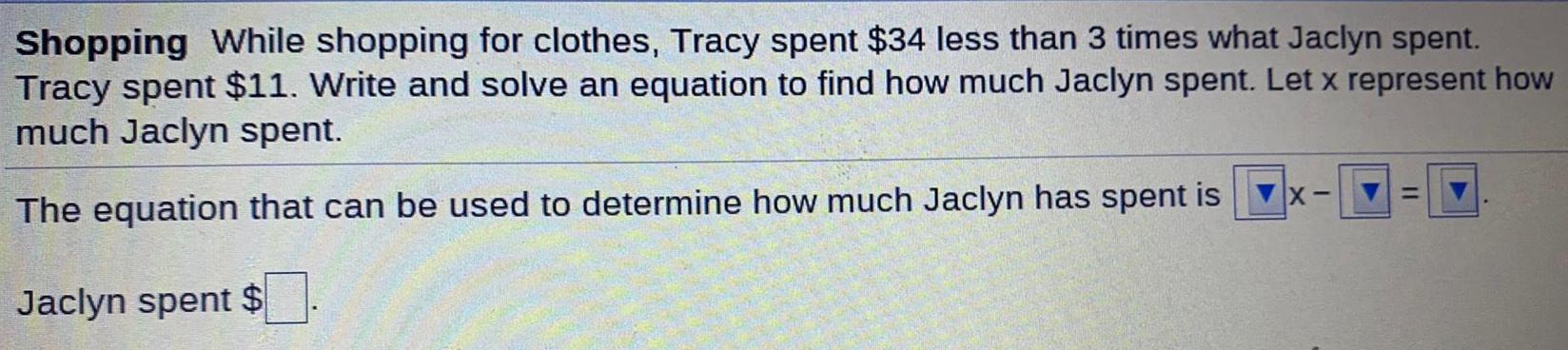
Math
Basic MathShopping While shopping for clothes, Tracy spent $34 less than 3 times what Jaclyn spent. Tracy spent $11. Write and solve an equation to find how much Jaclyn spent. Let x represent how much Jaclyn spent.
The equation that can be used to determine how much Jaclyn has spent is
Jaclyn spent $

Math
StatisticsIf a sample of 187 bowlers were taken from a population of 999 bowlers, x
could refer to the mean of how many bowlers' scores?
A. Both 187 and 999
B. 187
C. 999
D. Neither 187 nor 999

Math
Application of derivativesA road perpendicular to a highway leads to a farmhouse located 2 mile away. An automobile traveling on the highway passes through this intersection at a speed of 55mph. How fast is the distance between the automobile and the farmhouse increasing when the automobile is 2 miles past the intersection of the highway and the road?
The distance between the automobile and the farmhouse is increasing at a rate of ______miles per hour

Math
StatisticsThe mean is the average of the numbers.
Add up all the numbers, then divide by how many numbers there are.
Reminder: there are 15 numbers
7.5, 6.5, 8, 10, 9, 9.5, 5.5, 8, 7.5, 6.5, 6, 8, 7.5, 10, 10.5
Data set:
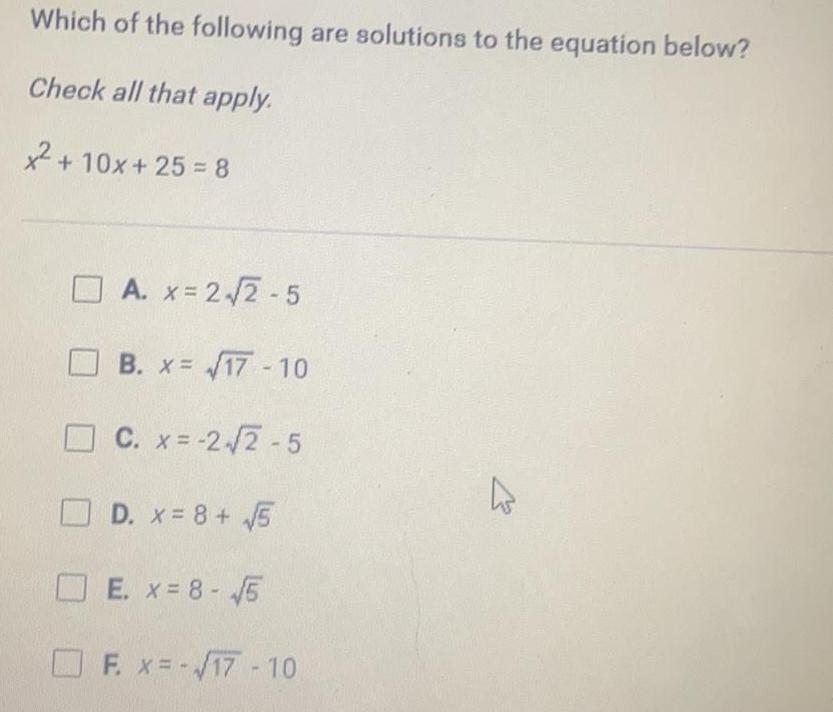
Math
Quadratic equationsWhich of the following are solutions to the equation below?
Check all that apply.
x² + 10x + 25 = 8
A. x = 2√2-5
B. x = √17-10
C. x = -2-√√2-5
D. x = 8 + √√5
E. x = 8 - √5
F. x = -√17-10

Math
Basic MathThe top and bottom margins of a poster are 2 cm and the side margins are each 2 cm. If the area of printed material on the poster is fixed at 388 square centimeters, find the dimensions of the poster with the smallest area
Width= Height=

Math
Application of derivativesA 16 ft ladder leans against a wall. The bottom of the ladder is 3 ft from the wall at time t = 0 and slides away from the wall at a rate of 3ft/sec Find the velocity of the top of the ladder at time t = 2
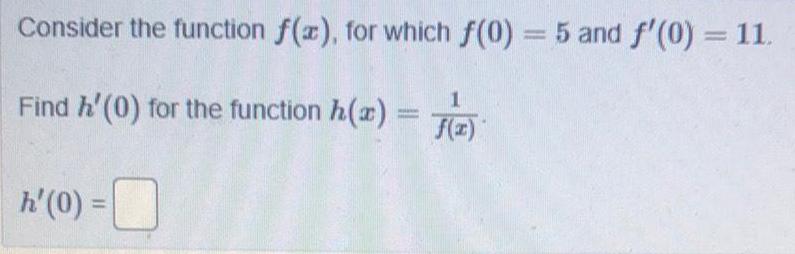
Math
DifferentiationConsider the function f(x), for which f(0) = 5 and f'(0) = 11.
Find h'(0) for the function h(x) = 1/ f(x)
h' (0) =
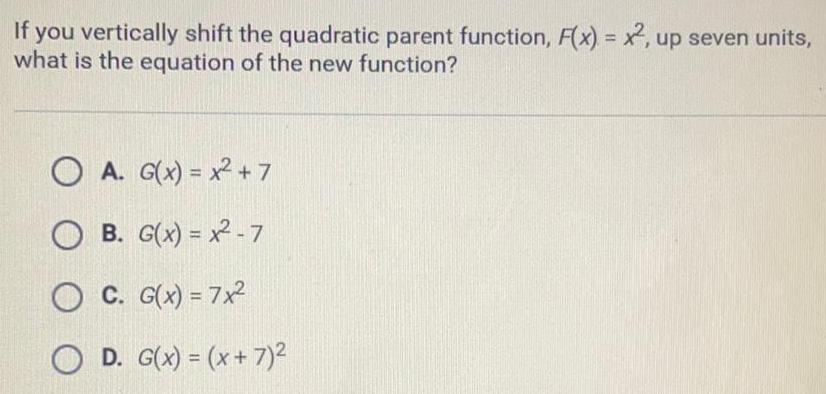
Math
ParabolaIf you vertically shift the quadratic parent function, F(x) = x2, up seven units,
what is the equation of the new function?
A. G(x) = x² +7
B. G(x)=x2-7
C. G(x) = 7x²
D. G(x) = (x + 7)²

Math
DifferentiationGiven that f(z) = 2x+cos(x) is one-to-one, use the formula (f ¹)'(x) = 1/ f'(f ¹(x))
to find (f ¹)'(1).
(ƒ˜¹)'(¹) =

Math
StatisticsA personnel director in a particular state claims that the mean annual income is the same in one of the state's counties (County A) as it is in another county (County B). In County A, a random sample of 15 residents has a mean annual income of $42,300 and a standard deviation of $8500. In County B, a random sample of 9 residents has a mean annual income of $39,600 and a standard deviation of $6000. At a=0.01, answer parts (a) through (e). Assume the population variances are not equal. Assume the samples are random and independent, and the populations are normally distributed.
(a) Identify the claim and state Ho and Ha
Which is the correct claim below?
A. "The mean annual income in County A is greater than in County B."
B. "The mean annual incomes in Counties A and B are not equal."
C. "The mean annual income in County A is less than in County B."
D. "The mean annual incomes in Counties A and B are equal."


Math
Basic MathSolve the system of equations below by graphing them with a pencil and paper. Choose the correct ordered pair (b, u).
u=-b+21
u=-2b+30
A. (5, 15)
B. (9,12)
C. (15,5)
D. (12,9)

Math
Basic MathA restaurant serves dessert in a cone-shaped dish with a diameter of 7 cm. If the dish is 10 cm deep, how many cubic centimeters of dessert can the dish hold?
Use 3.14 to approximate the answer to two decimal places if necessary.
512.87 cm3
128.22 cm³
384.65 cm³
73.27 cm³


Math
StatisticsWhich of these groups of relative frequencies would be best represented by a
pie chart?
A. 20%; 19%; 21%; 20%; 20%
B. 25%; 24%; 26%; 25%
C. 16% ; 18%; 17%; 16% ; 17%; 16%
D. 6%; 14%; 80%
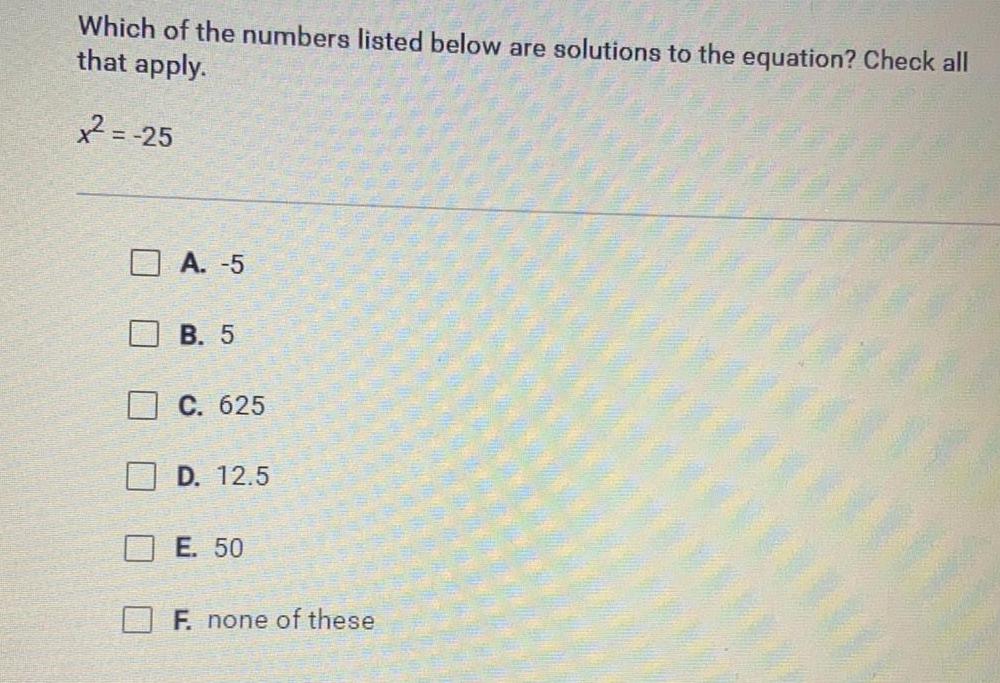
Math
Sets and RelationsWhich of the numbers listed below are solutions to the equation? Check all that apply.
x²=-25
A. -5
B. 5
C. 625
D. 12.5
E. 50
F. none of these

Math
Application of derivativesThe minute hand on a watch is 8 mm long and the hour hand is 4 mm long How fast is the distance between the tips of the hands changing at one o'clock? Round your answer to the nearest tent

Math
Basic MathFor the given data set, find the a. mean b. median c. mode (or state that there is no mode) d. midrange.
Ages of teachers in the mathematics department of a certain high school:
25, 53, 36, 59, 25, 53, 25, 47, 47, 43
a. 41.3
b. 45
c. 47
d. 42
a. 31
b. 45
c. 25
d. 42
a. 41.3
b. 45
c. 25
d. 42
a. 26.3
b. 45
C. 25
d. 42

Math
Basic MathWhich polynomial represents the sum below?
(x^8+2x+1)+ (2x^4 + x² + 1)
A. x^8 + 4x^4 + x² + 2
B. x^16 +16x^8 + x² + 2
C. 2x^8 + 8x^4 + 2x² +2
D. 16x^8 + x² + 2
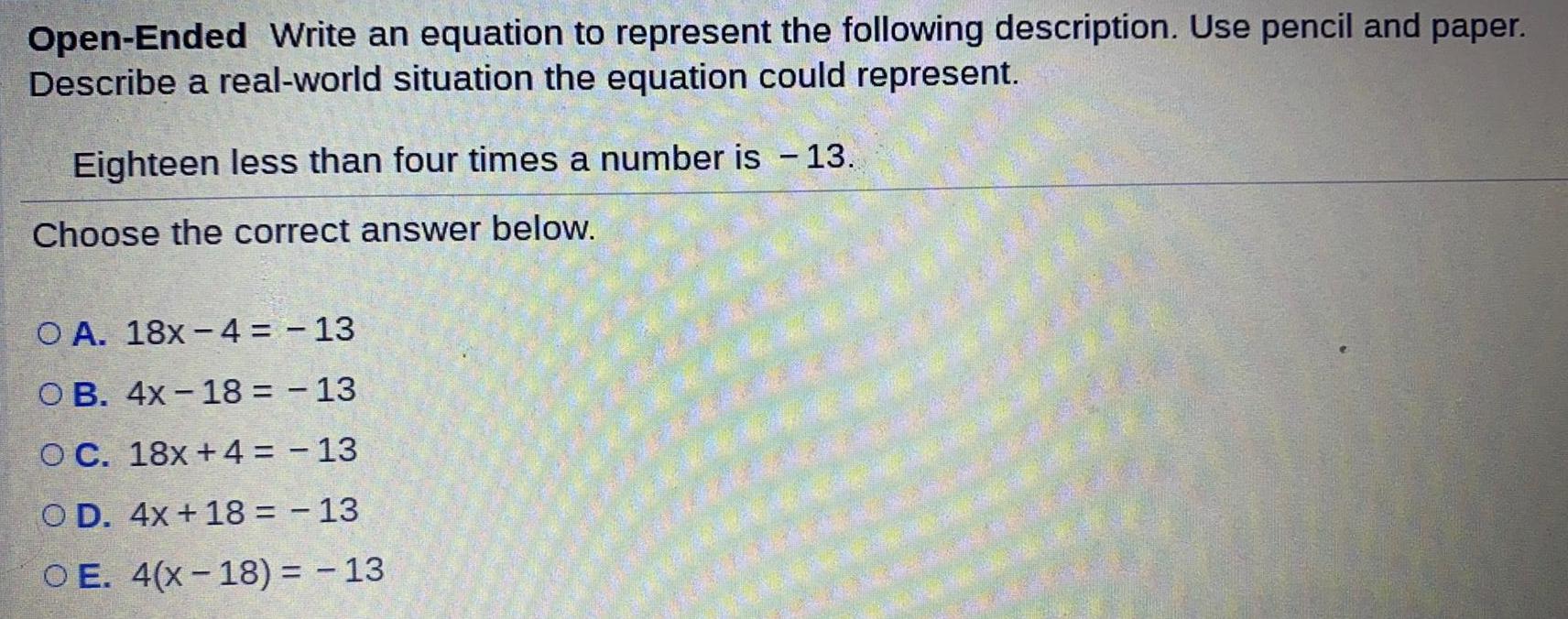
Math
Basic MathOpen-Ended Write an equation to represent the following description. Use pencil and paper. Describe a real-world situation the equation could represent.
Eighteen less than four times a number is - 13.
Choose the correct answer below.
A. 18x-4 = -13
B. 4x 18 = -13
C. 18x + 4 = −13
D. 4x+18 = -13
E. 4(x-18) = 13

Math
Application of derivativesA water trough is 10 m long and a cross-section has the shape of an isosceles trapezoid that is 30 cm wide at the bottom, 80 cm wide at the top, and has height 50 cm If the trough is being filled with water at a rate of 2 m³/min, how fast is the water level rising when the water is 30 cm deep?

Math
Quadratic equationsA child launches a toy rocket in the air, and the function f(x) = -10x² +90x+ 20 represents the flight of the rocket, where x is the time in seconds and f(x) is the height (in feet) at x seconds.
a. For how many seconds is the rocket higher than 100 feet above the ground?
b. Explain how you found your answer.

Math
StatisticsFind the annual percentage yield (APY).
A bank offers an APR of 3.1% compounded daily.
6.20%
3.15%
103.15%
3.22%
![If ƒ(x) = (3x − 4)² (6x² + 6)³ then:
ƒ'(x) =
[Suggestion: use logarithmic differentiation.]](https://media.kunduz.com/media/sug-question/raw/47839054-1658334915.8563726.jpeg?w=256)
Math
DifferentiationIf ƒ(x) = (3x − 4)² (6x² + 6)³ then:
ƒ'(x) =
[Suggestion: use logarithmic differentiation.]

Math
Basic MathSelect all of the sequences of transformations on the isosceles trapezoid below that would result in a congruent figure.
A horizontal reflection, followed by a 3 unit translation down.
A 5 unit translation to the left, followed by dilation by a scale factor of 1/2.
A vertical reflection, followed by a rotation of 90 degrees clockwise.
A vertical reflection, followed by a rotation 270 degrees counterclockwise.
A rotation 180 degrees clockwise, followed by dilation by a scale factor of 3.
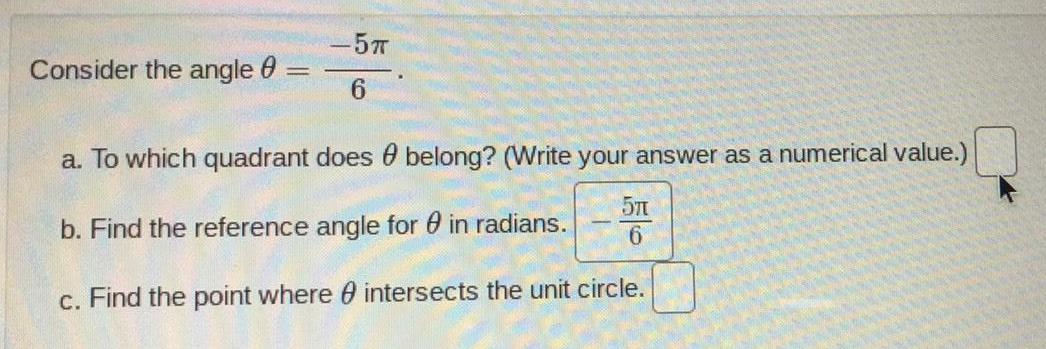
Math
TrigonometryConsider the angle θ=-5π/6
a. To which quadrant does belong? (Write your answer as a numerical value.)
b. Find the reference angle for in radians
c. Find the point where intersects the unit circle.
![If the value of "y" varies directly with "x" and y=-51 when x = 3, find "y" if x = 2.
Enter the number that belongs in the green box.
y = [?]](https://media.kunduz.com/media/sug-question/raw/47948996-1658334816.019678.jpeg?w=256)
Math
Basic MathIf the value of "y" varies directly with "x" and y=-51 when x = 3, find "y" if x = 2.
Enter the number that belongs in the green box.
y = [?]

Math
Basic MathFind the sum of the polynomials below:
(8x9 + 6x6 - 2x+6) + (9x⁹ + 4x6 + 9x+7)
A. 17x9 + 10x6-7x+13
B. 10x⁹ + 17x6 + 7x+ 13
C. 72x9 +24x6-18x² + 13
D. 17x + 10x + 7x+13

Math
Application of derivativesUse an appropriate local linear approximation to estimate the value of the given quantity.
(2.04)3
Math
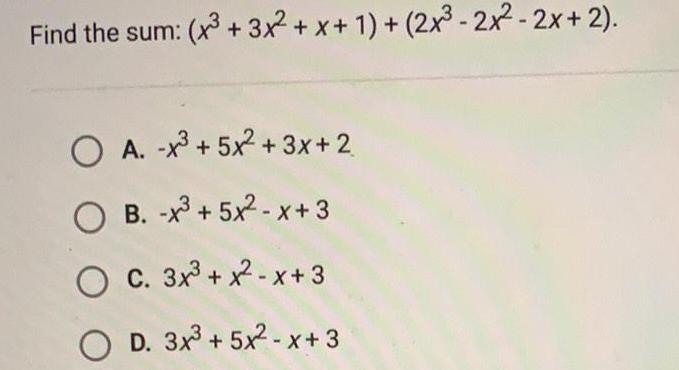
Quadratic equationsFind the sum: (x³ + 3x²+x+1)+ (2x³ - 2x² - 2x+2).
A. x³ +5x²+3x+2
B. -x³ +5x²-x+3
C. 3x³ + x²-x+3
D. 3x³ + 5x²-x+3

Math
FunctionsThe number of teams y remaining in a single elimination tournament can be found using the exponential function y=128(1/2)^x played in the tournament. Complete parts a through d below.
a. Determine whether the function represents exponential growth or decay. Explain.
.

Math
ProbabilityThe probability that a building's front door lock will jam on a random day is 5%, and the probability that the front door lock will jam and the locksmith will be out sick on a random day is 0.4%. Assuming these two events are independent, find the probability that the locksmith will be out sick on a random day.
(A) 2%
(B) 4.6%
(C) 8%
(D) 12.5%

Math
Quadratic equationsWhat number must you add to the polynomial below to complete the square?
x²-26x

Math
Basic MathWrite a function g(x) that represents the exponential function f(x) = 2x after a vertical stretch by a factor of 2 and a reflection across the x-axis. Graph both functions.
Find the equation for g(x).

Math
Basic MathFor what value of k will the function y = 3x²+4r-7/x²-5x+k have asymptotes at x = 6, x= -1, and y = 3?
(A) k=6
(B) k=-6
(C) No such value of k exists because regardless of the horizontal asymptote is y = 0
(D) No such value of k exists because there will be a hole, not a vertical asymptote, at x= -1


Math
Quadratic equations6/x= 2x+4/5 Multiply each side by the common denominator to find the quadratic equation equivalent to this equation.
A. x² + 4x-15 = 0
B. 2x² + 4x-30 = 0
C. x² + 4x-30 = 0
D. 2x² + 4x + 15 = 0