Math Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Math
Coordinate systemA sequence of transformations is described below:
A dilation with a scale factor of 3
A translation left 4 units and down 1 unit
Select the statement that describes the resulting image.
A. The angle measures are preserved, but the image is a reduction
B. The angle measures are preserved, but the image is an enlargement
C. The angle measures are not preserved, and the image is a reduction
D. The angle measures are not preserved, and the image is an enlargement

Math
Application of derivativesA rock is thrown off of a 100 foot cliff with an upward velocity of 50 m/s. As a result its height after t seconds is given by the formula:
h(t) = 100+ 50t - 5t²
What is its height after 3 seconds?
What is its velocity after 3 seconds?
(Positive velocity means it is on the way up, negative velocity means it is on the way down.)

Math
Basic MathA random sample of size n = 616 from a population whose parameter is p = 0.31.
a. What is the mean of the distribution of sample proportions? Round the answer accurate to 2 decimal places.
b. What is the standard deviation of the distribution of sample proportions? Round the answer accurate to 2 decimal places.

Math
StatisticsA population of values has a normal distribution with µ=68.9 and σ= 34.3.
A random sample of size n = 239 is drawn. Find the probability that a
sample of size n = 239 is randomly selected with a mean less than 75.1.
Round your answer to four decimal places.
P(M<75.1):

Math
Basic MathValentina's parents are planning a trip to the Typhoon Towers resort. They plan to get a 6- day Fun Pass, which will give Valentina access to all the slides and pools at the resort during their stay. Her parents also plan to get her a $30 arcade pass. Altogether, Valentina's parents will spend $129 on passes. What is the daily cost of a Fun Pass?

Math
Binomial theoremMagnetic resonance imaging (MRI) is a process that pro- duces internal body images using a strong magnetic field. Some patients become claustrophobic and require sedation because they are required to lie within a small, enclosed space during
the MRI test. Suppose that 21% of all patients undergoing MRI testing require sedation due to claustrophobia. If 7 patients are selected at random, find the probability that
Note: Please keep 4 decimal places in your final answer.
a. exactly 2 patients require sedation.
b. less than 2 patients require sedation.
c. exactly 5 patients require sedation.
d. at least 5 patients require sedation.

Math
Basic MathJavon is in a 26% tax bracket for his federal income tax. If the amount of money that he paid for federal income tax was $19,240, what was his taxable income?

Math
Basic MathConsider the Quadratic function f(x) = x² - 4x - 21.
Its vertex is
Its largest x-intercept is x =
Its y-intercept is y =


Math
ProbabilityA manufacturer knows that their items have a normally distributed lifespan, with a mean of 11.6 years, and standard deviation of 1.8 years If you randomly purchase one item, what is the probability it will last longer than 10 years? Round answer to three decimal places
Enter your answer as an integer or decimal number. Examples: 3, -4,
Enter DNE for Does Not Exist, oo for Infinity
Math
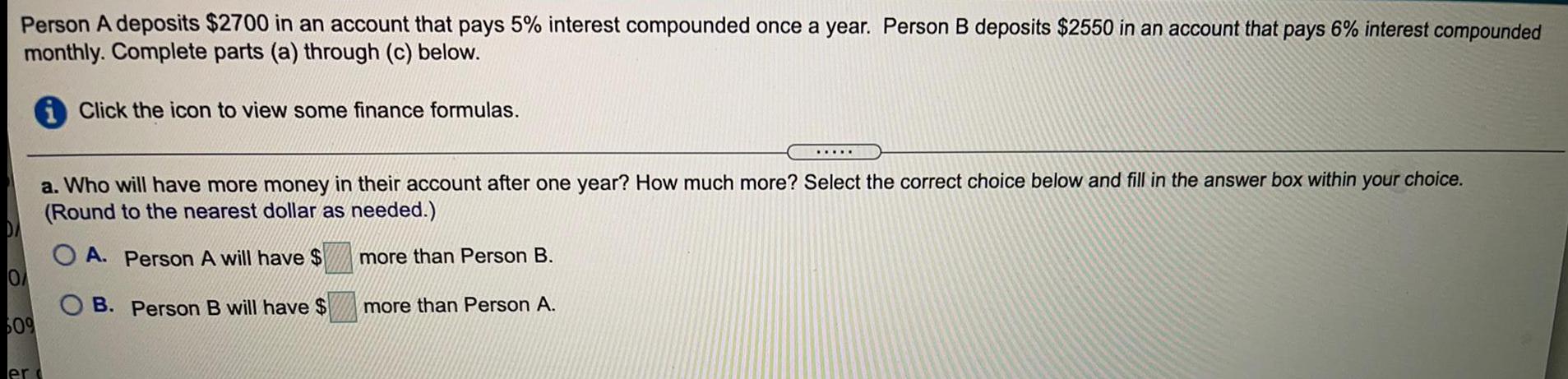
StatisticsPerson A deposits $2700 in an account that pays 5% interest compounded once a year. Person B deposits $2550 in an account that pays 6% interest compounded monthly. Complete parts (a) through (c) below.
a. Who will have more money in their account after one year? How much more? Select the correct choice below and fill in the answer box within your choice.
(Round to the nearest dollar as needed.)
A. Person A will have $ more than Person B.
B. Person B will have $ more than Person A.

Math
Basic MathCar Survey In a survey of 1,700 people who owned a certain type of car, 935 said they would buy that type of car again. What percent of the people surveyed were satisfied with the car? % of the people surveyed were satisfied with the car.
(Type a whole number.)

Math
Basic MathAt the time of her grandson's birth, a grandmother deposits $15,000 in an account that pays 9% compounded monthly. What will be the value of the account at the
child's twenty-first birthday, assuming that no other deposits or withdrawals are made during this period?
Click the icon to view some finance formulas.
The value of the account will be $
(Round to the nearest dollar as needed.)
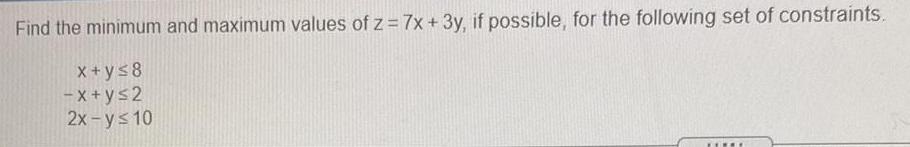
Math
FunctionsFind the minimum and maximum values of z = 7x + 3y, if possible, for the following set of constraints.
x+y≤8
-x+y≤2
2x-y≤ 10

Math
Basic MathYou have a choice between going to an in-state college where you would pay $6500 per year for tuition and an out-of-state college where the tuition is $9000 per
year. The cost of living is much higher at the in-state college, where you can expect to pay $700 per month in rent, compared to $450 per month at the other college.
Assuming all other factors are equal, which is the less expensive choice on an annual (12-month) basis?
The yearly expense of the in-state college is $
college.
the
and the yearly expense of the out-of-state college is $
Thus, on an annual basis, the less expensive choice is

Math
ProbabilityAccording to Masterfoods, the company that manufactures M&M's, 12% of peanut M&M's are brown, 15% are yellow, 12% are red, 23% are blue, 23% are orange and 15% are green. (Round your answers to 4 decimal places where possible)
a. Compute the probability that a randomly selected peanut M&M is not red.
b. Compute the probability that a randomly selected peanut M&M is red or blue.
c. Compute the probability that three randomly selected peanut M&M's are all green.
d. If you randomly select five peanut M&M's, compute that probability that none of them are brown.
e. If you randomly select five peanut M&M's, compute that probability that at least one of them is brown.

Math
StatisticsThe lengths of human pregnancies are normally distributed with a mean of 268 days and a standard deviation of 15 days. Given this information, find the probability of a pregnancy lasting 308 days or longer. Does that seem likely?

Math
Basic MathInflation causes things to cost more, and for our money to buy less (hence your grandparents saying "In my day, you could buy a cup of coffee for a nickel"). Suppose inflation decreases the value of money by 5% each year. In other words, if you have $1 this year, next year it will only buy you $0.95 worth of stuff. How much will $100 buy you in 25 years?

Math
Basic MathSelect the correct answer from each drop-down menu.
A square rotated about its center by 360° maps onto itself at _____ different lines of reflection.
across _____ different angles of rotation. You can reflect a square onto itself

Math
Basic MathFind the linear speed v for the following.
the tip of a propeller 1 m long, rotating 500 times per min (Hint: r=0.5 m)
The linear speed v for the tip of a propeller 1 m long, rotating 500 times per min is
min.
m per min.
m.

Math
Basic MathHow much should you deposit at the end of each month into an investment account that pays 7% compounded monthly to have $5 million when you retire in 38 years?
How much of the $5 million comes from interest?
Click the icon to view some finance formulas.
In order to have $5 million in 38 years, you should deposit $ each month.
(Round up to the nearest dollar.)

Math
Basic MathSelect the correct answer.
A regular octagon rotates 360° about its center. How many times does the image of the octagon coincide with the preimage during the rotation?
A. 1
B. 2
C. 4
D. 8
![Find all values of c that satisfy the mean value theorem for integrals on the following interval.
R(v)=v²-v; [5,8]
C=
(Round to two decimal places as needed. Use a comma to separate answers as needed.)](https://media.kunduz.com/media/sug-question/raw/56071056-1658145734.510638.jpeg?w=256)
Math
Basic MathFind all values of c that satisfy the mean value theorem for integrals on the following interval.
R(v)=v²-v; [5,8]
C=
(Round to two decimal places as needed. Use a comma to separate answers as needed.)

Math
Basic MathA container ship left the Dania Pier and traveled north at an average speed of 20
mph. Sometime later an aircraft carrier left traveling in the same direction but at an average speed of 30 mph. After traveling for two hours the aircraft carrier caught up with the container ship. Find the number of hours the container ship traveled before the aircraft carrier caught up.
3 hours
6 hours
4 hours
5 hours
7 hours

Math
StatisticsSuppose 50 students took an exam with results that were approximately normally distributed. If the mean was 68 and the standard deviation was 10.5, use the normal model to determine the proportion of students that scored at least a 70.

Math
FunctionsIf f(x)=x²-5x and g(x) = 8 - x³, evaluate the following.
a. (f+g)(4)
b. (g-f)(3)
c. (f.g)(-2)
d. (g/f)(-4)
a. (f+g)(4) = (Simplify your answer.)
Math
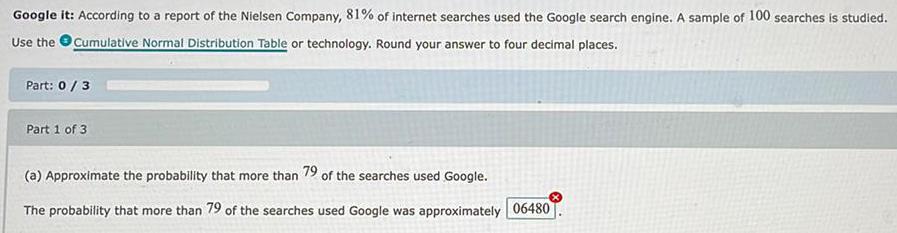
ProbabilityGoogle it: According to a report of the Nielsen Company, 81% of internet searches used the Google search engine. A sample of 100 searches is studied.
Use the Cumulative Normal Distribution Table or technology. Round your answer to four decimal places.
(a) Approximate the probability that more than 79 of the searches used Google.
The probability that more than 79 of the searches used Google was approximately 06480

Math
Basic MathA ball is launched into the air from the top of a building. Its initial velocity is 20 feet per second. The equation h - 16² +20 t + 50 can be used to model the height h of the ball in feet after t seconds. What is the height of the building the ball is being launched from? How long does it take for the ball to hit the ground?

Math
Basic MathInvestors buy a studio apartment for $200,000. Of this amount, they have a down payment of $60,000. Their down payment is what percent of the purchase price? What percent of the purchase price would an $80,000 down payment be?

Math
Basic MathThe number of asthma sufferers in the world was about 84 million in 1990 and 130 million in 2001. Let v represent the number of asthma sufferers (in millions) worldwide t years after 1990.
(a) Write N as a linear function of t. Use exact values in your formula, not decimal approximations.
N(t) =
(b) Write N as an exponential function of t. Use exact values in your formula, not decimal approximations.
N(t) =
(c) How many asthma sufferers are predicted worldwide in the year 2014 with the linear model?
(d) How many asthma sufferers are predicted worldwide in the year 2014 with the exponential model?

Math
Straight linesYou're a manager in a company that produces rocket ships. Machine A and Machine B both produce cockpits and propulsion sy stems. Machine A ran for 22 hours and produced 3 cockpits and 5 propulsion systems. Machine B ran for 44 hours and produc ed 6 cockpits and 10 propulsion systems. Assume both machines produce cockpits at the same rate and both produce propuls ion systems at the same rate. Can we use a system of linear equations in two variables to solve for a unique amount of time th at it takes each machine to produce a cockpit and to produce a propulsion system? Choose 1 answer: Yes; it takes Machine A a nd Machine B 4 hours to buduce a cockpit and 2 hours to produce a propulsion system. B Yes, it takes Machine A and Machine B 2 hours to produce a cockpit and 4 hours to produce a propulsion system. No: the system has many solutions. No, the syste m has no solution.

Math
Basic MathMr. Smith decides to feed his pet Doberman pinscher a combination of two dog foods.
Each can of brand A contains 4 units of protein, 1 unit of carbohydrates, and 2 units of fat and costs 60 cents. Each can of brand B contains 1 unit of protein, 1 unit of carbohydrates, and 4 units of fat and costs 40 cents. Mr. Smith feels that each day his dog should have at least 8 units of protein, 5 units of carbohydrates, and 16 units of fat. How many cans of each dog food should he give to his dog each day to provide the minimum requirements at the least cost?
Mr. Smith should give his dog can(s) of brand A and can(s) of brand B to provide the minimum requirements at the least cost.

Math
Basic MathSuppose that you borrow $2000.00 from a friend and promise to pay back $3170.00 in 3 years. What simple interest rate will you pay?
Math
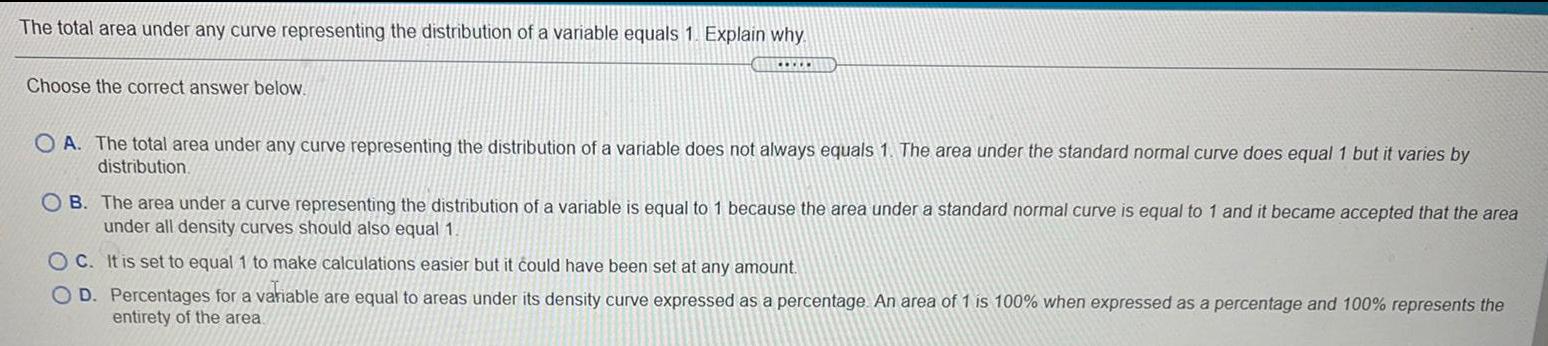
ProbabilityThe total area under any curve representing the distribution of a variable equals 1. Explain why.
.
A. The total area under any curve representing the distribution of a variable does not always equals 1. The area under the standard normal curve does equal 1 but it varies by distribution.
B. The area under a curve representing the distribution of a variable is equal to 1 because the area under a standard normal curve is equal to 1 and it became accepted that the area under all density curves should also equal 1.
C. It is set to equal 1 to make calculations easier but it could have been set at any amount.
D. Percentages for a variable are equal to areas under its density curve expressed as a percentage. An area of 1 is 100% when expressed as a percentage and 100% represents the entirety of the area.

Math
Basic MathSuppose that you earned a bachelor's degree and now you're teaching high school. The school district offers teachers the opportunity to take a year off to earn a master's degree. To achieve this goal, you deposit $3000 at the end of each year
in an annuity that pays 7.5% compounded annually.
How much will you have saved at the end of five years?
Find the interest.
b. Click the icon to view some finance formulas.
a. After 5 years, you will have approximately $
(Do not round until the final answer. Then round to the nearest dollar as
needed.)

Math
Basic MathChallenge in a company, 80% of the workers are men. If 600 people work for the company who aren't men, how many workers are there in all? Use pencil and paper. Show two different ways that you can solve this problem.

Math
Basic MathUse the problem-solving flowchart. The sum of three times a number and three is equal to the difference of the number and nine. Find the number. Round your answer to the neatest integer, if necessary.
The number is

Math
Quadratic equationsWhich shows the equation below written in the form ax2+bx+c=0?
x² +7x+9=3
A. x²+4x+6=0
B. x² +7x+6=0
C. x² + 4x+12=0
D. x² +7x+12=0

Math
Basic MathKarina has two investment options for $20,000 she is saving for her future college expenses. One account pays 2.5% interest compounded monthly. The second account pays 2.2% compounded weekly. Which account will have the larger balance after 5 years?
First account
both account
none of them
Second account

Math
Application of derivativesIf a person's temperature after x hours of strenuous exercise is T(x) = x²(7-x²) + 98.6 degrees Fahrenheit (for 0 ≤ x ≤ 2), find the rate of change of the temperature after 2 hours.
°F/hr

Math
StatisticsThe area under a particular normal curve between 8 and 11 is 0.7794. A normally distributed variable has the same mean and standard deviation as the parameters for this normal curve. What percentage of all possible observations of the variable lie between 8 and 11?

Math
StatisticsA variable is normally distributed with mean 10 and standard deviation 2.
a. Find the percentage of all possible values of the variable that lie between 9 and 14.
b. Find the percentage of all possible values of the variable that exceed 6.
c. Find the percentage of all possible values of the variable that are less than 5.

Math
StatisticsRecords taken from a hospital show that the times between arriving patients have a mean of 8.7 minutes with a standard deviation of 8.7 minutes. Based solely on the values of these two
parameters, explain why it is unreasonable to assume that the times between arriving patients is normally distributed or even approximately so.
Select the correct choice below.
*****
A. It is unreasonable because the standard deviation must be greater than the mean for a variable to be normally distributed. The given standard deviation is equal to the mean.
B. It is unreasonable because the time between arriving patients cannot be less than 0 minutes and all the values between 0 and the mean lie within one standard deviation.
C. It is unreasonable because the standard deviation must be less than the mean for a variable to be normally distributed. The given standard deviation is equal to the mean.
D. It is unreasonable because the time between arriving patients cannot be less than 0 minutes and all the values between 0 and the mean lie within two standard deviations.

Math
Basic MathA rectangle has a length of x − 6 and a width of x-7. Which equation below describes the perimeter, P, of the rectangle in terms of x?
P=2x-13
P-4x-26
p=x²-13x+42
P=x-13
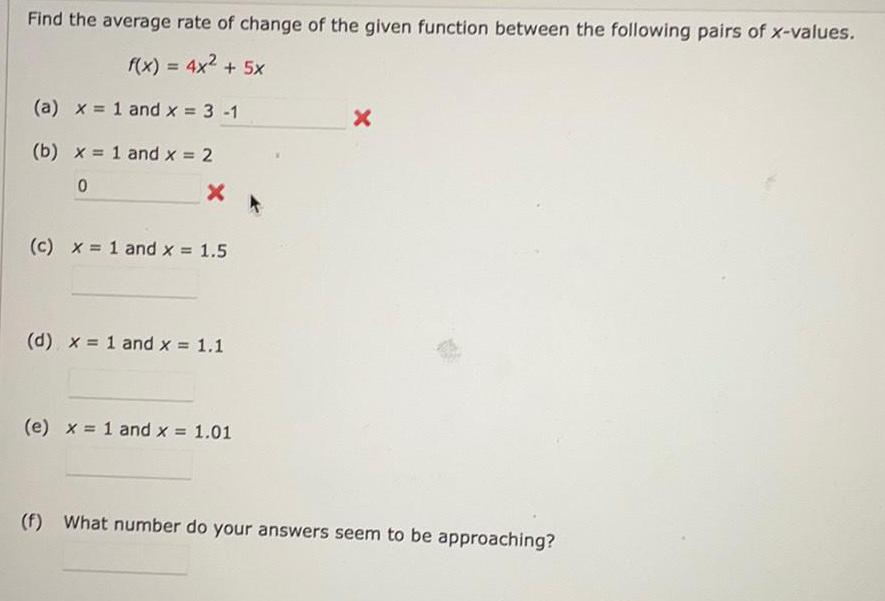
Math
Application of derivativesFind the average rate of change of the given function between the following pairs of x-values.
f(x) = 4x² + 5x
(a) x = 1 and x = 3
(b) x = 1 and x = 2
(c) x = 1 and x = 1.5
(d) x = 1 and x = 1.1
(e) x = 1 and x = 1.01
(f) What number do your answers seem to be approaching?

Math
Basic MathWe have seen that isosceles triangles have two sides of equal length. The angles opposite these sides have the same measure. Use the information to the right to help find the measure of angles 1 through 5.

Math
Basic MathA company wholesales shampoo in a particular city. Their marketing research department established the following weekly supply-and-demand equations.
p= x/600 + 1/2 Supply equation
p= 4500/x Demand equation
How many units are required for supply to equal demand? At what price per bottle will supply equal demand?

Math
Basic MathYou deposit $15,000 in an account that pays 4.5% interest compounded quarterly.
A. Find the future value after one year.
B. Use the future value formula for simple interest to determine the effective annual yield.
Click the icon to view some finance formulas.
A. The future value is $

Math
Basic MathOlivia sells solar panels to homeowners. She receives a 6% commission from the first $17,000 in sales and a 22% commission for any sales over $17,000. Last month he
sold $54,400 worth of solar panels. How much commission did Olivia earn from her first
$17,000 in sales?

Math
StatisticsAssume there is a certain population of fish in a pond whose growth is described by the logistic equation. It is estimated that the carrying capacity for the pond is 1600 fish. Absent constraints, the population would grow by 150% per year.
If the starting population is given by po = 200, then after one breeding season the population of the pond is given by
P1 =
After two breeding seasons the population of the pond is given by
P2=