Math Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
Math
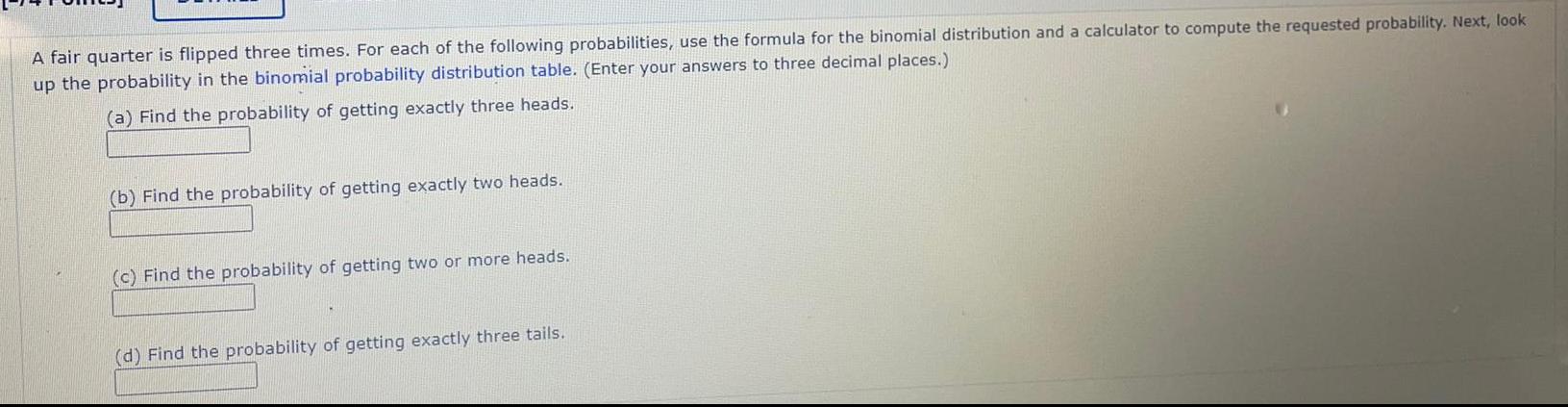
ProbabilityA fair quarter is flipped three times. For each of the following probabilities, use the formula for the binomial distribution and a calculator to compute the requested probability. Next, look up the probability in the binomial probability distribution table. (Enter your answers to three decimal places.)
(a) Find the probability of getting exactly three heads.
(b) Find the probability of getting exactly two heads.
(c) Find the probability of getting two or more heads.
(d) Find the probability of getting exactly three tails.

Math
Basic MathIn 4 minutes, a conveyor belt moves 100 pounds of recyclable aluminum from the delivery truck to a storage area. A smaller belt moves the same quantity of cans the same distance in 5 minutes. If both belts are used, find how long it takes to move the cans to the storage area. The conveyor belts together can move the 100 pounds of recyclable aluminum from the delivery truck to the storage area in minutes. (Simplify your answer. Type an integer, fraction, or mixed number.)
Math
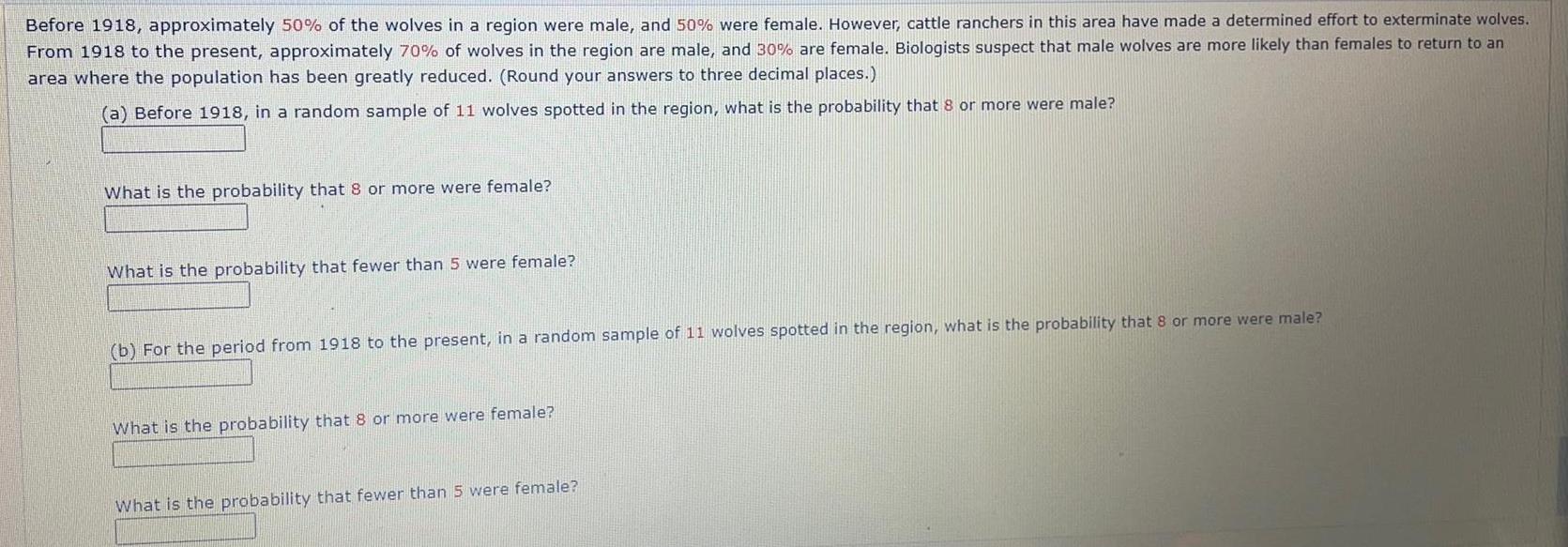
ProbabilityBefore 1918, approximately 50% of the wolves in a region were male, and 50% were female. However, cattle ranchers in this area have made a determined effort to exterminate wolves.
From 1918 to the present, approximately 70% of wolves in the region are male, and 30% are female. Biologists suspect that male wolves are more likely than females to return to an
area where the population has been greatly reduced. (Round your answers to three decimal places.)
(a) Before 1918, in a random sample of 11 wolves spotted in the region, what is the probability that 8 or more were male?
What is the probability that 8 or more were female?
What is the probability that fewer than 5 were female?
(b) For the period from 1918 to the present, in a random sample of 11 wolves spotted in the region, what is the probability that 8 or more were male?
What is the probability that 8 or more were female?
What is the probability that fewer than 5 were female?

Math
Basic MathIf a person can complete the following tasks in the following times, how much of the task can he complete in an hour? In other words, what is his rate at completing the task? a) Mow the lawn, 5 hours, (b) wash the car, 3 hours, (c) write a paper, 1.5 hours.
a) The person will have mowed of the lawn in an hour.
(Simplify your answer. Type an integer or a fraction)

Math
StatisticsA student deposits $300 in a savings account that pays 4% annual interest. At the end of 9 years, how much money will be in the savings account? Round your answer to the nearest cent.
The savings account will be worth $ at the end of 9 years.

Math
Permutations and CombinationsA baseball player comes up to bat 3 times during a league game. He either gets a hit or gets an out. How many different combinations are there for the three at bats? Make a
tree diagram to help see the situation.
8 different combinations
7 different combinations
6 different combinations
5 different combinations

Math
Basic MathIn 3 minutes, a conveyor belt moves 600 pounds of recyclable aluminum from the delivery truck to a storage area. A smaller belt moves the same quantity of cans the same distance in 7 minutes. If both belts are used, find how long it takes to move the cans to the storage area.

Math
Basic MathTwo angles are supplementary if the sum of their measures is 180°. Find two supplementary angles such that the larger angle is 148 more than 3 times the smaller angle. (Round to two decimal places if necessary.)

Math
Application of derivativesUse the Generalized Power Rule to find the derivative of the function.
f(x) = (3x + 1)^4 (3x - 1)^5
f'(x) =
Math
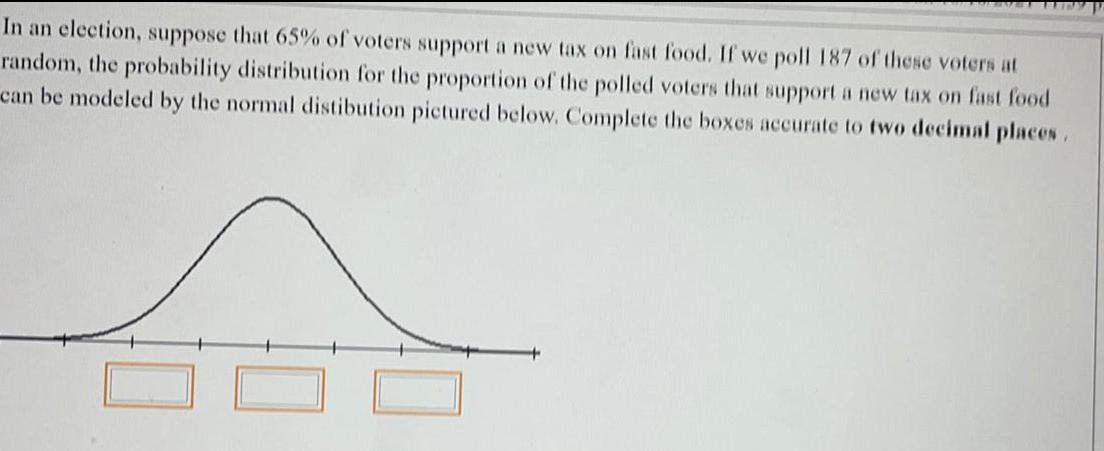
StatisticsIn an election, suppose that 65% of voters support a new tax on fast food. If we poll 187 of these voters at random, the probability distribution for the proportion of the polled voters that support a new tax on fast food can be modeled by the normal distibution pictured below. Complete the boxes accurate to two decimal places.

Math
Coordinate systemThe midpoint of AB is M(-1,-4). If the coordinates of A are (-3,-7), what are the coordinates of B?

Math
Basic MathUse the histogram and the normal probability plot of the data to assess the normality of the finger length data.
A. Both the histogram and the normal probability plot imply that the data is normal.
B. The normal probability plot implies normality but the histogram implies the data is not normal.
C. The histogram implies normality but the normal probability plot implies the data is not normal.
D. Both the histogram and the normal probability plot imply that the data is not normal.

Math
Basic MathSimplify sec² (t) - 1 / sec² (t) to an expression involving a single trig function with no fractions.
If needed, enter squared trigonometric expressions using the following notation.
Example: Enter sin² (t) as (sin(t))².

Math
Basic MathWhich reasoning process is shown in the following example? We examine the email addresses of 100 people. No two individuals from this group of people have identical email addresses. We conclude that for all people, no two people have identical email addresses.
A) deductive reasoning
B) reasoning by counterexample
C) theoretical reasoning
D) inductive reasoning
Math
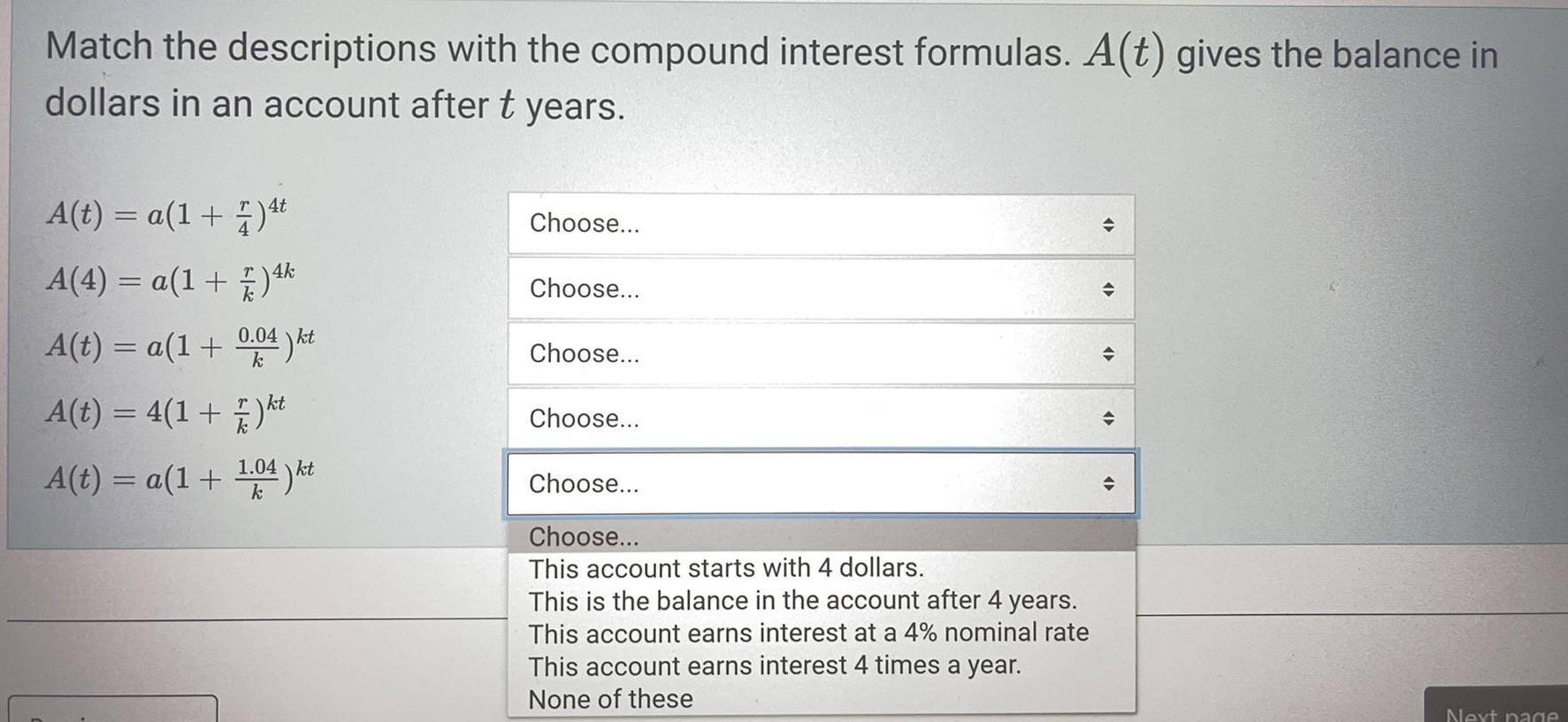
Basic MathMatch the descriptions with the compound interest formulas. A(t) gives the balance in dollars in an account after t years.
A(t) = a(1+ r/4)^4t
A(4) = a(1 + r/k)^4k
A(t) = a(1 + 0.04/k)^kt
A(t) = 4(1 + r/k)^kt
A(t) = a(1 + 1.04/k )^kt
This account starts with 4 dollars.
This is the balance in the account after 4 years.
This account earns interest at a 4% nominal rate
This account earns interest 4 times a year.
None of these

Math
Basic MathA piece of sheet metal, w = 24 inches wide, is bent to form the gutter shown in the illustration. If the cross-sectional area is 64 square inches, find the depth of the gutter. (Enter your answers as a comma-separated list.)

Math
Basic MathA shipping company is buying new trucks. The high-capacity trucks cost $50,000 and hold 340 cases of merchandise. The low-capacity trucks cost $30,000 and hold 200 cases of merchandise. The company has budgeted $1,140,000 for the new trucks and has a maximum of 30 people qualified to drive the trucks. Due to availability limitations, the company can purchase at most 15 high-capacity trucks. How many of each type of truck should the company purchase to maximize the number of cases shipped at one time?
To maximize the number of cases of merchandise that can be shipped simultaneously, the company should purchase trucks. high-capacity trucks and low-capacity

Math
Basic MathA certain store has a fax machine available for use by its customers. The store
charges $1.60 to send the first page and $0.45 for each subsequent page. Use an
inequality to find the number of pages that can be faxed for $7.00.
44 pages or fewer
16 pages or fewer
4 pages or fewer
13 pages or fewer

Math
Basic MathA dairy needs 270 gallons of milk containing 4 % butterfat. How many gallons each of milk containing 6% butterfat and milk containing 1% butterfat must be used to obtain the desired 270 gallons?
Math
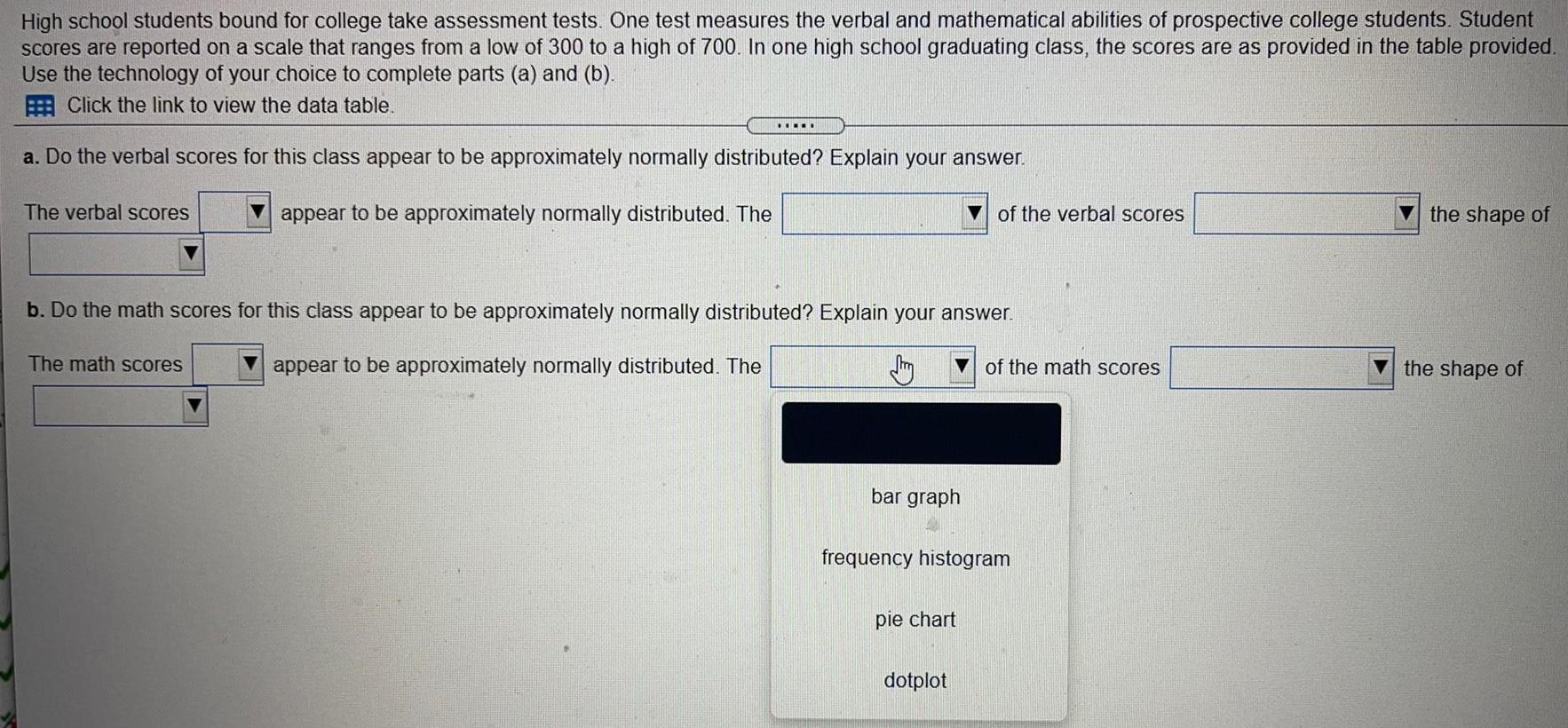
StatisticsHigh school students bound for college take assessment tests. One test measures the verbal and mathematical abilities of prospective college students. Student scores are reported on a scale that ranges from a low of 300 to a high of 700. In one high school graduating class, the scores are as provided in the table provided. Use the technology of your choice to complete parts (a) and (b). Click the link to view the data table.

Math
CircleIn the graph on the right, a line segment through the center of the circle intersects
the circle at the points (2,7) and (16, 9) as shown.
a. Find the coordinates of the circle's center.
b. Find the radius of the circle.
c. Use your answers from parts (a) and (b) to write the standard form of the circle's equation.
Math
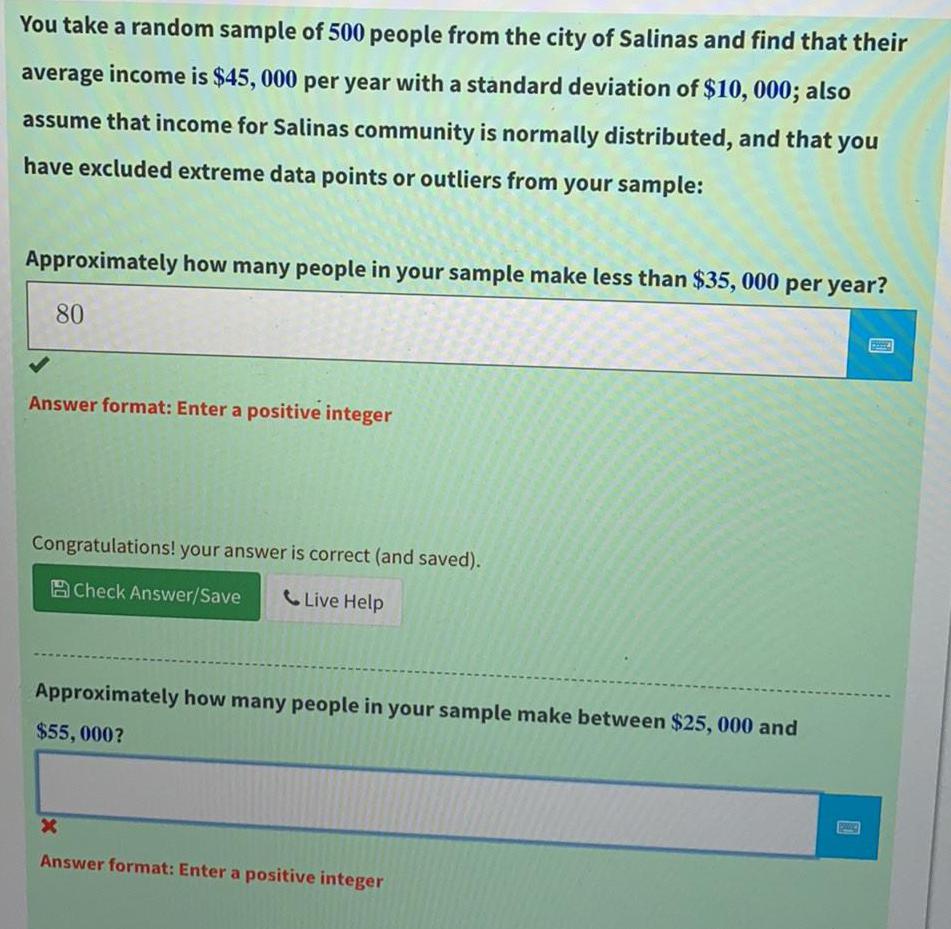
StatisticsYou take a random sample of 500 people from the city of Salinas and find that their
average e income is $45, 000 per year with a standard deviation of $10, 000; also
assume that income for Salinas community is normally distributed, and that you
have excluded extreme data points or outliers from your sample:
Approximately how many people in your sample make less than $35, 000 per year?
80
Answer format: Enter a positive integer
Congratulations! your answer is correct (and saved).
Check Answer/Save
Live Help
Approximately how many people in your sample make between $25,000 and
$55,000?
Answer format: Enter a positive integer

Math
Basic MathThink About the Process You deposit $3,900 into a bank account with a simple interest rate of 8%. How can you find the account balance after 6 years? Then find the account balance after 6 years.
How do you find your account balance after 6 years?
A. First use I = prt to find the simple interest earned after 6 years. Then add that to the rate.
B. First use I = prt to find the simple interest earned after 6 years. Then subtract that from the principal.
C. First use I = prt to find the simple interest earned after 6 years. Then add that to the principal.
D. First use I = prt to find the simple interest earned after 6 years. Then add that to the time.
After 6 years your account balance will be $
Resume later
Submit Quiz

Math
Basic MathOn the blueprint of a house, 55 millimeters represents 10 meters. The actual length of the living room is 8 meters. What is its length on the blueprint?
millimeters

Math
StatisticsOn a common measure of extroversion, the general population has an average score of 51 with a standard deviation of 30.
he probability of a researcher randomly selecting an individual who has an extroversion score of 62 or more?
Math
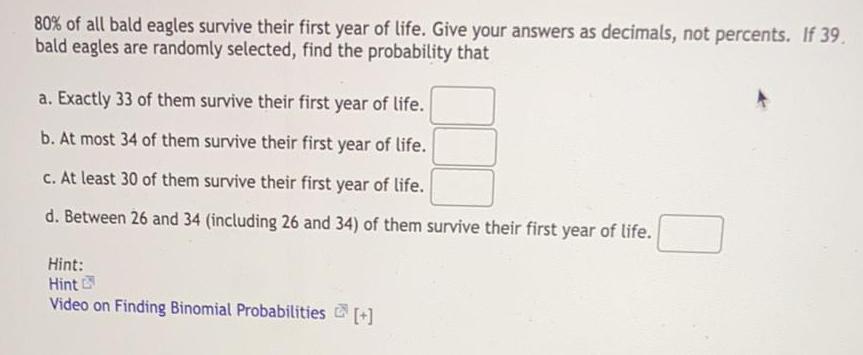
Probability80% of all bald eagles survive their first year of life. Give your answers as decimals, not percents. If 39.
bald eagles are randomly selected, find the probability that
a. Exactly 33 of them survive their first year of life.
b. At most 34 of them survive their first year of life.
c. At least 30 of them survive their first year of life.
d. Between 26 and 34 (including 26 and 34) of them survive their first year of life.

Math
Coordinate systemThe temperature in an industrial pasteurization tank is f(x) = x2 - 9x + 119 degrees centigrade after x minutes (for 0 ≤ x ≤ 13).
(a) Find f'(x) by using the definition of the derivative.
f'(x) =
(b) Use your answer to part (a) to find the instantaneous rate of change of the temperature after 2 minutes. Be sure to interpret the sign of your answer.
The temperature is ---Select--- at a rate of
degrees per minute after 2 minutes.
(c) Use your answer to part (a) to find the instantaneous rate of change after 6 minutes.
The temperature is ---Select--- at a rate of
degrees per minute after 6 minutes.
Math
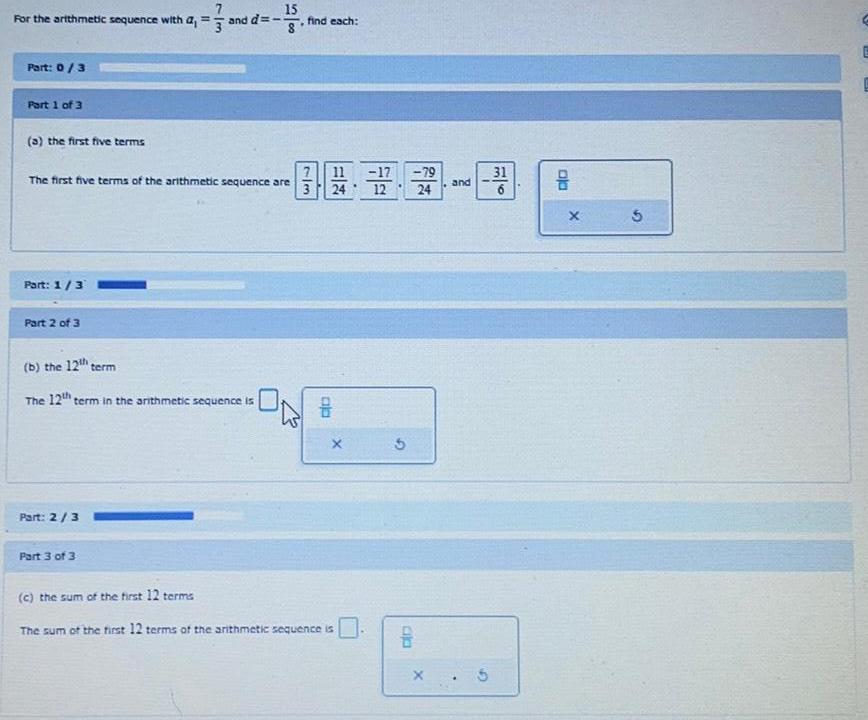
Sequences & SeriesFor the arithmetic sequence with a₁ =7/3 and d=-15/8
Part 1 of 3
(a) the first five terms
The first five terms of the arithmetic sequence are
(b) the 12th term
(c) the sum of the first 12 terms
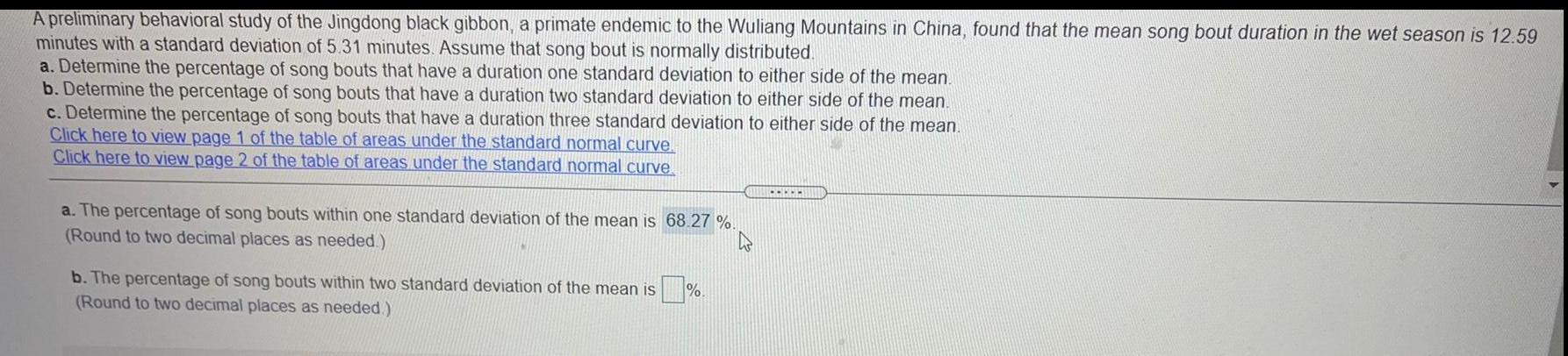
Math
StatisticsA preliminary behavioral study of the Jingdong black gibbon, a primate endemic to the Wuliang Mountains in China, found that the mean song bout duration in the wet season is 12.59
minutes with a standard deviation of 5.31 minutes. Assume that song bout is normally distributed.
a. Determine the percentage of song bouts that have a duration one standard deviation to either side of the mean.
b. Determine the percentage of song bouts that have a duration two standard deviation to either side of the mean.
c. Determine the percentage of song bouts that have a duration three standard deviation to either side of the mean.
Click here to view page 1 of the table of areas under the standard normal curve.
Click here to view page 2 of the table of areas under the standard normal curve
a. The percentage of song bouts within one standard deviation of the mean is 68.27 %.
(Round to two decimal places as needed.)
b. The percentage of song bouts within two standard deviation of the mean is
(Round to two decimal places as needed.)
%
.....
![ok so for this problem we need to write the answer in interval notation, and in the
answer key its [-5/3,2] and i understand where the points came from and why its
using brackets but why doesn't it use union? like (-infini, -5/3]U[2, infini) (edited)
4. 3x²-x-10 ≤0](https://media.kunduz.com/media/sug-question/raw/56022124-1658144510.3597875.jpeg?w=256)
Math
Quadratic equationsok so for this problem we need to write the answer in interval notation, and in the
answer key its [-5/3,2] and i understand where the points came from and why its
using brackets but why doesn't it use union? like (-infini, -5/3]U[2, infini) (edited)
4. 3x²-x-10 ≤0
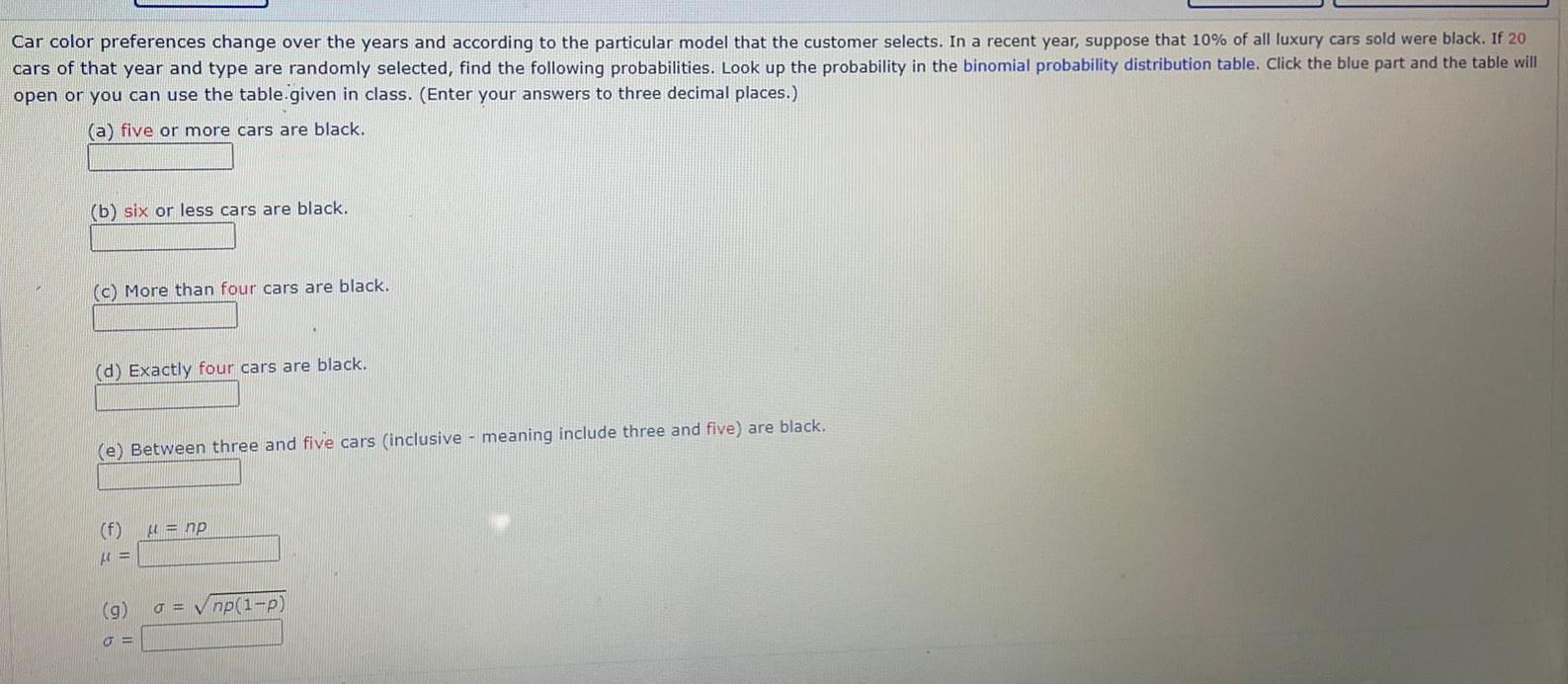
Math
ProbabilityCar color preferences change over the years and according to the particular model that the customer selects. In a recent year, suppose that 10% of all luxury cars sold were black. If 20 cars of that year and type are randomly selected, find the following probabilities. Look up the probability in the binomial probability distribution table. Click the blue part and the table will open or you can use the table.given in class. (Enter your answers to three decimal places.)
(a) five or more cars are black.
(b) six or less cars are black.
(c) More than four cars are black.
(d) Exactly four cars are black.
(e) Between three and five cars (inclusive - meaning include three and five) are black.
(f) μ = np
μ =
(g) σ = √(np(1-P))
σ =

Math
Basic MathDawn, Keith, and John are all working on a history project. Dawn spent 1.2 hours less than 6 times as many hours on the project as John did. Keith spent 0.8 hours more than 5 times as many hours on the project as John did. If Dawn and Keith spent the same amount of time working on the project, how many hours did John spend working on the project?

Math
Basic MathA company decided to fine its workers for parking violations on its property. The first offense carries a fine of $19, the second offense is $23, the third offense is $27, and so on. What is the fine for the eighth offense?

Math
Basic MathThe variable X denotes a binomial random variable with parameters n and p. Indicate which area under the approximate normal curve would be determined to approximate the given binomial probability.
P(X= 15)
The area between the lower delimiting x-value, and the upper delimiting x-value,
(Use integers or decimals for any numbers in the expressions. Do not round.) would be determined to approximate the binomial probability P(X = 15).

Math
Basic MathOn a park map, the distance from a picnic table to the hiking trail is 6 centimeters. The map uses a scale of 2 cm = 150 meters. What is the actual distance from the picnic table to the hiking trail?

Math
ProbabilityAn experiment consists of first rolling a die and then tossing a coin:
a. How many elements are there in the sample space?
b. Let A be the event that either a 2, 3 or 4 is rolled first, followed by landing a head on the coin toss.
P(A) = Present your answer as a decimal rounded to four decimal places.
c. Let B be the event that a number less than 2 is rolled, followed by landing a head on the coin toss. Are
the events A and B mutually exclusive?
Yes, they are Mutually Exclusive
No, they are not Mutually Exclusive
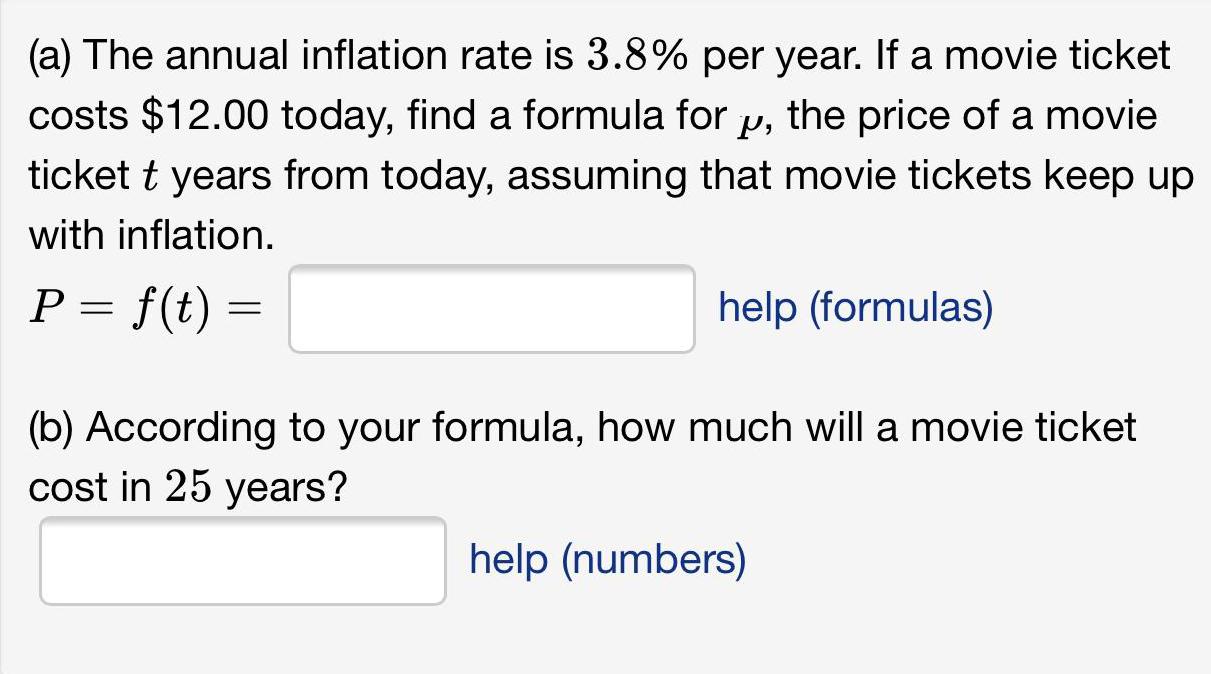
Math
Basic Math(a) The annual inflation rate is 3.8% per year. If a movie ticket costs $12.00 today, find a formula for y, the price of a movie ticket t years from today, assuming that movie tickets keep up with inflation.
(b) According to your formula, how much will a movie ticket cost in 25 years?

Math
Basic MathA variable is normally distributed with mean 18 and standard deviation 3.
a. Determine the quartiles of the variable.
b. Obtain and interpret the 85th percentile.
c. Find the value that 65% of all possible values of the variable exceed.
d. Find the two values that divide the area under the corresponding normal curve into a
middle area of 0.95 and two outside areas of 0.025. Interpret the answer.
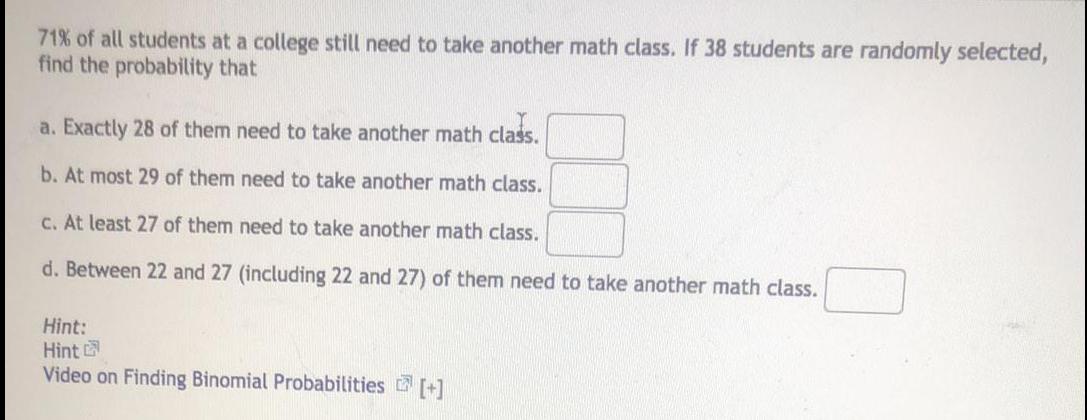
Math
Statistics71% of all students at a college still need to take another math class. If 38 students are randomly selected, find the probability that
a. Exactly 28 of them need to take another math class.
b. At most 29 of them need to take another math class.
c. At least 27 of them need to take another math class.
d. Between 22 and 27 (including 22 and 27) of them need to take another math class.
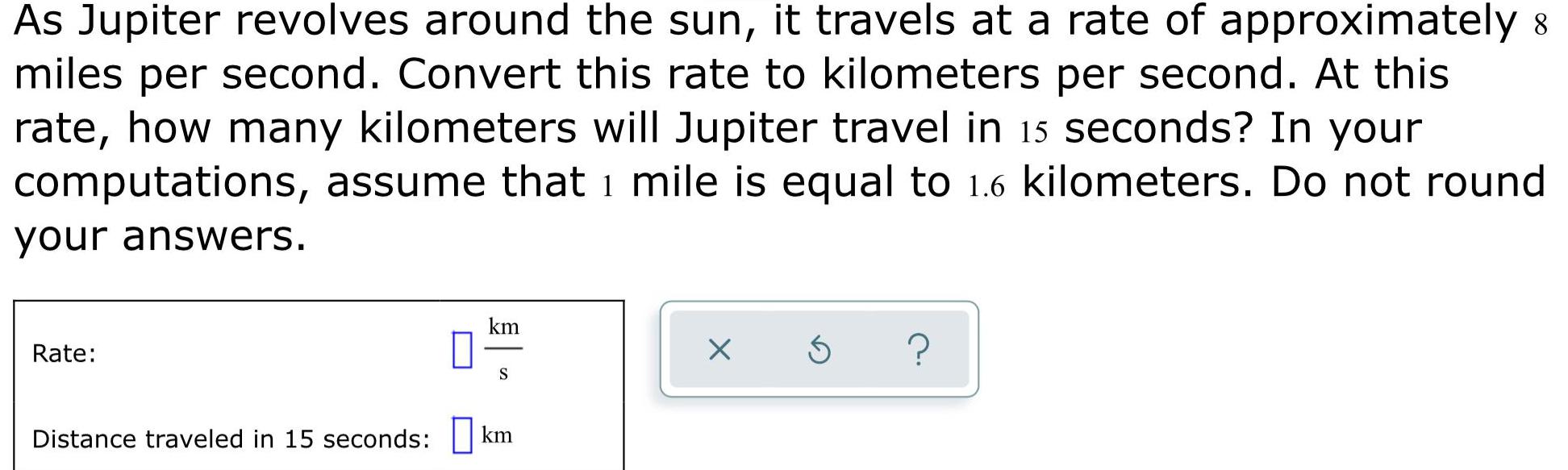
Math
Basic MathAs Jupiter revolves around the sun, it travels at a rate of approximately 8
miles per second. Convert this rate to kilometers per second. At this
rate, how many kilometers will Jupiter travel in 15 seconds? In your
computations, assume that 1 mile is equal to 1.6 kilometers. Do not round
your answers.
Rate:
Distance traveled in 15 seconds:

Math
Basic MathAt the city museum, child admission is $6.20 and adult admission is $9.80. On Friday, twice as many adult tickets as child tickets were sold, for a total sales of $722.40. How many child tickets were sold that day?

Math
Basic MathMs. Landry charges $40 an hour with a $5 flat fee for tutoring. Ms. Bowman charges $30 an hour with a flat fee of $10 to tutor. Which equation represents the situation when the cost is the same to be tutored by Ms. Landry and Ms. Bowman, where h is hours?
A) 40h + 30h-5+10
B) 40h+30h-10-5
40h+5-30h +10
D) 40h+ 10-30h+5

Math
Basic MathGraph y = f(x) by hand by first plotting points to determine the shape of the graph.
f(x) = -1

Math
Basic MathSolve the equation by hand, give an exact solution (the expression you arrived to without having to touch a calculator)
"2x³-1= 3.5
Type the expression you found so Desmos computes an approximate solution:
Check the solution works.
2( )³-1

Math
Basic MathAt the end of a snow storm, Savannah saw there was a lot of snow on her front lawn..
The temperature increased and the snow began to melt at a steady rate. The depth of
snow on Savannah's lawn, in inches, can be modeled by the equation S = -1.5t + 15, where t is the time, in hours, after the snow stopped falling. Wha is the slope of the equation and what is its interpretation in the context of the problem? The slope of the function is which reveals

Math
Basic MathYou and a group of friends participate in a game where you must use clues to escape from a room. You have a limited amount of time to escape and are allowed 3 free clues. Additional clues may be requested, but each removes 5 minutes from your remaining time. What integer represents the total change in the time when you use 5 clues?
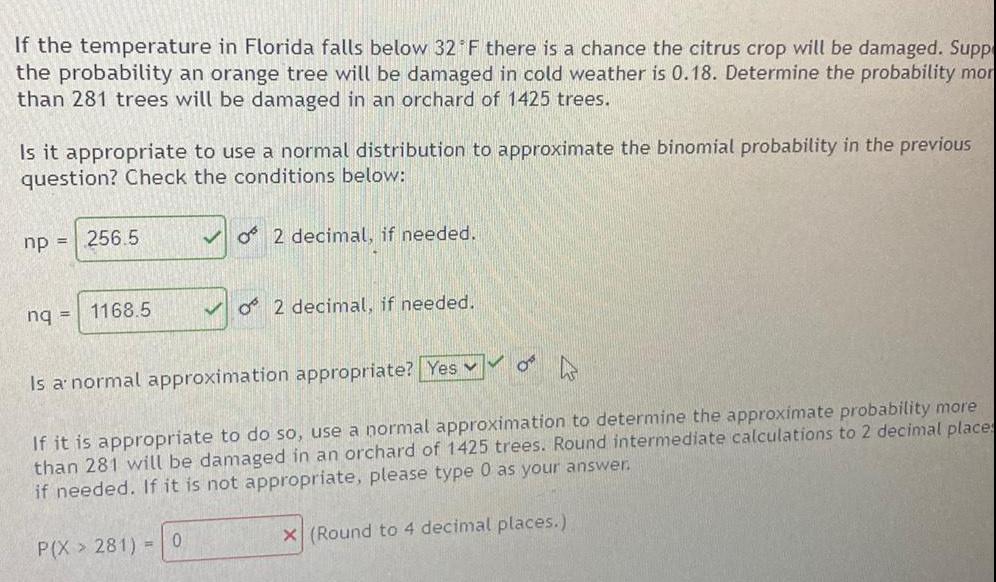
Math
ProbabilityIf the temperature in Florida falls below 32°F there is a chance the citrus crop will be damaged. Supp the probability an orange tree will be damaged in cold weather is 0.18. Determine the probability more than 281 trees will be damaged in an orchard of 1425 trees. Is it appropriate to use a normal distribution to approximate the binomial probability in the previous question? Check the conditions below:
np = 256.5
nq =
1168.5
✓ 2 decimal, if needed.
Is a normal approximation appropriate? Yes
P(X> 281) =
✓ 2 decimal, if needed.
If it is appropriate to do so, use a normal approximation to determine the approximate probability more than 281 will be damaged in an orchard of 1425 trees. Round intermediate calculations to 2 decimal places if needed. If it is not appropriate, please type 0 as your answer. x (Round to 4 decimal places.)

Math
ProbabilityAt a large high school outside of Chicago, there are two students running for class president, Ronald and Bo. 60% of the students in the school support Bo and the remaining 40% support Ronald. If you randomly sampled 12 students, what is the probability that more than half of your sample is comprised of Ronald supporters? Assume independence between students. Note: Round to the nearest thousandth.
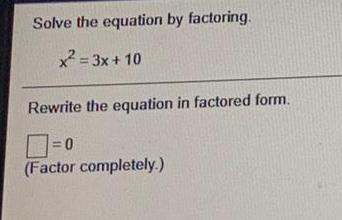
Math
Basic MathSolve the equation by factoring.
x² = 3x+10
Rewrite the equation in factored form.
= 0
(Factor completely.)
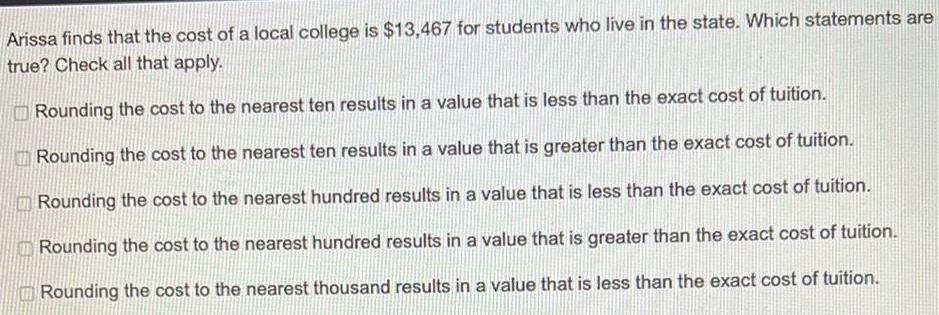
Math
Basic MathArissa finds that the cost of a local college is $13,467 for students who live in the state. Which statements are
true? Check all that apply.
Rounding the cost to the nearest ten results in a value that is less than the exact cost of tuition.
Rounding the cost to the nearest ten results in a value that is greater than the exact cost of tuition.
Rounding the cost to the nearest hundred results in a value that is less than the exact cost of tuition.
Rounding the cost to the nearest hundred results in a value that is greater than the exact cost of tuition.
Rounding the cost to the nearest thousand results in a value that is less than the exact cost of tuition.