Math Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Math
Sequences & SeriesSuppose a flu epidemic has broken out in all math 120 courses at your school. Assume a total of 12 people have the flu as of today and that each day the total number people who have the flu quadruples. Estimate numerically when the number of people will reach 3072. {your answer input will be number only)

Math
Basic MathA stone dropped into a still pond sends out a circular ripple whose radius increases at a constant rate of 3 ft/s. How rapidly is the area enclosed by the ripple increasing when the radius is 1 feet?
Math
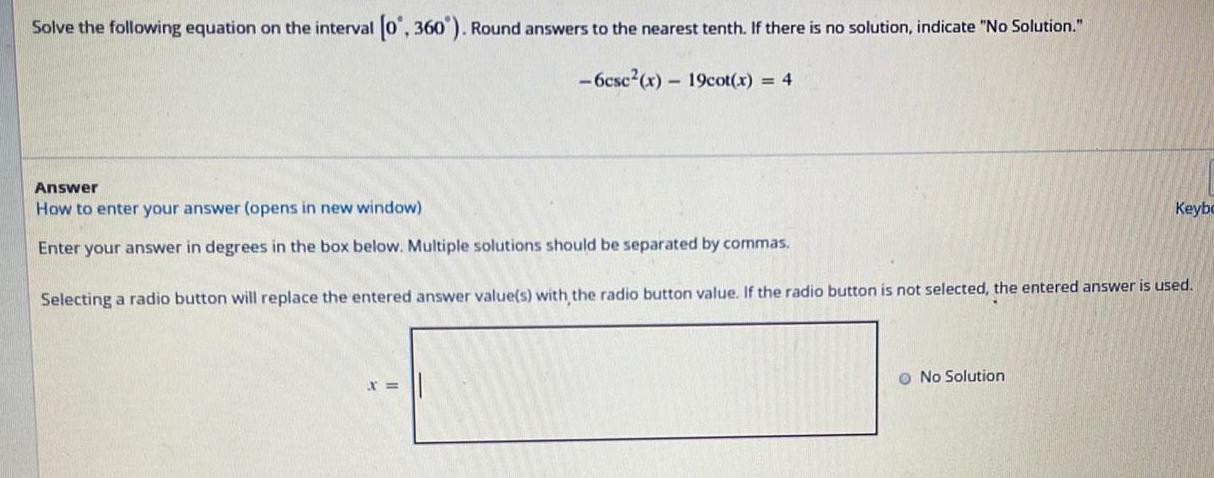
Trigonometric equationsSolve the following equation on the interval [0°, 360°). Round answers to the nearest tenth. If there is no solution, indicate "No Solution."
-6csc²(x) - 19cot(x) = 4
![Find all values of c that satisfy the mean value theorem for integrals on the following interval
f(x)=√x+9 . [0.4]](https://media.kunduz.com/media/sug-question/raw/56071020-1659004441.9720936.jpeg?w=256)
Math
DifferentiationFind all values of c that satisfy the mean value theorem for integrals on the following interval
f(x)=√x+9 . [0.4]

Math
Basic MathA linear function is given. Complete parts (a)-(d).
f(x)=1/5x-6
(a) Determine the slope and y-intercept of the function.

Math
Straight linesA cashier has a total of 48 bills in her cash drawer. There are only $20 bills and $5 bills in her drawer. The value of the bills is $465. How many $20 bills are in the drawer?
31 $20 bills
17 $20 bills
15 $20 bills
33 $20 bills

Math
Basic MathSelect the correct answer from each drop-down menu.
The barley plant has seven pairs of chromosomes. For a gamete, the number of genetic combinations that are possible through independent assortment is __. For a zygote produced by two barley parents, the number of possible genetic combinations is__
Math
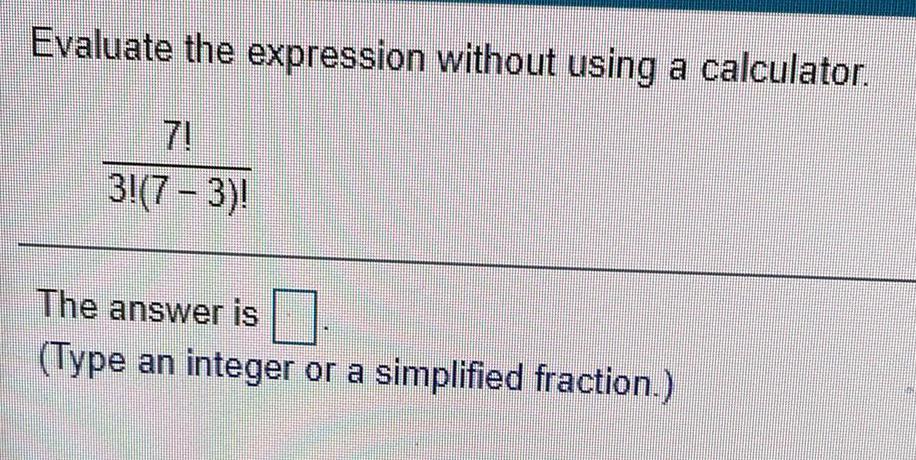
Permutations and CombinationsEvaluate the expression without using a calculator.
7!/3!(7-3)!
The answer is __
(Type an integer or a simplified fraction.)

Math
Mathematical ReasoningJohn wants to prepare a sandwich. He has 4 choices for the type of bread, 5 choices for the meat, and 3 choices for dressing. How many different sandwiches can John prepare? Show you work and answer in the text box given below.

Math
TrigonometryA building 29.94 feet tall has a shadow that is 33.11 feet long. Find the angle of elevation of the sun to the nearest hundredth of a degree.
The angle of elevation is degrees.
(Round to the nearest hundredth as needed.)

Math
FunctionsFor a given function f(x), the operation 1/2f(x) will
A) shrink the graph horizontally by a factor of 1/2.
B) stretch the graph horizontally by a factor of 2.
C) shrink the graph vertically by a factor of 1/2.
D) stretch the graph vertically by a factor of 2.

Math
Basic MathA right triangle has sides that measure 24 and 32, but the length of the hypotenuse is unknown. What is the perimeter measurement of this triangle? Round your
answer to the nearest hundredth
85.23
96
89
94.79

Math
Basic MathA candy company claims that 25% of the candies in its bags are colored green. Steve buys 32 bags of 32 candies, randomly selects one candy from each, and counts the number of green candies. If there are 7, 8, or 9 green candies, Steve will conclude that the company's claim is correct. What is the probability of Steve agreeing with the company's claim? Use Excel to find the probability
• Round your answer to three decimal places.

Math
Basic MathA gallon contains 231 cubic inches. A cylindrical barrel full of juice concentrate has a diameter of 3 feet and is 8 feet high. How many gallons of concentrate are in the barrel? Use π = 3.14.
There are __ gallons of concentrate in the barrel.
(Type an integer or a decimal. Round to two decimal places as needed.)
.....
![On the left-hand side, for the first term 9x³, we have the following.
d/dx[9x³]=_
Now, note that the second term x2y is a product, so we must use the product rule. We therefore have the following.
d/dx[x²y] = (x²)(y') + __](https://media.kunduz.com/media/sug-question/raw/55752619-1659003653.3623345.jpeg?w=256)
Math
DifferentiationOn the left-hand side, for the first term 9x³, we have the following.
d/dx[9x³]=_
Now, note that the second term x2y is a product, so we must use the product rule. We therefore have the following.
d/dx[x²y] = (x²)(y') + __
Math
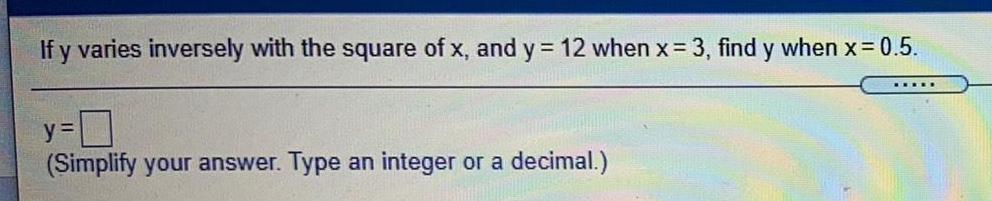
Basic MathIf y varies inversely with the square of x, and y = 12 when x = 3, find y when x = 0.5.
y=
(Simplify your answer. Type an integer or a decimal.)
*****

Math
Quadratic equationsWhich of the following statements is true for the quadratic equation x² - 16x+64 = 0?
The equation has no solutions.
The equation has two solutions.
It's impossible to determine how many solutions the equation has.
The equation has one solution.
Math
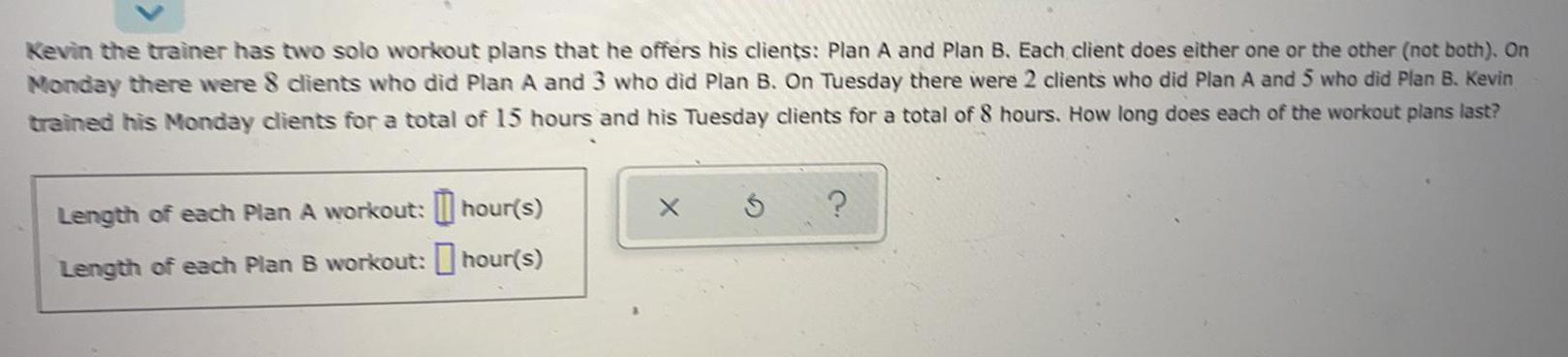
Basic MathKevin the trainer has two solo workout plans that he offers his clients: Plan A and Plan B. Each client does either one or the other (not both). On Monday there were 8 clients who did Plan A and 3 who did Plan B. On Tuesday there were 2 clients who did Plan A and 5 who did Plan B. Kevin trained his Monday clients for a total of 15 hours and his Tuesday clients for a total of 8 hours. How long does each of the workout plans last?
Length of each Plan A workout: _hour(s)
Length of each Plan B workout: _hour(s)
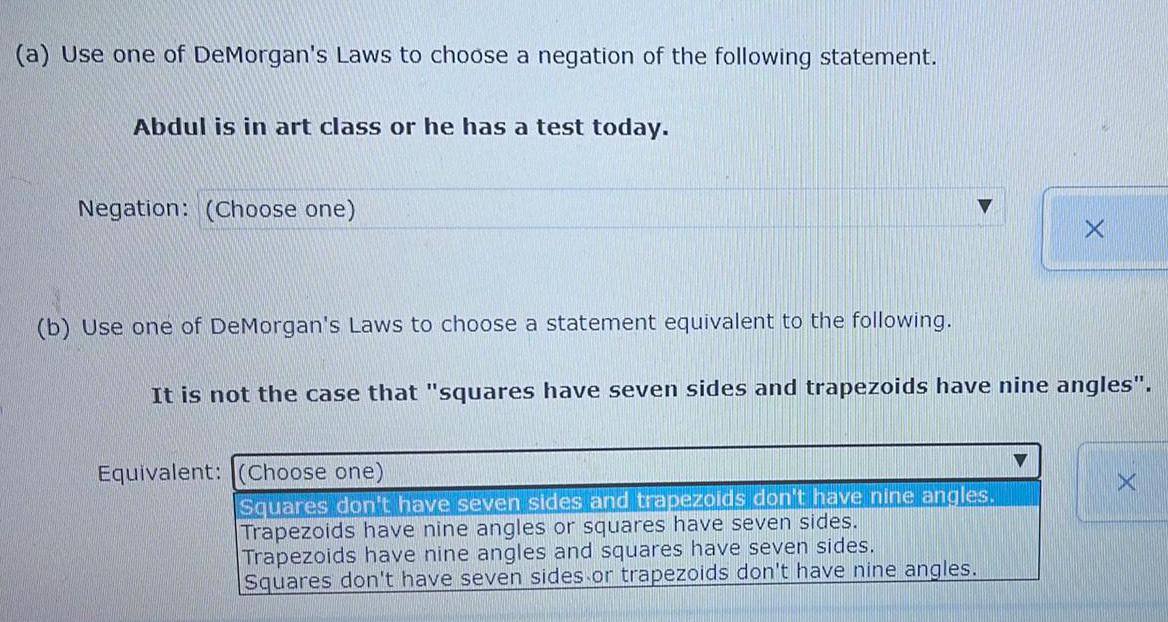
Math
Basic Math(a) Use one of DeMorgan's Laws to choose a negation of the following statement.
Abdul is in art class or he has a test today.
Negation: (Choose one)
(b) Use one of DeMorgan's Laws to choose a statement equivalent to the following.
It is not the case that "squares have seven sides and trapezoids have nine angles".
Equivalent: (Choose one)
Squares don't have seven sides and trapezoids don't have nine angles.
Trapezoids have nine angles or squares have seven sides.
Trapezoids have nine angles and squares have seven sides.
Squares don't have seven sides or trapezoids don't have nine angles.
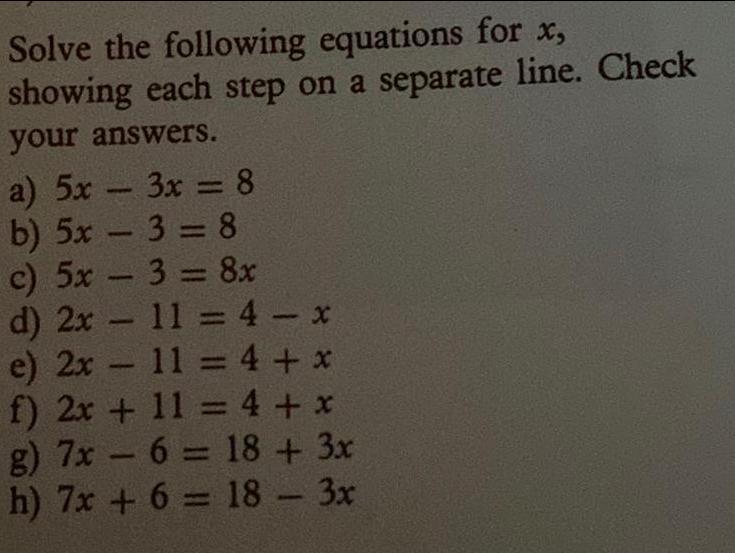
Math
Basic MathSolve the following equations for x,
showing each step on a separate line. Check your answers.
a) 5x - 3x = 8
b) 5x - 3 = 8
c) 5x - 3 = 8x
d) 2x - 11 = 4-x
e) 2x - 11 = 4+*
f) 2x + 11 = 4 + x
g) 7x 6 = 18 + 3x
h) 7x + 6 = 18 - 3x
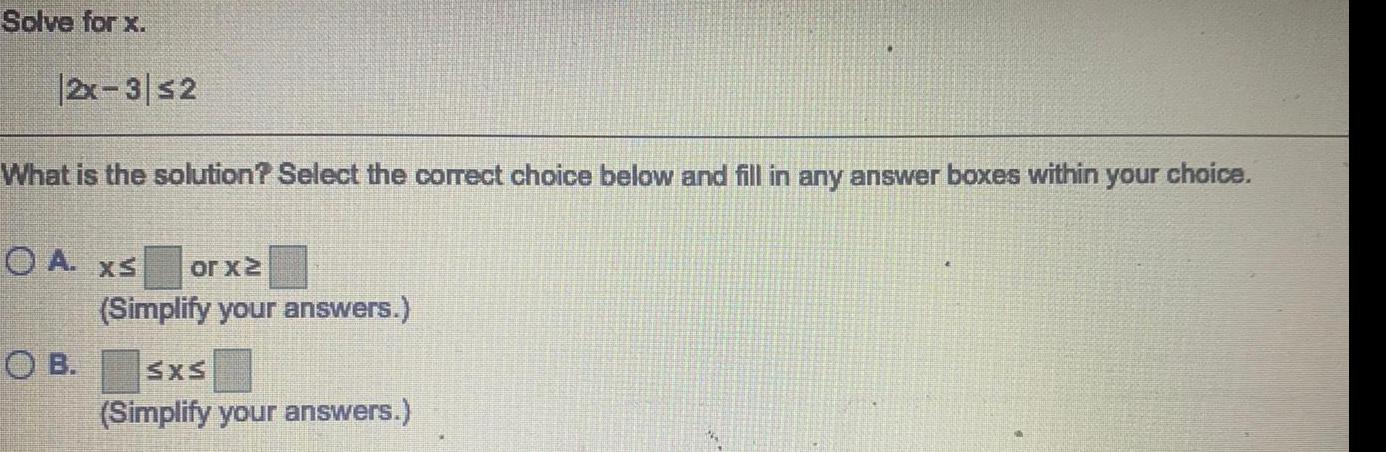
Math
Basic MathSolve for x.
|2x - 3| ≤2
What is the solution? Select the correct choice below and fill in any answer boxes within your choice.
A. x≤__ or x ≥__
(Simplify your answers.)
B. _≤x≤_
(Simplify your answers.)

Math
FunctionsAn endangered species of fish has a population that is decreasing exponentially (A - Agekt). The
population 9 years ago was 1500. Today, only 1000 of the fish are alive. Once the population
drops below 100, the situation will be irreversible. When will this happen, according to the
model? (Round to the nearest whole year.)
51 years from today
53 years from today
50 years from today
52 years from today
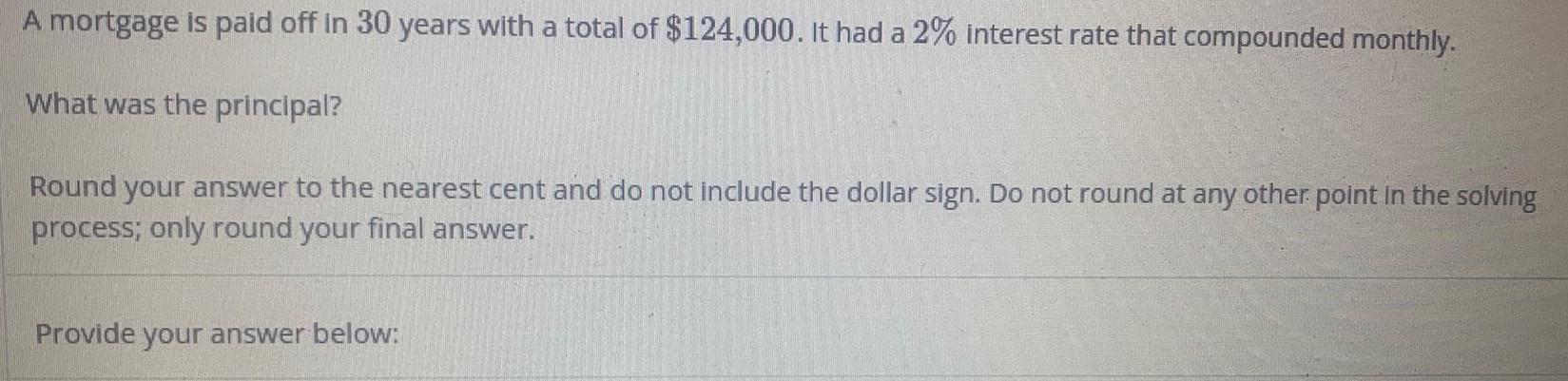
Math
Basic MathA mortgage is paid off in 30 years with a total of $124,000. It had a 2% interest rate that compounded monthly.
What was the principal?
Round your answer to the nearest cent and do not include the dollar sign. Do not round at any other point in the solving process; only round your final answer.
Provide your answer below:

Math
Permutations and CombinationsSuppose there is a list of fifteen jokes about marriage and divorce. In how many ways can people select their five favorite jokes from this list?
Five favorite jokes can be selected from a list of fifteen thoughts about marriage and divorce in different ways.
(Type a whole number.)
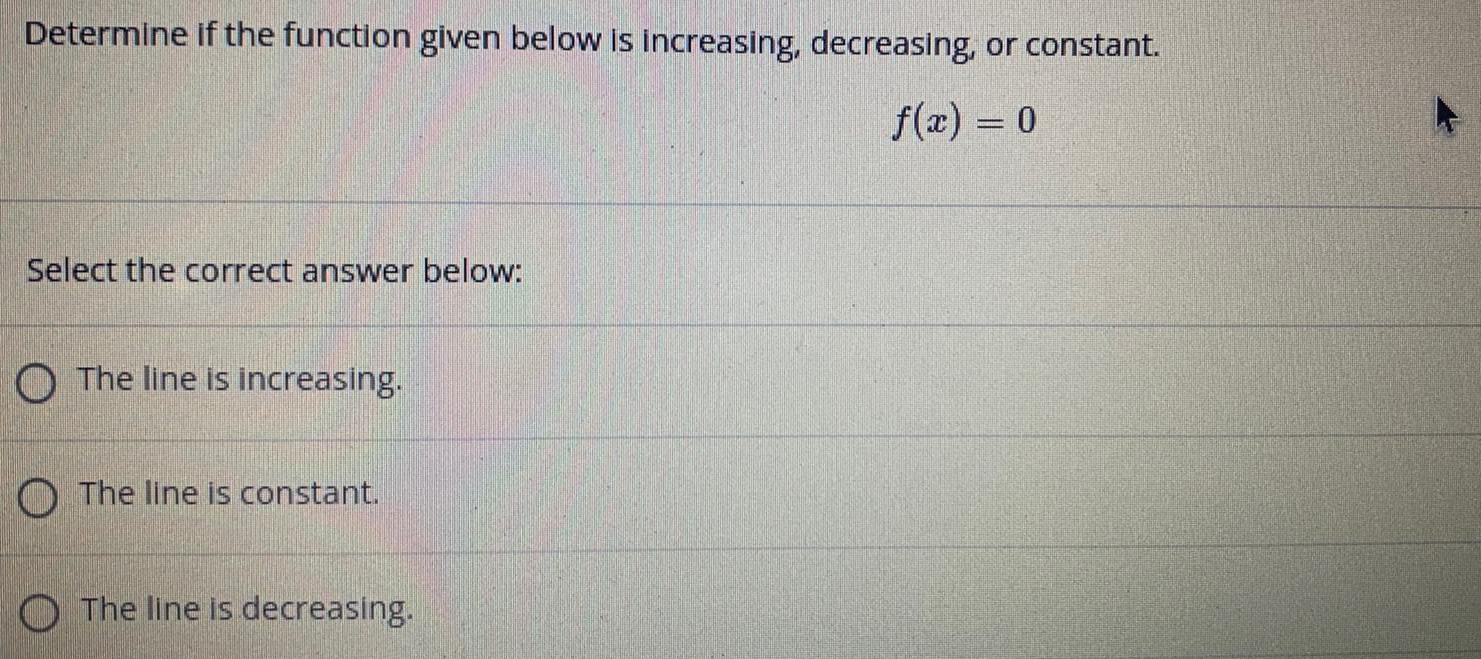
Math
Basic MathDetermine if the function given below is increasing, decreasing, or constant.
f(x) = 0
Select the correct answer below:
The line is increasing.
The line is constant.
The line is decreasing.

Math
Basic MathSelect a possible formula for the polynomial f(x), given that f(x) has degree three, f(-1) = f(3) = f(5) = 0, and limz⇒∞f(x) = -∞.
A. -(x + 1)(x - 3)(x - 5)
B. -(x + 1)2(x - 3)(x - 5)
C. (x + 1)(x+3)(x - 5)
D. -(x + 1)(x + 5)(x+3)
Is there more than one possible solution?
A. No, because there is only one function that meets all of the requirements.
B. Yes, because the leading coefficient could be any negative number.
C. Yes, because there could be different multiplicities for the roots.
D. No, because we know the three roots and it is a degree three polynomial.

Math
Basic Math"Princess Tower" in Dubai is considered the
world's tallest residential building, towering to
101 floors!
T(n) models the number of tenants living on
floor n of the tower.
What does the statement T(20) = T(c) mean?
Choose 1 answer:
(A).Floor 20 and floor c have the same number of tenants.
(B)The number of tenants on floor 20 is equal to C.
(C)The number of tenants on floor C is equal to 20.
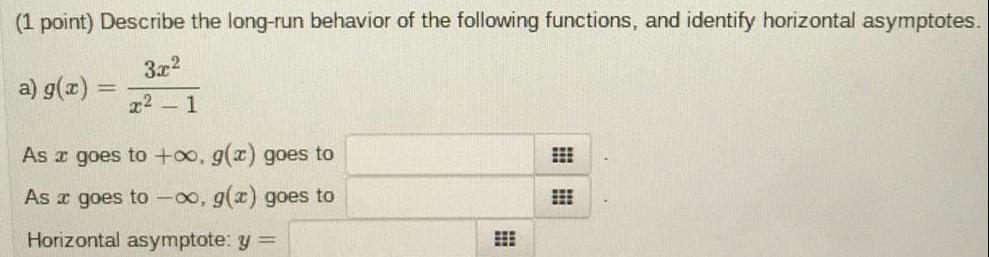
Math
Application of derivativesDescribe the long-run behavior of the following functions, and identify horizontal asymptotes.
a) g(x)=3x²/x² - 1
As a goes to +∞, g(x) goes to
As a goes to -∞, g(x) goes to
Horizontal asymptote: y =

Math
Basic MathQuadrilateral ABCD has vertices
A(-2, 1), B(4,4), C(5, 0), and D(-1, -2).
Which side is the longest?
CD
DA
AB
BC

Math
Basic MathIs the function below exponential?
m(t) = (2.3t) ³
If so, write the function in the form m(t) = abt and enter the
values you find for a and b in the indicated blanks below. If the
function is not exponential, enter NONE in both blanks below.
a
b

Math
StatisticsAt General Hospital, nurses are given performance evaluations to determine eligibility for merit pay raises. The supervisor rates the nurses on a scale of 1 to 10 (10
being the highest rating) for several activities: promptness, record keeping, appearance, and bedside manner with patients. Then an average is determined by giving
a weight of 4 for promptness, 2 for record keeping, 3 for appearance, and 1 for bedside manner with patients. What is the average rating for a nurse with ratings of 5
for promptness, 4 for record keeping, 9 for appearance, and 2 for bedside manner? (Enter your answer to one decimal place.)

Math
ProbabilityIn an article on Flurry Blog, a
gaming marketing gap for men
between the ages of 30 and 40 is
identified. You are researching a
startup game targeted at the 35-
year-old demographic. Your idea
is to develop a strategy game that
can be played by men from their
late 20s through their late 30s.
Based on the article's data,
industry research shows that the
average strategy player is 28
years old with a standard
deviation of 4.8 years. You take a
sample of 100 randomly selected
gamers. If your target market is
29- to 35-year-olds, should you
continue with your development
strategy?

Math
Quadratic equationsFind allercepts and y-intercepts of the graph of the function.
f(x)=3x² +17x+20
If there is more than one answer, separate them with commas.
Click on "None" if applicable.

Math
Basic MathA clothing business finds there is a linear relationship between the number of shirts, it can sell and the price, P, It cancharge per shirt. In particular, historical data shows that 3 thousand shirts can be sold at a price of $78 each, and that 7
thousand shirts can be sold at a price of $62 each.
Find the equation of the form P(n) = mn + b that gives the price P they can charge for n thousand shirts.
Select the correct answer below:
P(n) = 0n + 78
P(n) = -4n +95
P(n) = -4n +90
P(n) = On +62
P(n) = -6n +104
P(n) = -6n +96

Math
Basic MathUsing the slope formula, find the slope of the line through the given points.
(6,7) and (9,4)
What is the slope of the line? Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The slope of the line is
B. The slope of the line is undefined.
(Type an integer or a simplified fraction.)

Math
Basic MathMario has a 500-page novel which he is required to read
over summer break for his upcoming language arts class.
a. If Mario reads 24 pages each day, write a function to
represent the number of pages that Mario has left to read p
after d days.


Math
FunctionsA function of x contains the five ordered pairs
of the form (x, y). Four of these points are
given below.
(-2, 7), (0, 3), (1, -4), (5,-2)
Which ordered pair could
represent the fifth point?
A. (1,9)
B. (5,7)
C. (3,-4)
D. (0, -8)
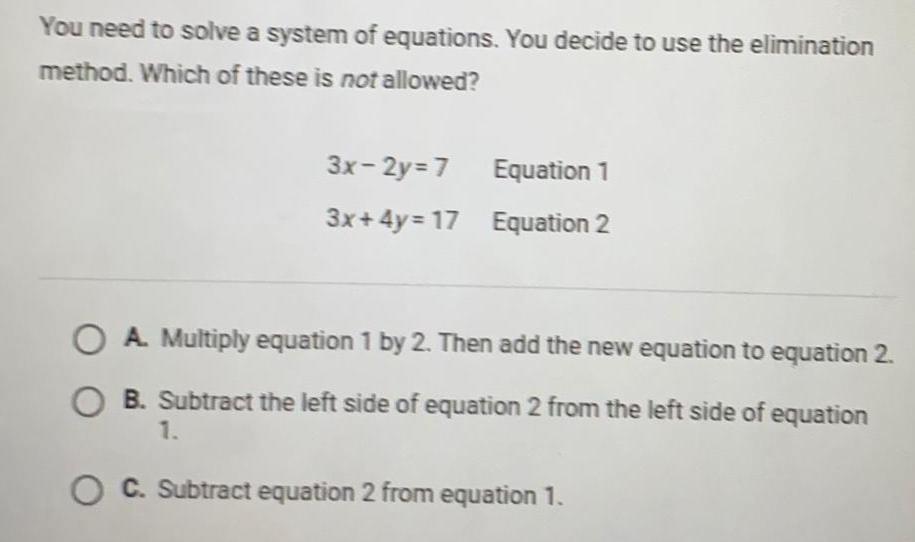
Math
Basic MathYou need to solve a system of equations. You decide to use the elimination
method. Which of these is not allowed?
3x-2y=7 Equation 1
3x+4y=17 Equation 2
A. Multiply equation 1 by 2. Then add the new equation to equation 2.
B. Subtract the left side of equation 2 from the left side of equation
C. Subtract equation 2 from equation 1.
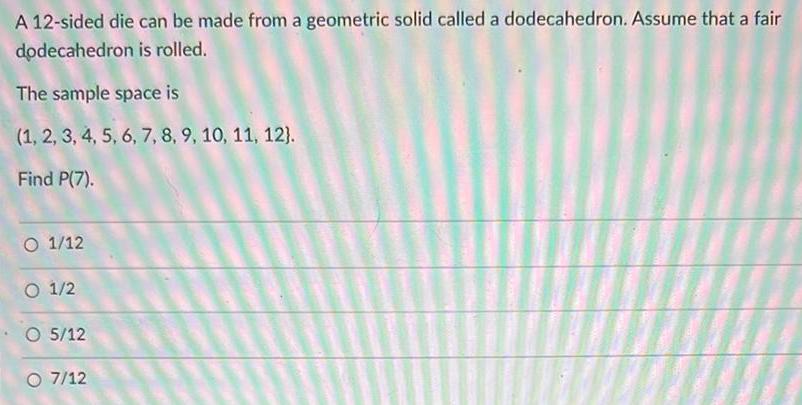
Math
Basic MathA 12-sided die can be made from a geometric solid called a dodecahedron. Assume that a fair dodecahedron is rolled.
The sample space is
(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12).
Find P(7).
1/12
1/2
5/12
7/12

Math
Basic MathWhen we throw a tennis ball into a lake for my dog she knows that if she swims straight for it she'll take longer to get to the ball. Instead, she
runs along the beach for a short distance and then turns and swims for the ball.
Let's say we throw the ball so that it lands 15 meters out into the water and 5 meters to the right of where we're standing. Draw a picture of this scenario.
Finally, let's say that the dog runs at a rate of 2.5 meters per second and swims at a rate of 1 meters per second.
(A) If the dog were to swim directly for the ball how long will it take? Recall that distance is equal to rate multiplied by time.
Direct Swim Time = seconds.
(B) If the dog were to run down the beach and make a 90 degree turn and then swim directly for the ball how long would it take to get to the ball?
Time for longest run and 90 degree turn to swim = seconds.
(C) My dog is smarter than either of the answers in parts (A) or (B). She knows that there is a better solution. Let be the amount of running that she
does down the beach (clearly r is less than 5 and greater than 0). The trip has now been broken into two parts: a running leg of length x meters and a
swimming leg at some angle to the beach. What is the length of the swimming leg as a function of r?
Length of swimming leg =
(D) Write a function T(r) that expresses the total time to get to the ball in terms of how far she runs down the beach.
T(r):

Math
Basic MathAt a point on the ground 80 ft from the base of a tree, the distance to the top of the tree is 11 ft more than 2 times the height of the tree. Find the height of the tree.

Math
Basic MathThe side of a square floor tile is measured to be 16 inches, with a possible error of 1/32 inch. Use differentials to approximate the possible error and the relative error in computing the area of the square.
Step 1
Recall that the formula for the area of a square is A = x2 where x is the side of the square.
We are given that the side of the square floor tile is x = 16 inches and the possible error
Δx = dx = ±1/32
Step 2
To approximate the possible propagated error in computing the area of the square, differentiate A =x² with respect to x.
dA /dx=
dA=
Step 3
Substitute the given values of x and dx into the equation.
dA = 2x dx
Step 4
Assuming that ΔA=dA, we can conclude that the approximate possible propagated error in computing the area of the square is
in².

Math
Basic MathComplete the missing measurement for each diagram. Then create an exponent equation and a square root equation that relate to the diagram
Diagram Exponent Equation Square Root Equation
Area =
Area = 144

Math
Matrices & DeterminantsSolve the 3 by 3 system of equations by using the matrix capabilities of your calculator to solve the system. For full credit you must write the augmented matrix you entered in your calculator, the matrix resulting from using the calculator function, and the solution as an ordered triple.
2x -y + 5z = -2
x+3y-z=6
4x + y + 3z = -2
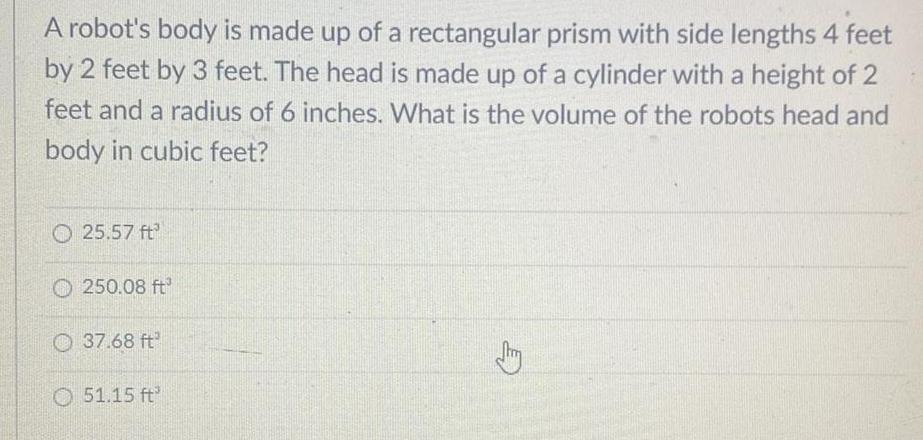
Math
Mathematical ReasoningA robot's body is made up of a rectangular prism with side lengths 4 feet by 2 feet by 3 feet. The head is made up of a cylinder with a height of 2 feet and a radius of 6 inches. What is the volume of the robots head and body in cubic feet?
25.57 ft^3
250.08 ft^3
37.68 ft^3
51.15 ft^3

Math
Application of derivatives4. Choose the appropriate answer for each of these questions:
A. The derivative of a function measures:
a. How steep its graph is
b. What value it takes for a given x
c.Where its graph crosses the x-axis
B. The derivative of a function at a given point is a:
a.An equation
b.A number
c.A function
C. The derivative of a function is closely related to the
a. Set of solutions of an equation
b. Slope of a line
c. Zero of a function
![The pH scale was designed to make it convenient to express hydrogen ion concentrations that are small in aqueous solutions. The definiton of pH is in terms of base 10 logarithms.
pH = -log[H+]
where [H+] is the hydrogen ion concentration.
a. If the hydrogen ion concentration in a solution is 7.60 × 10–5 mol/L, the pH is
b. If the pH of a solution is 3.165, the hydrogen ion concentration is
mol/L.](https://media.kunduz.com/media/sug-question/raw/55108014-1658998185.4569666.jpeg?w=256)
Math
LogarithmsThe pH scale was designed to make it convenient to express hydrogen ion concentrations that are small in aqueous solutions. The definiton of pH is in terms of base 10 logarithms.
pH = -log[H+]
where [H+] is the hydrogen ion concentration.
a. If the hydrogen ion concentration in a solution is 7.60 × 10–5 mol/L, the pH is
b. If the pH of a solution is 3.165, the hydrogen ion concentration is
mol/L.

Math
Basic MathPaul Curcio earns $7.45 per hour for regular time up to 40 hours, time-and-a-half for overtime, and double time for working on holidays. Find his gross pay (in $) if he worked 6 holiday
hours for a total of 58 hours Monday through Saturday.