Math Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
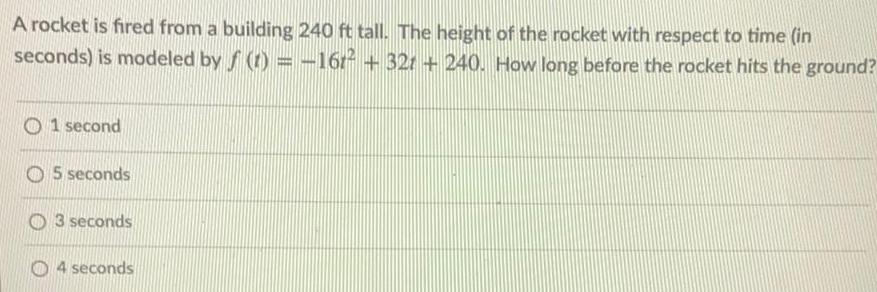
Math
Basic MathA rocket is fired from a building 240 ft tall. The height of the rocket with respect to time (in
seconds) is modeled by f(t) = -16r² +32 +240. How long before the rocket hits the ground?
1 second
5 seconds
3 seconds
4 seconds
Math
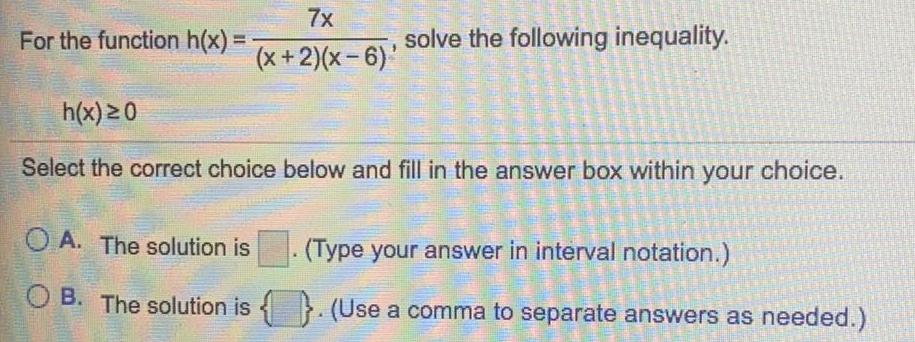
Basic Math7x
(x+2)(x-6).'
For the function h(x) = -
A. The solution is
B. The solution is
solve the following inequality.
h(x) ≥0
Select the correct choice below and fill in the answer box within your choice.
(Type your answer in interval notation.)
. (Use a comma to separate answers as needed.)

Math
Application of derivativesA rocket is fired from a building 240 ft tall. The height of the rocket with respect to time (in
seconds) is modeled by f (t) = -161² +32t + 240. What is the maximum height?
32 ft
240 ft
256 ft
120 ft
Math
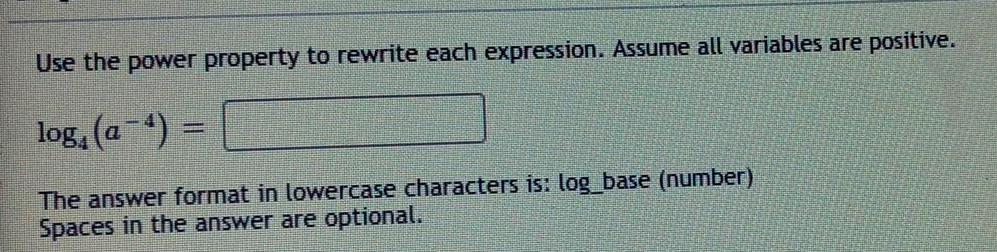
LogarithmsUse the power property to rewrite each expression. Assume all variables are positive.
log, (a-4)=
The answer format in lowercase characters is: log_base (number)
Spaces in the answer are optional.

Math
Basic MathYou decide to build a box with a square base and with a height equal to half the length of a bottom
side. The material you choose for the top of the box costs $6 per square foot. Since everyone will
see the top of the box, that material is more expensive than what you choose for the sides of the
box and the base: $4 per square foot. What equation expresses the cost of your box in terms of the
height of the box? Be sure to show a labeled picture of the box.

Math
Quadratic equationsA frog with bionic legs leaps from a stump with an initial velocity of 64 ft/sec. It is determined that
the height of the frog as a function of time can by modeled by h (t) = -16t² + 64r + 3. What is
the maximum height?
131 ft
99 ft
67 ft
195 ft
Math
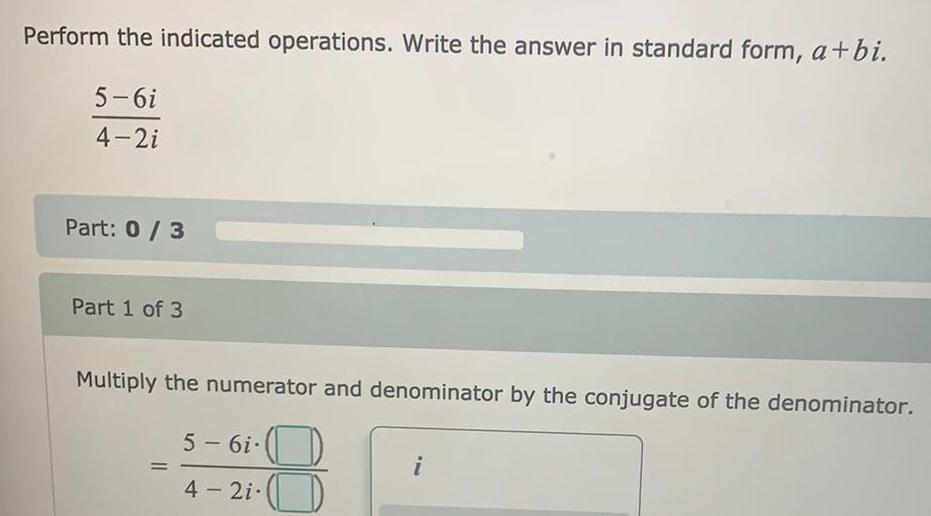
Complex numbersPerform the indicated operations. Write the answer in standard form, a+bi.
5-6i/4-2i
Multiply the numerator and denominator by the conjugate of the denominator.
5-6i-()/
4- 2i.()
i

Math
CircleFind the radius of a circle on which a central angle measuring 2 radians intercepts an arc on the circle with
a length of 35% kilometers.
A. 32.0 km
B. 20.0 km
C. 30.5 km
D. 52.5 km

Math
StatisticsQuarters are currently minted with weights normally distributed and having a standard deviation of 0.062. New equipment is being tested in an attempt to improve
quality by reducing variation. A simple random sample of 20 quarters is obtained from those manufactured with the new equipment, and this sample has a standard
deviation of 0.048. Use a 0.025 significance level to test the claim that quarters manufactured with the new equipment have weights with a standard deviation less
than 0.062. Does the new equipment appear to be effective in reducing the variation of weights?
(a) Write the claim mathematically and identify Ho and Ha-
A. Ho: 20.062; Ha: o<0.062 (Claim)
B. Ho: 20.062 (Claim); Ha: 0 <0.062
C.Ho: o≤ 0.062; Ha: o> 0.062 (Claim)
D. Ho: o≤ 0.062 (Claim); Ha: o> 0.062

Math
Basic MathSamantha invests $555 in an account that earns 14% interest compounded continuously. When will the value of the investment reach $1400? Graph the function on a graphing calculator or a desmos.com and use the graph to make the prediction.

Math
Basic MathWhich figure always has exactly one line of symmetry?
A. circle
B. rectangle
C. trapezoid
D. isosceles right triangle

Math
Basic MathA map using a scale of 1 inch : 5 miles
shows a section of land with an area
of 3.2 square inches. What is the
actual area of the section of land?
_________________square miles
Math
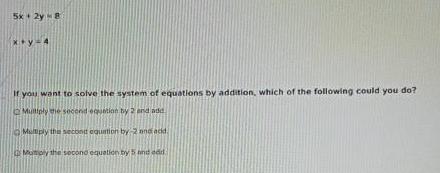
Basic Math5x+2y=8
x+y=4
If you want to solve the system of equations by addition, which of the following could you do?
Multiply the second equation by 2 and add
Multiply the second equation by 2 and acid
Mumply the second equation by 5 and add

Math
Basic MathWhich of the following represents the graph of the inequality?
-20x - 15 ≥ -30x - 45
Open circle and shaded to the left
Open circle and shaded to the right
Closed circle and shaded to the left
Closed circle and shaded to the right
Math
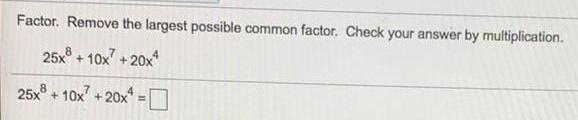
Basic MathFactor. Remove the largest possible common factor. Check your answer by multiplication.
25x8+10x7 +20x4
25x8+10x7 +20x =

Math
FunctionsFor the real-valued functions f(x)=x-2/x+1 and g(x)=4x-5, find the composition fog and specify its domain using interval notation.
(fog)(x)'=
Domain of fog :
Math
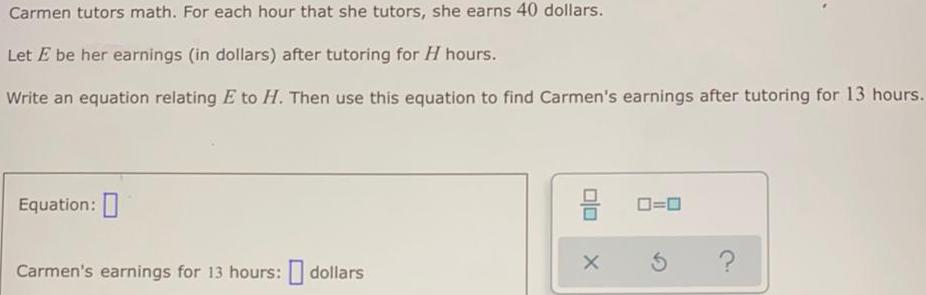
Basic MathCarmen tutors math. For each hour that she tutors, she earns 40 dollars.
Let E be her earnings (in dollars) after tutoring for H hours.
Write an equation relating E to H. Then use this equation to find Carmen's earnings after tutoring for 13 hours.

Math
Straight linesFind an equation of the line parallel to 10x-y=9 and passing through (3,8), Express the equation in standard form.
Which of the following is the equation of a line parallel to 10x-y=9 and passing through (3,8)?
A. x+10y=24
B. 10x-y=24
C. 10x-y=36
D. x+10y=36

Math
Basic MathA ladder leaning against a wall makes an angle of 68 degrees with
level ground. The foot of the ladder is 3 ft away from the wall. How
far up the wall does the ladder reach?

Math
LogarithmsFind the solution of the exponential equation
e²x+1= 32
in terms of logarithms, or correct to four decimal places.
x=

Math
StatisticsThe lengths of a certain species of crocodiles are
normally distributed with a mean of 12.5 ft and a
standard deviation of 2.1 ft.
Find the probability that a randomly selected
crocodile is more than 12 feet long.
0.51
0.53
0.59
0.57

Math
Functions2 Which of the following sets of ordered pairs
represents a relation that is not a function?
A.{(1, 1), (2,3), (6, 11), (10, 19), (50,99)}
B.{(-5, -2), (-4,-1), (1,4), (2,5), (3,4)}
C.{(1,3), (3, 9), (5, 15), (7, 21), (11,33)}
D. {(2,4), (8, 10), (8, 16), (11, 13), (15, 17)}
Math
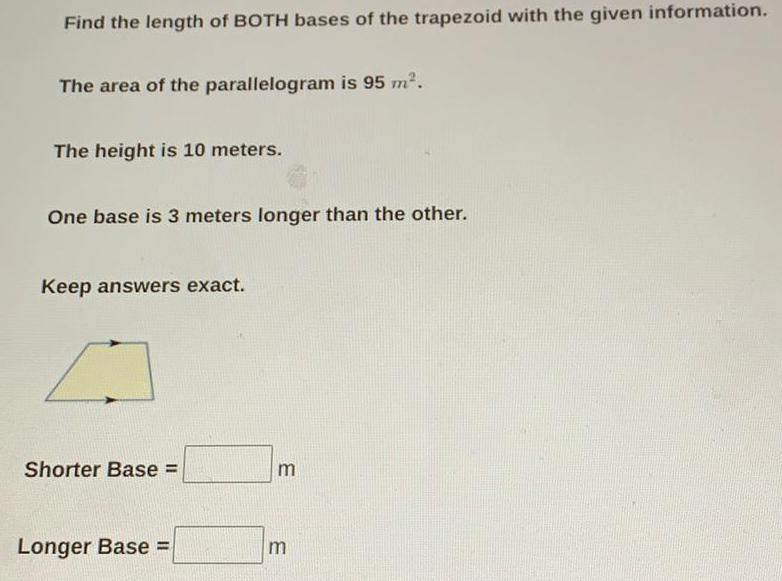
Basic MathFind the length of BOTH bases of the trapezoid with the given information.
The area of the parallelogram is 95 m².
The height is 10 meters.
One base is 3 meters longer than the other.
Shorter Base =
Longer Base=
Math
StatisticsIn a pizza takeout restaurant, the following probability
distribution was obtained.
The random variable x represents the number of
toppings for a large pizza.
Find the probability that more than one toppings
is ordered.
0.40
0.70
0.20
0.30
Math
StatisticsSelect the correct values of the five-number summary for the data set:
15, 17, 23, 21, 19, 20, 14, 25, 15, 24
Minimum: 14
Minimum: 15
Minimum: 13
1st quartile: 23
1st quartile: 14
1st quartile: 15
Median: 20
Median: 19
Median: 19.5
3rd quartile: 23
3rd quartile: 15
3rd quartile: 25
Maximum: 23
Maximum: 25
Maximum: 24

Math
Permutations and CombinationsDirections Answer the questions. All problems are with replacement.
1. How many 3-digit area codes can be made with the digits 0 through 9?
2. If area codes were changed from 3-digit to 4-digit numbers, how many more area codes would be made available?
3. How many 5-character PIN numbers can be made that contain 2 letters followed by 3 digits?
4. In a certain city, all phone numbers begin with one of 5 different 3-digit exchanges. How many different telephone numbers are possible for this area?
5. In the city in problem 4, how many new 3-digit exchanges would need to be added to allow for a total of 120,000 phone numbers?
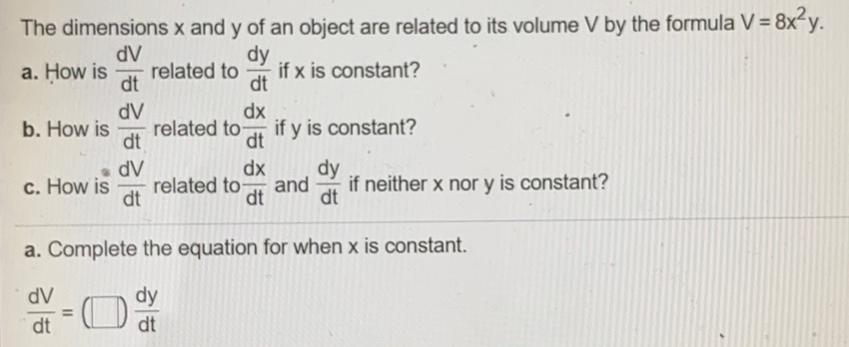
Math
DifferentiationThe dimensions x and y of an object are related to its volume V by the formula V = 8x²y.
a. How is dV/dt related to dy/dt if x is constant?
b. How is dV/dt related to dx/dt if y is constant?
c. How is dV/dt related to dx/dt and dy/dt if neither x nor y is constant?

Math
StatisticsA sample of students is selected and it is found that 25% own a computer.
Choose the correct statement below.
Parameter because the value is a numerical measurement describing a characteristic of a population.
Parameter because the value is a numerical measurement describing a characteristic of a sample.
Statistic because the value is a numerical measurement describing a characteristic of a population.
Statistic because the value is a numerical measurement describing a characteristic of a sample.

Math
Basic MathFind the exact and approximate area of a circle with the given radius r or diameter d. Use pi for π with no spaces in your exact answer. Round approximate answer to the nearest tenth.
d = 16 ft
A =
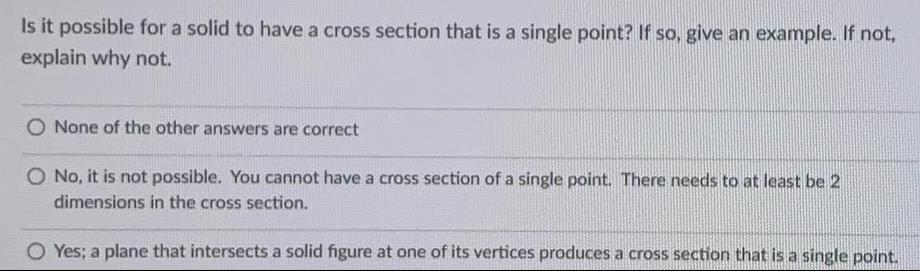
Math
Basic MathIs it possible for a solid to have a cross section that is a single point? If so, give an example. If not, explain why not.
None of the other answers are correct
No, it is not possible. You cannot have a cross section of a single point. There needs to at least be 2 dimensions in the cross section.
Yes; a plane that intersects a solid figure at one of its vertices produces a cross section that is a single point.

Math
Basic MathThe doubling time of a population of flies is 5 hours. By what factor does the population increase in 31 hours? By what factor does the population increase in 1 week?
By what factor does the population increase in 31 hours?
Math
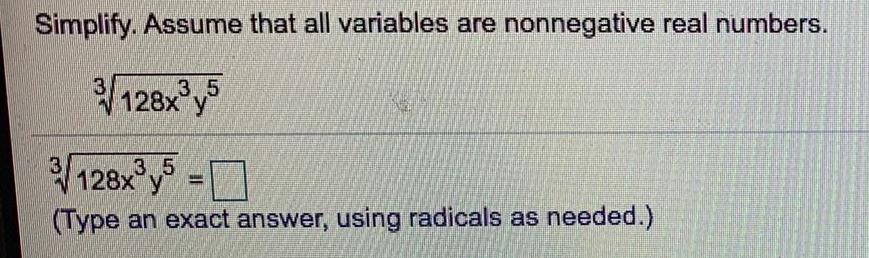
Basic MathSimplify. Assume that all variables are nonnegative real numbers.
3√128x³y^5
3√128x³y^5 =
(Type an exact answer, using radicals as needed.)

Math
Basic Mathbicycle riders start a race at the same time. The functions f(x) and g(x) give the distance in miles that each rider has traveled after x hours of riding. What does f(2)- g(2) = 5 mean in this context?
A The riders are 2 miles apart 5 hours after the race starts.
B The riders are 5 miles apart 2 hours after the race starts.
C Both riders travel 2 miles in the first 5 hours of the race.
D Both riders travel 5 miles in the first 2 hours of the race.

Math
VectorsLet V be a vector space with dimension n. Consider the following statements.
(i) Every independent set in V is a basis for V
(ii) Every set in V that spans V must be independent
(iii) Every set in V with less than n vectors must be independent.
Which of the above statements is always true?
(a) (ii) and (iii) only (b) (iii) only (c) (ii) only (d) none of them
(e) (i) only

Math
Basic MathA child flies a kite at a height of 50 ft, the wind carrying the kite horizontally away from the child at a rate of 26 ft/sec. How fast must the child let out the string when the kite is 130 ft away from the child?
The child must let out the string at a rate of___ft/sec when the kite is 130 ft away from the child.
(Simplify your answer.)

Math
StatisticsSuppose you arrive into a building and are about to take an elevator to the your floor.
Once you call the elevator, it will take between 2 and 40 seconds to arrive to you.
We will assume that the elevator arrives uniformly between 2 and 40 seconds after you press the button. Find µ.
22
21
11
19

Math
Application of derivativesGiven the function f(x) =1/x^2
a. Find the average rate of change between x=__and x= (choose two consecutive negative
Integers)
b. Find the instantaneous rate of change at x=_______ (choose a negative integer value for x)
c. Find the equation of the tangent line at your chosen point
d. Prove that f(x) is continuous at your chosen point
Math
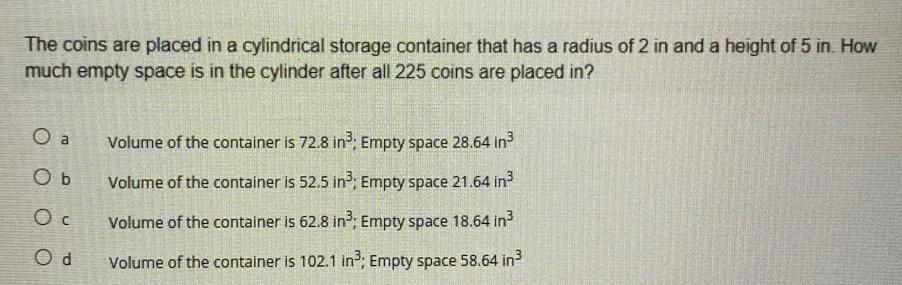
Basic MathThe coins are placed in a cylindrical storage container that has a radius of 2 in and a height of 5 in. How much empty space is in the cylinder after all 225 coins are placed in?
a. Volume of the container is 72.8 in³; Empty space 28.64 in³
b. Volume of the container is 52.5 in³; Empty space 21.64 in³
c. Volume of the container is 62.8 in³; Empty space 18.64 in³
d. Volume of the container is 102.1 in³; Empty space 58.64 in³
Math
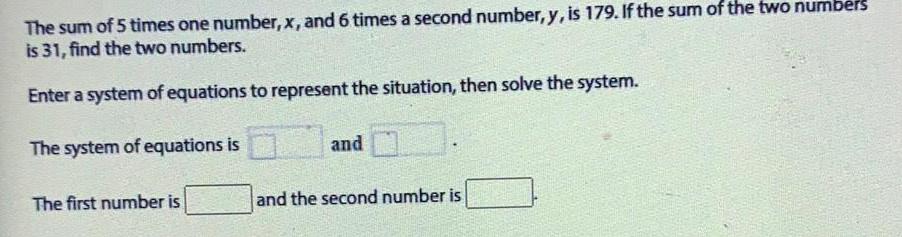
Basic MathThe sum of 5 times one number, x, and 6 times a second number, y, is 179. If the sum of the two numbers is 31, find the two numbers.
Enter a system of equations to represent the situation, then solve the system.
The system of equations is
The first number is__and the second number is___

Math
Basic MathFind the area and perimeter of a rectangle with sides 5 and 7.9 mi
None of the other answers are correct
area is 12√6 mi²
perimeter is 17.9 mi
area is 58.5 mi²
perimeter is 35 mi
area is 39.5 mi²
perimeter is 25.8 mi
area is 36.24 mi²
permeter is 12.9 mi

Math
Quadratic equationsConsider the Quadratic function f(x) = x² – 3x - 18.
Its vertex is
Its largest x-intercept is x =
Its y-intercept is y =

Math
Basic MathThe following list gives the home run totals for Barry Bonds from 1986 through 2007 (his total career).
16 25 24 19 33 25 34 46 37 34 49 73 46 45 45 5 26 28
Construct a stem-and-leaf plot for the data. Enter the leaves in ascending order, without spaces betweenb them. If a stem has no corresponding leaves, leave that space blank.

Math
DifferentiationGiven f(x)= x³-12x+5, find all local maxima and local minima.
B) local max:21, local min: - 11
A) local max: - 11, local min: - 21
D) local max: 11, local min:21
C) local max: -21, local min:11
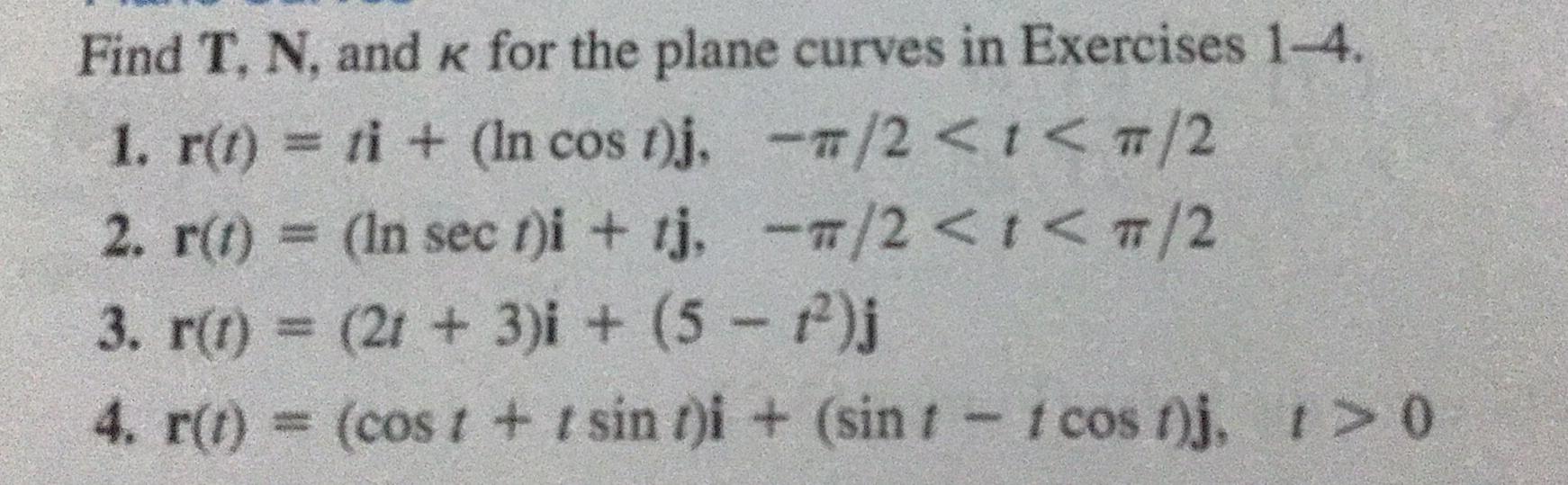
Math
DifferentiationFind T, N, and K for the plane curves in Exercises 1-4.
1. r(t) = ti + (In cos t)j,-π/2 < t< π/2
2. r(t) = (In sect)i + tj,-π/2 < t< π/2
3. r(t) = (2t+ 3)i + (5 −t²)j
4. r(t) = (cost + t sin t)i + (sin 1 - 1 cost)j, t> 0

Math
Basic MathAdam is also confused. He wonders why, if you take a rectangle and multiply the length of each side by 1.5. the area of the new rectangle isn't 1.5 times as big as the area of the old rectangle. How would you explain this to him?

Math
Quadratic equationsThe polynomial of degree 4, P(x) has leading coefficient 1, has a zero of multiplicity 2 at x = 4, a zero of multiplicity 1 at a x=0, and a zero of multiplicity 1 at x = - 4
Find a possible formula for P(x).
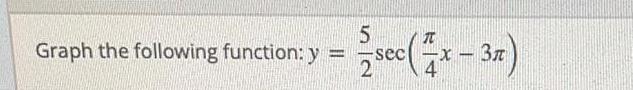
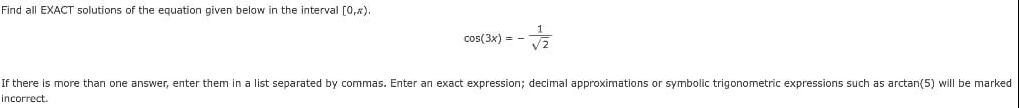
Math
Trigonometric equationsFind all EXACT solutions of the equation given below in the interval [0,π).
cos(3x)=-1/√2
If there is more than one answer, enter them in a list separated by commas. Enter an exact expression; decimal approximations or symbolic trigonometric expressions such as arctan (5) will be marked incorrect.
Math
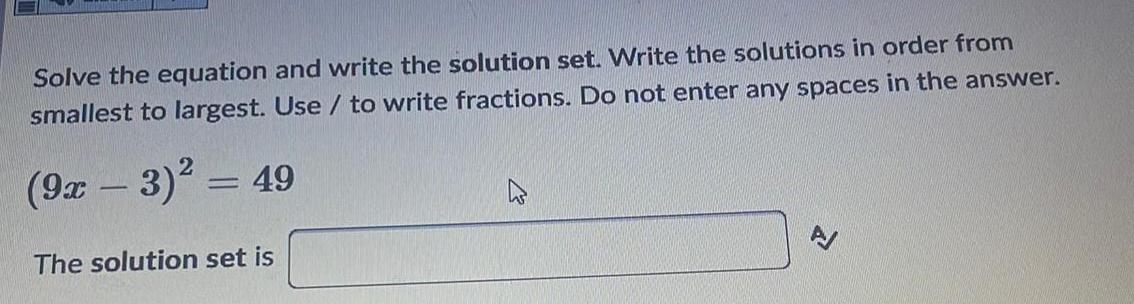
Sequences & SeriesSolve the equation and write the solution set. Write the solutions in order from
smallest to largest. Use / to write fractions. Do not enter any spaces in the answer.
(9x - 3)²=49
The solution set is
Math
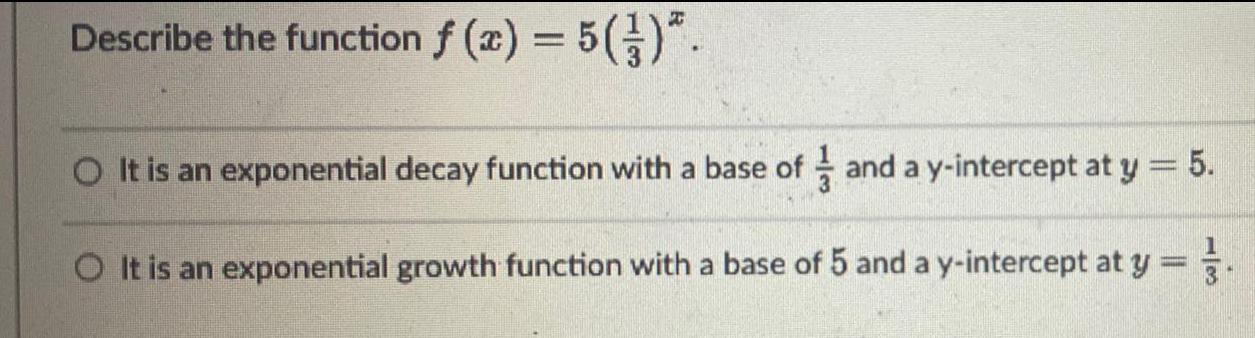
FunctionsDescribe the function f(x) = 5(1/3)^x.
O It is an exponential decay function with a base of 1/3 and a y-intercept at y=5.
O It is an exponential growth function with a base of 5 and a y-intercept at y=1/3