Math Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
Math
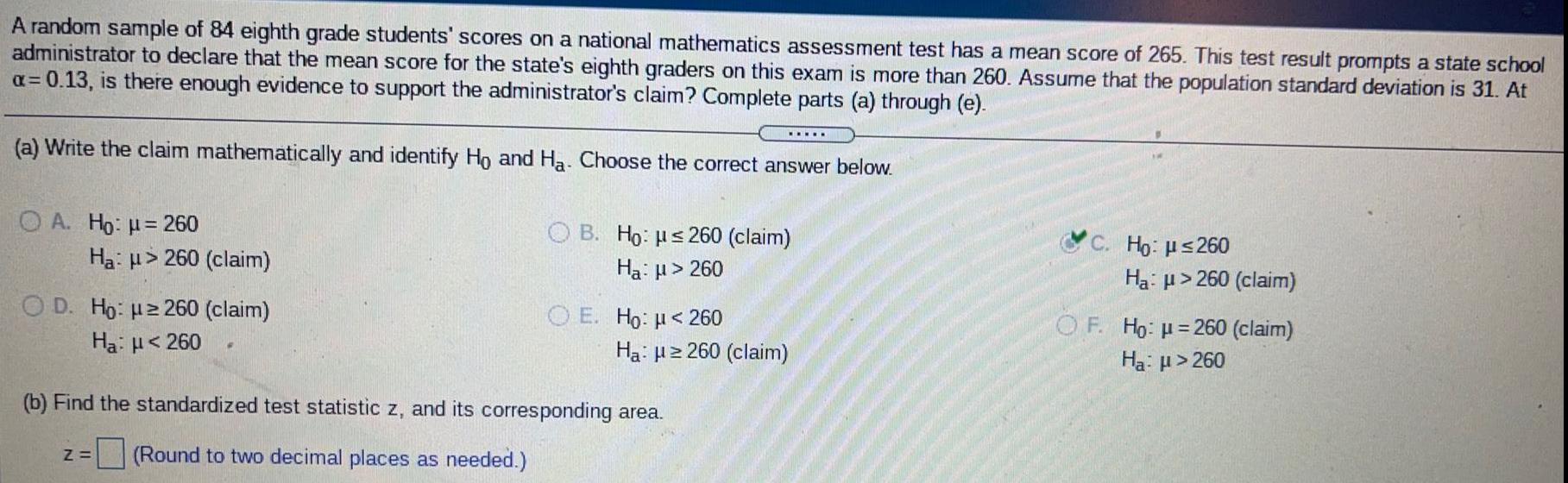
StatisticsA random sample of 84 eighth grade students' scores on a national mathematics assessment test has a mean score of 265. This test result prompts a state school administrator to declare that the mean score for the state's eighth graders on this exam is more than 260. Assume that the population standard deviation is 31. At a=0.13, is there enough evidence to support the administrator's claim? Complete parts (a) through (e).
(a) Write the claim mathematically and identify Ho and Ha. Choose the correct answer below.
(b) Find the standardized test statistic z, and its corresponding area.
Math
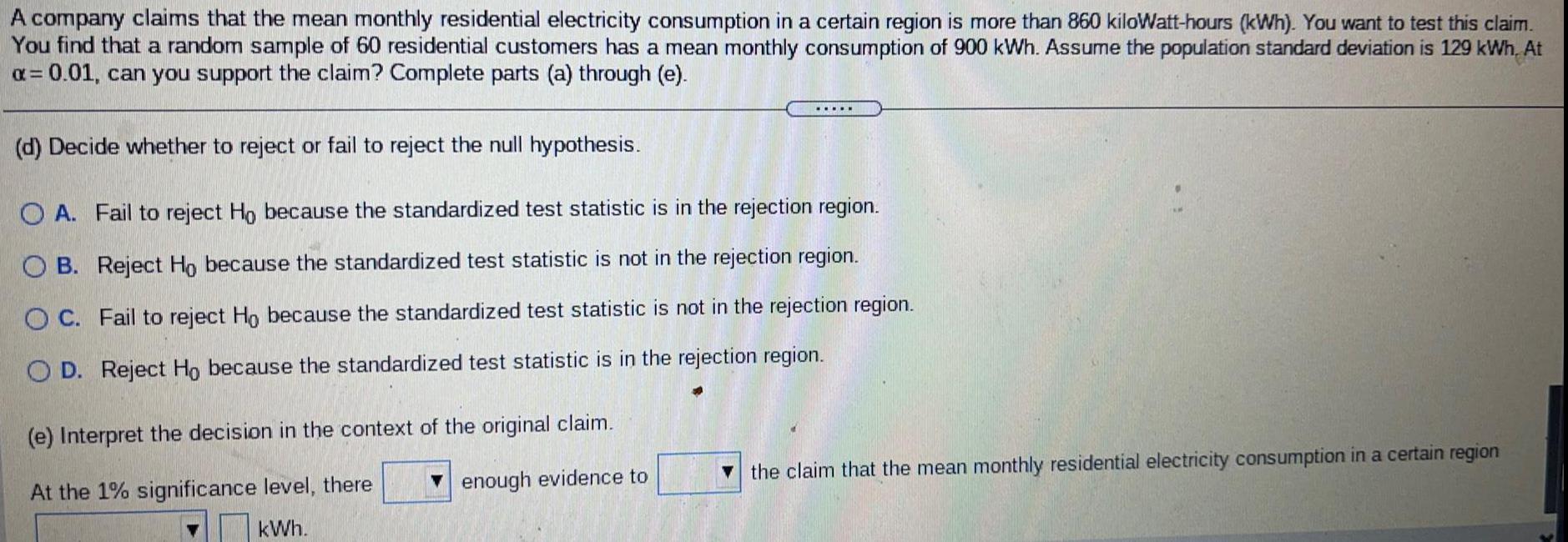
Basic MathA company claims that the mean monthly residential electricity consumption in a certain region is more than 860 kilowatt-hours (kWh). You want to test this claim. You find that a random sample of 60 residential customers has a mean monthly consumption of 900 kWh. Assume the population standard deviation is 129 kWh. At α = 0.01, can you support the claim? Complete parts (a) through (e)
(d) Decide whether to reject or fail to reject the null hypothesis.
A. Fail to reject Ho because the standardized test statistic is in the rejection region.
B. Reject Ho because the standardized test statistic is not in the rejection region.
C. Fail to reject Ho because the standardized test statistic is not in the rejection region.
D. Reject Ho because the standardized test statistic is in the rejection region.
(e) Interpret the decision in the context of the original claim.
At the1% significance level, there enough evidence to the claim that the mean monthly residential electricity consumption in a certain kWh.

Math
Basic MathSolve the following inequality.
⎮9x + 10⎮≤9
Choose the correct answer below and fill in the values. Round to three decimal places if needed.
≤x≤
x≤ OR x ≥
All real numbers.
There is no solution.


Math
Basic MathMomentum is mass times velocity. Suppose the momentum of a 275 g object is kg m measured to be 219 kg*m/s. Calculate the object's velocity. Be sure your answer has a unit symbol and the correct number of significant digits.
Math
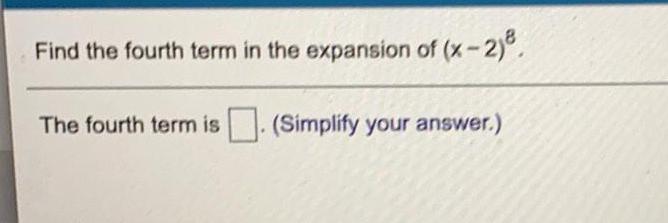
Basic MathFind the fourth term in the expansion of (x-2)^8.
(Simplify your answer.)
The fourth term is

Math
Sequences & SeriesUse the formula for the general term (the nth term) of a geometric sequence to find the indicated term of the following sequence with the given first term, a₁, and common ratio, r.
Find a6 when a₁ = 8 and r=3.

Math
Sequences & SeriesWrite the first six terms of the following arithmetic sequence.
an= a(n-1)-0.3, a₁ = 0.9
Math
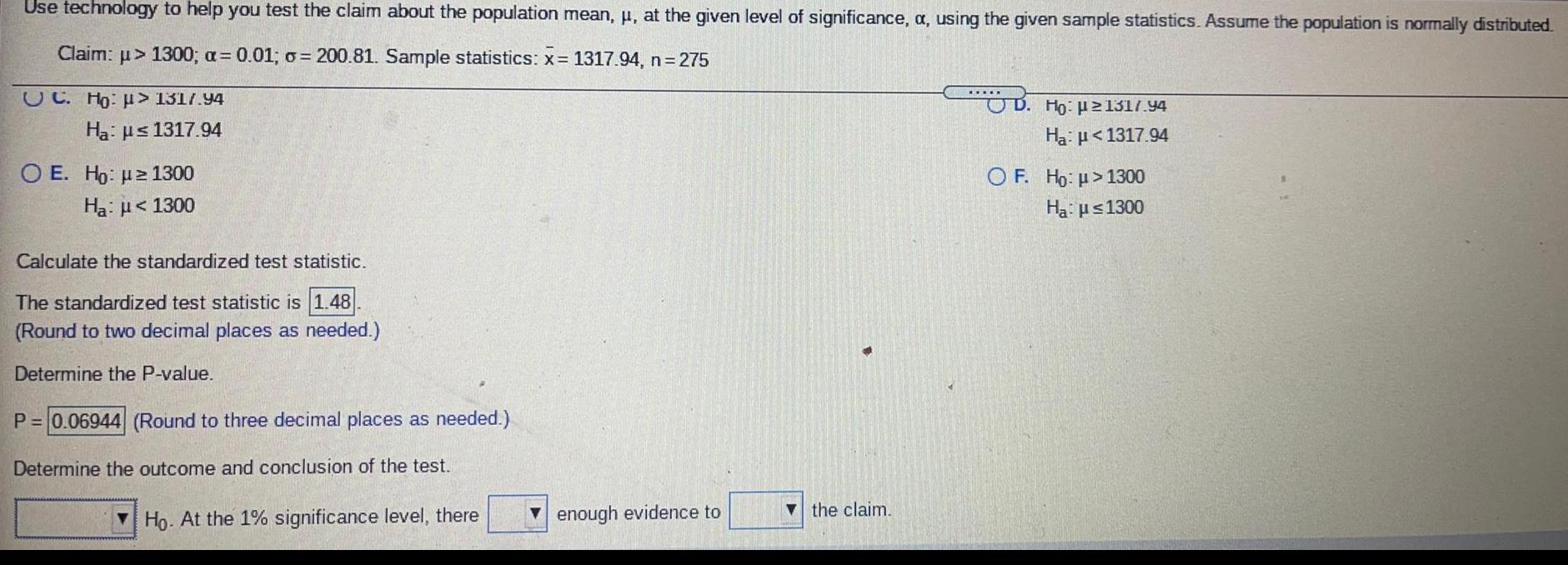
Basic MathUse technology to help you test the claim about the population mean, μ, at the given level of significance, a, using the given sample statistics. Assume the population is normally distributed.
Claim: μ> 1300; α= 0.01; σ = 200.81. Sample statistics: x= 1317.94, n=275
Calculate the standardized test statistic.
The standardized test statistic is
(Round to two decimal places as needed.)
Determine the P-value.
(Round to three decimal places as needed.)
Determine the outcome and conclusion of the test.
Ho. At the 1% significance level, thereenough evidence to the claim.

Math
Basic MathConsider a function that describes how a particular car's gas mileage depends on its speed. What would an appropriate domain for this function be? Choose the correct answer below.
A. An appropriate domain would be 0 to 50 miles per gallon because the gas mileage is the independent variable of the function, and the domain consists of all reasonable values of the independent variable.
B. An appropriate domain would be times from 0 to 10 minutes because the time is the dependent variable of the function, and the domain consists of all reasonable values of the dependent variable. C. An appropriate domain would be 0 to 100 miles per hour because the speed is the independent variable of the function, and the domain consists of all reasonable values of the independent variable.
D. An appropriate domain would be 0 to 100 miles per hour because the speed is the dependent variable of the function, and the domain consists of all reasonable values of the dependent variable. E. An appropriate domain would be 0 to 50 miles per gallon because the gas mileage is the dependent variable of the function, and the domain consists of all reasonable values of the dependent variable.

Math
Basic MathDescribe the basic differences between linear growth and exponential growth. Choose the correct answer below.
A. Linear growth occurs when a quantity grows by the same absolute amount in each unit of time, and exponential growth occurs when a quantity grows by the same relative amount, that is, by the same percentage, in each unit of time.
B. Linear growth occurs when a quantity grows by random amounts in each unit of time, and exponential growth occurs when a quantity grows by different, but proportional amounts, in each unit of time.
C. Linear growth occurs when a quantity grows by different, but proportional amounts, in each unit of time, and exponential growth occurs when a quantity grows by random amounts in each unit of time.
D. Linear growth occurs when a quantity grows by the same relative amount, that is, by the same percentage, in each unit of time, and exponential growth occurs when a quantity grows by the same absolute amount in each unit of time.

Math
Basic MathChoose the best answer to the following question. Explain your reasoning with one or more complete sentences.
Which of the following is necessary if you want to make monthly contributions to savings? Choose the correct answer below.
A. You must be spending less than 20% of your income on food and clothing. Spending less on food and clothing will increase cash flow exponentially every month.
B. You must not owe money on any loans. This means that you are not spending any money toward interest. If you are not paying interest, you have money to save.
C. You must be spending less than 20% of your income on food and clothing. As long as you don't increase your spending in any other category, you should be able to find money to save.
D. You must have a positive monthly cash flow. If you have a positive monthly cash flow, you can pay more towards your credit card balance. Once the balance is zero, you should start putting that extra money in the bank.
E. You must have a positive monthly cash flow. If your cash flow is positive, you will have money left over at the end of each month, which you can use for savings.
F. You must not owe money on any loans. If you do not owe any money on loans, you will have many Ieft overe at the end of each month, which you can use for savings.

Math
FunctionsGraph y = 5(2)^(x-1)-8
by clicking the icon below and then there are two main steps:
1st, click where the horizontal asympotote will be.
2nd, click two points on the graph to create the graph itself.

Math
Sequences & SeriesWrite the first six terms of the arithmetic sequence shown below.
an = a(n-1) +9, a₁ = -7

Math
Basic MathSummarize how average spending patterns change with age. How can comparing your own spending to average spending patterns help you evaluate your budget? Summarize how average spending patterns change with age. Choose the correct answer below.
A. As people get older, they tend to spend more on food and entertainment than younger people. They also tend to spend less on housing than younger people.
B. As people get older, they tend to spend more on health care and donations to charity than younger people. They also tend to spend less on personal insurance, pensions, clothing, and services than younger people.
C. As people get older, they tend to spend more on transportation and housing than younger people. They also tend to spend less on health care.
D. As people get older, they tend to spend more on clothing and services than younger people. They also tend to spend less on food and housing than younger people.
How can comparing your own spending to average spending patterns help you evaluate your budget?
A. It can be useful to check how you compare to the rest of the population. If you notice that most people donate less than you do to charity, it might be time to stop giving away so much.
B. If you are spending a higher percentage of your money on an item in your budget than the average person, you might want to consider finding lower-cost options or adjusting your budget.
C. It is a good idea to check how you compare to the rest of the population. If you find that people spend more than you on gas, you can give others advice on how to spend less.
D. If you are spending a higher percentage of your money on entertainment than the average person, you might be able to find cheaper ticket prices if you ask around.

Math
Basic MathBriefly summarize the story of the bacteria in the bottle. Explain the answers to the four questions in the text.
Briefly summarize the story of the bacteria in a bottle. Choose the correct answer below.
A. The number of bacteria in a bottle increases by 1 every minute. There is one bacteria at 11:00 and the bottle is full at 12:00, so the colony is doomed.
B. The number of bacteria in a bottle triples every minute. There is one bacteria at 11:00 and the bottle is full at 12:00, so the colony is doomed.
C. The number of bacteria in a bottle doubles every minute. There is one bacteria at 11:00 and the bottle is full at 12:00, so the colony is doomed.
D. The number of bacteria in a bottle increases by 2 every minute. There is one bacteria at 11:00 and the bottle is full at 12:00, so the colony is doomed.

Math
Basic MathWhat does the fact that the Dow Jones Industrial Average (DJIA) changes from day to day say?
Choose the correct answer below.
A. Time is a function of the DJIA because the DJIA, the dependent variable, changes with respect to time, the independent variable.
B. The DJIA and time are both functions because the DJIA, the dependent variable changes with respect to time, the independent variable.
C. The DJIA is a function of time because time, the dependent variable changes with respect to the DJIA, the independent variable.
D. The DJIA is a function of time because the DJIA, the dependent variable, changes with respect to time, the independent variable.
E. The DJIA and time are both functions because both the DJIA and time describe how one variable depends on another.
F. Time is a function of the DJIA because time, the dependent variable, changes with respect to the DJIA, the independent variable.

Math
Basic MathAll of the following are functions of time. Which one would you expect to be closest to being a periodic function of time? Choose the correct answer below.
A. The price of gasoline is closest to a periodic function of time because the price of gasoline repeats over and over with time.
B. The volume of traffic on an urban freeway is closest to a periodic function of time because the volume of traffic becomes larger with time.
C. The price of gasoline is closest to a periodic function of time because the price of gasoline gets larger over time.
D. The population of a given country is closest to a periodic function of time because the population decays exponentially over time.
E. The population of a given country is closest to a periodic function of time because the population grows exponentially over time.
F. The volume of traffic on an urban freeway is closest to a periodic function of time because the volume of traffic repeats over and over with time.
Math
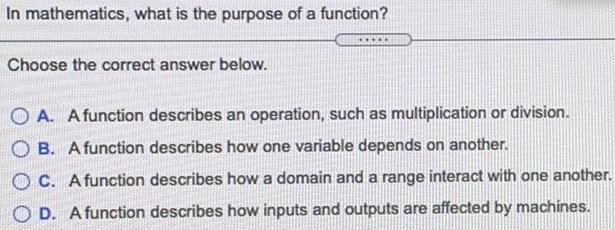
Basic MathIn mathematics, what is the purpose of a function?
Choose the correct answer below.
A. A function describes an operation, such as multiplication or division.
B. A function describes how one variable depends on another.
C. A function describes how a domain and a range interact with one another.
D. A function describes how inputs and outputs are affected by machines.

Math
Basic MathWrite and solve an equation for the following problem:
How many liters of pure acid should be added to 10 liters of 40% concentrate to raise the concentration to 55%?

Math
Basic MathThe general population has been scared of HIV/AIDS for more than twenty years. The Center for Disease Control (CDC) warns of other infectious diseases that the public should be fearful of as well. You don't have to be a germophobe to be leery of the H7N9 flu which is one of the newer forms of bird flu. Research has identified some alarming details which note that the infectious disease can be passed from animals to humans without making the infected animals sick. As such, identifying and containing infected animals is difficult at best. At the present, there is no vaccine for the H7N9 flu. Most human cases to date have been found from exposure to infected poultry. The one item that has prevented the H7N9 from turning into a global pandemic is the saving grace that the flu is not passed from person to person. Click the icon to view the graph. ..... From the information given in the graph above, determine which decade saw the largest decrease in volume of reported flues from the past 100 years of reported cases.
A. 1910-1920
B. 1980-1990
C. 1990-2010
D. 1920-1930

Math
Basic MathWhat is a mathematical model? Explain this statement: A model's predictions can only be as good as the data and the assumptions from which the model is built.
Choose the correct answer below.
*****
A. Mathematical models are based on relationships between quantities that remain constant and are described by mathematical tools called functions.
B. Mathematical models are based on relationships between quantities that change and are described by very complicated functions that can only be understood using supercomputers.
C. Mathematical models are based on relatickships between quantities that remain constant and can only be described by a graph.
D. Mathematical models are based on relationships between quantities that change and are described by mathematical tools called functions.

Math
Basic MathAt 11:00 you place a single bacterium in a bottle, and at 11:01 it divides into 2 bacteria, which at 11:02 divide into 4 bacteria, and so on. If the bacteria occupy a volume of 1 cubic meter at 12:02 and conti their exponential growth, when will they occupy a volume of 2 cubic meters?
The bacteria will occupy a volume of 2 cubic meters at

Math
Basic MathMathematical modeling abounds with algebraic applications such as quadratic graphs representing maximum and minimum cost equations. The mathematical principles involved are explored in typical high school algebra classes. In the past 30 years, computer modeling has catapulted our ability to mathematically model complex items in our world such as weather prediction, unemployment, and how buildings behave under stress such as those imposed by extreme weather. Computer mathematical modeling not only opens the door for evaluating these more complex models that are tedious to evaluate by hand but also saves time and financial resources. Car manufacturers no longer need to build prototypes of proposed car design changes to perform tests such as wind resistance, roll-over, and initial crash tests. The use of computer modeling has shortened the time from seeing a car move from a drawing to the assembly line.
Computer modeling can be found in which of the following arenas? Choose the correct answer below.
A. Unemployment models
B. Earthquake strength of skyscrapers
C. Weather
D. All of the above

Math
Basic MathThe impact of the recession of 2009 was widely felt across America. One response that continues well into 2013 is an effort to build local economies by thinking and spending locally. This decry has been heard in both large cities and small towns and has colored the shopping habits of a growing number of individuals even as some relief from the recession is felt. The results can be noteworthy. A national newspaper reported that if residents of New Orleans were to reallocate 10% of their spending to locally owned businesses and services, more than $200 million would be remain in the local economy. To meaningfully build local economies for the long haul, consumers as well as business owners must take the next step and produce more of what the community has imported over the years. Source: Christian Science Monitor, volume 101
Which of the following would not be an example of thinking and spending locally?
A. Holiday shopping at a craft fair featuring community vendors.
B. Contracting with a nationally known music group to provide entertainment for a town's centennial celebration.
C. Selling jams made from area berry farms to surrounding communities.
D. Using locally grown ingredients in country restaurants.

Math
Basic MathMr. Montoya instructs the students in his math class to draw a rectangle with a certain area. Catlynn draws a rectangle with a length of 18 centimeters and a width of 6 centimeters.
This proportional situation represents variation.
The constant of variation, k, is equal to
If Sergio draws a rectangle with a length of 27 centimeters, the width of the rectangle must be centimeters.

Math
Basic MathThe variable fvaries inversely as the square root of g. When f= 4, g = 4. Jordan's work finding the value of fwhen g = 100 is shown:
f√g = k
4(4) = k
16 = k
f√g = 16
f√100 = 16
10f=16
f= 1.6
What is the first error, if any, in Jordan's work?
A.He used an equation that models direct variation instead of inverse variation.
B.He substituted incorrectly when calculating the constant of variation.
C.He took the square root of the wrong variable.
D.He did not make any errors.
Math
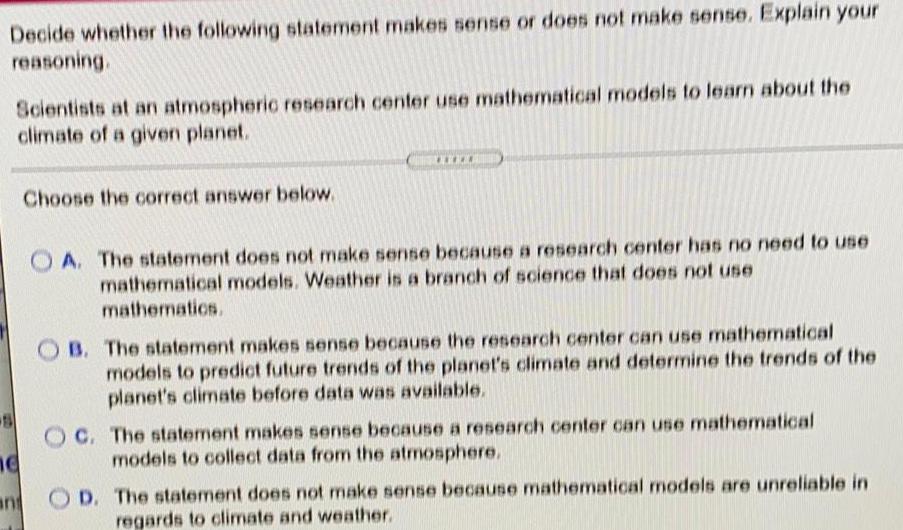
Basic MathDecide whether the following statement makes sense or does not make sense. Explain your reasoning.
Scientists at an atmospheric research center use mathematical models to learn about the climate of a given planet. ne Choose the correct answer below.
A. The statement does not make sense because a research center has no need to use mathematical models. Weather is a branch of science that does not use mathematics,
B. The statement makes sense because the research center can use mathematical models to predict future trends of the planet's climate and determine the trends of the planet's climate before data was available.
C. The statement makes sense because a research center can use mathematical models to collect data from the atmosphere.
D. The statement does not make sense because mathematical models are unreliable in regards to climate and weather.
Math
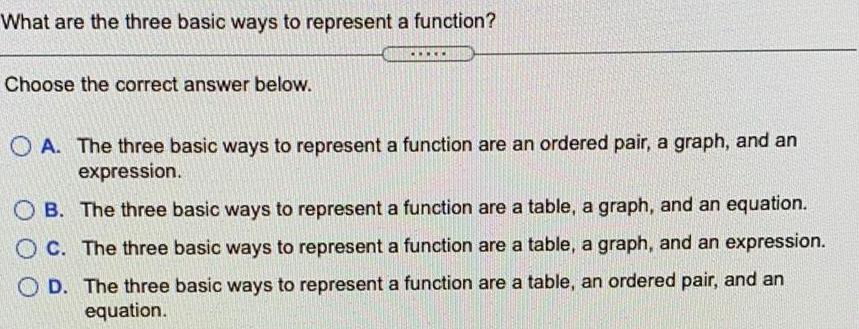
Basic MathWhat are the three basic ways to represent a function?
Choose the correct answer below.
A. The three basic ways to represent a function are an ordered pair, a graph, and an expression.
B. The three basic ways to represent a function are a table, a graph, and an equation.
C. The three basic ways to represent a function are a table, a graph, and an expression.
D. The three basic ways to represent a function are a table, an ordered pair, and an equation.

Math
Basic Math65% of a Carbon-14 sample has decayed and 56 grams remain.
What was the mass of the original sample? Round your answer to the nearest whole number.


Math
Basic MathA car company says that the mean gas mileage for its luxury sedan is at least 23 miles per gallon (mpg). You believe the claim is incorrect and find that a random sample of 6 cars has a mean gas mileage of 20 mpg and a standard deviation of 3 mpg. At a= 0.05, test the company's claim. Assume the population is normally distributed.
Which sampling distribution should be used and why?
A. Use a normal sampling distribution because n > 30.
B. Use a normal sampling distribution because the population is normal, and a is unknown.
C. Use a normal sampling distribution because the population is normal, and o is known.
D. Use a t-sampling distribution because the population is normal, and a is unknown.
E. Use a t-sampling distribution because the population is normal, and o is known.
F. Use a t-sampling distribution because n< 30.
State the appropriate hypotheses to test.
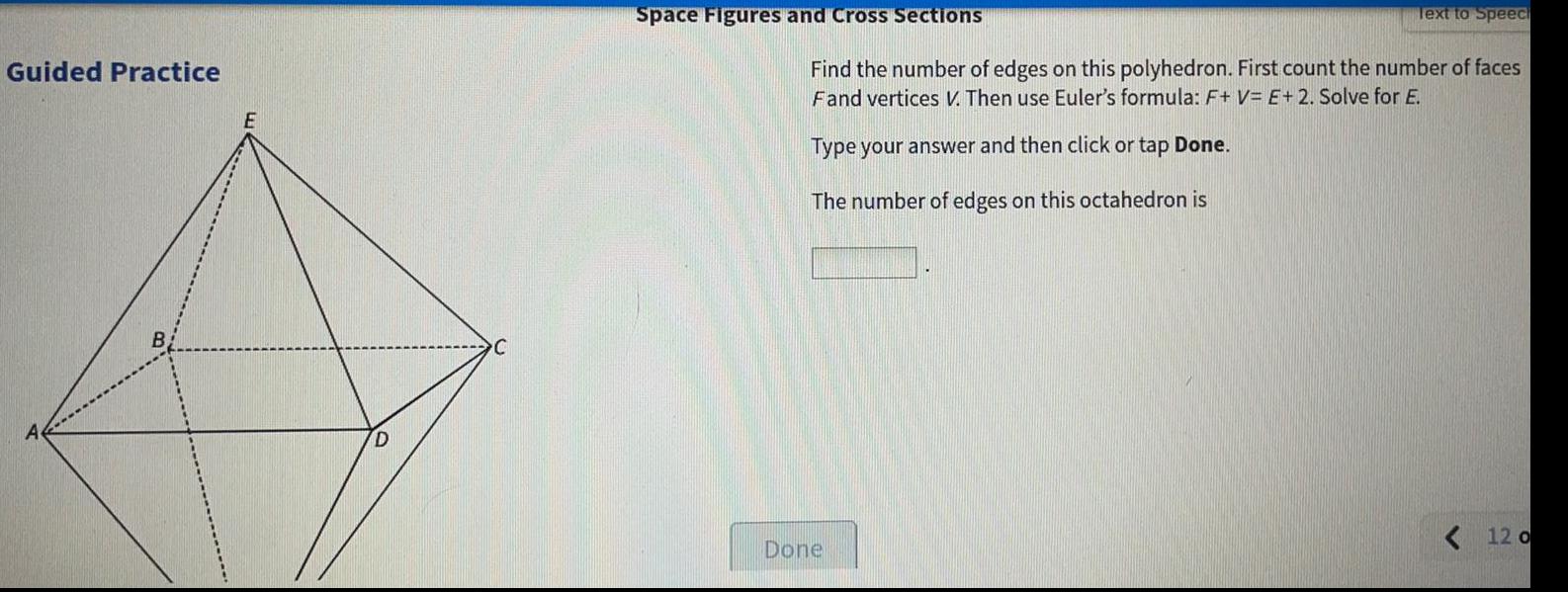
Math
Basic MathFind the number of edges on this polyhedron. First count the number of faces Fand vertices V. Then use Euler's formula: F+ V= E + 2. Solve for E. Type your answer and then click or tap Done. The number of edges on this octahedron is

Math
Basic MathA chemist has three different acid solutions. The first acid solution contains 20% acid, the second contains 30% and the third contains 50 %. They want to use all three solutions to obtain a mixture of 80 liters containing 40 % acid, using 3 times as much of the 50 % solution as the 30% solution. How many liters of each solution should be used?

Math
Basic MathMatch the one-to-one functions with their inverse functions.
Inverse Function
f^-1(x) = 5x
f^-1(x) = x^3/2
f^-1(x) = x+10
f^-1(x) = 3(x+17)/2

Math
Basic MathWhich statement describes the end behavior of the function?
f(x)=x^2-100/x^2-3x-4
A. The function approaches 0 as x approaches -∞ and ∞
B. The function approaches 1 as x approaches -∞ and ∞
C. The function approaches 5 as x approaches -∞ and ∞
D. The function approaches 25 as x approaches -∞ and ∞

Math
Basic MathWhich variable is plotted on the vertical axis when a graph of the function z = f(w) is created?
Choose the correct answer below.
A. f is plotted on the vertical axis because the horizontal axis is used for the dependent variable and the vertical axis is used for the independent variable.
B. f is plotted on the vertical axis because the horizontal axis is used for the independent variable and the vertical axis is used for the dependent variable.
C. z is plotted on the vertical axis because the horizontal axis is used for the dependent variable and the vertical axis is used for the independent variable.
D. w is plotted on the vertical axis because the horizontal axis is used for the independent variable and the vertical axis is used for the dependent variable.
E. z is plotted on the vertical axis because the horizontal axis is used for the independent variable and the vertical axis is used for the dependent variable.
F. w is plotted on the vertical axis because the horizontal axis is used for the dependent
variable and the vertical axis is used for the independent variable.

Math
Basic MathThe domain of function f is (-∞, 6) U (6, ∞). The value of the function approaches -∞ as x approaches -∞, and the value of the function approaches ∞ as x approaches ∞. Which function could be function f?
A f(x)=x²-36/x-6
B. f(x)=x-6/x²-36
C. f(x)=x+6/x-6
D. (x)=x-6/x+6

Math
Straight linesIf the point (1,4) is on the graph of an equation, which statement must be true?
A. There are solutions to the equation for the values x = 1 and x = 4.
B. The values x = 4 and y = 1 make the equation true.
C. The values x = 1 and y= 4 are the only values that make the
equation true.
D. The values x = 1 and y = 4 make the equation true.

Math
FunctionsThe domain of function r is (-∞, -7) U (-7, 5) U (5, ∞), and the value of the function approaches 1 as x approaches -∞ and ∞. Which function could be function r?
A. f(x) = x-5/x+7
B. f(x) = 2x-35/x^2+2x-35
C. f(x) = x^2-3x-15/x^2+2x-35
D. f(x) = x^2+2x-35/x^2-3x-15
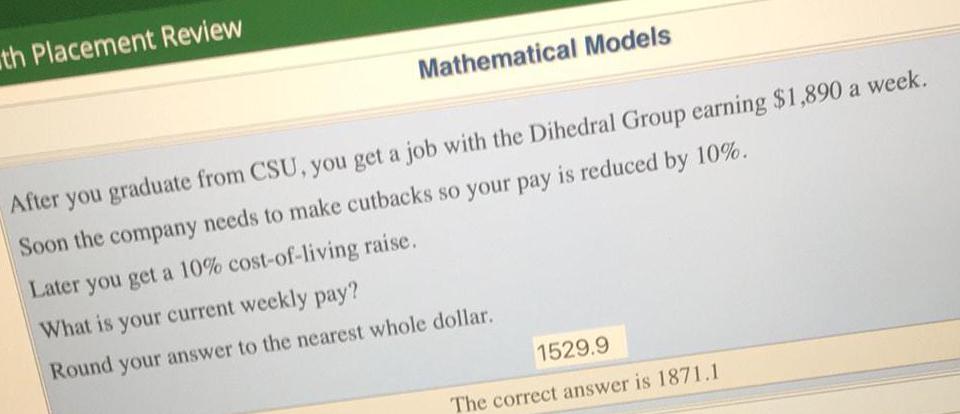
Math
Basic MathAfter you graduate from CSU, you get a job with the Dihedral Group earning $1,890 a week.
Soon the company needs to make cutbacks so your pay is reduced by 10%.
Later you get a 10% cost-of-living raise.
What is your current weekly pay?
Round your answer to the nearest whole dollar.

Math
Basic MathChange the following decimal to fraction form (or mixed number form) and reduce, if possible.
76.09


Math
Basic MathIf a minivan travels 306 miles on 25 gallons of gas, how many miles per gallon does it average (to the nearest tenth)?


Math
Basic MathThe use of linear and exponential models to predict growth patterns in science and medicine is not new. However, scientists and researchers continue to find new applications of the models to explain and predict growth patterns. Seiki Hamada and Makoto Takamiya of Japan have studied the growth patterns of a specific heart aneurism to better predict the estimated growth of an aneurism as well as to assist in determining when to recommend surgery. Hamada and Takamiya have found that aortic aneurisms grow in an exponential pattern rather than the hoped for linear pattern.
What shape best describes the graph of an exponential model?
A. A curve that starts slowly but then grows rapidly
B. A straight line that is decreasing in value
C. A curve that starts rapidly but then grows slowly
D. A straight line that is increasing in value

Math
Basic MathCarlos begins his workout by stretching. Then he spends an equal amount of time on each workout machine. The equation y=8x+10 represents the total time, in minutes, of Carlos' workout if he uses x workout machines.
Explain what the slope and y-intercept of the equation represent in this situation.
A. Carlos spends 10 minutes on one machine and 8 minutes on another.
B. Carlos uses 8 workout machines for 10 minutes each.
C. Carlos spends 8 minutes stretching and 10 minutes on each workout machine.
D. Carlos spends 10 minutes stretching and 8 minutes on each workout machine.

Math
Basic MathThe government of a large city needs to determine whether the city's residents will support the construction of a new gymnasium. The government decides to conduct a survey of a sample of the city's residents. Which one of the following procedures would be the most appropriate for obtaining a sample of the city's residents?
Survey a random sample of the future employees of the new gymnasium.
Survey every tenth person to use the public restroom.
Survey the last 100 residents listed in the telephone directory.
Survey a random sample of persons within each neighborhood.

Math
ProbabilityOne option in a roulette game is to bet $9 on red. (There are 18 red compartments, 18 black compartments, and two compartments that are neither red nor black.) If the ball lands on red, you get to keep the $9 you paid to play the game and you are awarded $9. If the ball lands elsewhere, you are awarded nothing and the $9 that you bet is collected. Complete parts (a) through (b) below.
a. What is the expected value for playing roulette if you bet $9 on red?
(Round to the nearest cent.)
b. What does this expected value mean? Choose the correct statement below.
A. This value represents the expected loss over the long run for each game played.
B. Over the long run, the player can expect to break even.
C. This value represents the expected win over the long run for each game played.

Math
Basic MathWhich situation is most likely to show a constant rate of change?
A. The amount of gasoline in a car's tank while driving on a highway at a constant speed compared with time
B. The distance of a student from home during a school day compared with the time of day
C. The speed of the wind on a stormy day compared with the time of day
D. The number of customers in a grocery store compared with the day of the week