Math Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Math
Basic MathThe half-life of radium-223 is approximately 11.43 days.
Step 3 of 3: How much of an 8 gram sample of radium-223 would remain after 9 days? Round to three decimal places.
Answer

Math
StatisticsTrue or False. The samples in sampling distribution must come from the same
population.
True
False

Math
Basic MathA museum gift shop sells hats with embroidered logos of the museum.
The hats are available in small, medium, and large sizes. They are available
in the colors red and green.
Make a tree diagram to represent all possible varieties of hats sold at the museum

Math
StatisticsAbout what percent of the data in a data set falls between the median value and the maximum value? Explain.
About___% of the data falls in this range because the minimum, first quartile, median, third quartile, and maximum divide a data set into___equal parts and the given range comprises___of these parts.

Math
Permutations and CombinationsA state makes auto license plates that have two letters (excluding I, O, and Q) followed by four digits of which the first digit is not zero. How many different license plates are possible?
3,085,128
3,470,769
O4,761,000
Math
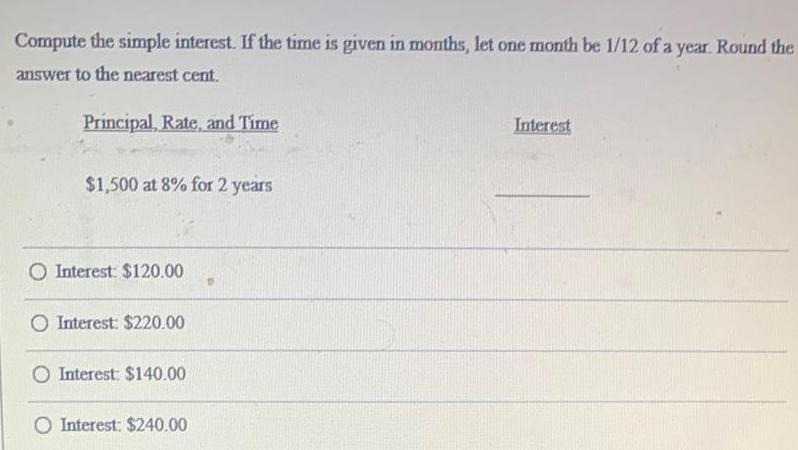
Basic MathCompute the simple interest. If the time is given in months, let one month be 1/12 of a year. Round the answer to the nearest cent.
Principal, Rate, and Time Interest
$1,500 at 8% for 2 years
Interest: $120.00
Interest: $220.00
Interest: $140.00
Interest: $240.00

Math
ProbabilityIn one town, 68% of adults have health insurance.
a. What is the probability that 6 adults selected at random from the town all have health insurance?
(Assume the population is large enough that we can consider events to be independent.)
A) 0.68
B) 0.099
C) 0.088
D) 4.08
b. What is the probability that 3 of the 6 adults have health insurance. (use binomial)

Math
Basic MathDirections: Simplify each of the following expressions. Partial credit will be given if enough work is shown to indicate some understanding of the process. You are highly encouraged to show every step so that you can earn as many points as possible even if your final answers are not correct, and so that I can help you figure out what exactly you do not understand if you do not simplify an expression correctly.
1. (3x-6) + 2xy + 4(x -3xy)-x
2. 8+(-7x+4)-(3x + y)
3. -(3x-5x + 7) + 4(-x-1)
4. 3(x-6) + (-2+4x)-2x
5. 3(xy)-5(x + y)-(- xy + x)

Math
StatisticsThe blue catfish (Ictalurus Furcatus) is the largest species of North American catfish. The current world record stands at 143 pounds, which was caught in the John H. Kerr Reservoir (Bugg's Island Lake) located in Virginia. According to American Expedition, the average weight of a blue catfish is between 20 to 40 pounds. Given that the largest blue catfish ever caught was at the John H. Kerr Reservoir, you believe that the mean weight of the fish in this reservoir is greater than 40 pounds. Use the data below, which represents the summary statistics for 42 blue catfish caught at this reservoir, and a 0.05 significance level to test the claim that the mean weight of the fish in the John H. Kerr Reservoir is greater than 40 pounds.
n = 42; = 40.71 pounds; s = 3.89 pounds
a) Identify the null and alternative hypotheses?
Ho:
HA:
b) What type of hypothesis test should you conduct (left-, right-, or two-tailed)?
left-tailed
right-tailed
two-tailed
c) Identify the appropriate significance level.
d) Calculate your test statistic. Write the result below, and be sure to round your final answer to two decimal places.
e) Calculate your p-value. Write the result below, and be sure to round your final answer to four
decimal places.

Math
Basic MathFind the interval I and radius of convergence R for the given power series. (Enter your answer for interval of convergence using interval notation.)
Σ k = 0 to ∝ k! (x - 3)k

Math
Application of derivativesWhat is the maximum vertical distance between the line y = x + 12 and the parabola y = x² for -3 ≤ x ≤ 4?

Math
Functionsa) Find and classify the critical point(s).
b) Find the interval(s) where f(x) is increasing.
c) Find the interval(s) where f(x) is decreasing.
1. f(x)=x²-x-1
2. f(x)=2x^4 - 4x² +1
3. f(x)=xe^1/x
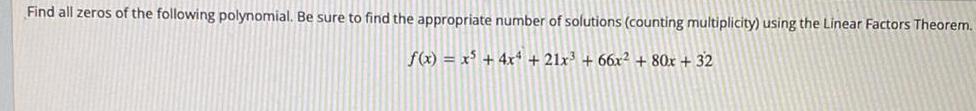
Math
Basic MathFind all zeros of the following polynomial. Be sure to find the appropriate number of solutions (counting multiplicity) using the Linear Factors Theorem.
f(x) = x^5 + 4x^4+21x³ +66x² + 80x + 32

Math
Basic MathThree different bacteria are cultured in one environment and feed on three nutrients. Each individual of species I consumes 1 unit of each of the first and second nutrients and 2 units of the third nutrient. Each individual of species II consumes 2 units of the first nutrient and 2 units of the third nutrient. Each individual of species III consumes 2 units of the first nutrient, 3 units of the second nutrient, and 5 units of the third nutrient. If the culture is given 5100 units of the first nutrient, 7200 units of the second nutrient, and 12,300 units of the third nutrient, how many of each species can be supported such that all of the nutrients are consumed? (Let x = species I, y = species II, and z = species III. If there are infinitely many solutions, express your answers in terms of z as in Example 3.)
(x, y, z) =____ where 2100 ≤ z ≤ 2400
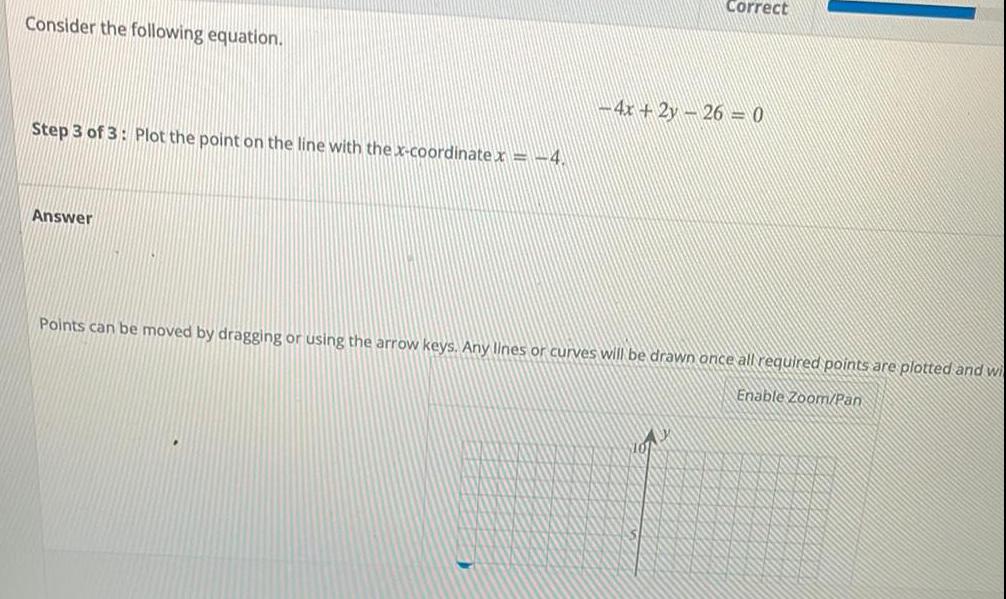
Math
Basic MathConsider the following equation.
-4x+2y-26 = 0
Step 3 of 3: Plot the point on the line with the x-coordinate x = -4.
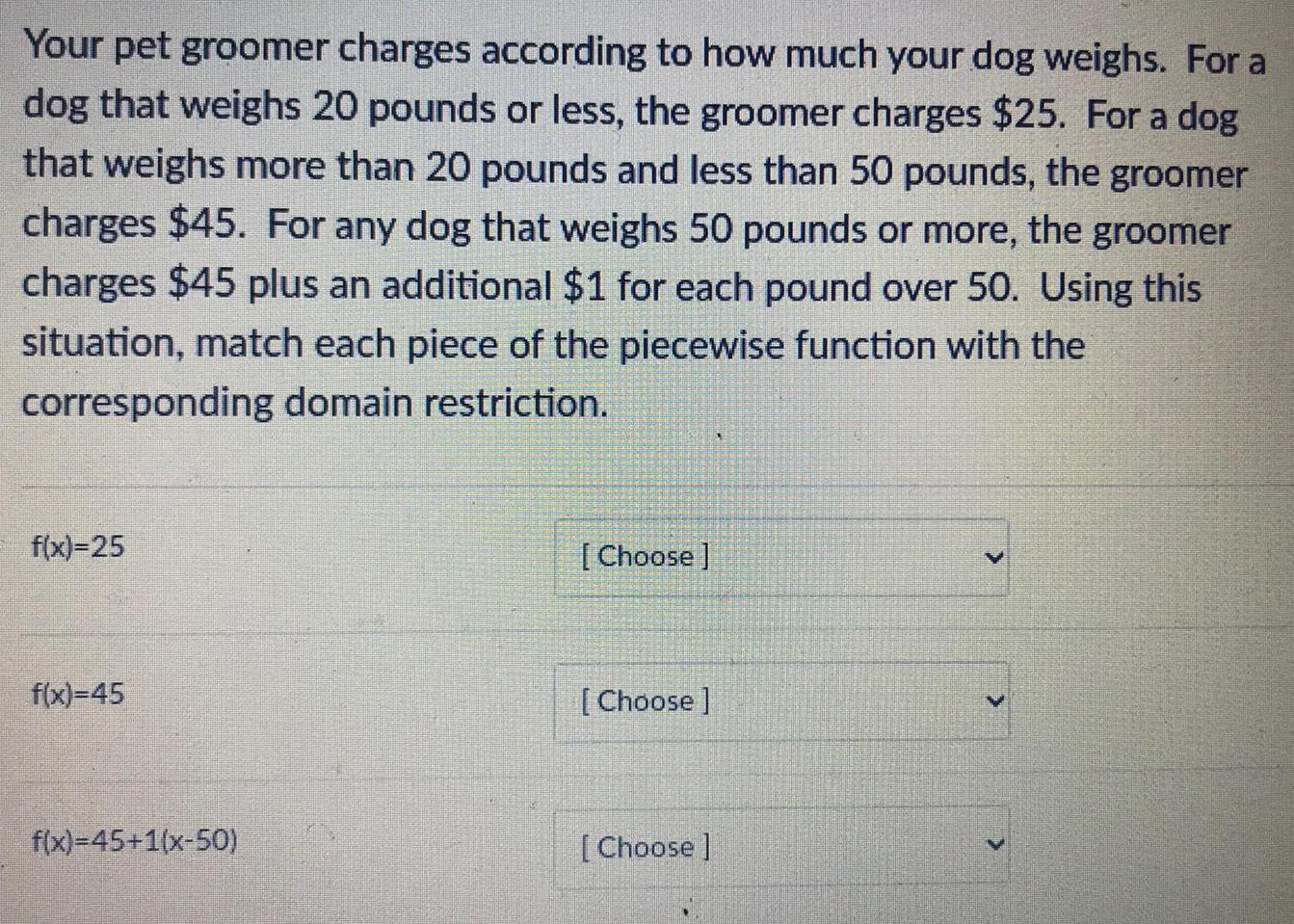
Math
Basic MathYour pet groomer charges according to how much your dog weighs. For a
dog that weighs 20 pounds or less, the groomer charges $25. For a dog
that weighs more than 20 pounds and less than 50 pounds, the groomer
charges $45. For any dog that weighs 50 pounds or more, the groomer
charges $45 plus an additional $1 for each pound over 50. Using this
situation, match each piece of the piecewise function with the
corresponding domain restriction.
f(x)=25
f(x)=45
f(x)=45+1(x-50)

Math
Basic MathYum Yum Sandwich Shop has a lunch special. Customers can choose one sandwich, one bag of chips, and one drink. The options are below.
Sandwich Chips Drinks
Ham Potato Chips Water
Egg Salad Corn Chips Tea
Tuna Salad Coke
BLT Sprite
Root Beer
Power Aid

Math
FunctionsLet f(x) = x² - 4x - 21 and g(x) = x² − 9x + 14. Find f.g and f/g respective domains. Simplify your answers.
1. f. g =
2. What is the domain of f. g ?
Answer (in interval notation):
3. f/g =
Answer (in interval notation):
4. What is the domain of f/g?
Answer (in interval notation):

Math
CircleComplete the square and write the given equation in standard form. Then give the center and radius of the circle and graph the equation.
x² + y² +6x-4y - 12 = 0
The equation of the circle in standard form is

Math
VectorsFind the vector w w of length 6 6 in the direction of v = 8 i +7j. v=8i+7j. (Give your answer using component form or standard basis vectors. Express numbers in exact form. Use symbolic notation and fractions where needed.)

Math
StatisticsRoper Through their Roper Reports Worldwide, GfK Roper conducts a global consumer survey to help mul- tinational companies understand different consumer attitudes throughout the world. Within 30 countries, the researchers interview 1000 people aged 13-65. Their samples are designed so that they get 500 males and 500 females in each country. (www.gfkamerica.com)
a) Are they using a simple random sample? Explain.
b) What kind of design do you think they are using?

Math
Application of derivativesA company found that new employees prefer training sessions of moderate length, shorter training sessions provided too little instruction to complete a task, while longer training sessions contain too much instruction to remember. For a training session on a particular task, the company determined that the ratings new employees gave for the training session could be approximated
by R(t)=32t/t²+256 where t is the length of the training session in minutes. Find the training session length that received the highest rating
The training session length that received the highest rating is____minutes
(Simplify your answer.)
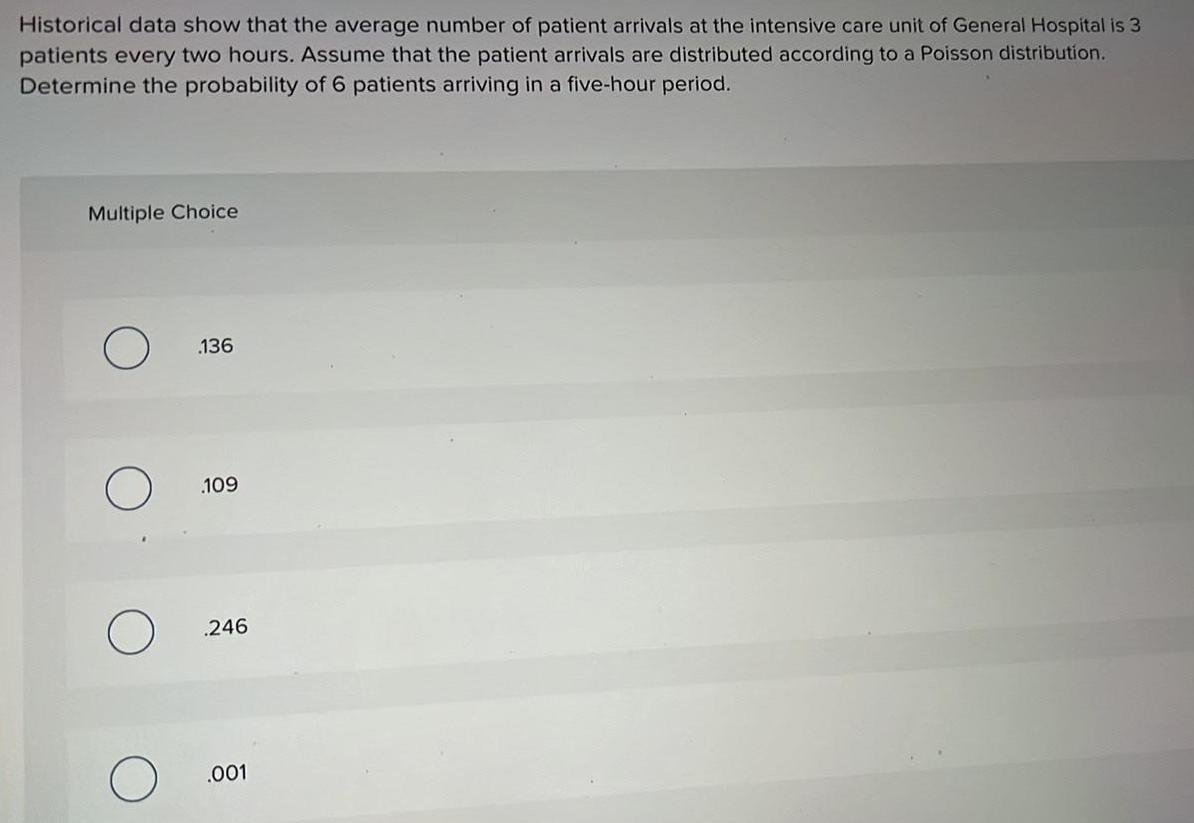
Math
Basic MathHistorical data show that the average number of patient arrivals at the intensive care unit of General Hospital is 3 patients every two hours. Assume that the patient arrivals are distributed according to a Poisson distribution.
Determine the probability of 6 patients arriving in a five-hour period.
136
.109
.246
.001
Math
TrigonometryDiscussion Board Topic: In this discussion board you will:
Part 1: Use a real life application to come up with a QUESTION utilizing the Law of Sines and Law of Cosines in Trigonometry.
Post the question on the discussion board.
Please use proper directions and equation editor for any mathematical notation.
You may post this as a pdf file.
Part 2: Solve one of your classmate's questions.
Part 3: Once someone has answered your question, provide feedback.

Math
ProbabilityA golf ball is selected at random from a golf bag. The golf bag contains the following golf ball brands: 9 Titleists, 8 Maxflis, and 3 Top-Flites. Find the probability that the golf ball is:
A Titleist or Maxfli

Math
Basic MathConsider the equation and the following ordered pairs: (-4, y) and (x, 2).
y = 2x + 8
Step 1 of 2: Compute the missing x and y values so that each ordered pair will satisfy the given equation.

Math
Basic MathHeather drove 268 miles using 12 gallons of gas. At this rate, how many miles would she drive using 9 gallons of gas?

Math
FunctionsWrite a rule for g described by the transformations the vertex. of the graph off. Then identify 2 f(x) = x²; vertical stretch by a factor of 4 and a reflection in the x-axis, followed by a translation 1 unit left.
a. g(x) = -4(x + 1)²; (-1,0)
b. g(x) = 4x² + 1; (0,1)
c. g(x)=-1/4 (x + 1)² ; (-1,0)
d. g(x) = 4(x + 1)²; (-1,0)

Math
Basic MathThe population in a certain town is increasing linearly each year. The population at time t = 3 is 1285 and at time t = 8 is 2460, where t is the number of years after 1990.
If P(t) is the population at time t, write the equation below that correctly represents this situation.

Math
Application of derivativesFind all relative extrema and saddle points of the function. Use the Second Partials Test where applicable. (If an answer does not exist, enter DNE.)
f(x, y) = -8x² - 5y^2 + 8x - 10y + 8
relative minimum.
relative maximum
saddle point


Math
Basic Math1. Which of the following rules correctly represents the translation from ABC to MNP?
A (x,y) → (x + 5,y - 2)
B (x,y) → (x-2, y + 5)
C (x,y) → (x-5,y + 2)
D (x,y) → (x+2, y-5)

Math
Application of derivativesThe radius r of a sphere is increasing at a rate of 2 inches per minute.
(a) Find the rate of change of the volume when r = 11 inches.
in.3/min
(b) Find the rate of change of the volume when r = 36 inches.
in.3/min
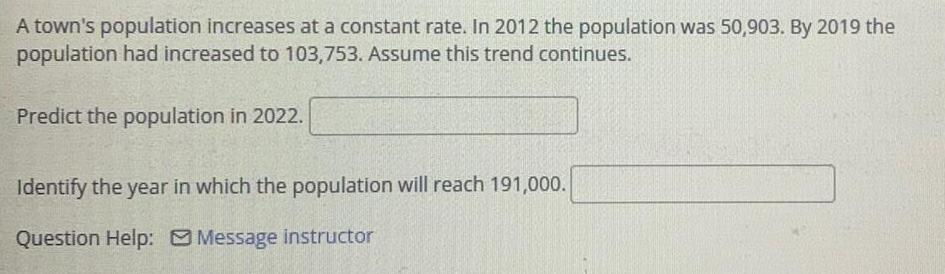
Math
Straight linesA town's population increases at a constant rate. In 2012 the population was 50,903. By 2019 the population had increased to 103,753. Assume this trend continues.
Predict the population in 2022.
Identify the year in which the population will reach 191,000.

Math
Basic MathThe rate R that a certain disease spreads is proportional to the number of infected individuals and is also proportional to the number of uninfected individuals. The total population is P and the number of infected individuals is D. Express the rate that the disease spreads in terms of this information. Use C as your proportionality constant.

Math
Basic MathA truck costs $80,000. It depreciates in value $6,000 per year. Write a linear model in the form v(t) = mt + b where v(t) represents the current value of the truck after t years of ownership.

Math
Basic MathInternetlivestats.com reported in December 2017 around 38% of the world population has an Internet connection today. If there are 3,074,488,191 users, what is the world population? (Round your answer to the nearest whole number.)

Math
Basic MathExpress the repeating decimal as a fraction in lowest terms.
0.97= 97/100 + 97/10,000 + 97/1,000,000 + ...

Math
Sequences & SeriesUse the formula for the general term (the nth term) of an arithmetic sequence to find the indicated term of the sequence with the given first term, a1 and common difference, d.
Find a250 when a₁ = -60, d = 5.

Math
Basic MathUse the distributive property to remove the parentheses.
2+14+26+...+ (12k-10)+(12(k+1)-10) = k(6k-4) + 12(k+1)-10
=6k²-4k+....
Then we simplify the right side of the formula.
2+14+26+...+ (12k-10)+(12(k+1)-10) = 6k²-4k+ 12k+12-10 = ....
Factor the right side.
2+14+26+...+(12k-10)+(12(k+1)-10) = 6k² +8k+2=...

Math
Functionsf(x) = (2x - 1)(3x + 5) (x + 1) has zeros at x = -5/3, x=-1 and x=1/2
What is the sign of f on the interval -5/3<x<1/2?
Choose 1 answer:
f is always positive on the interval.
f is always negative on the interval.
f is sometimes positive and sometimes negative on the interval.
![A statement S, about the positive integers is given below. Write statements Sk and Sk+ 1.
Sn: 4+10+16+...+(6n-2) = n(3n+1)
Sk: 4+10+16+...+(6k-2)=
Sk+1:4+10+16+...+ [6(k+ 1)-2] =](https://media.kunduz.com/media/sug-question/raw/53250425-1658586342.8074906.jpeg?w=256)
Math
Basic MathA statement S, about the positive integers is given below. Write statements Sk and Sk+ 1.
Sn: 4+10+16+...+(6n-2) = n(3n+1)
Sk: 4+10+16+...+(6k-2)=
Sk+1:4+10+16+...+ [6(k+ 1)-2] =

Math
Basic MathThe selling price of a refrigerator, is $537.90. If the markup is 10% of the dealer's cost, what is the dealer's cost of the refrigerator?
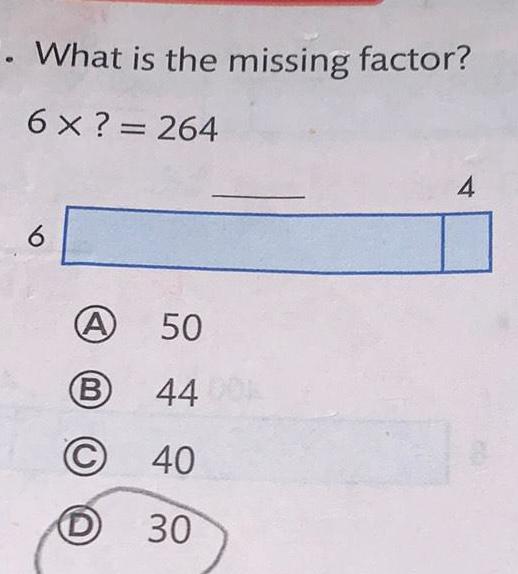

Math
Basic MathA farmer is building a fence to enclose a rectangular area consisting of two separate regions. The four walls and one additional vertical segment (to separate the regions) are made up of fencing, as shown below.
If the farmer has 234 feet of fencing, what are the dimensions of the region which enclose the maximal area?

Math
Sequences & SeriesWrite a formula for the general term (the nth term) of the arithmetic sequence shown below. Do not use a recursion formula. Then use the formula for an to find a20. the 20th term of the sequence.
an = an-1 - 10, a1 =32



