Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
Calculus
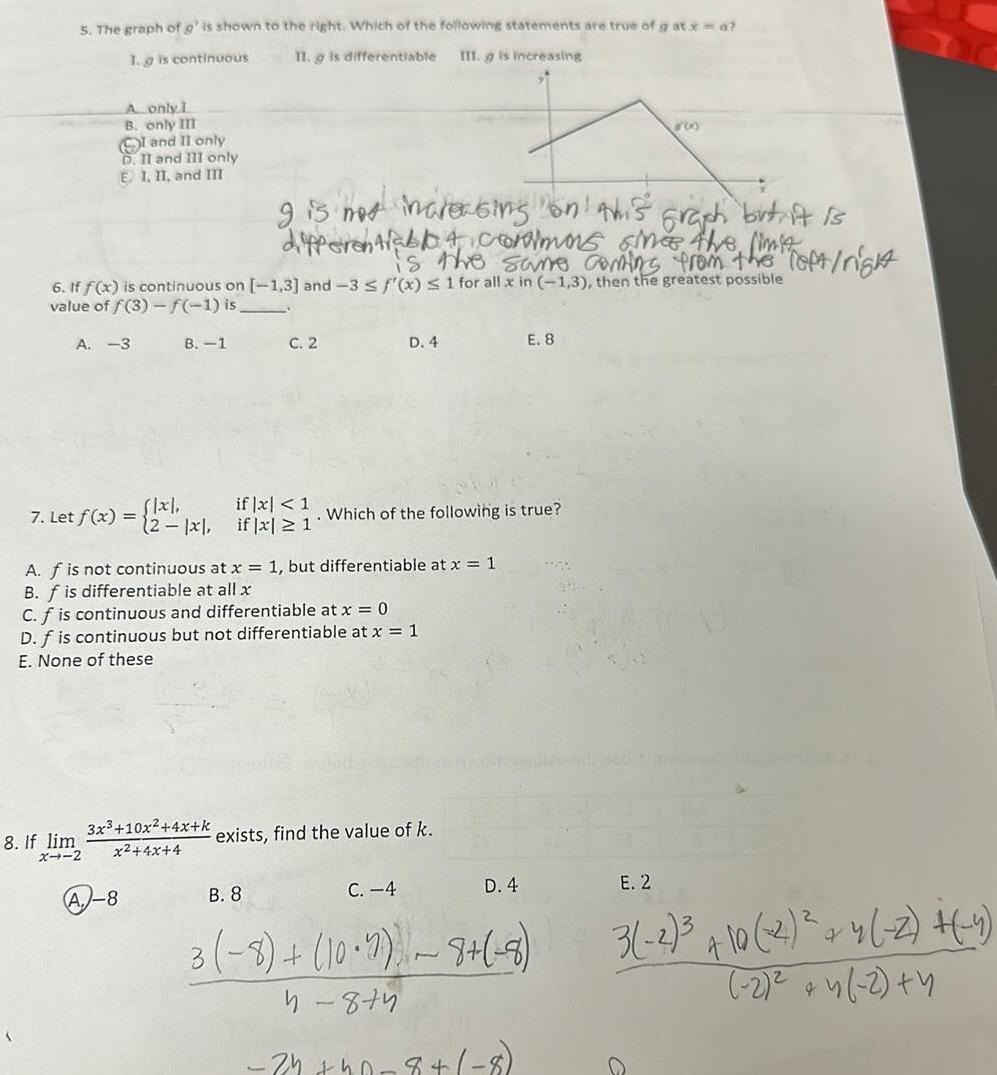
Limits & Continuity5 The graph of g is shown to the right Which of the following statements are true of g at x d 1 g is continuous 11 g is differentiable III g is increasing A only 1 B only III I and II only D II and III only E 1 II and III A 3 6 If f x is continuous on 1 3 and 3 f x 1 for all x in 1 3 then the greatest possible value of f 3 f 1 is 7 Let f x 8 If lim X4 2 B 1 flxl 2 x A 8 g is not increasing on this graph but it is differentiablo A Cormors sines the limit is the same coming from the Toft right 3x 10x 4x k x 4x 4 C 2 if x 1 if x 1 A f is not continuous at x 1 but differentiable at x 1 B f is differentiable at all x D 4 C f is continuous and differentiable at x 0 D f is continuous but not differentiable at x 1 E None of these Which of the following is true exists find the value of k E 8 D 4 3 B 8 C 4 3 8 10 2 8 8 4 874 34 40 8 8 E 2 3 2 10 2 4 2 4 2 4 2 4

Calculus
Definite Integralsf x x Let x be any arbitrary element of R then Right hand limit at x x lim f x lim f x h X X Institute of Lifelong Learning University of Delhi lim x h 40 lim x h 2xh 0 0 lim f x x X X Left hand limit at x x lim f x lim f x h lim x h 60 lim x h 2x h x 0 0 lim f x x x x Hence lim f x x 2 Au Since lim f x lim f x x2 X 195 Continuity of Functions Now the value of the function at x x is SITY f x x from equation 1 and 2 we have lim f x f x x X 30 f x f x Thus f x x is continuous at x x Since is an arbitrary element of R Therefore f x is continuous at each point of R Hence f x is continuous on R Example 4 Show that the function f x defined by if x 0 X 0 if x 0 is continuous on R Solution Given function is DELHI xsin if x 0 1 2
Calculus
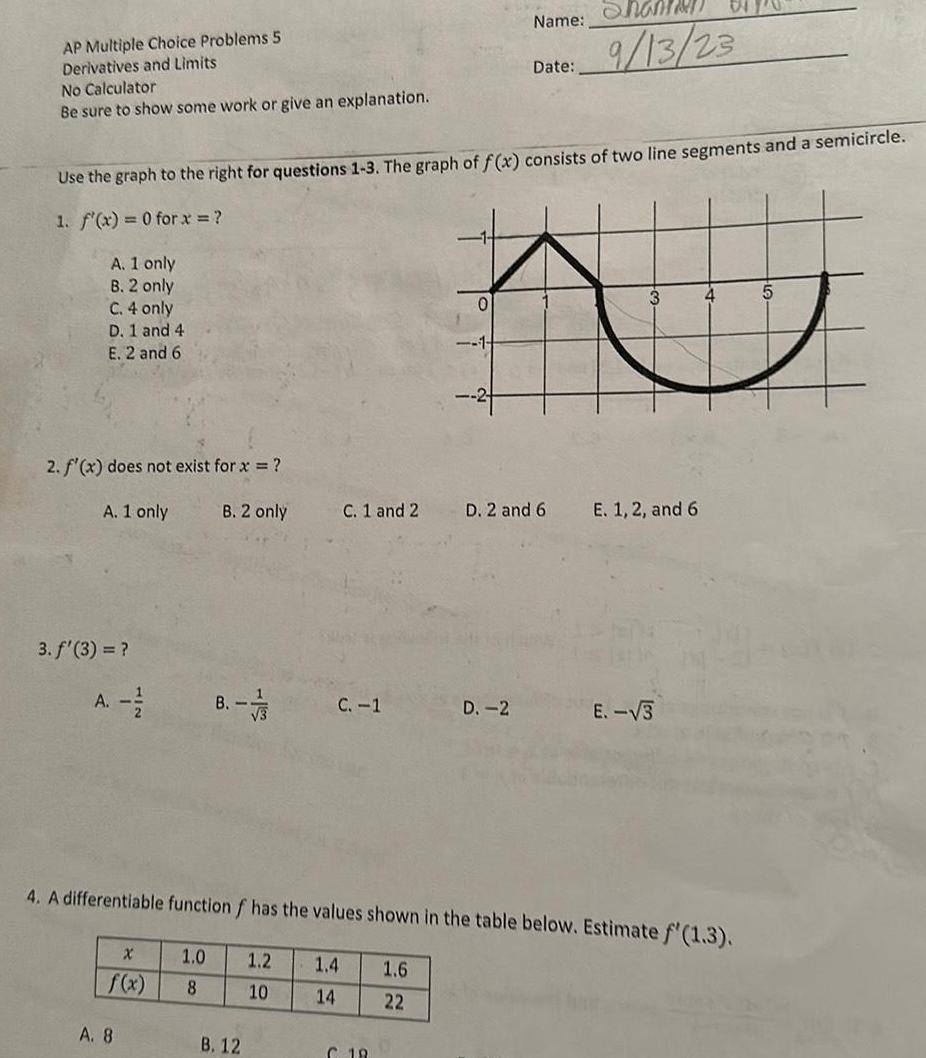
Limits & ContinuityAP Multiple Choice Problems 5 Derivatives and Limits No Calculator Be sure to show some work or give an explanation A 1 only B 2 only C 4 only D 1 and 4 E 2 and 6 2 f x does not exist for x Use the graph to the right for questions 1 3 The graph of f x consists of two line segments and a semicircle 1 f x 0 for x A 1 only 3 f 3 X f x B 2 only A 8 8 1 0 1 2 8 10 C 1 and 2 B 12 C 1 1 4 1 6 14 22 0 C 18 1 Name Date D 2 D 2 and 6 4 A differentiable function f has the values shown in the table below Estimate f 1 3 9 13 23 E 1 2 and 6 E 3 4 5

Calculus
Application of derivatives1 Suppose that the height of a skydiver t seconds after jumping from an airplane is given by s t 4500 20t 16t2 feet neglecting air resistance The skydiver pulls the ripcord after 10 seconds of free fall to deploy the parachute after he has fallen Write a velocity function for the skydiver t How fast is the skydiver falling the instant before he pulls the ripcord ft sec miles per hour Calculate the skydiver s average velocity over the time interval from 5 seconds to 10 seconds What is the skydiver s acceleration function 2 A car moves along the x axis so that at any time t t 0 the position is given by s t 4t 18t 15t 1 Write a velocity function for the car Write an acceleration function for the car What is the velocity of the car at t 2 What is the velocity of the car at t 4 What is the average velocity of the car on the time interval from 4 to 6 When is the car at rest circle

Calculus
Differential equationsII I Discontinuity of the First Kind from the Left at x The function f X R is said to have a discontinuity of first kind from the left at x if the left hand limit exist at x but not equal to the value of the function at x i e lim f x f x II II Discontinuity of the First Kind from the Right at The function f X R is said to have a discontinuity of first kind from the right atx if the right hand limit exist at x but not equal to the value of the function atx i e lim f x f x X III Discontinuity of the Second Kind at x The function f X R is said to have a discontinuity of second kind at if both the left hand limit and right hand limit do not exist at x i e lim f x and lim f x do not exist III I Discontinuity of the Second Kind from the Left at x The function f X R is said to have a discontinuity of second kind from the left at x if the left hand limit does not exist at x i e lim f x does not exist X x III II Discontinuity of the First Kind from the Right at x The function f X R is said to have a discontinuity of second kind from the right at x if the right hand limit does not exist at i e lim f x does not exist x Value Addition Jump of a Function at x If a function f X R has a discontinuity of first kind at x then the function f is said to have a jump at x and the value of the jump is equal to the difference of both the limits at x i e Institute of Lifelong Learning University of Delhi Value of the jump at x lim f x lim f x 1 94 1 g Example 5 Show that the function f defined by sin x Continuity of Functions f x x DEL x 0 x 0 dementimuit pg 10 10

Calculus
DifferentiationNow let a be any arbitrary element of R then there arise two cases Case I If a 0 then and 1 lim f x lim x sin X NI 2 M X Now f a asin 1 asin 1 a whenever Continuity of Functions a Then lim f x f a a sin X M SITY I Q 2 I Q 3 1 Thus f x is continuous at x a Case II If a 0 then by the definition of function f a f 0 0 a x 0 xsin 0 si S A Sin JO f x f 0 Now if we choose s then for a given 0 there exists a number 8 E 0 such that That f x f 0 e x 0 x 8 Thus f x is continuous at x 0 Hence f x is continuous on R OF DEL Institute of Lifelong Learning University of Delhi Continuity of Functions pg 8 8
Calculus
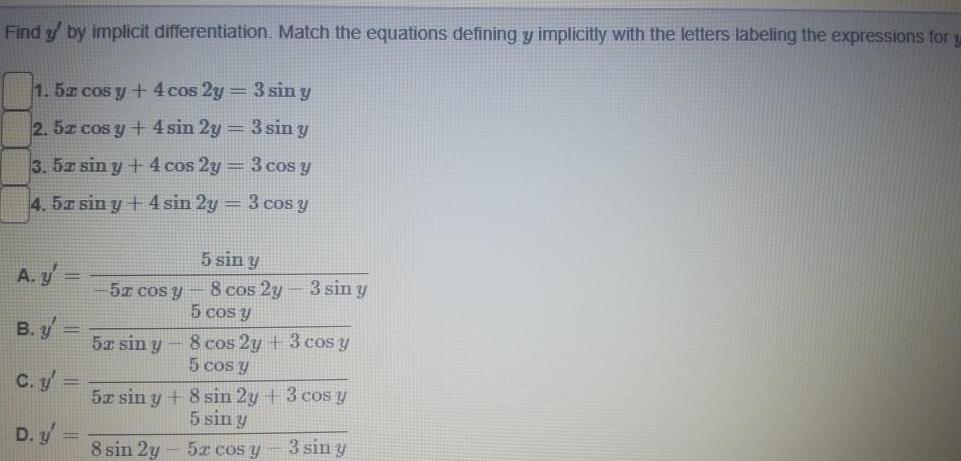
DifferentiationFind y by implicit differentiation Match the equations defining y implicitly with the letters labeling the expressions for y 1 5x cos y 4 cos 2y 3 sin y 2 5z cos y 4 sin 2y 3 sin y 3 5z sin y 4 cos 2y 3 cos y 4 52 sin y 4 sin 2y 3 cos y A y B y C y D y 5x cos y 5x sin y 5 sin y 8 cos 2y 5 cos y 3 sin y 8 cos 2y 3 cos y 5 cos y 5x sin y 8 sin 2y 3 cos y 5 sin y 8 sin 2y 5x cos y 3 sin y

Calculus
DifferentiationSammen A particle is moving along the curve y 3 4z 1 As the particle passes through the point 2 9 its coordinate increases at a rate of units per second Find the rate of change of the distance from the particle to the origin at this instant

Calculus
DifferentiationThe radius of a spherical balloon is increasing at a rate of 4 centimeters per minute How fast is the volume changing in cubic centimeters per minute when the radius is 14 centimeters Note The volume of a sphere is given by V 4 3 Tr Rate of change of volume in cubic centimeters per minute

Calculus
Application of derivativesHelium is pumped into a spherical balloon at a rate of 3 cubic feet per second How fast is the radius increasing after 2 minutes Note The volume of a sphere is given by V 4 3 TT Rate of change of radius in feet per second
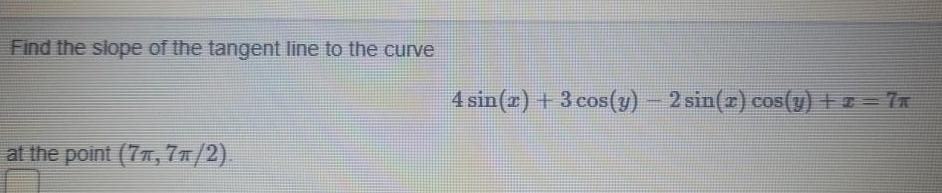
Calculus
DifferentiationFind the slope of the tangent line to the curve at the point 77 7 2 4 sin z 3 cos y 2 sin r cos y z 7
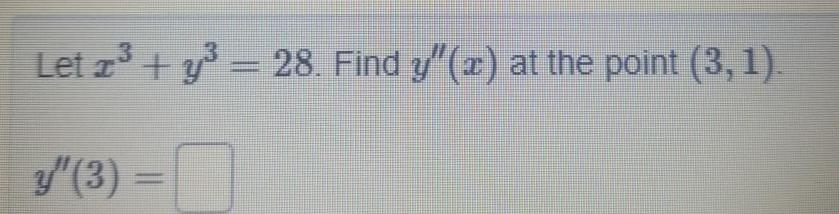
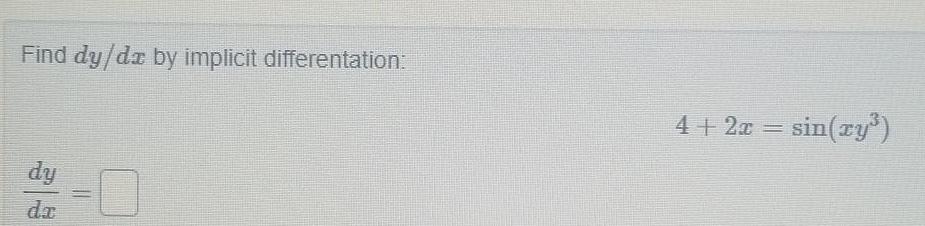

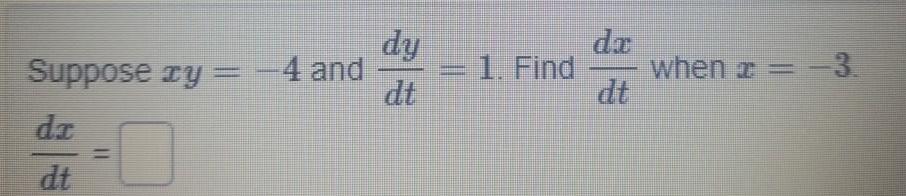
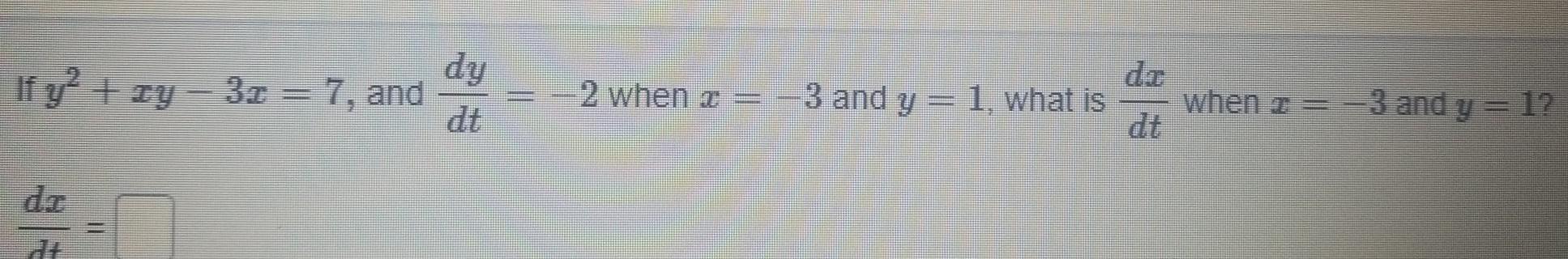
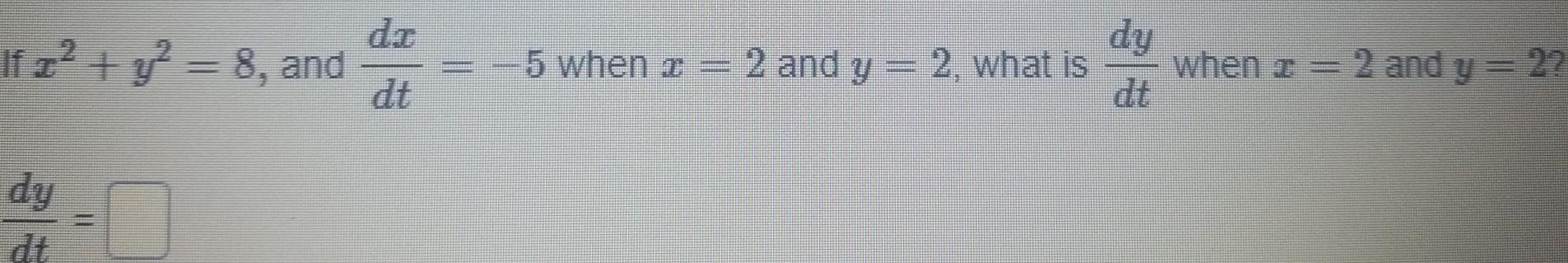
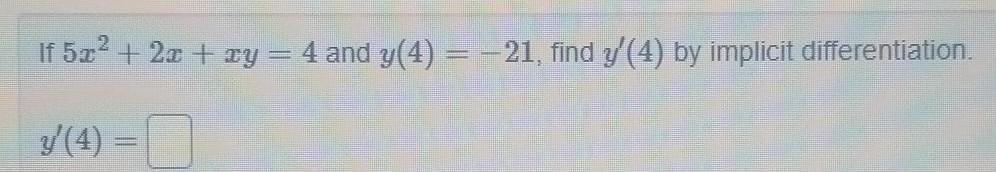
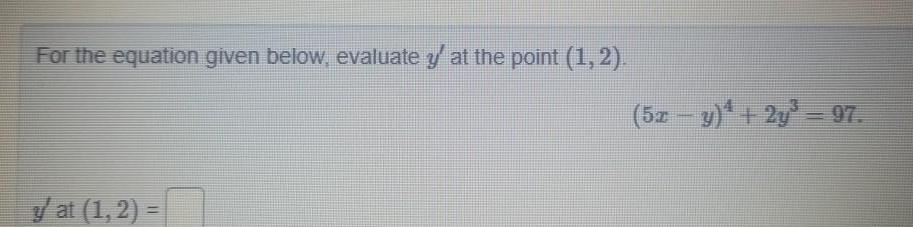

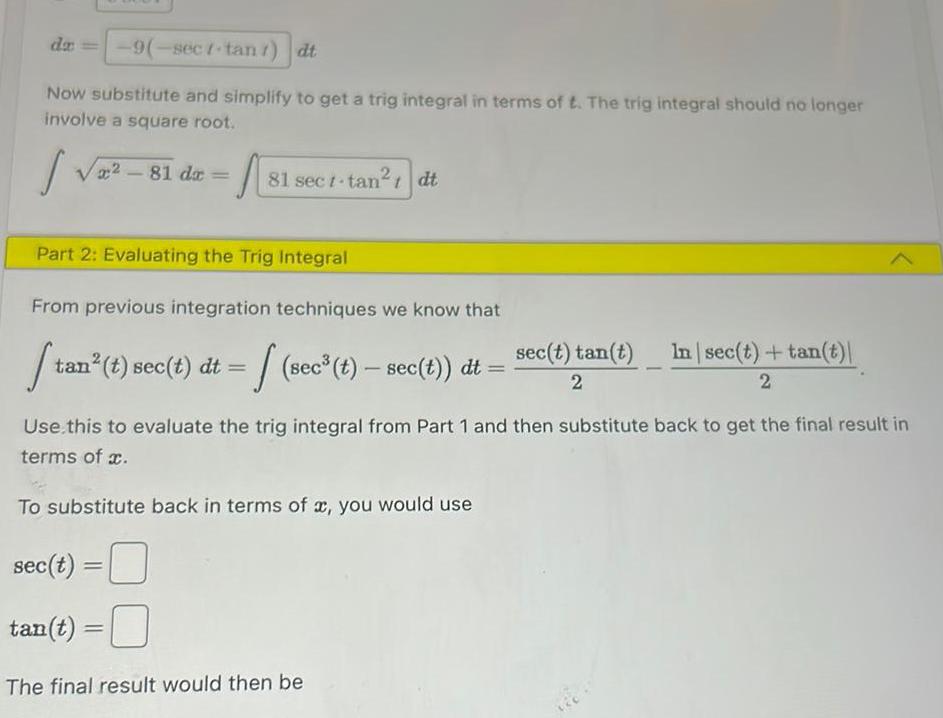
Calculus
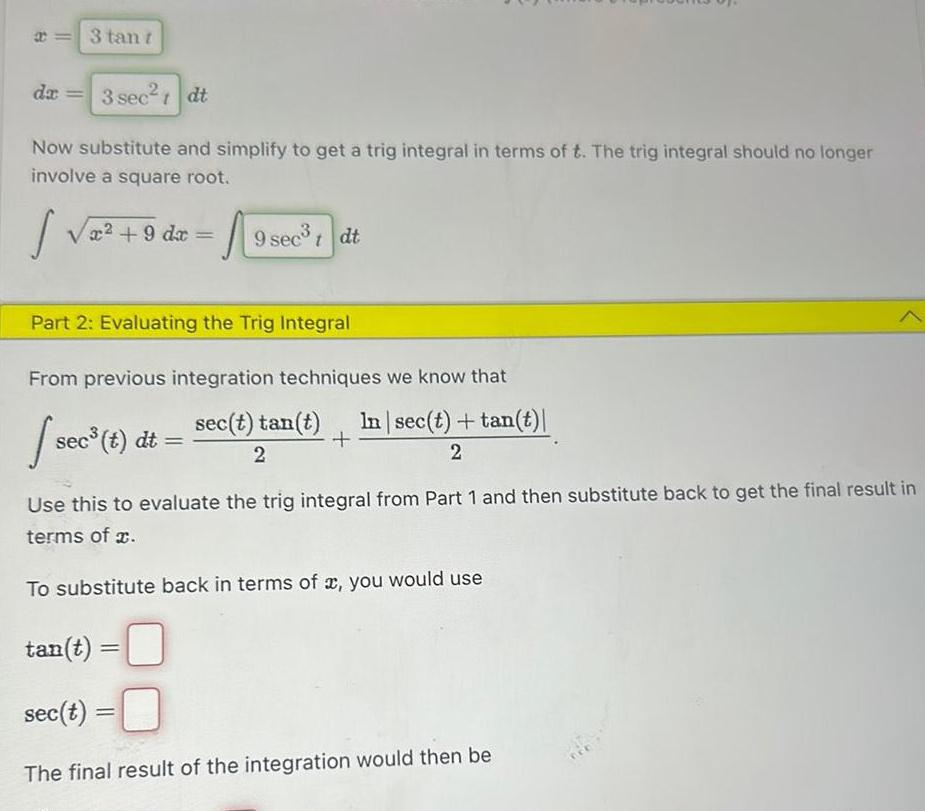
Application of derivativesda 9 sect tan dt Now substitute and simplify to get a trig integral in terms of t The trig integral should no longer involve a square root 81 da A 81 sect tan dt t Part 2 Evaluating the Trig Integral From previous integration techniques we know that St tan t sec t dt sec t sec t dt sec t tan t 2 The final result would then be In sec t tan t 2 Use this to evaluate the trig integral from Part 1 and then substitute back to get the final result in terms of x To substitute back in terms of x you would use sec t tan t

Calculus
Application of derivatives1 Assume that f x is a function on the interval 0 1 that has a Fourier sine series on 0 given by 00 give the value of ba 1 12 f x sin nx 71 1 Use a Fourier sine series to find a solution to This solution will have the form 3v x f x 0 x n v 0 v n 0 v x b sin nx n 1
Calculus
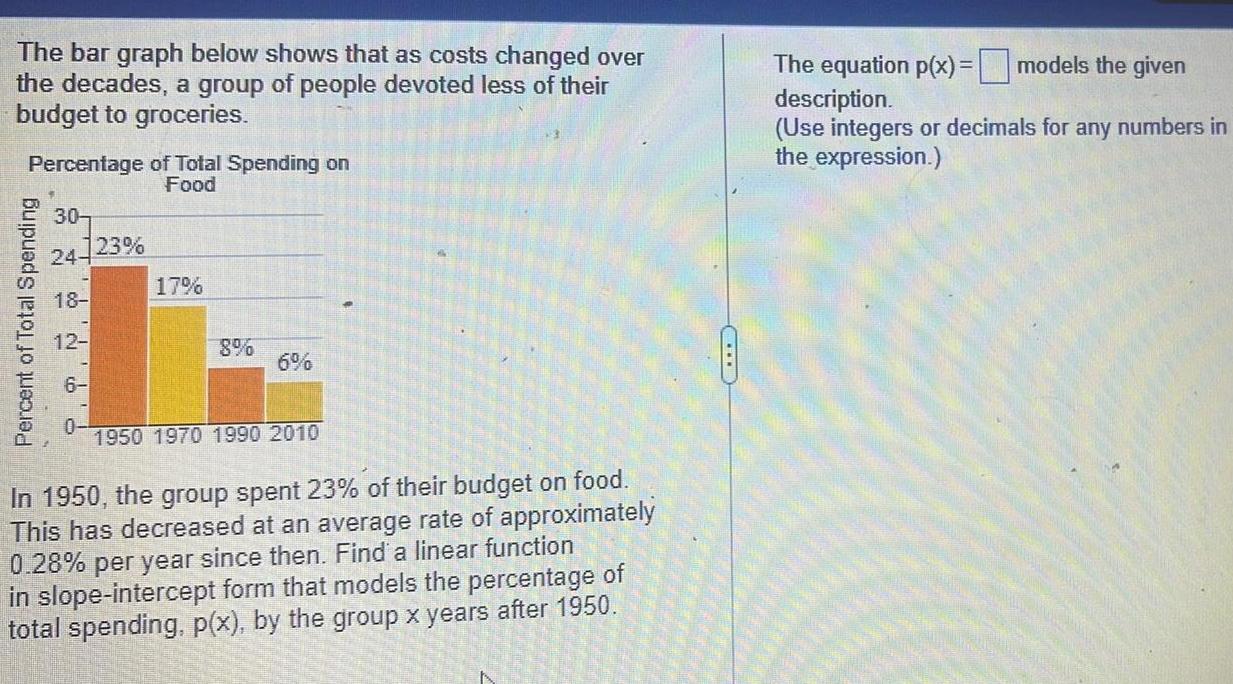
Application of derivativesThe bar graph below shows that as costs changed over the decades a group of people devoted less of their budget to groceries Percentage of Total Spending on Food Percent of Total Spending 30 24 18 12 6 23 17 8 6 1950 1970 1990 2010 In 1950 the group spent 23 of their budget on food This has decreased at an average rate of approximately 0 28 per year since then Find a linear function in slope intercept form that models the percentage of total spending p x by the group x years after 1950 The equation p x models the given description Use integers or decimals for any numbers in the expression

Calculus
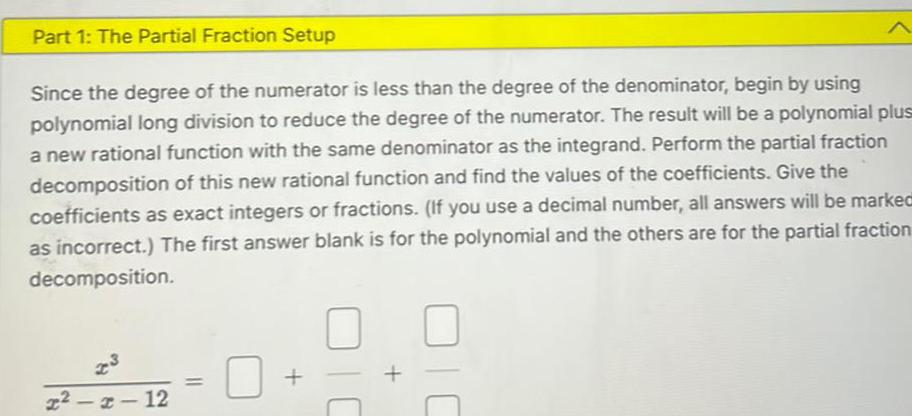
Definite IntegralsPart 1 The Partial Fraction Setup Since the degree of the numerator is less than the degree of the denominator begin by using polynomial long division to reduce the degree of the numerator The result will be a polynomial plus a new rational function with the same denominator as the integrand Perform the partial fraction decomposition of this new rational function and find the values of the coefficients Give the coefficients as exact integers or fractions If you use a decimal number all answers will be marked as incorrect The first answer blank is for the polynomial and the others are for the partial fraction decomposition x x 12
Calculus
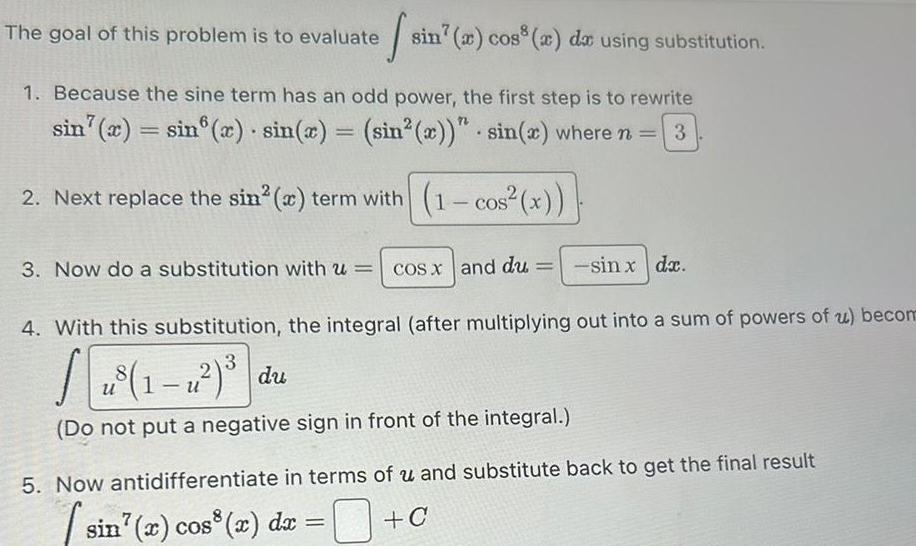
Indefinite IntegrationThe goal of this problem is to evaluate 1 Because the sine term has an odd power the first step is to rewrite sin x sin x sin x sin x sin x where n 3 2 Next replace the sin x term with 1 cos x 3 Now do a substitution with u sin a cos a da using substitution u cos x and du sin x dx 4 With this substitution the integral after multiplying out into a sum of powers of u becom SE u Do not put a negative sign in front of the integral 5 Now antidifferentiate in terms of u and substitute back to get the final result sin x cos x dx C

Calculus
Differential equationsPart 1 The Partial Fraction Setup 4x 3 and find the values of the 3x 5 x 3 Perform the partial fraction decomposition of coefficients Give the coefficients as exact integers or fractions If you use a decimal number all answers will be marked as incorrect 4z 3 3x 5 2 3
Calculus
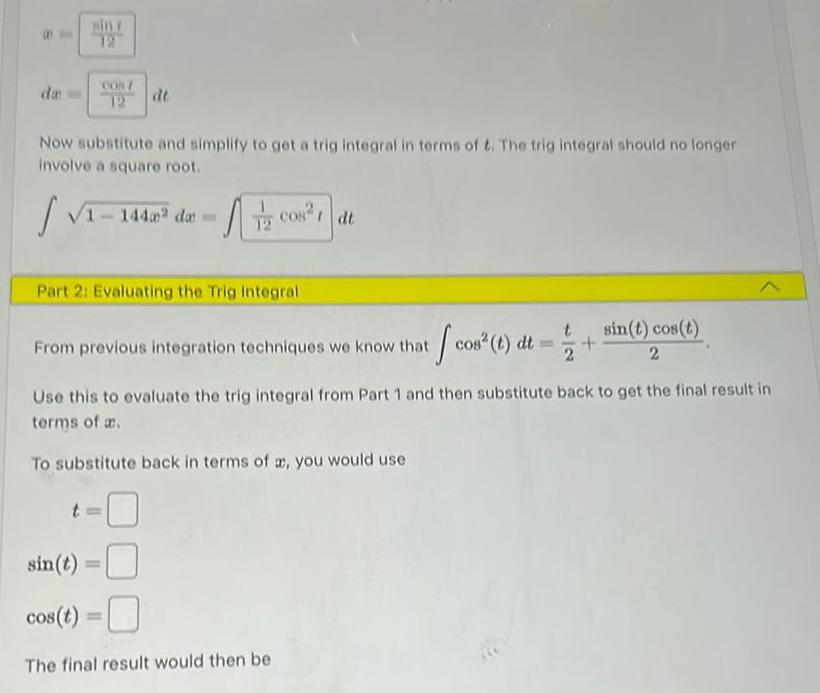
Application of derivativesda sin z 12 COS 12 Now substitute and simplify to get a trig integral in terms of t The trig integral should no longer involve a square root Tz cos 1 dt 1 14 dt 1 144m da Part 2 Evaluating the Trig Integral From previous integration techniques we know that cos t dt Use this to evaluate the trig integral from Part 1 and then substitute back to get the final result in terms of a To substitute back in terms of a you would use sin t cos t The final result would then be sin t cos t 2

Calculus
Indefinite IntegrationThe goal of this problem is to evaluate Part 1 The Partial Fraction Setup 82 16 x 8x Perform the partial fraction decomposition of 8x 16 x28x dx using partial fractions 8x16 x 8x and find the values of the coefficients
Calculus
Indefinite IntegrationB 3 tan t da 3 sec tdt Now substitute and simplify to get a trig integral in terms of t The trig integral should no longer involve a square root Sv x 9 dx sec Part 2 Evaluating the Trig Integral From previous integration techniques we know that sec t tan t In sec t tan t 2 2 sec t dt tan t 19 sec Use this to evaluate the trig integral from Part 1 and then substitute back to get the final result in terms of x To substitute back in terms of x you would use 9 sec t dt sec t 0 The final result of the integration would then be

Calculus
DifferentiationFor each of the following integrals give an appropriate trigonometric substitution of the form f t to simplify the integral x 9 x dx a 2 9 x 49 dx b C d 5x2 8 dx 6 dr H 11 x C
Calculus
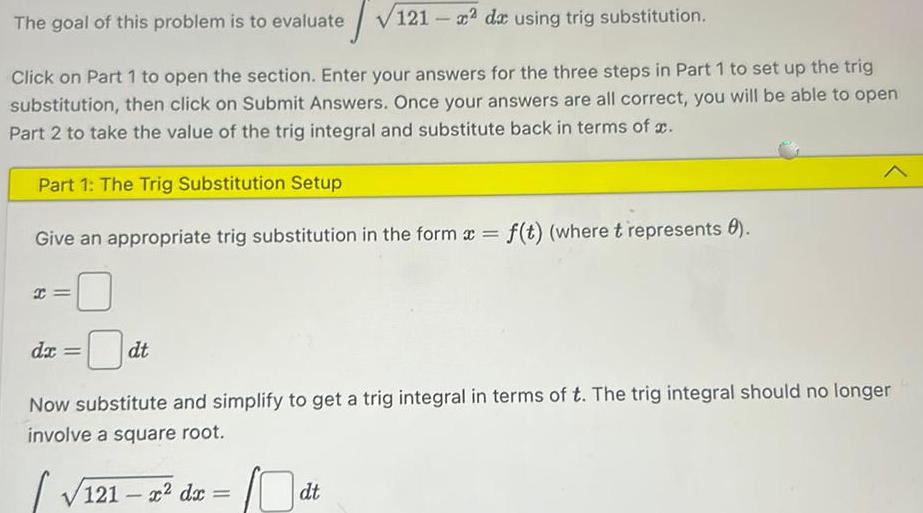
Indefinite IntegrationThe goal of this problem is to evaluate 121 2 de using trig substitution Click on Part 1 to open the section Enter your answers for the three steps in Part 1 to set up the trig substitution then click on Submit Answers Once your answers are all correct you will be able to open Part 2 to take the value of the trig integral and substitute back in terms of Part 1 The Trig Substitution Setup Give an appropriate trig substitution in the form x f t where t represents 8 I dx dt Now substitute and simplify to get a trig integral in terms of t The trig integral should no longer involve a square root 121 x dx dt
Calculus
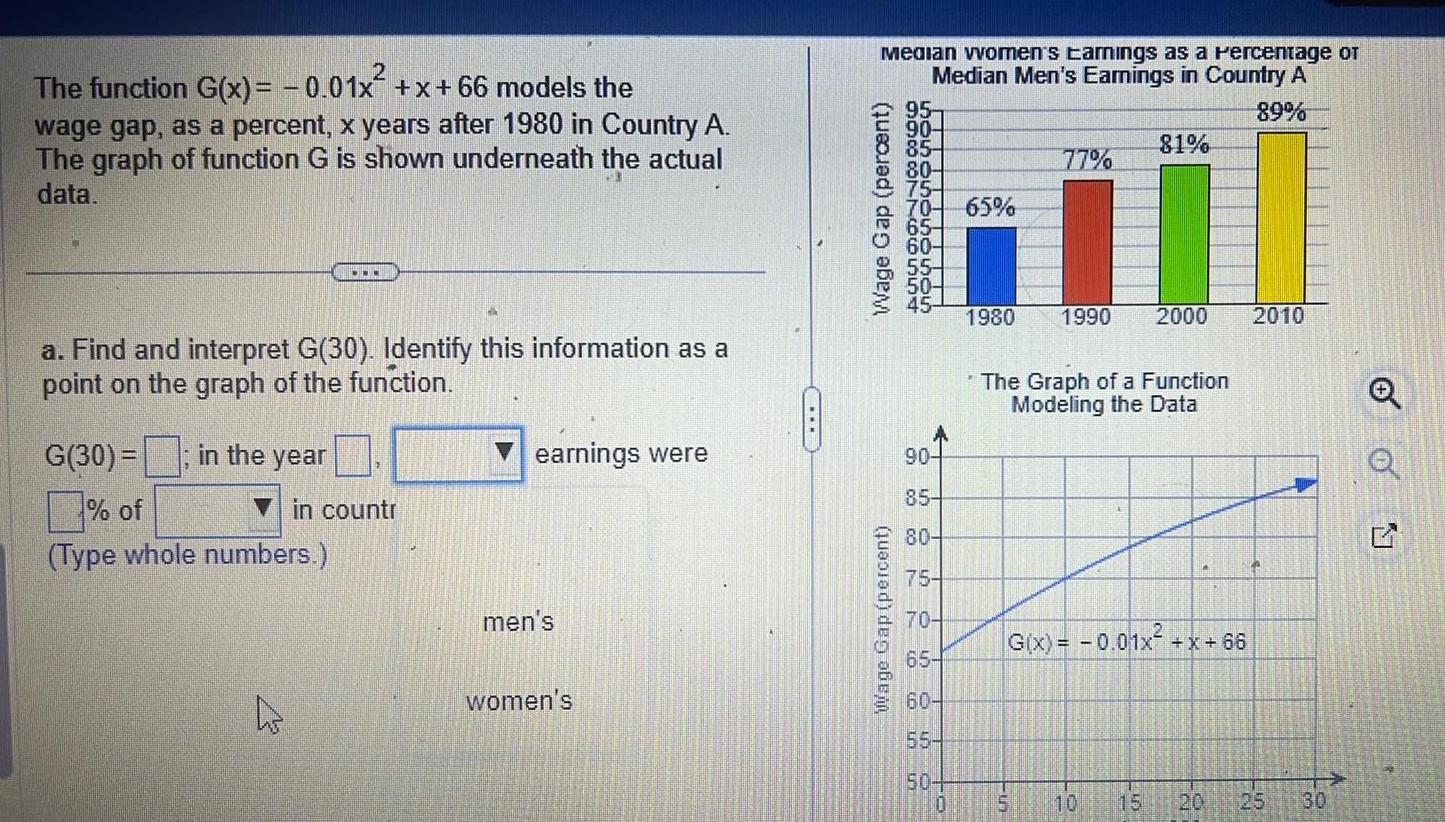
Vector Calculus2 The function G x 0 01x x 66 models the wage gap as a percent x years after 1980 in Country A The graph of function G is shown underneath the actual data a Find and interpret G 30 Identify this information as a point on the graph of the function G 30 of Type whole numbers in the year K in countr earnings were men s women s Median women s Earnings as a Percentage of Median Men s Earnings in Country A 89 Wage Gap percent quasjad des ab 95 90 85 otho LOLOS 80 75 70 65 65 60 55 50 90 85 80 75 70 65 60 55 504 77 1980 1990 The Graph of a Function Modeling the Data 10 5 0 81 G x 0 01x x 66 2000 15 18 20 2010 FN 2

Calculus
DifferentiationPlot the ordered pair 7 6 on the rectangular coordinate plane Plot 7 6 a 2 2 10 B 6 10 8 84 2 Ay 4 6 8

Calculus
Indefinite IntegrationThe goal of this problem is to evaluate J cos 2x cos x dx First convert this to a new integral with cos 2x cos x rewritten as the sum of two trig functions rather than the product of two trig functions then integrate this new integral J cos 2x cos x dx C dx SO sin 3x 6 sin x 2
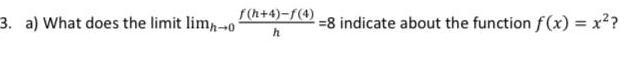
Calculus
Differentiation3 a What does the limit lim 0 f h 4 f 4 h 8 indicate about the function f x x

Calculus
Application of derivatives2 Evaluate each limit Use algebraic methods if possible If not use graphs or tables x 7x 12 x 9 2K 4K a limx 31 X 8 b limx 8 2
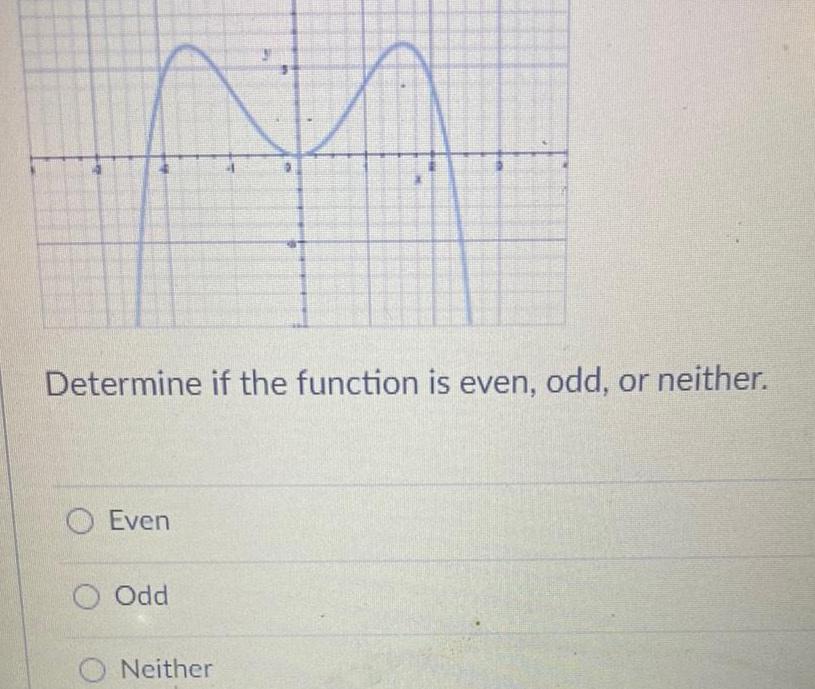
Calculus
Differential equationsNA Determine if the function is even odd or neither Even O Odd ONeither

Calculus
Application of derivativesa Are the events A and C independent Justify your answer b Are the events A and D independent Justify your answer c Compute 1 P AB and P AB Are they equal d Compute 1 P AB and P AB Are they equal 26 A large corporation has spent considerable time developing employee performance g scales to evaluate an employee s job performance on a regular basis so major adjustments e made when needed and employees who should be considered for a fast track can be isolat eys to this latter determination are ratings on the ability of an employee to perform to his or pabilities and on his or her formal training for the job


Calculus
Application of derivativesWhich inequality has a solution set of 5 00 0 1 4 0 1 4 0 1 4 02 124
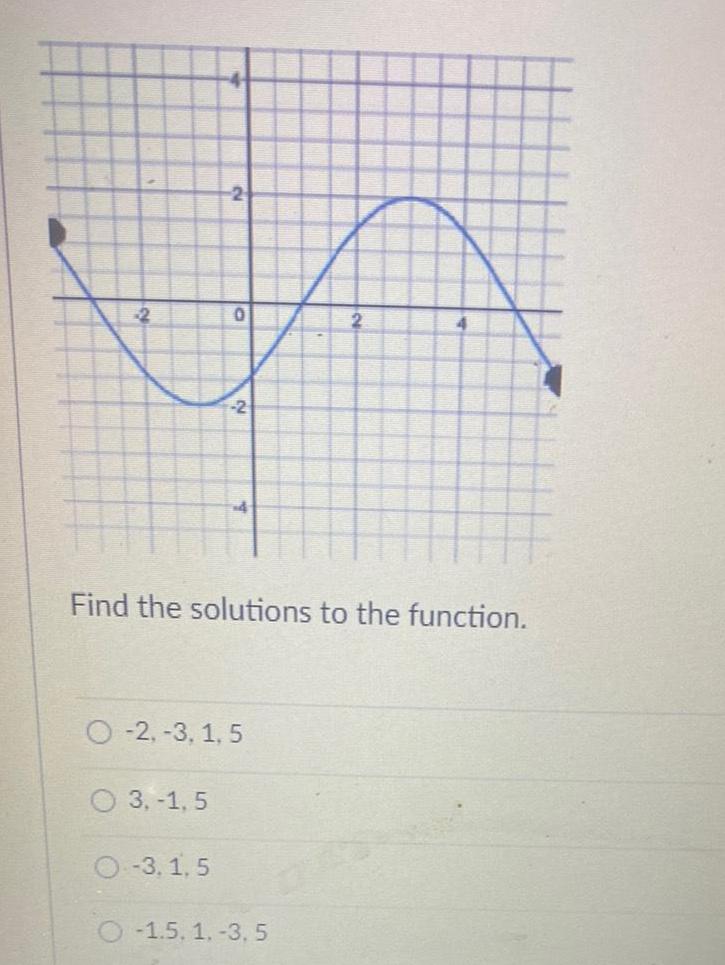
Calculus
Limits & Continuity2 4 3 1 5 2 O 3 1 5 0 2 O 2 3 1 5 Find the solutions to the function 2 O 1 5 1 3 5 4
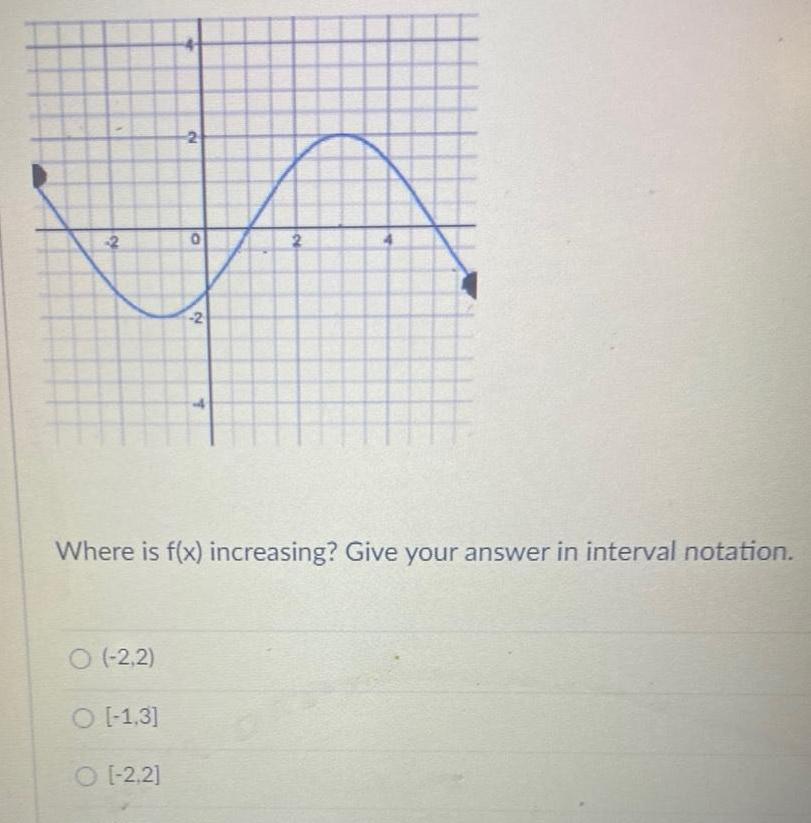
Calculus
Application of derivatives2 O 2 2 O 1 3 O 2 2 0 2 T Where is f x increasing Give your answer in interval notation

Calculus
Application of derivativesWhich function has an x intercept of 12 and a y intercept of 3 Oy 4x 3 Oy 3x 12 O y 12x 3 Oy z 3
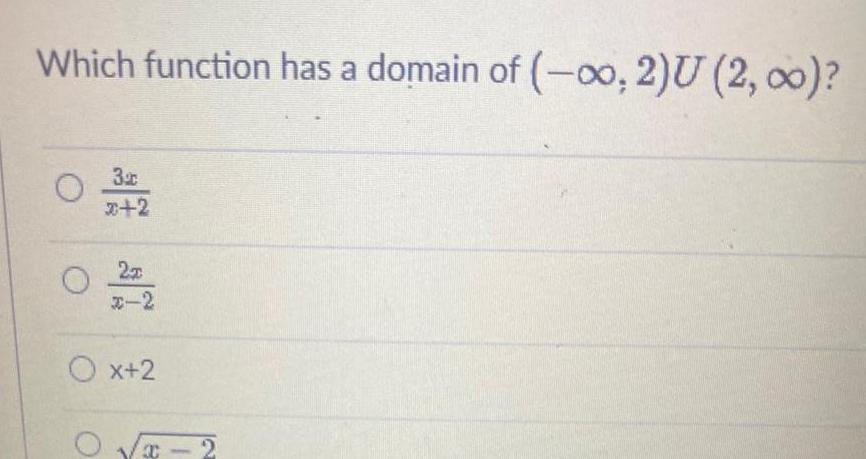
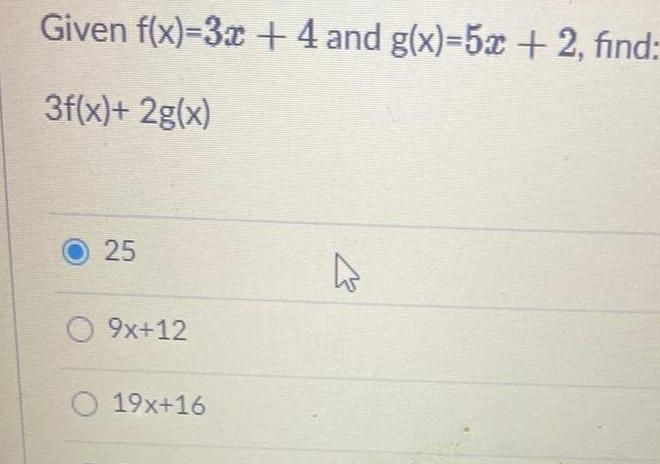


Calculus
Application of derivativesThe goal of this problem is to evaluate sin cos da using substitution 1 Because the cosine term has an odd power the first step is to rewrite cos5 x cos x cos x cos x cos x where n 0 2 Next replace the cos x term with 3 Now do a substitution with u and du dx 4 With this substitution the integral after multiplying out into a sum of powers of u becomes Odu Do not put a negative sign in front of the integral 5 Now antidifferentiate in terms of u and substitute back to get the final result siz C sin x cos5 x dx
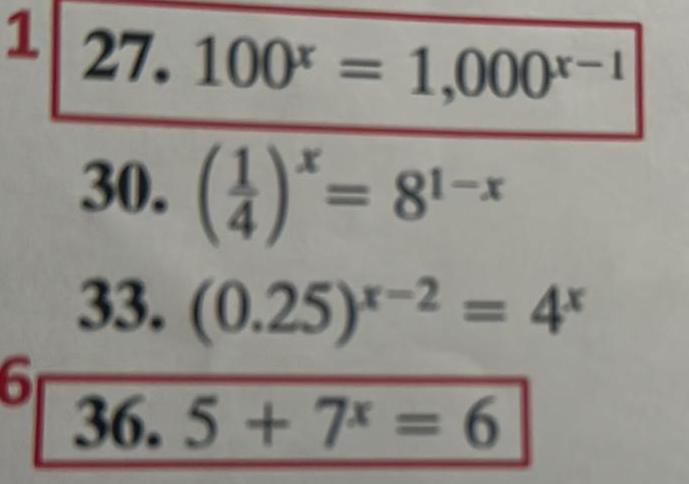

Calculus
Indefinite IntegrationThe goal of this problem is to evaluate cos 2x cos x dx First convert this to a new integral with cos 2x cos x rewritten as the sum of two trig functions rather than the product of two trig functions then integrate this new integral cos cos 2x cos x dx da C