Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
Calculus
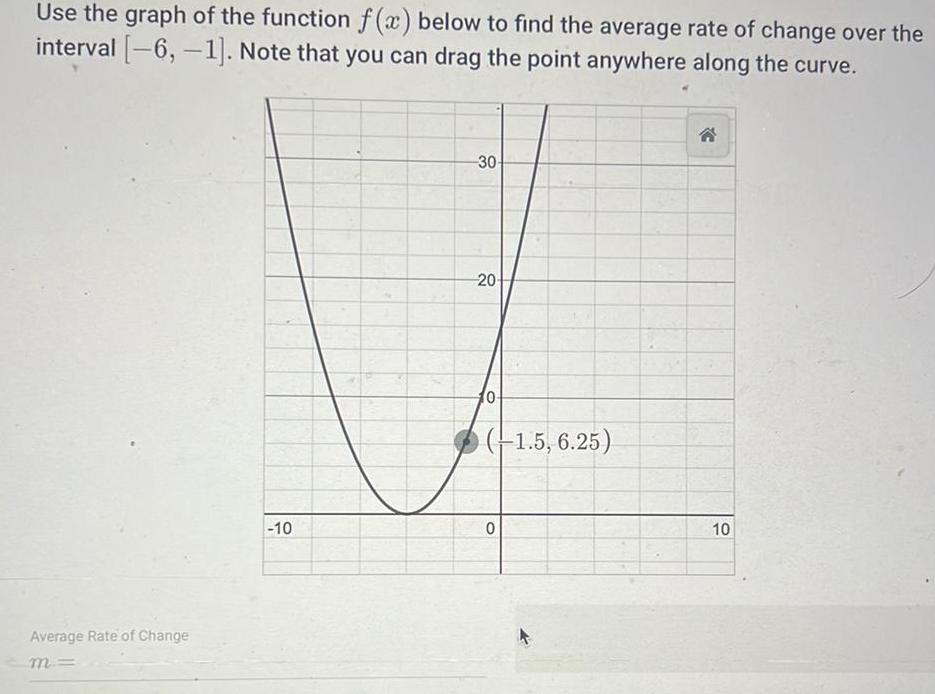
DifferentiationUse the graph of the function f x below to find the average rate of change over the interval 6 1 Note that you can drag the point anywhere along the curve Average Rate of Change m 10 30 20 10 1 5 6 25 0 10
Calculus
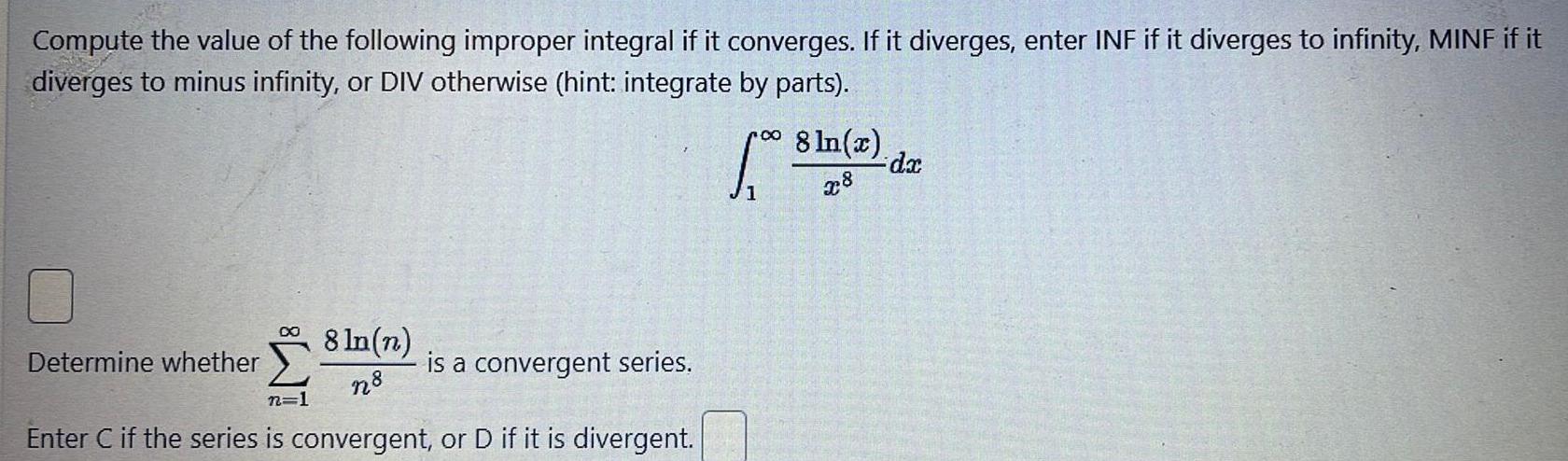
Definite IntegralsCompute the value of the following improper integral if it converges If it diverges enter INF if it diverges to infinity MINF if it diverges to minus infinity or DIV otherwise hint integrate by parts 8 ln n n8 n 1 Enter C if the series is convergent or D if it is divergent Determine whether is a convergent series 1 8 ln x x8 dx

Calculus
Limits & ContinuityFind the average rate of change of f x x 3x 2 over the following intervals a From 4 to 2 b From 1 to 1 c From 1 to 4 a The average rate of change from 4 to 2 is 25 b The average rate of change from 1 to 1 is 2 c The average rate of change from 1 to 4 is
Calculus
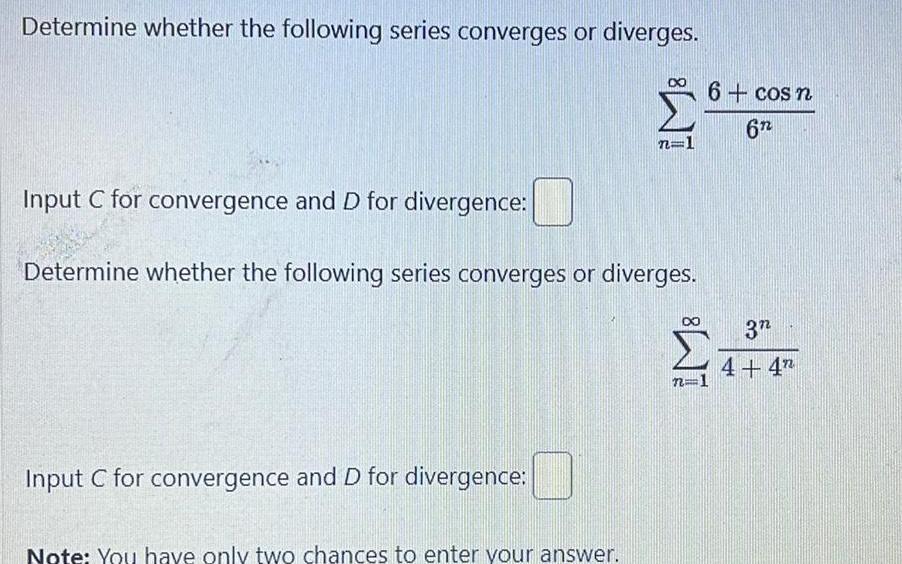
Application of derivativesDetermine whether the following series converges or diverges Input C for convergence and D for divergence Determine whether the following series converges or diverges Input C for convergence and D for divergence 7 Note You have only two chances to enter your answer 6 cos n 6n 3 4 4
Calculus
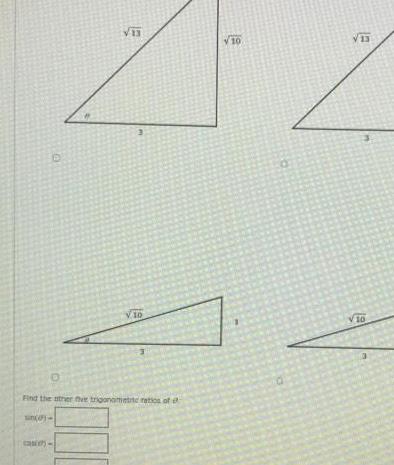
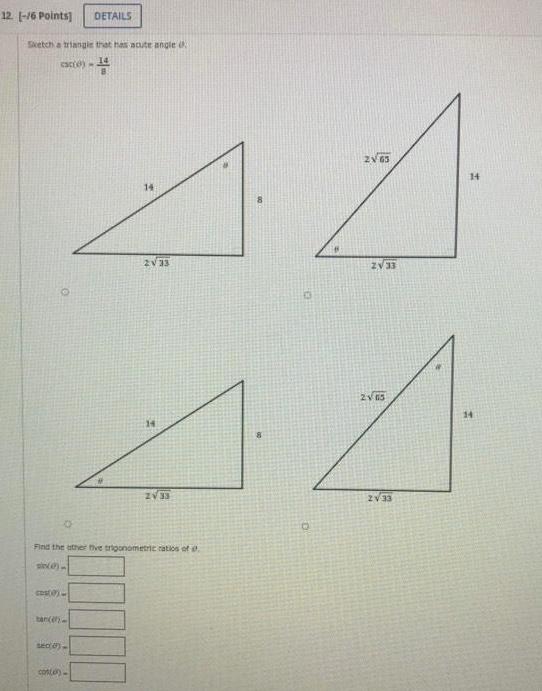
Application of derivatives12 16 Points Sketch a triangle that has acute angle cace COS 0 tan en DETAILS sec 0 con e 14 14 2 33 Find the other five trigonometric ratios of si 14 44 2 33 2V 63 O ZV 33 2165 2 33 14 14
Calculus
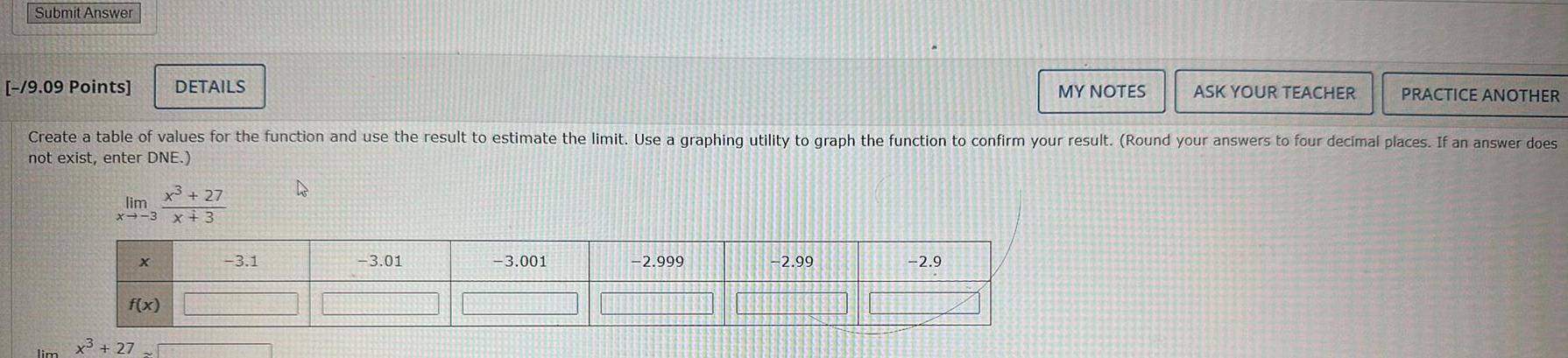
Limits & ContinuitySubmit Answer 9 09 Points Create a table of values for the function and use the result to estimate the limit Use a graphing utility to graph the function to confirm your result Round your answers to four decimal places If an answer does not exist enter DNE lim x 27 lim x 3 x 3 X f x DETAILS x 27 3 1 A 3 01 3 001 2 999 2 99 2 9 MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER
Calculus
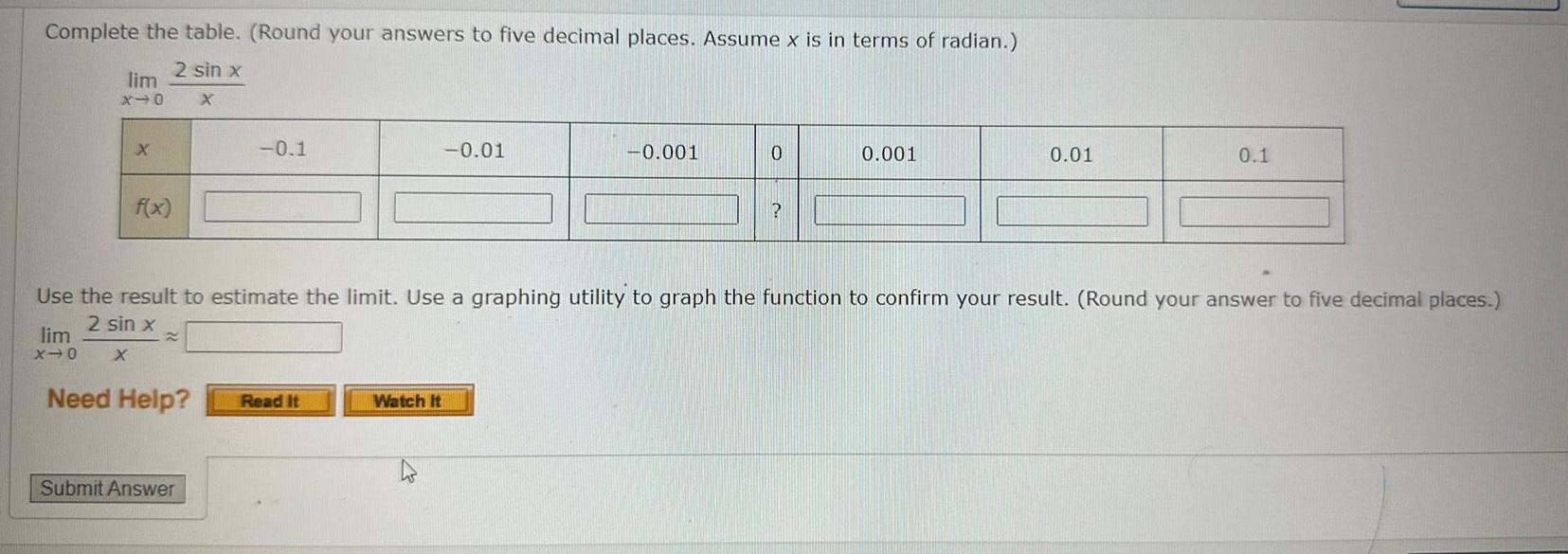
Limits & ContinuityComplete the table Round your answers to five decimal places Assume x is in terms of radian 2 sin x X lim X 0 lim X 0 X f x Need Help 0 1 Submit Answer Read It 0 01 Watch It 0 001 0 Use the result to estimate the limit Use a graphing utility to graph the function to confirm your result Round your answer to five decimal places 2 sin x X 0 001 0 01 0 1
Calculus
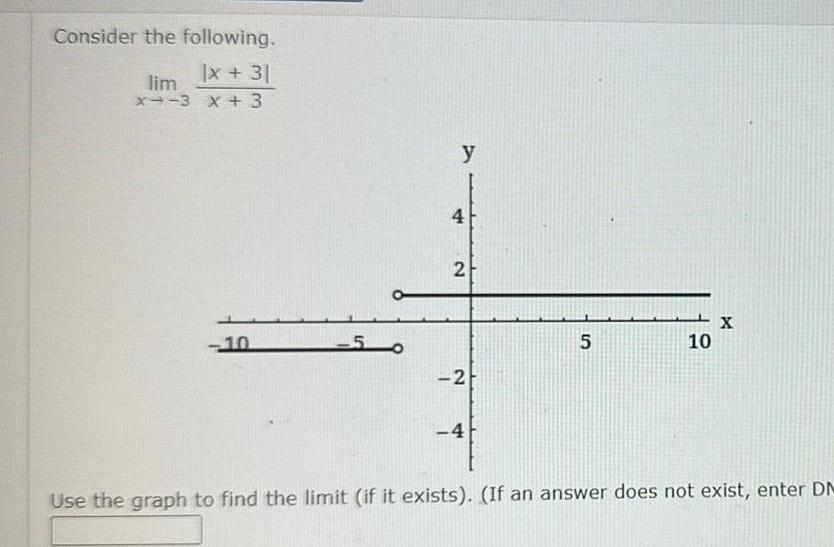
Limits & ContinuityConsider the following x 31 lim x 3 x 3 10 50 y 4 2 2 4 5 10 X Use the graph to find the limit if it exists If an answer does not exist enter DM
Calculus
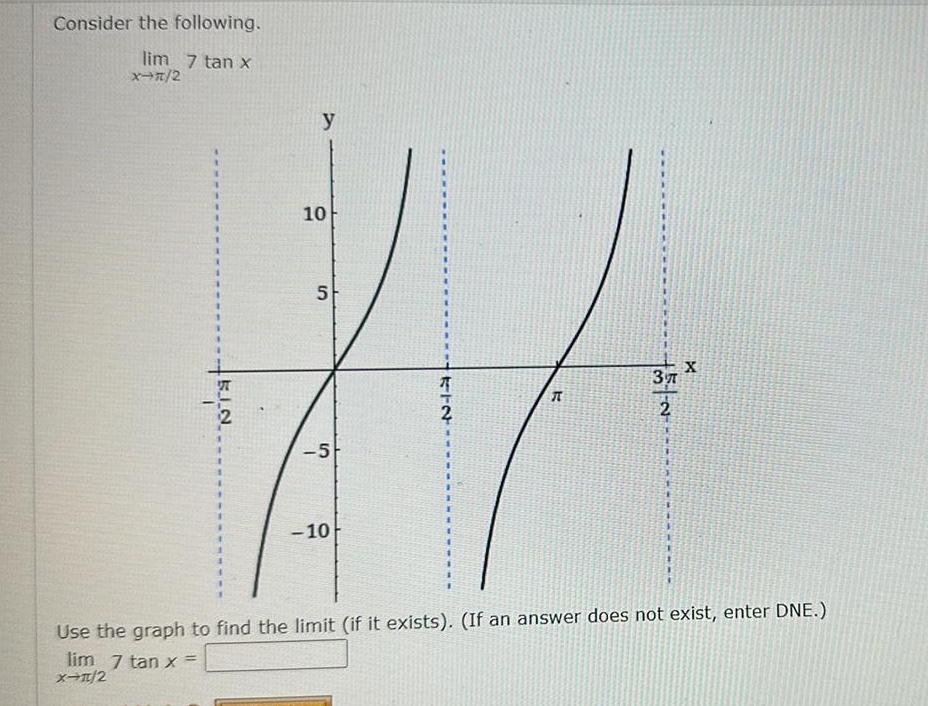
Limits & ContinuityConsider the following lim 7 tan x X 2 27 X 1 2 y 10 5 5 10 712 E 5 37 2 X Use the graph to find the limit if it exists If an answer does not exist enter DNE lim 7 tan x
Calculus
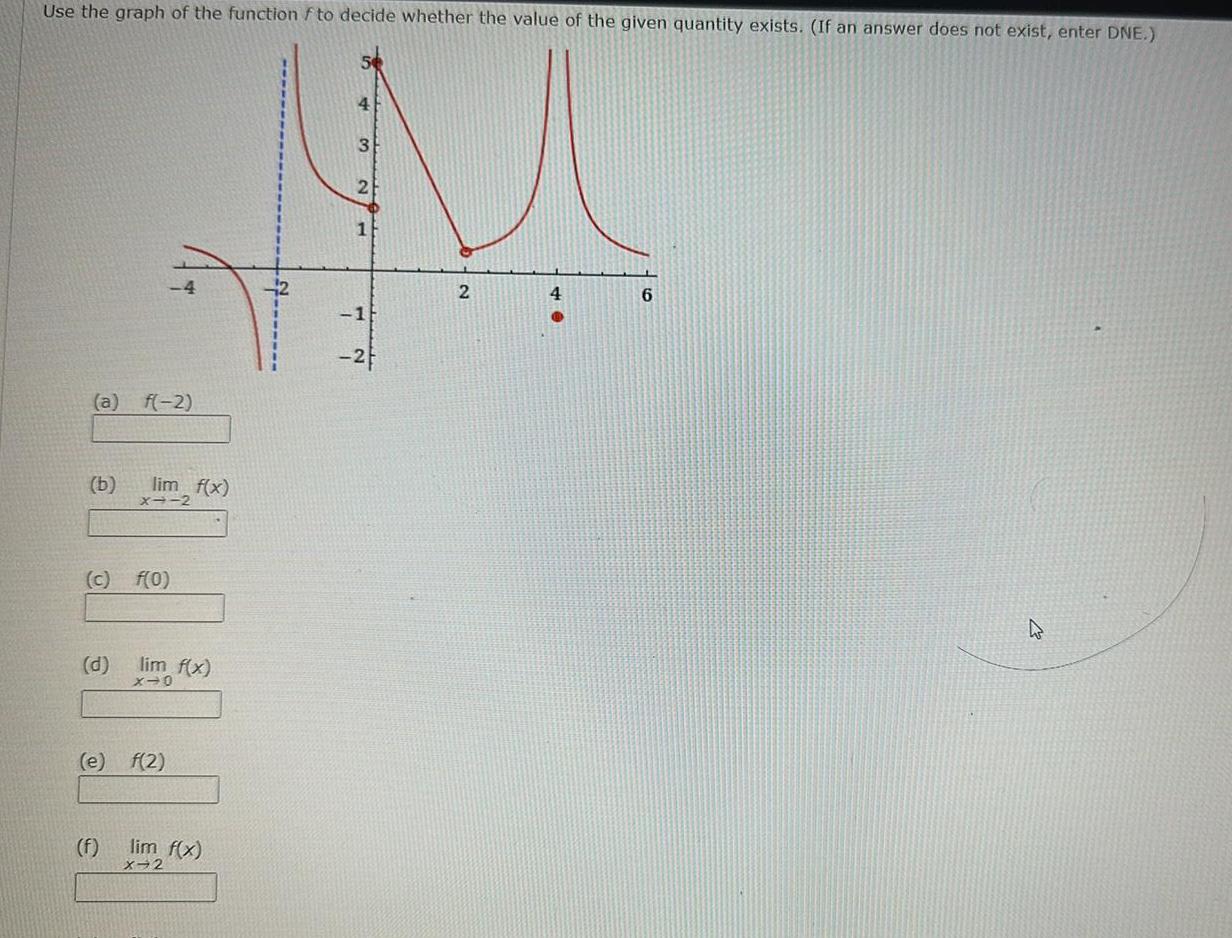
Limits & ContinuityUse the graph of the function f to decide whether the value of the given quantity exists If an answer does not exist enter DNE 4 M 2 1 2 a f 2 b d c f 0 4 lim f x f X 2 e f 2 lim f x X 0 lim f x X 2 1 2 6 2

Calculus
Application of derivatives60 For what value of x does the graph of f x e 2x have a horizontal tangent
Calculus
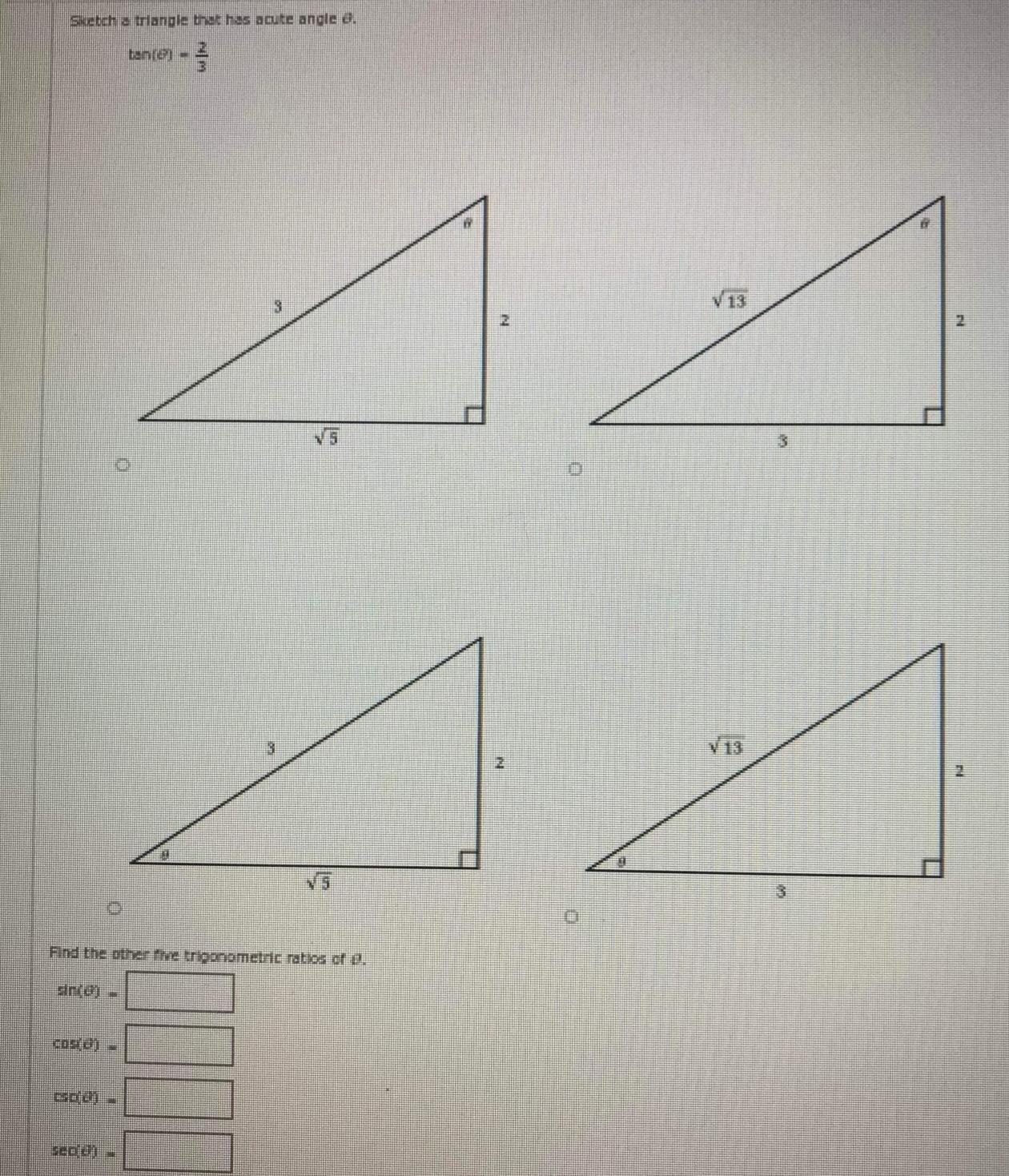
Application of derivativesSketch a triangle that has acute angle COS 2 GOU SCD UI tantel Find the other the trigonometric ratios of t drid THE NM 3 3 D VA 2 2

Calculus
Application of derivativesA cardiac monitor is used to measure the heart rate of a patient after surgery It compiles the number of heartbeats after t minutes When the data in the table are graphed the slope of the tangent line represents the heart rate in beats per minute t min 36 38 40 42 44 Heartbeats 2505 2640 2773 2906 3042 The monitor estimates this value by calculating the slope of a secant line Use the data to estimate the patient s heart rate after 42 minutes using the secant line between the points with the given values of t Round your answers to one decimal place a t 36 and t 42 67 8 x b t 38 and t 42 67 25 X c t 40 and t 42 66 5 d t 42 and t 44 69
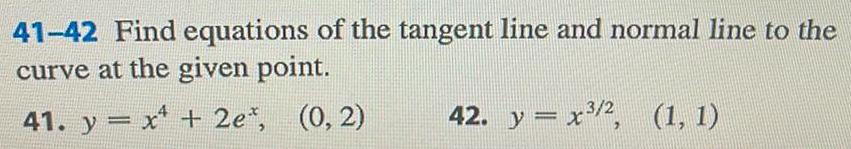
Calculus
Differentiation41 42 Find equations of the tangent line and normal line to the curve at the given point 41 y x 2e 0 2 42 y x 2 1 1
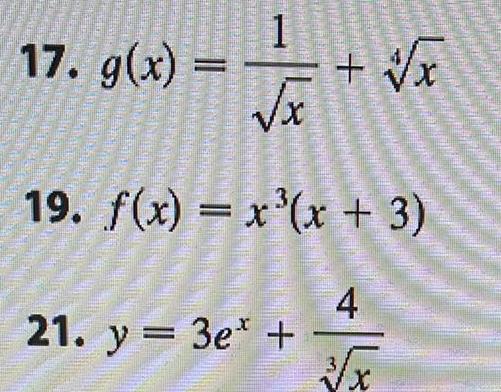
Calculus
DifferentiationROME WAST OVERNAN ARRAY THEATER 20 2 2 WHISTE DAE 1950 17 g x DONE 1 x x 19 f x x x 3 4 x 21 y 3e

Calculus
Limits & ContinuityCOS X a By graphing the function f x cos 2x and zooming in toward the point where the graph crosses the y axis estimate the value of limx o f x 5 Check your answer in part a by evaluating f x for values of x that approach 0
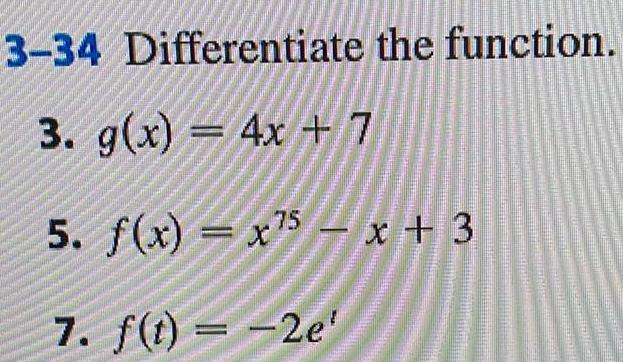

Calculus
Limits & ContinuityFind the points on the curve y x 3x 9x 8 where the tangent is horizontal smaller x value x y larger x value x y Enhanced Feedback Please try again Find the x value where X dy is equa h

Calculus
Limits & Continuitya How is the number e defined b Use a calculator to estimate the values of the limits 2 7h 1 lim h 0 h and lim h 0 2 8h 1 h correct to two decimal places What can you conclude about the value of e
Calculus
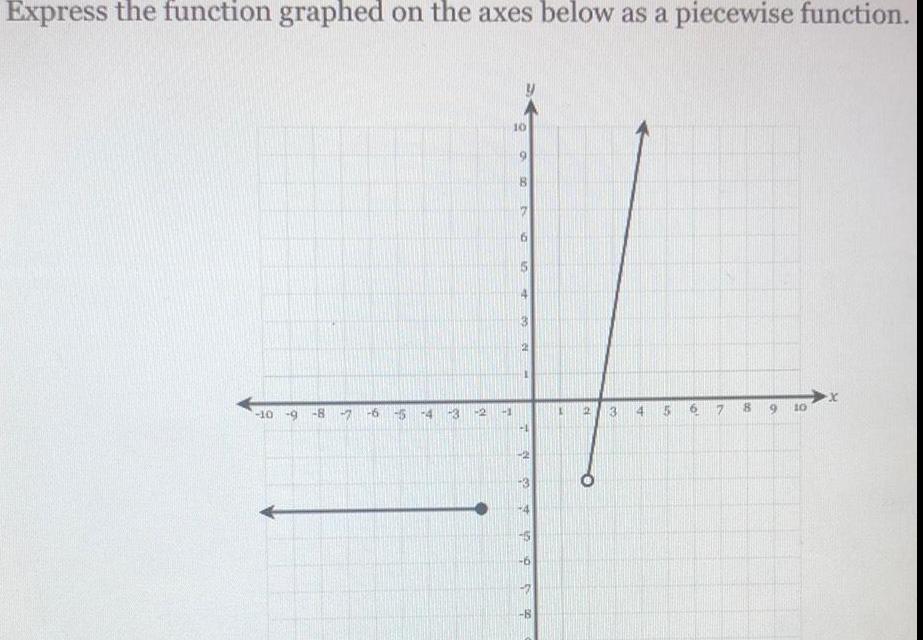
Limits & ContinuityExpress the function graphed on the axes below as a piecewise function 10 9 8 7 6 S T 8 15 4 10 6 00 P 10 t 45 7 35 8 15 O 3 MT 45 vo 7 8 9 10
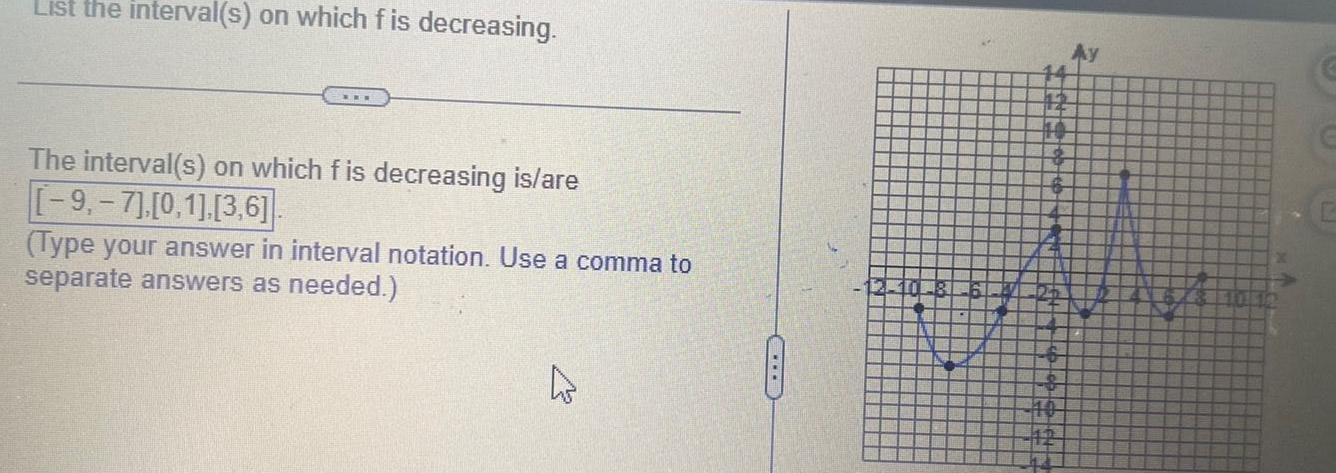
Calculus
Application of derivativesList the interval s on which f is decreasing The interval s on which f is decreasing is are 9 7 0 1 3 6 Type your answer in interval notation Use a comma to separate answers as needed 4 14 12 14 10 4 Ay

Calculus
Differentiation5 Suppose lim f x 1 lim f x 1 and f 3 is not defined Which if any of the following Statements may be false A lim f x 1 3113 B f is continuous everywhere except at x 3 C If we redefine f 3 to be equal to 1 then the new function will be continuous at x 3 D f has a removable discontinuity at x 3 E All of the preceding statements are true
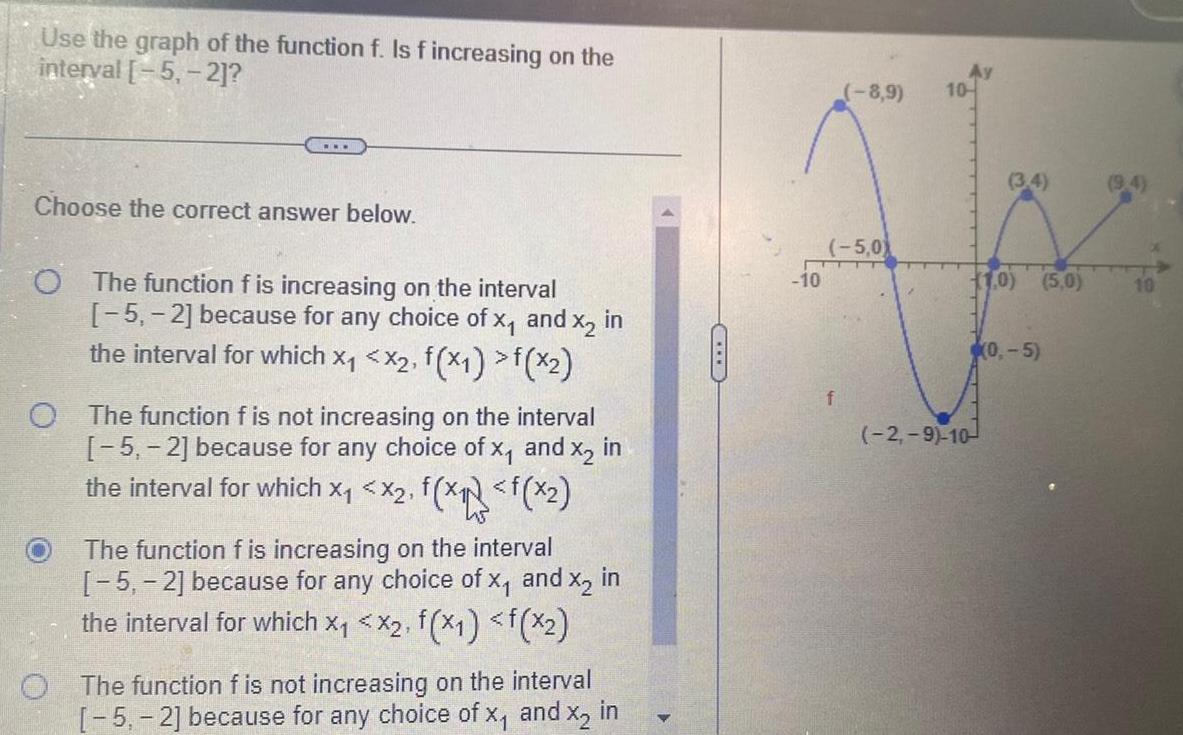
Calculus
Limits & ContinuityUse the graph of the function f Is f increasing on the interval 5 2 Choose the correct answer below O The function f is increasing on the interval 5 2 because for any choice of X and x in the interval for which x x2 f x1 f x2 O The function f is not increasing on the interval 5 2 because for any choice of x and x2 in the interval for which X X2 f x f x The function f is increasing on the interval 5 2 because for any choice of x and x in the interval for which x x2 f x1 f x2 O The function f is not increasing on the interval 5 2 because for any choice of x and x in CIT 10 8 9 5 0 T f 10 3 4 1 0 2 9 10 0 5 5 0 10

Calculus
Indefinite IntegrationEvaluate the integral sint dt 5 3 cost OA 1 4 3 cost 4 OB 4 3 cost OC C 1 3 cost 4 OD C C 1 6 3 cost 6 C

Calculus
DifferentiationSolve the initial value problem d s dt 162 cos 9t s 0 13 s 0 8 OA s 18 cos 9t 13t 10 OB S 18 sin 9t 13 OC s 2 cos 9t 13t 6 OD s 2 cos 9t 6

Calculus
Differential equationsEvaluate the integral fe cot e 6 dt O A e In sin t 6 C OB Incos e 6 C OC In sin 6 C OD In sin t 6 C

Calculus
Indefinite IntegrationEvaluate the integral 3x 1 10 2x dx OA 12 10 2x3 5 4 C OB 2 10 2x 3 4 C OC 3 10 2x3 5 4 C 2 OD 10 2x 5 4 C C
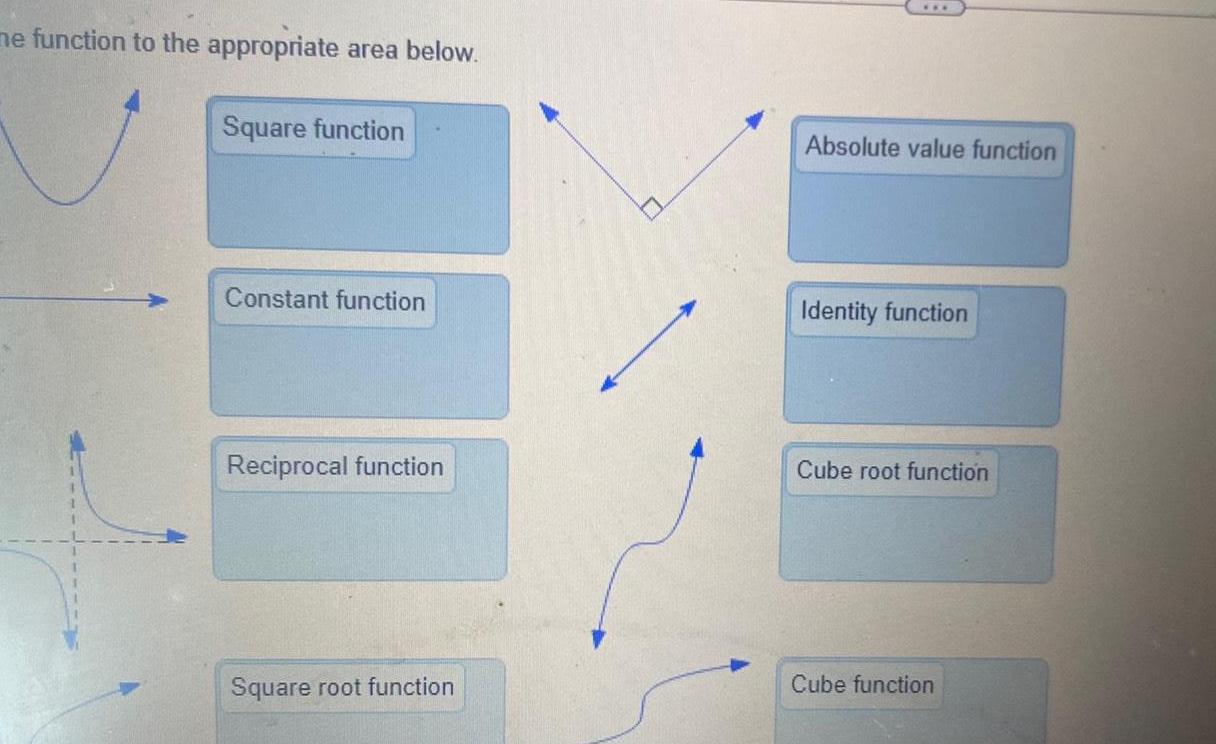
Calculus
Vector Calculusme function to the appropriate area below Square function Constant function Reciprocal function Square root function Absolute value function Identity function Cube root function Cube function
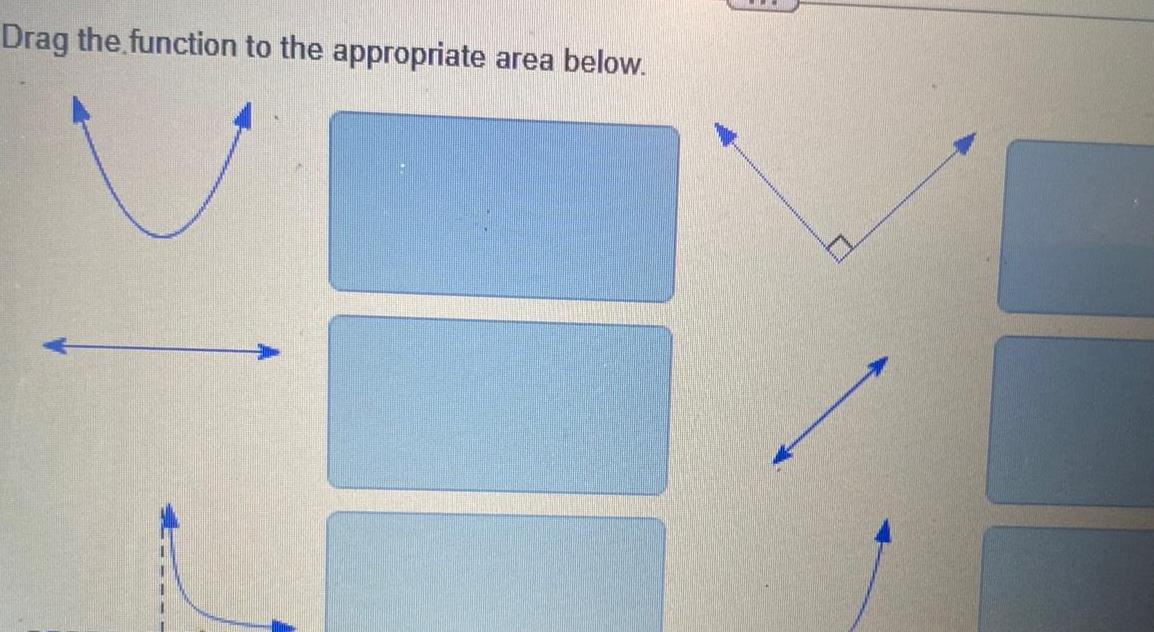
Calculus
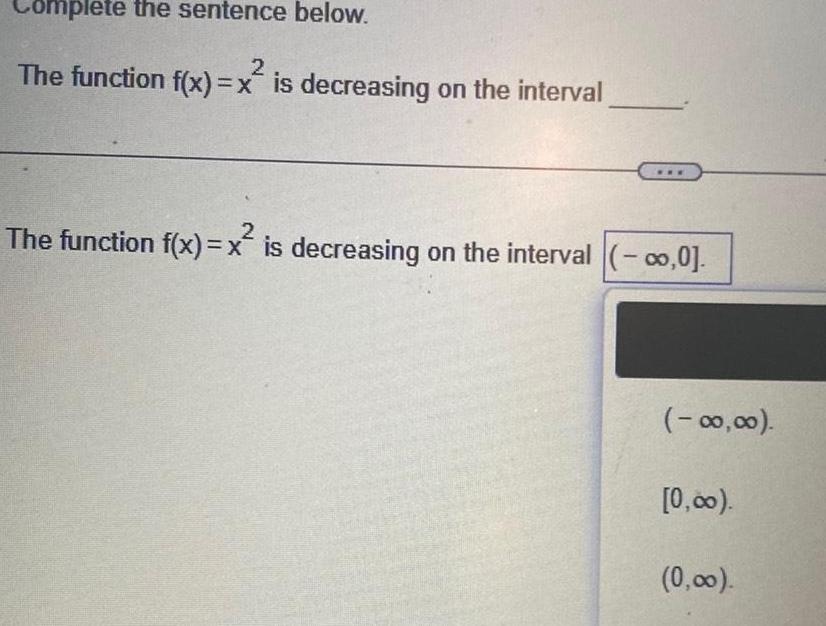
Application of derivativesComplete the sentence below 2 The function f x x is decreasing on the interval 2 The function f x x is decreasing on the interval 0 00 00 0 00 0 00

Calculus
DifferentiationUse the English and metric equivalents to the right along with dimensional analysis to convert the given measurement to the unit indicated 20 m to yd yd Round to the nearest hundredth Approximate English and Metric Equiv 2 54 cm 30 48 cm 1 in 1 ft 1 yd 1 mi 0 9 m 1 6 km
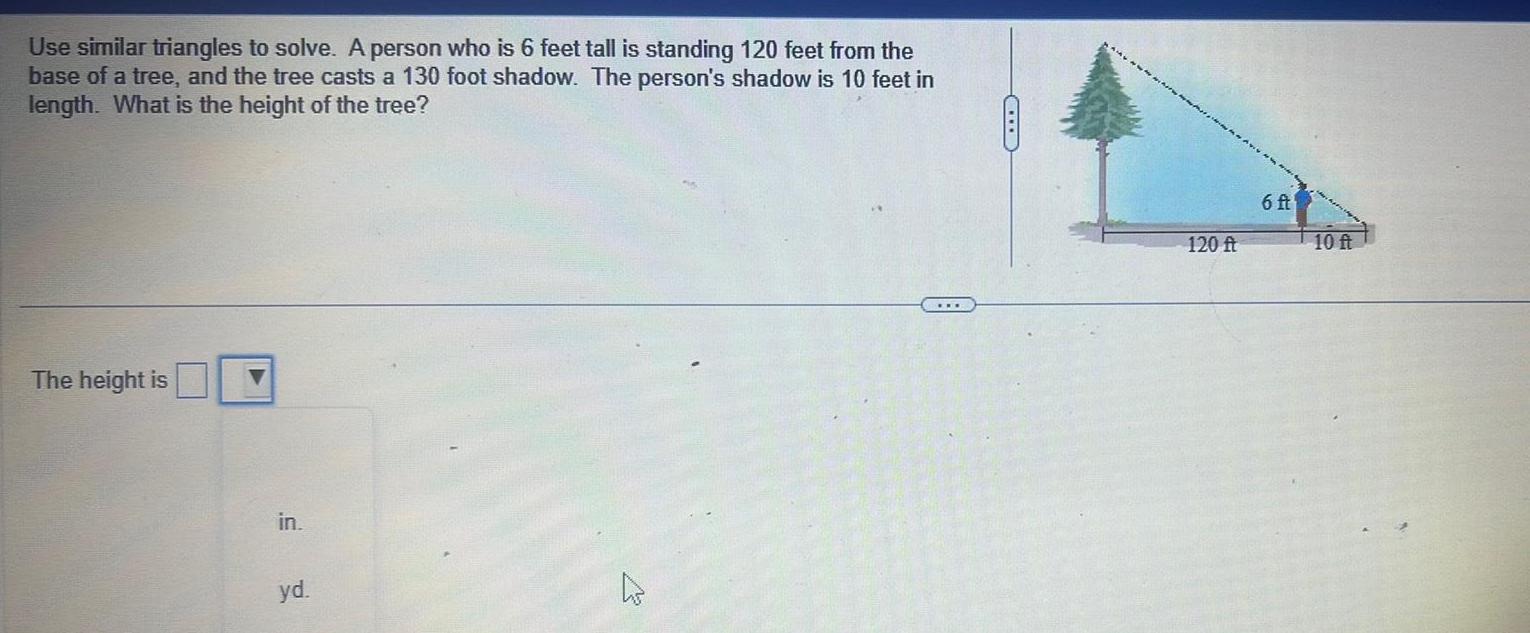
Calculus
Application of derivativesUse similar triangles to solve A person who is 6 feet tall is standing 120 feet from the base of a tree and the tree casts a 130 foot shadow The person s shadow is 10 feet in length What is the height of the tree The height is in yd C 120 ft 6 ft 10 ft
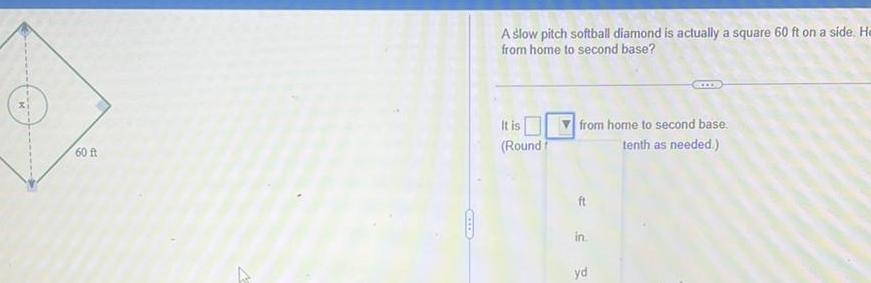
Calculus
Differentiation60 ft A GOOOD A slow pitch softball diamond is actually a square 60 ft on a side He from home to second base It is Round from home to second base tenth as needed ft in yd

Calculus
Differential equationsIf construction costs are 144 000 per kilometer find the cost of building the new road in the figure shown to the right The cost of building the new road is s Round to the nearest dollar as needed new road 24 000 m 10 000 m


Calculus
Application of derivatives8 12 11 U 19 find 12 9Find f 0 the graph of f x shown 10 Solve f x 0 11 Find f 0 12 Solve f x 0 13 Sketch f x 12 Using the graph shown a Find g 1 b Solve g x 1 X f x c Find g 1 d Solve g x 1 e Sketch f x t h t 13 Use the table below to find the indicated quantities 0 1 2 3 7 1 14 Find f 7 15 Solve f x 4 16 Find f 8 17 Solve f x 2 3 9 a Find h 3 b Solve h t 5 c Find h 0 10 4 6 14 Use the table below to fill in the missing values 0 1 2 3 4 9 4 7 2 5 10 If 1 7 find 1 5 2 2 3 2 1 f x 1 2 3 5 1 6 8 g x 2 3 6 8 7 5 4 7 0 8 0 9 4 8 3
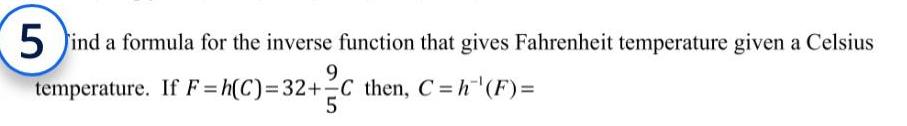
Calculus
Application of derivatives5 ind a formula for the inverse function that gives Fahrenheit temperature given a Celsius 9 temperature If F h C 32 C then C h F 5
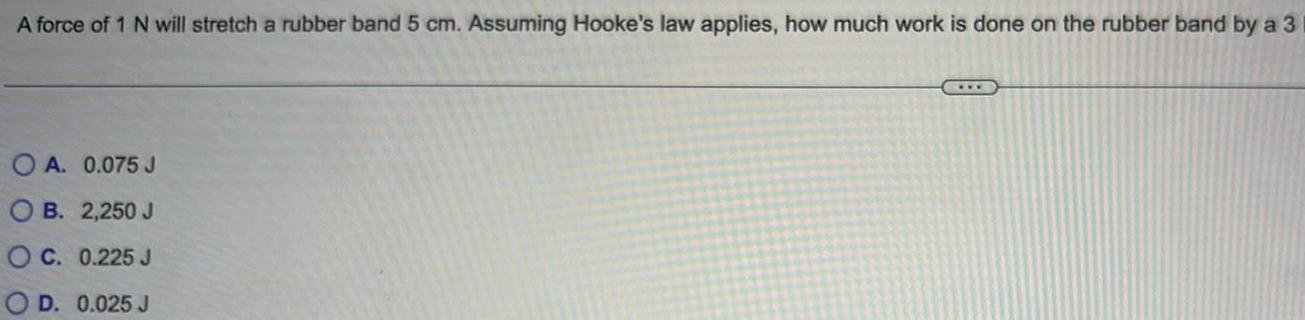
Calculus
Definite IntegralsA force of 1 N will stretch a rubber band 5 cm Assuming Hooke s law applies how much work is done on the rubber band by a 3 A 0 075 J OB 2 250 J C 0 225 J D 0 025 J
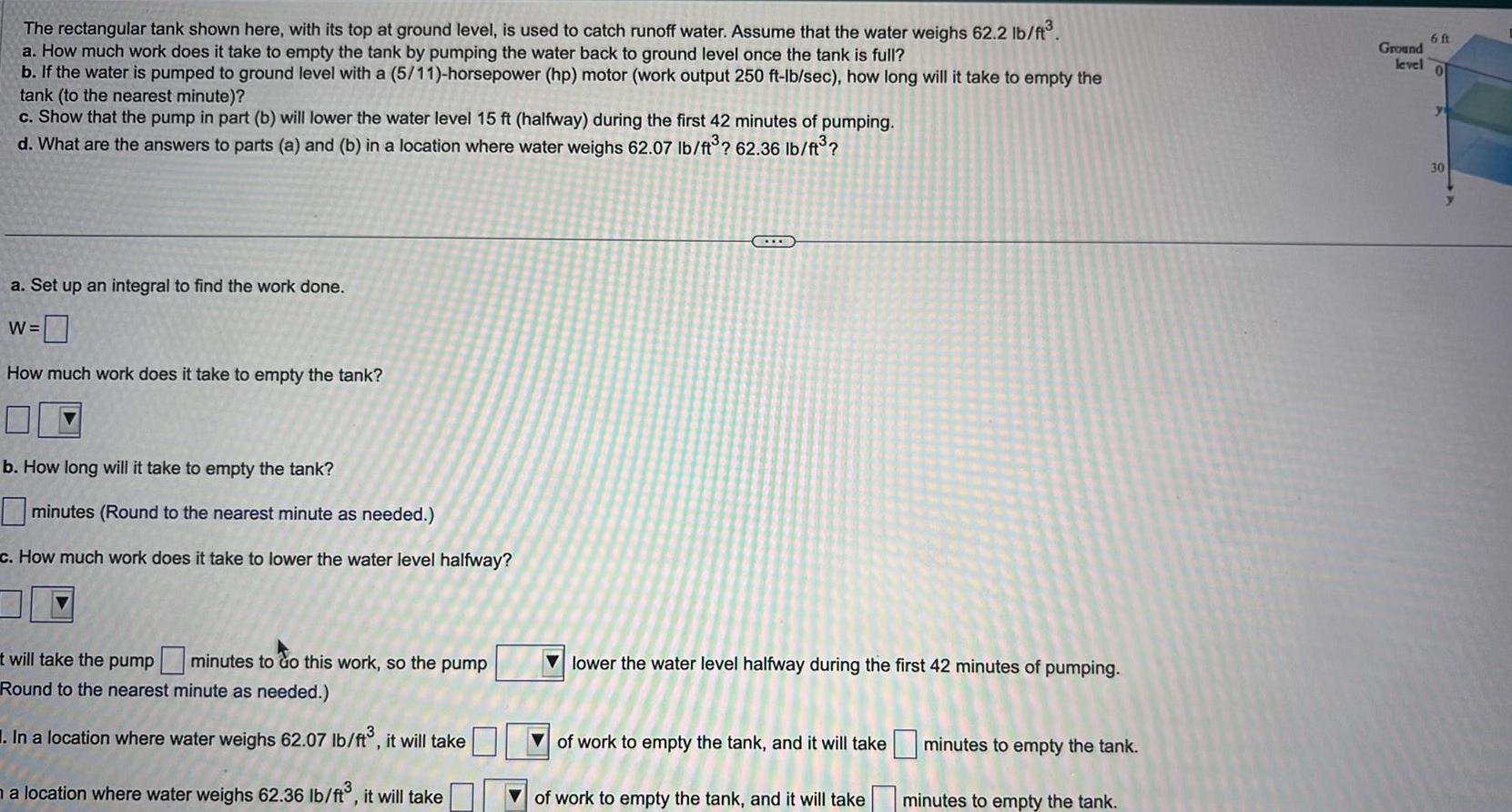
Calculus
Application of derivativesThe rectangular tank shown here with its top at ground level is used to catch runoff water Assume that the water weighs 62 2 lb ft a How much work does it take to empty the tank by pumping the water back to ground level once the tank is full b If the water is pumped to ground level with a 5 11 horsepower hp motor work output 250 ft lb sec how long will it take to empty the tank to the nearest minute c Show that the pump in part b will lower the water level 15 ft halfway during the first 42 minutes of pumping d What are the answers to parts a and b in a location where water weighs 62 07 lb ft 62 36 lb ft a Set up an integral to find the work done W How much work does it take to empty the tank b How long will it take to empty the tank minutes Round to the nearest minute as needed c How much work does it take to lower the water level halfway t will take the pump minutes to do this work so the pump Round to the nearest minute as needed In a location where water weighs 62 07 lb ft it will take a location where water weighs 62 36 lb ft it will take TE lower the water level halfway during the first 42 minutes of pumping of work to empty the tank and it will take of work to empty the tank and it will take minutes to empty the tank minutes to empty the tank Ground level 6 ft 0 30

Calculus
DifferentiationSolve the initial value problem d s dt 3 2 7 81 sin 9t OA s sin 9t 91 OB s sin 9t n st 3 2 OC s sin 9t 3 2 O D s 9cos 9t s 0 8 s 0 2 7 3 2 3 2 8t 3 7t 2 8

Calculus
Application of derivativesbtract Simplify by collecting like radical terms if possible assuming that all expressions under radicals represent non negative numbers 54x 3 2x4 54x 3 2x 3 2x x 2x Simplify your answer Type an exact answer using radicals as needed

Calculus
Definite IntegralsA water tank in the shape of a hemispherical bowl of radius 6 m is filled with water to a depth of 3 m rm dm How much work is required to pump all the water over the top of the tank The density of water is 1000 kg m Use symbolic notation and fractions where needed

Calculus
Definite IntegralsMultiply and simplify Assume that all expressions under the radicals represent nonnegative numbers 9 n Type an exact answer using radicals as needed

Calculus
DifferentiationSimplify by taking roots of the numerator and the denominator 3 3 729 8 729 8 Simplify your answer Type an exact answer using radicals as needed
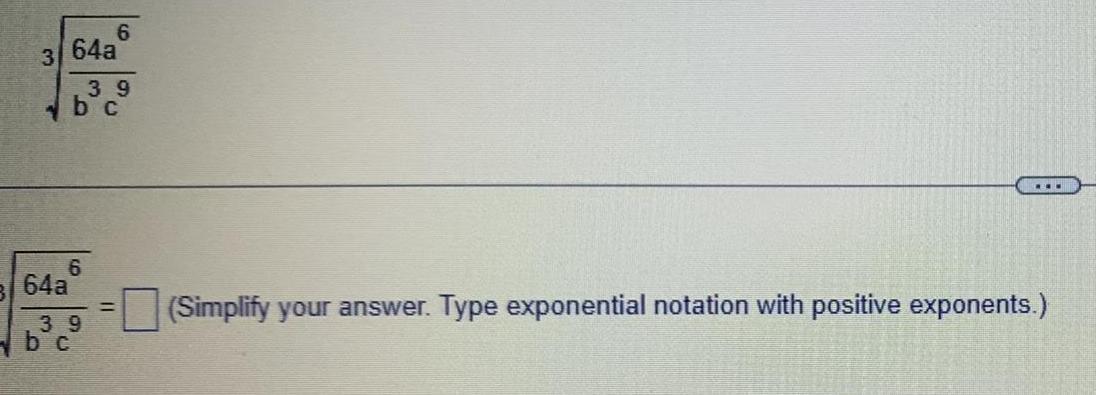
Calculus
Indefinite Integration3 64a 6 39 bc 6 64a 39 bc Simplify your answer Type exponential notation with positive exponents
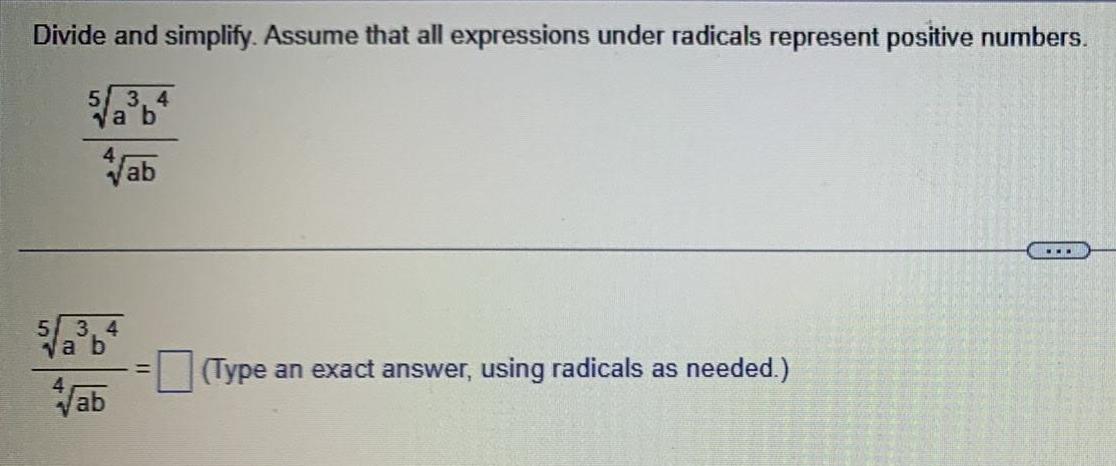
Calculus
Limits & ContinuityDivide and simplify Assume that all expressions under radicals represent positive numbers 5 3 4 va b Vab 5 3 4 va b Vab Type an exact answer using radicals as needed