Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
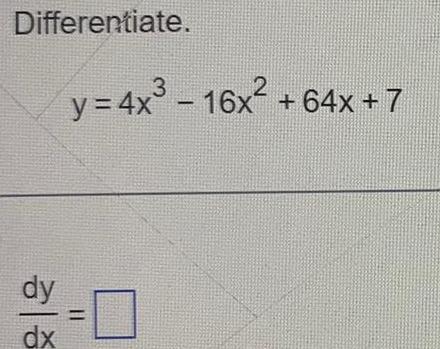
Differentiation6 6 Suppose a is expanded in descending powers of a a Write down the r 1 th term of the expansion where 0 r 6 b Write down the first and the middle term of the expansion
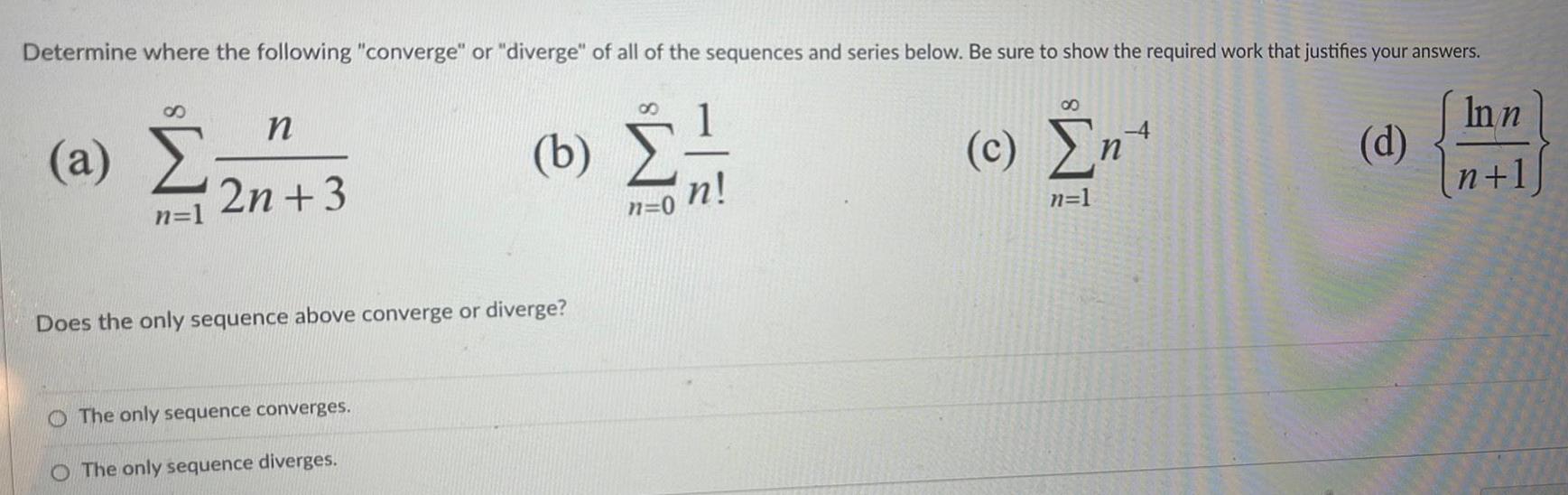
Calculus
Application of derivativesDetermine where the following converge or diverge of all of the sequences and series below Be sure to show the required work that justifies your answers S a n 1 n 2n 3 b n 0 Does the only sequence above converge or diverge The only sequence converges O The only sequence diverges n 8 c Ent n 1 d Inn n 1
Calculus
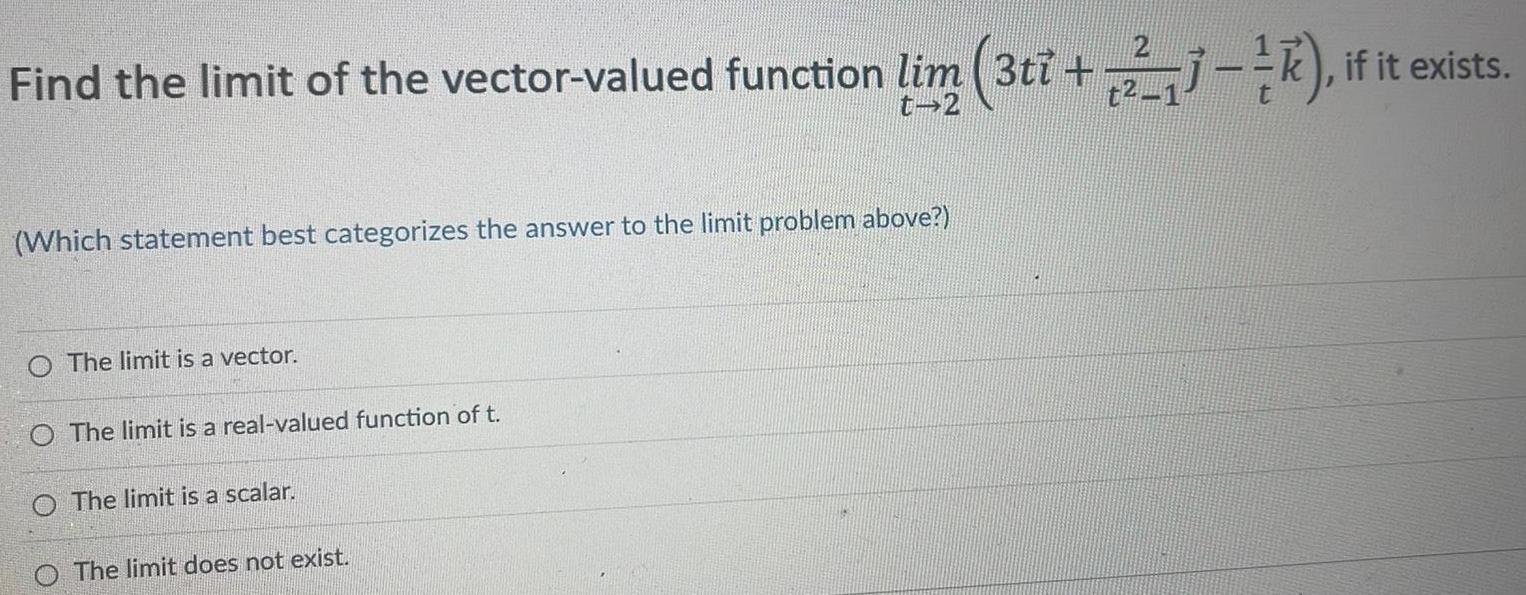
Application of derivativesFind the limit of the vector valued function lim 3ti 23 if it exists t2 t 2 Which statement best categorizes the answer to the limit problem above O The limit is a vector O The limit is a real valued function of t O The limit is a scalar The limit does not exist

Calculus
Vector CalculusUse the given vector valued function to find each of the following r t t i 2t 3 j 3t 5 k a t b 7 t c t d r t t e t x 7 t Which choice below best describes the third derivative of the given vector valued function O The third derivative is a vector The third derivative is a scalar The third derivative is a real valued function of t The third derivative does not exist
Calculus
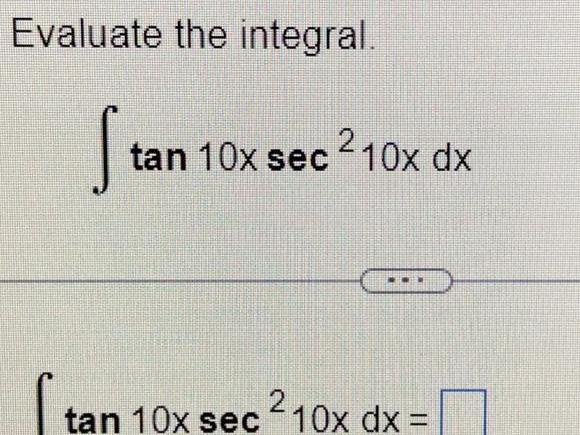
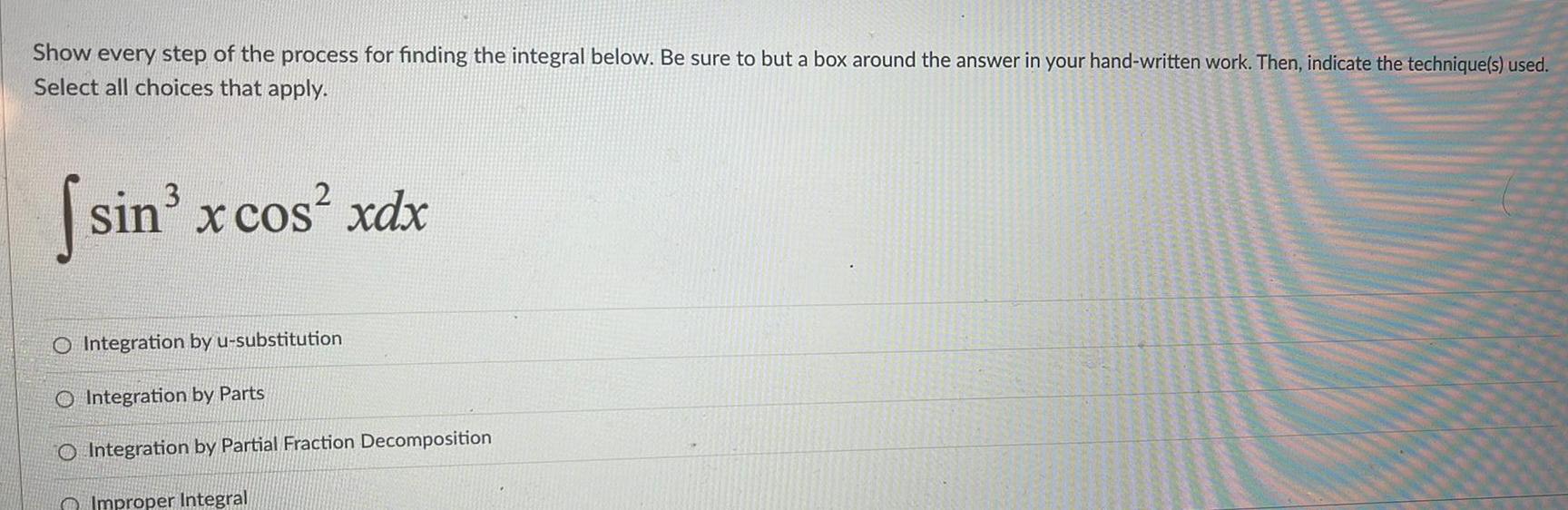
Definite IntegralsShow every step of the process for finding the integral below Be sure to but a box around the answer in your hand written work Then indicate the technique s used Select all choices that apply sin x cos xdx O Integration by u substitution O Integration by Parts O Integration by Partial Fraction Decomposition Improper Integral

Calculus
Vector CalculusGiven that u 3 4 2 and v 1 2 3 find a The vector component of u along w b The vector component of u orthogonal to v W Which of the vector components that you found above is the projection of vector u onto vector v Select the choice part a O part b
Calculus
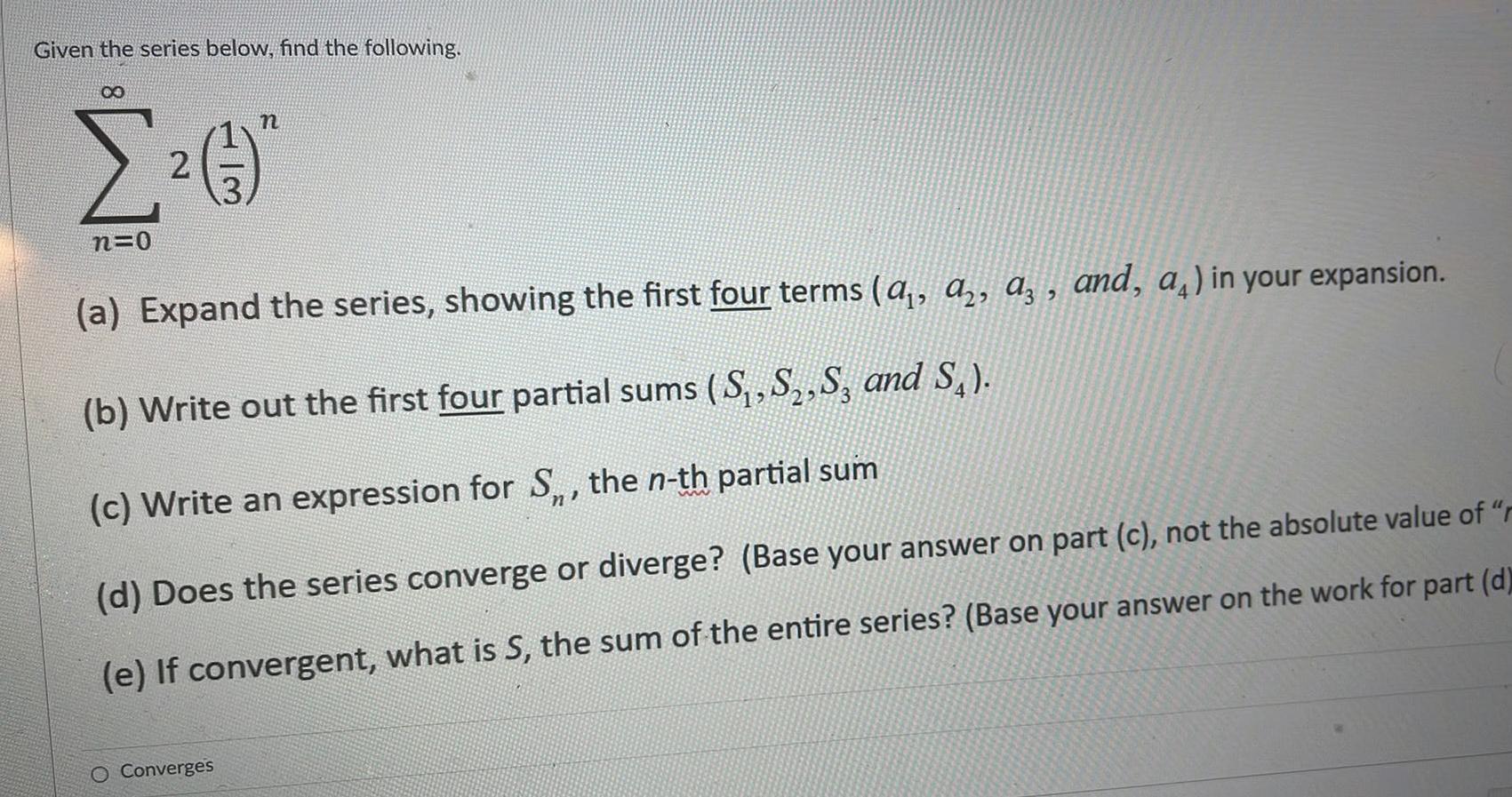
Definite IntegralsGiven the series below find the following 8 n 2 n 0 a Expand the series showing the first four terms a a a and a in your expansion b Write out the first four partial sums S S S3 and S c Write an expression for S the n th partial sum d Does the series converge or diverge Base your answer on part c not the absolute value of r e If convergent what is S the sum of the entire series Base your answer on the work for part d O Converges

Calculus
Application of derivativesa Create a table of values for the variables found in the given parametric equations below b Write the corresponding rectangular equation by eliminating the parameter c Sketch the curve represented by the parametric equations indicate the orientation of the cur x t 1 y t 3t 3 t 2 According to your table of values when x 0 what does y equal Enter this answer in the space provided
Calculus
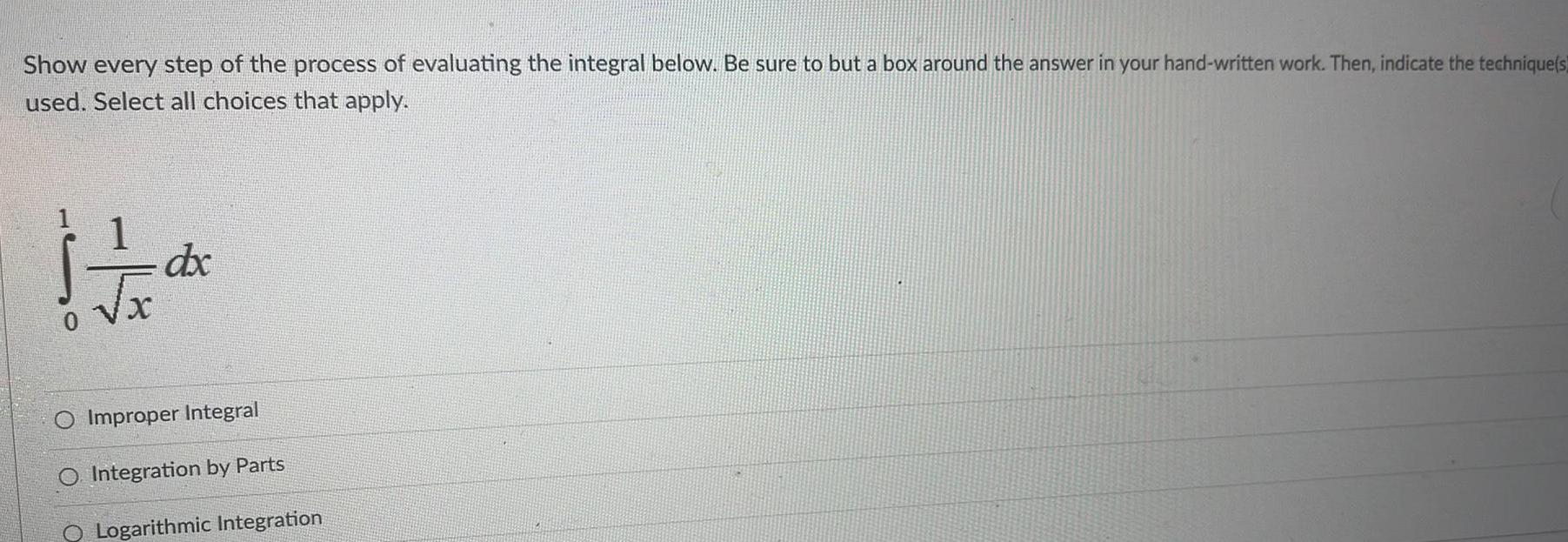
Limits & ContinuityShow every step of the process of evaluating the integral below Be sure to but a box around the answer in your hand written work Then indicate the technique s used Select all choices that apply 11 x dx O Improper Integral O Integration by Parts O Logarithmic Integration
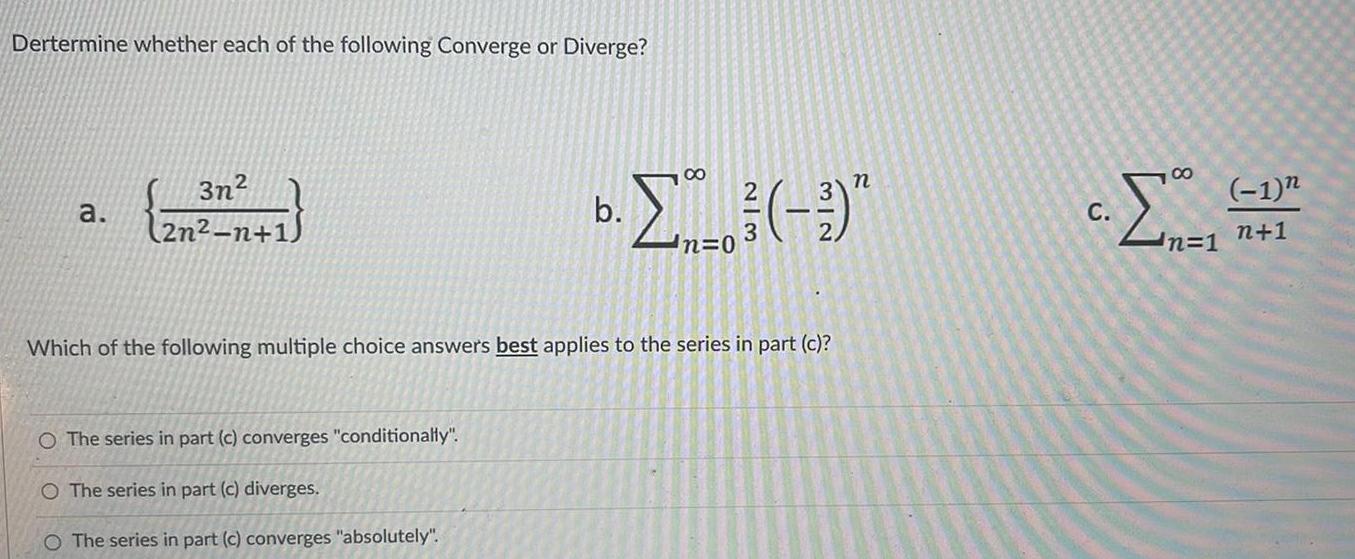
Calculus
Limits & ContinuityDertermine whether each of the following Converge or Diverge a 3n 2n n 1 8 n b n 0 Which of the following multiple choice answers best applies to the series in part c The series in part c converges conditionally O The series in part c diverges O The series in part c converges absolutely C 221 n 1 1 n 1

Calculus
Application of derivativesConsider the function f x sin x Write the fifth Maclaurin polynomial P5 x for sin x b Write the Maclaurin series representation in sigma notation for sim Use P5 x to approximate sin 0 8 to six decimal places a C Enter part c rounded to six decimal places in the space provided

Calculus
Application of derivativesGiven that u 3 4 2 and 1 2 3 find a u b uxi Enter the answer to part a in the space provided c the unit vector in the same direction as

Calculus
Limits & ContinuityFor the given conic section determine each of the following a the type of conic section b the center if applicable c the focus or foci d the vertex or vertices e the eccentricity Which of the choices below is the correct type of conic section for the equation above O Ellipse O Circle 9x 4y 36x 24y 36 0 Parabola O Hyperbola Degenerate Conic

Calculus
Application of derivativesFind the interval of convergence of the power series Express your answer in interval notation n 1 x 5 n n Do not skip any spaces when entering the interval of convergence

Calculus
Application of derivatives3 Consider the following system of linear equations 3Z X 2x 2y 5z X 2Z 1 2 0 a Write down the coefficient matrix A i e the matrix of coefficients of the above syster and determine A 0 4 2 2 4 b Show that AA and A A I where is the 3 x 3 identity matrix c Use A to solve the system d Evaluate Al by expanding by the second column e Use Cramer s rule to solve the above system

Calculus
Definite Integrals2 Use the Integral Test to determine whether the following series converge after showing that the conditions of the Integral Test are satisfied a b en 1 en 1 k lnk

Calculus
DifferentiationOut of pocket spending in a country for health care increased between 2003 and 2008 The function f x 2573e0 0359x models average annual expenditures per household in dollars In this model x represents the year where x 0 corresponds to 2003 a Estimate out of pocket household spending on health care in 2008 b Determine the year when spending reached 2778 per household a The total expenditures per household in the year 2008 were approximately Round to the nearest dollar as needed b During the year spending reached 2778 per household Round down to the nearest year
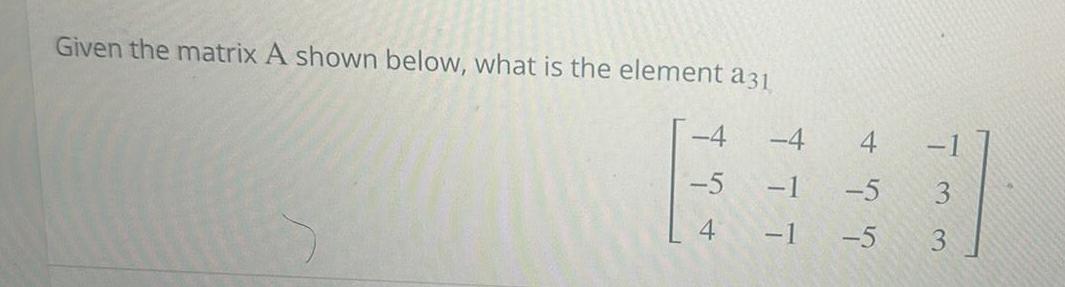
Calculus
Application of derivativesGiven the matrix A shown below what is the element a31 4 5 4 4 1 5 1 5 3
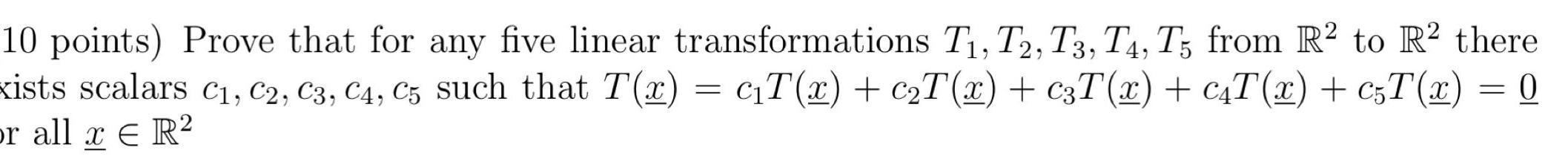
Calculus
Application of derivatives10 points Prove that for any five linear transformations T T2 T3 T4 T5 from R to R there xists scalars C C2 C3 C4 C5 such that T x c T x c T x c3T x c T x c5T x 0 or all x R E R2


Calculus
Application of derivativesA sample of 500 g of radioactive lead 210 decays to polonium 210 according to the function A t 500e 0 032t where t is time in years Find the amount of radioactive lead remaining after a 4 yr b 8 yr c 20 yr d Find the half life a The amount of radioactive lead remaining after 4 yr will be Round to the nearest integer as needed b The amount of radioactive lead remaining after 8 yr will be g Round to the nearest integer as needed c The amount of radioactive lead remaining after 20 yr will be Round to the nearest integer as needed g d The half life is about yr Round to two decimal places as needed g

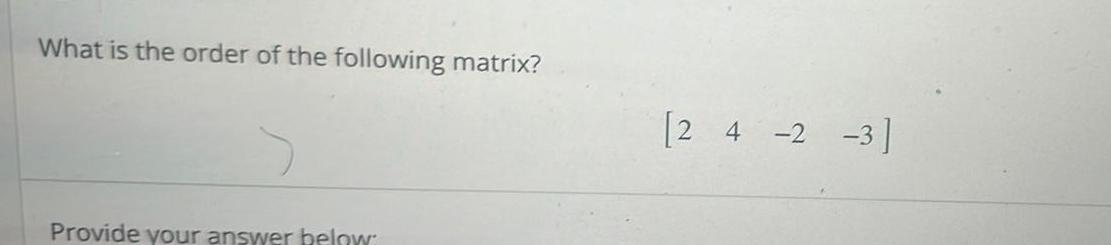
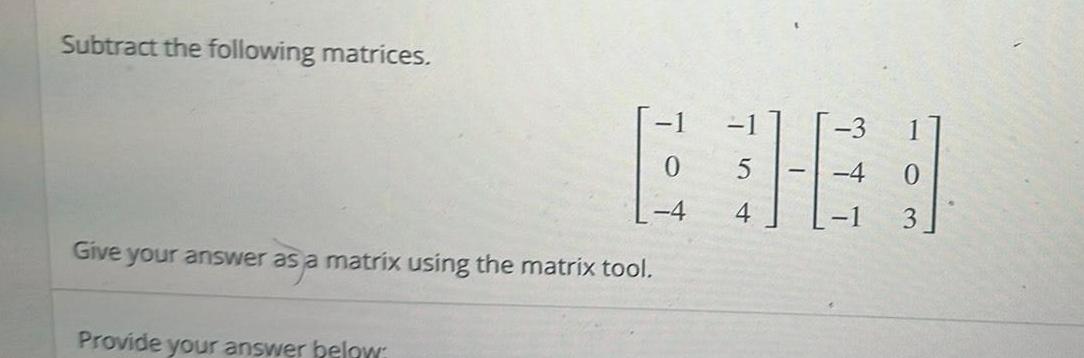
Calculus
Vector CalculusSubtract the following matrices Give your answer as a matrix using the matrix tool Provide your answer below 0 4 4 4 0 3

Calculus
Application of derivativesThe average monthly temperature T m in degrees Celsius in a particular city varies according to the model T m 4 sin sin m 2 1 2 where m represents the months of the year and January begins at m 0 Between what months will the temperature be above 0 C O February and April January and July January and April January and May
Calculus
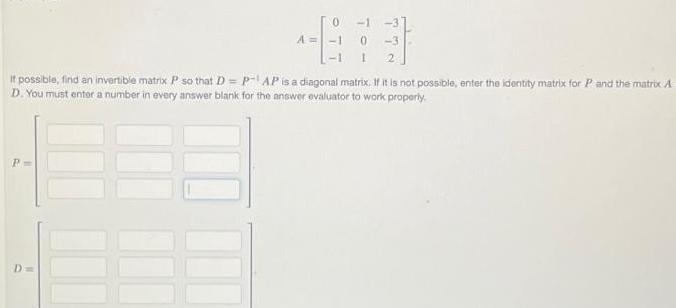
Vector CalculusP 67 1 2 If possible find an invertible matrix P so that D P AP is a diagonal matrix If it is not possible enter the identity matrix for P and the matrix A D You must enter a number in every answer blank for the answer evaluator to work properly D A
Calculus
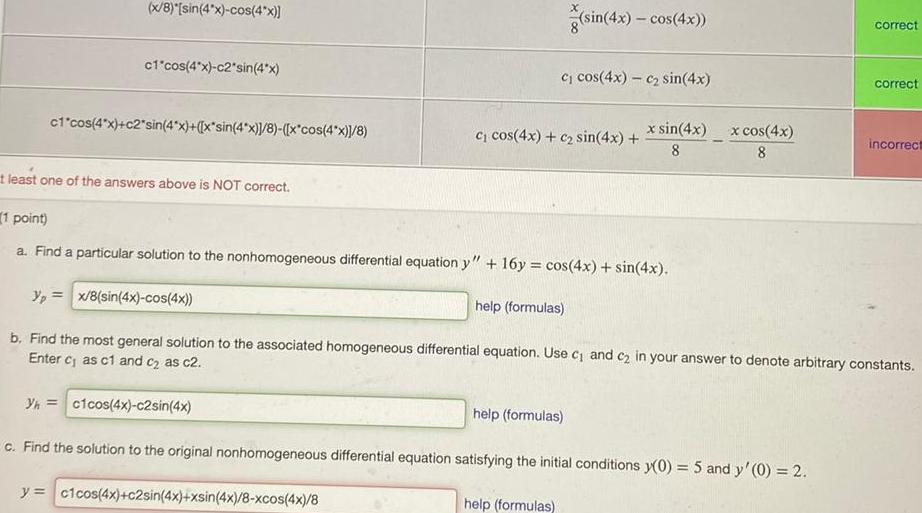
Differential equationsx 8 sin 4x cos 4x c1 cos 4x c2 sin 4x c1 cos 4x c2 sin 4x x sin 4x 8 x cos 4x 8 t least one of the answers above is NOT correct c cos 4x c sin 4x c cos 4x c sin 4x sin 4x cos 4x 1 point a Find a particular solution to the nonhomogeneous differential equation y 16y cos 4x sin 4x help formulas help formulas help formulas x sin 4x 8 x cos 4x 8 correct yp x 8 sin 4x cos 4x b Find the most general solution to the associated homogeneous differential equation Use c and c in your answer to denote arbitrary constants Enter c as c1 and c as c2 Yh c1cos 4x c2sin 4x c Find the solution to the original nonhomogeneous differential equation satisfying the initial conditions y 0 5 and y 0 2 y c1cos 4x c2sin 4x xsin 4x 8 xcos 4x 8 correct incorrect

Calculus
Vector Calculus12 Set up but do not Evaluate Use sperical cordinates to set up the integral for the volumenof the solid bounded above by the sphere x y z 1 and below by the cone Z x y
Calculus
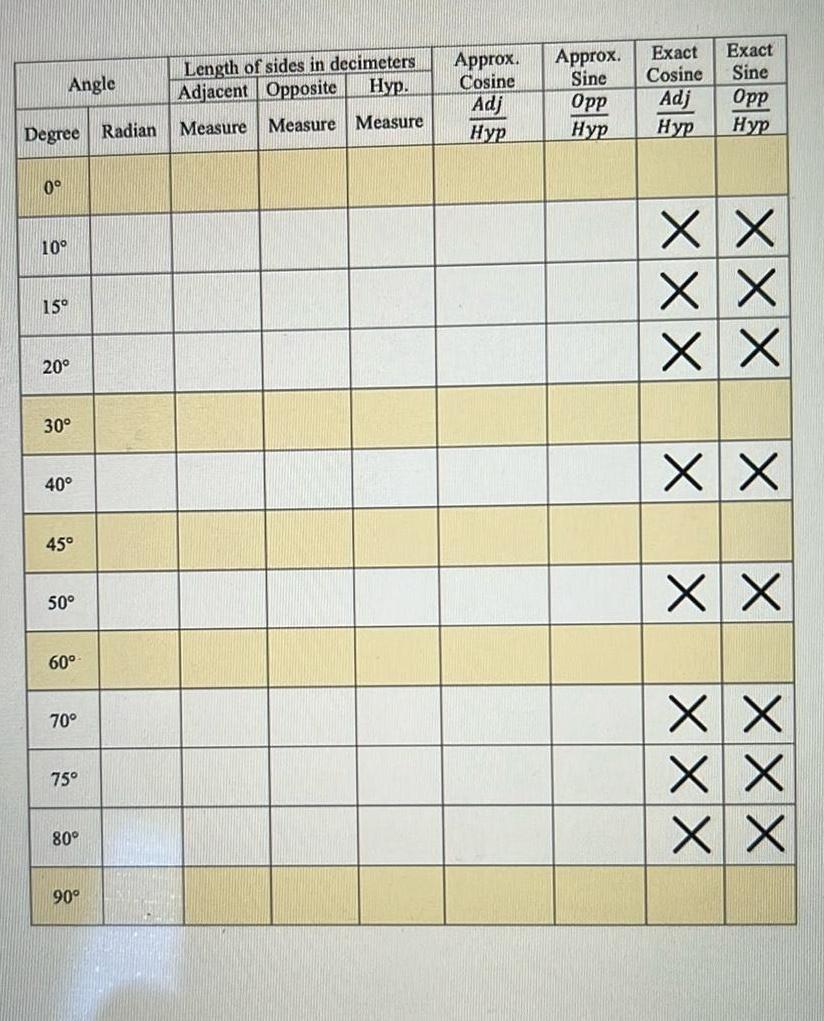
Vector CalculusAngle Degree Radian 0 10 15 20 30 40 45 50 60 70 75 80 90 Length of sides in decimeters Adjacent Opposite Hyp Measure Measure Measure Approx Approx Cosine Sine Adj Opp Hyp Hyp Exact Exact Cosine Sine Adj Opp Hyp Hyp XX XX X X XX XX XX X X X X
Calculus
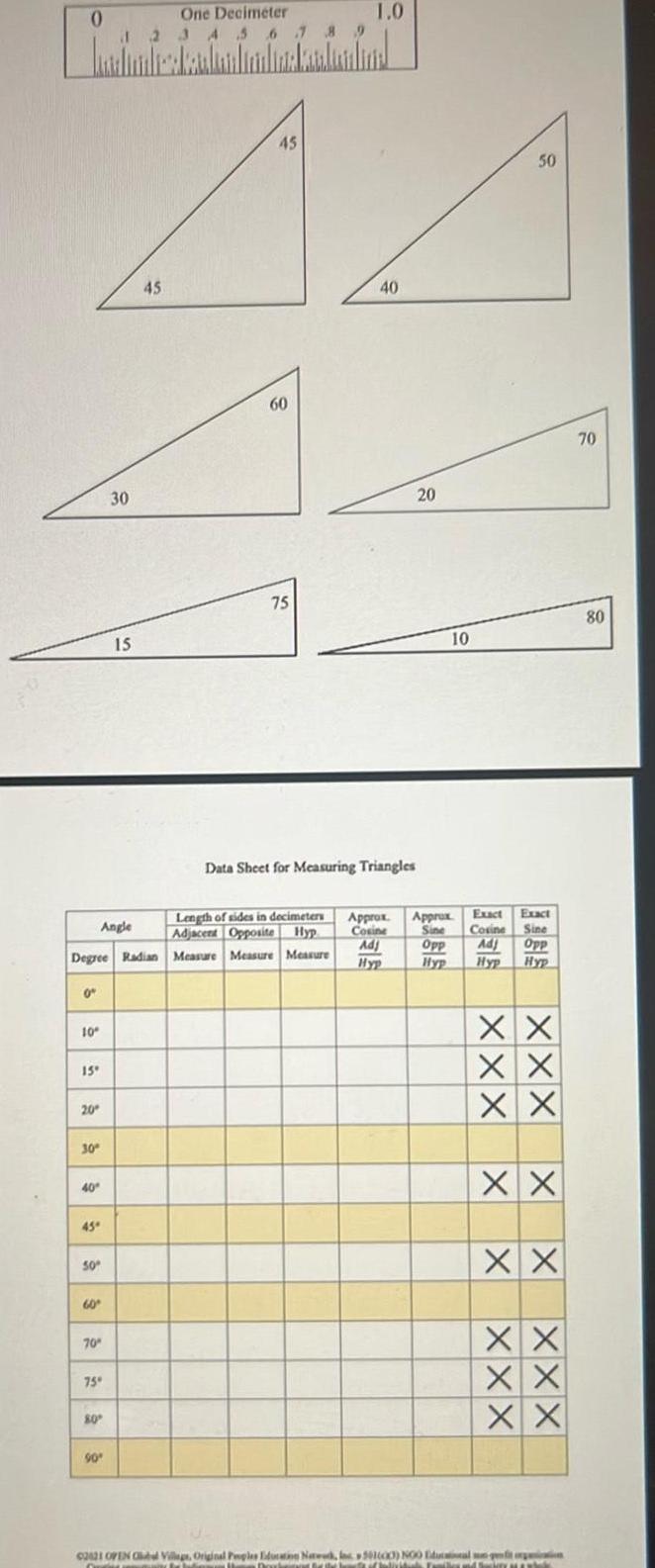
Vector Calculus0 0 10 15 20 Degree Radian 30 40 45 50 60 Angle 70 75 One Decimeter 1 2 3 4 5 6 7 8 9 80 30 90 15 45 45 60 75 1 0 Length of sides in decimeters Adjacent Opposite Hyp Measure Measure Measure 40 Data Sheet for Measuring Triangles Approx Cosine Adj Hyp 20 10 50 Exact Exact Approx Sine Cosine Sine Opp Adj Opp Hyp Hyp Hyp XX XX XX XX XX XX XX XX C2821 OPEN Clubel Village Original Peoples Education Network Inc 501000 NOO Edualun qefit organization Th Be the home of health Fember and Semberyanbok 70 80

Calculus
Limits & ContinuityQuestion 3 2 2 4 points Compute the following limits or else prove that they do not exist using methods from algebra and Calculus You must justify your steps with reference to theorems or definitions learned in class correctly and legibly and use correct notation to earn full credit 14 2r 2x 4 a lim

Calculus
Application of derivativesQuestion 4 4 points Our goal is to estimate the value of In 0 9 using a Taylor polynomial a 1 point Write down the formula for the Taylor polynomial of degree 3 of a function f r centered at z a

Calculus
Indefinite IntegrationEvaluate the cylindrical coordinate integral The value is 0 0 r r dz dr d

Calculus
Definite Integralsfr F dr where F x y z yi zjxk and C is a triangle with vertices 0 0 0 Use Stokes theorem to evaluate 9 0 0 and 0 9 9 oriented counterclockwise when viewed from above
Calculus
Definite IntegralsSet up and evaluate an integral for the surface area of the surface defined by z x y 1 with 1 z 5
Calculus
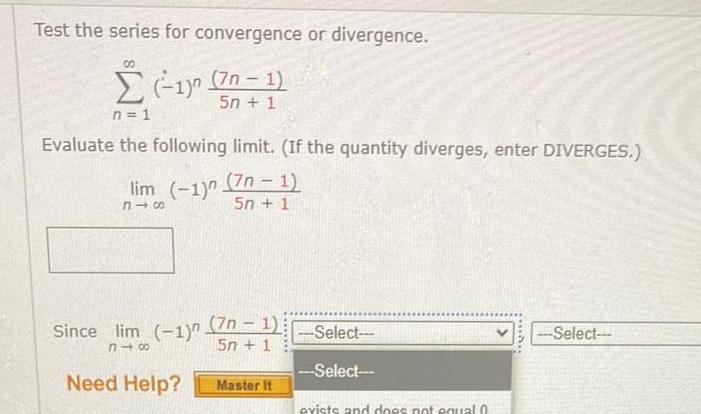
Limits & ContinuityTest the series for convergence or divergence 1 7n 1 5n 1 n 1 Evaluate the following limit If the quantity diverges enter DIVERGES lim 1 318 Since lim 1 818 Need Help 7n 1 5n 1 7n 1 5n 1 Master it Select Select exists and does not equal 0 Select

Calculus
Limits & Continuity5 12 Consider the rational function r x Evaluate the local behavior As x 1 r x As x 1 r x As x 2 r x As x 2 r x As x 4 r x As x 4 r x 750 x 1 7x 3 x 1 x 1 x 4 x 2

Calculus
Application of derivatives9 End Behavior Give the equation of the horizontal asymptote of eac rational function If there is no horizontal asymptote state that fact 5x4 12x 120x 100 2x 20x 25 a b C 12x 25x 75x 125 100 2x3 7x 55x 125 4x3 125

Calculus
Differential equationsProblem 3 6 points Compute the rate of change of the function f x y ln xy in the direction of k 1 at the point 1 1

Calculus
Differential equationsUse the Laplace transform to solve the given differential equation subject to the indicated initial conditions y 7y 6y et 8 t 3 8 t 7 y 0 0 y 0 0 1 u t 3 y t X X X u t 7

Calculus
Vector CalculusDetermine the correct partial fraction decomposition for 9x 14x 2 5x 4 x2 x 2
Calculus
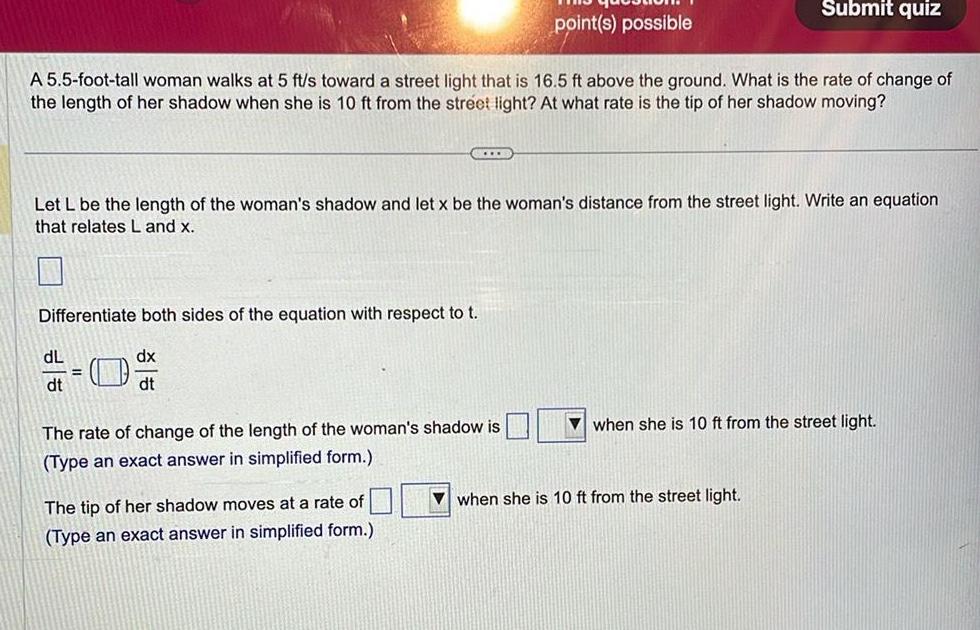
Application of derivativesA 5 5 foot tall woman walks at 5 ft s toward a street light that is 16 5 ft above the ground What is the rate of change of the length of her shadow when she is 10 ft from the street light At what rate is the tip of her shadow moving CLE Differentiate both sides of the equation with respect to t dx dt dL dt Let L be the length of the woman s shadow and let x be the woman s distance from the street light Write an equation that relates L and x point s possible The rate of change of the length of the woman s shadow is Type an exact answer in simplified form The tip of her shadow moves at a rate of Type an exact answer in simplified form Submit quiz when she is 10 ft from the street light when she is 10 ft from the street light
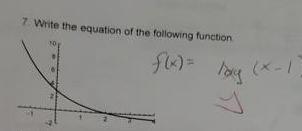


Calculus
DifferentiationUse the definition to find an expression for the instantaneous velocity of an object moving with rectilinear motion according to the given function relating s in ft and t in s Then calculate the instantaneous velocity for the given value of t s 3t 4t t 6 The expression for the instantaneous velocity of the object is

Calculus
Application of derivativesFind the average rate of change of y with respect to x from P to Q Then compare this with the instantaneous rate of change of y with respect to x at P by finding ma y 7 x P 3 20 Q 3 4 32 304 Enter the average rate of change of y with respect to x from point P to Q below mpo Type an integer or a decimal