Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
DifferentiationA bacteria culture starts with 100 bacteria and the growth rate is proportional to the number of bacteria After 2 hours the population is 5000 Find an expression for the number of bacteria after t hours OP 100 25t In 50 OP 100e 2 OP 100e In 25 t O P 5000et t
Calculus
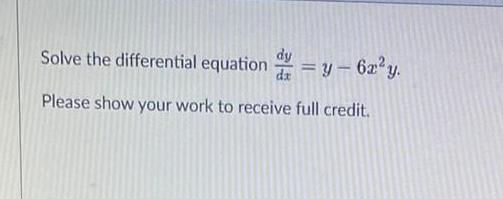
Differential equationsSolve the differential equation dy y 6z y Please show your work to receive full credit

Calculus
Differential equationsGiven that all members of the family y Ce are solutions of the differential equation y 3x y find a solution that satisfies the initial condition y 0 15 O y 15e Oy 30e O y 45e O y 5e
Calculus
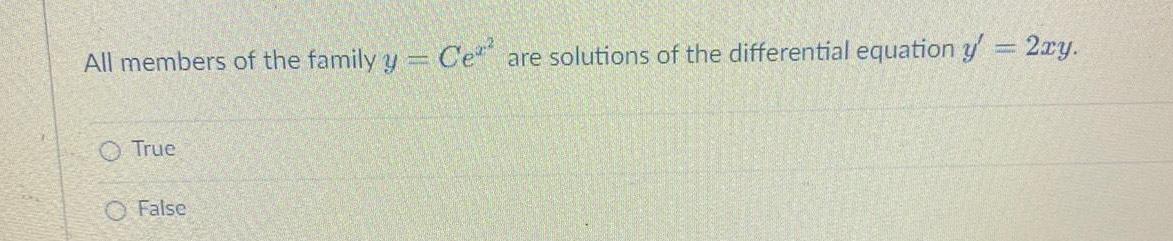
DifferentiationAll members of the family y Ce are solutions of the differential equation y 2xy True False
Calculus
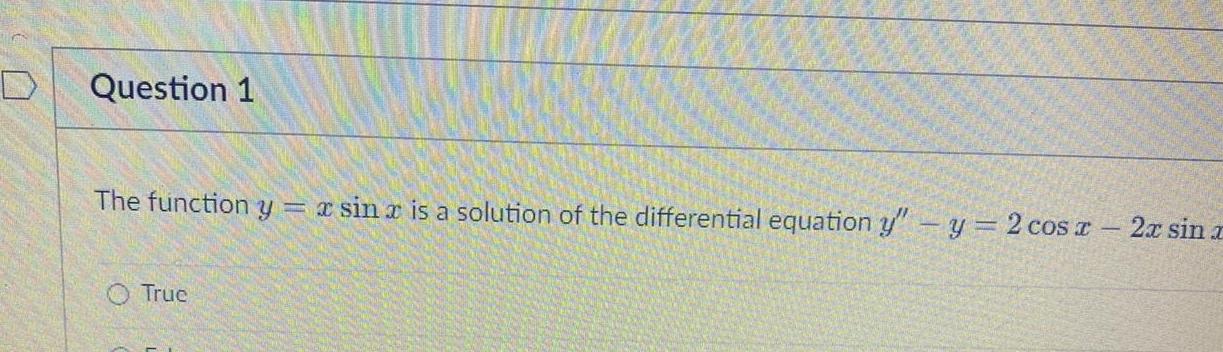
DifferentiationQuestion 1 The function y x sin x is a solution of the differential equation y y 2 cos x True 2x sin x
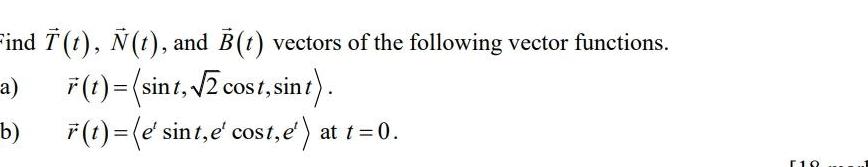
Calculus
Vector CalculusFind t t and B t vectors of the following vector functions a F t sint 2 cost sint b r t e sint e cost e at t 0 10

Calculus
Vector Calculus110 101 101 101 Find and parameterize the set of all least squares solutions to this system 6 5 points Consider the inconsistent system A16 where A and b 3 6 5 4
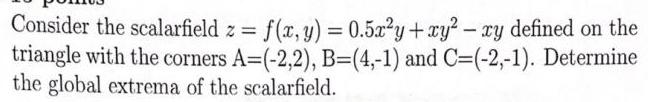
Calculus
DifferentiationConsider the scalarfield z f x y 0 5x y xy xy defined on the triangle with the corners A 2 2 B 4 1 and C 2 1 Determine the global extrema of the scalarfield

Calculus
Differential equations1 point Let y be the solution of the initial value problem The maximum value of y is y y sin 2x y 0 0 y 0 0
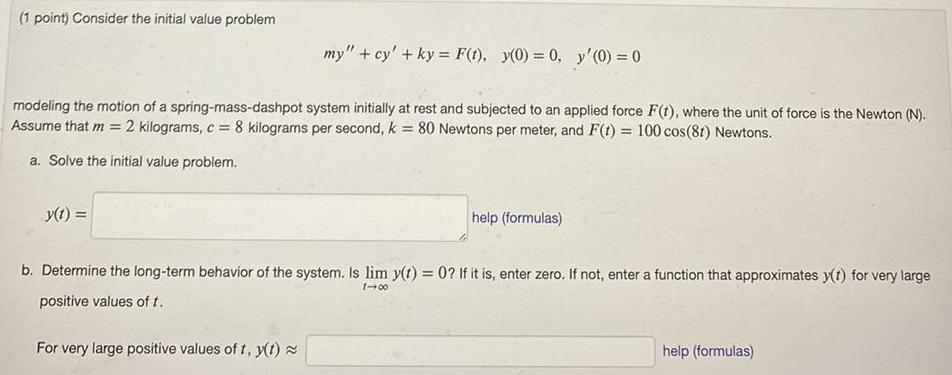
Calculus
Application of derivatives1 point Consider the initial value problem my cy ky F t y 0 0 y 0 0 modeling the motion of a spring mass dashpot system initially at rest and subjected to an applied force F t where the unit of force is the Newton N Assume that m 2 kilograms c 8 kilograms per second k 80 Newtons per meter and F t 100 cos 8t Newtons a Solve the initial value problem y t help formulas b Determine the long term behavior of the system Is lim y t 0 If it is enter zero If not enter a function that approximates y t for very large positive values of t 1 00 For very large positive values of t y t help formulas
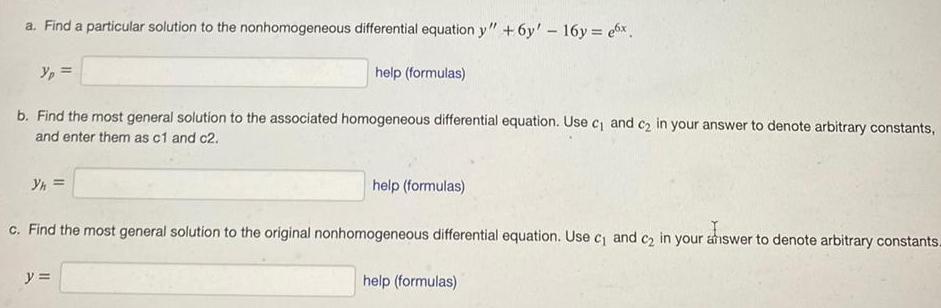
Calculus
Differential equationsa Find a particular solution to the nonhomogeneous differential equation y 6y 16y ex b Find the most general solution to the associated homogeneous differential equation Use c and c in your answer to denote arbitrary constants and enter them as c1 and c2 Yh help formulas y help formulas c Find the most general solution to the original nonhomogeneous differential equation Use c and c in your answer to denote arbitrary constants help formulas
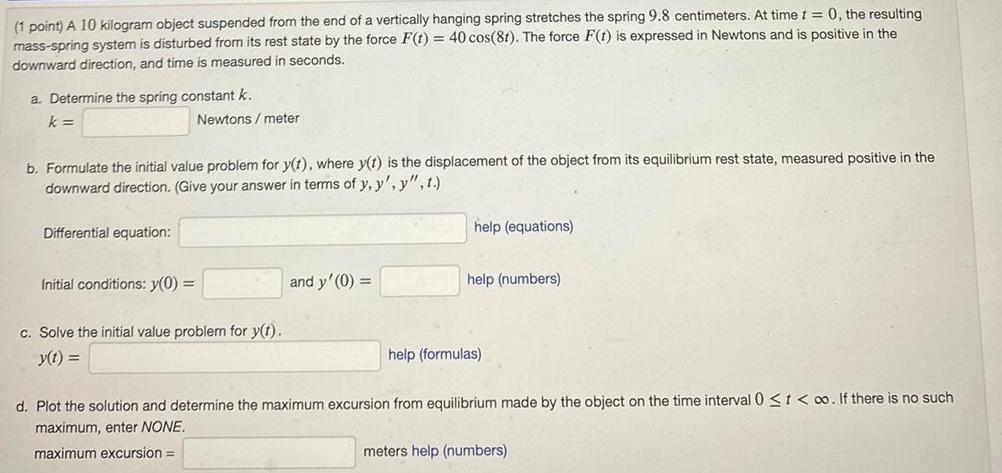
Calculus
Application of derivatives1 point A 10 kilogram object suspended from the end of a vertically hanging spring stretches the spring 9 8 centimeters At time t 0 the resulting mass spring system is disturbed from its rest state by the force F t 40 cos 81 The force F t is expressed in Newtons and is positive in the downward direction and time is measured in seconds a Determine the spring constant k k b Formulate the initial value problem for y t where y t is the displacement of the object from its equilibrium rest state measured positive in the downward direction Give your answer in terms of y y y t Differential equation Newtons meter Initial conditions y 0 c Solve the initial value problem for y t y t and y 0 help equations help numbers help formulas d Plot the solution and determine the maximum excursion from equilibrium made by the object on the time interval 0 t o If there is no such maximum enter NONE maximum excursion meters help numbers

Calculus
Vector Calculus6z 6z 140 z 5 3z 5 Determine the correct partial fraction decomposition for the expression above Provide your answer below
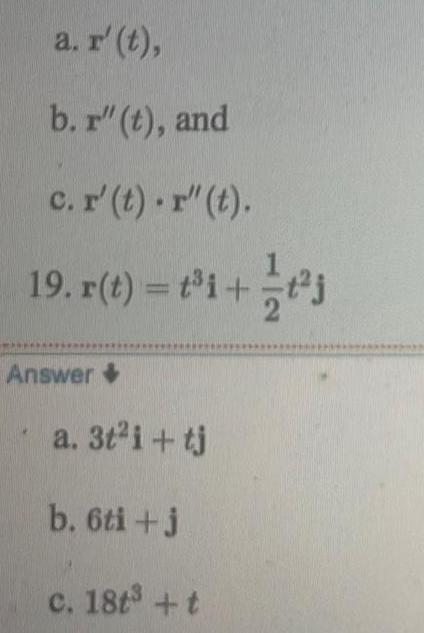
Calculus
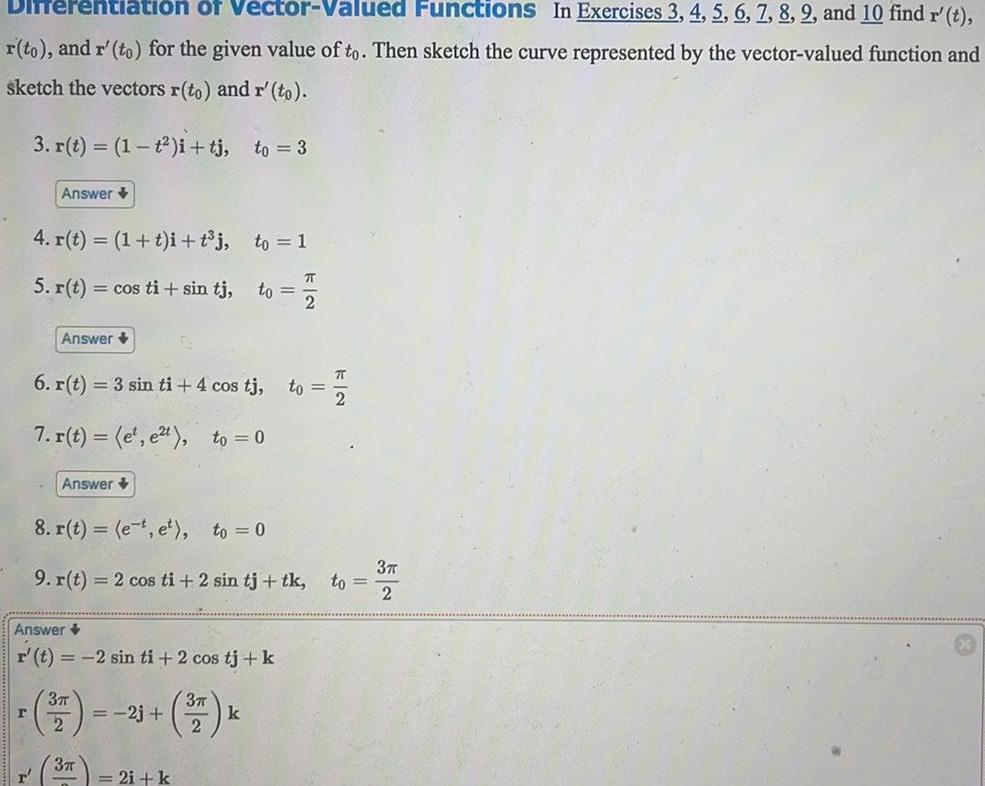
Differentiationentiation of Vector Valued Functions In Exercises 3 4 5 6 7 8 9 and 10 find r t r to and r to for the given value of to Then sketch the curve represented by the vector valued function and sketch the vectors r to and r to 3 r t 1 t i tj to 3 r Answer 4 r t 1 t i t j 5 r t cos ti sin tj Answer Answer 6 r t 3 sin ti 4 cos tj to 7 r t e e to 0 Answer r t 2 sin ti 2 cos tj k 3 2 8 r t e t et to 0 9 r t 2 cos ti 2 sin tj tk 3 2j to 1 2i k 3 2 to 7 2 2 k KN to 3 2
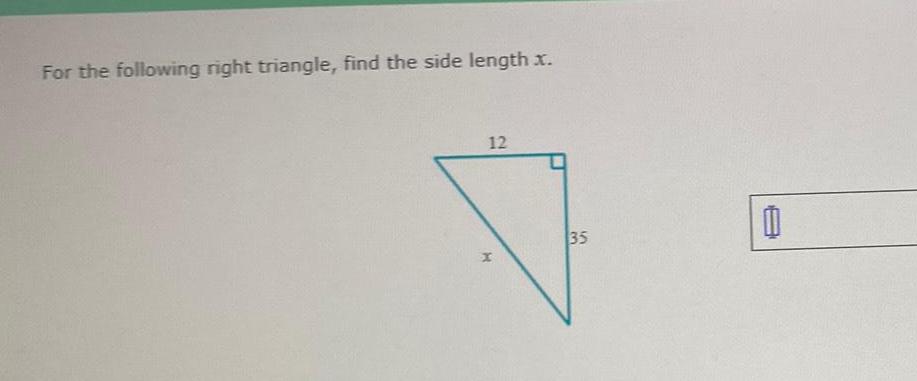

Calculus
Application of derivativesFind the centroid of the region bounded by the xy plane the cylinder x y 2401 and the 1 Assume the density of 8 x y z 1 Use symbolic notation and fractions where needed Express numbers in exact form Give your answer as point coordinates ins the form x J Z 0 0 100
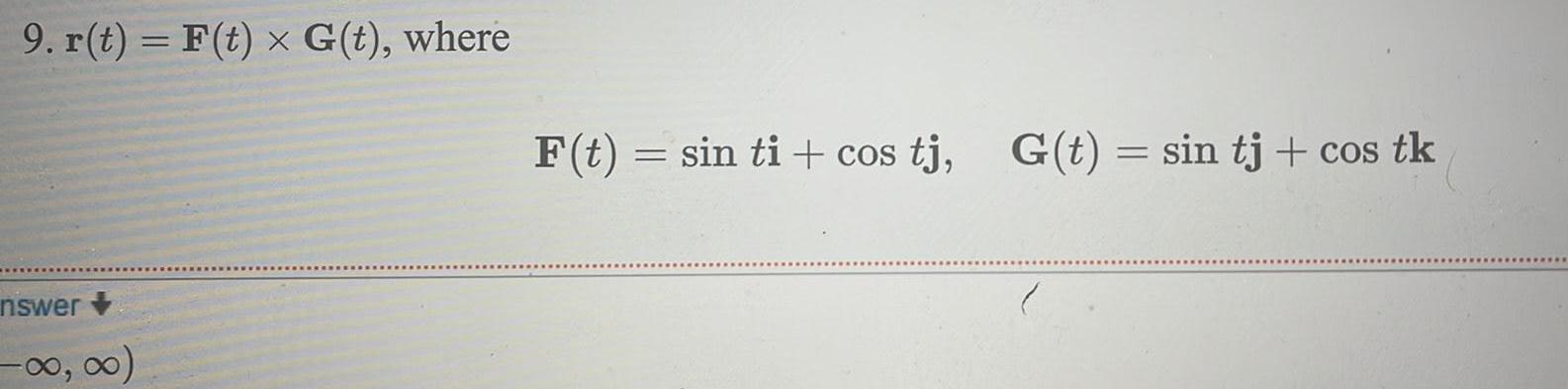
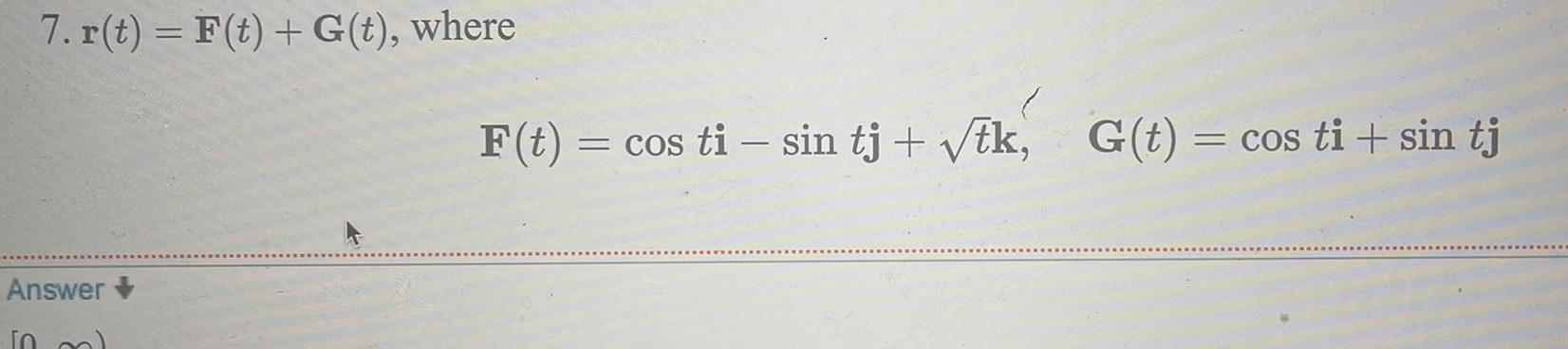

Calculus
Definite IntegralsAt the end of every 3 months Mayan deposits 200 into an account that pays 5 compounded quarterly After 2 years she puts the accumulated amount into a certificate of deposit paying 6 compounded monthly for 1 year When this certificate matures how much will Mayan have accumulated How much interest was earned overall
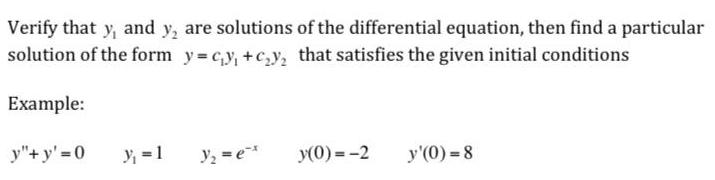
Calculus
Application of derivativesVerify that y and y are solutions of the differential equation then find a particular solution of the form y c y c y that satisfies the given initial conditions Example y y 0 y 1 y ex y 0 2 y 0 8

Calculus
Indefinite IntegrationMake a substitution to express the integrand as a rational function and then evaluate the integral Use C for the constant of integration 7e2x 11e 18 e2x dx 9 ln e 9 2 ln e 2 C X

Calculus
Vector CalculusO Correct Consider a triangle ABC like the one below Suppose that c 66 a 31 and C 124 The figure is not drawn to scale Solve the triangle Carry your intermediate computations to at least four decimal places and round your answers to the nearest tenth If no such triangle exists enter No solution If there is more than one solution use the button labeled or B A 22 9 B 33 1 b 43 5 or X No solution S
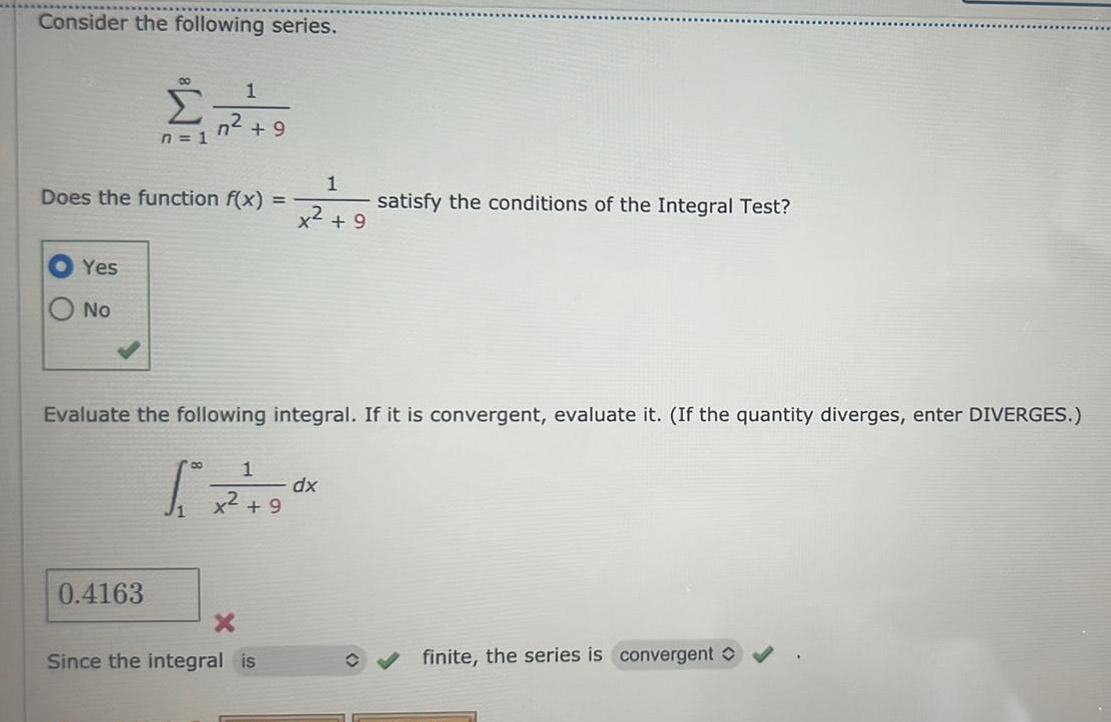
Calculus
Application of derivativesConsider the following series Yes No 00 n 1 Does the function f x 1 n 9 0 4163 1 x 9 Evaluate the following integral If it is convergent evaluate it If the quantity diverges enter DIVERGES 80 1 5 x 2 9 9 X Since the integral is satisfy the conditions of the Integral Test dx finite the series is convergent
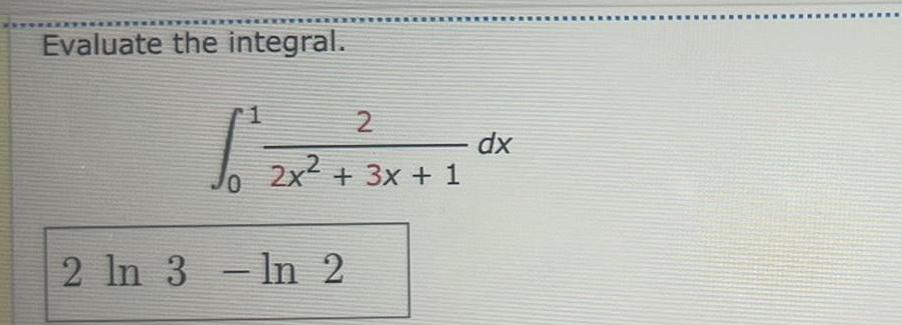
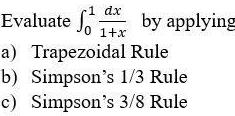
Calculus
Definite Integrals1 dx Evaluate 1 x by applying Rule a Trapezoidal Simpson s 1 3 Rule b c Simpson s 3 8 Rule

Calculus
Vector CalculusSuppose you have just poured a cup of freshly brewed coffee with temperature 94 C in a room where the temperature is 20 C a When do you think the coffee cools most quickly What happens to the rate of cooling as time goes by Explain The coffee cools most quickly as soon as it is removed from the heat source The rate of cooling decreases towards 0 coffee approaches room temperature b Newton s law of cooling states that the rate of cooling of an object is proportional to the temperature difference between the object and its surroundings provided that this difference is not too large Write a differential equation that expresses Newton s law of cooling for this particular situation Use t as the independent variable y as the dependent variable R as the room temperature and k as a proportionality constant dy k dt X What is the initial condition y 0 94 In view of your answer to part a do you think this differential equation is an appropriate model for cooling The answer and the model support each other because as y approaches R dy dt approaches 0 since the so the model seems appropriate

Calculus
Differentiation2 Bessel functions are useful in the analysis of problems that involve oscillations Very impor tant equations in differential equations involve Bessel functions in their solutions If a is a positive integer the Bessel function Ja r of the first kind of order a is defined by the power series Ja 3 n a 2 n 0 Show that this power series is convergent for every real number x 2n a

Calculus
Differentiation16 X Find an equation of the curve that passes through the point 0 4 and whose slope at x y is x y is X
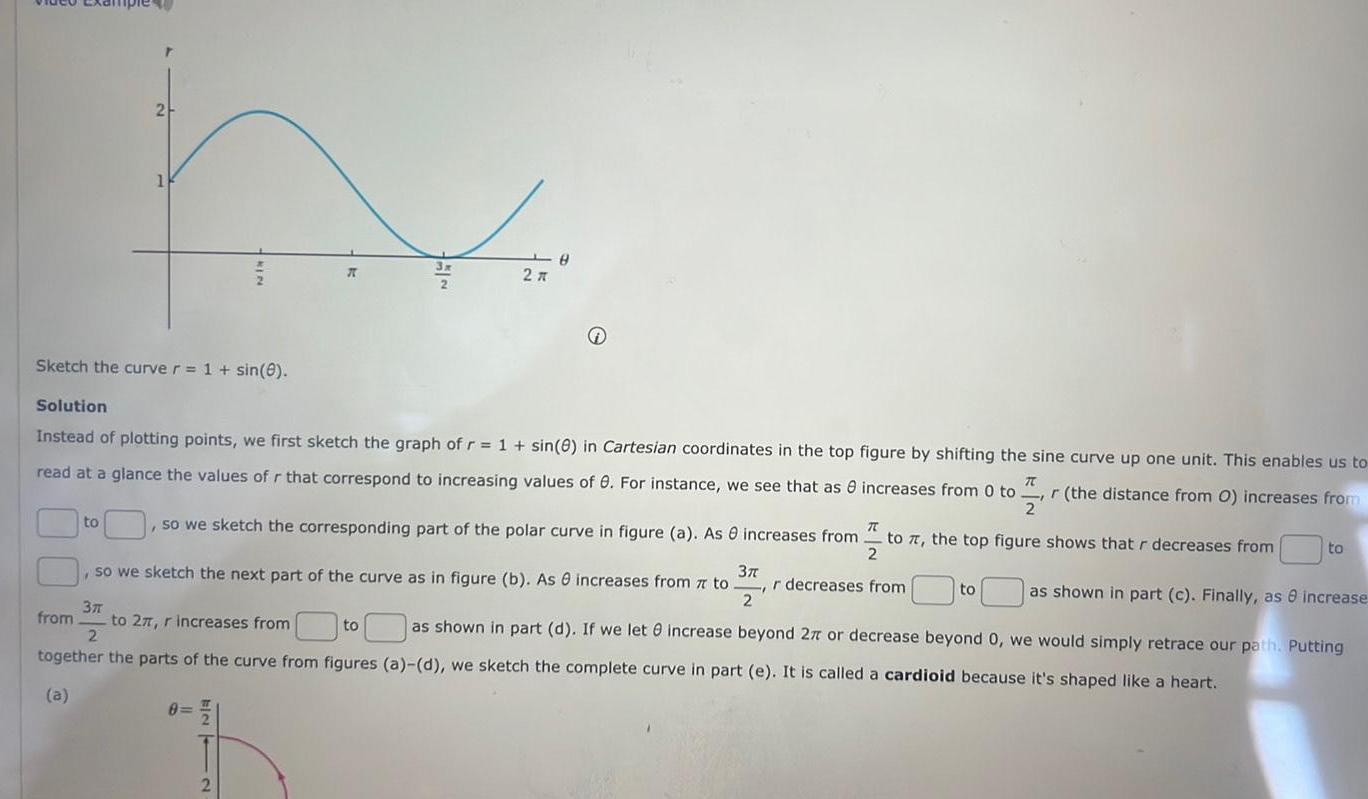
Calculus
Application of derivativesSketch the curve r 1 sin 0 2 h to from Solution Instead of plotting points we first sketch the graph of r 1 sin 8 in Cartesian coordinates in the top figure by shifting the sine curve up one unit This enables us to read at a glance the values of r that correspond to increasing values of 0 For instance we see that as r the distance from O increases from 2 increases from 0 to 70 TC 2 so we sketch the corresponding part of the polar curve in figure a As increases from to 7 the top figure shows that r decreases from as shown in part c Finally as 8 increase as shown in part d If we let increase beyond 27 or decrease beyond 0 we would simply retrace our path Putting KIN 37 8 so we sketch the next part of the curve as in figure b As increases from 7 to r decreases from 2 8 2 x 2 8 3T 2 to 27 r increases from together the parts of the curve from figures a d we sketch the complete curve in part e It is called a cardioid because it s shaped like a heart a to to to

Calculus
Application of derivativesFind a polar equation for the curve represented by the given Cartesian equation Assume 0 0 2 3x 3 y
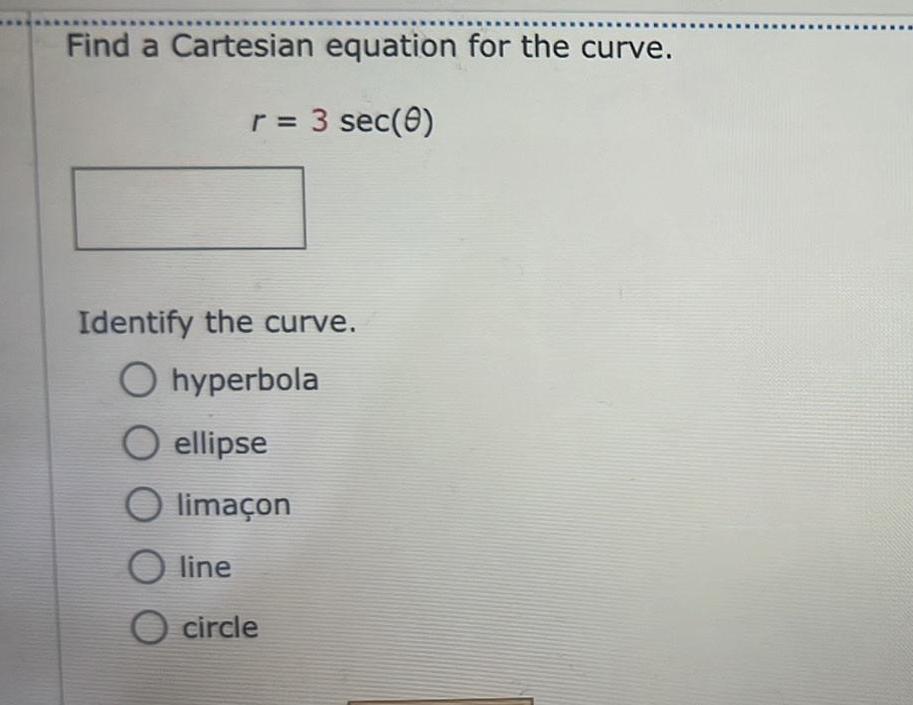
Calculus
Differential equationsFind a Cartesian equation for the curve r 3 sec 0 Identify the curve O hyperbola O ellipse O lima on O line O circle
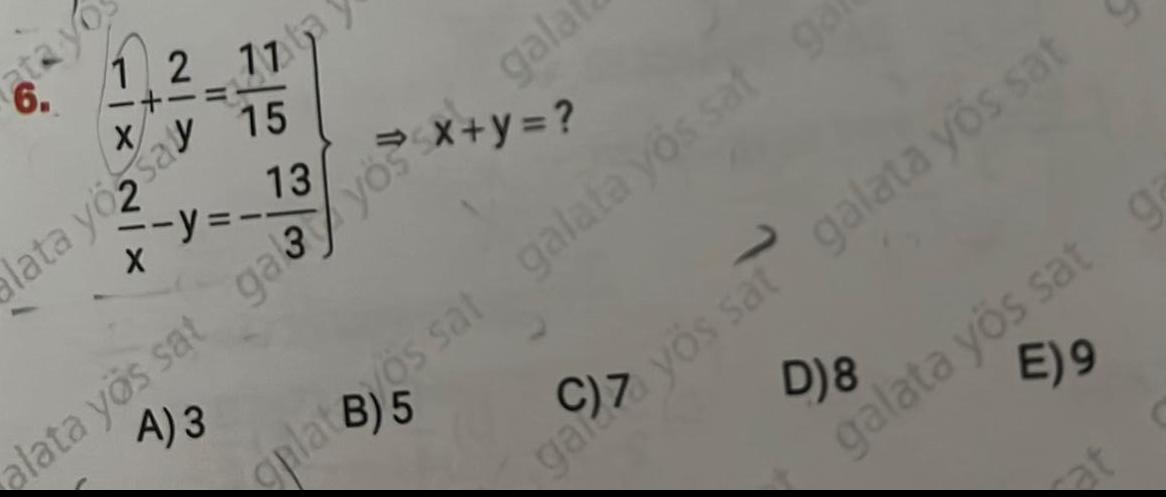
Calculus
Application of derivatives6 FIX 12 11 X lata you sa A 3 1767 13 D 8 galata y s sat E 9 gar a y s sat galata y s sat plats sat galata y s sat ga alata y s sat gale yogalaf

Calculus
Application of derivativesFind the maximum volume of a box that is resting on the xy plane with one vertex at the origin and the opposite vertex in the given plan 7x By 2z24

Calculus
Differential equations2 A tank with a capacity of 500 liters originally contains 200 liters of water with 100 kilograms of salt in the solution Water containing 1 kg of salt per liter is entering at a rate of 3 liter min and the mixture is allowed to flow out of the tank at a rate of 2liter min Find the amount of salt in the tank at any time prior to the instant when the solution begins to overflow Find the concentration in kilograms per liter of salt in the tank at the instant it starts to overflow

Calculus
Application of derivativesA tank initially contains 120 liters of pure water A mixture containing a concentration of y g liter of salt enters the tank at a rate of 3liters min and the well stirred mixture leaves the tank at the same rate Find an expression in terms of y for the amount of salt in the tank at any time t Also find the limiting amount of salt in the tank as t

Calculus
Differential equationsCheck if the equation is exact if it is solve it If there is an initial value find the particular solution satisifying the initial value 1 3x 2 y 2 4xy y 2y 2 2xy 3

Calculus
Differential equations1 An object stretches a spring 4cm in equilibrium Find its displacement for t 0 if it is initially displaced 36 cm above equilibrium and given a downward velocity of 25 cm s

Calculus
Differential equationsFind the general solution and if an initial value is given solve the IVP 1 y 5y 6y 18x 2 18x 22

Calculus
Application of derivativesTechnetium 99m is a radioactive substance used to diagnose brain diseases Its half life is approximately 6 hours Initially you have 220 mg of technetium 99m a Write an equation that gives the amount of technetium 99m remaining after t hours NOTE Round any values to four decimal places if required R t 220 e6t b Determine the number of hours needed for your sample to decay to 132 mg NOTE Round your answer to three decimal places It takes approximately hours for the sample to decay to 132 mg c Determine the concavity of the graph that models the quantity of technetium 99m using average rates of change over intervals of length 2 between t 0 and t 6 The graph is concavo

Calculus
Differential equationsSolve the differential equation If there is an initia value find the particular solution satisfying the initial value 1 xy 2y 4x 2 y 1 4
Calculus
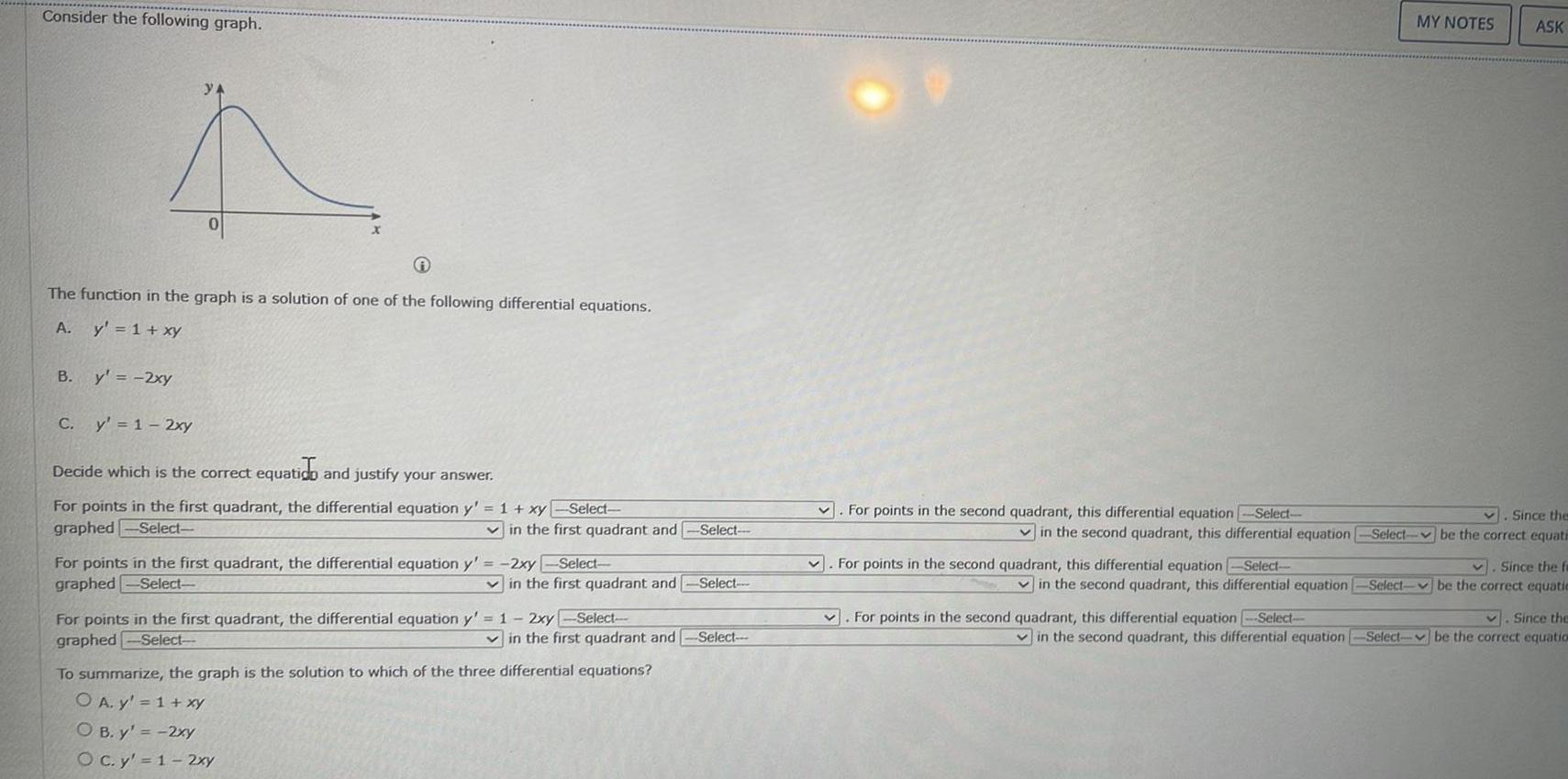
Differential equationsConsider the following graph The function in the graph is a solution of one of the following differential equations A y 1 xy B y 2xy C y 1 2xy Decide which is the correct equatico and justify your answer For points in the first quadrant the differential equation y 1 xy Select graphed Select in the first quadrant and Select For points in the first quadrant the differential equation y 2xy Select graphed Select in the first quadrant and Select For points in the first quadrant the differential equation y 1 2xy Select graphed Select in the first quadrant and Select To summarize the graph is the solution to which of the three differential equations O A y 1 xy OB y 2xy O c y 1 2xy For points in the second quadrant this differential equation Select v For points in the second quadrant this differential equation Select MY NOTES Since the in the second quadrant this differential equation Select be the correct equati V Since the fa in the second quadrant this differential equation Select be the correct equatie v Since the in the second quadrant this differential equation Select be the correct equation For points in the second quadrant this differential equation Select ASK


Calculus
Indefinite IntegrationEvaluate the integral Remember to use absolute values where appropriate Use C for the constant of integration y 2 5y 1 dy In y 2 In 5y 1 C 11 X
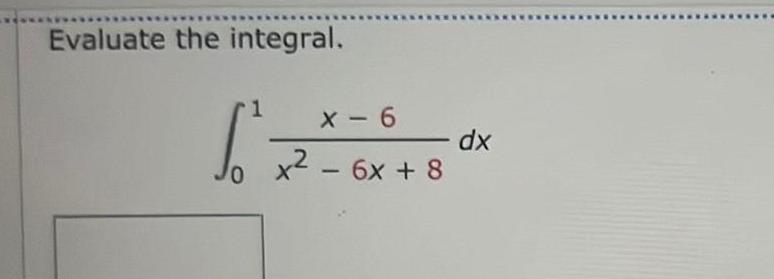
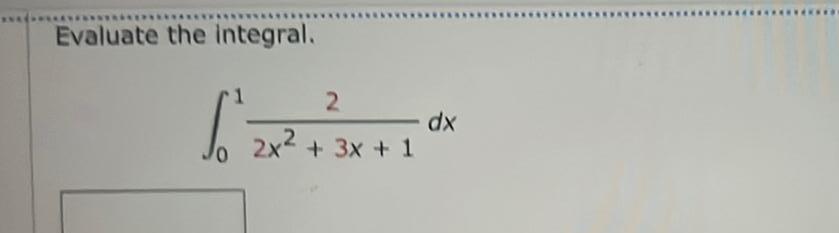
Calculus
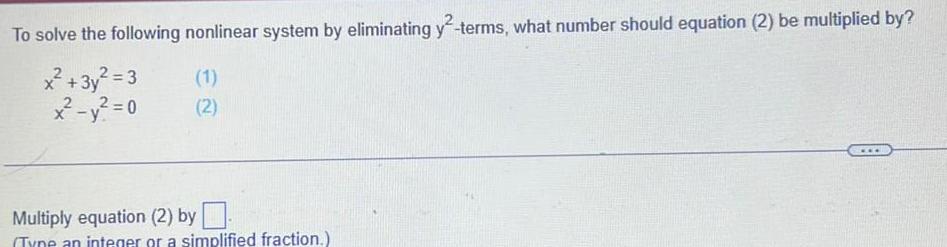
Application of derivativesTo solve the following nonlinear system by eliminating y terms what number should equation 2 be multiplied by x 3y 3 x y 0 1 2 Multiply equation 2 by Tyne an integer or a simplified fraction
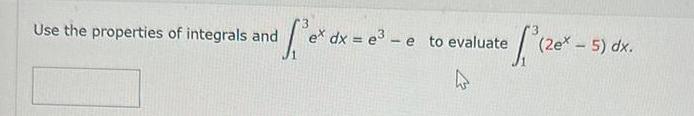
Calculus
Definite Integrals1f ex dx e Use the properties of integrals and 1 zex dxe3e to evaluate 4 ex 5 dx

Calculus
DifferentiationFind the cofactor of each element in the second row 2 6 3 15 1 1 1 5 The cofactor of 1 is