Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
Limits & ContinuityA 11 2 resistor and a variable resistor of resistance R are placed in parallel The expression for the resulting resistance RT is given by RT value of RT as R o The limiting value of R is Simplify your answer 11R 11 R Determ

Calculus
DifferentiationDetermine the values of x for which the function f x Where is the function continuous or not continuous 4 2 4X is continuous If the function is not continuous determine the reason OA The function is not continuous at x 4 OB The function is continuous for all values of x OC The function is continuous for all values of x greater than 0 OD The function is not continuous at x 0 OE The function is not continuous at x 4 OF The function is continuous for all values of x less than 4 OG The function is continuous for all values of x between 0 and 4 H The function is not continuous at x 0 and x 4

Calculus
Differential equationsompute the following limits using I H opital s rule if appropriate Use INF to denote and MINF to denote x mx 0 X 3 512 2 3 dt
Calculus
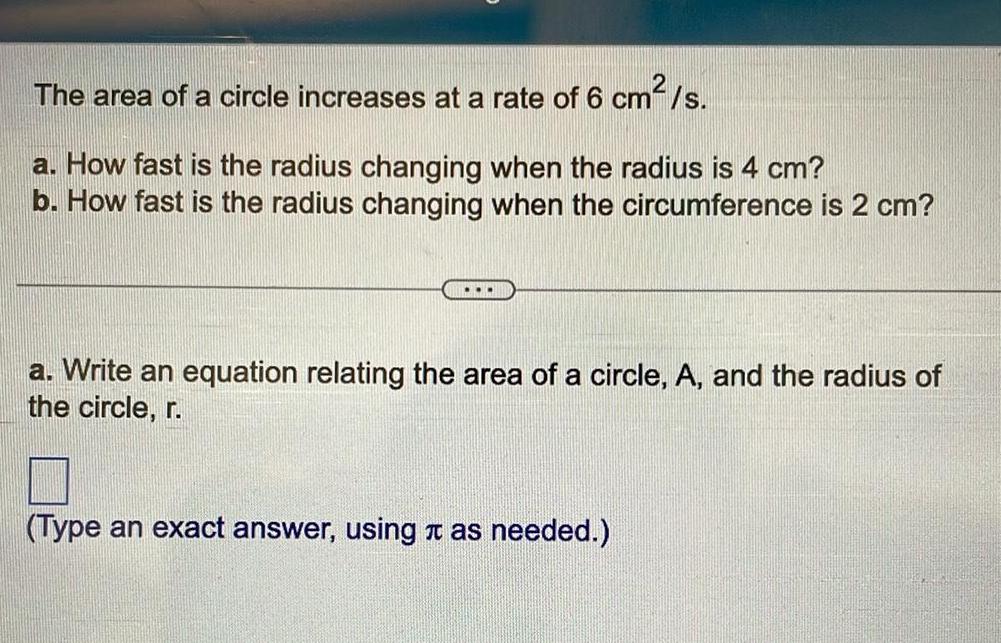
Application of derivatives2 The area of a circle increases at a rate of 6 cm s a How fast is the radius changing when the radius is 4 cm b How fast is the radius changing when the circumference is 2 cm a Write an equation relating the area of a circle A and the radius of the circle r Type an exact answer using it as needed
Calculus
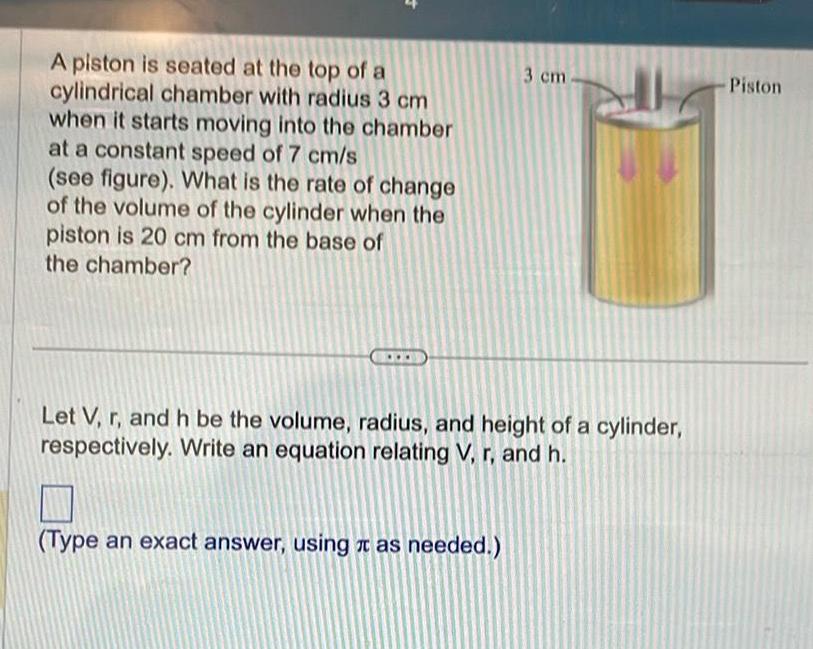
Application of derivativesA piston is seated at the top of a cylindrical chamber with radius 3 cm when it starts moving into the chamber at a constant speed of 7 cm s see figure What is the rate of change of the volume of the cylinder when the piston is 20 cm from the base of the chamber 3 cm Let V r and h be the volume radius and height of a cylinder respectively Write an equation relating V r and h Type an exact answer using as needed Piston

Calculus
DifferentiationFind values of the trigonometric functions of the angle in standard position whose terminal side passes through the given point 4 3 sin 0 cos tan 0 cot 0 3 5 4 5 3 Type an exact answer in simplified form Type an exact answer in simplified form Type an exact answer in simplified form Type an exact answer in simplified form
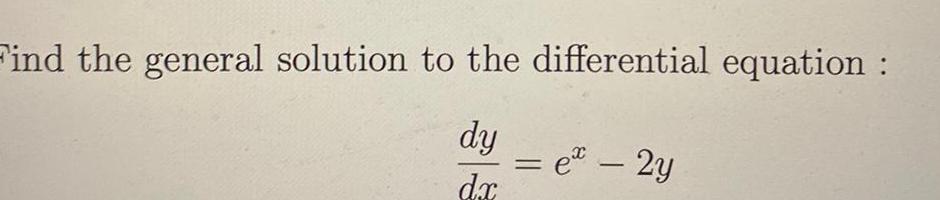
Calculus
Application of derivativesFind the general solution to the differential equation dy dx ex 2y
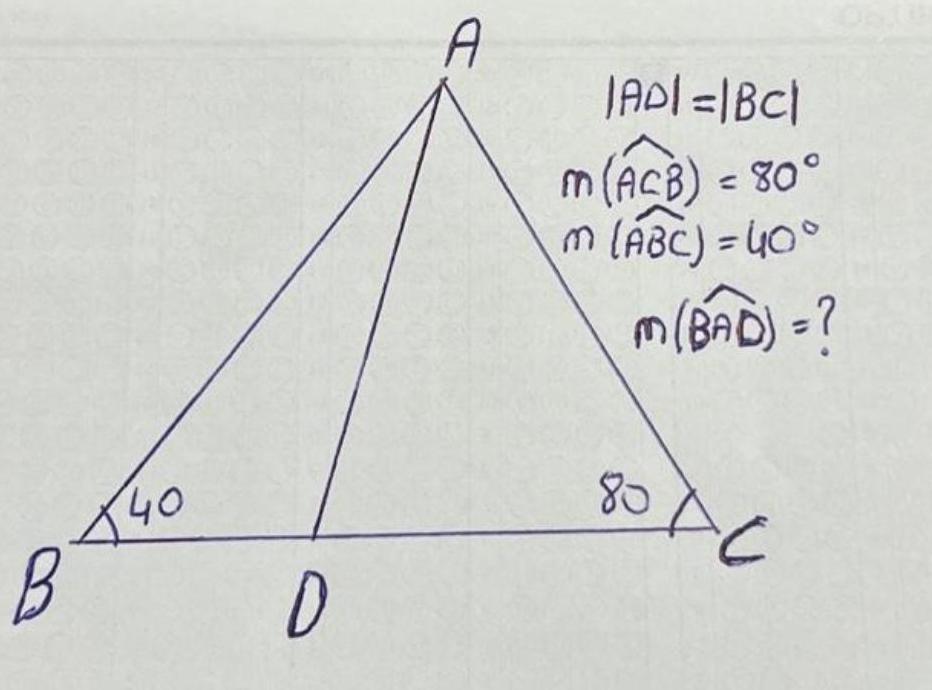
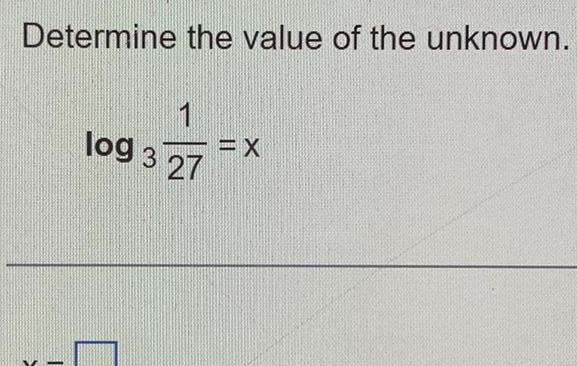
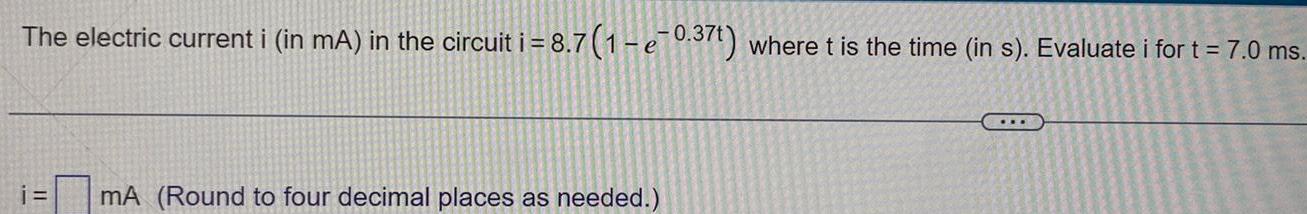
Calculus
DifferentiationThe electric current i in mA in the circuit i 8 7 1 e 0 37t where t is the time in s Evaluate i for t 7 0 ms i mA Round to four decimal places as needed

Calculus
Application of derivativesA 13 foot ladder is leaning against a vertical wall see figure when Jack begins pulling the foot of the ladder away from the wall at a rate of 0 5 ft s How fast is the top of the ladder sliding down the wall when the foot of the ladder is 5 ft from the wall 13 ft Let x be the distance from the foot of the ladder to the wall and let y be the distance from the top of the ladder to the ground Write an equation relating x and y

Calculus
Application of derivativesAn angler hooks a trout and reels in his line at 3 in s Assume the tip of the fishing rod is 13 ft above the water and directly above the angler and the fish is pulled horizontally directly toward the angler see figure Find the horizontal speed of the fish when it is 20 ft from the angler 13 ft Decreasing at 3 in s Let x be the horizontal distance from the angler to the fish and z be the length of the fishing line where both x and z are measured in inches Write an equation relating x and z

Calculus
DifferentiationBy means of the definition of a radian change the given angles in radians to an equal angle expressed in degrees 4 498 rad O 4 498 rad Round to two decimal places as needed

Calculus
Differential equationscomplete a Sketch at least 2 cycles of the graph showing the height of a rider above the ground as a function of time if the rider gets on at a height of 0 5 metres at t 0 minutes 4 marks b Determine the equation which expresses the height of the rider with respect to time Show all calculations Use radian measure 5 marks

Calculus
Application of derivativesA rocket burns up at the rate of 5 tons min after falling out of orbit into the atmosphere If the rocket weighed 5400 tons before reentry express its weight w as a function of the time t in minutes of reentry Write the weight of the rocket as the function w t w t Simplify your answer Do not factor

Calculus
Application of derivativesA rectangle initially has dimensions 2 cm by 5 cm All sides begin increasing in length at a rate of 2 cm s At what rate is the area of the rectangle increasing after 16 s Let A b and h be the area base and height of a rectangle respectively Write an equation relating A b and h
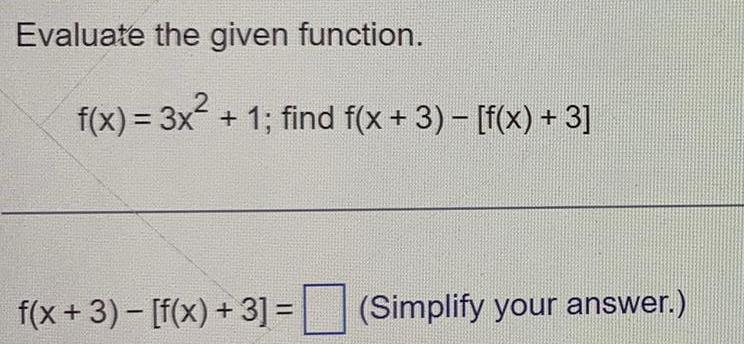
Calculus
DifferentiationEvaluate the given function f x 3x 1 find f x 3 f x 3 f x 3 f x 3 Simplify your answer

Calculus
Definite IntegralsA rope passing through a capstan on a dock is attached to a boat offshore The rope is pulled in at a constant rate of 2 ft s and the capstan is 6 ft vertically above the water How fast is the boat traveling when it is 5 ft from the dock Let x be the horizontal distance from the boat to the dock and z be the length of the rope Write an equation relating x and z

Calculus
Application of derivativesOnce Kate s kite reaches a height of 57 ft above her hands it rises no higher but drifts due east in a wind blowing 6 ft s How fast is the string running through Kate s hands at the moment that she has released 119 ft of string Let x be the horizontal distance from Kate to the kite and z be the length of the string Write an equation relating x and z


Calculus
Application of derivativesThe volume of a cube decreases at a rate of 0 2 ft min What is the rate of change of the side length when the side lengths are 7 ft Write an equation relating the volume of a cube V and an edge of the cube s
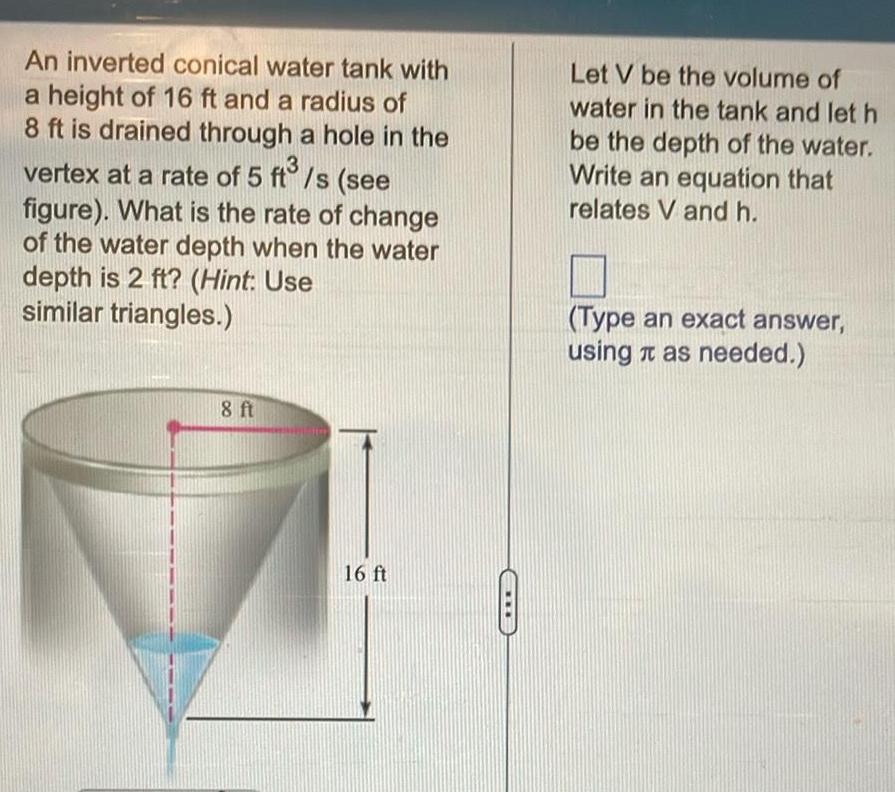
Calculus
DifferentiationAn inverted conical water tank with a height of 16 ft and a radius of 8 ft is drained through a hole in the vertex at a rate of 5 ft s see figure What is the rate of change of the water depth when the water depth is 2 ft Hint Use similar triangles 8 ft 16 ft Let V be the volume of water in the tank and let h be the depth of the water Write an equation that relates V and h Type an exact answer using as needed
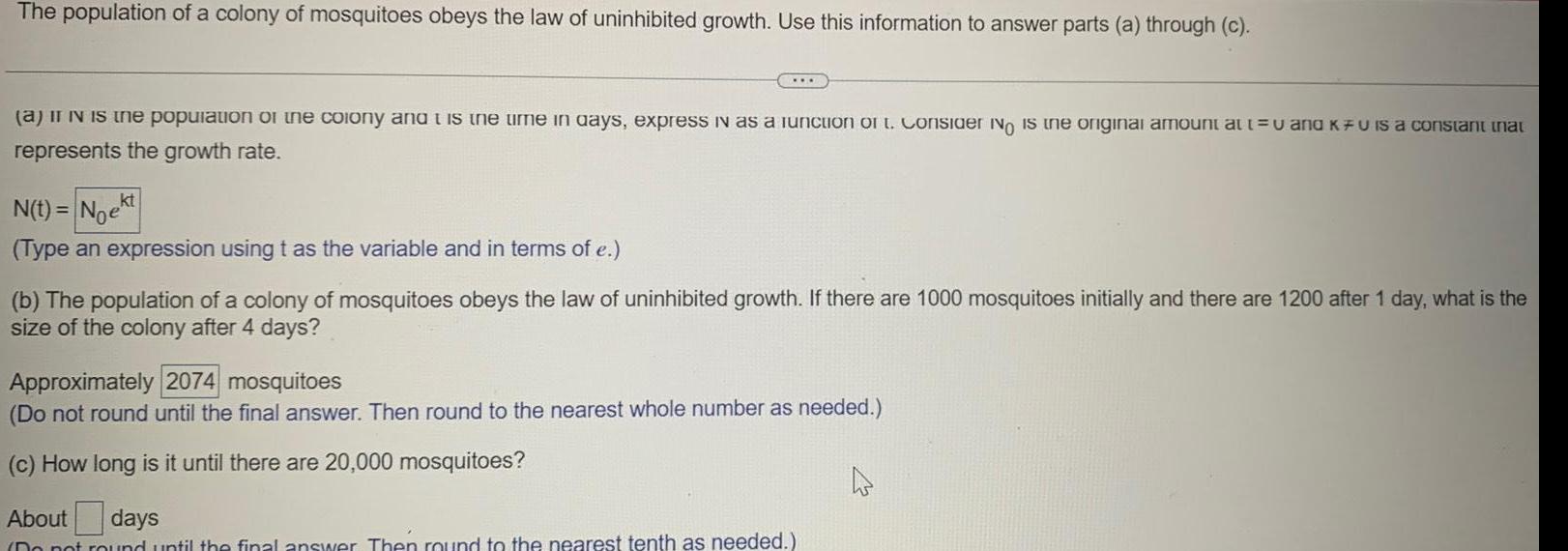
Calculus
Application of derivativesThe population of a colony of mosquitoes obeys the law of uninhibited growth Use this information to answer parts a through c a it iN is the population of the colony and is the time in days express in as a function of t Consider No is the original amount at t u and KFU is a constant that represents the growth rate N t Noekt Type an expression using t as the variable and in terms of e b The population of a colony of mosquitoes obeys the law of uninhibited growth If there are 1000 mosquitoes initially and there are 1200 after 1 day what is the size of the colony after 4 days Approximately 2074 mosquitoes Do not round until the final answer Then round to the nearest whole number as needed c How long is it until there are 20 000 mosquitoes About days Do not round until the final answer Then round to the nearest tenth as needed 4

Calculus
Application of derivativesA thermometer reading 10 C is brought into a room with a constant temperature of 32 C If the thermometer reads 17 C after 2 minutes what will it read after being in the room for 4 minutes For 9 minutes C After 4 minutes the thermometer will read Do not round until the final answer Then round to the nearest hundredth as needed
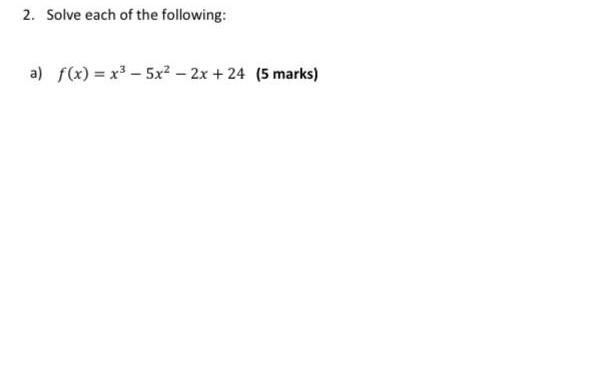

Calculus
Application of derivatives1 Given f x 3x and g x x 4 determine the expression for f g x 3 marks

Calculus
Application of derivativesDetermine the volume of the largest rectangular box in the first octant with three faces in the coordinate planes one vertex at the origin and its opposite vertex in the plane 3r 6y z 18 6 pts
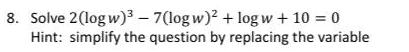
Calculus
Limits & Continuity8 Solve 2 logw 7 logw log w 10 0 Hint simplify the question by replacing the variable

Calculus
Limits & Continuity6 As a tornado moves its speed increases The function S d 93 log d 65 relates the speed of the wind S in miles per hour near the center of a tornado to the distance that the tornado has travelled d in miles Determine the distance that a tornado has travelled if the speed of the wind at the center of the tornado reaches 150 miles per hour 3 marks

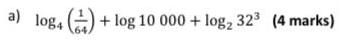
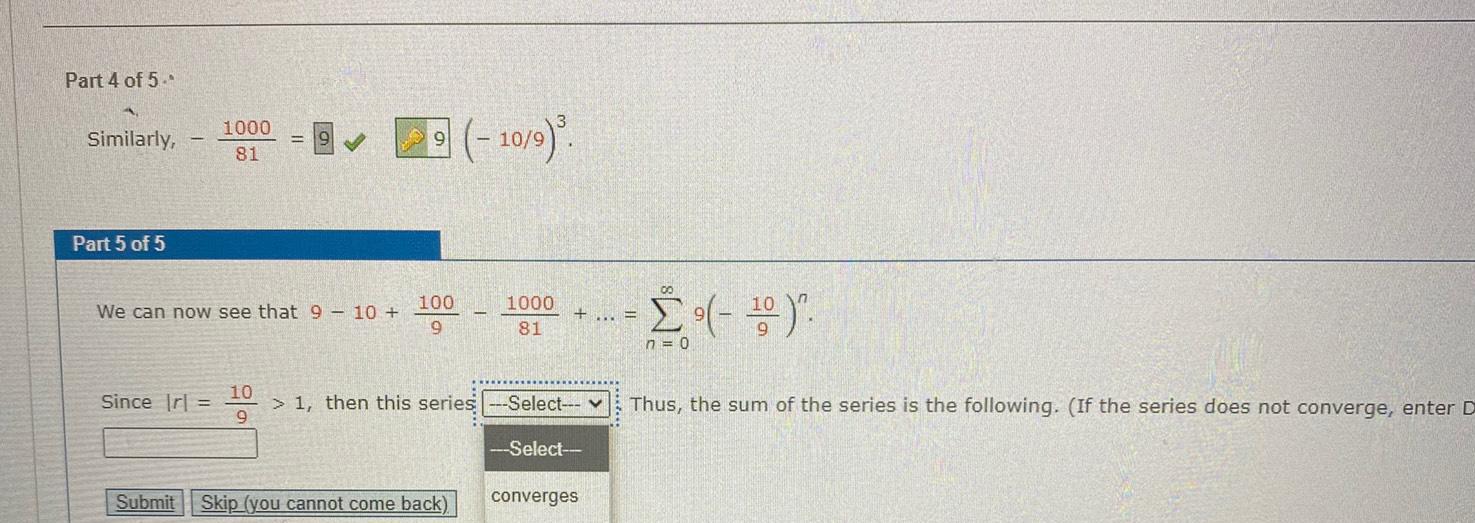
Calculus
Application of derivativesPart 4 of 5 Similarly Part 5 of 5 1000 81 Since Irl We can now see that 9 10 10 9 100 9 10 9 Submit Skip you cannot come back 1000 81 1 then this series Select Select converges 00 n 0 Thus the sum of the series is the following If the series does not converge enter D
Calculus
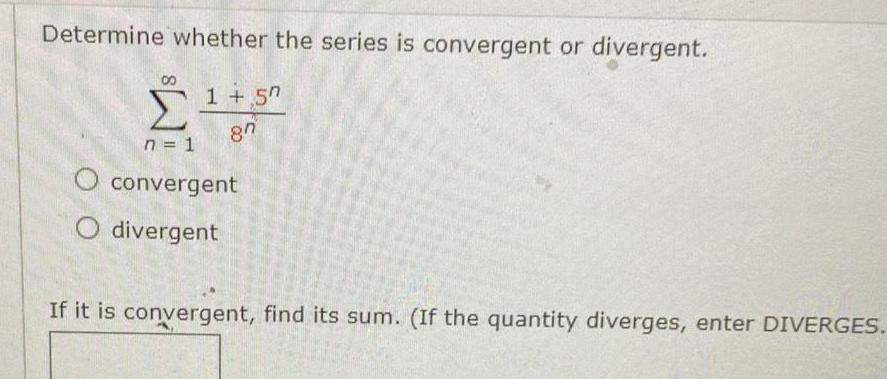
Differential equationsDetermine whether the series is convergent or divergent 1 57 87 n 1 O convergent O divergent If it is convergent find its sum If the quantity diverges enter DIVERGES
Calculus
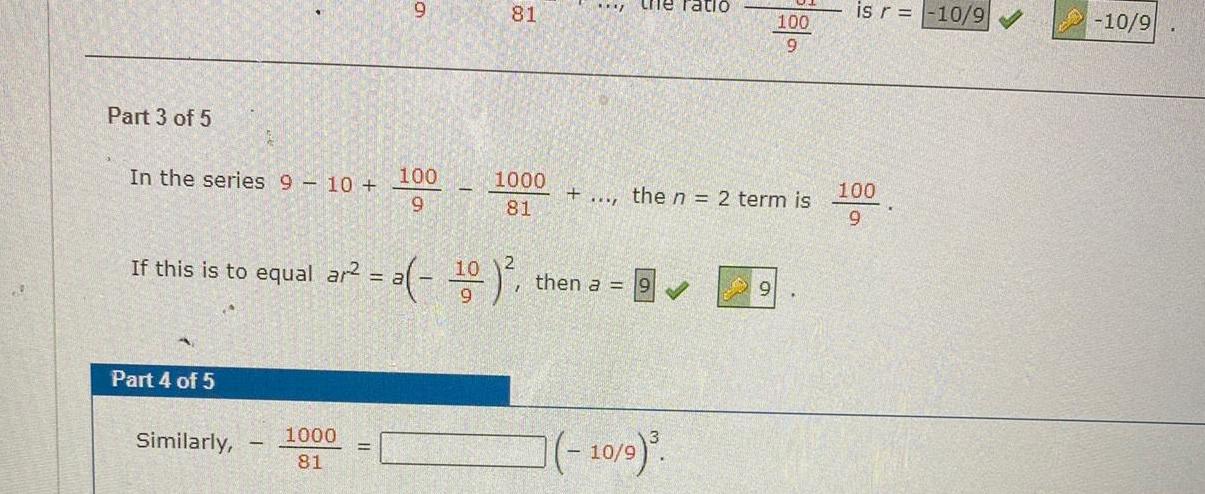
Application of derivativesPart 3 of 5 In the series 9 10 100 9 Part 4 of 5 9 Similarly 1000 81 81 1000 81 the ratiO If this is to equal ar a 10 a 10 then a P the n 2 term is 100 9 10 9 is r 10 9 100 9 10 9
Calculus
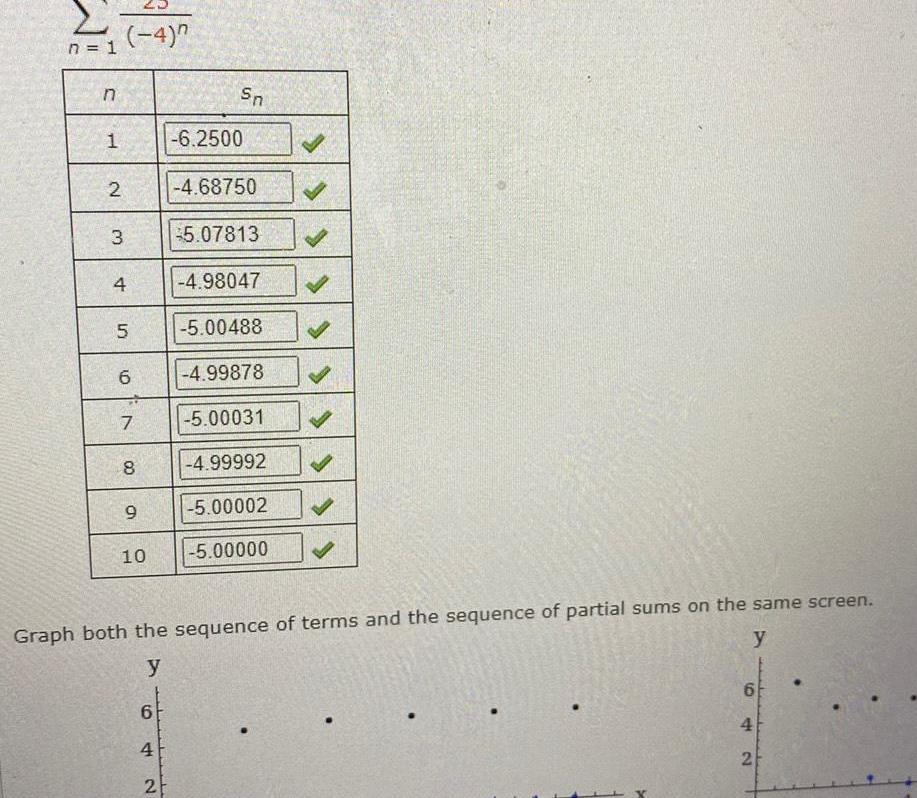
Differentiationn 1 n 1 2 4 3 4 5 6 7 8 9 10 6 4 2 Sn MIRAS 6 2500 Graph both the sequence of terms and the sequence of partial sums on the same screen y y 4 68750 5 07813 4 98047 5 00488 4 99878 5 00031 4 99992 5 00002 5 00000 6 4 42
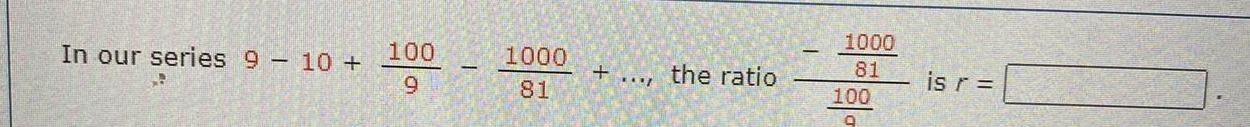
Calculus
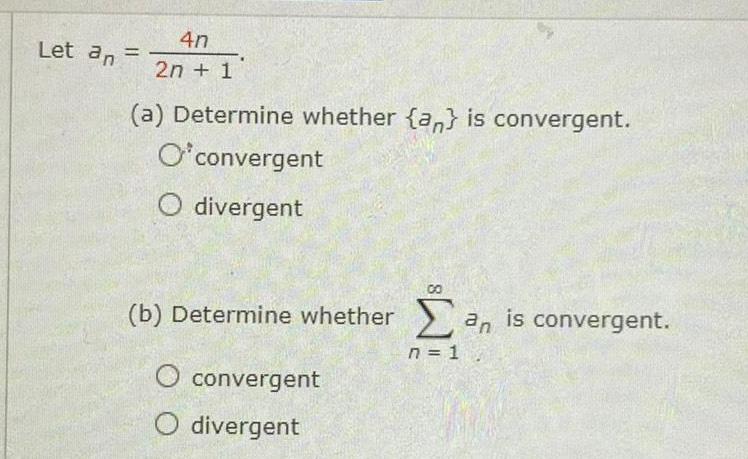
Application of derivativesLet an 4n 2n 1 a Determine whether a is convergent O convergent O divergent b Determine whether an is convergent n 1 convergent CO O divergent
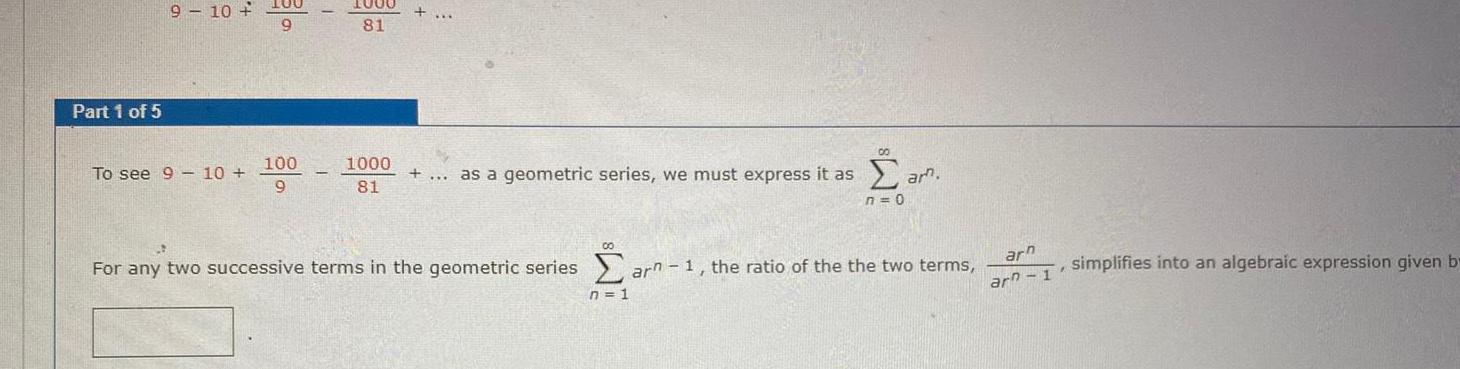
Calculus
DifferentiationPart 1 of 5 9 10 To see 9 10 100 9 100 9 1000 81 1000 81 as a geometric series we must express it as 00 00 n 1 ar am n 0 For any two successive terms in the geometric series arn 1 the ratio of the the two terms arn arn 1 I simplifies into an algebraic expression given b
Calculus
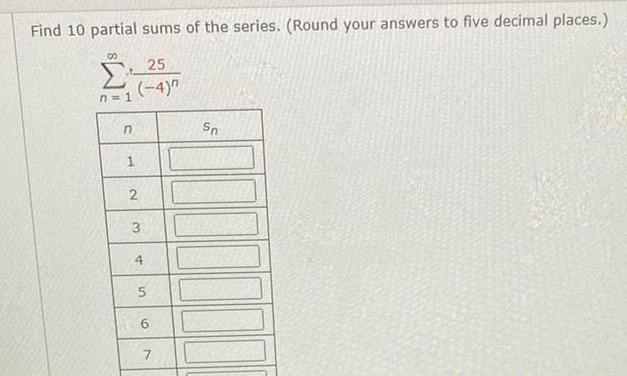
Limits & ContinuityFind 10 partial sums of the series Round your answers to five decimal places n 1 n 25 4 1 2 3 4 5 6 7 7 Sn
Calculus
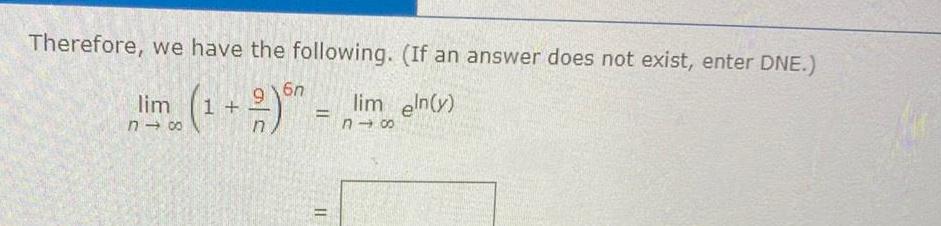
Limits & ContinuityTherefore we have the following If an answer does not exist enter DNE 6n lim 24 1 2 60 II lim eln y n

Calculus
Limits & ContinuityCancelling T from the numerator and denominator gives us lim In y lim x 00 X 54
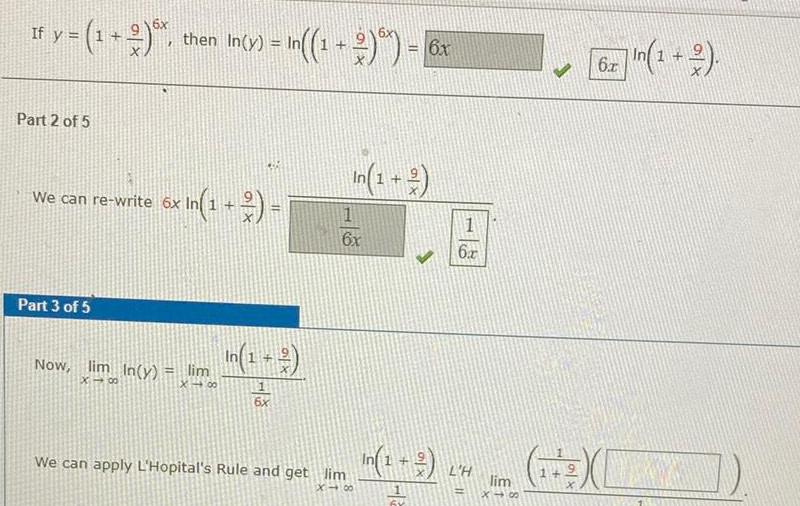
Calculus
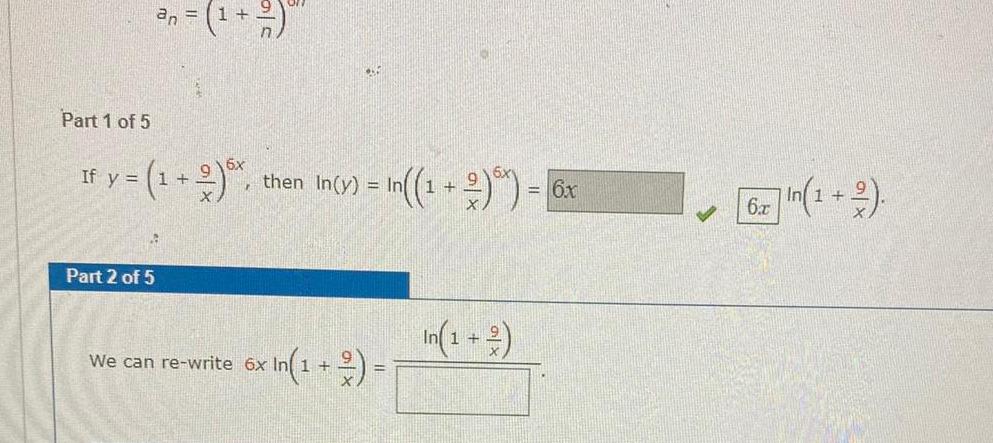
Limits & ContinuityIf y 1 2 x then In y Part 2 of 5 We can re write 6x Part 3 of 5 6x In 1 Now lim In y lim X 00 X 00 In In 1 6x 6x In 1 6x We can apply L Hopital s Rule and get lim X78 6x 1 6 L H 11 lim 818 m 1 6x
Calculus
Limits & ContinuityPart 1 of 5 an 2 1 If y 1 2 A Part 2 of 5 r n 1 2 then In y In 1 We can re write 6x 6x In 1 2 6x n 1 2

Calculus
Limits & ContinuityTutorial Exercise Determine whether the sequence converges or diverges If it converges find the limit 6n Part 1 of 5 an If y 1 2 916x X then In y In 1 2 In 1 2 1
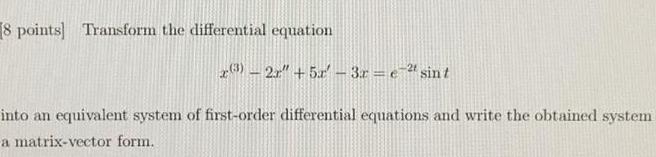
Calculus
Application of derivatives8 points Transform the differential equation 3 2r 5r 3r etsint into an equivalent system of first order differential equations and write the obtained system a matrix vector form
Calculus
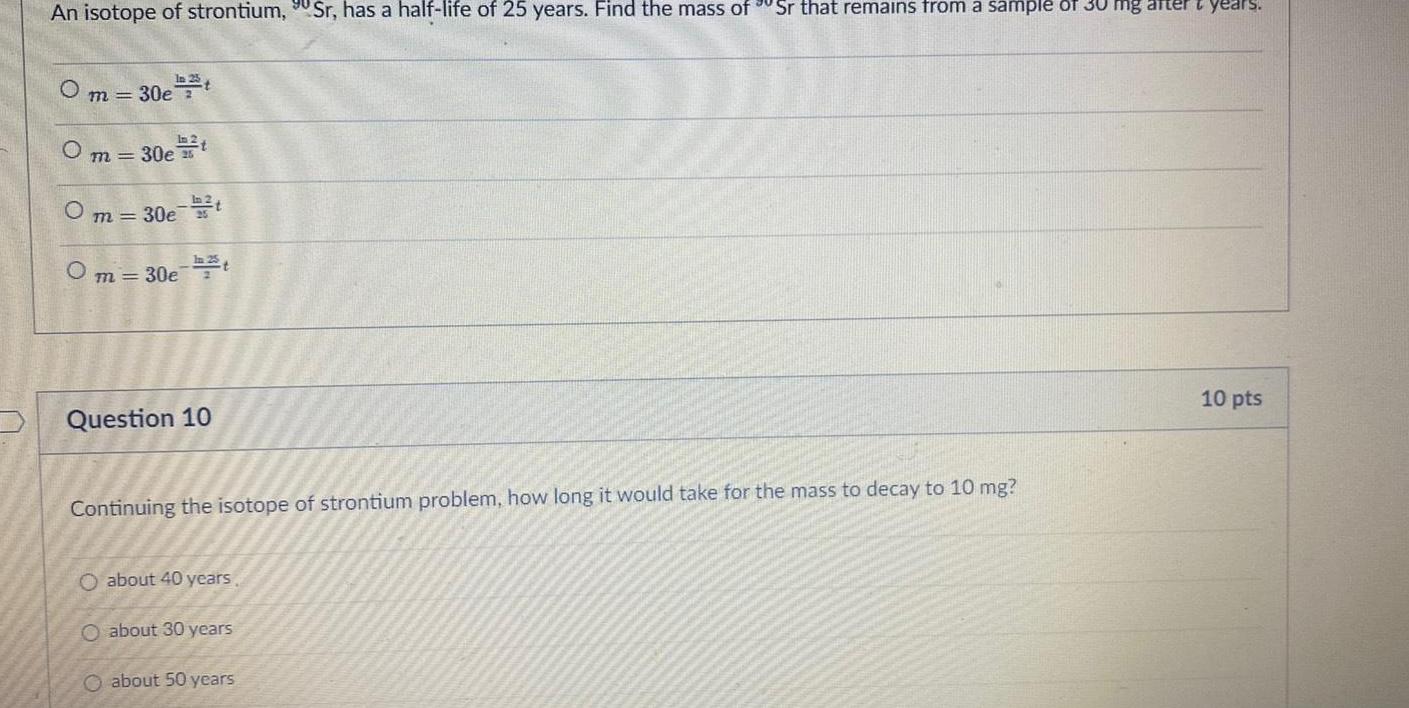
Differential equationsAn isotope of strontium Sr has a half life of 25 years Find the mass of Sr that remains from a sample of 30 mg after years Om 30e t m 30e t Om 30e t Om 30et Question 10 Continuing the isotope of strontium problem how long it would take for the mass to decay to 10 mg O about 40 years O about 30 years O about 50 years 10 pts
Calculus
Differentiationpopulation is 5000 Find an expression for the number of bacteria after t hours OP 100 25t OP 100e OP 100e In 25 t OP 5000et Question 8 In 50 Continuing from the bacteria culture problem find the number of bacteria after 4 hours 250000 O 200000 O 100000 10 pts