Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
Application of derivativesAILS n 1 SCALCET9 11 2 019 Determine whether the series is convergent or divergent by expressing s as a telescoping sum If it is convergent find its sum If the quantity diverges enter DIVERGE 27 n n 3 M

Calculus
Limits & ContinuityFind the radius interval of convergency of the power series 1 22 1 05 0 1
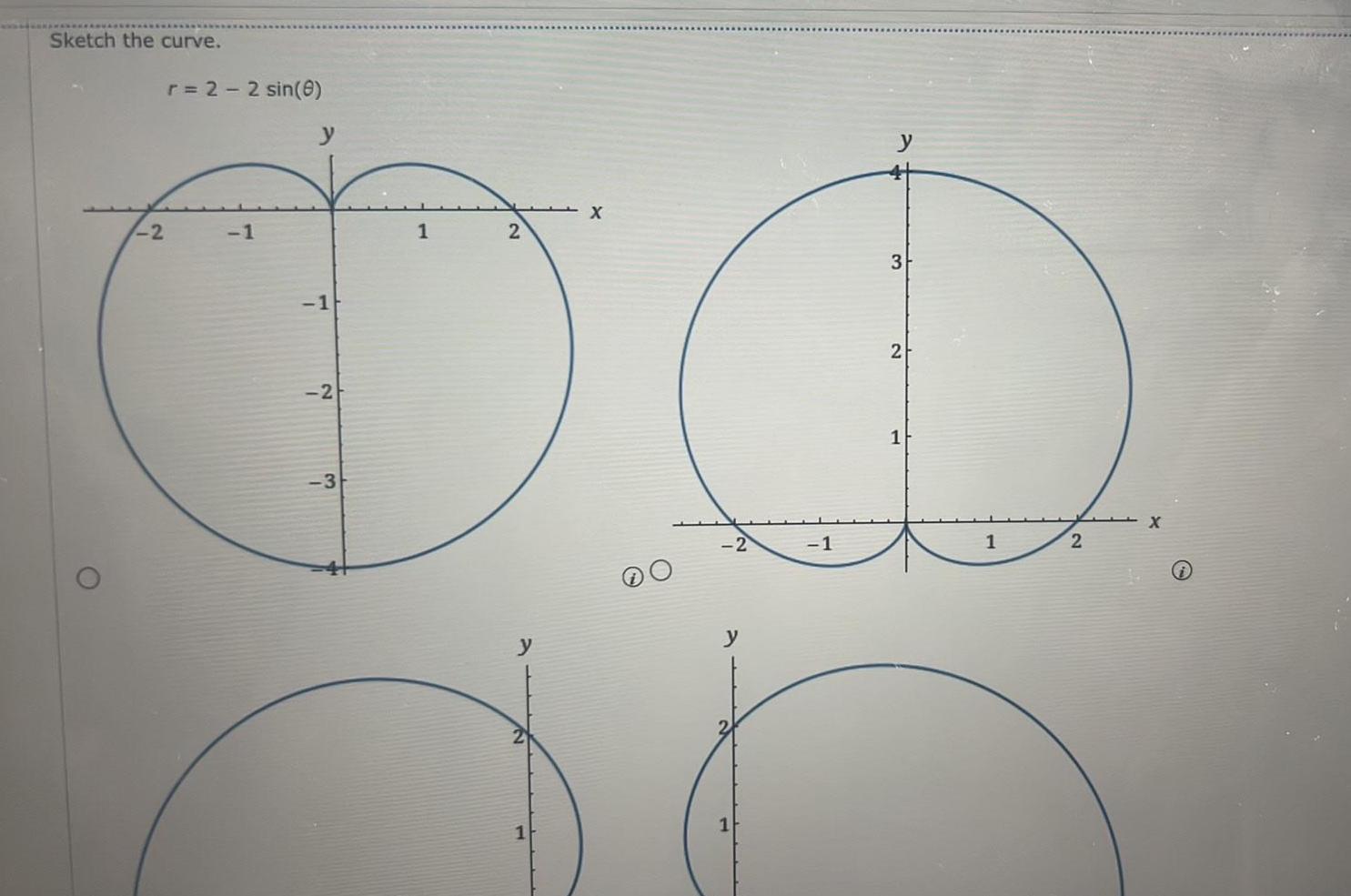



Calculus
DifferentiationFind the area of the region that is bounded by the given curve and lies in the specified sector st 2 r 180 0 es

Calculus
Limits & ContinuityDetermine whether the sequence converges or diverges If it converges find the limit If the sequence diverges enter DIVERGES an e4n n 4 lim a

Calculus
DifferentiationFind the Maclaurin series for f x using the definition of a Maclaurin series Assume that f has a power series expansion Do not show that R x 0 f x In 1 5x f x 00 R n 1 Find the associated radius of convergence R 1 n 1 x 1 5 1 n 15 11 10 012 X
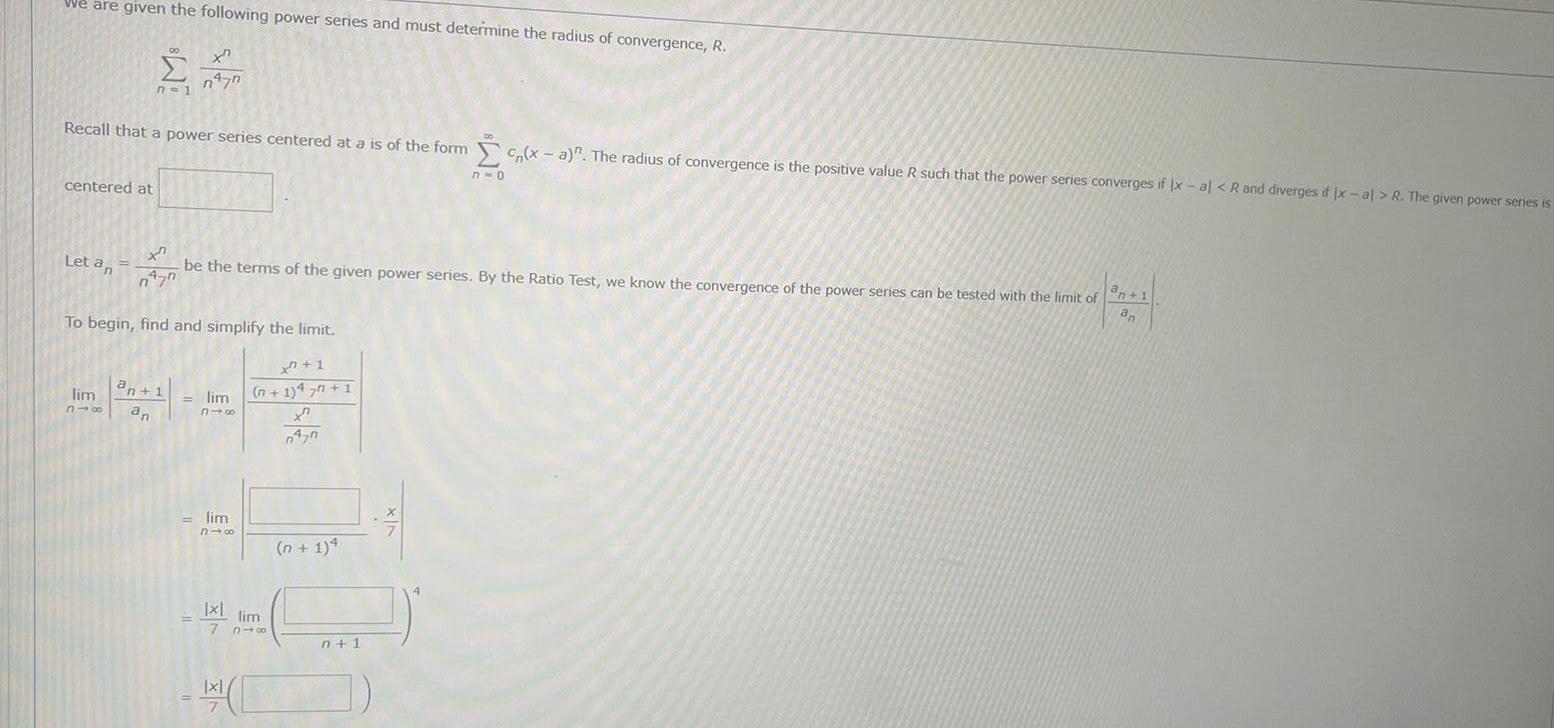
Calculus
Application of derivativesWe are given the following power series and must determine the radius of convergence R centered at Recall that a power series centered at a is of the form x a The radius of convergence is the positive value R such that the power series converges if x al R and diverges if Ix al R The given power series is n 1 Let an xn n 70 be the terms of the given power series By the Ratio Test we know the convergence of the power series can be tested with the limit of an 1 an To begin find and simplify the limit xn 1 n 1 47n 1 X 0470 n477 lim an 1 318 an lim 318 lim 310 Ixl lim le 7 816 x n 1 4 7 0 n 1

Calculus
Application of derivativesConsider the following series n 1 Evaluate the following limit where an R 7427 lim 818 I Find the radius of convergence R of the series an 1 an Find the interval I of convergence of the series Enter your answer using interval notation
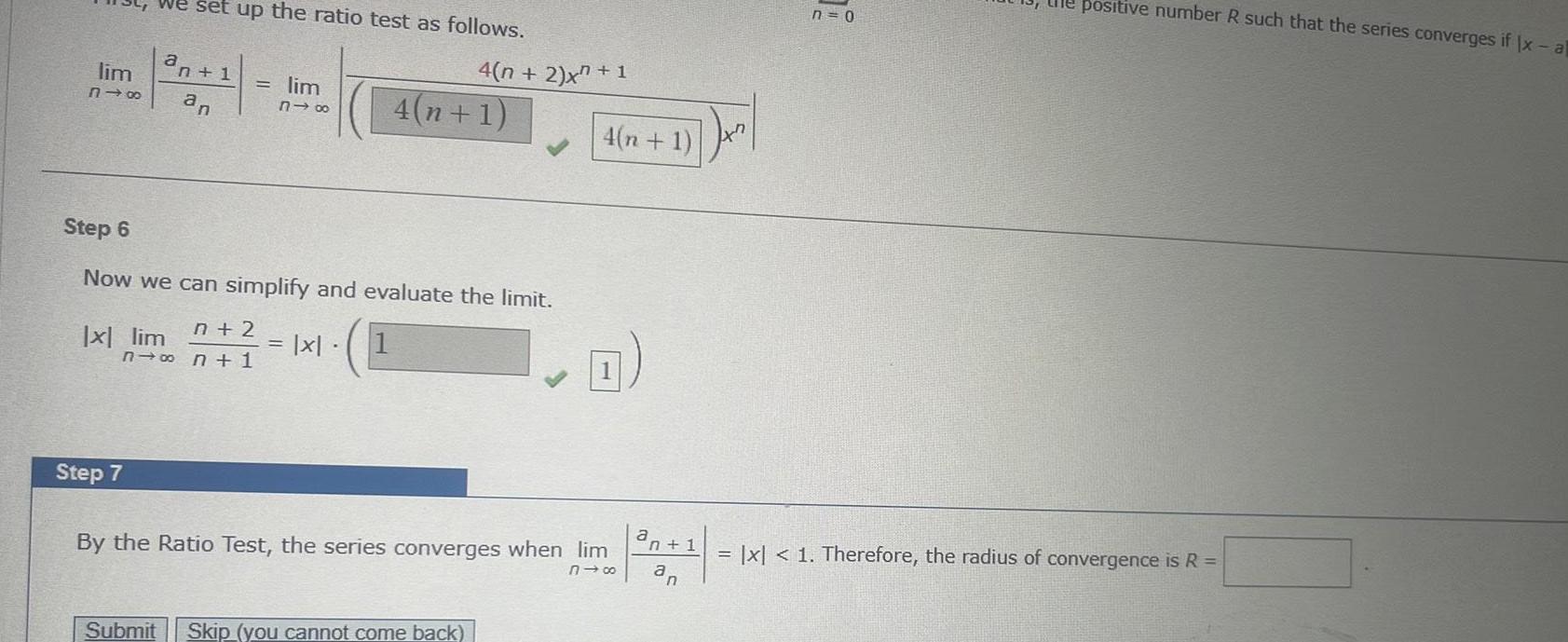
Calculus
Application of derivativesWe set up the ratio test as follows an 1 318 an lim x lim Step 7 lim 818 Step 6 Now we can simplify and evaluate the limit n 2 n n 1 1 x 4 n 2 x 1 4 n 1 Submit Skip you cannot come back 4 n 1 By the Ratio Test the series converges when lim 818 a n 1 an Jx n 0 positive number R such that the series converges if Ix al x 1 Therefore the radius of convergence is R

Calculus
Application of derivativesSCALCET9 11 10 006 Use the definition of a Taylor series to find the first four nonzero terms of the series for f x centered at the given value of a Enter your answers as a comma separated list 4 1 x 4 3 4 31 f x x 2 4 a 2 x 2 2 4 x 2 3 MY NOTES

Calculus
Limits & Continuitya What is a sequence A sequence is an ordered list of numbers A sequence is the product of an ordered list of numbers A sequence is an unordered list of numbers A sequence is the sum of an ordered list of numbers A sequence is the sum of an unordered list of numbers b What does it mean to say that lim 818 8 an The terms a approach infinity as n become large The terms an approach 8 as n becomes small The terms an approach infinity as 8 approaches n The terms a approach infinity as 8 approaches n n O The terms a approach 8 as n becomes large c What does it mean to say that liman n O The terms a The terms a The terms a n o become small as n becomes small become small as n becomes large become large as n becomes large become large as n becomes small The terms an The terms a approach zero as n becomes large

Calculus
Limits & ContinuityList the first five terms of the sequence 3 0 2 n n 22 23 24 25 a6 11 11 11 MI

Calculus
Indefinite IntegrationWrite the given function as a power series cos x 1 X n 1 1 n 1 1 X Evaluate the indefinite integral as an infinite series cos X 1 1 x2n 2n 2n x2n 2n 2n dx C c



Calculus
Application of derivativesThe shaded region in the figure consists of all points whose distances from the center of the square are less than their distances from the edges of the square Find the area of the region Round your to three decimal places 64 5 y 5 5 5

Calculus
Application of derivativesla Assignment Status Click here for incorrect Answer ded answer is not correct and ecific feedback is available e hints and review the relevant material and stay on this question 3 4 5 6 7 S 9 10 11 Completed Completed Completed kicked over flat ground and the acceleration due to gravity on the planet is 5 18 m s The planet has no atmosphere Partial Partial Partial Partial How far horizontally does the ball travel in meters while it is in flight x 109 758 sin cos cotan asin atan acotan cosh 789 HOME tan acos ET 45 6 sinh 123 tanh cotanh C 0 Degrees O Radians NO BACKSPACE INL CLEAR END Submit Hint Frothick I give not 1 Grade Summary Deductions Potential 29 98 Submissions Attempts remaining 2 2 per attempt detailed view 1 296

Calculus
Differential equations1 point Estimate f x g x dx if f x x and g x has the values given in the following table 3 o f x g x dx 26 169 x 00 5 1 1 5 2 2 5 3 g x 11 11 62 63 64 14 3

Calculus
Application of derivativesNow we must find the radius of convergence for the Maclaurin series First we set up the ratio test as follows lim 816 an 1 an lim 818 n 2 n n 1 4 n 2 x 1 Step 6 Now we can simplify and evaluate the limit Ixl lim x 4 n 1 4 n 1 B n 0 4 n 1 x That is the positive number R such that the series converges if Ix al R and diverges of La

Calculus
Limits & ContinuityStep 5 Now we must finde radius of convergence for the Maclaurin series First we set up the ratio test as follows 4 n 2 x 1 an 1 lim 816 an lim 510 Submit Skip you cannot come back n o 4 n 1 x That is the positive number R such that the series converges if x al R and diverges if Ix al R We can use the ratio test to find R

Calculus
Limits & Continuityf x f 0 f 0 x 4 00 n 0 f 0 2 begins as 8 f 0 3 3 Submit Skin you cannot come back 8 x 12 4 0 4 12 x 16 V 16 x 20 20 4 x Step 4 Now that we have the beginning of the Maclaurin series continuing this pattern we find the general formula as follows f x 4 8x 12x 16x 20x

Calculus
Limits & Continuity2 Points f x Find a power series representation for the function Center your power series representation at x 0 00 n 0 DETAILS f x SCALCET9 11 9 003 MI 1 9 x Determine the interval of convergence Enter your answer using interval notation

Calculus
Application of derivativesStep 3 We have found the following values of the function and its derivatives f 0 4 f 0 8 f 0 24 f 0 96 4 0 480 Therefore the Maclaurin series begins as f x f 0 f 0 x f 0 2 f 0 x3 4 0 x4 3 4 X x ARK

Calculus
Application of derivatives480 1 x 6 Step 2 We have found the following derivatives of f x f x 4 1 x f x 8 1 x f x 24 1 x 4 96 1 x 5 4 x 480 1 x 6 The Maclaurin series uses the function and its derivatives evaluated at 0 which we find as follow f 0 f 0 F 0 f 0 4 0 480 1 x 6 f x Submit Skip you cannot come back

Calculus
Application of derivativesIf f x b x 4 for all x write a formula for b n 0 O by O b O b Ob by O by f 7 7 4 f 4 4 f 4 7 f 7 4 7 f 4 4 7

Calculus
Application of derivatives6 sin x 5 sin x 1 0 0 2 X Select 4 correct answer s 1 30 3 31 0 T 4 5T 4 2 3 5 94 5


Calculus
Application of derivatives2 cos x 3 cos x 1 0 0 2 X Select 3 correct answer s 0 5 3 3 2 5 6 11

Calculus
Application of derivativestan x 3 X Select 2 correct answer s HO 130 TU 57 6 11 6 3 0 2 No solution 5 3

Calculus
Vector Calculus40 sin x 5 15 0 2 X Select 2 correct answer s 0 5n 6 11 6 27 3 500 4x 3 1 30 Search


Calculus
Application of derivativesProblems 4 7 Simplify each rational expression If the rational expression cannot be simplified so state 4 5 7 48y5 15y3 4a 9b 2a 3b 3x 1 3x 29x 10 3 x 5r 15

Calculus
Differential equationsWe now have u t tan t C Since u 0 9 we can substitute into the equation and solve for C 81 Part 5 of 5 Noting that u 0 9 is negative then when we solve for u we must get u Submit Skip you cannot come back 81

Calculus
Application of derivativesIgnoring the constant of integration integrating the right side gives Part 4 of 5 We now have u t tan t C Since u 0 9 we can substitute into the equation and solve for C Submit Skip you cannot come back sec t

Calculus
Differentiation2 Ignoring the constant of integration integrating the left side gives zu 2u du u Part 3 of 5 1 Ignoring the constant of integration integrating the right side gives 2t sec t dt

Calculus
Differential equationsTutorial Exercise Find the solution of the differential equation that satisfies the given initial condition du 2t sec t 2u Part 1 of 5 Separating du dt u 0 9 2t sec t 2u gives us 2u du dt

Calculus
Limits & ContinuityAnswer Above the xy plane and above Quadrants II or IV or below the xy plane and below Quadrants I or III

Calculus
Definite Integralsthe equation of the sphere in standard form Find the center and radius 43 x y 2 2x 6y 8z 1 0 Answer 44 a y z 9x 2y 10z 19 0 45 9x 9y 92 6x 18y 1 0 Answer x 1 Center 2 y 1 1 1 0 exercises 43 44 45 and 40 complete Radius 1

Calculus
Vector Calculus21 xy 0 2 3 Answer Three units below the xy plane and below either Quadrant I or Quadrant

Calculus
Differential equations10 Points DETAILS Find the solution of the differential equation that satisfies the given initial condition dy 4 y 0 5 dx y Submit Answer 5 10 Points SCALCCCH4 DETAILS SCALCCCH4 7 3 013 MI SA This question has several parts that must be completed sequentially If you skip a par able to come back to the skipped part Tutorial Exercise Find the solution of the differential equation that satisfies the given initial condit 2t sec t 0 9

Calculus
Indefinite IntegrationWe can now solve 1 u Ke 2 2t for u 1 Notice that since u 1 is a solution This also means that K could be 0 and so we could simply write u

Calculus
Indefinite IntegrationPart 5 of 6 We now have In 1 ul 11 2 2 2t C 2 2t C This can be re written as 11 u e 2 2t C Letting K e e can be re written as K
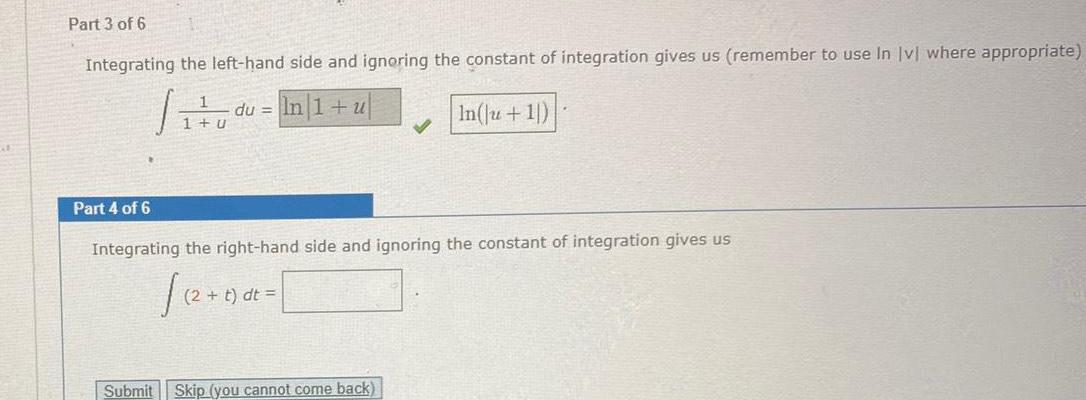
Calculus
Indefinite IntegrationPart 3 of 6 Integrating the left hand side and ignoring the constant of integration gives us remember to use In lvl where appropriate In 1 u In Ju 1 Part 4 of 6 1 u du Integrating the right hand side and ignoring the constant of integration gives us t dt Submit Skip you cannot come back
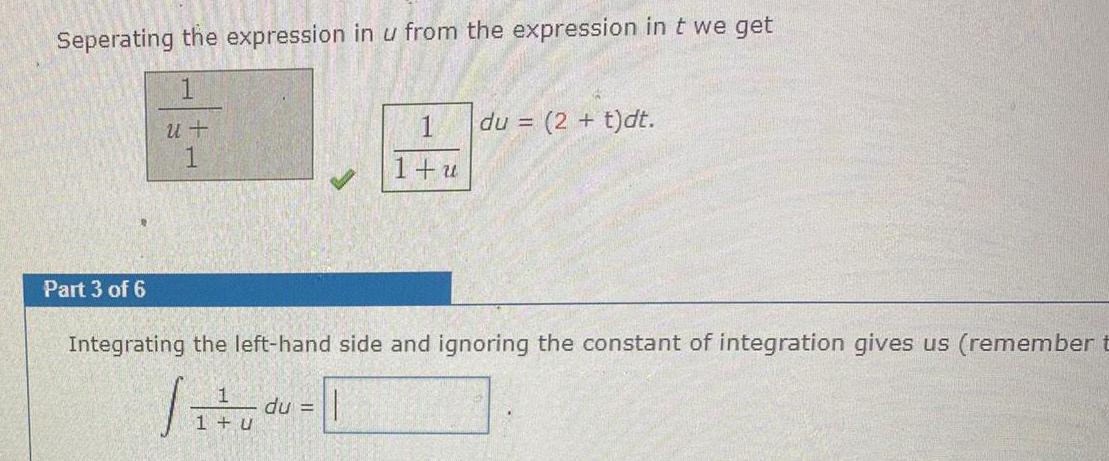
Calculus
Indefinite IntegrationSeperating the expression in u from the expression in t we get 1 u 1 Part 3 of 6 1 1 u du 2 t dt Integrating the left hand side and ignoring the constant of integration gives us remember t du 1 u

Calculus
Differential equationsdu To separate 2 2u t tu factor the right hand side to get dt Part 2 of 6 Seperating the expression in u from the expression in t we get du 2 t dt du dt 2 t 1 u 1 u

Calculus
Vector CalculusIf cost is represented by C x 2 8x 100 000 and revenues are represented by R x 5 3x which equation could be used to find the break even point Select the correct answer below 8 1x 100 000 O 2 5x 100 000 O 5 3x 100 000 O 2 5x 100 000 O 8 1x 100 000
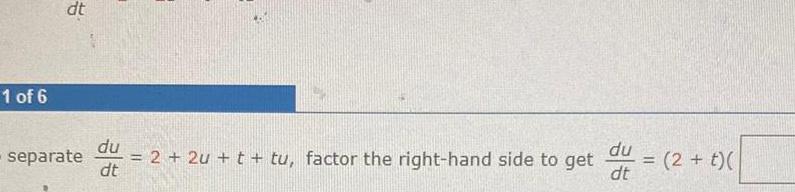
Calculus
Indefinite Integration1 of 6 dt separate du 2 2u t tu factor the right hand side to get dt du dt 2 t

Calculus
Limits & ContinuityFinding the Equation of a Sphere In Exercises 37 38 39 40 41 and 42 find the standard equation of the sphere with the given characteristics 37 Center 7 1 2 Radius 1 Answer x 7 y 1 z 2 1 38 Center 1 5 8 Radius 5 39 Endpoints of a diameter 2 1 3 1 3 1 Answer X 1 2 3 y 2 z 1 21 4