Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
Calculus
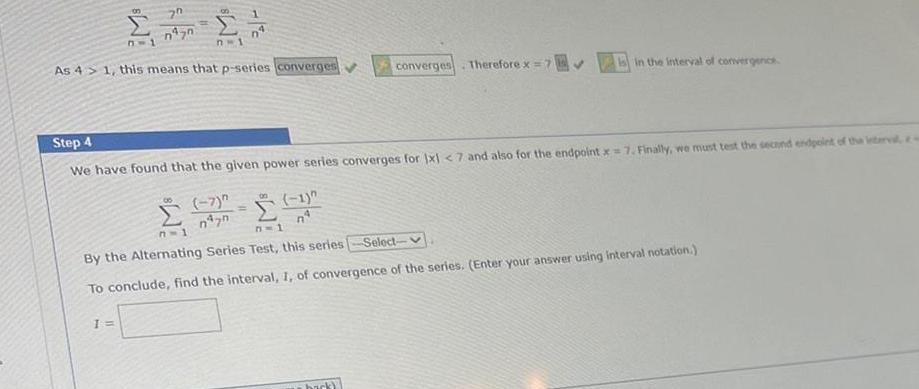
Application of derivatives8 7 1 70 1 n Lan n 1 As 4 1 this means that p series converges 09 7 07 Step 4 We have found that the given power series converges for 1x1 7 and also for the endpoint x 7 Finally we must test the second endpoint of the interval e 8 1 n converges Therefore x 7 in the interval of convergence n 1 7 1 By the Alternating Series Test this series Select To conclude find the interval 1 of convergence of the series Enter your answer using interval notation back

Calculus
Definite IntegralsDETAILS b sin br 114 0 1 Points Find the solution of the differential equation that satisfies the given initial condition dA Ab cos br A 0 6 dr Need Help x PREVIOUS Read It

Calculus
Application of derivativesTherefore k 30 In 2 30 Step 4 Now remembering that In x n In x and that eln z z we have y t 50e t 30 In 2 mg

Calculus
Application of derivativesP 3 0 1 Points Find the solution of the differential equation that satisfies the given initial condition dp dt DETAILS 7 3 ad Help 7 Pt P 1 3 3 PREVIOUS 7 3 Read It X

Calculus
Application of derivativesDETAILS 9 0 1 Points PREVIOUS ANSW Find the area of the region that lies inside the first curve and outside the second curve r 16 sin 8 11 71 x r 8
Calculus
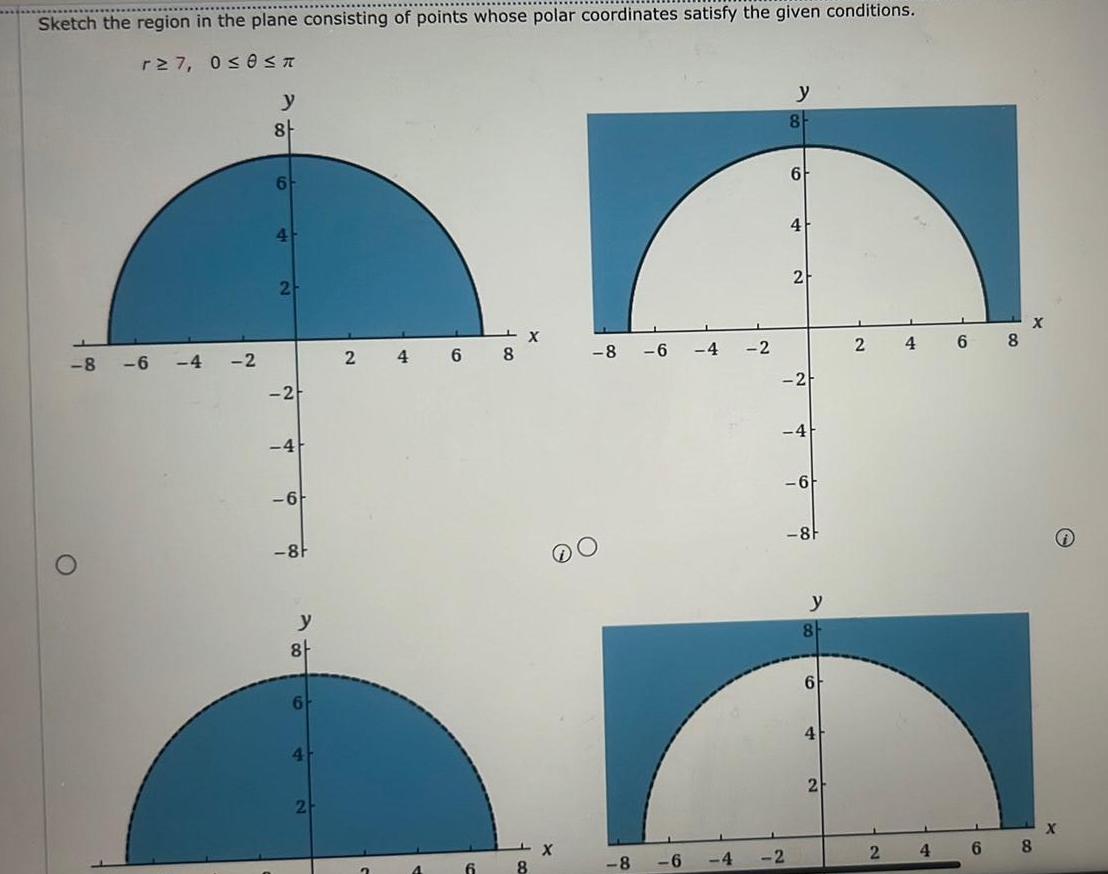
Definite IntegralsSketch the region in the plane consisting of points whose polar coordinates satisfy the given conditions r 7 0 0 8 6 4 2 y 8 6 4 2 2 4 6 8F y 8 6 4 2 2 4 6 8 X 8 8 6 4 2 4 6 y 8 6 2 4 2 2 4 6 8F y 8 6 2 2 2 4 4 6 6 8 X 8

Calculus
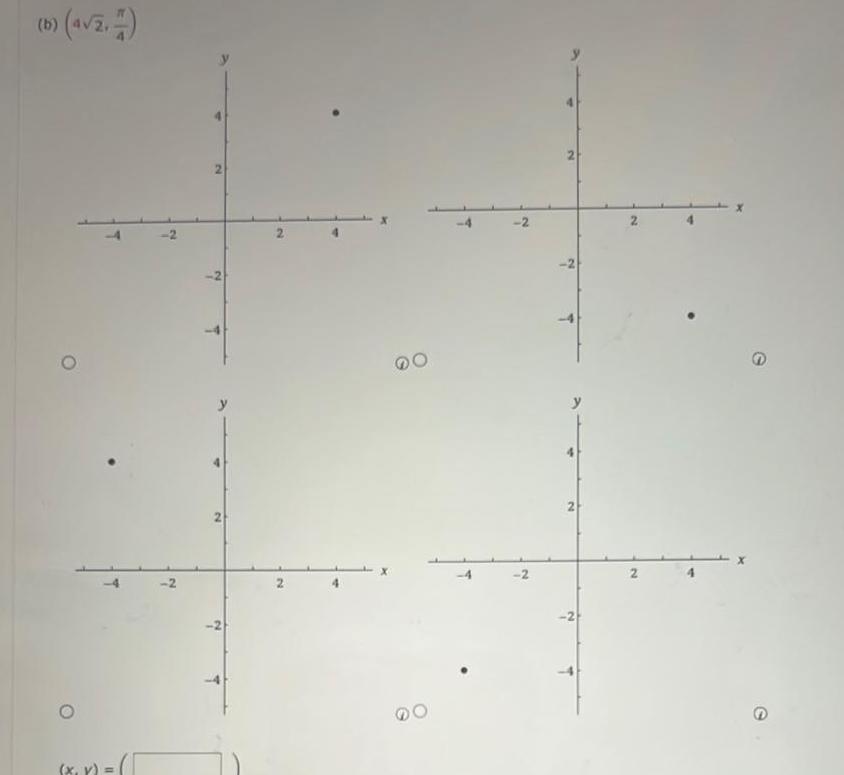
Definite IntegralsDETAILS 11 0 1 Points Find the area of the region that lies inside the first curve and outside the second curve r 3 cos 8 r 1 cos 8 A T x Enhanced Feedback Please try again keeping in mind that you should first find the intersection points Then use the formula for the area between two parametric curves which is A toll
Calculus
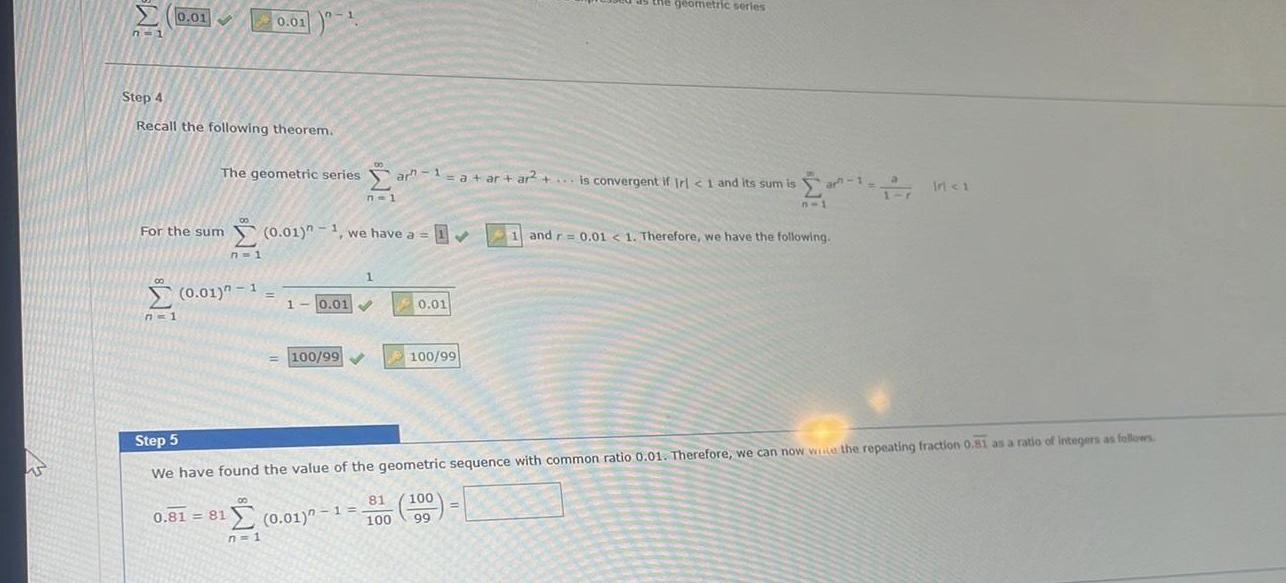
Limits & ContinuityW S 0 01 n 1 Step 4 Recall the following theorem 8 n 1 For the sum 0 01 n 1 we have a 0 01 The geometric seriesar 1 a ar ar a ar ar is convergent if Irl 1 and its sum is n 1 7 1 0 01 n 1 0 81 81 n 1 1 10 01 0 01 100 99 0 01 100 99 the geometric series ar 1 n 1 Step 5 We have found the value of the geometric sequence with common ratio 0 01 Therefore we can now wice the repeating fraction 0 81 as a ratio of integers as follows 0 01 1 81 100 100 99 17 Inci 1 and r 0 01 1 Therefore we have the following
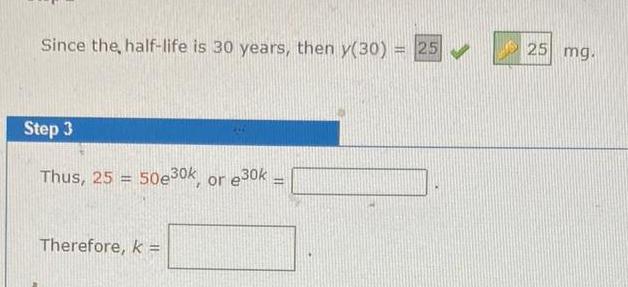
Calculus
Application of derivativesSince the half life is 30 years then y 30 25 Step 3 Thus 25 50e30k or 30k Therefore k H 25 mg
Calculus
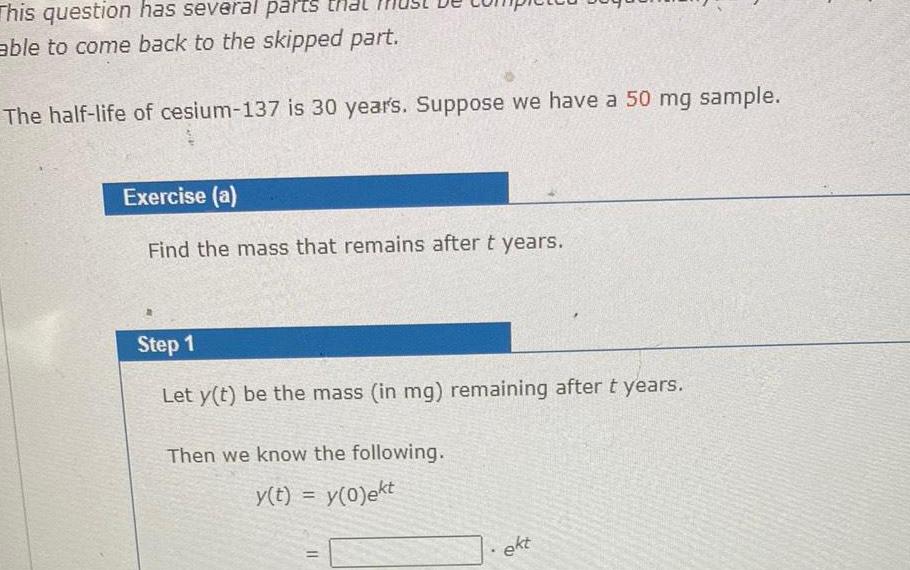
Application of derivativesThis question has several parts that able to come back to the skipped part The half life of cesium 137 is 30 years Suppose we have a 50 mg sample Exercise a Find the mass that remains after t years Step 1 Let y t be the mass in mg remaining after t years Then we know the following y t y 0 ekt ekt

Calculus
Application of derivativesSolve for x cos x cos 2x 0 0 2n X Select 3 correct answer s KO 4 60 03 Gla co No solution 02 2 W H 560 n
Calculus
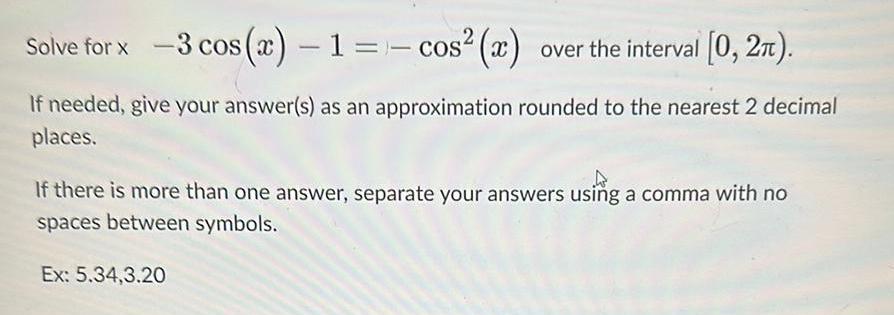
Differential equationsSolve for x 3 cos x 1 cos x over the interval 0 2 If needed give your answer s as an approximation rounded to the nearest 2 decimal places If there is more than one answer separate your answers using a comma with no spaces between symbols Ex 5 34 3 20
Calculus
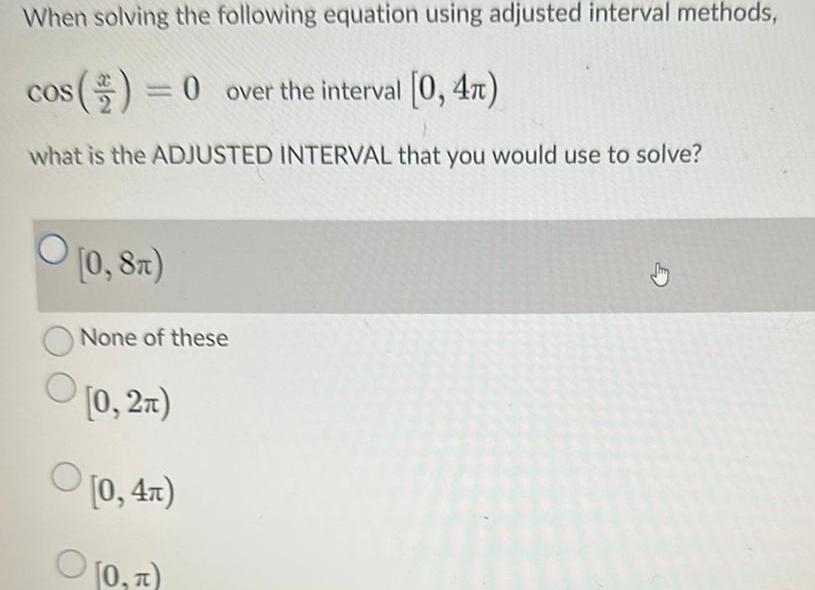
DifferentiationWhen solving the following equation using adjusted interval methods cos 0 over the interval 0 4 what is the ADJUSTED INTERVAL that you would use to solve 0 8T None of these 0 2x 0 4 0
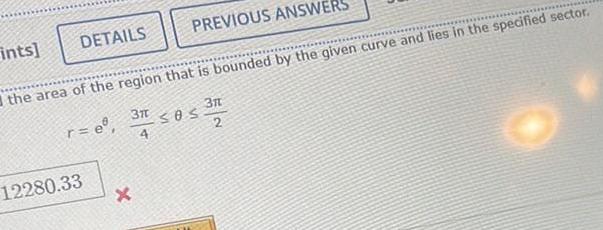
Calculus
Application of derivativesPREVIOUS ANSWERS the area of the region that is bounded by the given curve and lies in the specified sector r e 3 t 4 Os 3128 2 DETAILS ints 12280 33 X
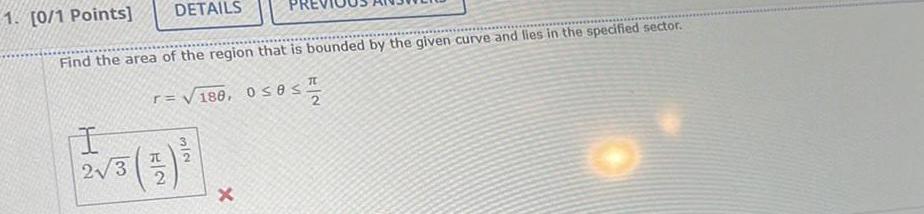
Calculus
Application of derivatives1 0 1 Points DETAILS Find the area of the region that is bounded by the given curve and lies in the specified sector r 180 0 8 I 2 3 x T

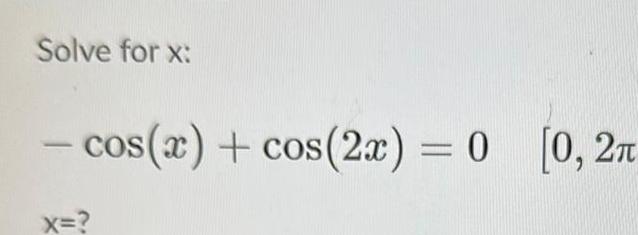

Calculus
Application of derivativesX Select 4 correct answer s 4 3 00 11 57 12 03 017 No solution 12 13m 12 2 5 6
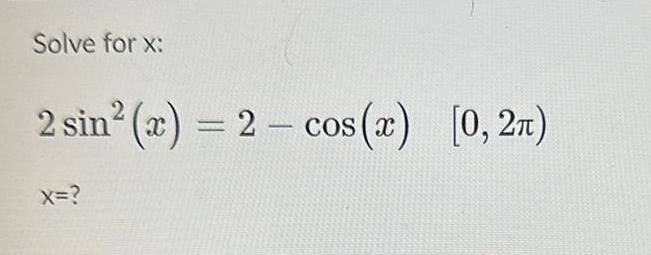
Calculus
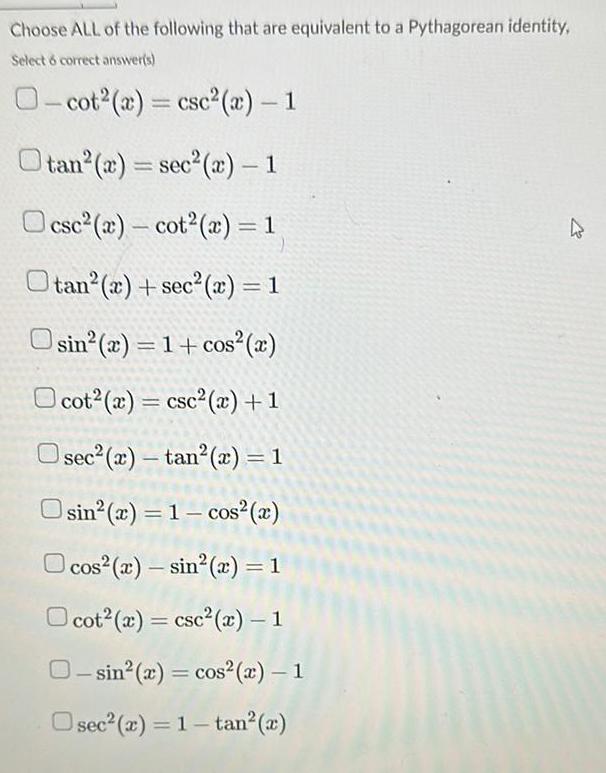
Limits & ContinuityChoose ALL of the following that are equivalent to a Pythagorean identity Select 6 correct answer s O cot x csc x 1 Otan x sec x 1 csc a cot x 1 tan x sec x 1 Osin x 1 cos x Ocot x csc x 1 Osec x tan x 1 sin x 1 cos x cos r sin x 1 Ocot x csc x 1 O sin x cos x 1 Osec x 1 tan x K
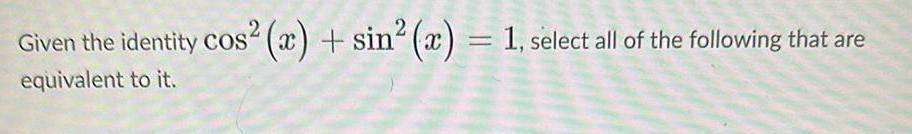
Calculus
Limits & ContinuityGiven the identity cos x sin x 1 select all of the following that are equivalent to it
Calculus
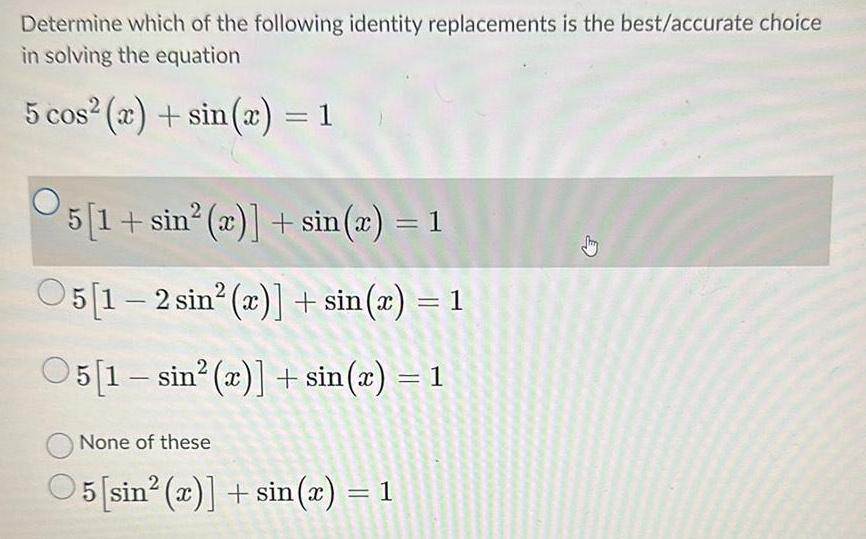
Limits & ContinuityDetermine which of the following identity replacements is the best accurate choice in solving the equation 5 cos x sin x 1 5 1 sin x sin x 1 05 1 2 sin r sin x 1 05 1 sin x sin x 1 None of these O5 sin 2 sin x 1 D

Calculus
Application of derivativesDetermine which of the following double identity replacements is the best accurate choice in solving the equation cos x cos 2x 0 cos x 2 cos x sin x 0 None of these O cos x cos r sin x 0 cos x 2 cos x 1 0 cos x 1 2 sin x 0 G
Calculus
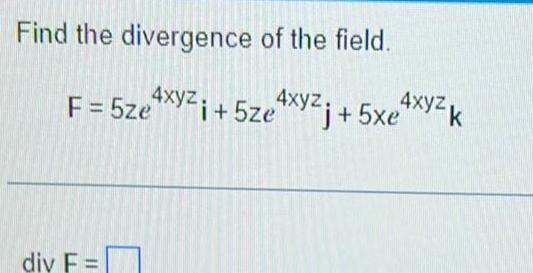
Application of derivativesFind the divergence of the field F 5ze4xyzi 5ze i 5ze div F j 5x4xyzk
Calculus
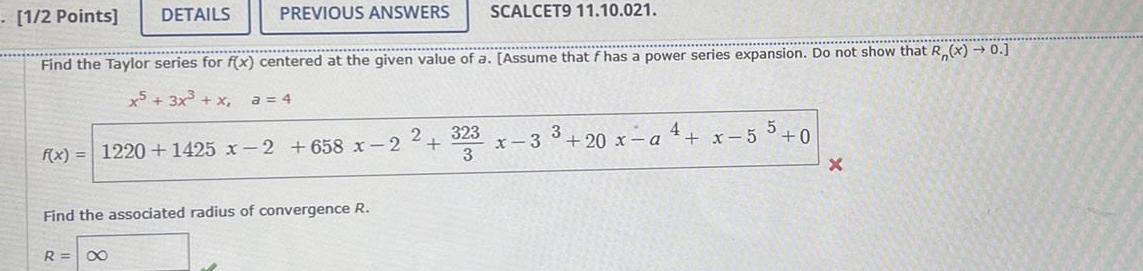
Limits & Continuity1 2 Points DETAILS PREVIOUS ANSWERS SCALCET9 11 10 021 Find the Taylor series for f x centered at the given value of a Assume that f has a power series expansion Do not show that R x 0 x5 3x x a 4 f x 1220 1425 x 2 658 x 2 R Find the associated radius of convergence R 2 323 3 x 3 3 20 x a 4 x 55 0 X
Calculus
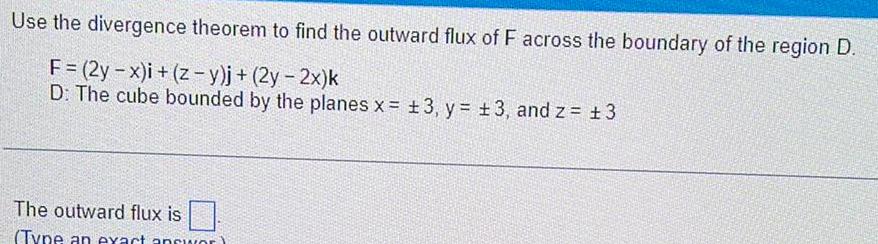
Differential equationsUse the divergence theorem to find the outward flux of F across the boundary of the region D F 2y x i z y j 2y 2x k D The cube bounded by the planes x 3 y 3 and z 3 The outward flux is Type an exact answor
Calculus
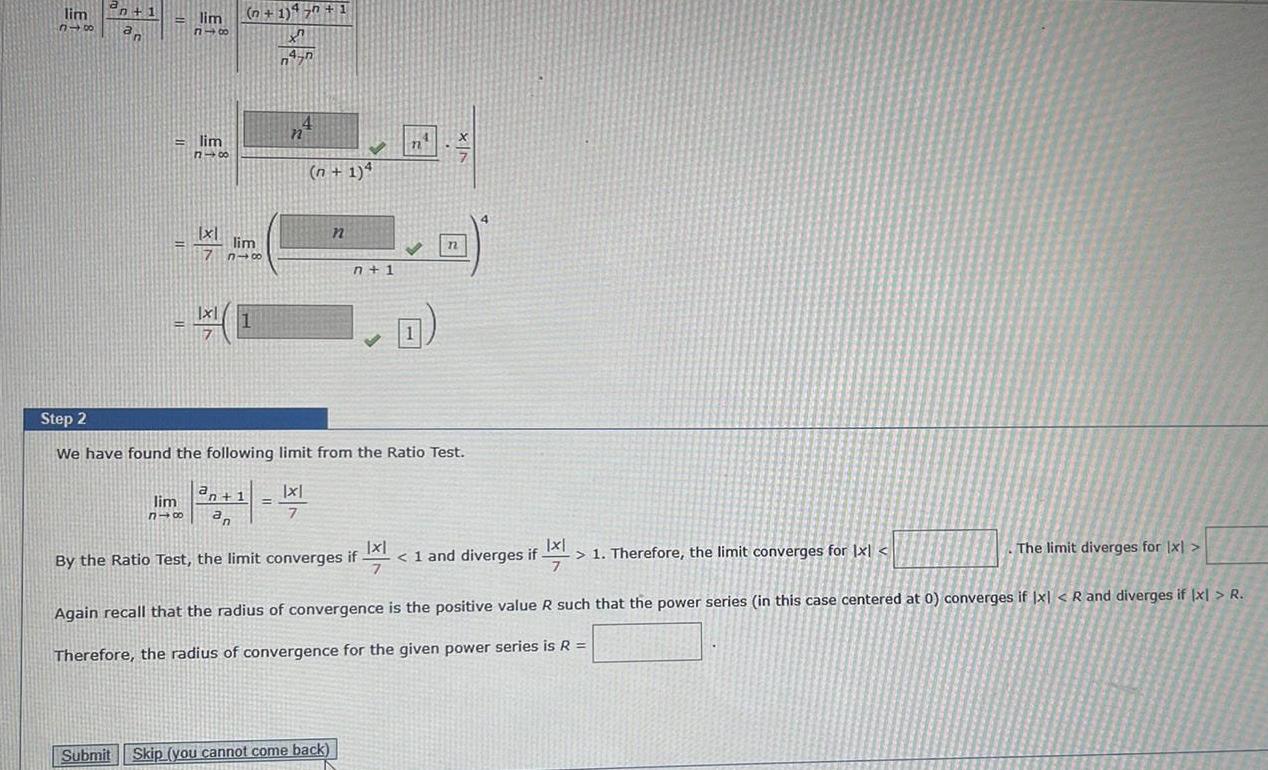
Limits & Continuitylim 318 n 1 an lim 816 lim 818 x1 7 n 1 450 1 X 4 n n lim n 1 a n 1 lim 818 an 4 n n 1 4 Step 2 We have found the following limit from the Ratio Test x 7 n n 1 Submit Skip you cannot come back 71 By the Ratio Test the limit converges if Q n x FIX 1 and diverges if 1 Therefore the limit converges for Ixl if 21 The limit diverges for x Again recall that the radius of convergence is the positive value R such that the power series in this case centered at 0 converges if x R and diverges if x R Therefore the radius of convergence for the given power series is R
Calculus
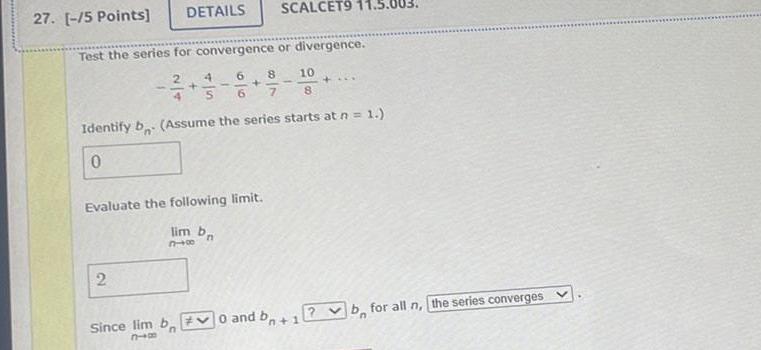
Limits & Continuity27 5 Points DETAILS Test the series for convergence or divergence 2 2 4 6 8 S 6 7 SCALCET9 Evaluate the following limit lim bn 318 Identify b Assume the series starts at n 1 0 10 8 Since lim b 0 and bo 1 810 4 b for all n the series converges
Calculus
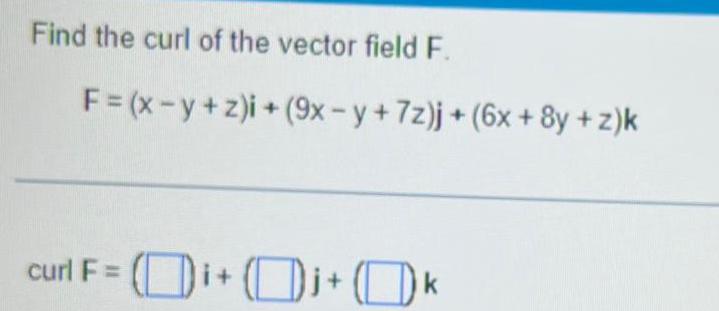
Application of derivativesFind the curl of the vector field F F x y z i 9x y 7z j 6x 8y z k curl F i j k
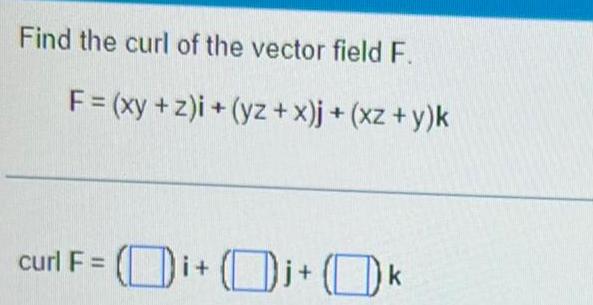
Calculus
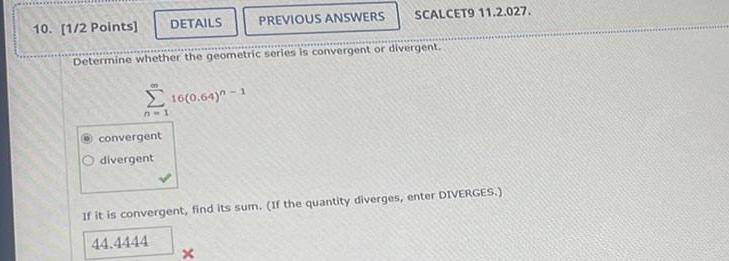
Indefinite Integration10 1 2 Points DETAILS Determine whether the geometric series is convergent or divergent n 1 convergent divergent 16 0 64 1 PREVIOUS ANSWERS SCALCET9 11 2 027 x If it is convergent find its sum If the quantity diverges enter DIVERGES 44 4444
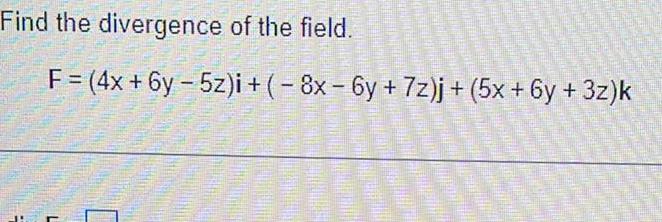
Calculus
Application of derivativesFind the divergence of the field F 4x 6y 5z i 8x 6y 7z j 5x 6y 3z k AMAN neuen Einfl Wirtu duben
Calculus
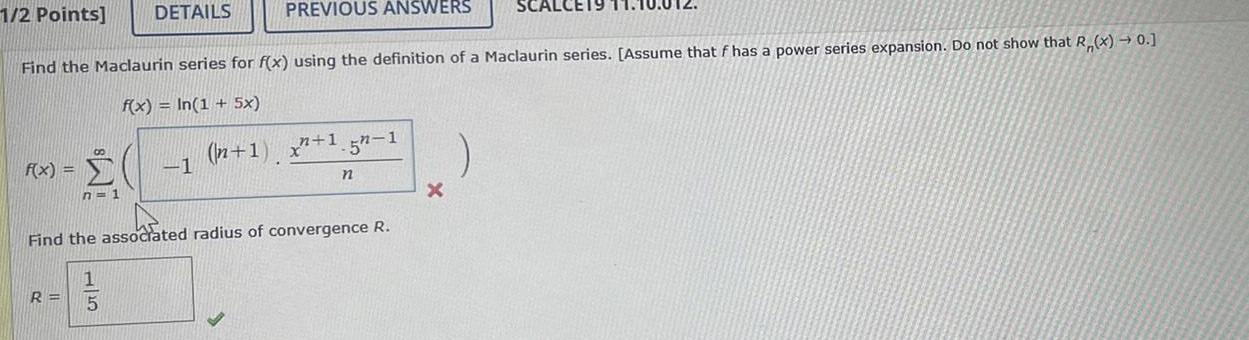
Application of derivativesf x n 1 1 2 Points Find the Maclaurin series for f x using the definition of a Maclaurin series Assume that f has a power series expansion Do not show that R x 0 f x In 1 5x DETAILS R 15 PREVIOUS ANSWERS 1 Find the associated radius of convergence R n 1 x 1 5 1 n X SCALCE19
Calculus
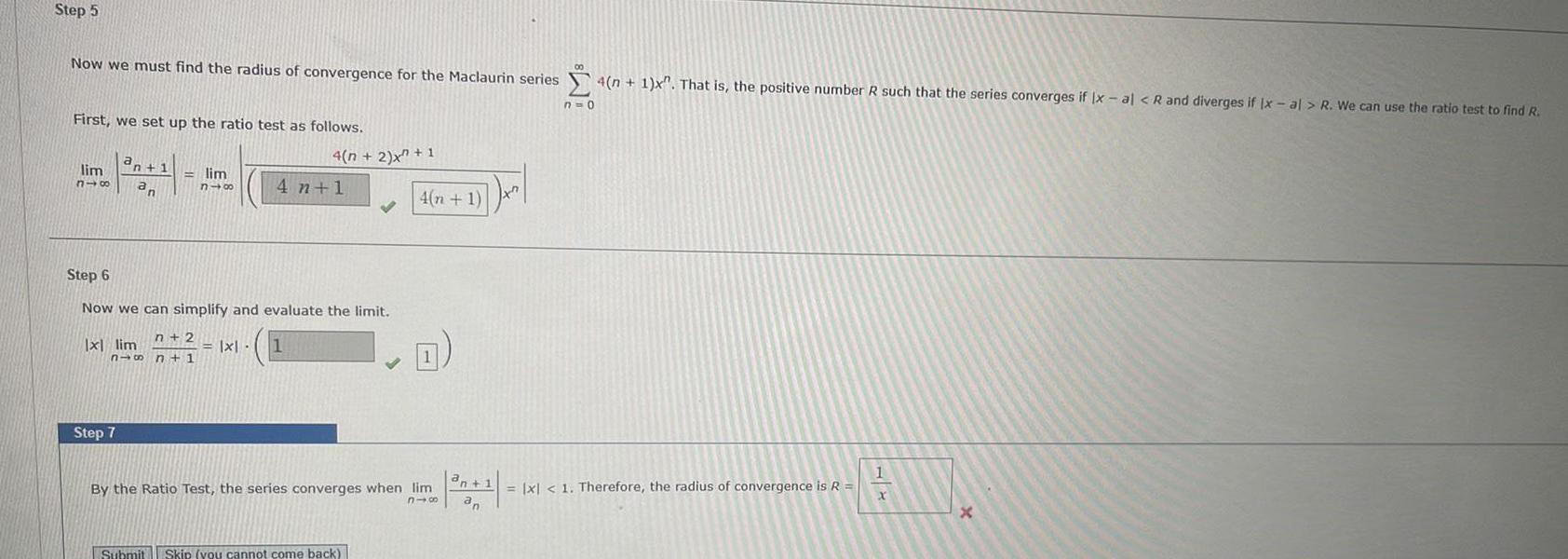
Application of derivativesStep 5 Now we must find the radius of convergence for the Maclaurin series First we set up the ratio test as follows a lim n 1 318 an lim n48 n 2 816 n 1 x lim Step 7 Step 6 Now we can simplify and evaluate the limit 4 n 2 x 1 4 n 1 x 1 Submit Skip you cannot come back 4 n 1 x By the Ratio Test the series converges when lim 816 an 1 an 4 n 1 x That is the positive number R such that the series converges if x al R and diverges if Ix al R We can use the ratio test to find R n 0 x 1 Therefore the radius of convergence is R 1 X X
Calculus
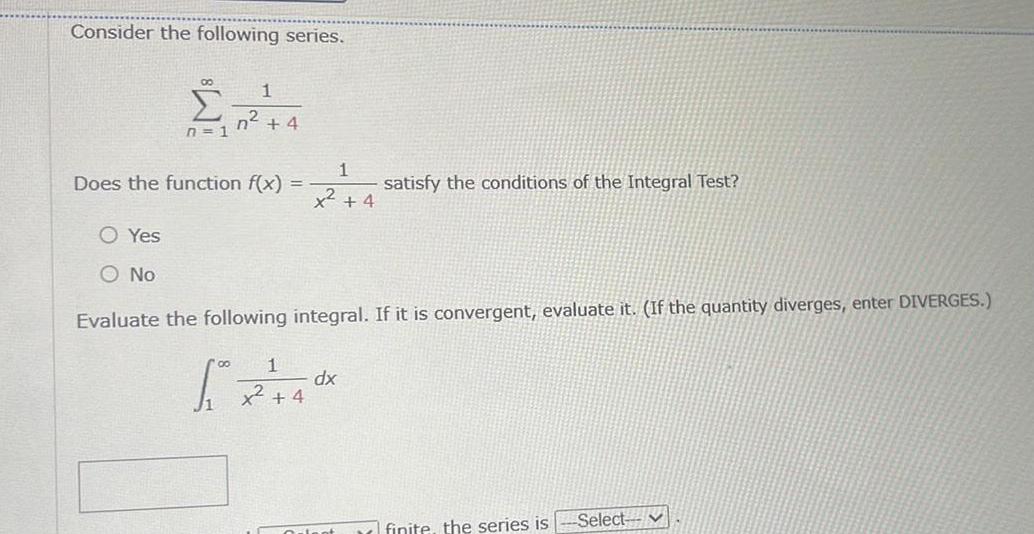
Indefinite IntegrationConsider the following series 1 2 4 4 n 1 Does the function f x O Yes O No 1 x 4 satisfy the conditions of the Integral Test Evaluate the following integral If it is convergent evaluate it If the quantity diverges enter DIVERGES 1 x 2 40x dx 4 Orient finite the series is Select
Calculus
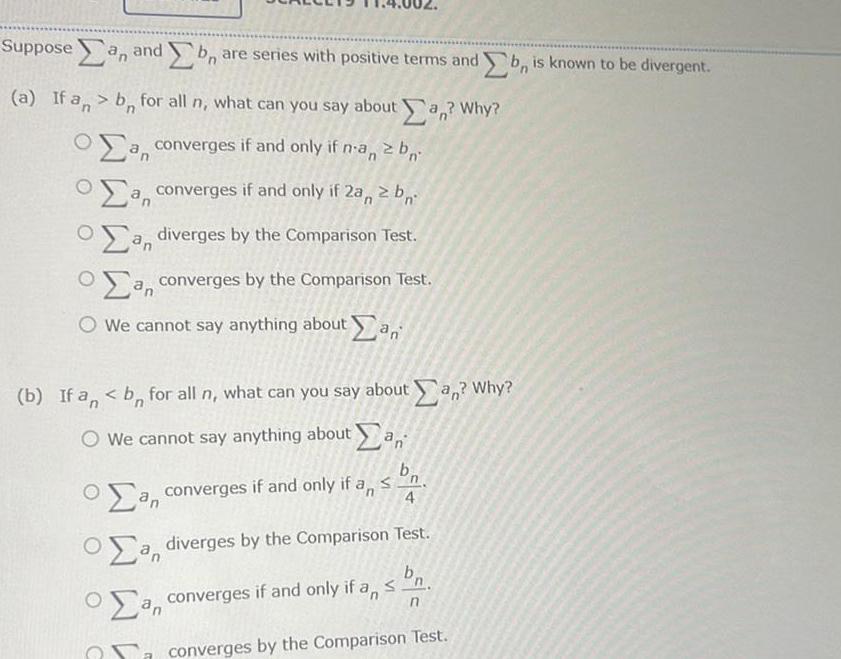
Application of derivativesSuppose an and b are series with positive terms and b is known to be divergent a If an bn for all n what can you say about an Why a converges if and only if n an 2 b a converges if and only if 2a 2b a diverges by the Comparison Test a converges by the Comparison Test We cannot say anything about an b If an b for all n what can you say about an Why O We cannot say anything about an S a converges if and only if an 4 a diverges by the Comparison Test a converges if and only if an an n converges by the Comparison Test
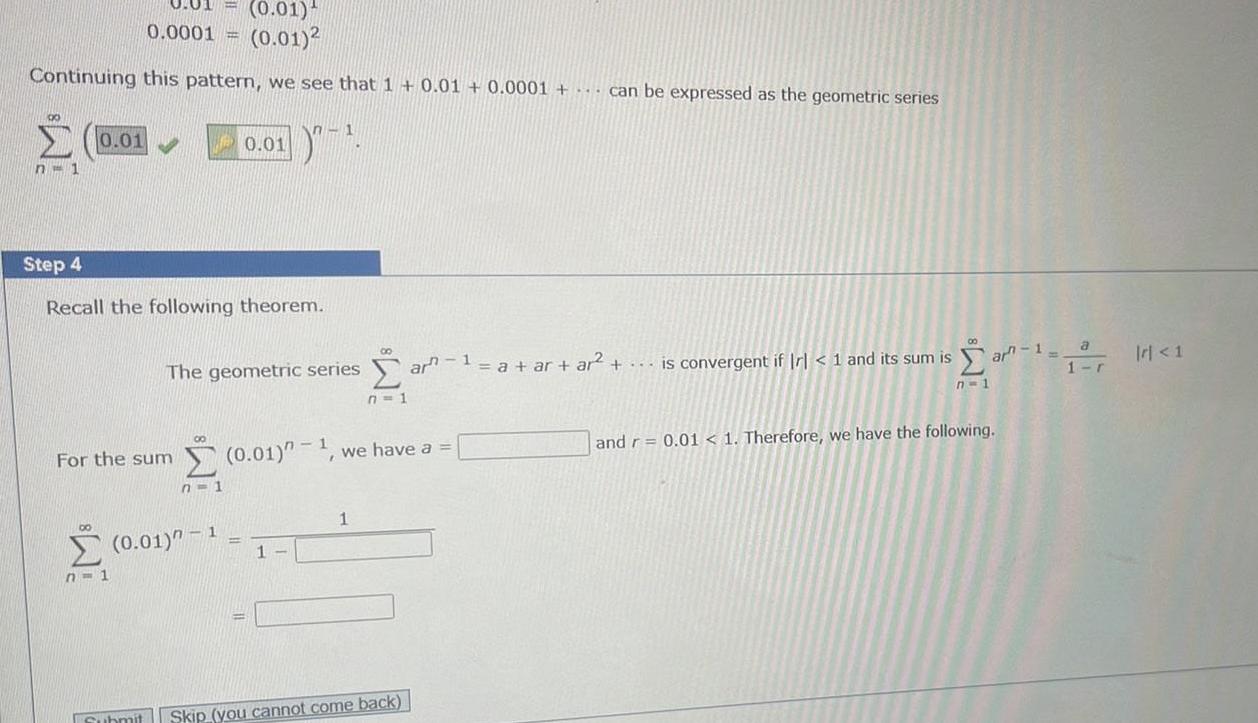
Calculus
Application of derivatives0 01 0 01 0 0001 0 01 2 Continuing this pattern we see that 1 0 01 0 0001 can be expressed as the geometric series 00 0 01 n 1 Step 4 Recall the following theorem For the sum n 1 00 0 01 The geometric series n 1 n 1 0 01 1 1 0 01 1 1 ar 1 a ar ar is convergent if r 1 and its sum is we have a 1 Submit Skip you cannot come back n 1 ar 1 a and r 0 01 1 Therefore we have the following 1 r r 1

Calculus
Application of derivativesSupposea and b bare series with positive terms and b is known to be convergent n a If a b for all n what can you say about a Why Oa diverges by the Comparison Test a converges if and only if a 2b a converges if and only if a 4b a converges by the Comparison Test an O O We cannot say anything about an b If an b for all n what can you say about an Why O We cannot say anything about an b a converges if and only if n sans br an 2 a converges by the Comparison Test a diverges by the Comparison Test bn converges if and only if n sans br 4 Ox an

Calculus
Limits & Continuity9 0 1 Points DETAILS 8 7 PREVIOUS ANSWERS Determine whether the geometric series is convergent or divergent If it is convergent find its sum If the quantity diverges enter DIVERGES 49 343 8 64 SCALCET9 11 2 024 MY NO
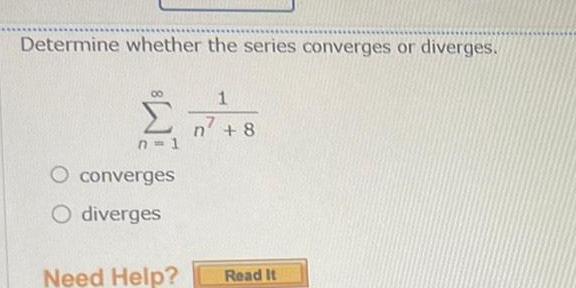
Calculus
Application of derivativesDetermine whether the series converges or diverges 1 n 8 n 8 n 1 converges O diverges Need Help Read It
Calculus
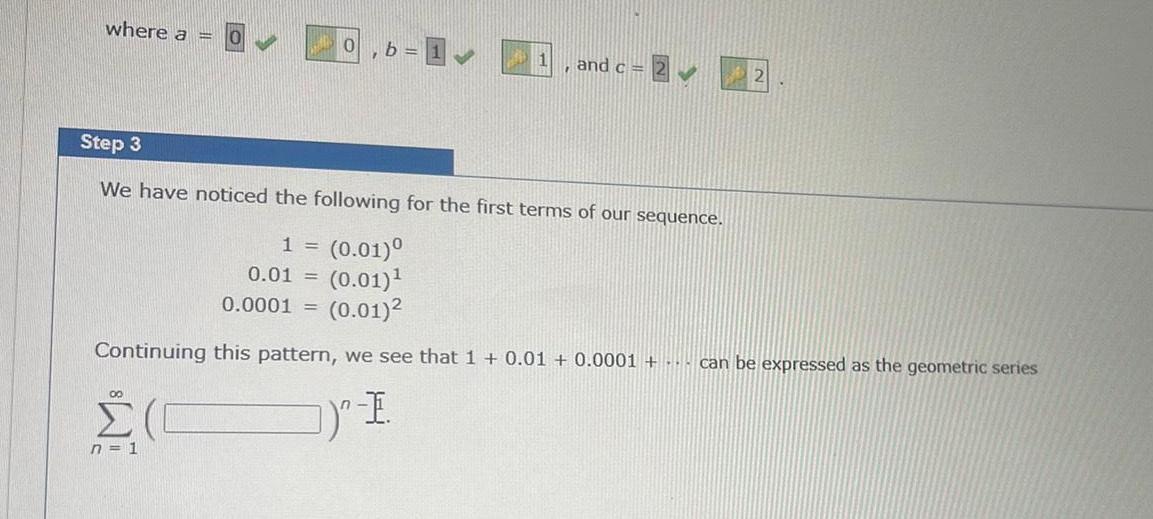
Application of derivativeswhere a 0 00 n 1 b 1 1 and c 2 Step 3 We have noticed the following for the first terms of our sequence 1 0 01 0 01 0 01 0 0001 0 01 Continuing this pattern we see that 1 0 01 0 0001 can be expressed as the geometric series I
Calculus
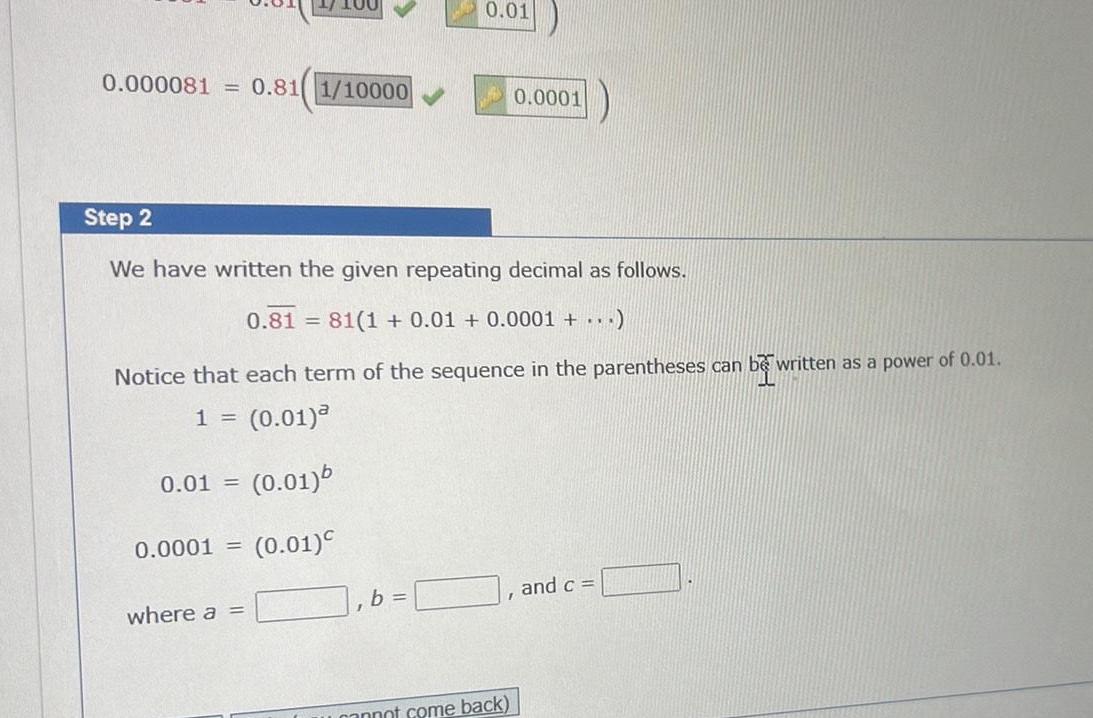
Vector Calculus0 000081 0 81 1 10000 0 01 Step 2 We have written the given repeating decimal as follows 0 81 81 1 0 01 0 0001 Notice that each term of the sequence in the parentheses can 1 0 01 0 01 b 0 0001 0 01 where a 0 01 b 0 0001 cannot come back and c be written written as a power of 0 01
Calculus
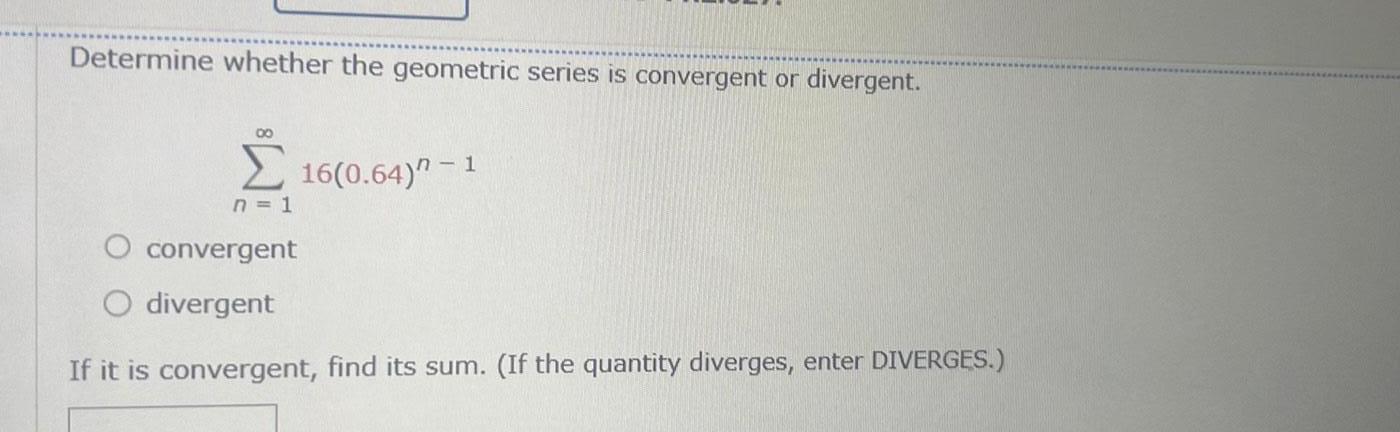
Application of derivativesDetermine whether the geometric series is convergent or divergent 80 16 0 64 1 n 1 O convergent O divergent If it is convergent find its sum If the quantity diverges enter DIVERGES
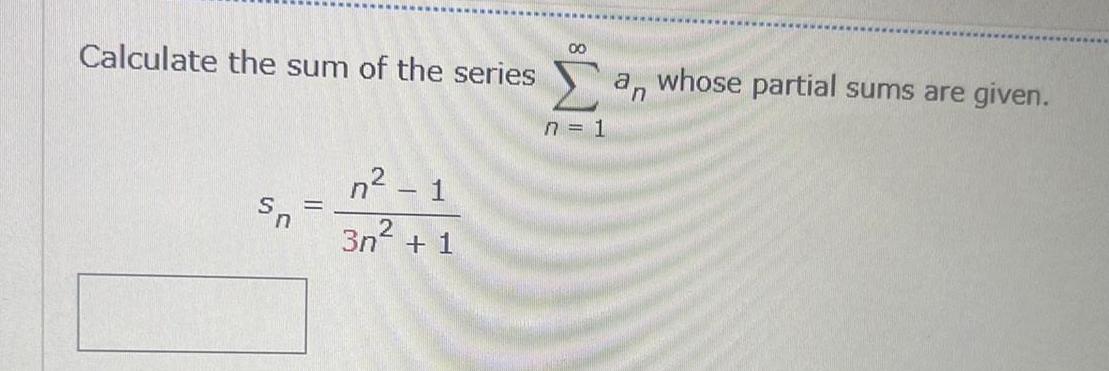
Calculus
Limits & ContinuityCalculate the sum of the series Sn n 1 3n 1 00 n 1 an whose partial sums are given
Calculus
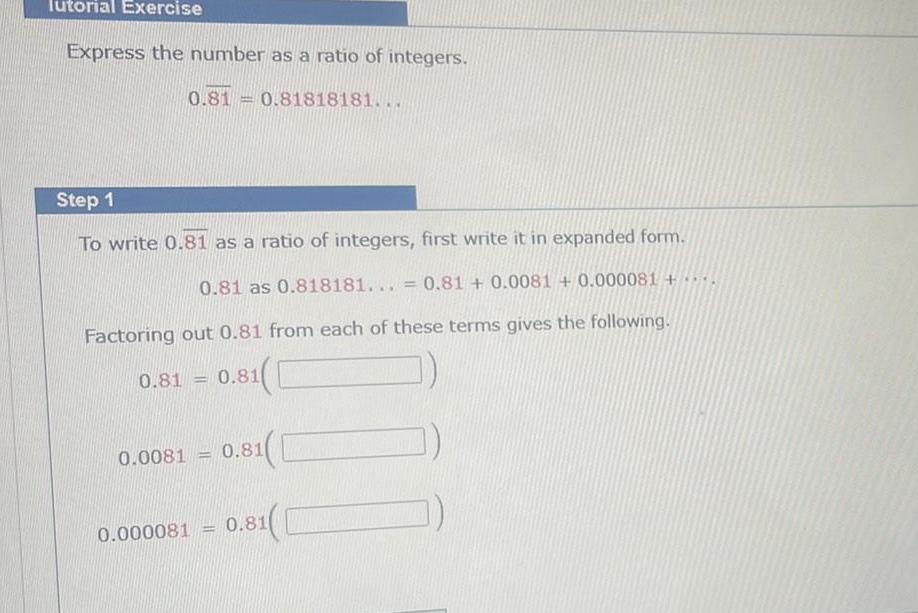
Definite IntegralsTutorial Exercise Express the number as a ratio of integers 0 81 0 81818181 Step 1 To write 0 81 as a ratio of integers first write it in expanded form 0 81 as 0 818181 0 81 0 0081 0 000081 Factoring out 0 81 from each of these terms gives the following 0 81 0 81 0 0081 1 0 81 1 0 000081 0 81
Calculus
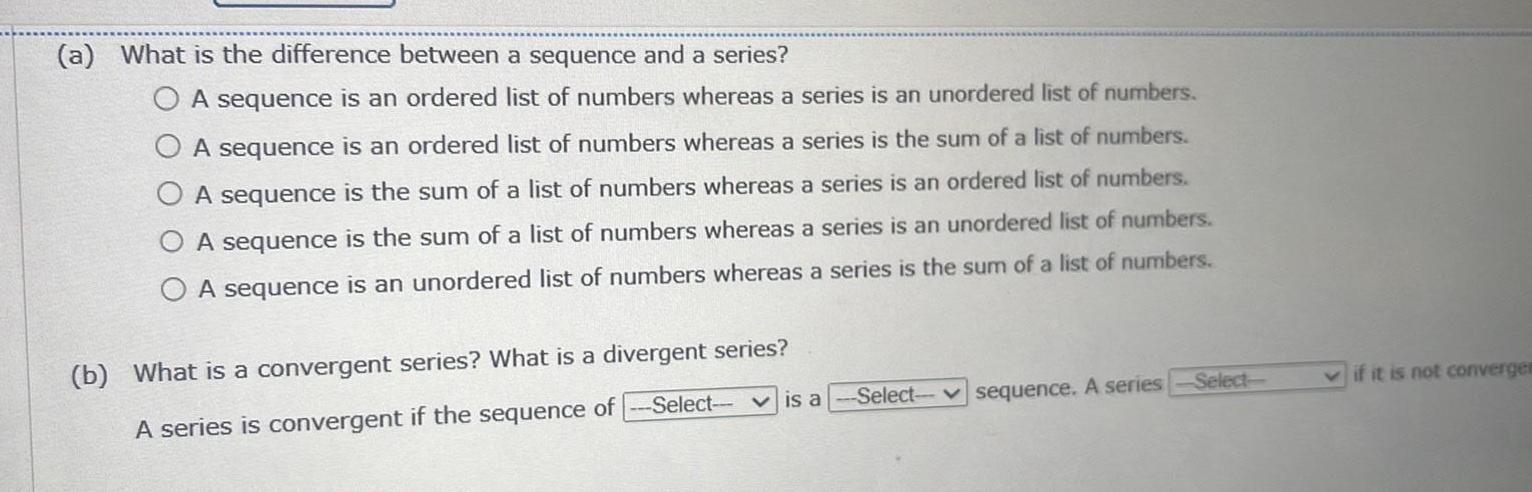
Limits & Continuitya What is the difference between a sequence and a series b A sequence is an ordered list of numbers whereas a series is an unordered list of numbers A sequence is an ordered list of numbers whereas a series is the sum of a list of numbers A sequence is the sum of a list of numbers whereas a series is an ordered list of numbers A sequence is the sum of a list of numbers whereas a series is an unordered list of numbers A sequence is an unordered list of numbers whereas a series is the sum of a list of numbers What is a convergent series What is a divergent series A series is convergent if the sequence of Select is a Select sequence A series Select if it is not convergen

Calculus
Application of derivativesFind the area of the region that lies inside the first curve and outside the second curve r 16 sin 8 r 8
Calculus
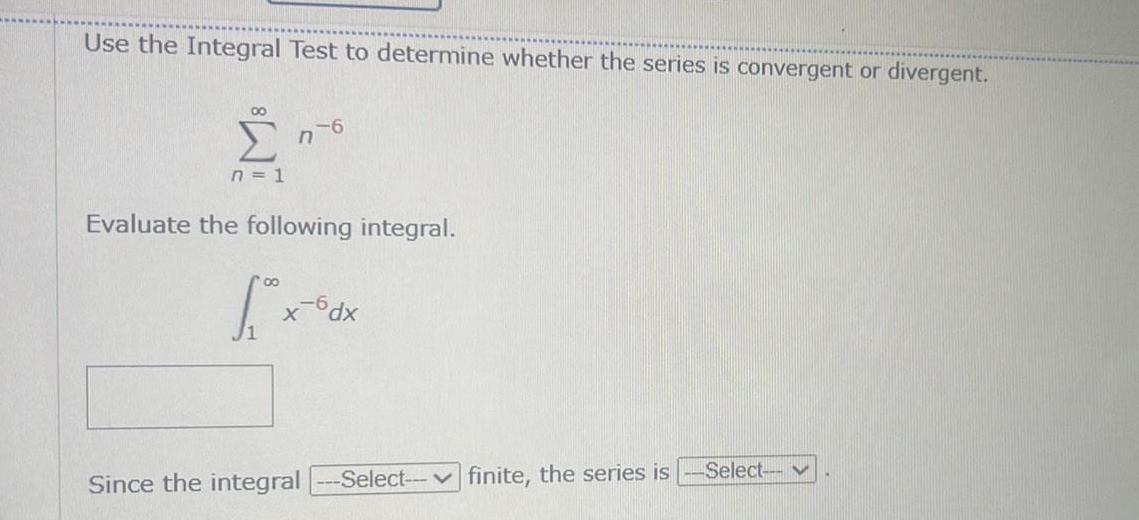
Application of derivativesUse the Integral Test to determine whether the series is convergent or divergent 00 n 1 76 Evaluate the following integral X 6dx Since the integral Select finite the series is Select
Calculus
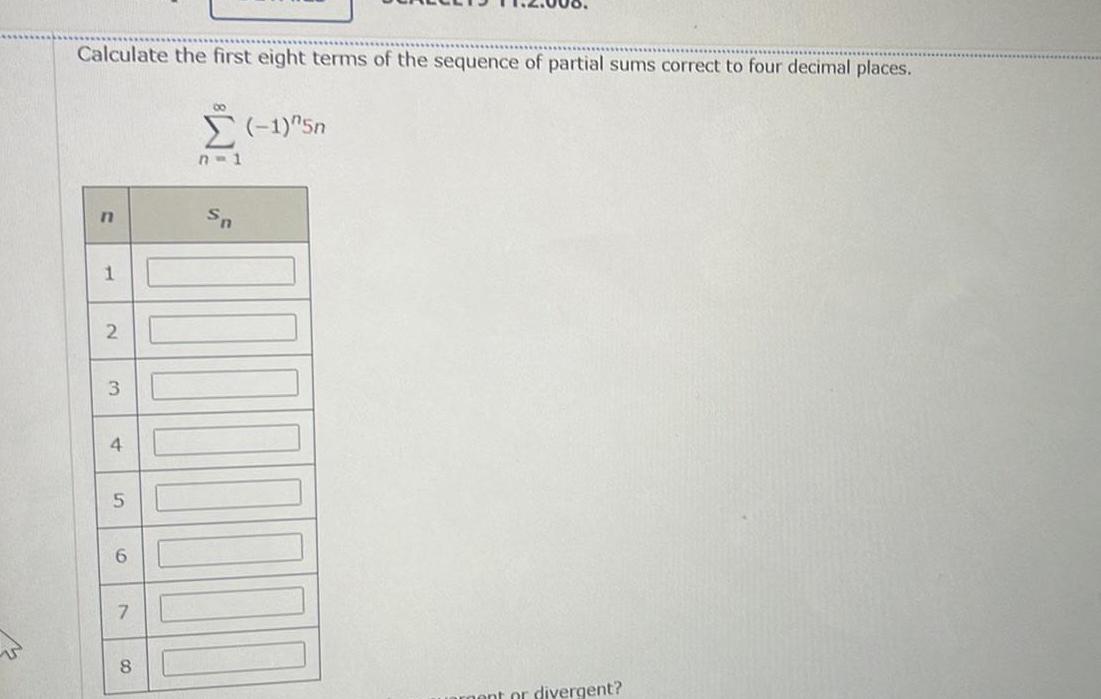
Limits & ContinuityCalculate the first eight terms of the sequence of partial sums correct to four decimal places n 1 2 3 4 5 6 7 8 8 1 5n n 1 nent or divergent