Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
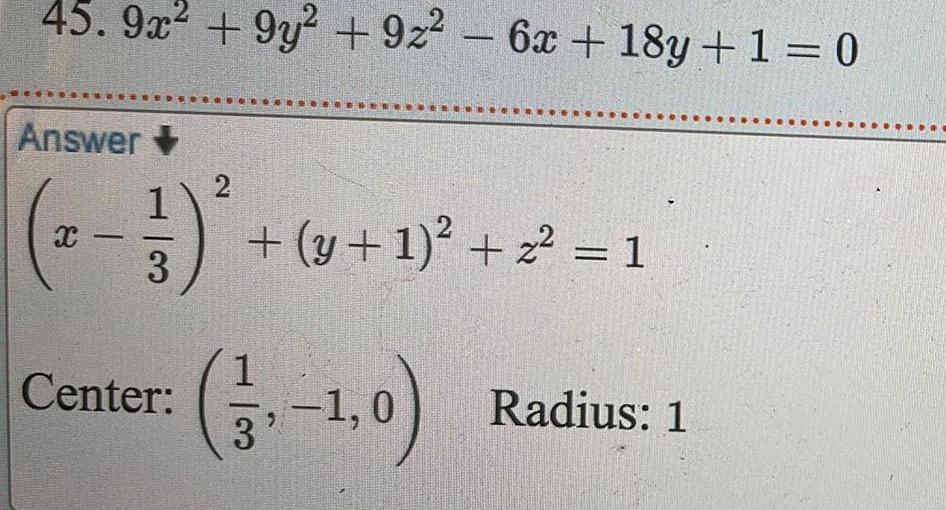

Calculus
Limits & ContinuityPlotting Points In Exercises 5 6 7 and 8 plot the points in the same three dimensional coordinate system 5 a 2 1 3 b 1 2 1

Calculus
Vector CalculusFinding the Midpoint In Exercises 33 34 35 and 36 find the coordinates of the midpoint of the line segment joining the points 33 4 0 6 8 8 20 Answer 6 4 7 34 7 2 2 5 2 3 35 3 4 6 1 8 0 Answer

Calculus
Vector CalculusOf the following which is most likely to improve employee motivation and satisfaction Allowing employees to set their own schedules Providing additional job training Upgrading the physical workplace with new furnishings and d cor Allowing employees to work from home

Calculus
Vector CalculusHinding the Distance Between Two Points in Space In Exercises 25 26 27 and 28 find the distance between the points 25 4 1 5 8 2 6 Answer 3 2 26 1 1 1 3 5 3 27 0 2 4 3 2 8

Calculus
Vector Calculus75 Resultant Force Forces with magnitudes of 500 pounds and 200 pounds act on a machine part at angles of 30 and 45 respectively with the x axis see figure Find the direction and magnitude of the resultant force Answer 10 7 584 6 lb 30 45 200 lb 500 lb X
Calculus
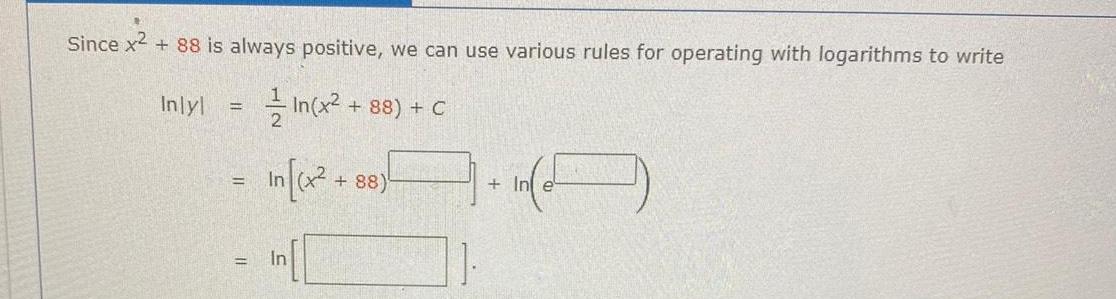
Vector CalculusSince x 88 is always positive we can use various rules for operating with logarithms to write In x in x Inlyl In 88 C 88 In

Calculus
Indefinite IntegrationUsing the substitution u x2 88 and again ignoring the constant of integration gives us du
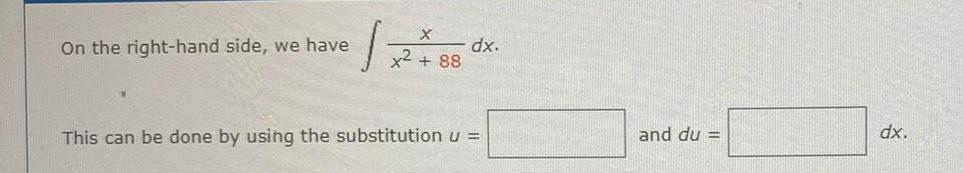
Calculus
Indefinite IntegrationOn the right hand side we have X 12 x2 88 dx This can be done by using the substitution u and du dx

Calculus
Application of derivativesWe now integrate each side of the differential equation Ignoring the constant of integration we can integrate the left hand side of the equation to obtain integral 10 dy

Calculus
Application of derivativesWriting y dy then we have to solve x 88 dx xy dx Our strategy is to separate the variables so that all x terms are on one side of the equation and all y terms are on the other We also avoid positioning dy or dx in denominator With that in mind we can rewrite the original equation as dy dx
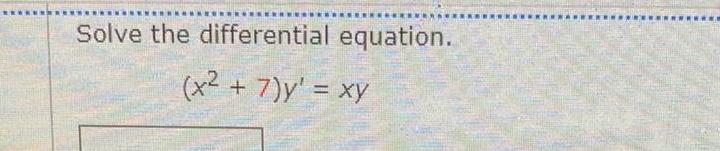

Calculus
DifferentiationQuestion 9 R duis l expression ci dessous l aide de la notation exponentielle sans d exposants n gatifs 27 5 C

Calculus
Application of derivatives8 pts 5 For the functions below sketch the graph of the function labeling the axes Use the graph to determine whether f x has an inverse that is also a function Give a specific reason for your answer If the function has an inverse that s also a function find a formula for the inverse function f x showing all work on how your reached your answer a f x 6 2x x 4 5
Calculus
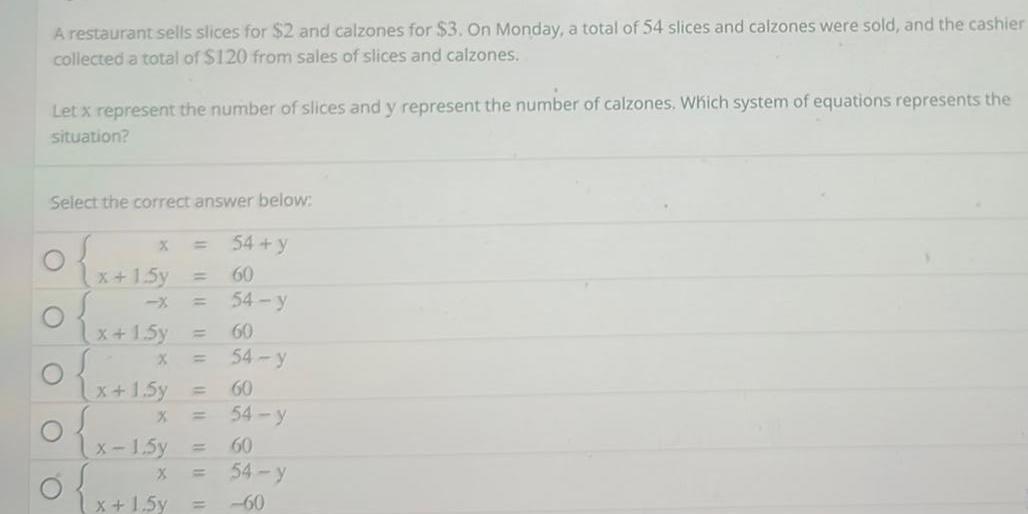
Application of derivativesA restaurant sells slices for 2 and calzones for 3 On Monday a total of 54 slices and calzones were sold and the cashier collected a total of 120 from sales of slices and calzones Let x represent the number of slices and y represent the number of calzones Which system of equations represents the situation Select the correct answer below 54 y 60 54 y 60 54 y 60 54 y 60 54 y 60 O O O O x 1 5y x 1 5y X x 1 5y 1111 x 1 5y x 1 5y X
Calculus
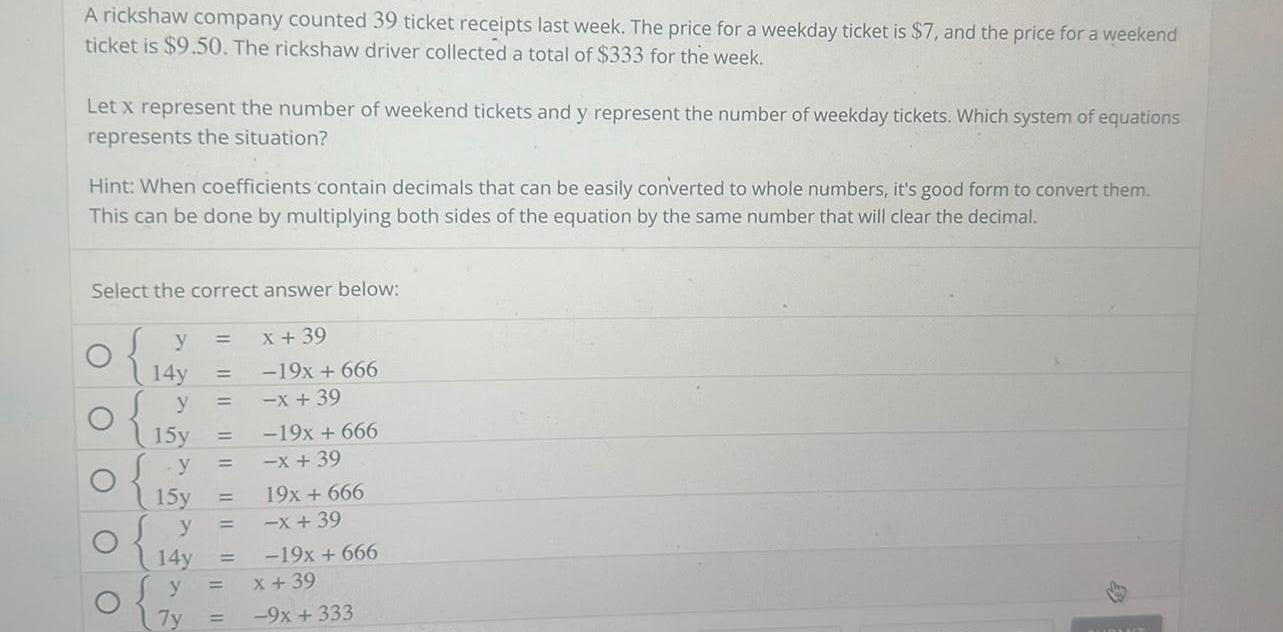
DifferentiationA rickshaw company counted 39 ticket receipts last week The price for a weekday ticket is 7 and the price for a weekend ticket is 9 50 The rickshaw driver collected a total of 333 for the week Let x represent the number of weekend tickets and y represent the number of weekday tickets Which system of equations represents the situation Hint When coefficients contain decimals that can be easily converted to whole numbers it s good form to convert them This can be done by multiplying both sides of the equation by the same number that will clear the decimal Select the correct answer below y x 39 O O 14y y 15y y 15y y 14y y 7y 19x 666 x 39 19x 666 x 39 19x 666 x 39 19x 666 x 39 9x 333
Calculus
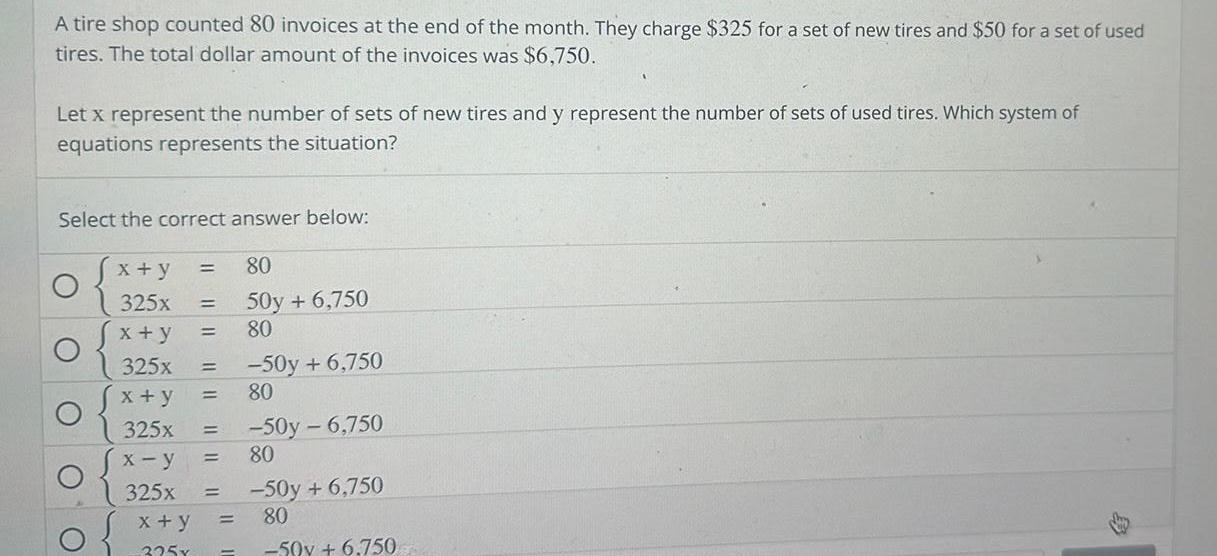
Vector CalculusA tire shop counted 80 invoices at the end of the month They charge 325 for a set of new tires and 50 for a set of used tires The total dollar amount of the invoices was 6 750 Let x represent the number of sets of new tires and y represent the number of sets of used tires Which system of equations represents the situation Select the correct answer below C C O O x y 325x x y 325x x y 325x x y 325x x y 325x 80 50y 6 750 80 50y 6 750 80 50y 6 750 80 50y 6 750 80 50y 6 750 B

Calculus
DifferentiationA company sells widgets The company s fixed and variable costs are modeled by the function C x 0 74x 25000 Their revenue is modeled by the function R x 2 3x How many widgets do they have to sell to break even Round your answer up to the nearest whole number and do not include units Provide you olour
Calculus
Application of derivativesThe costs of a company are represented by the function C x 0 22x 1 750 Its revenues are represented by function R x 4 1x Find the function that represents the company s profits Provide your answer below
Calculus
DifferentiationA concert manager counted 33 ticket receipts the day after a concert The price for an adult ticket was 14 and the price fo a student ticket was 9 50 The register confirms that 403 50 was taken in How many adult tickets and student tickets were sold Provide your answer below
Calculus
Vector CalculusFind the general solution of the following system of equations Select the correct answer below x 7 O x 7 O x 4x 7 O x 4x 11 O x 4x 7 O x 4 7 4x y 12x 3y 21

Calculus
DifferentiationThe range of h x X 2x 1 1 3 x 21 O A 0 1 B 0 3 C 3 00 D All real numbers D E 0 3 F 0 1 is
Calculus
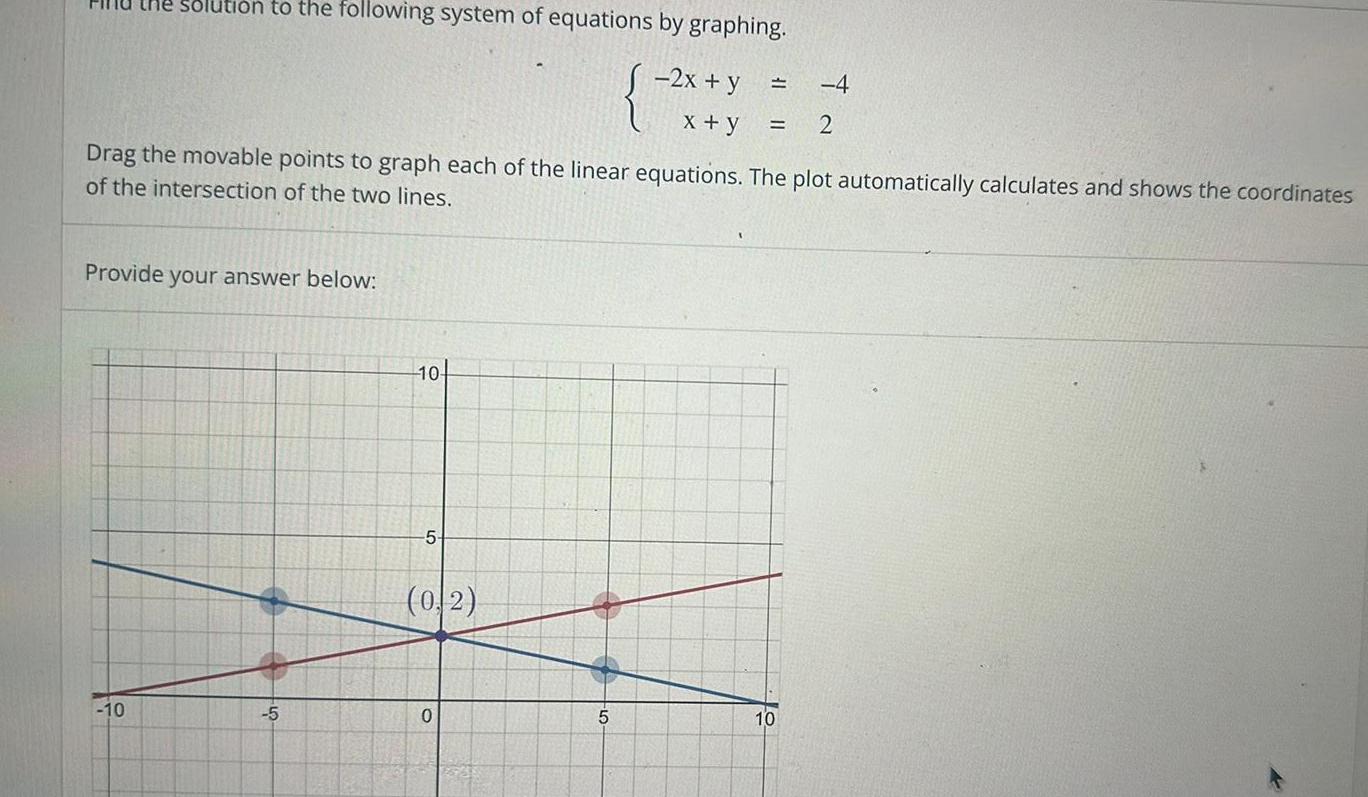
Application of derivativessolution to the following system of equations by graphing 2x y x y Drag the movable points to graph each of the linear equations The plot automatically calculates and shows the coordinates of the intersection of the two lines Provide your answer below 10 5 10 5 0 2 0 t 4 2 5 10 4
Calculus
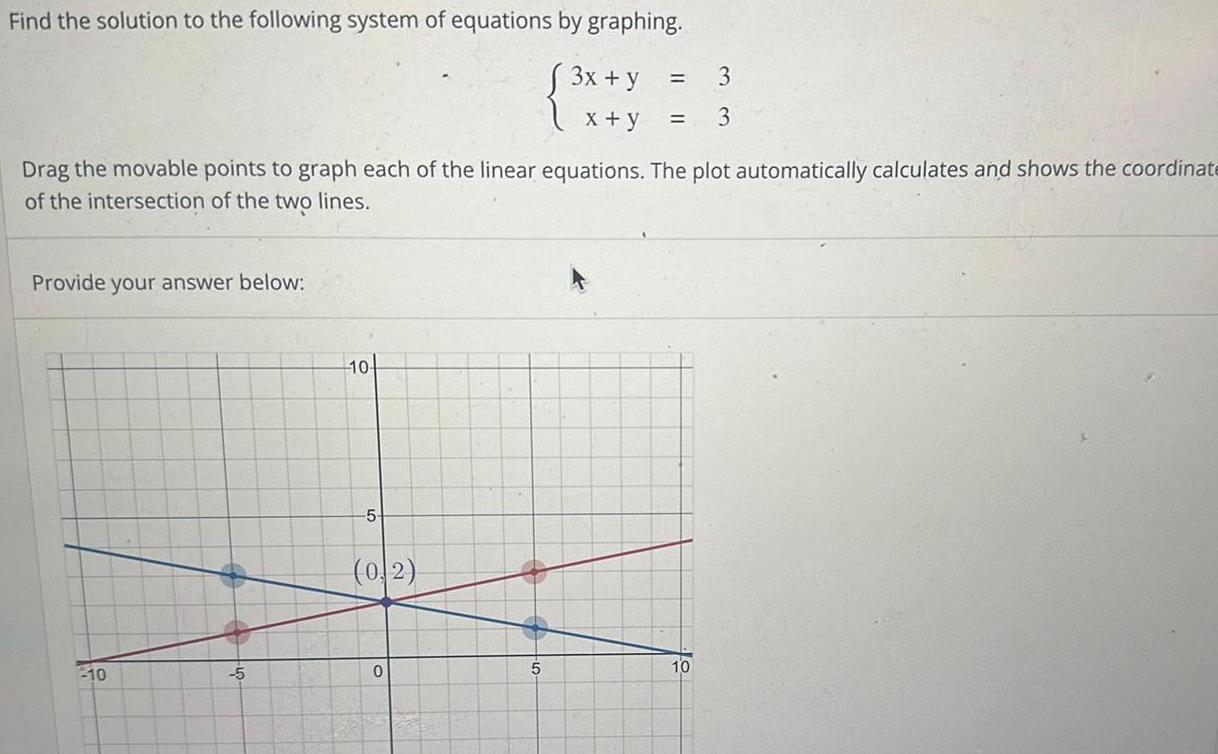
DifferentiationFind the solution to the following system of equations by graphing 3x y x y Drag the movable points to graph each of the linear equations The plot automatically calculates and shows the coordinate of the intersection of the two lines Provide your answer below 10 5 10 5 0 2 0 3 3 5 10
Calculus
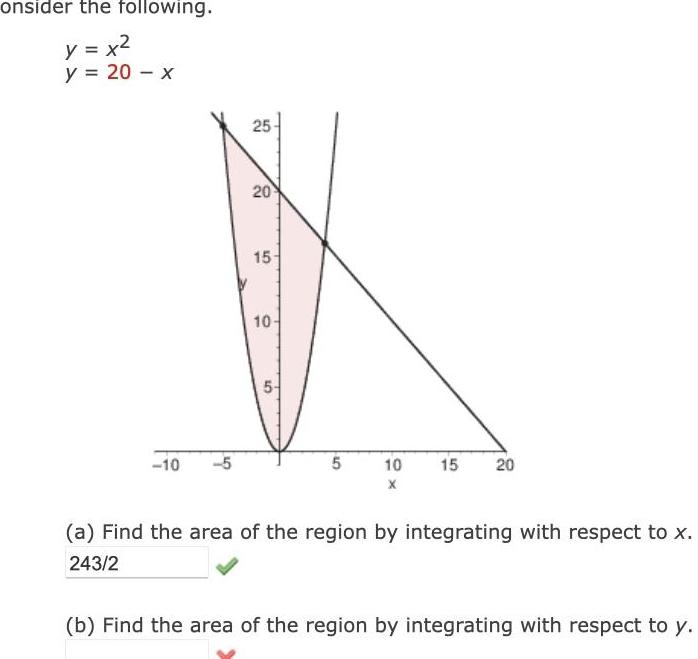
Definite Integralsonsider the following y x y 20 x 10 5 25 20 15 10 10 5 10 X 15 20 a Find the area of the region by integrating with respect to x 243 2 b Find the area of the region by integrating with respect to y
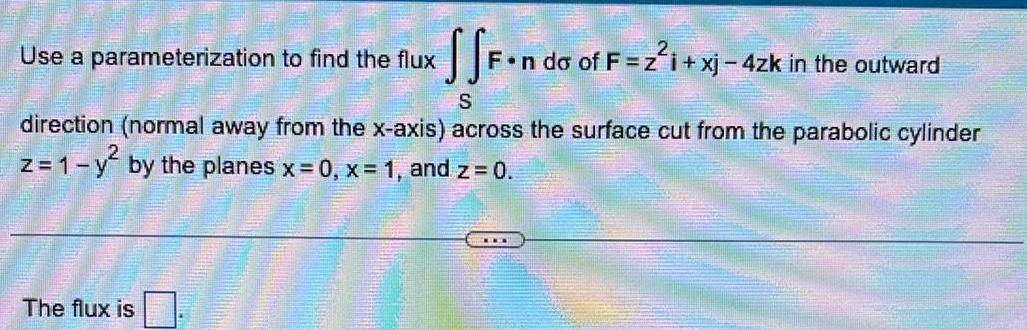
Calculus
Vector CalculusSSF n do of F 2 xj 4zk in the outward S direction normal away from the x axis across the surface cut from the parabolic cylinder z 1 y by the planes x 0 x 1 and z 0 Use a parameterization to find the flux The flux is
Calculus
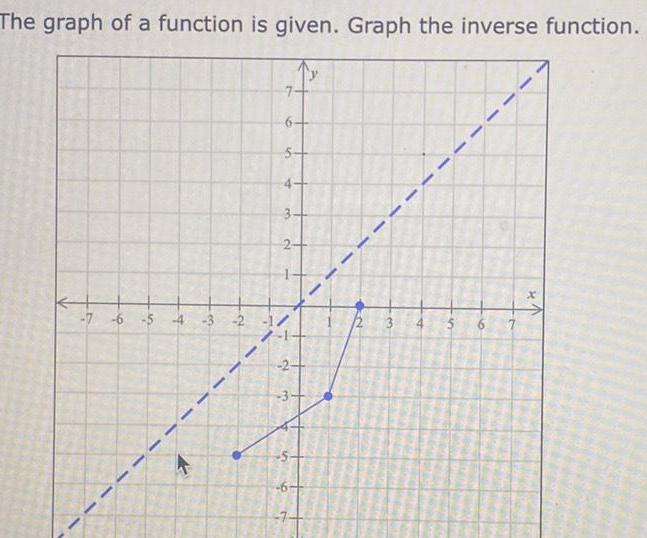
Application of derivativesThe graph of a function is given Graph the inverse function 7 6 5 44 3 2 6 5 4 3 2 1 2 3 S 4 6

Calculus
Limits & Continuity3 Use the data below for the temperature in degrees Celsius for a wood fire oven App Time in Minutes 058 10 13 15 19 21 25 290 285 285 Temp C 25 120 205 250 290 280 a find the average rate of change of the temperature between 0 and 25 minutes Show proper units and notation b Estimate the instantaneous rate of change of the temperature at 10 minutes Use 2 methods

Calculus
Vector CalculusUse a parameterization to find the flux The flux is SSF ndoo F n do of F z i xj 2zk in the outward direction normal away from the x axis across the surface cut from the parabolic cylinder z 1 y by the planes x 0 x 1 and z 0 S EXT
Calculus
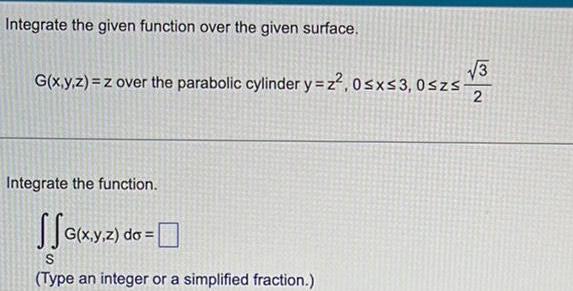
Definite IntegralsIntegrate the given function over the given surface 3 G x y z z over the parabolic cylinder y z 0 x 3 0szs 2 Integrate the function G x y z do S Type an integer or a simplified fraction
Calculus
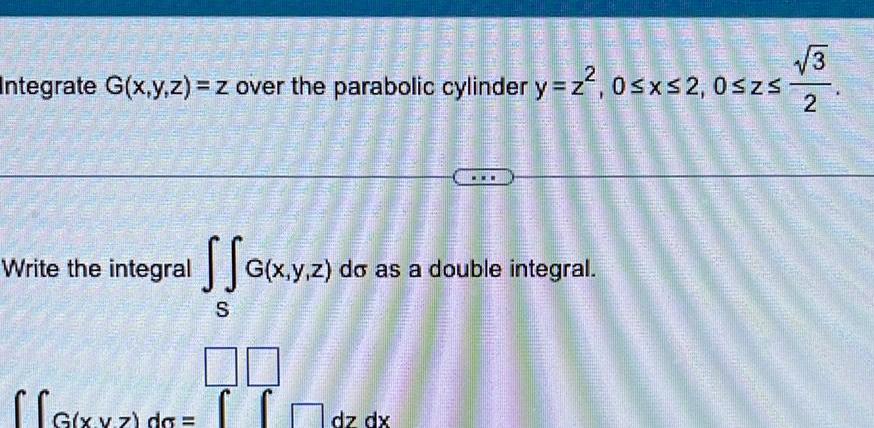
Definite Integrals100727 MANUE G x y z dg PHILADE PERUMS S 2009 40 Integrate G x y z z over the parabolic cylinder y z 0 x 2 0 zs Write the integral G x y z do as a double integral 777 SPORT dz dx 15M 2

Calculus
Definite Integrals1 2 SSG x y 2 do 2 1 42 S S dzdx S 00 Evaluate the integral found in the previous step SJ G x y z do S
Calculus
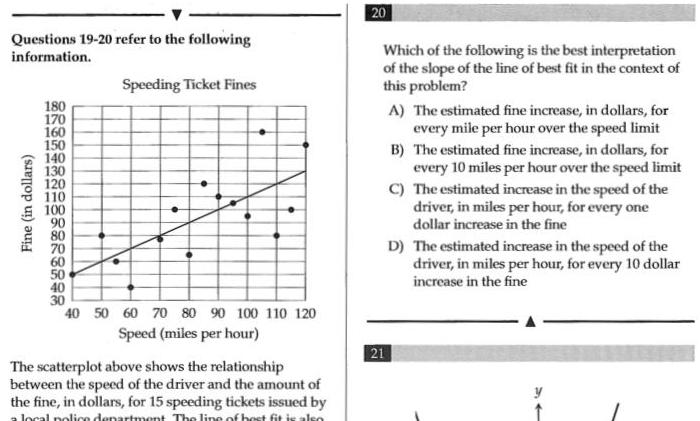
Vector CalculusQuestions 19 20 refer to the following information Fine in dollars 180 170 160 150 140 130 120 110 100 30 40 Speeding Ticket Fines 50 60 70 80 90 100 110 120 Speed miles per hour The scatterplot above shows the relationship between the speed of the driver and the amount of the fine in dollars for 15 speeding tickets issued by a local police department The line of best fit is also 20 Which of the following is the best interpretation of the slope of the line of best fit in the context of this problem 21 B A The estimated fine increase in dollars for every mile per hour over the speed limit The estimated fine increase in dollars for every 10 miles per hour over the speed limit C The estimated increase in the speed of the driver in miles per hour for every one dollar increase in the fine D The estimated increase in the speed of the driver in miles per hour for every 10 dollar increase in the fine
Calculus
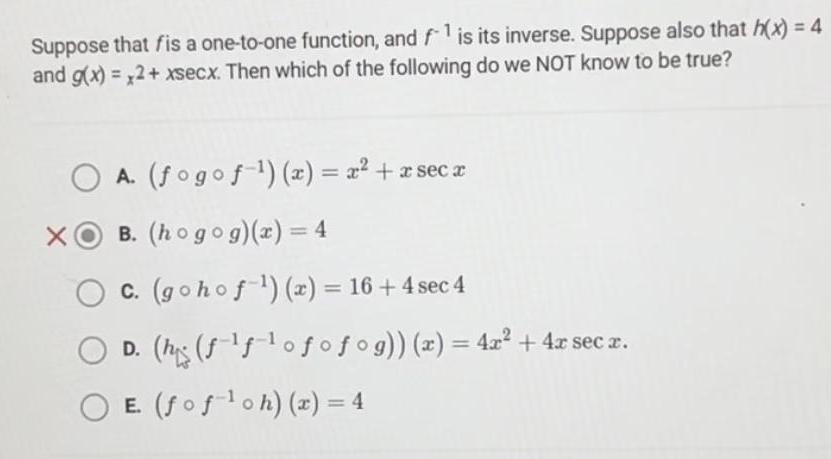
Limits & ContinuitySuppose that fis a one to one function and f is its inverse Suppose also that h x 4 and g x x2 xsecx Then which of the following do we NOT know to be true X A fogof x x x secx B hogog x 4 OC gohof x 16 4 sec 4 D his f f ofofog x 4x 4x sec x E fof oh x 4

Calculus
Limits & ContinuityIf f x x2 on the domain 2 2 then f OA has domain 4 4 OB equals C doesn t exist D has range 2 2 hos doma

Calculus
Limits & ContinuitySuppose P x and the F x hog x Then which of the following are possible definitions for hand g I h x x g II h x x g x X x 2 x 7 H III h 2 37 9 2 IV h x 7 9 x x x 7 x 7 8 OA II and III only B I and II only C I and IV only D I III and IV only E I II III and IV

Calculus
Definite IntegralsWhich of the following functions described does not have an inverse A None of these they all have inverses B Vm the volume of m kilograms of sand OC K t the temperature in Kelvin as a function of the temperature tin Fahrenheit D A d your age as a function of the date d E A t the altitude of an airplane as a function of time t between take off and landing
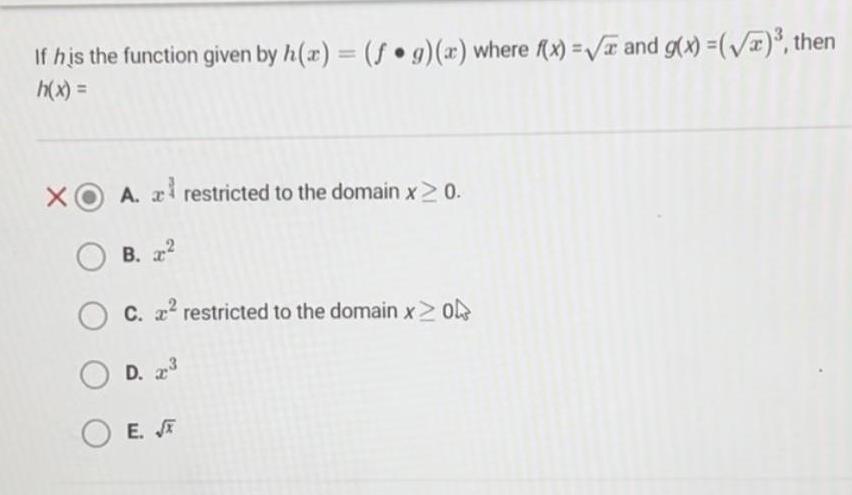
Calculus
Application of derivativesIf his the function given by h x f g x where f x and g x then h x O A a restricted to the domain x 0 OB OC 2 restricted to the domain x 0 OD 23 OE J

Calculus
Application of derivativesSuppose the following about a certain object 1 The object s altitude is a function of time represented by the function A x where here x is time II The temperature of the object is a function of its velocity represented by the function T x where here x is the object s velocity III The weight of the object is a function of its altitude represented by the function x where here x is the object s altitude IV The velocity of the object is a function of its weight represented by the function V x where here x is the object s weight The function F 1 which gives us the object s temperature at time t can be represented as A F t A o WoVoT t XO B F t TO Vo AoW t OC F t To Wo VoA t F t To VoWo A t OE F t To Wo AoV t

Calculus
Application of derivatives1 sin x on the domain the domain of g is If g x OA O B 4 4 C all real numbers OD 1 1 O E 0 1
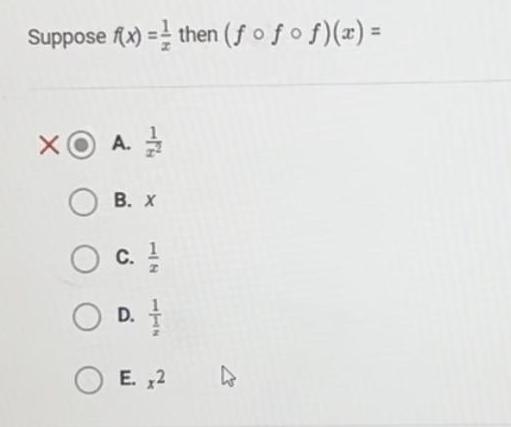
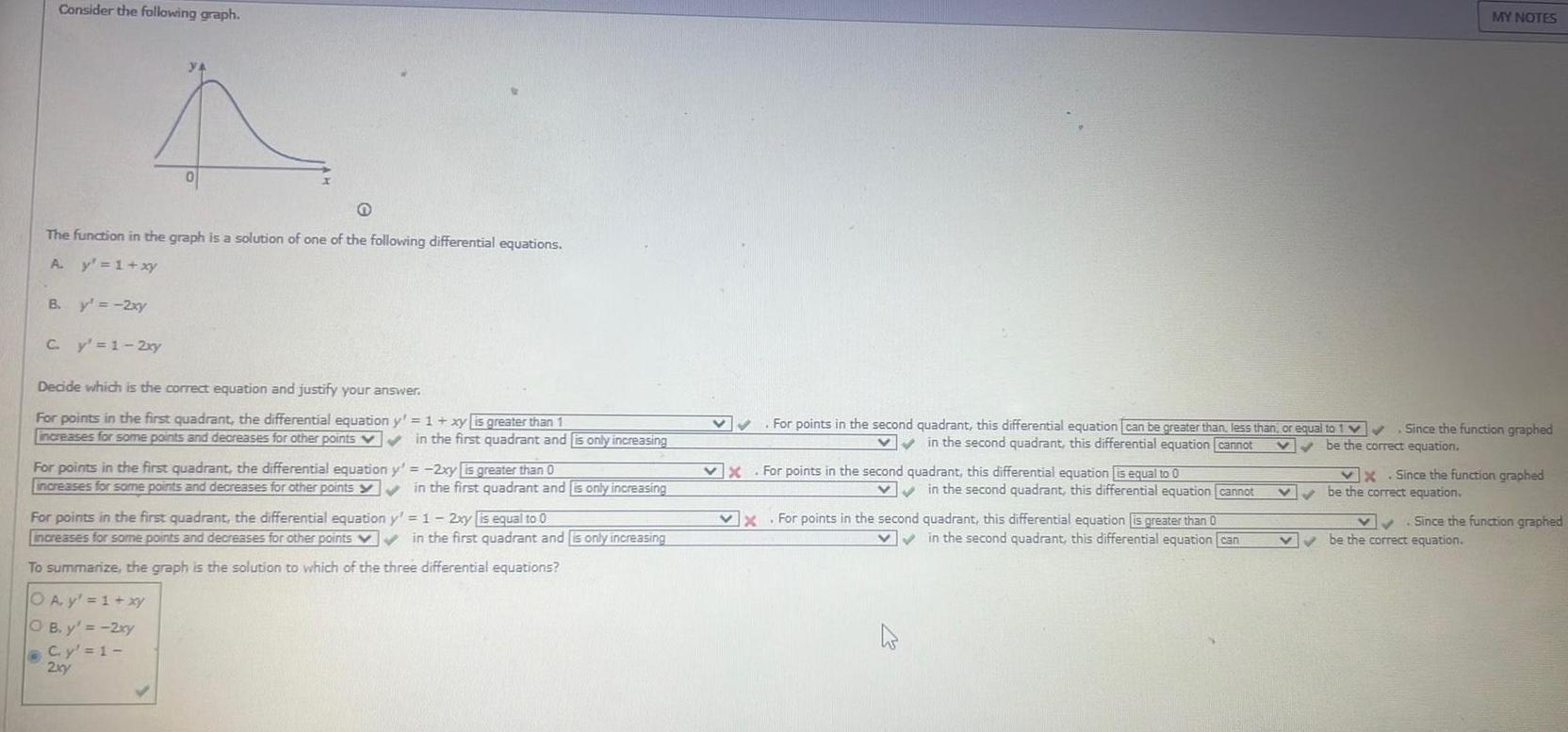
Calculus
Application of derivativesConsider the following graph Q The function in the graph is a solution of one of the following differential equations A y 1 xy B y 2xy O 0 C y 1 2xy Decide which is the correct equation and justify your answer For points in the first quadrant the differential equation y 1 xy is greater than 1 increases for some points and decreases for other points v in the first quadrant and is only increasing For points in the first quadrant the differential equation increases for some points and decreases for other points y 2xy is greater than 0 in the first quadrant and is only increasing For points in the first quadrant the differential equation y 1 2xy is equal to 0 increases for some points and decreases for other points in the first quadrant and is only increasing To summarize the graph is the solution to which of the three differential equations OA y 1 xy OB y 2xy C y 1 2xy For points in the second quadrant this differential equation can be greater than less than or equal to 1 Since the function graphed in the second quadrant this differential equation cannot V be the correct equation X For points in the second quadrant this differential equation is equal to 0 in the second quadrant this differential equation cannot X For points in the second quadrant this differential equation is greater than 0 x in the second quadrant this differential equation can MY NOTES v X Since the function graphed be the correct equation Since the function graphed be the correct equation

Calculus
Vector Calculus1 Determine the approximate radian measure 252 2 Determine the approximate degree measure to the nearest tenth 4 78 3 Draw both special triangles using radian measures

Calculus
Definite IntegralsUse the given transformation to evaluate the integral J R 12x 12y da where R is the parallelogram with vertices 2 4 2 4 4 2 and 0 6 x 1 u v y v2u

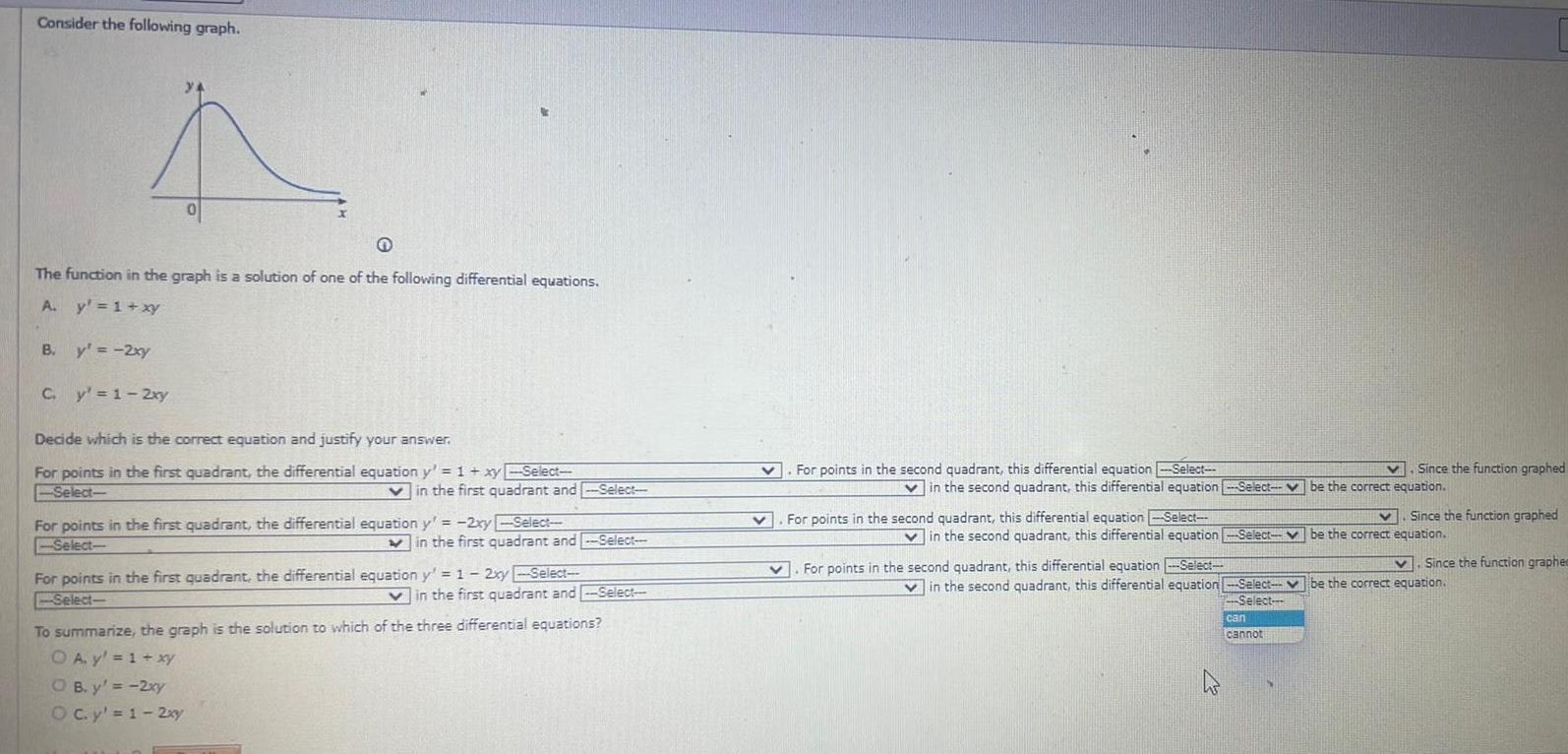
Calculus
Vector CalculusConsider the following graph 4 The function in the graph is a solution of one of the following differential equations A y 1 xy B y 2xy C y 1 2xy Decide which is the correct equation and justify your answer For points in the first quadrant the differential equation y 1 xy Select Select Vin the first quadrant and Select For points in the first quadrant the differential equation y 2xy Select Select in the first quadrant and Select For points in the first quadrant the differential equation y 1 2xy Select Select OB y 2xy O c y 1 2xy in the first quadrant and Select To summarize the graph is the solution to which of the three differential equations O A y 1 xy v For points in the second quadrant this differential equation Select v v in the second quadrant this differential equation Select be the correct equation For points in the second quadrant this differential equation Select in the second quadrant this differential equation Select For points in the second quadrant this differential equation Select 4 Since the function graphed Select be the correct equation Select Since the function graphed V in the second quadrant this differential equation Select be the correct equation can cannot Since the function graphee
Calculus
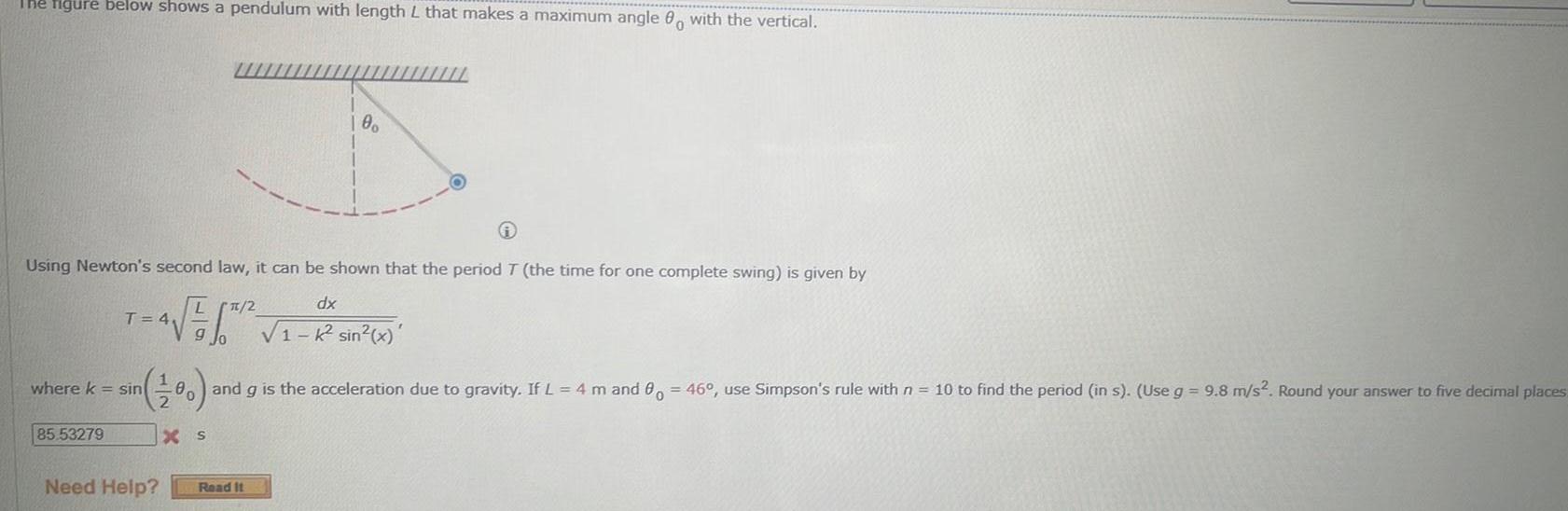
Application of derivativesThe figure below shows a pendulum with length L that makes a maximum angle 00 with the vertical Using Newton s second law it can be shown that the period T the time for one complete swing is given by LT 2 dx T 4 4 K sin x where k sin 100 and g is the acceleration due to gravity If L 4 m and 0 46 use Simpson s rule with n 10 to find the period in s Use g 9 8 m s Round your answer to five decimal places XS 85 53279 100 Need Help Read It

Calculus
Limits & ContinuityTutorial Exercise Find the Maclaurin series for f x using the definition a Maclaurin series Assume that f has a power series expansion Do not show that R x 0 Find the associated radius of convergence R f x 4 1 x