Math Questions

A basketball player routinely hits 100% of their free throws. What is the probability this player at practice only makes 2 out of 11 free throws? Express your answer as a percent rounded to the nearest tenth. 0.0% 0.5% 1.4% 2.9%

A soda machine dispenses abnormally distributed amounts of soda with a mean of 20 ounces and a standard deviation of 0.2 ounces. What is the probability of selecting a sample of eight bottles with a mean amount dispensed between 19.8 and 20.2 ounces? Population Mean: μ = Population Standard Deviation: σ = Normally Distributed (yes or no): Sample Sizes: n = What does this mean? Can the problem be completed? (Yes or No):

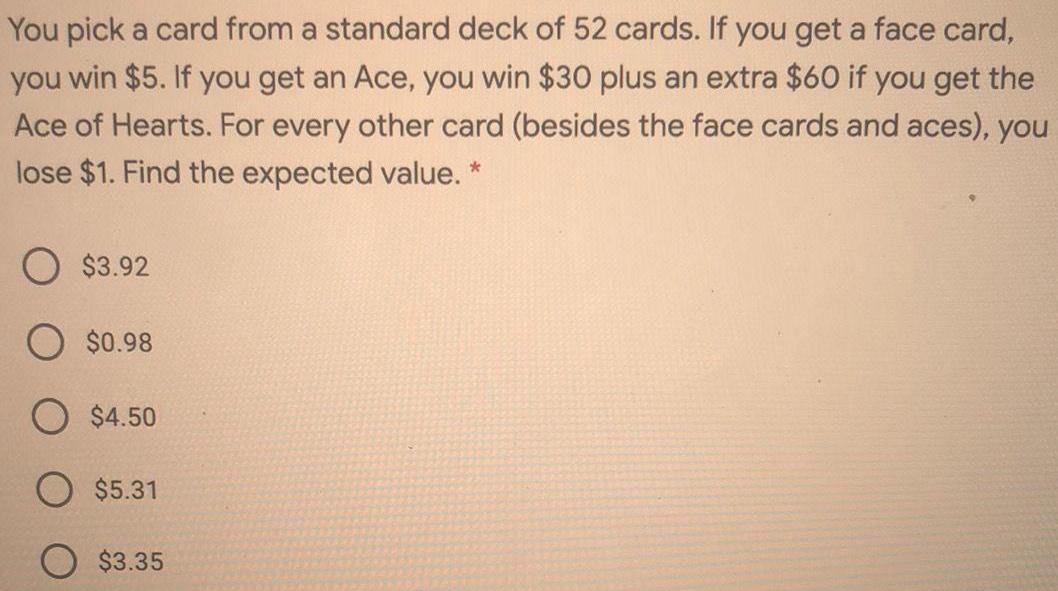
You pick a card from a standard deck of 52 cards. If you get a face card, you win $5. If you get an Ace, you win $30 plus an extra $60 if you get the Ace of Hearts. For every other card (besides the face cards and aces), you lose $1. Find the expected value. * $3.92 $0.98 $4.50 $5.31 $3.35

37% of U.S. adults say they are more likely to make purchases during a sales tax holiday. You randomly select 10 adults. Find the probability that the number of adults who say they are more likely to make purchases during a sales tax holiday is (a) exactly two, (b) more than two, and (c) between two and five, inclusive. (a) P(2)= 0.153 (Round to the nearest thousandth as needed.) (b) P(x > 2) = 0.779 (Round to the nearest thousandth as needed.) (c) P(2 ≤x≤5)=(Round to the nearest thousandth as needed.)

A company is interested in learning if employees are satisfied with their jobs. To find out, the company hires an independent market research company to conduct a survey. Every survey filled out by an employee is anonymous. Which of the following statements is correct? A. This method of sampling is unbiased. B. This method of sampling can be considered both biased and unbiased. C. This method of sampling is blased. D. This method of sampling is neither biased nor unbiased.

Show complete work on your worksheet! You many use the !, nCr and nPr functions on your calculator to CHECK your calculations, but you must show the formulas with appropriate values substituted in first. There are 15 members on a city council. On a recent agenda item, 8 of the council members voted in favor of a budget increase. How many possible groups of council members could have voted in favor? Permutation Combination n= T= There can be groups.

A square pyramid measuring 6 km along each edge of the base with a height of 9 km. 123 km³ 108 km³ 324 km³ 106 km³

The denarius was a unit of currency in ancient Rome. Suppose it costs the Roman government 10 denarius per day to support 3 legionaries and 3 archers. It only costs 3 denarius per day to support one legionary and one archer. Use a system of linear equations in two variables. Can we solve for a unique cost for each soldier? Choose 1 answer: Yes; a legionary costs 1 denarius per day to support, and an archer costs 2 denarius per day to support. Yes; a legionary costs 2 denarius per day to support, and an archer costs 4/3 denarius per day to support. No; the system has many solutions. No: the system has no solution.

A coin of questionable fairness is tossed 10 times per set of trials for two sets of trials. The outcomes are THTHTHTHHT and TTTHTTHTTH (T= Tails; H = Heads). Which model can you most likely rule out on the basis of this simulation? A. The probability of heads is 40%. B. The probability of heads is 30%. C.The probability of heads is 35%. D. The probability of heads is 70%.

Ricardo and Kim rowed their canoes from their base camp to a fishing camp. They rowed a distance of x miles upstream on one river, (3x² - 9) miles downstream on another river, and (2x + 9) miles across a calm lake. Which expression is equivalent to the total distance, in miles, Ricardo and Kim rowed their canoes? 5x² 6x² 3x²+2x 3x² + 3x

Pepperoni, green olives, black olives, tomatoes, green peppers, bacon, and hamburger are topping selections for a pizza. How many 2-topping possibilities are there, in which the toppings are not used more than once? 21 49 36 64

A cereal company packs its oatmeal into cylindrical containers. The height of each container is 10 inches, and the radius of the bottom is 5 inches. What is the volume of the container to the nearest cubic inch?

A recent survey found that 69% of all adults over 50 wear glasses for driving. In a random sample of 70 adults over 50, what is the mean and standard deviation of those that wear glasses? mean: 48.3; standard deviation: 6.95 mean: 48.3; standard deviation: 3.87 mean: 21.7; standard deviation: 3.87 mean: 21.7; standard deviation: 6.95

The Academy of Orthopedic Surgeons states that 80% of women wear shoes that are too small for their feet. A researcher wants to be 98% confident that this proportion is within 3% of the true proportion. How large a sample is necessary? 484 966 683 1183

Which of the following best describes the process for finding the interquartile range for a set of data? * Find the difference between the Maximum and Minimum values in the data set. ADD Q1 and Q3 and divide by 2. ADD the biggest and smallest values in the data set. Place the numbers in order from least to greatest and find the middle. SUBTRACT Q1 from Q3.

Find the equation of the line and write in the specified form: a. the line parallel to d = (2, 3) that hits the point (1,4), in parametric form. b. the line that passes through the points (2, 4) and (5, 13), in vector form.

Jacksonville, Florida is due south of Charleston, West Virginia. Find the distance between Jacksonville (30°20') and Charleston (38°21'). Assume that the radius of the Earth is 3960 miles. Round your answer to the nearest whole mile. The distance is miles.

Choose the answer that describes the set of ordered pairs below. Be prepared to justify your answer. {(Ford, blue), (Nissan, red), (Toyota, silver), (Subaru, black), (Chevy, blue), (Volvo, red)} A function with domain of (Ford, Nissan, Toyota, Subaru, Chevy, Volvo} A relation with domain of {Ford, Nissan, Toyota, Subaru, Chevy, Volvo} A function with domain of (blue, red, silver, black} A relation with domain of {blue, red, silver, black}

There are seven white dogs, five black dogs, six white cats, and three black cats. What is the probability of randomly selecting a white animal or a dog?

A fruit company delivers its fruit in two types of boxes: large and small. A delivery of 3 large boxes and 8 small boxes has a total weight of 162 kilograms. A delivery of 5 large boxes and 2 small boxes has a total weight of 117 kilograms. How much does each type of box weigh? Weight of each large box: kilogram(s) Weight of each small box: kilogram(s)

The standard deviation of the mass of 50 mice in a normal population is 5 g. How many mice are within one standard deviation of the mean?

Fiona's Fashion Store is world renowned for its buttoned uniforms. A collection of 36 shirts and 42 jackets contains 842 buttons. A collection of 6 shirts and 7 jackets contains 137 buttons. Each shirt has the same number of buttons, and each jacket has the same number of buttons. How many buttons are there in a Fiona's Fashion shirt, and how many buttons are there in a jacket?

Beth bought 15 tickets to a movie, where adult tickets cost $6.00 and senior citizen tickets cost $4.00. She spent a total of $76. Which system of equations will determine the number of adult tickets, a, and the number of senior citizen tickets, s, Beth purchased? a. a + s = 76 6a + 4s = 15 c. a+s=15 4a + 6s = 76 b. a + s = 15 6a + 4s = 76 d. a + s = 76 6a + 4s = 15

53% of U.S. adults have very little confidence in newspapers. You randomly select 10 U.S. adults. Find the probability that the number of U.S. adults who have very little confidence in newspapers is (a) exactly five, (b) at least six, and (c) less than four. (a) P(5)= (Round to three decimal places as needed.) (b) P(x ≥ 6) = (Round to three decimal places as needed.) (c) P(x<4)= (Round to three decimal places as needed.)

56% of U.S. adults have very little confidence in newspapers. You randomly select 10 U.S. adults. Find the probability that the number of U.S. adults who have very little confidence in newspapers is (a) exactly five, (b) at least six, and (c) less than four.

In a recent survey, 73% of the community favored building a police substation in their neighborhood. If 14 citizens are chosen, find the probability that exactly 8 of them favor the building of the police substation. 0.094 0.571 0.730 0.013

The Internal Revenue Service claims that the mean wait time for callers during a recent tax filing season was less than 7 minutes. A random sample of 11 callers had a mean wait time of 6.7 minutes and a standard deviation of 3.2 minutes. Does the data support the idea that the wait time was less than 7 minutes. Use a 5% level of significance.

If the population of a country increases at a rate of 1.5% annually and its current population is 430,000, how many years will it take for the population to triple? A. 74 years B. 3 years C. 2 years D. 150 years

Given the equation solve for x and identify if it is an extraneous solution. x = 4, solution is extraneous x = 4, solution is not extraneous x = 5, solution is extraneous x = 5, solution is not extraneous

f(x)=2x³+2x²-8x-8 If there is more than one answer, separate them with commas. Click on "None" if applicable.

Using your knowledge of exponential and logarithmic functions and properties, what is the intensity of a fire alarm that has a sound level of 120 decibels? 10 * 10-12 watts/m² 1.0 x 100 watts/m² 12 watts/m² 1.10 x 102 watts/m²

Determine which numbers could not be used to represent the probability of an event. Select all that apply. A. 320/1058 because probability values cannot be in fraction form. B. 33.3%, this is because probability values cannot be greater than 1. C. 64/25, because probability values cannot be greater than 1. D. 0, because probability values must be greater than 0. E. 0.0002, because probability values must be rounded to two decimal places. F. -1.5, because probability values cannot be less than 0.

Situation: There is a linear relationship between the total cost of a gym membership for the month and the number of fitness class taken that month. One month Mari took 10 classes and it cost her $75. Another month she took 8 classes and paid $60. Question: If the total cost of a gym membership for the month was $97.50, how many fitness classes did Mari take? Answer: Mari attended fitness classes.

Use TVM Solver on your calculator to answer the following questions. Round each answer to the nearest cent. You deposit $300 each month into an account earning 8% interest compounded monthly. a) How much will you have in the account in 15 years? b) How much total money will you put into the account? c) How much total interest will you earn?

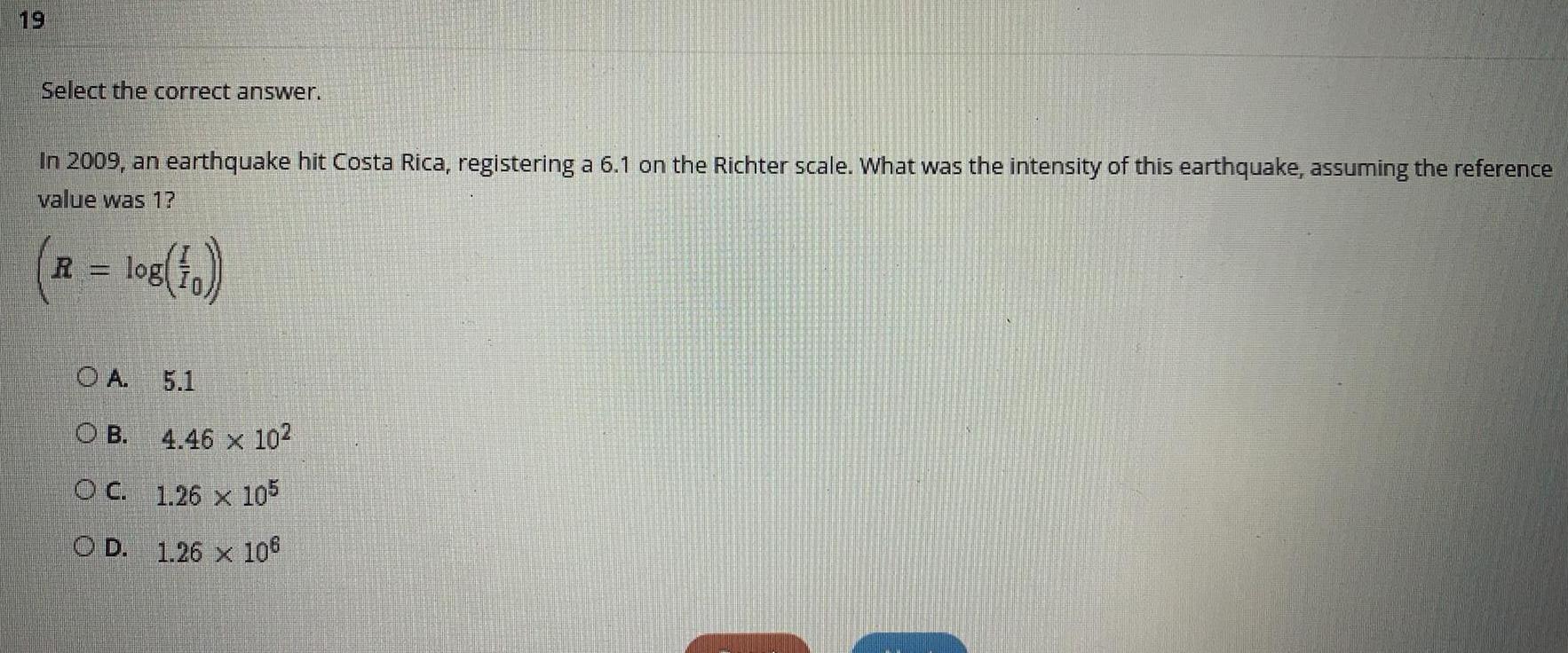
In 2009, an earthquake hit Costa Rica, registering a 6.1 on the Richter scale. What was the intensity of this earthquake, assuming the reference value was 1? (R =log(I/I₀)) A. 5.1 B. 4.46 x 10^2 C. 1.26 x 10^5 D. 1.26 x 10^6

In a learning theory project, psychologists discovered that f(t) = 0.8 / (1+e^-0.2t) is a model for describing the proportion of correct responses, f(t), after t learning trials. a. Find the proportion of correct responses prior to learning trials taking place. b. Find the proportion of correct responses after 10 learning trials. c. What is the limiting size of f(t), the proportion of correct responses, as continued learning trials take place?

Bentley invested $1700 in an account that pays 1.5% interest compounded annually. Assuming no deposits or withdrawals are made, write a recursive formula that represents the amount of money Bentley has in the account n years after his initial investment. ao= an =

Avocado Pickers are paid as shown below. What would be the gross earnings for a worker that picks 1,108 avocados? 1-500 Avocados $0.10 each 501 - 700 Avocados $0.14 each Over 700 Avocados $0.18 each

The rod on a pump rises and falls as the pump operates. Function /gives the height of the top of the rod above the pumping unit in feet, L(t), as a function of time in seconds, t, after the pump is activated. L(t) = sin(πt +π/2 ) + 3/2 What is the range of the given function? A. 0 feet to 3 feet B. 0 feet to feet C. 1-foot to feet D. 1 foot to 3 feet

17% adults favor the use of unmanned drones by police agencies. Twelve U.S. adults are randomly selected. Find the probability that the number of U.S. adults who favor the use of unmanned drones by police agencies is (a) exactly three, (b) at least four, (c) less than eight.

Given the equation 2√x-5=2, solve for x and identify if it is an extraneous solution. a. x = 6, solution is not extraneous b. x = 6, solution is extraneous c. x= 11, solution is not extraneous d. x= 11, solution is extraneous

Ian is a teacher and takes home 46 papers to grade over the weekend. He can grade at a rate of 11 papers per hour. Write a recursive sequence to represent how many papers Ian has remaining to grade after working for n hours. ao = an =

Allison kicks a stone off the edge of a tall cliff. The distance d (in feet), between the rock and the ground seconds after being kicked is d(t)= -t^2 +4t+474. a. How many seconds elapse before the rock is at a height of 424 feet above the ground? Round your answer to the nearest tenth of a second. b. What is the maximum height that the rock reaches? Round your answer to the nearest whole foot.

Complete the table to determine the balance A for P dollars invested at rate r for t years, compounded n times per year. (Round your answers to the nearest cent.) Rate r = 7.5% Time t = 15 years Principal P = $1500 n 1 4 12 365 Continuous compounding A

To get from point A to point B, you must avoid walking through a pond. To avoid the pond, you must walk 34 meters south and 41 meters east. To the nearest meter, how many meters would be saved if it were possible to walk through the pond? 45 meters 34 meters 22 meters 53 meters

A population of fish in a pond is decreasing by 4% each year. The population starts with 250 fish. Which of the following functions represent the population of fish as a function of time? P (t) = 250(4)^t-1 P (t) = 250(1 + .04)^t P (t) = 250(.04)^t-1 P (t) = 250(1-.04)^t

Tomas sells cars and there is a linear relationship between the number of cars he sells each week and his weekly pay. One week Tomas sold 4 cars and he made $820 that week. Another week he sold 6 cars and made $980. Write an equation that models the linear relationship between the number of cars Tomas sells in a week and his pay for that week. DO NOT USE ANY SPACES between variables, constants, equals signs, and operation signs. For example, DO NOT enter y = 2x + 1. DO ENTER: y=2x+1. Put parentheses around constants that are fractions like this: y=(2/3)x-(1/2) To write your equation, use the variables: p = total weekly pay ($) n = number of cars sold during the week The equation in slope-intercept form is

Select the correct answer. Consider the equation below (x - 2)³ - 6=3 √x + 4. Which statement explains why the solution to the equation is x= 4? A. The x-value of 4 is a x-intercept for both f(x)=(x - 2)³ - 6 and g(x)=3 √x + 4. B. The x-value of 4 produces the same y-value in both f(x)=(x - 2)³ - 6 and g(x) =3√x + 4. C. The x-value of 4 is undefined for both f(x) = (x - 2)³ - 6 and g(x)=3√x + 4. D. The x-value of 4 is defined on the graphs of both f(x) = (x - 2)³ — 6 and g(x) =3√x + 4.

Kaylee is looking to take out a mortgage for $260, 000 from a bank offering an annual interest rate of 5.7%, compounded monthly. Using the formula below, determine her monthly payment, to the nearest dollar, if the loan is taken over 10 years. M = Pr(1+r)"/(1+r)" - 1

There are 3 apples, 4 oranges, and a pear in a basket. Determine each probability that you select an orange and then a pear at random without replacement. Write your answer as a fraction. 2 out of 5 would be typed as 2/5.