Math Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Math
Basic MathDaniela measures her math book and records its width as 21.9 cm to the nearest tenth of a centimeter. The actual measurement of the book's width is 22.0 cm. What is the percent error of her measurement? Round your answer to the nearest tenth of a percent.
A. 0.2%
B. 0.5%
C. 2.3%
D. 4.5%

Math
Basic MathTara works in a clothing store where she earns a base salary of $100 per day plus 12% of her daily sales. She sold $800 in clothing on Saturday and $1500 in clothing on Sunday. How much did she earn over the two days?
A. $276
B. $376
C. $476
D. $576

Math
TrigonometryThe average monthly temperature, T, in degrees Celsius, for any month m, for the town of Someplace, is modeled by the function T(m) = 19.1 sin(3π/9 x) + 7.5.
a. What is the period of the function and what does it mean?
b. Plot one full cycle of the function below. Show all of your thinking work and be sure to label your axes correctly.

Math
Basic MathUse the function equation to find the n-intercept of the linear function algebraically.
C(n)=8n-1240
Write the ordered pair using parentheses like this: (x,y) with no spaces but with the appropriate numerical coordinates instead of x and y. If there is no
'x'-intercept type "N/A" in the blank.
The n-intercept is

Math
ProbabilityA shipment of 12 microwave ovens contains 2 defective units. A restaurant buys four of these units. What is the probability of the restaurant buying at least three nondefective units?
The probability of the restaurant buying at least three nondefective units is

Math
Basic MathKatherine just started a running plan where she runs 8 miles the first week and then increases the number of miles she runs by 5% each week. If she keeps up this plan for 19 weeks, how many total miles would Katherine have run, to the nearest whole number?

Math
FunctionsMia opens a coffee shop in the first week of January. The function W(x) = 0.002x3 -0.01x2 models the total number of customers visiting the shop since it opened after x days. She then opens an ice cream parlor in the month of February. The function R(x) = x2 - 4x + 13 models the total number of customers visiting the parlor since it opened after x days.
Which function represents the difference of the number of customers visiting the two shops?
A. D(x) = 0.002x3 +1.01x2 - 4x + 13
B. D(x) = 0.002x3 - 1.01x2 + 4x - 13
C. D(x) = 0.002x3 - 0.99x2 - 4x + 13
D. D(x) = 0.002x3 +0.99x2 + 4x - 13
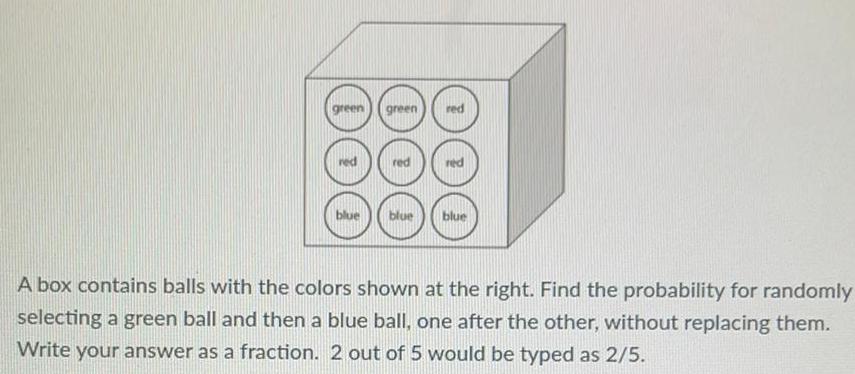
Math
Probabilitygreen green red
red red red
blue blue blue
A box contains balls with the colors shown at the right. Find the probability for randomly
selecting a green ball and then a blue ball, one after the other, without replacing them.
Write your answer as a fraction. 2 out of 5 would be typed as 2/5.
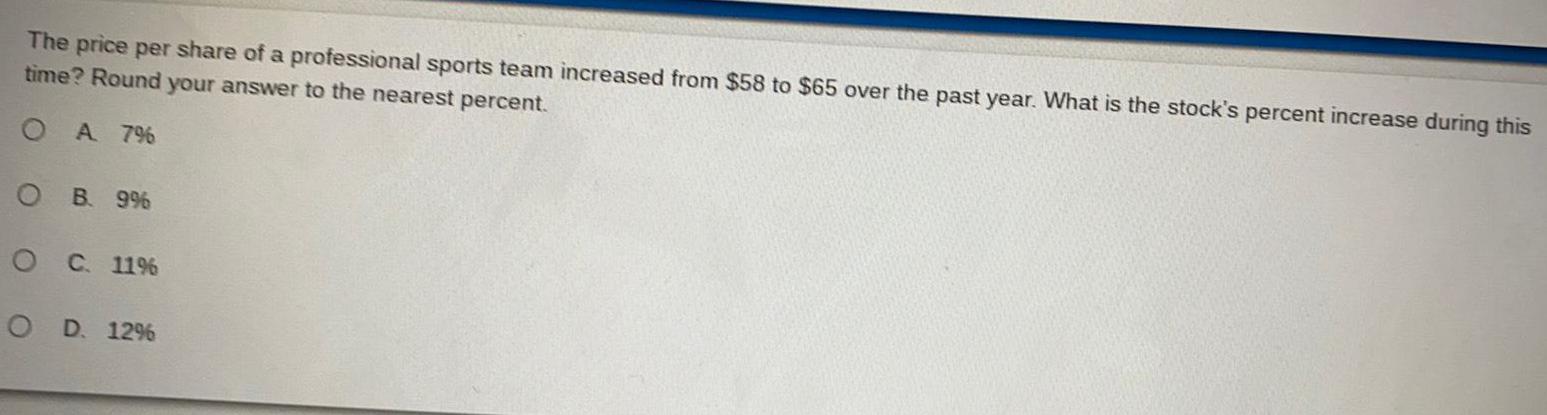
Math
Basic MathThe price per share of a professional sports team increased from $58 to $65 over the past year. What is the stock's percent increase during this time? Round your answer to the nearest percent.
A 7%
B. 9%
C. 11%
D. 12%

Math
ProbabilityDetermine whether the distribution is a discrete probability distribution.
Is the distribution a discrete probability distribution? Why? Choose the correct answer below.
A. No, because some of the probabilities have values greater than 1 or less than 0.
B. Yes, because the probabilities sum to 1 and are all between 0 and 1, inclusive.
C. No, because the total probability is not equal to 1.
D. Yes, because the distribution is symmetric.

Math
Basic MathAnswer the following questions about P(x)=x^3-4x²-3x+18:
a. The polynomial P(x) has no remainder when divided by (x+2). List all of the roots of P(x).
showing how you found the roots algebraically.
b. Sketch a graph of the function f(x) =x+2/P(x) and explain or show algebraically how you found P(x) the asymptotes and holes, if any.

Math
ProbabilityAn analog stopwatch has 60 tick marks, one for each second. After the stopwatch has been running for a few minutes, it is stopped randomly. What is the probability of the stopwatch's hand landing on the 9, 30, 45, or 51?
9.1%
7.9%
7.3%
6.7%

Math
Linear ProgrammingA calculator company produces a scientific calculator and a graphing calculator. Long-term projections indicate an expected demand of at least 100 scientific and 80 graphing calculators each day. Because of limitations on production capacity, no more than 200 scientific and 170 graphing calculators can be made daily. To satisfy a shipping contract, a total of at least 200 calculators must be shipped each day. If each scientific calculator sold results in a $2 loss, but each graphing calculator produces a $5 profit, how many of each type should be made daily to maximize net profits?

Math
ProbabilityA warehouse employs 21 workers on first shift, 15 workers on second shift, and 10 workers on third shift. Eight workers are chosen at random to be interviewed about the work environment. Find the probability of choosing exactly five first-shift workers.
The probability of choosing exactly five first-shift workers is

Math
Basic MathPriya starts with $50 in her bank account. She then deposits $20 each week for 12 weeks.
1. Write an equation that represents the relationship between the dollar amount in her
bank account and the number of weeks of saving.
2. Graph your equation using graphing technology. Mark the point on the graph that
represents the amount after 3 weeks.
3. How many weeks does it take her to have $250 in her bank account? Mark this point on
the graph.

Math
ProbabilityA probability experiment consists of rolling a 6-sided die. Find the probability of the event below. rolling a number less than 3
The probability is

Math
FunctionsDrag the values to the correct locations on the image. Not all values will be used.
Function fis a logarithmic function with a vertical asymptote at x = 0 and an x-intercept at (4,0). The function is decreasing over the interval (0,infinity).
Function g is represented by the equation g(x)= log₂ (x + 3) - 2
Over which interval are both functions positive?

Math
FunctionsWhich function defines (g - f)(x)?
f(x) = 3√12x + 1 + 4
g(x) = log(x − 3) + 6
A. (g-f)(x) = log x - 3√12x - 12
B. (g - f)(x) = log(x − 3) - 3√12x+1 - 10
C. (g - f)(x) = log(x - 3) - 3√12x+1 + 2
D. (g - f)(x) = log(x - 3) - 3√12x+1 +10

Math
Straight linesYour school is printing programs for the honor society induction ceremony. L & L Printing will print the programs for $350 plus an additional $1.50 per program. Red Baron will print the programs for $1.82.
Identify the y-intercept for each of the Printing Companies.
L & L Printing =
Red Baron =

Math
Solution of trianglesTriangle ABC has sides with lenths of 3, 6, and 8. Classify each of the transformations described as producing a triangle similar to triangle ABC or a triangle not similar to triangle ABC.
Match each transformation to either similar to triangle ABC or not similar to triangle ABC.
Column A Column B
1. ___ Multiply each side length by 3.5. a.Similar to triangle ABC.
2. ____ Add 12 to each side length. b. Not similar to triangle ABC.
3. _____Subtract 2 from each side length.
4. ___Divide each side length by 0.75.
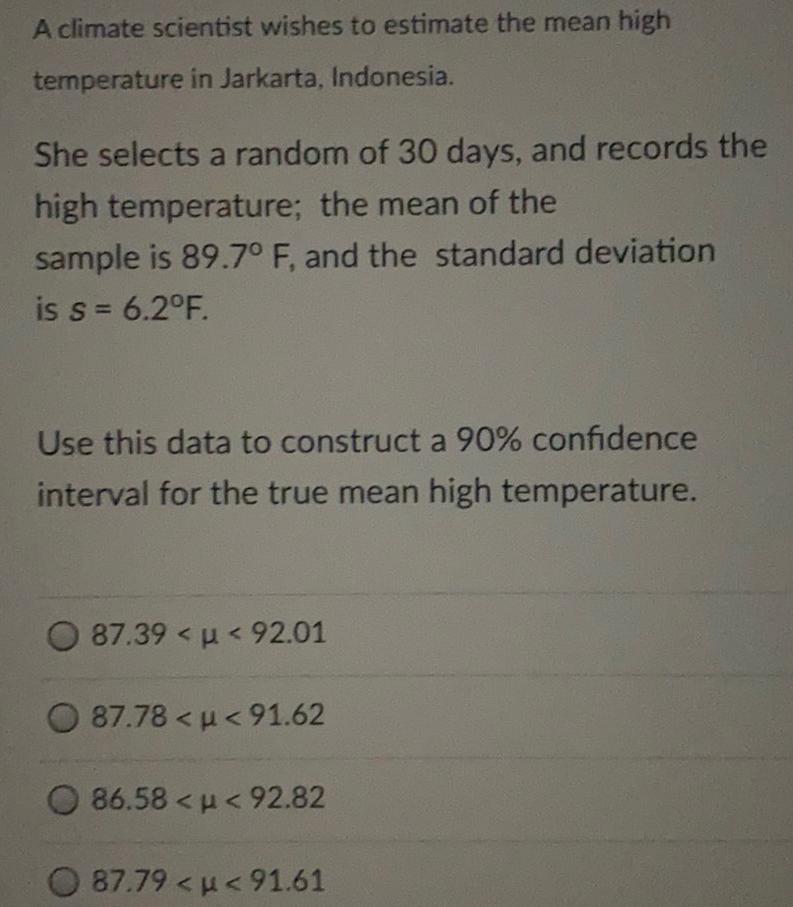
Math
StatisticsA climate scientist wishes to estimate the mean high
temperature in Jarkarta, Indonesia.
She selects a random of 30 days, and records the
high temperature; the mean of the
sample is 89.7° F, and the standard deviation
is s = 6.2°F.
Use this data to construct a 90% confidence
interval for the true mean high temperature.
87.39<µ< 92.01
87.78 <µ< 91.62
86.58 <µ< 92.82
87.79 <µ< 91.61

Math
AreaA cylindrical cup is 8 centimeters in height. When filled to the very top, it holds 480 cubic centimeters of water. What is the radius of the cup, rounded to the nearest tenth?
a 4.4
b 19.1
c 8.5
d 15.6

Math
Basic MathA cylinder with a diameter of 16 yd and a height of 12 yd.
3467.84 yd³
2412.74 yd³
1781.32 yd³
1321.15 yd³

Math
Parabola1. Select the best choice for the definition of a parabola. *
A. The graph of a quadratic function that is a U-shaped curve.
B. Is defined by an ordered pair and is considered the minimum point or the maximum point.
C. A vertical line that passes through the vertex of the graph of a quadratic function.
D. A term that describes the x-intercept(s) of the graph of a quadratic function.
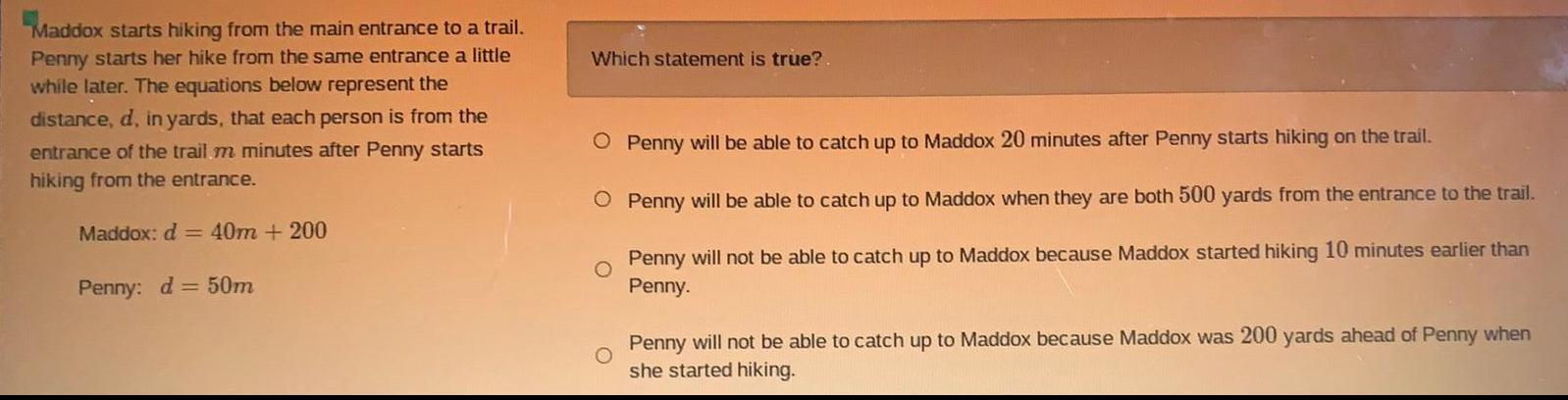
Math
Basic Math"Maddox starts hiking from the main entrance to a trail. Penny starts her hike from the same entrance a little while later. The equations below represent the distance, d, in yards, that each person is from the entrance of the trail m minutes after Penny starts hiking from the entrance.
Maddox: d = 40m + 200
Penny: d = 50m
Which statement is true?
Penny will be able to catch up to Maddox 20 minutes after Penny starts hiking on the trail.
Penny will be able to catch up to Maddox when they are both 500 yards from the entrance to the trail.
Penny will not be able to catch up to Maddox because Maddox started hiking 10 minutes earlier than Penny.
Penny will not be able to catch up to Maddox because Maddox was 200 yards ahead of Penny when she started hiking.

Math
Sequences & SeriesAubrey opened a savings account with $1400 that pays no interest. She deposits an additional $70 each week thereafter. Write a recursive formula to show how much money Aubrey has in the account n weeks after opening the account.

Math
ProbabilityA local ice cream store sells three flavors of ice cream during a busy summer month. During this month, there were 566 orders of vanilla ice cream, 400 orders of strawberry ice cream, and 1,224 orders of chocolate ice cream. What is the experimental probability that chocolate ice cream was ordered during this month?

Math
Basic MathMadison was given a large box of 42 chocolates for her birthday. If she eats exactly 5 chocolates each day, how many chocolates would Madison have remaining 5 days after her birthday?

Math
ProbabilityYou randomly select an integer from 0 to 7 (inclusively) and then randomly select an integer from 0 to 4 (inclusively). What is the probability of selecting a 3 both times?
The probability is
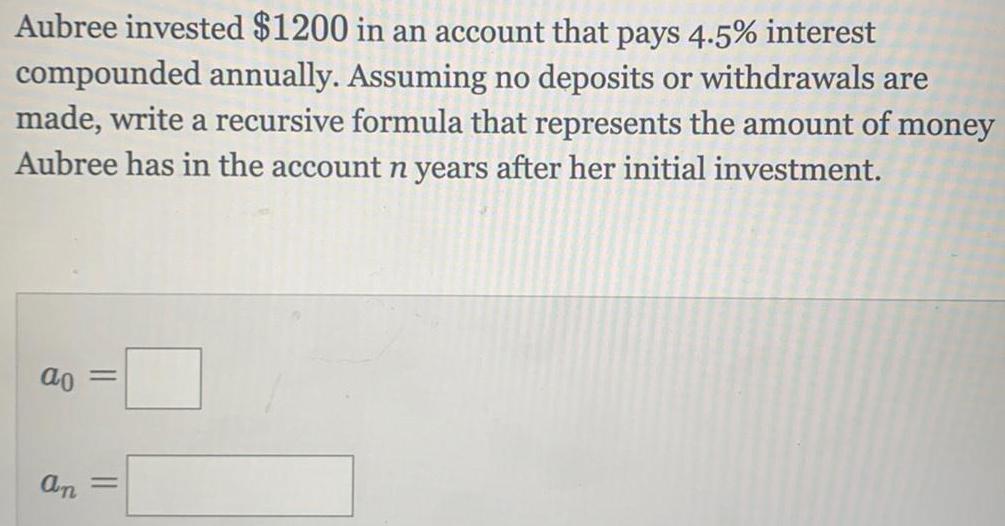
Math
Sequences & SeriesAubree invested $1200 in an account that pays 4.5% interest compounded annually. Assuming no deposits or withdrawals are made, write a recursive formula that represents the amount of money Aubree has in the account n years after her initial investment.

Math
StatisticsWhich of the following statements is false regarding randomization?
A Randomization protects against unknown factors.
B.Randomization allows each member of the population to have an equal probability of being selected for the sample population.
C. Randomization can be replaced by accurately matching the sample to the population.
D. Randomization helps avoid bias.

Math
StatisticsA laboratory tested 73 chicken eggs and found that the mean amount of cholesterol was 247 milligrams; the population SD for all eggs is a = 15.2 milligrams.
Use this data to construct a 95 percent confidence interval for the true mean cholesterol content, m, of all such eggs.
244 <m < 250
243 <m< 249
245 <m < 251
243 <m < 250

Math
FunctionsWhich statement best demonstrates why the following is a non-example of a polynomial?
33y² /x²-62y2xz-35z2y2
The expression has a variable raised to a negative exponent.
The expression has a negative coefficient.
The expression has a variable raised to a fraction.
The expression has a variable in the denominator of a fraction.

Math
Basic MathRhett decides to build a square room for his movie and music collection. If the area of the room is 4x² + 28x + 49 square feet, what is the length of one side of the room?
(7x + 2) feet
(2x + 7) feet
(2x-7) feet
(7x-2) feet

Math
StatisticsA truck from Lakeland Trucking, Inc. carries boxes of canned goods. Records of past trips show that the weights of boxes that it carries have a mean of 72 lb. and a standard deviation of 16 lb. For samples of size 64, find the mean and standard deviation of the sampling distribution for x.
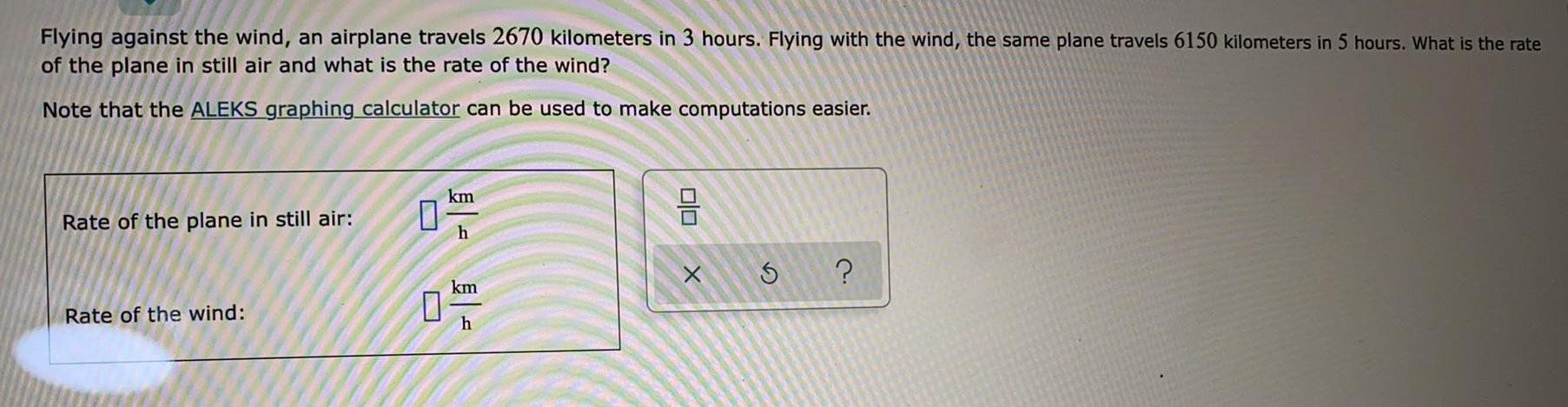
Math
Basic MathFlying against the wind, an airplane travels 2670 kilometers in 3 hours. Flying with the wind, the same plane travels 6150 kilometers in 5 hours. What is the rate of the plane in still air and what is the rate of the wind?
Note that the ALEKS graphing calculator can be used to make computations easier.
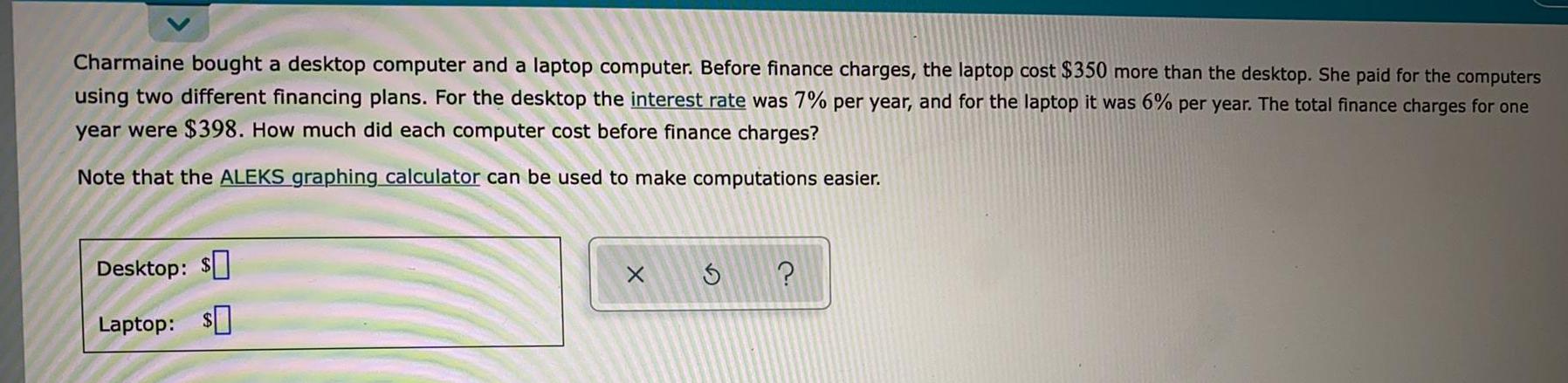
Math
Basic MathCharmaine bought a desktop computer and a laptop computer. Before finance charges, the laptop cost $350 more than the desktop. She paid for the computers using two different financing plans. For the desktop the interest rate was 7% per year, and for the laptop it was 6% per year. The total finance charges for one year were $398. How much did each computer cost before finance charges? Note that the ALEKS graphing calculator can be used to make computations easier.
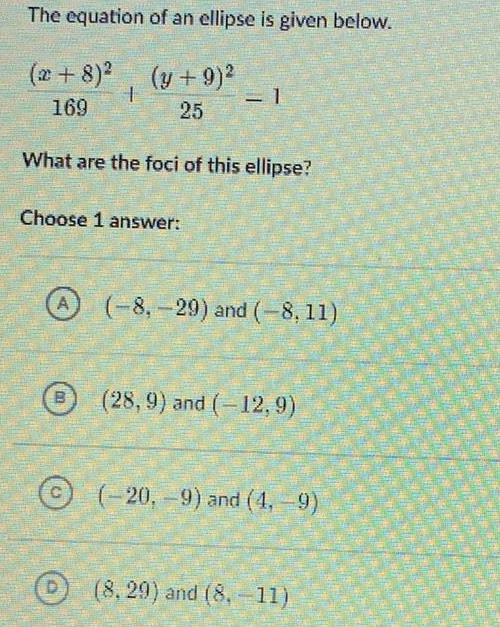
Math
EllipseThe equation of an ellipse is given below.
(x+8)²/169 + (y + 9)²/25 =1
What are the foci of this ellipse?
Choose 1 answer:
A(-8,-29) and (-8, 11)
(28,9) and (-12,9)
(-20, -9) and (4, 9)
(8.29) and (8, −11)

Math
ProbabilitySuppose the weights of all DVC students are normally distributed with mean 168.2 pounds and standard deviation 22.1 pounds.
(a) If one student is randomly selected, find the probability that the student weighs more than 180 pounds.
(b) The elevator in the Math Building can safely lift 1,800 pounds; it is dangerous if the total weight is over 1,800 pounds. If 10 people are in the elevator, find the probability that their mean weight is greater than 180 pounds (hence, the total weight exceeds 1,800 pounds). Is it safe to have 10 people in the elevator? Explain.

Math
FunctionsA sample of a radioactive isotope had an initial mass of 540 mg in the year 2009 and decays exponentially over time. A measurement in the year 2011 found that the sample's mass had decayed to 300 mg. What would be the expected mass of the sample in the year 2021, to the nearest whole number?
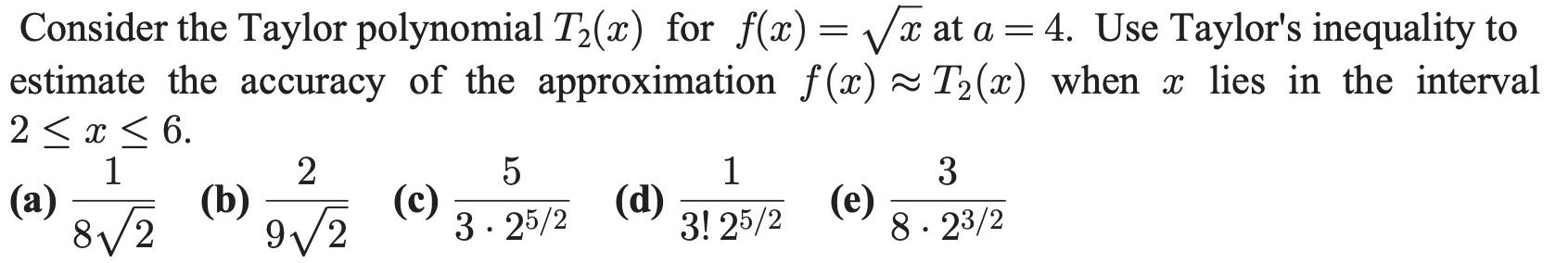
Math
Sequences & SeriesConsider the Taylor polynomial T₂(x) for f(x)=√x at a = 4. Use Taylor's inequality to estimate the accuracy of the approximation f(x)≈ T₂(x) when x lies in the interval 2 ≤ x ≤ 6.
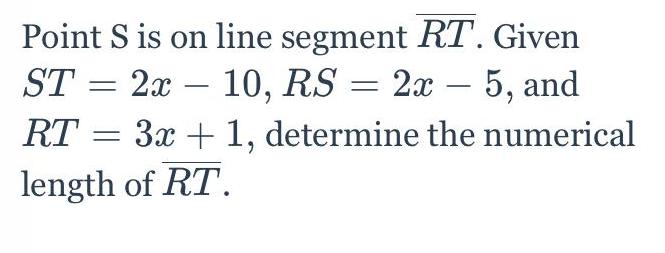
Math
Basic MathPoint S is on line segment RT. Given ST= 2x- 10, RS = 2x - 5, and RT = 3x + 1, determine the numerical length of RT.

Math
FunctionsA sample of a radioactive isotope had an initial mass of 560 mg in the year 1995 and decays exponentially over time. A measurement in the year 2002 found that the sample's mass had decayed to 90 mg. What would be the expected mass of the sample in the year 2012, to the nearest whole number?

Math
DifferentiationSelect the best choice for the definition of average rate of change.
A. The rate at which a function's y-values (output) are changing as compared to the function's x-values (input).
B. The graph of a quadratic function that is a U-shaped curve.
C. Is defined by an ordered pair and is considered the minimum point or the maximum point.
D. A vertical line that passes through the vertex of the graph of a quadratic function.
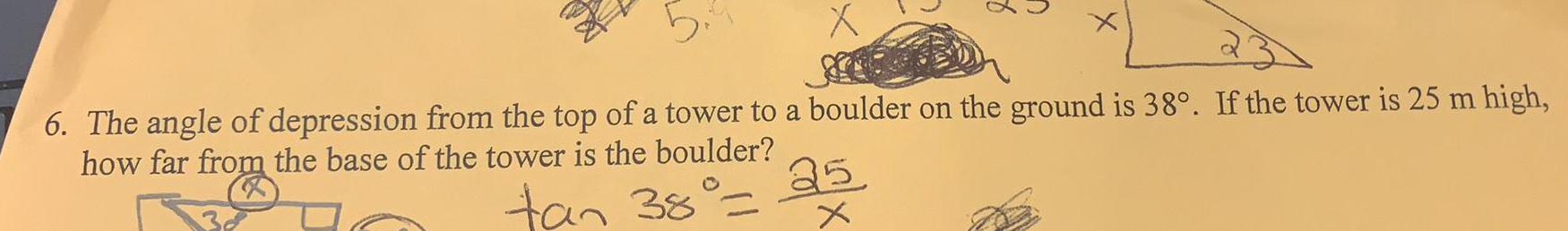
Math
TrigonometryThe angle of depression from the top of a tower to a boulder on the ground is 38°. If the tower is 25 m high, how far from the base of the tower is the boulder?
Math
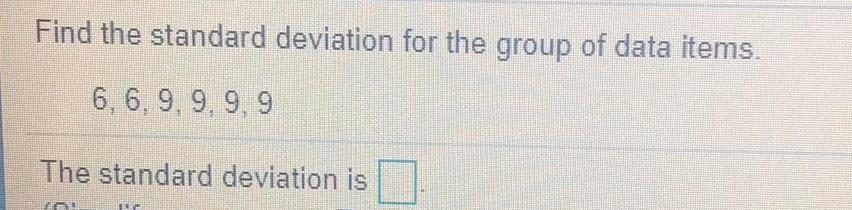
StatisticsFind the standard deviation for the group of data items.
6, 6, 9, 9, 9, 9
The standard deviation is

Math
Basic MathCertain radioactive material decays in such a way that the mass remaining after t years is given by the function
m(t) = 275e-0.045
where m(t) is measured in grams.
(a) Find the mass at time t = 0.
Your answer is
(b) How much of the mass remains after 10 years?
Your answer is
Math
Sequences & SeriesYou rent an apartment that costs $1300 per month during the first year, but the rent is set to go up $120 per year. What would be the monthly rent during the 8th year of living in the apartment?

Math
Basic MathFind the circumference and area of a circle with a diameter of 22 inches. Leave your answers in terms of pl.

Math
Basic MathA wheel with three numbers on it--0, 1, and 2--is spun so that there is a 40% chance that the wheel lands on zero, a 10% chance the wheel lands on one, and a 50% chance the wheel lands on two. You get back the amount in dollars of the number that the wheel lands on. If it costs $1 to
play, what is the expected value of the game? *
-$1.10
-$0.10
$0.10
$0.20
$1.10