Math Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Math
ProbabilityDetermine whether the events are independent or dependent. Explain your reasoning.
Returning a rented movie after the due date and receiving a late fee

Math
Binomial theoremFind the mean, variance, and standard deviation of the binomial distribution with the given values of n and p.
n = 50, p=0.9
The mean, µ, is
The variance, σ2, is
The standard deviation, σ, is (Round to the nearest tenth as needed.)

Math
CircleThe formula for the circumference C of a circle, in terms of the radius, is C=2πr, where r stands for the radius. Rearrange the quantities in this formula to give a new formula for the radius of a circle in terms of the circumference.
Math
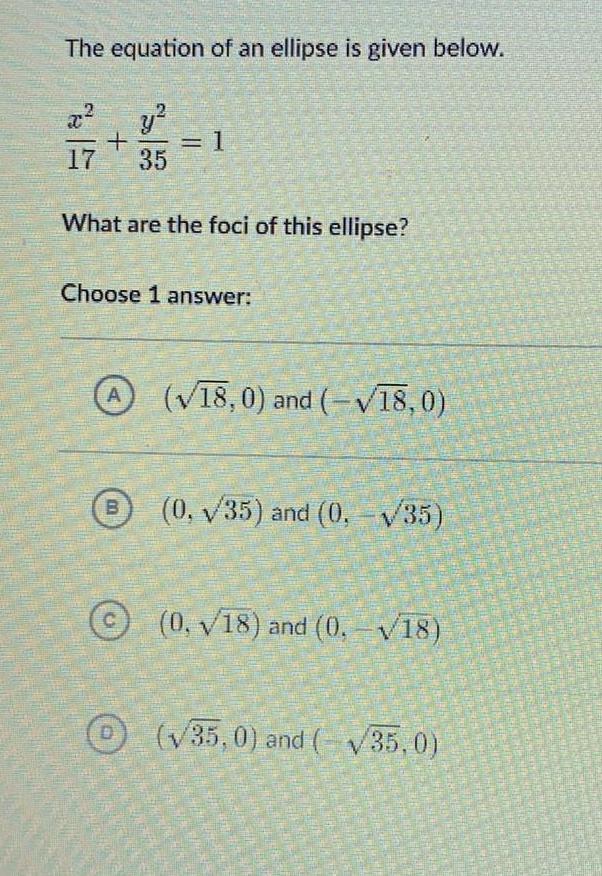
Basic MathThe equation of an ellipse is given below.
x2/17+y²/35= 1
What are the foci of this ellipse?
Choose 1 answer:
A(√18,0) and (-√18,0)
B (0, √35) and (0, -√/35)
c (0, 18) and (0, -√18)
D (√35,0) and (-√35,0)

Math
Logarithms1. The logistic growth function f(t) = 100,00 / (1 + 5000e-t) describes the number of people, f(t), who have become ill with influenza t weeks after its initial outbreak in a particular community.
a. How many people became ill with the flu when the epidemic began?
b. How many people were ill by the end of the fourth week?
c. What is the limiting size of the population that becomes ill?

Math
FunctionsAn object dropped from a tower has its height in feet above the ground t seconds into the fall given by s(t) = 160 -16t2. Include appropriate units in your answers to all questions:
a) What is the object's velocity, speed, and acceleration at time t?
b) How long does it take the object to hit the ground?
c) What is the object's velocity at the moment of impact?

Math
Basic MathA company makes electronic gadgets. One out of every 50 gadgets is faulty, but the company doesn't know which ones are faulty until a buyer complains. Suppose the company makes a $3 profit on the sale of any working gadget, but suffers a loss of $80 for every faulty gadget because they have to repair the unit. Can the company expect a profit in the long term? *
Yes, they can expect a profit.
No, they will lose money in the long term.
Math
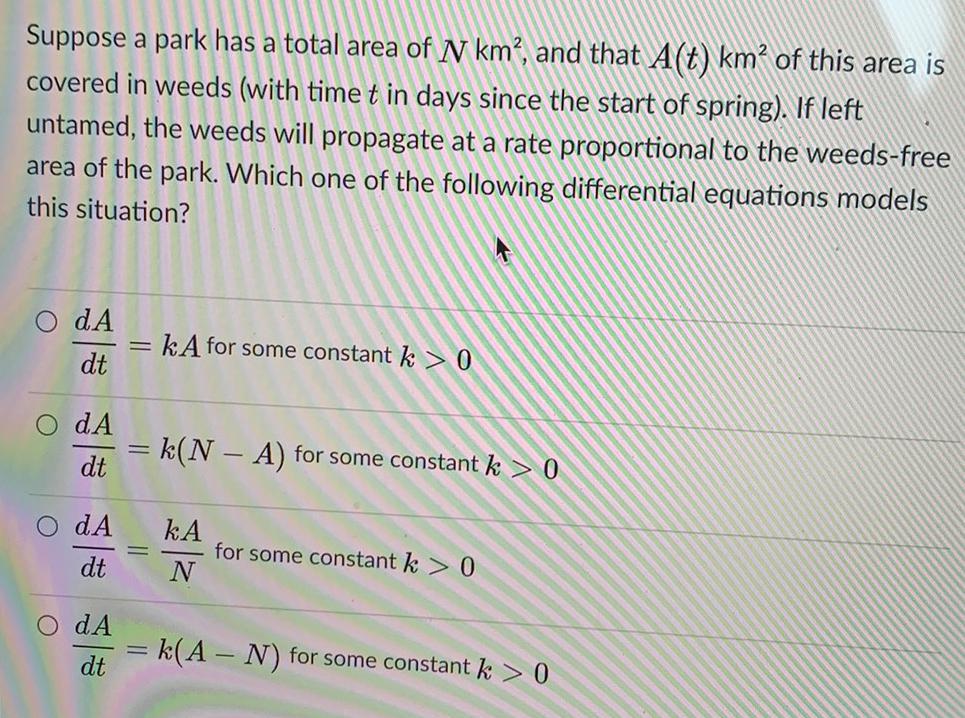
Differential equationsSuppose a park has a total area of N km², and that A(t) km² of this area is
covered in weeds (with time t in days since the start of spring). If left
untamed, the weeds will propagate at a rate proportional to the weeds-free
area of the park. Which one of the following differential equations models
this situation?

Math
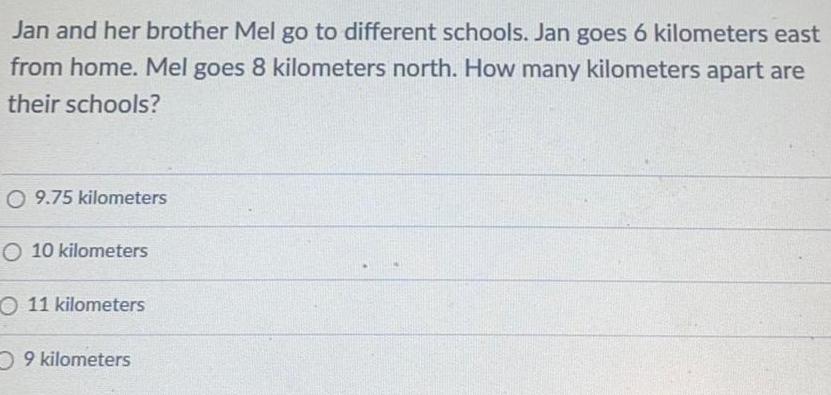
TrigonometryJan and her brother Mel go to different schools. Jan goes 6 kilometers east from home. Mel goes 8 kilometers north. How many kilometers apart are their schools?
9.75 kilometers
10 kilometers
11 kilometers
9 kilometers

Math
Probability32% of college students say they use credit cards because of the rewards program. You randomly select 10 college students and ask each to name the reason he or she uses credit cards. Find the probability that the number of college students who say they use credit cards because of the rewards program is (a) exactly two, (b) more than two, and (c) between two and five inclusive. If convenient, use technology to find the probabilities. )


Math
ProbabilityA 12-sided die is rolled. The set of equally likely outcomes is {1,2,3,4,5,6,7,8,9,10,11,12). Find the probability of rolling a number greater than 2.
The probability of rolling a number greater than 2 is
(Type an integer or a simplified fraction.)

Math
Basic MathYou rent an apartment that costs $1500 per month during the first year, but the rent is set to go up 11.5% per year. Write a recursive formula to show what the rent is during the nth year of living in the apartment.

Math
DifferentiationThe equation y = 664(1.031)t models the number of students in a certain state that go to out of state colleges/universities each year from 1992 through 1999, where y is the number of students that study out of state and t is the number of years after 1992. Round answers to the nearest whole student.
Assuming that the above equation remains valid in the future, estimate
1) the number of students from above that studied out of state in 2002.
2) the number of students from above that studied out of state in 2018.

Math
FunctionsWhich function defines(ƒ ÷ g)(x),
ƒ(1) = (3.6)x+2
g(x) = (3.6)³x+1
A (g ÷ f)(x) = (1.8)3x²+7+2
B. (g = f)(x) = (1.8)−2x+3
C. (g ÷ 1)(x) = (3.6)4x+3
D. (g = f)(x) = (3.6)-2x+1

Math
Basic MathWhich property should be used next in this solution process?
3x +2+3= 7 (x - 1)-4
3x+5= 7 (x-1) - 4
A Commutative Property of Addition
B. Identity Property of Multiplication
C. Associative Property of Multiplication
D. Distributive Property
Math
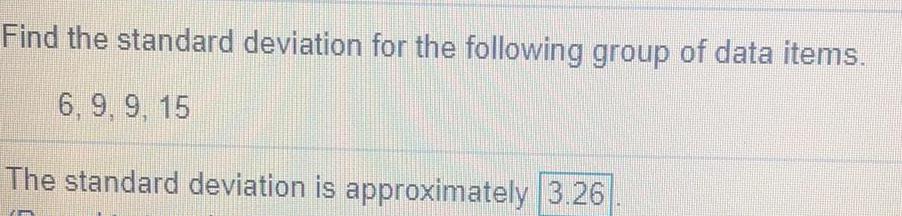
StatisticsFind the standard deviation for the following group of data items.
6, 9, 9, 15
The standard deviation is approximately

Math
Basic MathA company manufactures computers. Function represents the number of components that a new employee can assemble per day. Function E represents the number of components that an experienced employee can assemble per day. In both functions, t represents the number of hours worked in one day.
N(t) = 50t/t + 4
E(t) = 70t/t + 3
Which function describes the difference of the number of components assembled per day by the experienced and new employees?

Math
Basic MathFind the volume of a cylinder with a diameter of 8 inches and a height that is three times the radius. Use 3.14 for pl and round your answer to the nearest hundredth. (Hint: You may only enter numerals, decimal points, and negative signs in the answer blank)

Math
Basic MathSuppose the points from a class total 1000 points and are divided into 600 points on the Exams and 400 points on Homeworks. If you averaged 75% on the exams and 90% on the homeworks, what is your overall percentage? Try to answer this with rate and mixture equation that we have used in many contexts.

Math
Basic MathIdentify whether the following equation represents an exponential function.
g(x) = -22.85x - 50.75
NOT an exponential function
exponential function

Math
Application of derivativesA girl flies a kite at a height of 300 ft, and the wind carries the kite horizontally away from her at a rate of 25 ft/sec. How fast must she let out the string when the kite is 500 ft away from her?

Math
StatisticsUnder which condition is the sample proportion, P, a point estimate of the population proportion?
A. The sample proportion is never a point estimate of the population proportion.
B. The sample proportion is unbiased.
C. The sample represents a proportion of the population.
D. The sample size, n, is small enough.

Math
FunctionsThe size of a stray cat population at the bay area of a certain city grows at a rate of 8% monthly. If there are 350 stray cats currently, find how many stray cats should be expected in 24 months. Use P(t)= 350e0.08t, and let t be 24 months. (Round your answer to the nearest whole number.)
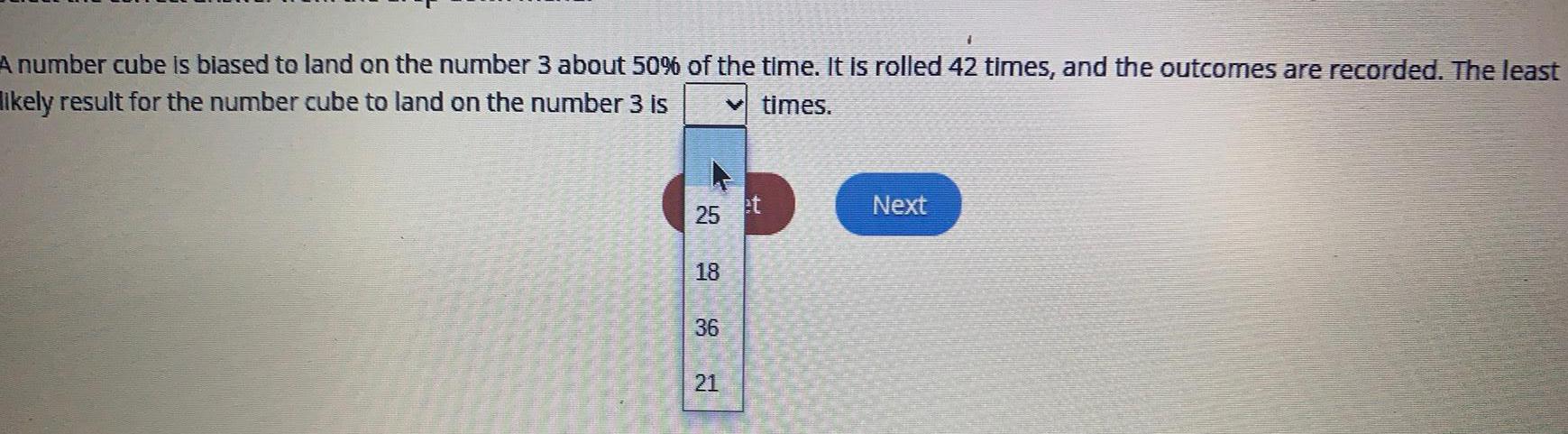
Math
ProbabilityA number cube is biased to land on the number 3 about 50% of the time. It is rolled 42 times, and the outcomes are recorded. The least likely result for the number cube to land on the number 3 is times.
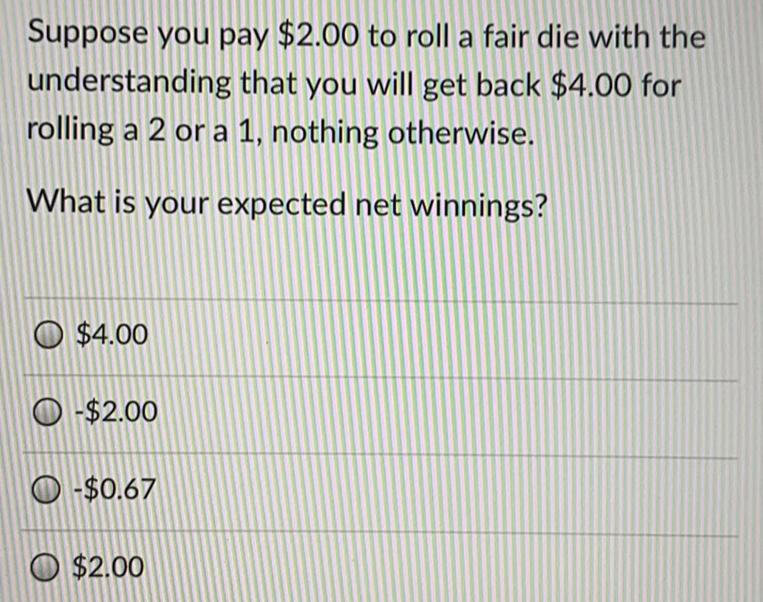
Math
Mathematical InductionSuppose you pay $2.00 to roll a fair die with the understanding that you will get back $4.00 for rolling a 2 or a 1, nothing otherwise.
What is your expected net winnings?
$4.00
-$2.00
-$0.67
$2.00

Math
Application of derivativesThe length, width, and height of a box are measured as 8 ft, 7 ft, and 6 ft, respectively, with an error in measurement of at most 0.1 ft in each. Use differentials to estimate the maximum error (in feet) in the calculated volume of the box.
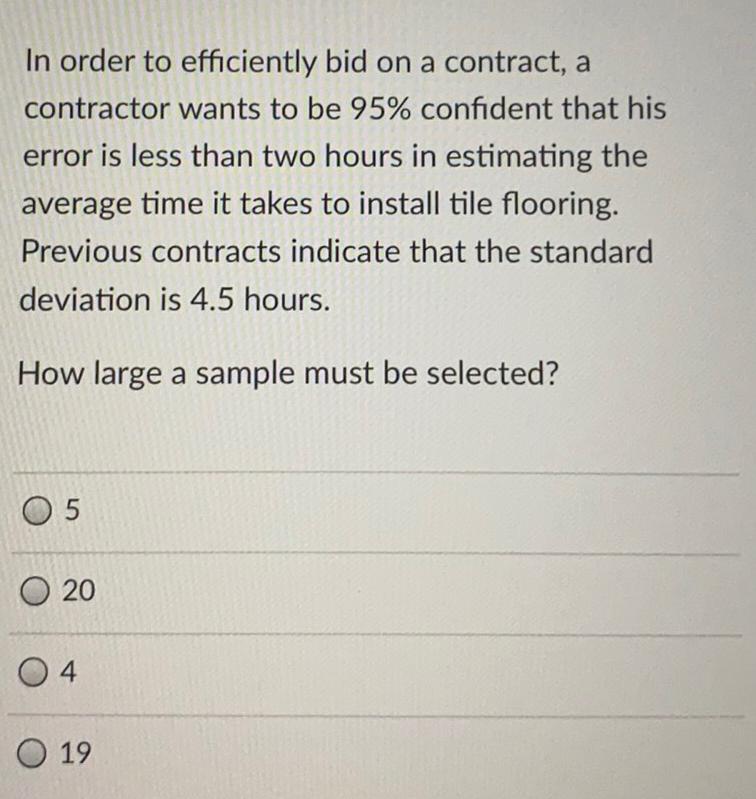
Math
Basic MathIn order to efficiently bid on a contract, a contractor wants to be 95% confident that his error is less than two hours in estimating the average time it takes to install tile flooring. Previous contracts indicate that the standard deviation is 4.5 hours.
How large a sample must be selected?
5
20
4
19
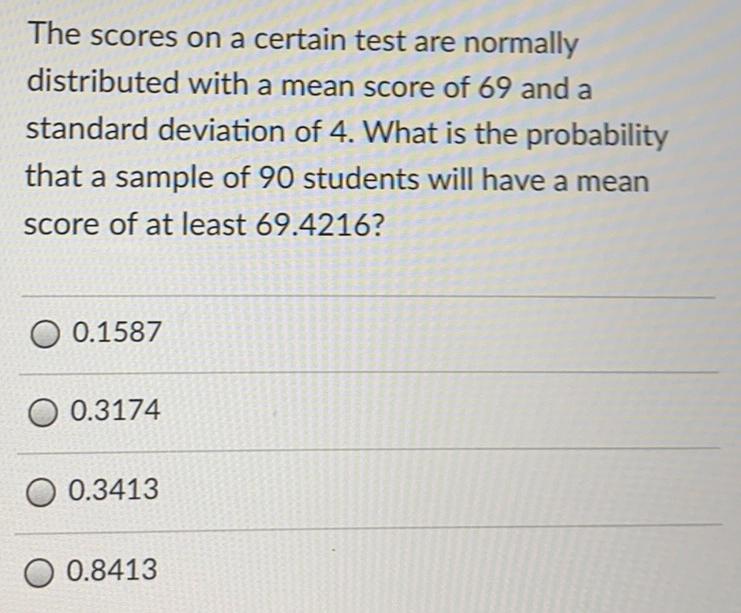
Math
ProbabilityThe scores on a certain test are normally distributed with a mean score of 69 and a standard deviation of 4. What is the probability that a sample of 90 students will have a mean score of at least 69.4216?
0.1587
0.3174
0.3413
0.8413

Math
StatisticsAt one college, the distributions of GPA's is bell- shaped with a mean of 2.8 and a standard deviation of 0.4.
According to the Empirical rule, about what percentage of students at the college have a GPA between 2.4 and 3.2?
99.74%
95.44%
84.13%
68.26%
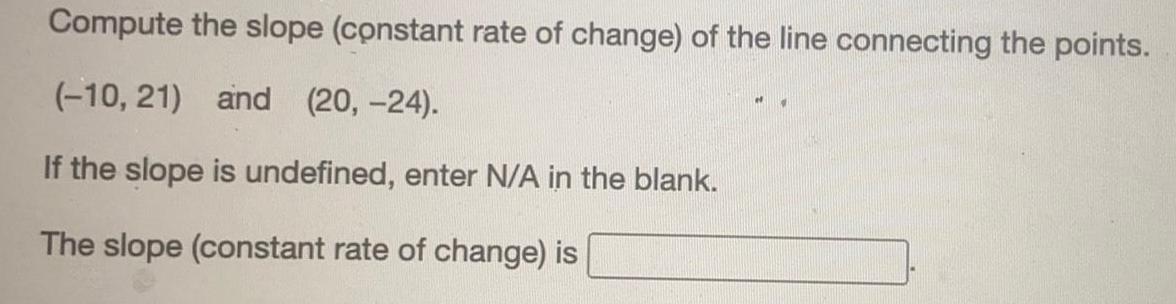
Math
Straight linesCompute the slope (constant rate of change) of the line connecting the points.
(-10, 21) and (20,-24).
If the slope is undefined, enter N/A in the blank.
The slope (constant rate of change) is

Math
Straight linesMs. Scott will pay $2,000 to have her house painted. The amount each painter earns, A, varies inversely for the number of painters, n, that will paint the house. Which equation best represents this situation?
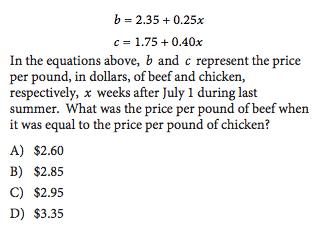
Math
Basic Mathb = 2.35 +0.25x
c = 1.75 +0.40x
In the equations above, b and c represent the price per pound, in dollars, of beef and chicken, respectively, x weeks after July 1 during last summer. What was the price per pound of beef when it was equal to the price per pound of chicken?
A) $2.60
B) $2.85
C) $2.95
D) $3.35

Math
Mathematical ReasoningHans is performing an experiment examining how salt affects the speed at which water freezes. He fills four equally sized containers with the same amounts of water. Then, In three of the containers, he stirs in varying amounts of salt. The fourth container remains plain water.
Hans places all four of the containers in the same freezer and checks the containers every five minutes, recording when the water in each container freezes solid.
In this situation, what do Hans's time measurements represent?
A the response group
B. the explanatory variable
C. the control group
D. the response variable

Math
Basic MathLook at an example of a polynomial 7x³ - 2x²+x-5, we say that the degree of this polynomial is 3, which is the highest power.
For this week's discussion, briefly explain how the degree of a divider is compared to the degree of the remainder. Divide the following expression, and compare the degree of the divider:
x+3 and the degree of the remainder: (7x3-2x²+x-5)/x + 3

Math
ProbabilityIt has been reported that 47% of the general consumer population in the United States is loyal to the automobile manufacturer of their choice. Suppose Chevrolet did a study of a random sample of 1006 Chevrolet owners and found that 490 said that they would buy another Chevrolet. Does this indicate that the population proportion of consumers loyal to Chevrolet is more than 47%? Use a = 0.01.

Math
Permutations and CombinationsOutside a home, there is a 6-key keypad with letters A, B, C, D, E and F that can be used to open the garage if the correct six-letter code is entered. Each key may be used only once. How many codes are possible?
The number of possible codes is

Math
DifferentiationA fast food restaurant estimates that the mean sodium content in one of its breakfast sandwiches is 940 milligrams. A random sample of 44 breakfast sandwiches had a mean sodium content of 944 milligrams with a standard deviation of 18 milligrams. Is there sufficient evidence to say that the sodium content is more than 940 milligrams. Use a 1% level of significance. Conduct the appropriate hypothesis test.
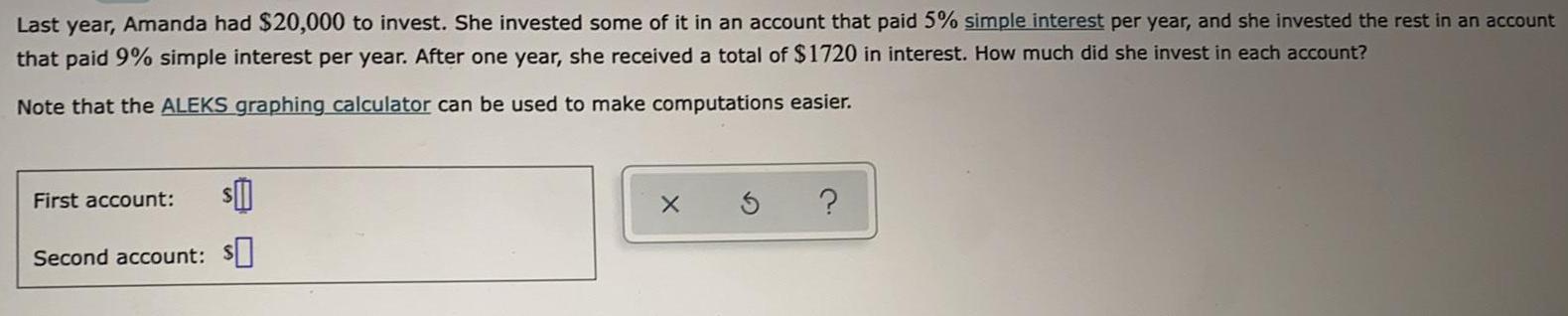
Math
Basic MathLast year, Amanda had $20,000 to invest. She invested some of it in an account that paid 5% simple interest per year, and she invested the rest in an account that paid 9% simple interest per year. After one year, she received a total of $1720 in interest. How much did she invest in each account?
Note that the ALEKS graphing calculator can be used to make computations easier.
First account: $
Second account: $

Math
StatisticsIn order to be accepted into a top university, applicants must score within the top 5% on the SAT exam. Given that the test has a mean of 1000 and a standard deviation of 200, what is the lowest possible score a student needs to qualify for acceptance into the university?
1250
1100
1329
1400

Math
Basic MathP(q) = -0.01(q-250) (q - 80)
The equation above gives the profit, P(q), in dollars, earned by a cupcake bakery when q
cupcakes are produced. What is the best interpretation of the number 80 in this context?
A 80 is a number of cupcakes for which the profit is equal to $0.
B 80 is the number of cupcakes that corresponds to the maximum profit.
C 80 is the number of cupcakes that corresponds to the minimum profit.
D $80 is the maximum profit, in dollars.

Math
TrigonometryTwo ships leave the same port at the same time. The Explorer is traveling at a bearing of N 17° W at
43 miles per hour and the Adventurer is traveling at a bearing of S 73° W at 37 miles per hour.
a) How far apart are the two ships after 3 hours of travel?
b) If the ships lay anchor after three hours and a small boat travels directly from The Explorer to the
Adventurer, at what bearing should the boat travel?

Math
Basic MathYou want to create a custom border for a picture of you and your family. The picture measures 8 inches by 10 inches. What should the width of the
picture frame be if the final area, including the picture, is three times the area of the picture by itself?
• Write answer as a number only.
Round answer to two decimal places in needed.
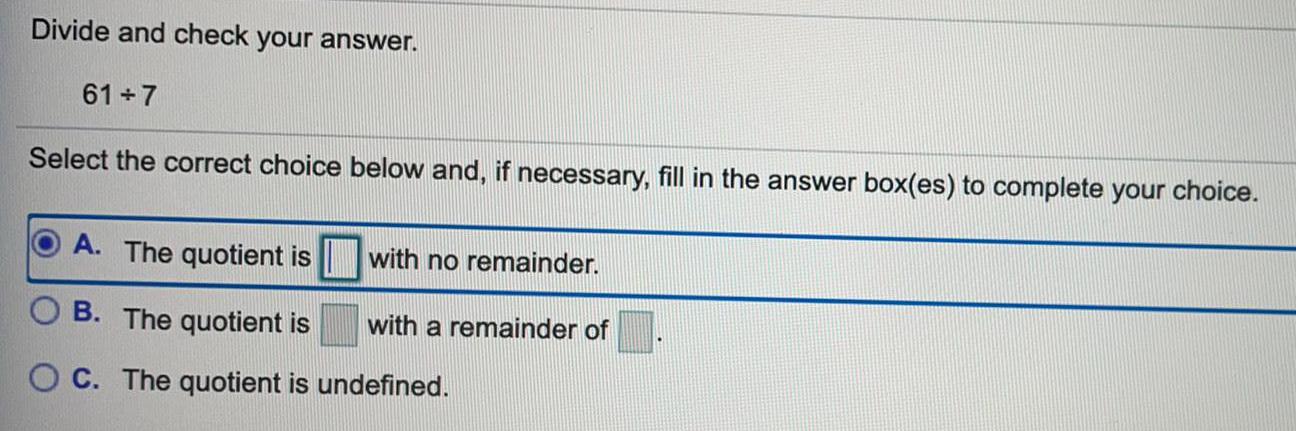
Math
Basic MathDivide and check your answer.
61+7
Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice.
A. The quotient is
with no remainder.
B. The quotient is with a remainder of
OC. The quotient is undefined.

Math
Basic MathRicardo transformed the quadratic parent function f(x) to create g(x). After the transformation, he noticed that the domain and range were the same for f(x) and g(x). Which of the following could NOT represent g(x)?
Math
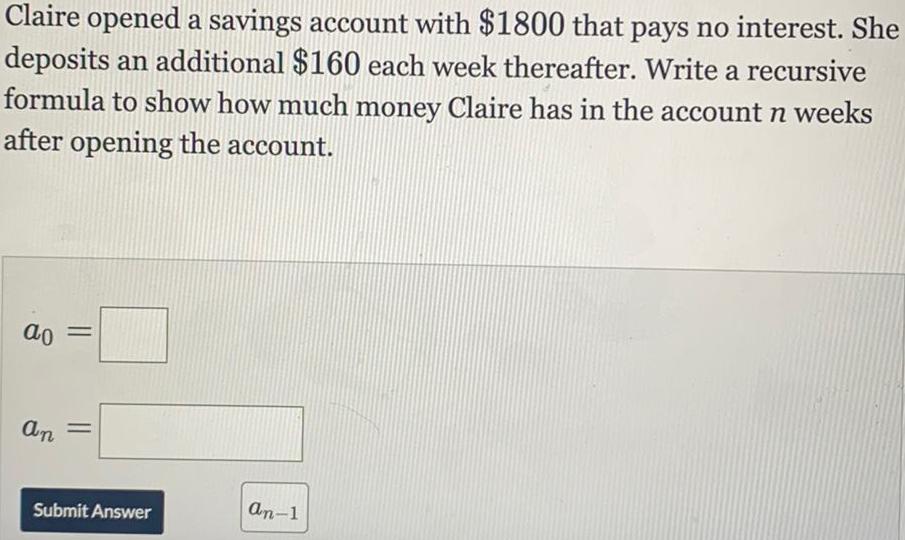
Sequences & SeriesClaire opened a savings account with $1800 that pays no interest. She
deposits an additional $160 each week thereafter. Write a recursive
formula to show how much money Claire has in the account n weeks
after opening the account.
ao =
an
Math
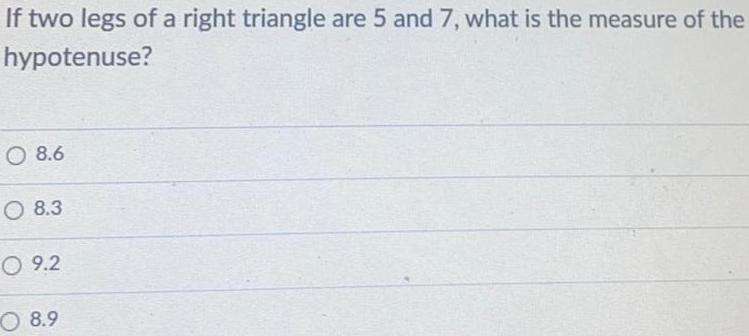
Solution of trianglesIf two legs of a right triangle are 5 and 7, what is the measure of the hypotenuse?
8.6
8.3
9.2
8.9

Math
ProbabilityA math class has 7 girls and 1 boy in the seventh grade and 2 girls and 6 boys in the eighth grade. The teacher randomly selects a seventh grader and an eighth grader from the class for a competition. What is the probability that the students she selects are both boys? Write your answer as a fraction in simplest form.

Math
FunctionsIdentify the independent and dependent variables for the given linear situation.
Write an equation that represents the linear relationship between the variables.
Use the equation to answer the question. Be prepared to show how you used the function equation to answer the question.
Situation: There is a linear relationship between the price a shop charges for a product and the quantity of that product that will sell at that price. If the
shop charges $6 for a t-shirt, they will sell 27 of them that week. If the shop charges $14 for a t-shirt, they will sell only 3 of them that week.
Question: How much did the shop charge for a t-shirt if they sold 45 t-shirts in one week?
Round final answers to the nearest cent if rounding is necessary.
Answer: They charged $