Math Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Math
Basic Math4. (Like 2003 Exit) Myesha makes hand-painted pots. Her overhead costs are $650 per week, and she pays an additional $12 per pot in material costs. What will be her total expenses if she sells 50 pots this week.
A $250
B $650
C $1250
D $1650

Math
StatisticsThe heights of adult men in America are normally distributed, with a mean of 69.3 inches and a standard deviation of 2.63 inches. The heights of adult women in America are also normally distributed, but with a mean of 64.4 inches and a standard deviation of 2.52 inches.
a) If a man is 6 feet 3 inches tall, what is his z-score (to two decimal places)?
Z=
b) What percentage of men are SHORTER than 6 feet 3 inches? Round to nearest tenth of a percent.
%
c) If a woman is 5 feet 11 inches tall, what is her z-score (to two decimal places)?
Z=
d) What percentage of women are TALLER than 5 feet 11 inches? Round to nearest tenth of a percent.
%

Math
Basic MathYou pick a card from a deck. If you get a face card (J,Q,K), you win $5. If you get an ace, you win $30 plus an extra $60 for the ace of hearts. For any other card you win nothing. Find the expected value you will win. *

Math
StatisticsThe number of cartoons watched by Mrs. Kelly's first grade class on Saturday morning is shown below:
X P(x)
0 0.15
1 0.20
2 0.30
3 0.10
4 0.20
5 0.05
Find the probability that a student watches at most two cartoons.
0.85
0.20
0.35
0.65

Math
Basic MathJustin opened a savings account with $900 that pays no interest. He deposits an additional $190 each week thereafter. How much money would Justin have in the account 30 weeks after opening the account?

Math
Permutations and CombinationsHow many different arrangements of 4 letters can be formed if the first letter must be W or K (repeats of letters are allowed)?
There are different 4-letter combinations that can be formed. (Simplify your answer.)

Math
Permutations and CombinationsLicense plates in a particular state display 2 letters followed by 2 numbers. How many different license plates can be manufactured for this state?
There are different license plates that can be manufactured for this state.

Math
ProbabilityThe probability that a tennis set will go to a tiebreaker is 16%. In 420 randomly selected tennis sets, what is the mean and the standard deviation of the number of tiebreakers?
mean: 67.2; standard deviation: 8.2
mean: 63; standard deviation: 7.51
mean: 67.2; standard deviation: 7.51
mean: 63; standard deviation: 8.2

Math
Basic MathDakota wants cover his patio with concrete pavers. If the patio is shaped like a trapezoid whose bases are 16 feet and 18 feet and whose height is 14 feet, how many square feet of pavers will he need?

Math
Basic Math2. A student bought a pair of sunglasses in the USA and paid $35.50. In England, an
identical pair of sunglasses costs £26.99. The exchange rate is £1 = $1.42. In which
country were the sunglasses cheaper, and by how much?
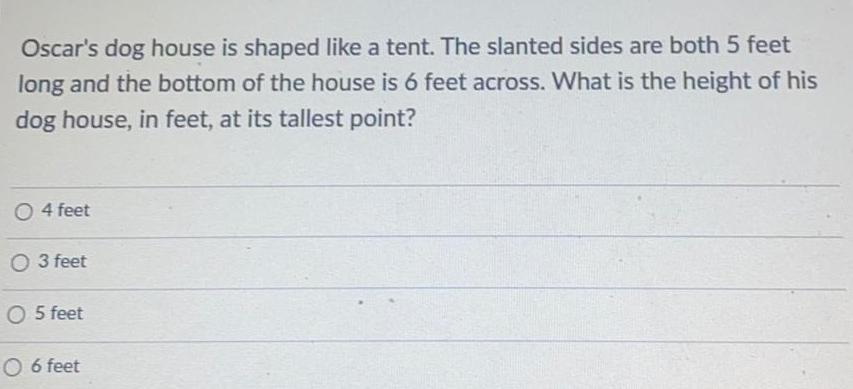
Math
Basic MathOscar's dog house is shaped like a tent. The slanted sides are both 5 feet
long and the bottom of the house is 6 feet across. What is the height of his
dog house, in feet, at its tallest point?
4 feet
3 feet
5 feet
6 feet

Math
Basic Math7) It takes a hose 5 minutes to fill a rectangular aquarium 9 inches long, 10 inches wide, and 13
inches tall. How long will it take the same hose to fill an aquarium measuring 1.5 feet by 2 feet by
2.5 feet?

Math
ProbabilityA doctor gives a patient a 60% chance of surviving bypass surgery after a heart attack. If the patient survives the surgery, then the patient has a 25% chance that the heart damage will heal. Find the probability that the patient survives the surgery and the heart damage heals.
The probability is

Math
Basic MathA survey of 2450 golfers showed that 281 of them are left-handed. Use this data to construct a 98% confidence interval for the proportion of golfers that are left- handed.
(0.369, 0.451)
(0.203, 0.293)
(0.100, 0.130)
(0.683, 0.712)

Math
Basic MathA random sample of 40 students has a mean annual earnings of $3120 and a population standard deviation of $677. Use this sample data to construct a 95% confidence interval for the population mean, μ, of all student earnings.
($2910, $3330)
($1987, $2346)
($4812, $5342)
($210, $110)
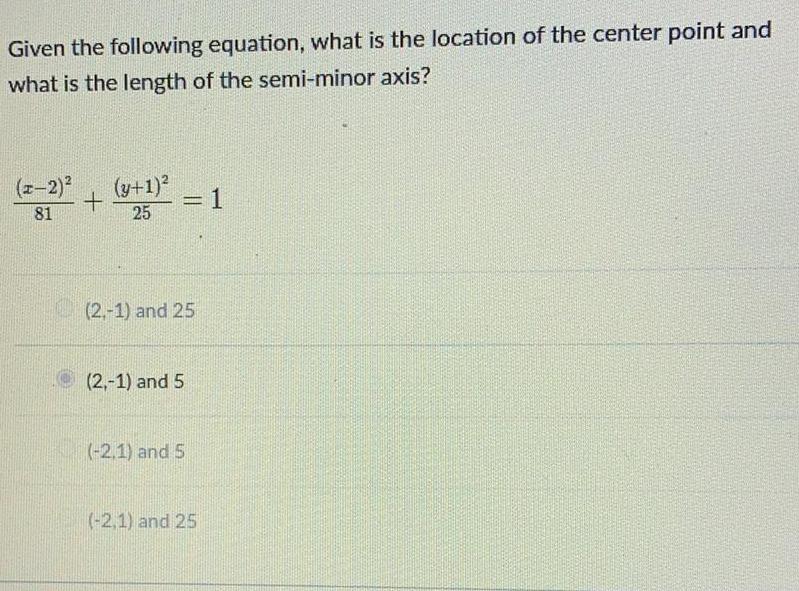
Math
EllipseGiven the following equation, what is the location of the center point and what is the length of the semi-minor axis?
(x-2)²/81 + (y+1)²/25 =1
(2,-1) and 25
(2,-1) and 5
(-2,1) and 5
(-2,1) and 25
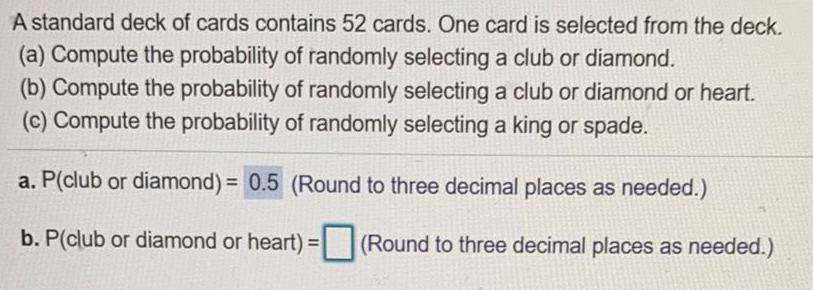
Math
ProbabilityA standard deck of cards contains 52 cards. One card is selected from the deck.
(a) Compute the probability of randomly selecting a club or diamond.
(b) Compute the probability of randomly selecting a club or diamond or heart.
(c) Compute the probability of randomly selecting a king or spade.
a. P(club or diamond) = 0.5 (Round to three decimal places as needed.)
b. P(club or diamond or heart) = (Round to three decimal places as needed.)

Math
StatisticsThe population of rabbits on an island is growing exponentially. In the year 2001, the population of rabbits was 2400, and by 2004 the population had grown to 2900. Predict the population of rabbits in the year 2012, to the nearest whole number.

Math
Basic MathAn object is dropped from a tower, 166 ft above the ground. The object's height above ground t sec into the fall is s=166-16t²
a. What is the object's velocity, speed, and acceleration at time t?
b. About how long does it take the object to hit the ground?
c. What is the object's velocity at the moment of impact?
The object's velocity at time t is

Math
Basic MathA class has 35 students. In how many different ways can six students form a group for an activity?
(Assume the order of the students is not important.)
There are different ways that the six students can form a group for an activity.
(Type a whole number.)

Math
ProbabilityA small corporation must appoint four officers (a president, a chief executive officer, a chief operating
officer, and a chief financial officer). It must also appoint a Strategic Planning Committee with four people on
it. There are a total of 9 qualified candidates, and the chosen officers may also serve on the committee.
(a) How many different ways can the four officers be appointed?
(b) How many different ways can the committee of four be appointed?
(c) What is the probability of randomly selecting the committee members and getting the four youngest of the
qualified candidates?

Math
Quadratic equationsWhich of the following shows that polynomials are closed under addition when two polynomials 4x + 6 and 2x²-8x-4 are added? (1 point)
a. 2x²-4x+2 will be a polynomial
b. 2x²-4x+2 may or may not be a polynomial
c. 2x²-12x-10 will be a polynomial
d. 2x²-12x-10 may or may not be a polynomial

Math
FunctionsSal is running on a treadmill at the gym. He is going to run for 7 miles at a constant speed of 1 mile per 8 minutes.
Graph the distance Sal will run as a function of time.
y= 1/8 x+0

Math
Statistics6 calculate how much you can borrow with a $800 per month payment at today's mortgage rates and determine if it would be enough money to purchase the home you selected in #4. Do this for BOTH loans.
a. For a 30-year mortgage. State your findings in a complete sentence.

Math
FunctionsFind the end behavior of the following polynomial: f(x)=-7(x-11)^3(x+13)³(x+2)(x-3)5
As x → ∞, f(x)→→ -∞
As x→ -∞, f(x) → ∞
As x→∞, f(x)→∞
As x→ -∞, f(x) → ∞
As x→ -∞, f(x) → -∞
As x→→ -∞, f(x)→ -∞
As x→ ∞, f(x) → ∞
As x→ -∞, f(x) → -∞

Math
StatisticsA sample of 14 squirrels were found to have an average weight of 9.8 ounces
with a sample standard deviation is 0.30.
Use this data to find the 95% confidence interval of the true mean weight.
(9.59, 10.01)
(8.92, 10.68)
(9.63, 9.97)
(9.72, 9.88)

Math
Basic MathThe expression is given in standard form. Rewrite it in factored form. If it cannot be rewritten in factored form, write "cannot be done."
p² + 18p-40
a (p-20)(p+2)
b (p+20)(p+2)
c (p+20)(p-2)
d (p-20)(p-2)

Math
Application of derivativesThe original 24 m edge length x of a cube decreases at the rate of 5 m/min.
a. When x = 5 m, at what rate does the cube's surface area change?
b. When x = 5 m, at what rate does the cube's volume change?
a. When x = 5 m, the surface area is changing at a rate of m²/min.
(Type an integer or a decimal.)

Math
Basic MathA long year-end status report for work is 82 pages long. You need to print 19 copies for a meeting next week. How much is the paper going to cost for those reports? Paper is sold in reams (500 pages) for $3.99 each. Give your answer to the nearest cent, only for the paper you use (partial reams are OK)

Math
Basic MathEvery year in Delaware there is a contest where people create cannons and catapults designed to launch pumpkins as far in the air as possible. The equation y = 15 + 110x -16x² can be used to represent the height, y, of a launched pumpkin, where x is the time in seconds that the pumpkin has been in the air. What is the maximum height that the pumpkin reaches? How many seconds have passed when the pumpkin hits the ground? (Hint: If the pumpkin hits the ground, its height is 0 feet.)

Math
ProbabilityYou randomly select an integer from 0 to 24 (inclusively) and then randomly select an integer from 0 to 39 (inclusively). What is the probability of selecting an 18 both times?

Math
FunctionsWhich of the following describes the zeroes of the graph of f(x) = 3x6 + 30x5 + 75x4?
-5 with multiplicity 2 and 1/3 with multiplicity 4
5 with multiplicity 2 and 1/3 with multiplicity 4
-5 with multiplicity 2 and 0 with multiplicity 4
5 with multiplicity 2 and 0 with multiplicity 4
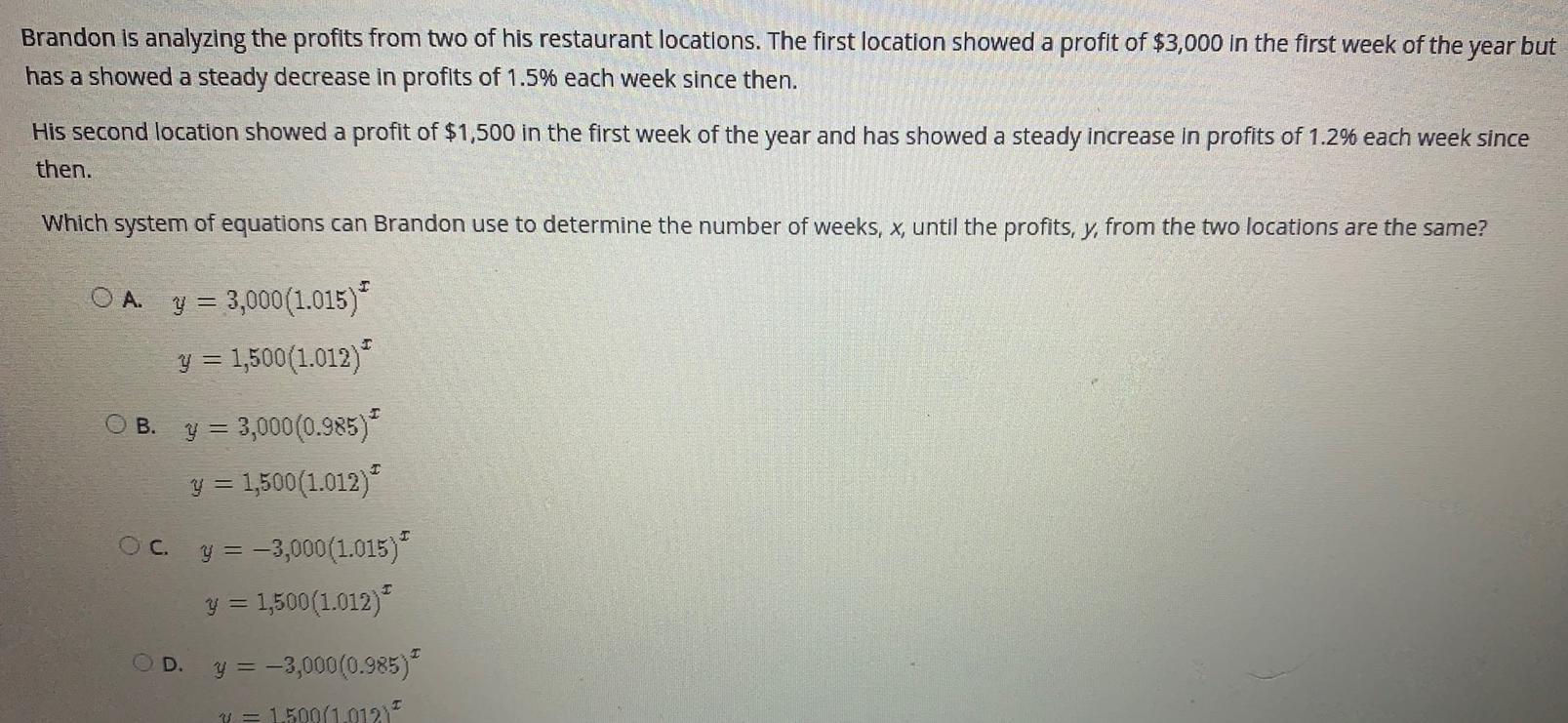
Math
Basic MathBrandon is analyzing the profits from two of his restaurant locations. The first location showed a profit of $3,000 in the first week of the year but has a showed a steady decrease in profits of 1.5% each week since then.
His second location showed a profit of $1,500 in the first week of the year and has showed a steady increase in profits of 1.2% each week since then.
Which system of equations can Brandon use to determine the number of weeks, x, until the profits, y, from the two locations are the same?
A. y = 3,000 (1.015)^x
y = 1,500 (1.012)^x
B. y = 3,000(0.985)^x
y = 1,500(1.012)^x
C. y = -3,000 (1.015)^x
y = 1,500(1.012)^x
D. y = -3,000(0.985)^x
Y = 1,500/(1,012)^x

Math
StatisticsA tire company tested a particular model of super radial tire and found the tires to be normally distributed with respect to wear. The "average" (mean) tire wore out at 59,000 miles, and the standard deviation was 2500 miles.
a. If 2000 tires are tested, about how many are likely to wear out before 54,000 miles?
b. What if the company wanted to guarantee 55,000 miles? What percent of the tires are likely to wear out before 55,000 miles? In this case, you cannot get an "exact" answer. What could you do to increase the accuracy of your estimate?

Math
Basic MathAlma bought a laptop computer at a store that gave a 20 percent discount off its original price. The total amount she paid to the cashier was p dollars, including an 8 percent sales tax on the discounted price. Which of the following represents the original price of the computer in terms of p?
A) 0.88p
B) p / 0.88
C) (0.8) (1.08) p
D) p / (0.8) (1.08)
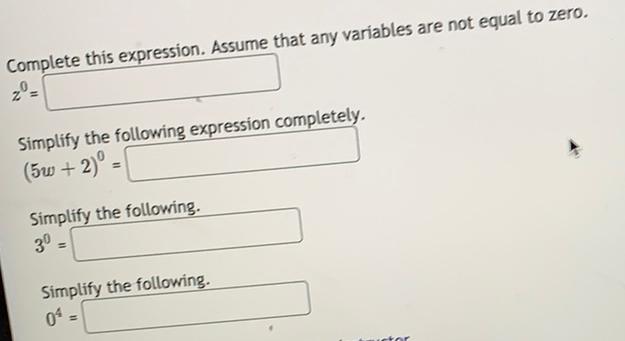
Math
Basic MathComplete this expression. Assume that any variables are not equal to zero.
z⁰ =
Simplify the following expression completely.
(5w+2)⁰ =
Simplify the following.
3⁰ =
Simplify the following.
0⁴ =

Math
StatisticsSuppose you and your brother each invest $5000 in a bank account. Both banks offer 6.5% annual interest. However, your brother's account is compounded annually, while yours is compounded monthly.
a. How much do each of you have in your accounts after 3 years?
b. How much more is your account worth than your brother's after 100 years? Find the Absolute difference (one is this many dollars more than the other) and the relative difference (one is this percent more than the other).
c. What is the r ='annual percentage yield' for the account that is compounded monthly?

Math
StatisticsA report states that 42% of home owners had a vegetable garden. How large a sample is needed to estimate the true proportion of home owners who have vegetable gardens to within 3% with 96% confidence?
672
1142
336
571

Math
StatisticsAn insurance company will insure a $220,000 home for its total value for an annual premium of
$510.
The company spends $30 per year to service such a policy, and the probability of total loss for such a home in a given year is 0.001.
Assuming that either total loss or no loss will occur, what is the company's expected annual
gain (or profit) on each such policy?
-$220
$260
$290
$210

Math
Basic MathFactor each trinomial. Then match the polynomial (term) on the left with its factored form (definition) on the right.
Column A Column B
1. x²-8x-20 a. Prime
2. x²+8x-20 b. (x-2)(x+10)
3. x² - x-20 c. (x-10)(x + 2)
4. x²-9x-20 d. (x - 5)(x+4)

Math
Coordinate systemThe parent cosine function is shifted 5 units left, then vertically stretched by a factor of 4 and shifted up 2 units. Which statement is true about the graph of the transformed function?
A. The midline is y = 2.
B. The midline is y = 4.
C. The midline is y = 8.
D. The midline is y = 5.

Math
FunctionsThe monthly rent for a pizza parlor is $1,200. The average production cost per pizza is $6.75. The monthly expenses for the pizza parlor are given by the function E(x) = 1,200 +6.75x, where x is the number of pizzas sold. For x pizzas sold, the pizza parlor's revenue is given by the function R(x) = 12.5x
The monthly profit of the pizza parlor is the difference between its revenue and its expenses. Which function represents the monthly profit, P(x) ?
A. P(x) =5.75x + 1,200
B. P(x) = 1,200 + 19.25x
C. P(x) = 6.25x - 1,200
D. P(x) = 5.75x - 1,200

Math
FunctionsBetty has a checking account and a non-interest-bearing savings account. Function Crepresents her checking account balance, where x is the number of months. Function S represents her saving account balance.
C(x) = -|240x -140| + 1,400
S(x) = 450x + 100
Which function represents Betty's total account balance, T(x)?
A. T(x) = -|240x - 140| + 450x + 1,500
B. T(x) = -|240x - 140| + 450x + 1,400
C. T(x) = |240x + 140| +450x + 1,500
D. T(x) = -|240x - 140| +450x + 1,300

Math
Basic MathThe function h defined by h(t) + (49+4.9t) (10-t) models the height, in meters, of an object t seconds after it is dropped from a helicopter.
From what height is the object dropped?
a 500
b 490
c 480
d 460

Math
AreaGiven a soda can with a volume of 36 and a diameter of 4, what is the volume of a cone that fits perfectly inside the soda can? (Hint: only enter numerals in the answer blank). (4 points)

Math
AreaA piece of cardboard is being used to make a container that will have no lid. Four square cutouts of side length h will be cut from the corners of the cardboard. The container will have a square base of side s, height h, and a volume of 80 in³. Which is the correct order of steps for finding minimum surface area A of the container?
s²h = 80 and A = s² + 4sh
I. A'=2s - 320/s²
II. 0=2s - 320/s²
III. A = s² + 320/s²
s = 5.429 in and h = 2.714 in
I, III, II
III, I, II
III, II, I
I, II, III

Math
Basic MathA car company tested a sports car on a road with different inclines. The test driver tested the car by driving a distance of x miles on a flat road,
(x² + 3) miles downhill, and (x-7) miles uphill. Which simplified expression is equivalent to the total distance, in miles, for which the car was
tested? (2 points)
a. 3x²-4
b. 3x² +10
c. x²+2x-4
d. x²+2x+10

Math
Basic MathAnswer the following.
(a) The total surface area of Asia is approximately 17,200,000 square miles. Write this number in scientific notation.
(b) The signal from a certain satellite takes approximately 4.1 x 10^-2 seconds to reach Earth. Write this number in standard notation.

Math
AreaA company that manufactures and ships canned vegetables is designing boxes in the shape of square prisms to meet specific requirements. The vegetables are packed into cans that are 2.5 inches in diameter and 4 inches in height. Company regulations state that boxes must be filled with two layers of 16 cans each, and be completely closed with no overlapping material. What is the smallest amount of cardboard needed to meet the company's requirements.
They will need at least inches of cardboard. square
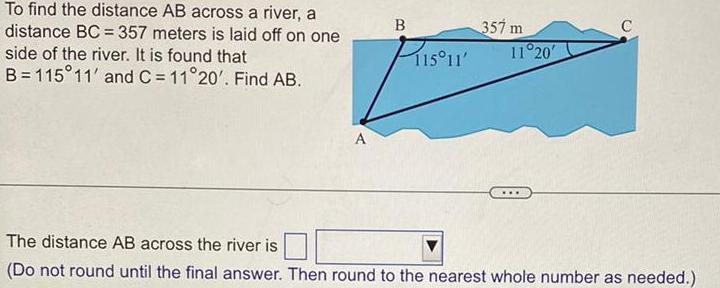
Math
Basic MathTo find the distance AB across a river, a distance BC= 357 meters is laid off on one side of the river. It is found that B=115°11' and C = 11°20'. Find AB.
The distance AB across the river is
(Do not round until the final answer. Then round to the nearest whole number as needed.)