Math Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Math
3D Geometry(b) What is the group of all symmetries of the tetrahedron, including those that
reverse orientation (and are therefore no longer rotations in 3-space)? (Hint: it's S₁. Why?)

Math
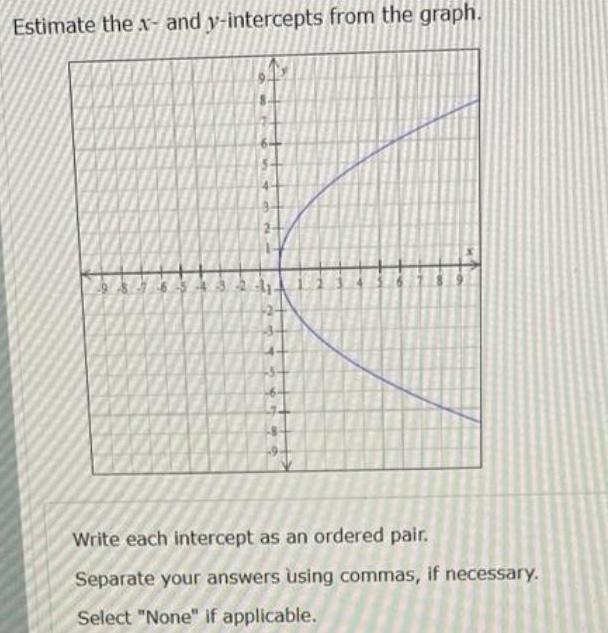
Basic MathEstimate the - and y-intercepts from the graph.
Write each intercept as an ordered pair.
Separate your answers using commas, if necessary.
Select "None" if applicable.
Math
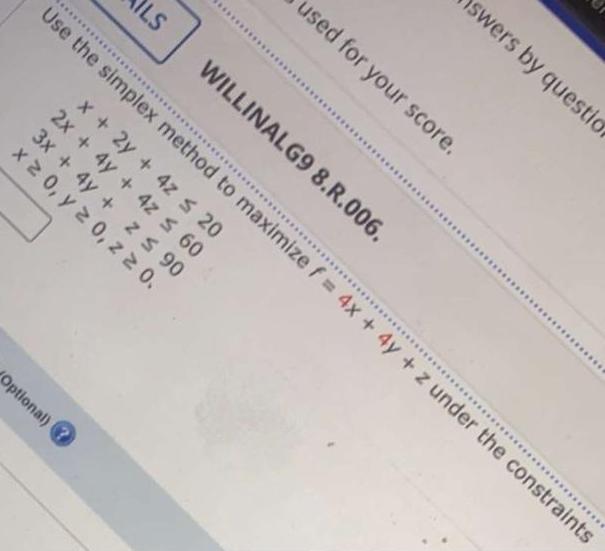
Linear ProgrammingUse the simplex method to maximize f= 4x + 4y + z under the constraints
x + 2y + 4z ≤ 20
2x + 4y + 4z ≤ 60
3x + 4y + z ≤ 90
x ≥ 0, y ≥ 0, z ≥ 0.
Math
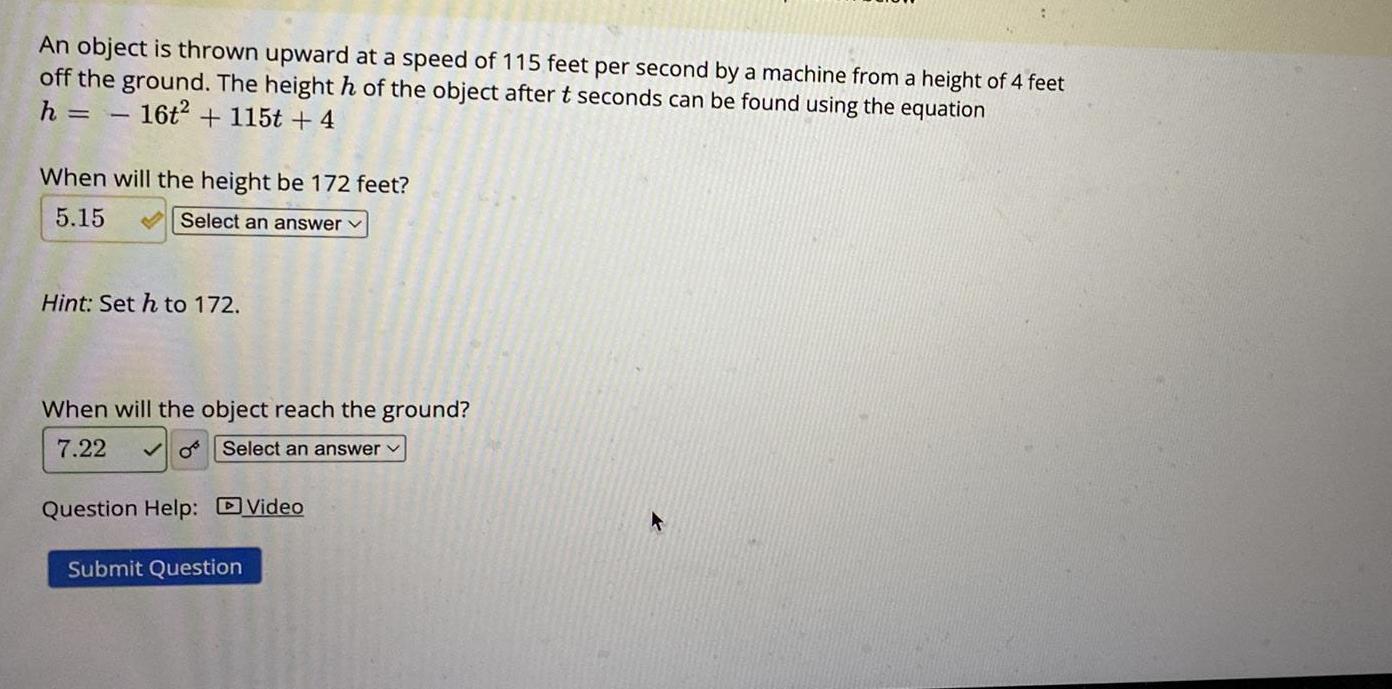
Heights and DistancesAn object is thrown upward at a speed of 115 feet per second by a machine from a height of 4 feet off the ground. The height h of the object after t seconds can be found using the equation
h = 16t² + 115t +4
When will the height be 172 feet?
Hint: Set h to 172.
When will the object reach the ground?
7.22

Math
Basic MathSome mathematics professors would like to purchase a $140 microwave oven for the
department workroom. If 5 of the professors do not contribute, everyone's share will
increase by $50. How many professors are in the department?
A) 26
B) 21
C) 14
D) 7
E) 9

Math
TrigonometryGiven right triangle ABC, right angle at C, side b = 6 inches, side c = 15 inches.
Solve the triangle completely.
Round all angles to the nearest degree and all sides to the nearest tenth of an inch.
a=
A=
B=
Math
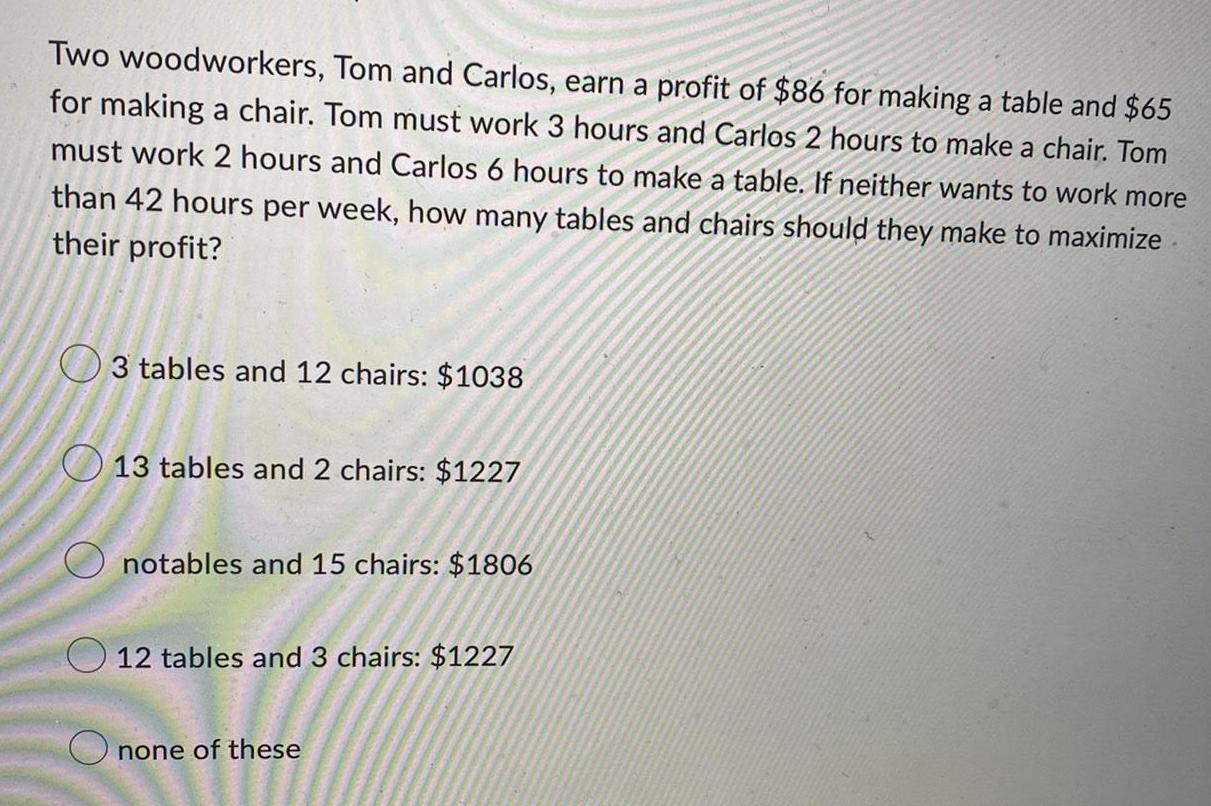
Linear ProgrammingTwo woodworkers, Tom and Carlos, earn a profit of $86 for making a table and $65
for making a chair. Tom must work 3 hours and Carlos 2 hours to make a chair. Tom
must work 2 hours and Carlos 6 hours to make a table. If neither wants to work more
than 42 hours per week, how many tables and chairs should they make to maximize
their profit?
3 tables and 12 chairs: $1038
13 tables and 2 chairs: $1227
notables and 15 chairs: $1806
12 tables and 3 chairs: $1227
none of these

Math
Basic MathYou drove 10,000 miles last year. Your expenses were $3,100 in gasoline, $150 in oil and lubrication, $780 in minor repairs, $1,900 in insurance and $60 for license and vehicle sticker. True or False: Your cost for maintaining your vehicle per mile is $0.58.
True
False

Math
Basic MathHow many solutions does the following system have?
3x - 2y + 3z = 3
9x + 3y + z = -3
-27x11z = -3
Select the correct answer below:
No solutions
1 solution
Infinitely many solutions

Math
Basic MathSketch the logarithmic function h(x)=-4 log(x+2)+4 Find two points on the graph, and determine the domain and the equation of any vertical asymptotes.
Fill in the missing coordinates of the points that lie on the graph of y= log 4 x and the corresponding points that lie on the graph of h(x)=-4 log(x+2)+4.

Math
Basic MathA new restaurant is to contain two-seat tables and four-seat tables. Fire code limits
the restaurant's maximum occupancy to 56 customers. If the owners have hired
enough servers to handle 17 tables of customers, how many of each kind of table
should they purchase?
two-seat 7; four-seat 10
two-seat 10; four-seat 7
two-seat 12; four-seat 5
two-seat 5; four-seat 12
two-seat 6; four-seat 11
two-seat 11; four-seat 6

Math
Basic MathSimplify the fraction. If the fraction is already simplified, so state.
72/88
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. 72/88= (Simplify your answer. Type a whole number or a fraction.)
B. The expression cannot be simplified.


Math
Basic MathSolve the system of equations:
4x = 3y + 8
2x - 5y = -14
(-41/7, 36/7)
(41/7, -36/7)
no solutions
infinite solutions
(41/7, 36/7)
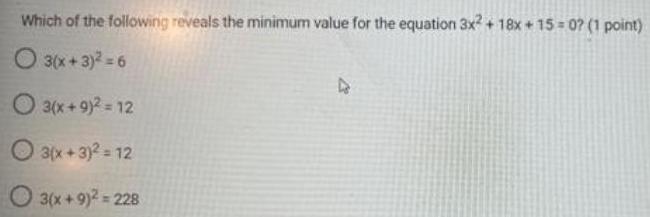
Math
Quadratic equationsWhich of the following reveals the minimum value for the equation 3x2 + 18x+15=0?
3(x+3)² = 6
3(x+9)² = 12
3(x+3)² = 12
3(x+9)² = 228

Math
FunctionsThe following models describe wages for low-skilled labor.
p = -0.325x+5.8 demand model
p = 0.375x +3 supply model
where p represents the price of labor per hour and x is the number of workers
available in millions. Determine the equilibrium number of workers, in millions,
associated with the equilibrium wage per hour.
5 million workers @ $4.88 an hour
3 million workers @ $4.12 an hour
4.5 million workers @ $4.68 an hour
4 million workers @ $4.50 an hour

Math
StatisticsDescribe the sampling distribution of p. Assume the size of the population is 30,000.
n=1300, p=0.288
Describe the shape of the sampling distribution of p. Choose the correct answer below.
A. The shape of the sampling distribution of p is approximately normal because n ≤0.05N and np(1-p) ≥ 10.
B. The shape of the sampling distribution of p is not normal because n ≤0.05N and np(1-p) ≥ 10.
C. The shape of the sampling distribution of p is approximately normal because n ≤0.05N and np(1-p) < 10.
D. The shape of the sampling distribution of p is not normal because n ≤0.05N and np(1-p) < 10.


Math
TrigonometrySuppose cos(a)=4/5, where 0 ≤ a ≤ π/2.
Find all solutions in [0, 2π):
cos(2x) = 4/5.

Math
Trigonometric equationsSuppose sin(a)= 7/10, where 0 ≤ a ≤ π/2
Find all solutions in [0, 2π):
sin(2x) = 7/10

Math
StatisticsBelow is a sample of share prices (in dollars) for a particular stock, selected at random over several years:
242 253 261 269 271 235 240 242 230
259 243 242 274 255 232 259 230 273
Use Excel (or other form of electronic assistance) to find the mean, median, mode, and standard deviation for this sample. Round answers to the nearest tenth.
Mean =
Median =
Mode =
Standard Deviation =
Using the Empircal Rule, what percent of values would be 235.4 or less?
%
What percent of values would be 281 or more?
%
If you haven't answered the question correctly in 3 attempts, you can get a hint.

Math
Basic MathFind all angles between 0 and 360° such that sec =2.705. Round to the nearest degree.
a) Find the reference angle.
b) Determine the Quadrants in which the solutions are in
c) Find the angles in the two quadrants, rounded to the nearest degree.
Be sure to type your answers to all parts in the answer box. Be sure to show all work on loose leaf as a file upload question at the end.

Math
Coordinate systemConsider the function: f(x) = x² + 8x - 20
The direction of the graph is like which of the following:
The y-intercept is at y =
The x-intercepts are at x =
The vertex is at the point
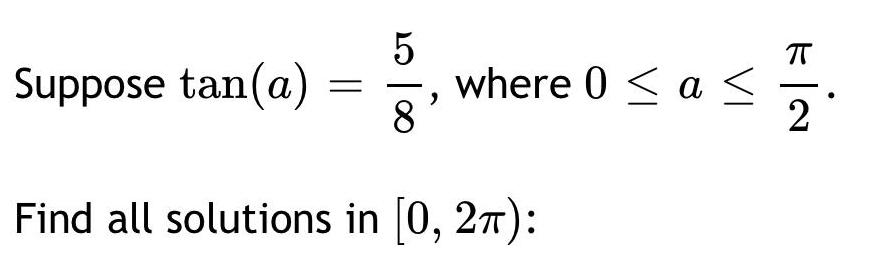

Math
Basic MathThe table below shows the number of individuals infected with a disease t days after its first detected by the CDC.
For each of the following problems, enter regression equation values with at least 3 decimal places. Enter predictions to the nearest whole individual.
1) Use regression to find an exponential equation that best fits the data above. The equation has form y =
abt where:
a =
b=
Use the model to predict the number of individuals infected with the disease after 16 days.
individuals
2) Use regression to find a linear equation that best fits the data above. The equation has form
y = mt + b where:

Math
StatisticsA research center claims that 31% of adults in a certain country would travel into space on a commercial flight if they could afford it. In a random sample of 1000 adults in that country, 35% say that they would travel into space on a commercial flight if they could afford it. At a = 0.01, is there enough evidence to reject the research center's claim? Complete parts (a) through (d) below.
(a) Identify the claim and state Ho and Ha
Identify the claim in this scenario. Select the correct choice below and fill in the answer box to complete your choice.
(Type an integer or a decimal. Do not round.)
A. % of adults in the country would travel into space on a commercial flight if they could afford it.
B. The percentage adults in the country who would travel into space on a commercial flight if they could afford it is not
C. At least % of adults in the country would travel into space on a commercial flight if they could afford it.
D. No more than % of adults in the country would travel into space on a commercial flight if they could afford it.
Let p be the population proportion of successes, where a success is an adult in the country who would travel into space on a commercial flight if they could afford it. State Ho and H₂. Select the correct choice below and fill in the answer boxes to
complete your choice.
(Round to two decimal places as needed.)
A. Ho: P
Ha:p=
D. Ho: P
H₂: p
B. Ho: P<
H₂: p2
E. Ho: p2
H₂: p<
C. Ho:p>
Haps
F. Ho: PS
H₂:p>
(b) Use technology to find the P-value.
Identify the standardized test statistic.
Z=

Math
Basic MathPick the system of inequalities satisfied by the point (-4,2).
y< x +7 and y> 7x-3
y>-x+7 and y> 7x-3
y> -x + 7 and y <7x - 3

Math
Quadratic equationsConsider the parabola given by the equation:
y = 1x² + 14x - 33
Find the following for this parabola:
A) The vertex = (
B) The y intercept is the point (0,
C) Find the two values of a that correspond to the intercepts of the parabola and write them as a list, separated by commas:

Math
StatisticsProfessor Ivy has the following scores on her final exam:
76, 51, 81, 57, 62, 70, 98
41, 50, 100, 86, 93, 48
Compute the values indicated below. Express your answers rounded to the nearest tenth.
Mean:
Standard Deviation:
Use the 68-95-99.7 Rule to answer the following question.
What is the probability of an exam score more than 49.9 ?
Express your probability answer as a decimal.
If you haven't answered the question correctly in 3 attempts, you can get a hint.


Math
Basic MathWillie bought a CD for $16.95 and eight blank videotapes. The total cost was $52.55 excluding the tax. Find the cost of each blank videotape.
$4.45
$5.35
$3.25

Math
TrigonometryIf construction costs are $156,000 per kilometer, find the cost of building the new road in the figure shown to the right.
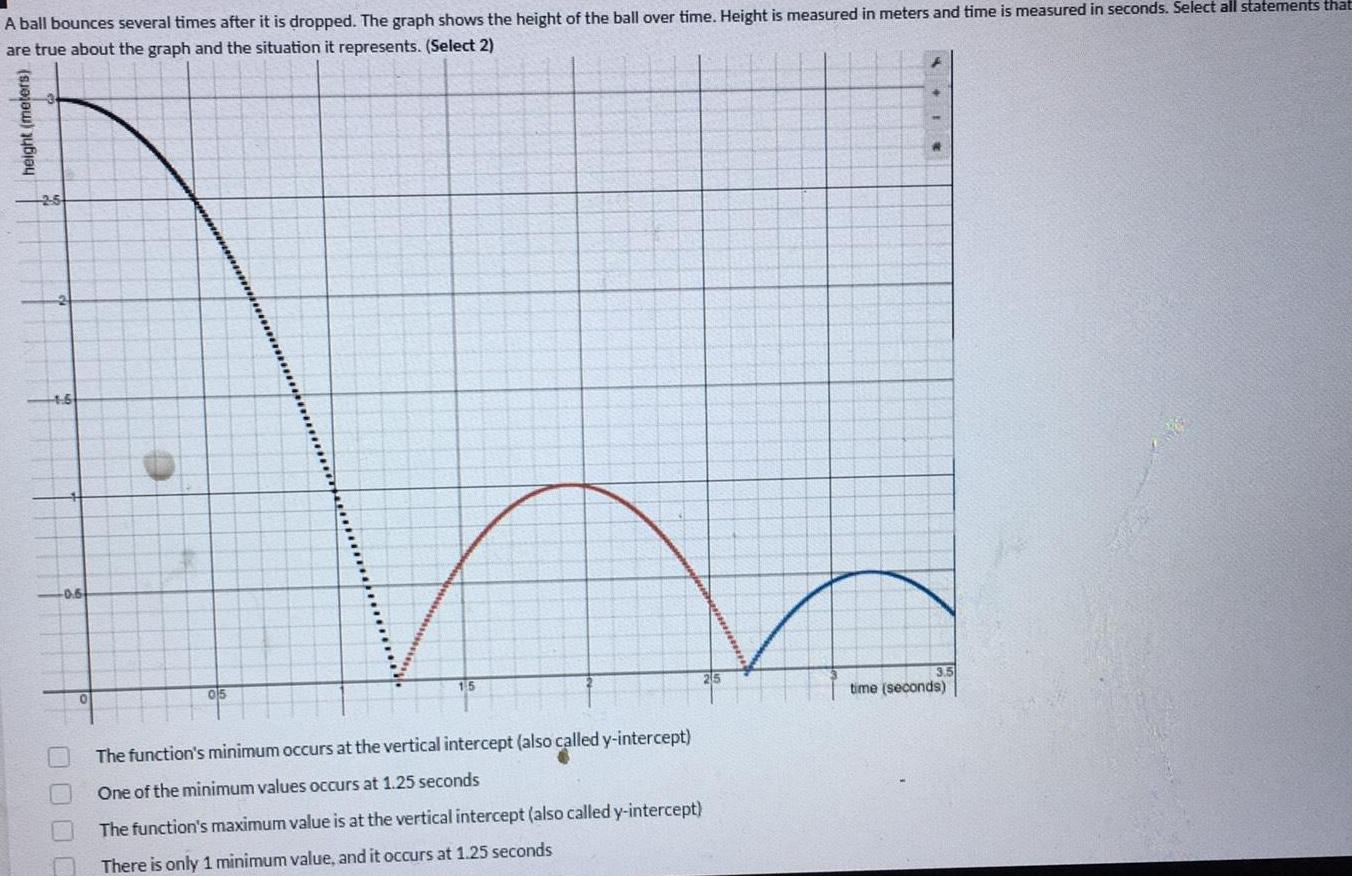
Math
Application of derivativesA ball bounces several times after it is dropped. The graph shows the height of the ball over time. Height is measured in meters and time is measured in seconds. Select all statements that are true about the graph and the situation it represents.
The function's minimum occurs at the vertical intercept (also called y-intercept)
One of the minimum values occurs at 1.25 seconds
The function's maximum value is at the vertical intercept (also called y-intercept)
There is only 1 minimum value, and it occurs at 1.25 seconds

Math
Basic MathThe volume of a cone is 113.04 mm2. What is the approximate volume of a sphere that has the same height and a circular base with the same diameter? Use 3.14 for π and round to the nearest hundredth.
113.04 mm³
226.08 mm³
904.32 mm³
3,052 mm³

Math
ParabolaUse the information provided to write the vertex form equation of each parabola.
Vertex: (-7,-5), Focus: (-7,-41/8)
y = (x +9) ² - 7
y = 2(x - 5)² +7
y- 1/2(x-5)²-7
y = -2(x+7)² - 5
y = 1/2( x − 4 )² + 6
![Suppose g (z) = -(z − a)³ (z - b)²(z − 1)². Describe the graph of g (z)
a. The graph the x-axis at x = d.
b. The graph [zero2] the x-axis at x = b.
c. The graph [zero3] the x-axis at x = 1.
d. At the ends, the graph (end).](https://media.kunduz.com/media/sug-question/raw/77312392-1660470183.0140185.jpeg?w=256)
Math
FunctionsSuppose g (z) = -(z − a)³ (z - b)²(z − 1)². Describe the graph of g (z)
a. The graph the x-axis at x = d.
b. The graph [zero2] the x-axis at x = b.
c. The graph [zero3] the x-axis at x = 1.
d. At the ends, the graph (end).

Math
Basic MathIdentify the number of solutions the following equation has: 7-5(z-6) +4=3-2(z-5)-3z +28.
No Solution
Unique Solution
Infinitely Many Solutions

Math
Application of derivativesConsider the function f(x) = 5x² - 10x + 1, 0≤x≤ 8.
The absolute maximum of f(x) (on the given interval) is at
x =
and the absolute maximum of f(x) (on the given interval) is
The absolute minimum of f(x) (on the given interval) is at
x=
and the absolute minimum of f(x) (on the given interval) is
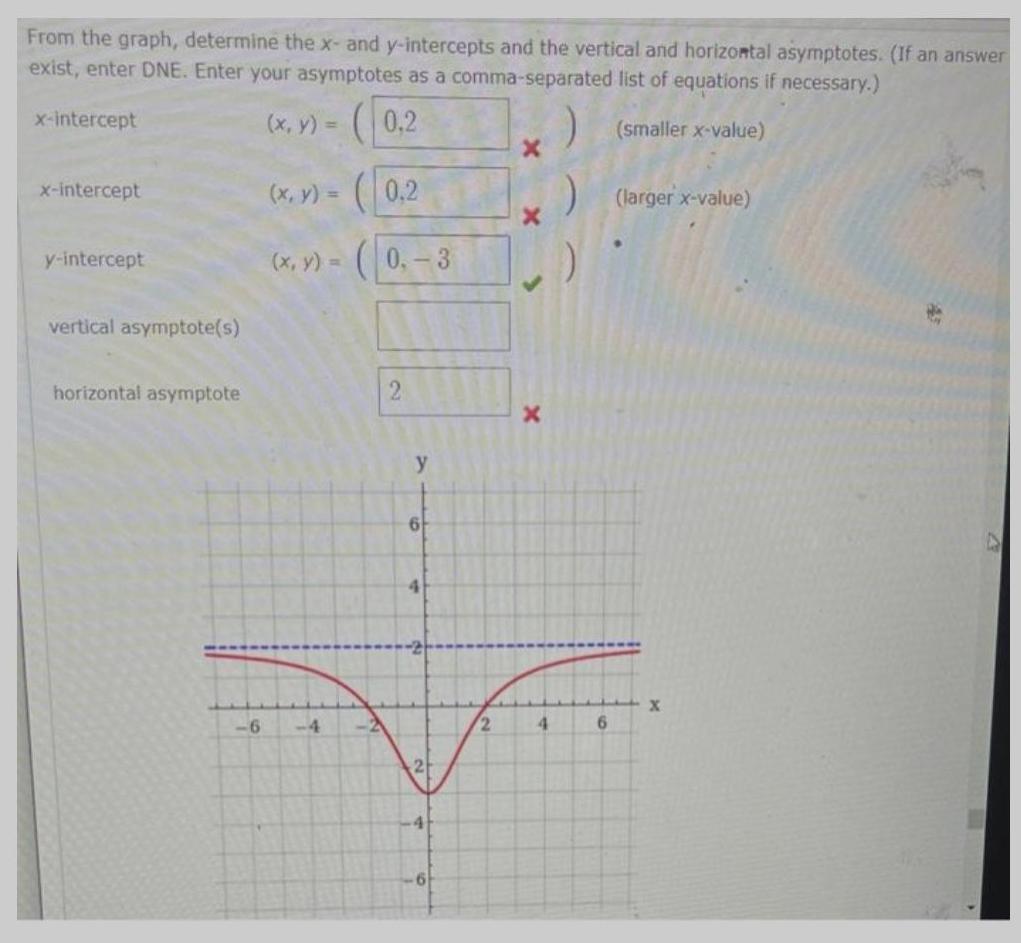
Math
FunctionsFrom the graph, determine the x- and y-intercepts and the vertical and horizontal asymptotes. (If an answer exist, enter DNE. Enter your asymptotes as a comma-separated list of equations if necessary.)
x-intercept (x, y) = (0,2 (smaller x-value)
x-intercept
y-intercept
vertical asymptote(s)
horizontal asymptote

Math
TrigonometrySketch the angle and write the sec and tan of the angle if the terminal side of the angle passes through (3, -6). Express each answer as a decimal rounded to the nearest hundredth.
Be sure to type your answers to all parts in the answer box. Be sure to show all work on loose leaf as a file upload question at the end.

Math
ProbabilitySuppose the random variable is best described by a normal distribution with μ = 20 and a = 8.2. Find the z-score that corresponds to each of the following a values.
Express your answers rounded correctly to the hundredths place.
(a) x = 15
z=
(b) x = 32
z=
(c) x= 10
z=
(d) x = 25
z=
(e) x= 25
z=
(f) x=17
z=

Math
3D GeometryThe diagram represents a regular pentagonal pyramid. The measurements unit is feet. (Round your answers to two decimal places.)
(a) Find the area of the base.
ft²
(b) Find the lateral area of the pyramid.
ft²
(c) Find the surface area of the pyramid.
ft²
(d) Find the volume of the pyramid.
ft3

Math
Quadratic equationsA person standing close to the edge on top of a 112-foot building throws a ball vertically upward. The quadratic function h(t)=16t² +96t+ 112 models the ball's height about the ground, h(t), in feet, t seconds after it was thrown.
a) What is the maximum height of the ball?
b) How many seconds does it take until the ball hits the ground?

Math
StatisticsA simple random sample of size n = 15 is obtained from a population with µ = 67 and σ = 17.
(a) What must be true regarding the distribution of the population in order to use the normal model to compute probabilities involving the sample mean? Assuming
that this condition is true, describe the sampling distribution of x.
(b) Assuming the normal model can be used, determine P(x < 70.9).
(c) Assuming the normal model can be used, determine P(x ≥ 68.3).
(a) What must be true regarding the distribution of the population?
A. The population must be normally distributed and the sample size must be large.
B. Since the sample size is large enough, the population distribution does not need to be normal.
C. The sampling distribution must be assumed to be normal.
D. The population must be normally distributed.

Math
StatisticsnSeveral years ago, 51% of parents with children in grades K-12 were satisfied with the quality of education the students receive. A recent poll found that 495 of 1,095 parents with children in grades K-12 were satisfied with the quality of education the students receive. Construct a 90% confidence interval to assess whether this represents evidence that parents' attitudes toward the quality of education have changed.
Find the 90% confidence interval.
The lower bound is 0.485
The upper bound is 0.535
(Round to three decimal places as needed.)
What is the correct conclusion?
A. Since the interval contains the proportion stated in the null hypothesis, there is sufficient evidence that parents' attitudes toward the quality of education
have changed.
B. Since the interval contains the proportion stated in the null hypothesis, there is insufficient evidence that parents' attitudes toward the quality of education
have changed.
C. Since the interval does not contain the proportion stated in the null hypothesis, there is sufficient evidence that parents' attitudes toward the quality of
education have changed.
D. Since the interval does not contain the proportion stated in the null hypothesis, there is insufficient evidence that parents' attitudes toward the quality of
education have changed.

Math
Basic MathWhich of the following represents vector t = -8i + 6j in trigonometric form?
t= 10 (cos 36.87°, sin 36.87°)
t= 10 (cos 143.13°, sin 143.13%)
t= 10 (sin 36.87°, cos 36.87°)
t= 10 (sin 143.13°, cos 143.13%)

Math
Sequences & SeriesDetermine whether the following statement is true or false, and explain why.
In a Markov chain, the outcome of an experiment depends only on the present state and not on any past states.
Is the statement true or false?
A. True.
B. False. In a Markov chain, the outcome of an experiment depends on past states found using transition matrice
C. False. In a Markov chain, the outcome of an experiment depends on past states found using probability vector
D. False. In a Markov chain, the outcome of an experiment depends on both past and present states.

Math
StatisticsThe average daily volume of a computer stock in 2011 was μ = 35.1 million shares, according to a reliable source. A stock analyst believes that the stock volume in
2018 is different from the 2011 level. Based on a random sample of 30 trading days in 2018, he finds the sample mean to be 32.1 million shares, with a standard
deviation of s = 12.3 million shares. Test the hypotheses by constructing a 95% confidence interval. Complete parts (a) through (c) below.
(a) State the hypotheses for the test.
Ho: µ ≠ 35.1 million shares
H₁: µ = 35.1 million shares
(b) Construct a 95% confidence interval about the sample mean of stocks traded in 2018. million shares and million shares.
With 95% confidence, the mean stock volume in 2018 is between
(Round to three decimal places as needed.)
(c) Will the researcher reject the null hypothesis
A. Do not reject the null hypothesis because μ = 35.1 million shares falls in the confidence interval.
B. Do not reject the null hypothesis because μ = 35.1 million shares does not fall in the confidence interval.
C. Reject the null hypothesis because μ = 35.1 million shares does not fall in the confidence interval.
D. Reject the null hypothesis because μ = 35.1 million shares falls in the confidence interval

Math
Straight linesGraph each of the lines in the following system to find the solution.
y = -2x + 6
y=-3x+9