Math Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Math
Coordinate systemDetermine the slope and intercepts of the graph below.
Vertical Intercept
Horizontal Intercept

Math
TrigonometryChoose all the right statements. Use Capital Letters ONLY. If you choose more than one letters, please arrange them in alphabetical order, please.
A. cos 2A = cos² A- sin² A
B. cos 2A = (cos A-sin A) (cos A + sin A)
C. cos 2A = 2 cos² A-1
D. cos 2A = 1-2 sin² A
E. cos 2A = cos² A+ sin² A

Math
Basic MathThree times a first number decreased by a second number is one. The first number increased by twice the second number is twelve. Determine the numbers.
6 and 12
0 and 12
-2 and -7
1 and 2
2 and 5

Math
Basic Mathwhere P is the power (in watts) and vis the velocity of the wind (in mph). Determine the velocity of the wind when the windmill is generating 600 watts of power.
A) v = 965.42 mph
B) v 19.88 mph
C) v = 31.07 mph
D) v = 173.19 mph
E) v = 37.28 mph

Math
Basic MathAngelize wants to buy pumpkin and autumn squash for a fall display. She has a budget of no more than $117 but wants to buy more than 10 vegetables for the decorations. The pumpkins are $5.50 each and the autumn squash are $3.50 each.
Identify the possible solution below to Angelize's situation.
8 pumpkins and 4 squash
4 pumpkins and 5 squash
15 pumpkins and 11 squash
5 pumpkins and 5 squash
CE

Math
Basic MathDetermine the pattern and complete the table. Then write a formula to describe then relationship between the input and output variables.
Math
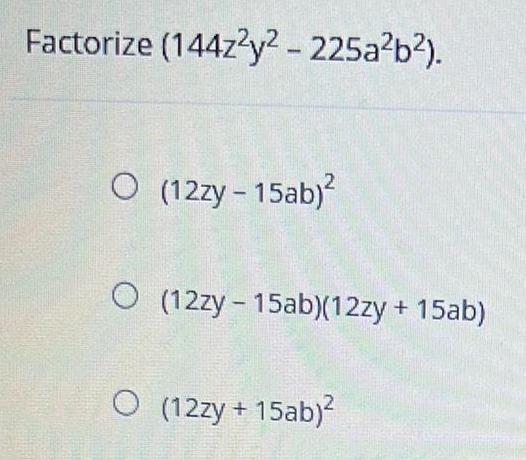
Quadratic equationsFactorize (144z2y² - 225a²b²).
(12zy - 15ab)²
(12zy-15ab)(12zy + 15ab)
(12zy + 15ab)²

Math
Basic MathSolve the system of equations-
10x - 5y = 5
80x+7y=181
Ono solutions
(2, 3)
(5,0)
(-2, -3)
(-1, 6)
infinite solutions
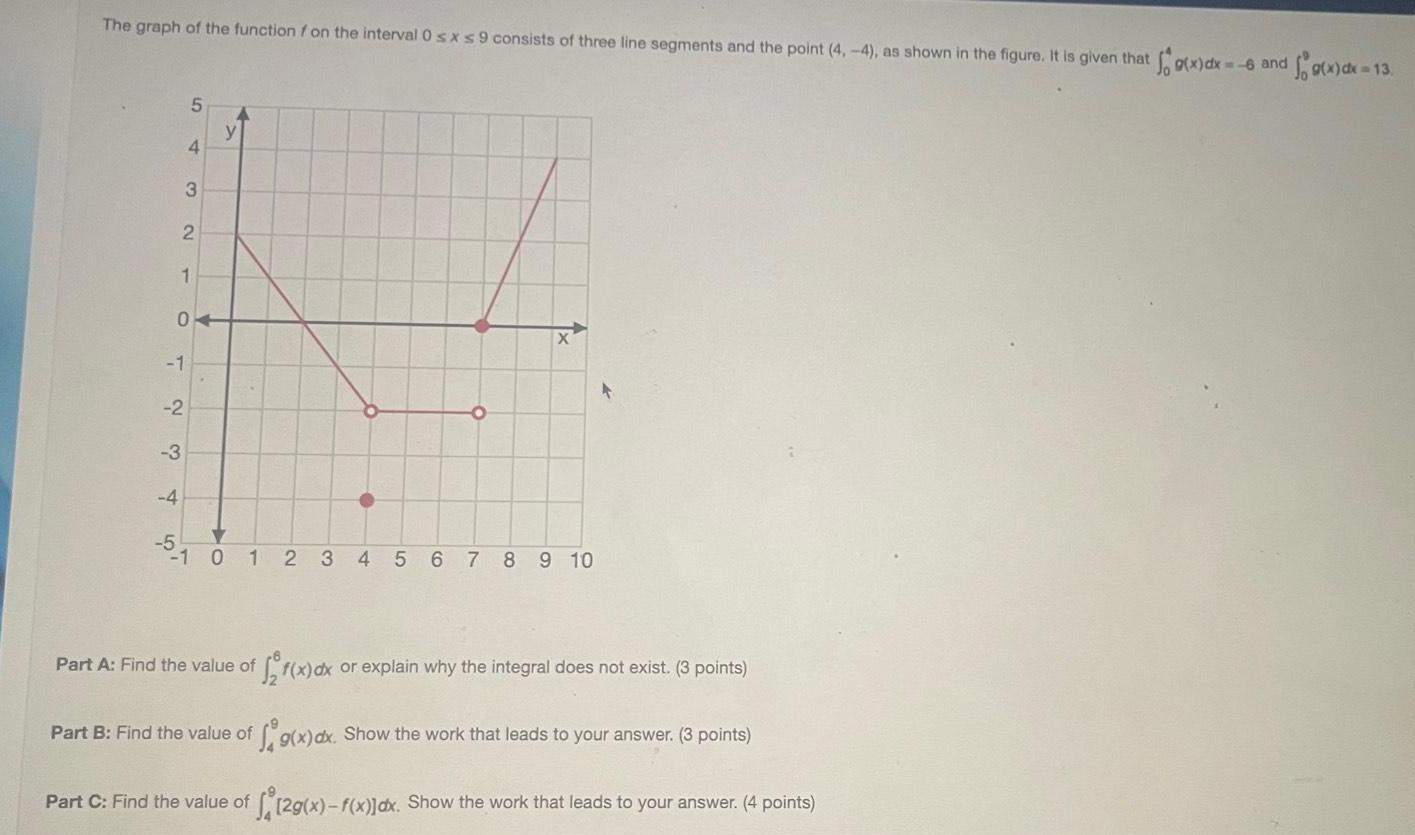
Math
Definite IntegralsThe graph of the function f on the interval 0 s x s9 consists of three line segments and the point (4,-4), as shown in the figure. It is given that
Sog(x) dx =
Find the value of
Part B: Find the value of
Part C: Find the value of
f5₂f(x) dx or explain why the integral does not exist. (3 points) g(x) dx. Show the work that leads to your answer.

Math
Complex numbersFind zw and Write each answer in polar form and in exponential form.
The product zw in polar form is
and in exponential form is

Math
Differential equationsSolve the initial value problem x'(t) = Ax(1) for 120, with x(0)=(3,1) Classify the nature of the origin as an attractor, repeller, or saddle point of the dynamical system described by x¹=Ax. Find the directions of greatest attraction and/or repulsion
2 -4
6-8
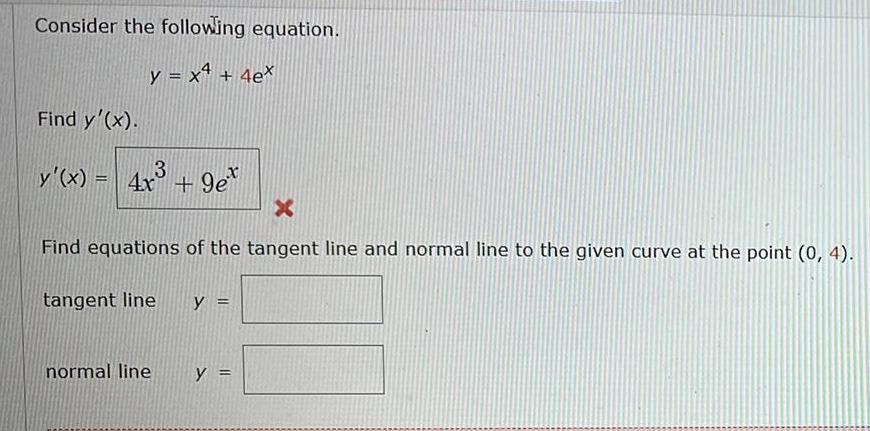
Math
Basic MathConsider the following equation.
y = x² + 4e^x
Find y'(x).
y'(x) = 4x³ + 9e^x
Find equations of the tangent line and normal line to the given curve at the point (0, 4).
tangent line
normal line

Math
AreaFor the regions A and B shown in the graph:
Part A: Discuss the limits of integration. (3 points)
Part B: Set up an integral expression that represents the total area. (4 points)
Part C: Calculate the total area. (3 points)

Math
Differential equations5. Consider differential equation
dy/dx + (2/x) y = xy³, y(1) = 1/2
Find y(10) numerically using the following methods and h = 0.5, 0.25, 0.125 and calculate
the errors in each case. You have to use MATLAB for this problem. (10 Points each)
a. Forward Euler's method
b. Backward Euler's method
c. Modified Euler's method
d. Improved Euler's method
e. Fourth-Order Runge Kutta Method

Math
Solution of trianglesUse Heron's Area Formula to find the area of the triangle. (Round your answer to two decimal places.)
A = 80°, b = 74, c = 42

Math
Basic MathA volleyball team sold raffle tickets to raise money for the upcoming season. They sold three different types of tickets: premium for $10, deluxe for $4, and regular for $2. The total number of tickets sold was 208, and the total amount of money from raffle tickets was $714. If 78 more regular tickets were sold than deluxe tickets, how many premium tickets were sold?

Math
Definite IntegralsA graph consists of the line y=5 for 1 sxs 5 and y=-1 for-3 sxs 1. Find the accumulation of change under the curve from x=-3 to x = 5 using geometric formule
-4 square units
4 square units
16 square units
24 square units

Math
Basic MathWhen talking about budgets, what should ALWAYS be the inequality symbol?
everything you're buying ≤ Total
everything you're buying < Total
everything you're buying > Total
everything you're buying ≥ Total

Math
Basic MathTwo buses, which are 2400 miles apart, travel towards each other. Their speeds differ by 60 miles per hour. They pass each other after 5 hours. Find their speeds.
210, 270
220, 270
250, 250

Math
Sequences & SeriesA bottle contains 95 milliliters of lemon extract solution. If. the extract contains 25 milliliters of alcohol, what is the volume percent (v/v) of the alcohol in the solution? Make sure to include a correct unit symbol with the answer choice.

Math
Basic MathYou decide to begin selling glow sticks at the local star wars convention. Your cost for each glow stick is $0.59 plus you have to pay a fixed weekly fee of $220 for the booth. Your plan is to sell each glow stick for $2.59.
1. Write an algebraic expression to represent your total costs for the week if you sell n glow sticks.
Total Costs:
2. Write an algebraic expression to represent the revenue from the sale of n glow sticks during the week.
Revenue:
3. Write an algebraic expression that represents the profits for selling n glow sticks in a given week.
Profit
If you sell 300 items, your total costs for the week will be $
Your revenue from selling 300 glow sticks is $
Your profit for selling 300 glow sticks is $

Math
CircleGraph the equation to find symmetry. (Let 0 ≤ θ< 2π. Select all that apply.) r = 7 The graph is symmetric with respect to θ = 2π The graph is symmetric with respect to the polar axis. The graph is symmetric with respect to the pole. The graph has no symmetry.

Math
DifferentiationSuppose that f(4) = 3, g(4) = 4, f'(4) = -5, and g'(4) = 2. Find h'(4).
(a) h(x) = 3f(x) + 2g(x)
h'(4) =
(b) h(x) = f(x)g(x)
h'(4) =
(c) h(x) =f(x)/g(x)
h'(4) =
(d) h(x) =(g(x))/(f(x) + g(x))
h'(4) =

Math
Basic MathJuan had $21600 and chose to split the money into two different mutual funds. During the first year, Fund A earned 8% interest and Fund B earned 6% interest. If he received a total of $1504 in interest, how much had he invested into each account?
Juan invested $ into Fund A.
Juan invested $ into Fund B.

Math
Basic MathIdentify the type of solution of the equation x + 4 = x+3. Unique solution No solution Infinite solutions

Math
StatisticsSuppose a survey of 551 women in the United States found that more than 63% are the primary investor in their household. Which part of the survey represents the descriptive branch of statistics? Make an inference based on the results of the survey.
Choose the best statement of the descriptive statistic in the problem.
A. 63% of women in the sample are the primary investor in their household.
B. There is an association between the 551 women and being the primary investor in their household.
C. There is an association between U.S. women and being the primary investor in their household.
D. 551 women were surveyed.
Choose the best inference from the given information.
A. There is an association between the 551 women and being the primary investor in their household.
B. 63% of women in the sample are the primary investor in their household.
C. There is an association between U.S. women and being the primary investor in their household.
D. 551 women were surveyed.


Math
StatisticsA random sample of 225 observations were selected from a population with a mean μ = 20 and variance σ2 = 144.
Find mean and standard deviation of the sampling distribution of the sample mean.
mean = 20, s.d. = 12
mean = 20, s.d. = 0.64
mean = 0.9, s.d. = 0.8
mean = 20, s.d. = 0.8
mean = 0.9, s.d. = 12

Math
Basic MathCompute the sum of all the solutions of the equation I2x−2/xI = 1 8 A) -4/3 B) 8/3 c) -8 D) 8 E) 38/3

Math
ProbabilityThe theoretical probability of a coin landing heads up is Does this probability mean that if a coin is flipped two times, one flip will land heads up? If not, what does it mean?
Choose the correct answer below.
A. No, it means that if a coin was flipped many times, at most 1/2 of the tosses would land heads up.
B. Yes, it means that if a coin was flipped two times, at least one of the tosses would land heads up.
C. No, it means that if a coin was flipped many times, about 1/2 of the tosses would lands heads up.
D. Yes, it means that if a coin was flipped two times, exactly one of the tosses would land heads up.

Math
Basic MathDetermine all the solutions of the equation. Give the sum of all the solutions. √9x+4= √7x+8 A) O B) 8 C) 2 D) -2 E) -8

Math
Basic MathSteinway piano should be placed in an environment where the relative humidity h is between 36% and 62%. Express this range with an inequality containing an absolute value. A) h + 13% ≤ 49% B) h-49% ≤ -13% C) h-49% ≤ 13% D) |h + 13% < 49% E) |h-49% > 13%

Math
Straight linesGraph the linear function by finding x- and y-intercepts. Then write the equation using function notation.. 2x - 4y= -4

Math
Basic MathWe are interested in the first few Taylor Polynomials for the function f(x) = 3e + 7e * centered at a a=0. To assist in the calculation of the Taylor linear function, T₁(x), and the Taylor quadratic function, T₂(x), we need the following values: f(0) = ƒ'(0) f''(0) = Using this information, and modeling after the example in the text, what is the Taylor polynomial of degree one: T₁(x) = What is the Taylor polynomial of degree two: T₂(x) =

Math
StatisticsThe null and alternative hypotheses are given. Determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed. What parameter is being tested? Ho: 0 = 5 H₁: 0 # 5 What type of test is being conducted in this problem? Left-tailed test Right-tailed test Two-tailed test

Math
Basic MathThe payments of a lease are $190 a month for 60 months. Jessica paid a deposit of $580, a title fee of $95, and a license fee of $65. At the end of the lease she can buy the car for a residual value of $3,900. True or False: The total cost if she buys the car at the end of the lease is $16,040.

Math
Mathematical ReasoningDetermine whether the variable is qualitative or quantitative. Explain your reasoning. Age of car driven Is the variable qualitative or quantitative? A. The variable is quantitative because age describes an attribute or characteristic. B. The variable is quantitative because age is found by measuring or counting. C. The variable is qualitative because age is found by measuring or counting. D. The variable is qualitative because age describes an attribute or characteristic.

Math
Basic MathMaude and Matilda each have a bank CD. Maude's is $1000 larger than Matilda's, but Maude's interest rate is 2% less. Last year Maude received interest of $840, and Matilda received $800. Determine the interest rate of each CD. A) Maude at 14%: Matilda at 16% B) Maude at 12%: Matilda at 14% C) Maude at 13%: Matilda at 15% D) Maude at 15%: Matilda at 17% E) Maude at 17%: Matilda at 19%

Math
Trigonometry6. Draw a graph of at least two periods of the function gir) -3 cos (x/2t+ x/2)-2 by
(a) plotting the points where the graph intersects the midline and
(b) plotting the points where the graph achieves maximum and minimum values and
(c) connecting these points with an appropriately curved sinusoidal wave
List the period, midline, and amplitude of the function and label the scale on the axes

Math
Trigonometry29. Determine the amplitude, period, midline, and an equation involving cosine for the graph shown in Figure 32.
30. Determine the amplitude, period, midline, and an equation involving sine for the graph shown in Figure 33.

Math
Basic MathConsider the quadratic function f(x) = x² + 3x -4
Determine the following: (enter all numerical answers as integers, fractions, or decimals):
The smallest x-intercept is x =
The largest x-intercept is x =
The y-intercept is y =
The vertex is (
The line of symmetry has the equation
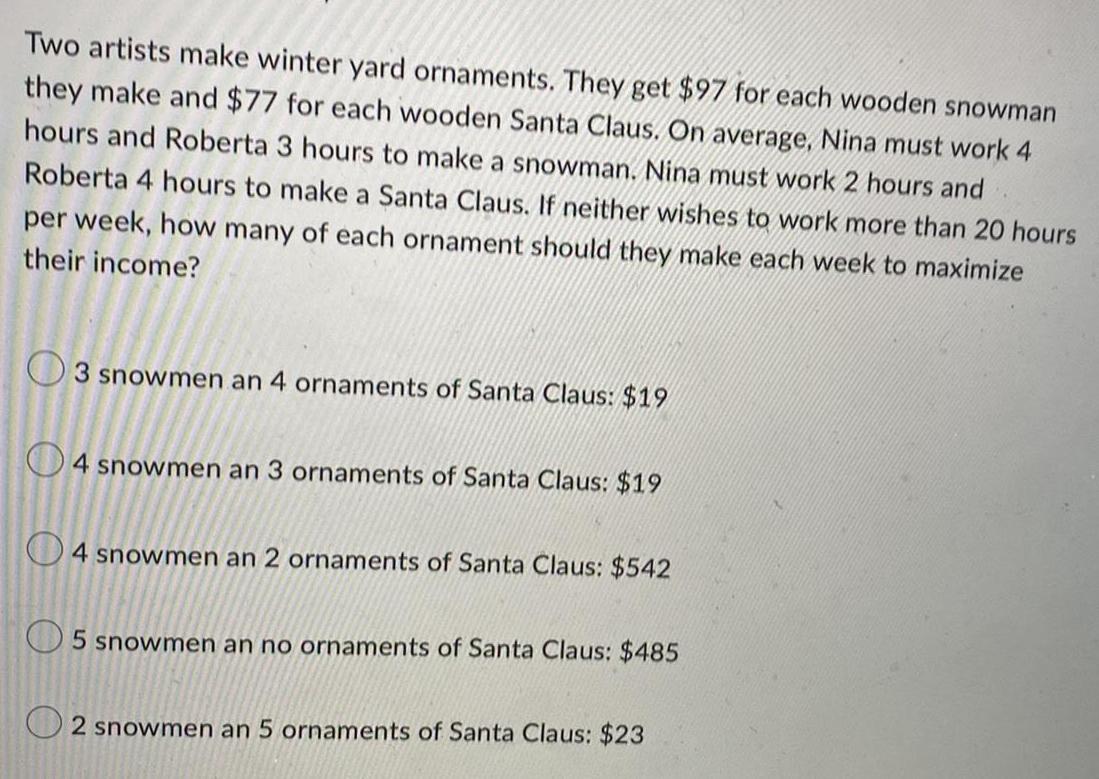
Math
Linear ProgrammingTwo artists make winter yard ornaments. They get $97 for each wooden snowman
they make and $77 for each wooden Santa Claus. On average, Nina must work 4
hours and Roberta 3 hours to make a snowman. Nina must work 2 hours and Roberta 4 hours to make a Santa Claus. If neither wishes to work more than 20 hours per week, how many of each ornament should they make each week to maximize their income?
3 snowmen an 4 ornaments of Santa Claus: $19
4 snowmen an 3 ornaments of Santa Claus: $19
4 snowmen an 2 ornaments of Santa Claus: $542
5 snowmen an no ornaments of Santa Claus: $485
2 snowmen an 5 ornaments of Santa Claus: $23

Math
Basic MathThe height of a projectile fired upward with an initial velocity of 160 feet per second
is given by the formula
h = -16t² + 160t
where h is the height in feet and t is the time in seconds. Determine the time required for the projectile to return to earth.
A) 35 sec
B) 25 sec
C) 10 sec
D) 5 sec
E) 20 sec
Math
FunctionsFind a quadratic function f(x) = ax²+bx+c whose vertex is (1, 3) and whose y-intercept is (0, 1).
f(x) =
![A continuously-decreasing function that is concave up on the interval [2, 6] is represented by the table.
Part A: Find the left Reimann sum estimate of f(x) dx, based on the subintervals given in the table. (4 points)
Part B: Write the midpoint Reimann sum that estimates f(x) dx, based on the subintervals given in the table. (4 points)
Part C: Determine whether the left Reimann sum estimate is an overestimate or an underestimate, based on the properties of the function. (2 points)](https://media.kunduz.com/media/sug-question/raw/77433702-1660473130.8209841.jpeg?w=256)
Math
Basic MathA continuously-decreasing function that is concave up on the interval [2, 6] is represented by the table.
Part A: Find the left Reimann sum estimate of f(x) dx, based on the subintervals given in the table. (4 points)
Part B: Write the midpoint Reimann sum that estimates f(x) dx, based on the subintervals given in the table. (4 points)
Part C: Determine whether the left Reimann sum estimate is an overestimate or an underestimate, based on the properties of the function. (2 points)

Math
Quadratic equations3. Find the zeros of the quadratic function by graphing. Round to the nearest tenth if necessary.
f(x) = -2x² + 3x + 1
0.8,2.1) is a zero of the quadratic function because it is the peak of the parabola.
(-0.3,0) and (1.8,0) are zeros of the quadratic function because it is where the parabola crosses the x-axis.
(0.8,2.1) and (0,1) are zeros of the quadratic function because it is where the parabola crosses the x-axis...
(0.1) is a zero of the quadratic because it is where the parabola crosses the y-axis.

Math
Basic MathEstimation A ramp is being built to a building to help with deliveries. The angle that the bottom of the ramp makes with the ground is 38.1°. Estimate the measure of the other acute angle. Find the exact measure of the other acute angle.
Which of the following is a good estimate for the measure of the other acute angle?
A. 57°
B. 62
C. 47°
D. 52°
![In the figure, m∠1 = (x+7)°, m∠2 = (3x+3)°, and m∠4 = (5x-6). Write an expression for m∠3. Then find m∠3.
Which is an expression for mZ3? Select all that apply.
A. 180° -(5x-6)°
B. 180° - (x+7)°
C. 180° -[(3x+3)° + (x+7)°]
D. 180° + (x + 7)°](https://media.kunduz.com/media/sug-question/raw/77312505-1660472985.195318.jpeg?w=256)
Math
Basic MathIn the figure, m∠1 = (x+7)°, m∠2 = (3x+3)°, and m∠4 = (5x-6). Write an expression for m∠3. Then find m∠3.
Which is an expression for mZ3? Select all that apply.
A. 180° -(5x-6)°
B. 180° - (x+7)°
C. 180° -[(3x+3)° + (x+7)°]
D. 180° + (x + 7)°

Math
Basic MathHelena is going to drive a distance of 245 miles each way on a trip. She used 14 gallons of gas going there and 10 gallons returning. What was her gas mileage to the nearest mile for the entire trip?
19 miles per gallon
20 miles per gallon

Math
TrigonometryTo get a better look at the graph, you can click on it.
The curve above is the graph of a sinusoidal function. It goes through the point (2, 0). Find a sinusoidal function that matches the given graph. If needed, you can enter π as pi in your answer.