Math Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Math
Solution of trianglesIn the figure, m∠1 = (7x+7)°, m∠2 = (5x+14)°, and m∠4 = (13x +9)°. Your friend incorrectly says that m∠4 = 15°. What is m∠4? What mistake might your friend have made?

Math
Basic MathThe path of the object thrown above the ground level is given by the function s(t) = 2t2 + 5t + 3. Rewrite it in factored form.
(2t+3)(t-1)
(2t+3)(t+1)
(2t-3)(t+1)

Math
Basic MathSolve for x and write the solution set using set-builder notation: 1.5-0.25x ≤ 6
{x|x ≥-18}
{x|x ≥-10}
{x|x ≤ 8}

Math
Basic MathFunction W gives the weight of a cat t weeks after it was born. The weight is measured in pounds.
Use function notation to represent this statement:
10 weeks after the cat was born, it weighed 8 pounds.
t=8, W=10
10(8) = W
W(10)=8
W(8)=10
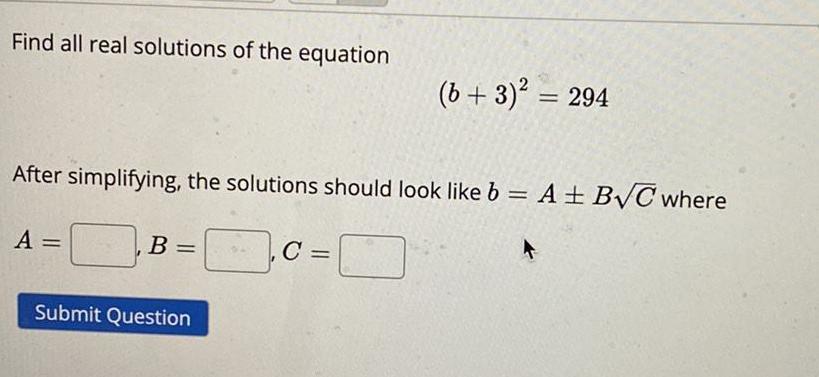
Math
Quadratic equationsFind all real solutions of the equation
(b + 3)² = 294
After simplifying, the solutions should look like b = A +- B√C where
A =
B =
C =

Math
Basic MathDan traveled to his friend's house and back. The trip there took two hours and the trip back took three hours. What was Dan's average speed on the trip there if he averaged 20 mph on the return trip?
25 mph
50 mph
42 mph
43 mph
30 mph

Math
ProbabilityA spinner has an equal chance of landing on each of its five numbered regions. You spin twice. The first spin lands in region two and the second spin lands in region one.
21/55≈ 0.382
1/25≈0.04
1/4≈0.25
4/15≈0.267
7/22≈0.318

Math
Basic MathWrite an equation for a line perpendicular to y = 2x - 5 and passing through the point (2,2)
y =

Math
Basic MathA bike shop rents bikes for $4 per hour, and helmets for $8 per day. Justin has less than $ 20 to rent
a helmet and a bike for x hours. Which of following inequality represents this situation?
4x+8 = 20
4x+8<20
4x-8<20

Math
Basic MathIf a couple has $50,000 in a retirement account, how long will it take the money to grow to $1,000,000 if it grows by 6% compounded continuously? Write your answer as an exact value.

Math
Basic MathThe perimeter of a rectangular swimming pool is 154 m. Its length is 2 m more than twice its width
Find the length and width of the pool.
I=30, w = 30
I=52, w = 25
I=25, w = 35

Math
Basic MathSimplify the following expressions completely. Assume all variables represent non-negative
numbers.
A)√16p26
B)√81m22 =

Math
TrigonometryThe following problem refers to triangle ABC. Solve it. Round your degrees and minutes to the nearest whole number. Round the sides to the 3 decimal places.
b = 0.75, c = 0.507, A = 46°20'

Math
StatisticsThe most famous geyser in the world, Old Faithful in Yellowstone National Park, has a mean time between eruptions of 85 minutes. If the interval of time between the eruptions is normally distributed with standard deviation 21.25 minutes, complete parts (a) through (f).
(a) What is the probability that a randomly selected time interval between eruptions is longer than 94 minutes?
The probability that a randomly selected time interval is longer than 94 minutes is approximately 0.3192
(Round to four decimal places as needed.)
(b) What is the probability that a random sample of 14 time intervals between eruptions has a mean longer than 94 minutes?
The probability that the mean of a random sample of 14 time intervals is more than 94 minutes is approximately noruptions has a mean longer than 94 minutes?
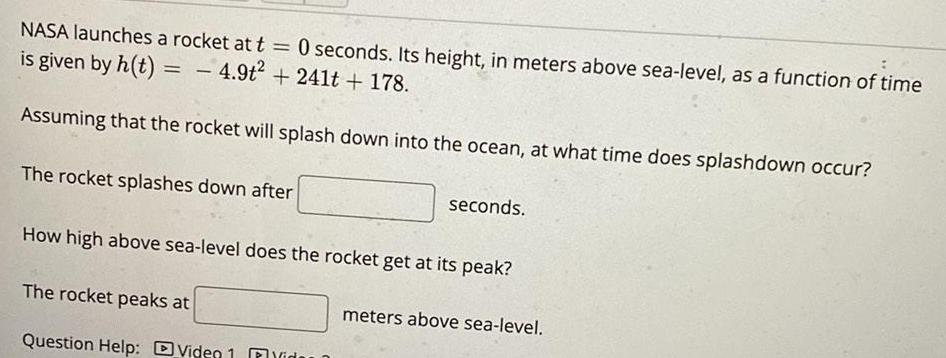
Math
Quadratic equationsNASA launches a rocket at t = 0 seconds. Its height, in meters above sea-level, as a function of time is given by h(t) = -4.9t² +241t+ 178. Assuming that the rocket will splash down into the ocean, at what time does splashdown occur? The rocket splashes down after seconds. How high above sea-level does the rocket get at its peak?
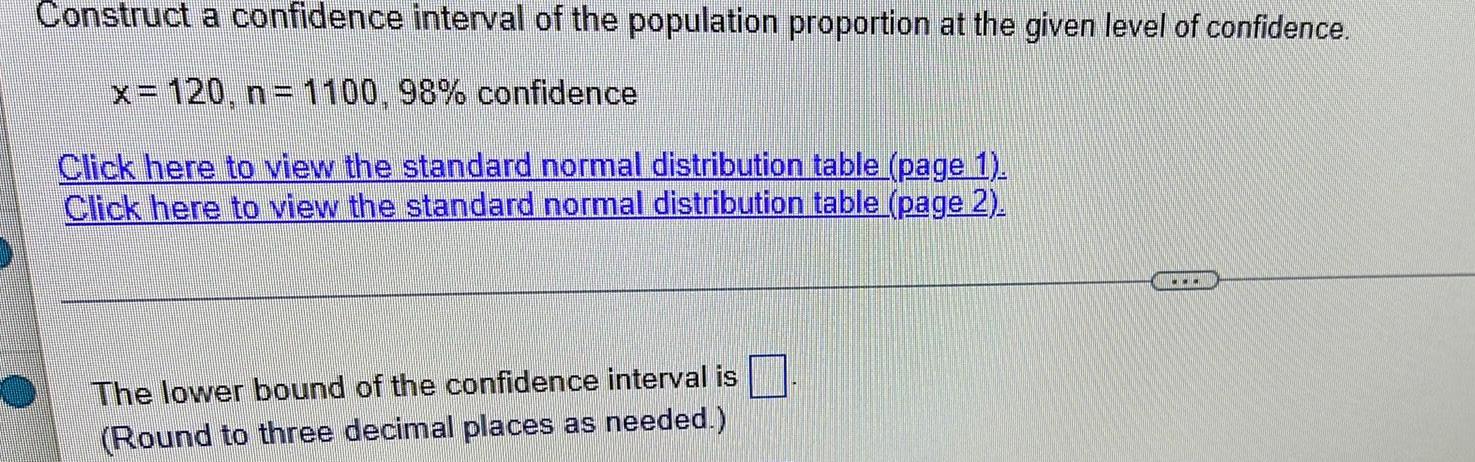
Math
StatisticsConstruct a confidence interval of the population proportion at the given level of confidence.
x= 120, n= 1100, 98% confidence
The lower bound of the confidence interval is

Math
Basic MathWhich is the equation of a circle with diameter AB where A(5, 4) and B(-1,-4)?
Select one:
a. (x + 2)² + y² = 5
b. (x + 5)² + (y - 4)² = 100
c. (x-2)² + y² = 25
d. (x - 5)² + (y-4)² = 10

Math
Quadratic equationsAn object is thrown upward at a speed of 132 feet per second by a machine from a height of 17 feet
off the ground. The height of the object after t seconds can be found using the equation
s(t) = 16t² + vot + so, where is the initial velocity and so is the initial height. Give all
numerical answers to 2 decimal places.
(a) When will the object reach its maximum height?
(b) What is its maximum height?
(c) When will the object reach the ground?
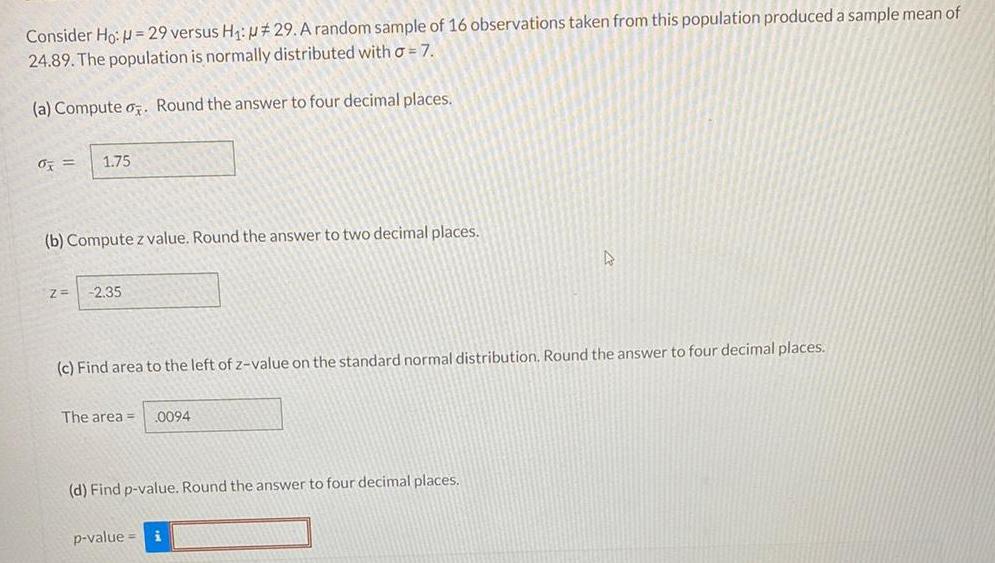
Math
StatisticsConsider Ho: = 29 versus H₁: #29. A random sample of 16 observations taken from this population produced a sample mean of 24.89. The population is normally distributed with a = 7.
(a) Compute . Round the answer to four decimal places.
% = 1.75
(b) Compute z value. Round the answer to two decimal places.
(c) Find area to the left of z-value on the standard normal distribution. Round the answer to four decimal places.
(d) Find p-value. Round the answer to four decimal places.
Math
Linear ProgrammingWhich of the following points lies in the solution region for y> 3 and y < -3.
(3,-3)
No solution
(0, 0)

Math
ProbabilitySuppose a simple random sample of size n = 11 is obtained from a population with μ-66 and o=14
(a) What must be true regarding the distribution of the population in order to use the normal model to compute probabilities regarding the sample mean? As
the normal model can be used, describe the sampling distribution x.
(b) Assuming the normal model can be used, determine P(x <69.3).
(c) Assuming the normal model can be used, determine P(x ≥ 67.9).
(a) What must be true regarding the distribution of the population?
A. The population must be normally distributed.
B. There are no requirements on the shape of the distribution of the population
C. The population must be normally distributed and the sample size must be large
D. Since the sample size is large enough, the population distribution does not need to be normal.

Math
Basic MathMary has $18.50 to buy pizza. A cheese pizza costs $14. Each extra topping cost $0.75. How many
extra toppings can she buy?
4 toppings
6 toppings
3 toppings
Math
Quadratic equationsSolve this equation using the square root property. If possible, simplify radicals. All answers should be exact.
(c - 9)² = 29
The solution(s) to this equation have the form c = A ± √B

Math
StatisticsAccording to a food website, the mean consumption of popcorn annually by Americans is 63 quarts. The marketing division of the food website unleashes an
aggressive campaign designed to get Americans to consume even more popcorn. Complete parts (a) through (c) below.
(a) Determine the null and alternative hypotheses that would be used to test the effectiveness of the marketing campaign.
(b) A sample of 866 Americans provides enough evidence to conclude that marketing campaign was effective. Provide a statement that should be put out by the
marketing department.
A. There is sufficient evidence to conclude that the mean consumption of popcorn has stayed the same.
B. There is not sufficient evidence to conclude that the mean consumption of popcorn has stayed the same.
OC. There is not sufficient evidence to conclude that the mean consumption of popcorn has risen.
D. There is sufficient evidence to conclude that the mean consumption of popcorn has risen.

Math
Basic MathA website uses the formula above to calculate a seller's rating, R, based on the number of favorable reviews, F, and unfavorable reviews, N. Which of the following expresses the number of favorable reviews in terms of the other variables?

Math
Application of derivativesThe radius of a circular oil spill after t minutes is given by r(t) = √4t. Find the instantaneous rate at which the radius is growing after 31 minutes.
Give your answer as a decimal approximation with at least 3 decimal places.
Math
StatisticsIs the hypothesis test left-tailed, right-tailed, or two-tailed?
The null and alternative hypotheses are given. Determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed. What parameter is being tested?
Ho μ = 125
H₁: μ < 125
Right-tailed test
Left-tailed test
Two-tailed test
Submit test

Math
Basic MathFind the Z-scores that separate the middle 75% of the distribution from the area in the tails of the standard normal distribution
The Z-scores are

Math
Basic MathDetermine the following limits. Enter DNE if a limit fails to exist, except in case of an infinite limit. If an infinite limit exists, enter ∞ or -∞, as appropriate.
Determine the equation of the horizontal asymptote that corresponds to the limit as n → ∞.
Equation of horizontal asymptote:
No horizontal asymptote corresponds to the limit as n→∞.
Determine the equation of the horizontal asymptote that corresponds to the limit as n → -∞.
Equation of horizontal asymptote:
No horizontal asymptote corresponds to the limit as n→-8

Math
TrigonometryGiven oblique triangle ABC, side a = 12 ft., side b = 17 ft., side c = 10 ft., find the degree of the smallest angle (round to the nearest whole degree). DO NOT FIND ALL THREE ANGLES AND THEN CHOOSE THE MALLEST. Remember that the smallest angles is across from the smallest side. Be sure to type your answers to all parts in the answer box. Be sure to show all work on loose leaf as a file upload question at the end. This question is worth 8 points total. 1 for the answer and 7 for the work.
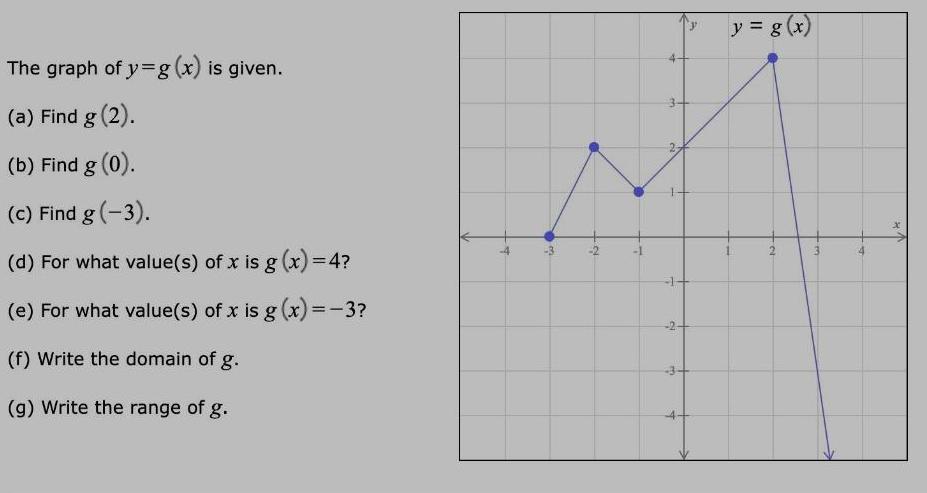
Math
FunctionsThe graph of y=g (x) is given.
(a) Find g (2).
(b) Find g (0).
(c) Find g (-3).
(d) For what value(s) of x is g (x)=4?
(e) For what value(s) of x is g(x)=-3?
(f) Write the domain of g.
(g) Write the range of g.
![Let x)=x², and compute the Riemann sum off over the interval [4, 51, choosing the representative points to be the midpoints of the subintervals and using the following number of subintervals
(n). (Round your answers to two decimal places.)
(a) two subintervals of equal length (n=2)
(b) five subintervals of equal length (n = 5)
(c) ten subintervals of equal length (n = 10)
(d) Can you guess at the area of the region under the graph of fon the interval [4, 5]?](https://media.kunduz.com/media/sug-question/raw/77311801-1660454184.3500469.jpeg?w=256)
Math
Definite IntegralsLet x)=x², and compute the Riemann sum off over the interval [4, 51, choosing the representative points to be the midpoints of the subintervals and using the following number of subintervals
(n). (Round your answers to two decimal places.)
(a) two subintervals of equal length (n=2)
(b) five subintervals of equal length (n = 5)
(c) ten subintervals of equal length (n = 10)
(d) Can you guess at the area of the region under the graph of fon the interval [4, 5]?

Math
ProbabilityIn a survey, it was found that 78% of the population of a certain urban area lived in single-family dwellings and 22% in multiple housing. Five years later, of those who had been living in single-family dwellings, 91% still did so, but 9% had moved to multiple-family dwellings. Of those in multiple housing, 96% were still living in that type of housing, while 4% had moved to single-family housing. Assume that these trends continue. Answer parts (a) through (f).

Math
ParabolaFarmer Jones, and his wife, Dr. Jones, decide to build a fence in their field, to keep the sheep safe. Since Dr. Jones is a mathematician, she suggests building fences described by y = 112² and y = x² + 4. Farmer Jones thinks this would be much harder than just building an enclosure with straight sides, but he wants to please his wife. What is the area of the enclosed region?
Math
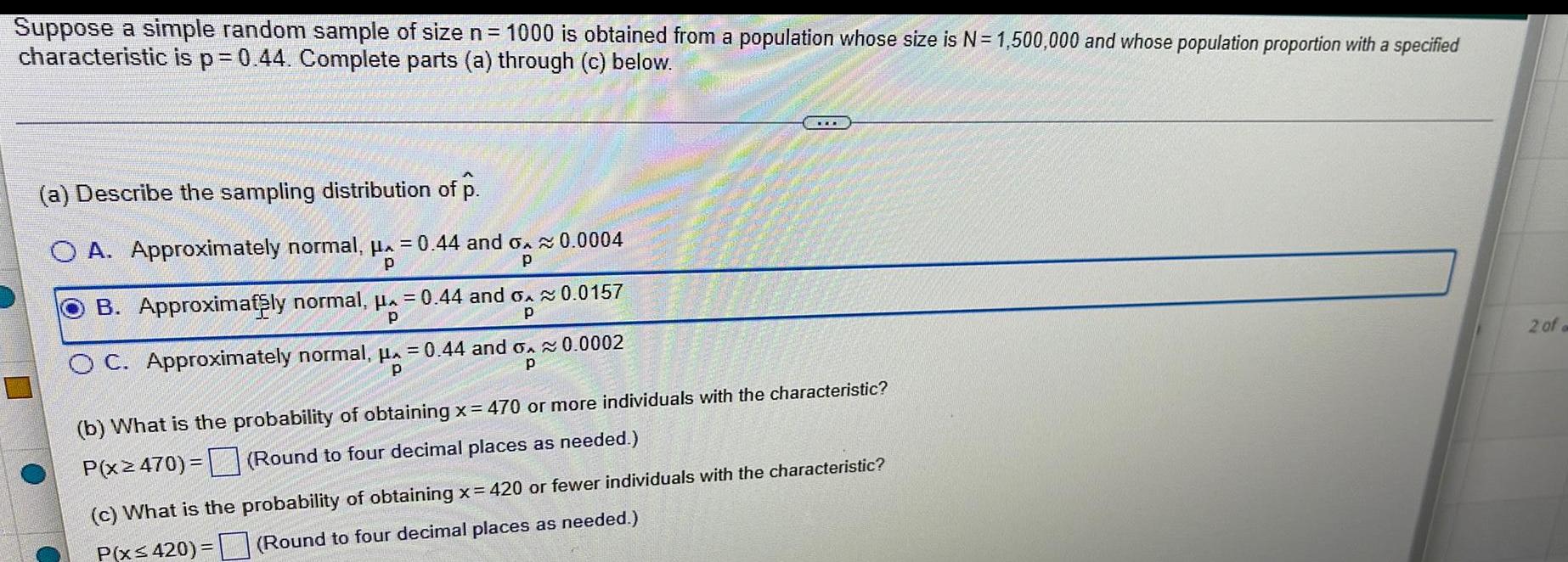
StatisticsSuppose a simple random sample of size n = 1000 is obtained from a population whose size is N= 1,500,000 and whose population proportion with a specified
characteristic is p = 0.44. Complete parts (a) through (c) below.
(a) Describe the sampling distribution of p.
A. Approximately normal, μ = 0.44 and o≈ 0.0004
B. Approximately normal, μ = 0.44 and ≈ 0.0157
C. Approximately normal, μ = 0.44 and o.≈ 0.0002
(b) What is the probability of obtaining x = 470 or more individuals with the characteristic?

Math
Basic MathHow many real and imaginary solutions does the equation x² + x = 11 contain?
1 real solution; 1 imaginary solution
No real solutions; 2 imaginary solutions
1 real solution; no imaginary solutions
2 real solutions; no imaginary solutions

Math
Basic MathA certain forest covers an area of 1800 km². Suppose that each year this area decreases by 3%. What will the area be after 13 years? Use the calculator provided and round your answer to the nearest square kilometer.

Math
StatisticsDetermine the point estimate of the population proportion, the margin of error for the following confidence interval, and the number of individuals in the sample with the specified characteristic, x, for the sample size provided. Lower bound = 0.201, upper bound = 0.469, n = 1000

Math
StatisticsA TV station wants to estimate the popular support for each of the candidates in an upcoming election. Which procedure would be most appropriate for obtaining a statistically unbiased sample?
a. interviewing the school board about the students' opinions
b. inviting all viewers to participate in a mail-in poll
c. calling a random sample selected from a list of eligible voters
d. setting up a booth in the local shopping mall and interviewing every tenth person that passes by is asked

Math
StatisticsA certain drug can be used to reduce the acid produced by the body and heal damage to the esophagus due to acid reflux. The manufacturer of the drug claims that more than 92% of patients taking the drug are healed within 8 weeks. In clinical trials, 217 of 233 patients suffering from acid reflux disease were healed after 8 weeks. Test the manufacturer's claim at the α = 0.1 level of significance.

Math
StatisticsSeveral years ago, 45% of parents who had children in grades K-12 were satisfied with the quality of education the students receive. A recent poll asked 1,035 parents who have children in grades K-12 if they were satisfied with the quality of education the students receive. Of the 1,035 surveyed, 456 indicated that they were satisfied. Construct a 90% confidence interval to assess whether this represents evidence that parents' attitudes toward the quality of education have changed What are the null and alternative hypotheses? Use technology to find the 90% confidence interval. What is the correct conclusion? We are 90% confident the proportion of parents who had children in grades K-12 that were satisfied with the quality of education the students receive is between idence that parents' attitudes toward the quality of education
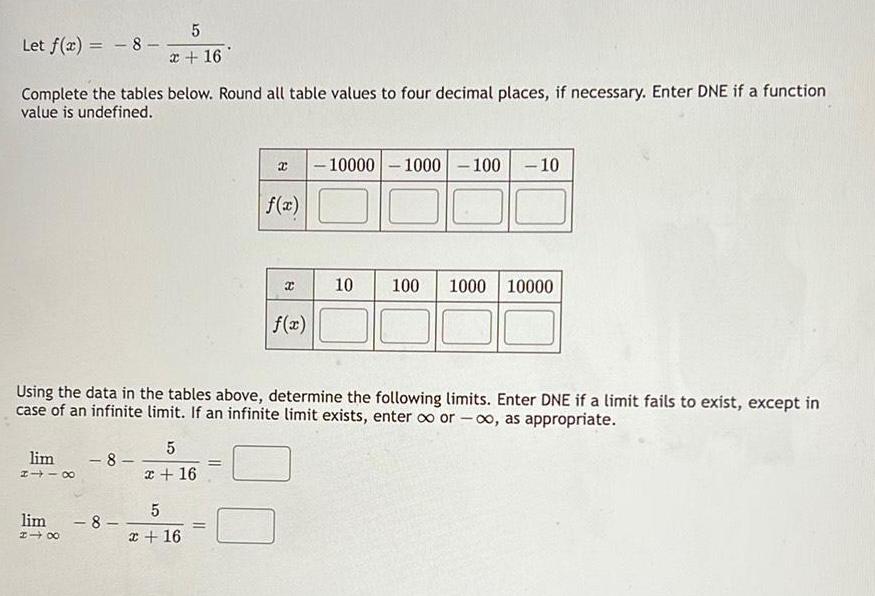
Math
Limits and ContinuityLet f(x) = -8 - 5/x+16
Complete the tables below. Round all table values to four decimal places, if necessary. Enter DNE if a function value is undefined.
Using the data in the tables above, determine the following limits. Enter DNE if a limit fails to exist, except in case of an infinite limit. If an infinite limit exists, enter ∞ or -∞, as appropriate.

Math
StatisticsFind the z-scores that separate the middle 14% of the distribution from the area in the tails of the standard normal distribution.

Math
TrigonometryJason sees a tall building from across town. He turns 90° and walks 100 yards. Jason then turns to face the building, and the angle between his line of sight and his path is 35° as shown below. Which of the following is the closest to the distance from Jason's original position to the building, in yards?

Math
Limits and ContinuityLet f(x)=√x6 +5x - x³ - 3.
Complete the tables below. Round all table values to four decimal places, if necessary. Enter DNE if a function value is undefined.
Using the data in the tables above, determine the following limits. Enter DNE if a limit fails to exist, except in case of an infinite limit. If an infinite limit exists, enter ∞ or -∞, as appropriate.

Math
StatisticsA simple random sample of size n = 81 is obtained from a population that is skewed right with µ-84 and σ = 27.
(a) Describe the sampling distribution of x.
(b) What is P (x>87)?
(c) What is P (x≤77.85) ?
(d) What is P (80.1<x<88.95)?
(a) Choose the correct description of the shape of the sampling distribution of x.
A. The distribution is approximately normal.
B. The distribution is uniform.
C. The distribution is skewed left.
D. The distribution is skewed right.
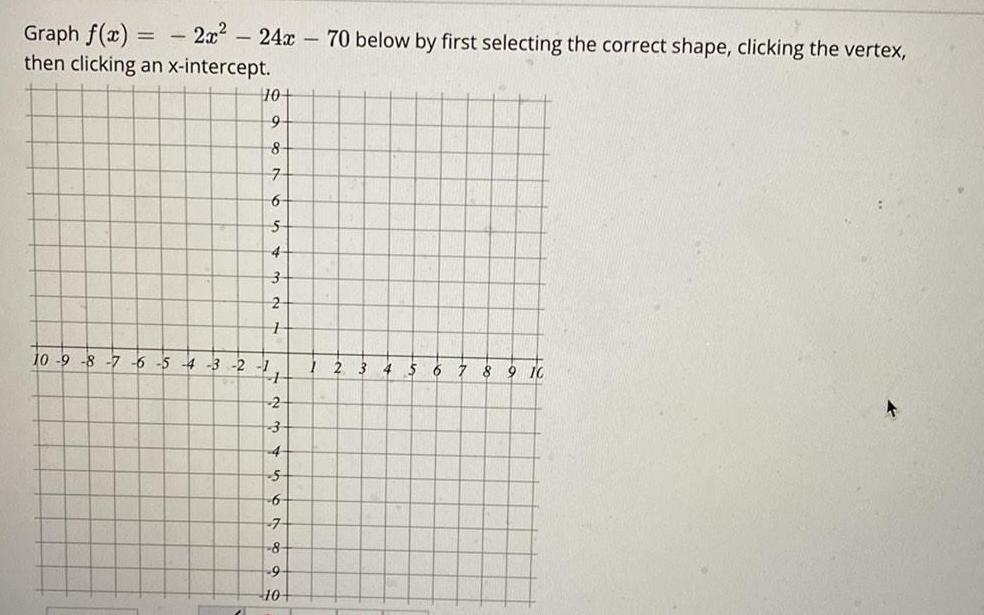
Math
Quadratic equationsGraph f(x) = 2x² 24x70 below by first selecting the correct shape, clicking the vertex, then clicking an x-intercept.
Math
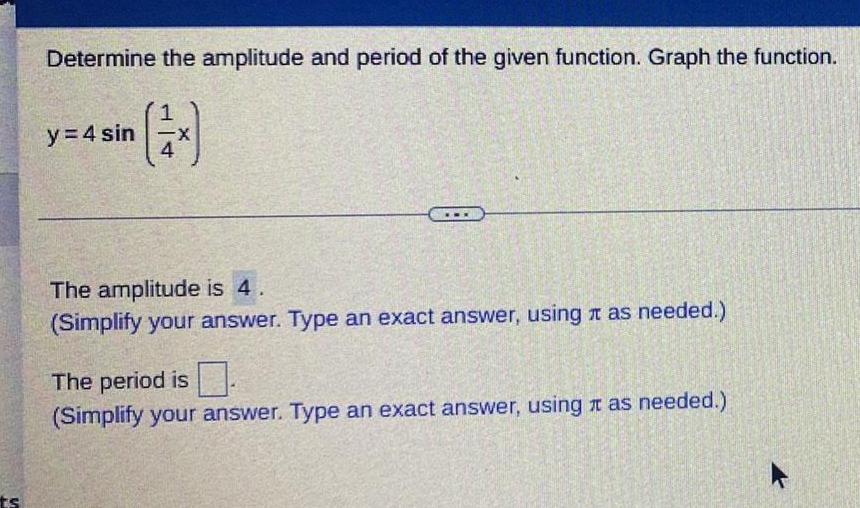
FunctionsDetermine the amplitude and period of the given function. Graph the function.
y = 4 sin (x/4)
The amplitude is 4
The period is

Math
ProbabilityAt one liberal arts college, students are classified as humanities majors, science majors, or undecided. The chances are 10% that a humanities major will change to a
science major from one year to the next, and 45% that a humanities major will change to undecided. A science major will change to humanities with probability 0.25,
and to undecided with probability 0.25. An undecided will switch to humanities or science with ptobabilities of 0.30 and 0.40, respectively. Complete parts (a) and (b)
below.
(a) Find the long-range prediction for the fraction of students in each of these three majors.
First, find the transition matrix P. Let the first state be that a student is a humanities major, the second that a student is a science major, and the third state that a
student is undecided.

Math
Quadratic equationsConsider the quadratic function f(x) = x² - 2x - 24.
Determine the following: (enter all numerical answers as integers, fractions, or decimals):
The smallest x-intercept is =
The largest x-intercept is x =
The y-intercept is y =
The vertex is =
The line of symmetry has the equation