Math Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Math
Basic MathGraph the linear equation. f(x) = -(1/3)x.
Use the graphing tool to graph the equation.

Math
Basic MathThe demand equation for a certain product is 8p² +5q² = 1400, where p is the price per unit in dollars and q is the number of units demanded.
(a) Find and interpret dq/dp.
(b) Find and interpret dp/dq.
(b) How is ap/dq calculated?
A. Use implicit differentiation. Differentiate with respect to q and assume that p is a function of q.
B. Use implicit differentiation. Differentiate with respect to q and assume that q is a function of p.
C. Use implicit differentiation. Differentiate with respect to p and assume that p is a function of q.
D. Use implicit differentiation. Differentiate with respect to p and assume that q is a function of p.
Find and interpret dq/dp, Select the correct choice below and fill in the answer box to complete your choice.
Math
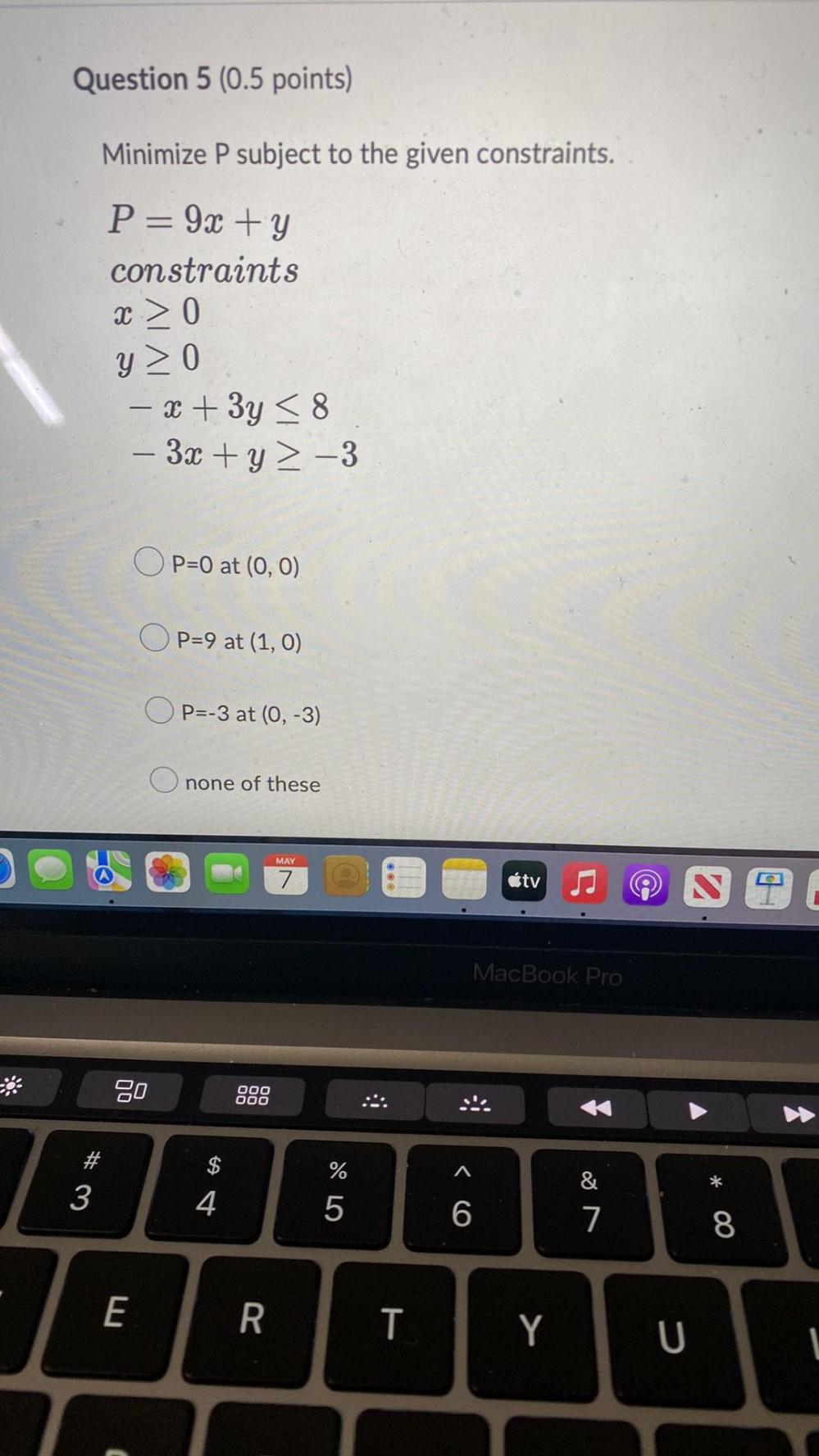
Linear ProgrammingMinimize P subject to the given constraints.
P= 9x + y constraints
x ≥ 0
y ≥ 0
-x + 3y ≤ 8
-3x + y ≥ -3
a. P=0 at (0, 0)
b. P=9 at (1, 0)
c. P=-3 at (0, -3)
d. none of these

Math
Basic MathThe height of a cylinder is three times the diameter of the base. The surface area of the cylinder is 126π ft^2? What is the radius of the base?
Math
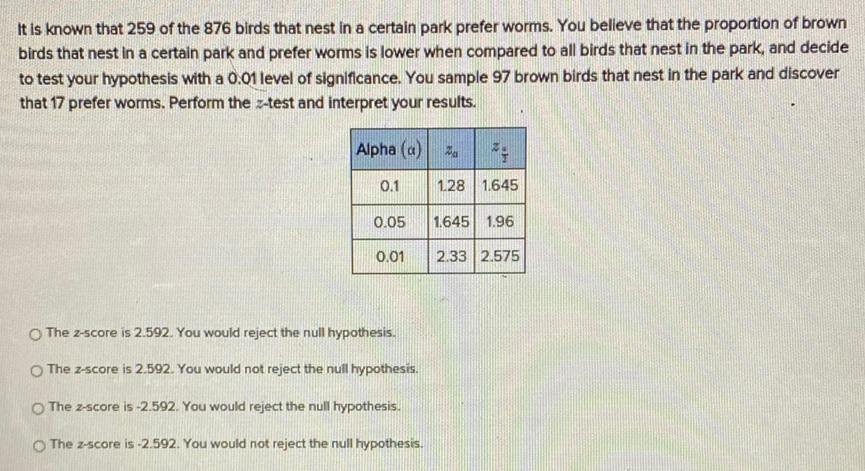
StatisticsIt is known that 259 of the 876 birds that nest in a certain park prefer worms. You believe that the proportion of brown birds that nest in a certain park and prefer worms is lower when compared to all birds that nest in the park, and decide to test your hypothesis with a 0.01 level of significance. You sample 97 brown birds that nest in the park and discover that 17 prefer worms. Perform the z-test and interpret your results.
Alpha (a) Zₐ zₐ/₂
0.1 1.28 1.645
0.05 1.645 1.96
0.01 2.33 2.575
The z-score is 2.592. You would reject the null hypothesis.
The z-score is 2.592. You would not reject the null hypothesis.
The z-score is -2.592. You would reject the null hypothesis.
The z-score is -2.592. You would not reject the null hypothesis.

Math
Binomial theoremSuppose the binomial expansion of (x - y)n includes the term – 84x6y3
The x5y4 term in the expansion will be ___
The x6y8 term in the expansion will be ___

Math
Matrices & DeterminantsUsing the information below to create the initial simplex matrix. Assume all variables are nonnegative.
Maximize f = 6x₁ +5x₂ + 7x₃ subject to
9x₁ + 7x₂ + 10x₃ ≤ 65
10x₁ + 3x₂ + 6x₃ ≤ 50
4x₁ + 10x₂ + 6x₃ ≤ 45
x₁ ≥0
x₂ ≥ 0
x₃ ≥ 0

Math
Permutations and CombinationsMs. Bell's mathematics class consists of 13 sophomores, 6 juniors, and 11 seniors. How many different ways can Ms. Bell create a 5-member committee of seniors if each senior has an equal chance of being selected?

Math
Binomial theoremSuppose the binomial expansion of (x + y)^n includes the term 3003x⁶y⁸.
The x⁵y⁹ term in the expansion will be?
The x⁴y³ term in the expansion will be?


Math
StatisticsYou intend to estimate a population mean μ with the following sample.
35.6
53.7
48.1
42.9
7.5
5.6
11.6
You believe the population is normally distributed. Find the 99% confidence interval. Enter your answer as an open-interval (i.e., parentheses) accurate to two decimal places (because the sample data are reported accurate to one decimal place).
99% C.I. =(______,_______).
Answer should be obtained without any preliminary rounding.

Math
Basic MathSolve the compound inequality.
- 2x < -8 and x-4 <5
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The solution set of the compound inequality is ___ . (Type your answer in interval notation.)
B. The solution set is Ø.

Math
ProbabilityA local restaurant manager wants to survey customers about the service they receive. Each night the manager randomly chooses a number between 1 and 10. He then gives a survey to that customer, and to every 10th customer after them to fill it out before they love.
Cluster Sample
Systematic Sample
Simple Random Sample
Convenience Sample

Math
Basic MathUse Gauss-Jordan elimination to find the solution to the following system of equations.
9x + 20y + 4z = 11
4x + 9y + 3z = -3
X+ 2y – 2z = 5
Select the correct choice below and fill in any answer boxes within your choice.
A) There is one solution. The solution is x= ______, y= _____and z= ______.
(Simplify your answer.)
B) There are infinitely many solutions. If z is any real number, x= _____ and y= _______.
(Type an expression using z as the variable.)
C) There is no solution.

Math
Basic MathA company uses two vans to transport workers from a free parking lot to the workplace between 7:00 and 9:00 a.m. One van has 5 more seats than the other. The smaller van makes two trips every morning while the larger one makes only one trip. The two vans can transport 65 people, maximum.
Let x be the seats in the small van and y the seats in the large van. How many seats does the larger van have?


Math
Basic MathPythagoras and Esky both put $400 into a bank at the same time. Pythagoras's bank calculates 5% interest compounded annually. Esky's bank compounds continuously using 4.5% interested. Who will have more after 10 years and by how much?
Pythagoras will have $24.24 more
Esky will have $24.24 more
Pythagoras will have $21.24 more
Esky will have $36.15 more

Math
ProbabilityIn a survey of families, the following data were obtained relating to the number of pets in their household:
Number of pets Frequency
0 10
1 15
2 10
3 10
4 5
total 50
What is the probability of calling a random family from the list that has less than 3 pets?
What is the probability of calling a random family from the list that has less than 3 pets?
![Consider the function f(x) = 3x^5/3 + 60x^2/3.
(a) Show that f'(x) = {[5(x + 8)] / ∛x}. Then find and classify all local extrema of f.
b) Find the values of the global extrema of f on the domain [-1,1].
c) Justify briefly, but precisely, why f has global extrema on the interval [-1, 1]](https://media.kunduz.com/media/sug-question/raw/77914624-1658831057.2986515.jpeg?w=256)
Math
FunctionsConsider the function f(x) = 3x^5/3 + 60x^2/3.
(a) Show that f'(x) = {[5(x + 8)] / ∛x}. Then find and classify all local extrema of f.
b) Find the values of the global extrema of f on the domain [-1,1].
c) Justify briefly, but precisely, why f has global extrema on the interval [-1, 1]

Math
Basic MathSolve the compound inequality.
-2x≤-8 or 7x-21≥21
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A). The solution set is _____.
B). The solution set is Ø.
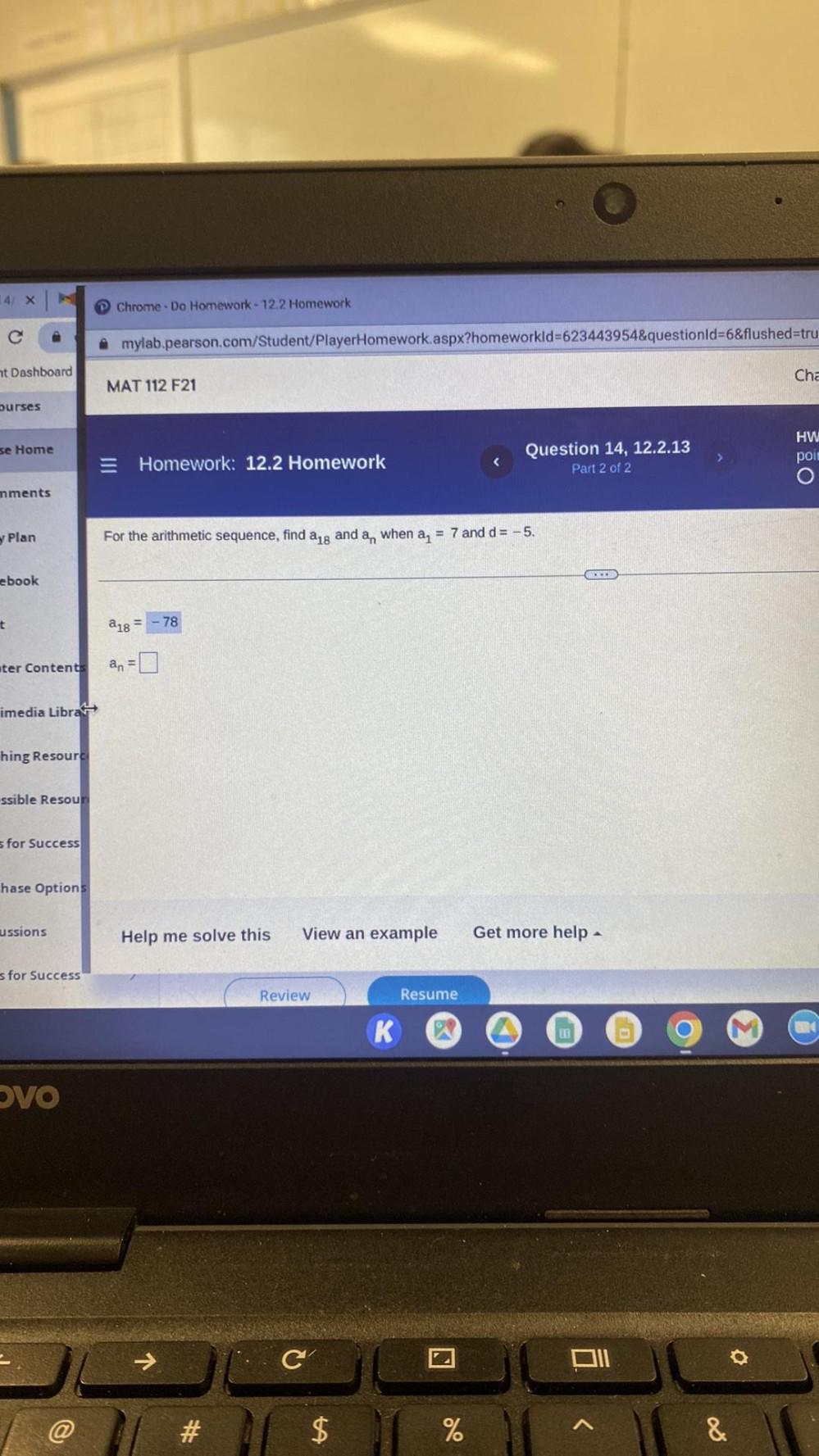
Math
Sequences & SeriesFor the arithmetic sequence, find a18 and an when a1 = 7 and d = -5.
a18 = -78.
an = ____.

Math
Basic MathConsider the quadratic equation
y = x² + 2x + 9.
Complete the square to express the quadratic in standard form y = a(x – h)²+k
a =_______
h =_______
k =_______

Math
FunctionsFor the given functions f and g, find the requested function and state its domain.
f(x) = 9x - 2; g(x) = 7x - 8.
Find f-g.
(f - g)(x) = 2x + 6; all real numbers
(f - g)(x) = 2x - 10; {x|x ≠ 5}
(f - g)(x) = -2x - 6; all real numbers
(f - g)(x) = 16x - 10; {x|x ≠ 1}

Math
Basic MathOliver wants to have $13,000 in 15 years after investing in an account that earns 4.2% compounded quarterly. How much should he invest?
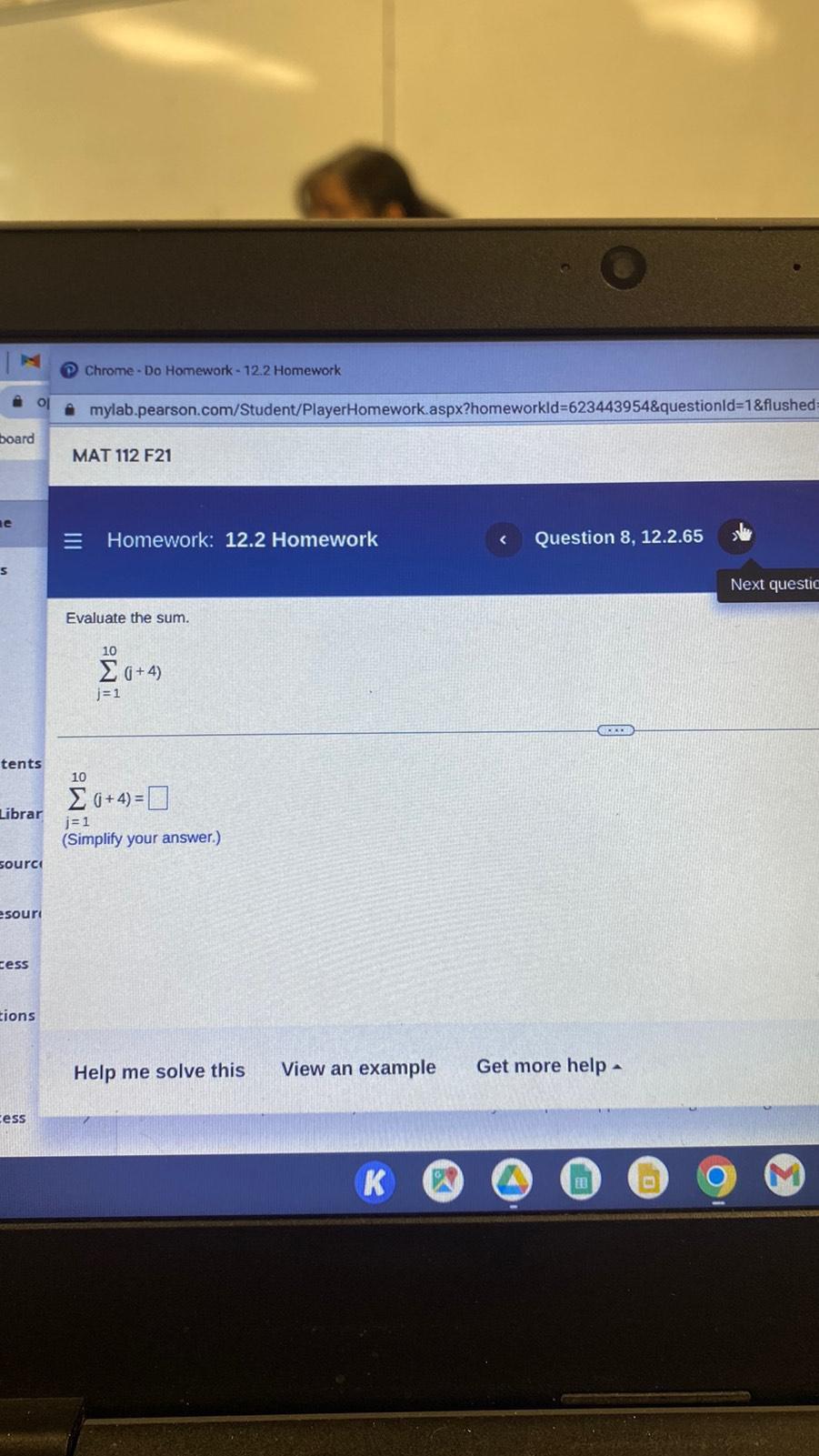

Math
Basic MathWrite an algebraic expression to represent each of the scenarios below.
Your answers must be simplified completely.
Scenario Algebraic Expression
a)Sales tax is currently 9.1 %. Write an algebraic expression
to represent the total amount paid for an item that costs D
dollars after tax is added to the purchase.
b)A store is having a 45% off sale. Write an algebraic expression
to represent the sale price for an item that is originally priced at
D dollars.
c)Carmen receives a 3% raise every year. Write an algebraic
expression to represent Carmen's salary after one year if her
current salary is S dollars.
d)Let B represent the bill for dinner at your favorite restaurant.
You decide to leave a 18% tip. Write an algebraic expression to
represent the total amount paid for dinner, including tip.
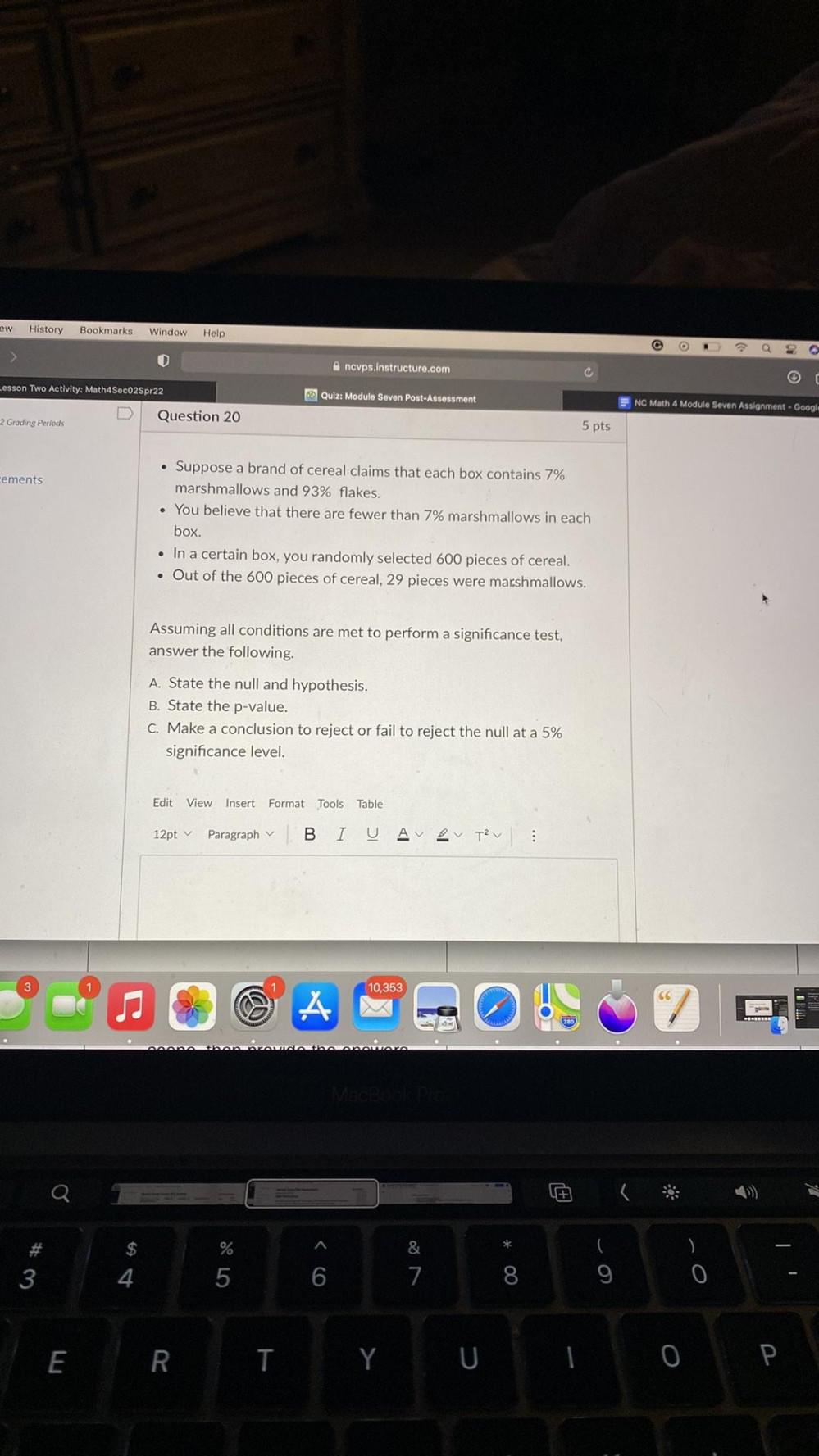
Math
Statistics• Suppose a brand of cereal claims that each box contains 7%
marshmallows and 93% flakes.
• You believe that there are fewer than 7% marshmallows in each box.
• In a certain box, you randomly selected 600 pieces of cereal.
• Out of the 600 pieces of cereal, 29 pieces were marshmallows.
Assuming all conditions are met to perform a significance test,
answer the following.
A State the null and hypothesis.
B State the p-value.
C Make a conclusion to reject or fail to reject the null at a 5%
significance level.

Math
Basic MathFill in the blank with the appropriate word.
A group that also satisfies the commutative property is called a(n)___________ (or abelian) group.
A group that also satisfies the commutative property is called a(n) __________ (or abelian) group.
→ finite
→ commutative
→ associative
→ infinite
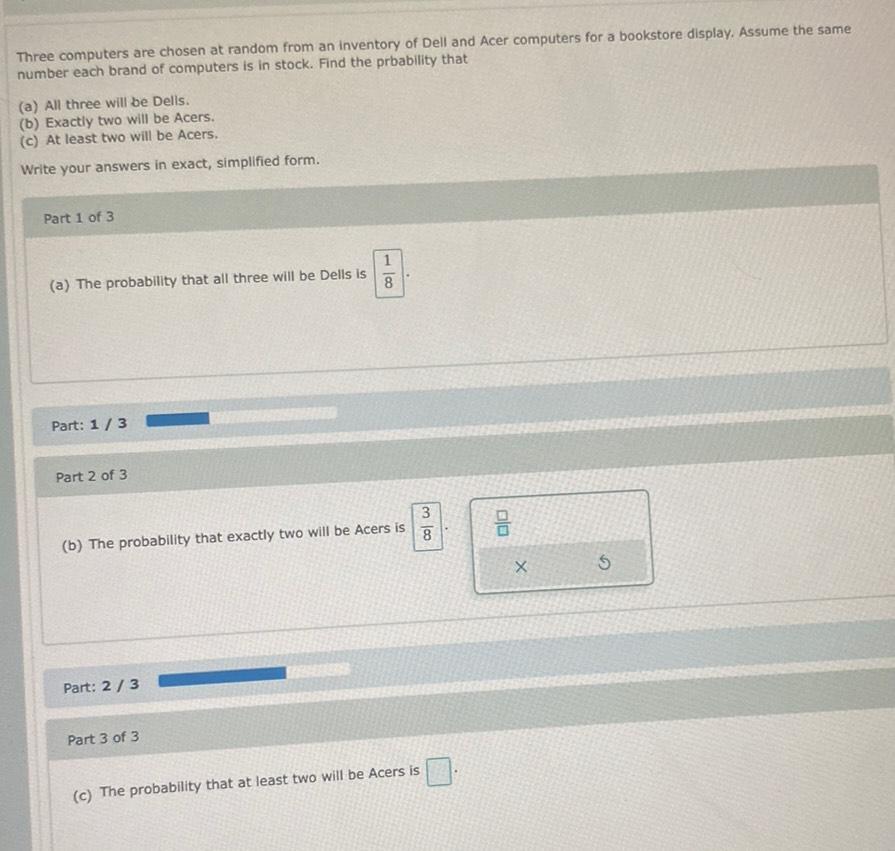
Math
ProbabilityThree computers are chosen at random from an inventory of Dell and Acer computers for a bookstore display. Assume the same number each brand of computers is in stock. Find the probability that
(a) All three will be Dells.
(b) Exactly two will be Acers.
(c) At least two will be Acers.

Math
Quadratic equationsChris operates a small sign-making business. He finds that if he charges x dollars for each sign, he sells 40 - x signs per week. What is the smallest number of signs that he can sell to have an income of $256 in one week?

Math
ProbabilityInside a bag there are 3 green balls, 2 red balls and 2 yellow balls. Two balls are randomly drawn without replacement. Calculate the probability of drawing one green ball and one yellow ball. The tree diagram has been started. ▢

Math
ProbabilityFind the probability for the experiment of selecting one card from a standard deck of 52 playing cards such that the card is a 10 or higher (aces are low).
4/13
11/13
9/26
12/13
3/13
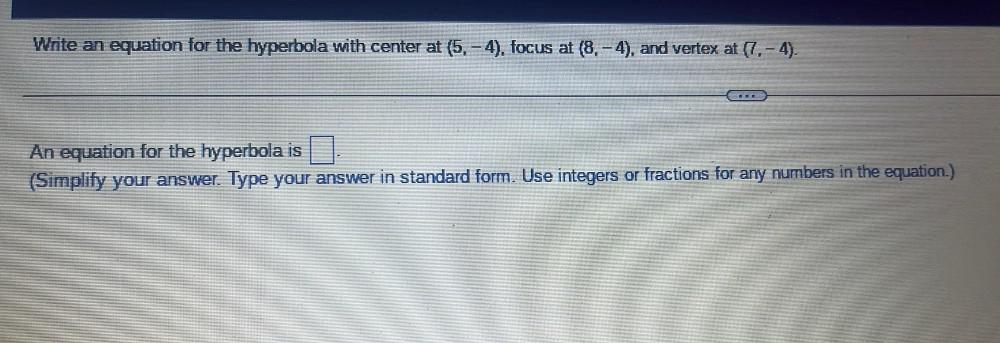
Math
HyperbolaWrite an equation for the hyperbola with center at (5, – 4), focus at (8, – 4), and vertex at (7, - 4).
An equation for the hyperbola is ____ .

Math
Straight linesFor each function below, identify the Slope, horizontal-intercept and vertical-intercept Write your numerical answers as whole numbers or reduced fractions. Write your intercepts as ordered pairs. If a slope or intercept Does Not Exist, write DNE
Function Slope Vertical Intercept Horizontal Intercept
y = 4x + 3
y = -8x + 7x
y = 10x
y = 2
x= -6

Math
FunctionsIsaac invested $1,800 in an account paying an interest rate of 4.7% compounded
continuously. Assuming no deposits or withdrawals are made, how much money, to the nearest hundred dollars, would be in the account after 15 years?

Math
StatisticsYou are interested in estimating the mean weight of the local adult population of female white-tailed deer (doe). From past data, you estimate that the standard deviation of all adult female white-tailed deer in this region to be 17 pounds. What sample size would you need to in order to estimate the mean weight of all female white-tailed deer, with a 95% confidence level, to within 5 pounds of the actual weight?
Sample Size: n≥
![Consider a two sector economy with input-output matrix
A= [0.4 0.5]
[0.2 0.6]
(a) Are the sectors in the economy profitable? Give a reason for your answer.
(b) Is the economy productive? Give a reason for your answer.](https://media.kunduz.com/media/sug-question/raw/77460694-1658830183.086395.jpeg?w=256)
Math
Matrices & DeterminantsConsider a two sector economy with input-output matrix
A= [0.4 0.5]
[0.2 0.6]
(a) Are the sectors in the economy profitable? Give a reason for your answer.
(b) Is the economy productive? Give a reason for your answer.

Math
Basic MathUse synthetic division to decide whether the given number k is a zero of the given polynomial function. If it is not, give the value of f(k).
f(x) = x³+2x²–2x+1, k=2+ i
Is 2+ i a zero of the function? Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
○ A. The given k is not a zero of the polynomial function. f(2 + i) = ▢
(Simplify your answer. Express complex numbers in terms of i.)
○ B. The given k is a zero of the polynomial function.

Math
Basic MathSolve the compound inequality. - X+9 > 10 and 1 + 2x ≤ -7
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A). The solution set is____
B). The solution set is Ø.

Math
Basic MathLet B represent the bill for dinner at your favorite restaurant. Write an algebraic expression to represent the total amount paid for dinner if you decide to leave a 15% tip. Simplify your answer.

Math
Basic MathThe demand equation for a certain product is 8p² + 5q² = 1400, where p is the price per unit in dollars and is the number of units demanded.
(a) Find and interpret dq/dp.
(a) How is dq/dp calculated?
A. Use implicit differentiation. Differentiate with respect to q and assume that q is a function of p.
B. Use implicit differentiation. Differentiate with respect to q and assume that p is a function of q.
C. Use implicit differentiation. Differentiate with respect to p and assume that p is a function of q.
D. Use implicit differentiation. Differentiate with respect to p and assume that q is a function of p.
Find and interpret dq/dp. Select the correct choice below and fill in the answer box to complete your choice.
A. dq/dp is the rate of change of price with respect to demand dq/dp = ▢.

Math
Basic MathThe metal bismuth melts at a temperature of 271 °C and boils at 1560 °C, whereas the metal cobalt melts at a temperature of 1495 °C and boils at 2870 °C.
(a) Which metal will be more volatile at room temperature?
(b) Predict which of the two molten metals has the larger surface tension at its melting point.

Math
ProbabilityDescribe how and when to use multiplication rule 1, P (A and B)=P(A) . P(B), and how and when use multiplication rule 2, P(A and B) = P(A) P(B, given that A has already occured).
Use multiplication rule 1 when two events are joined by "and" and the events are. Use multiplication rule 2 when the events are joined by "and" and the events are .

Math
FunctionsLet T: P₃->P₃, be the linear transformation such that
T(2x²) = -2x² + 3x. T(-0.5x - 2) = -4x² - 4x -2, T(5x² + 1) = 2x - 1.
Find T(1), T(x), T(x²), and T(ax² + bx + c), where a, b, and c are arbitrary real numbers.
T(1) =
T(x) =
T(ax² + bx + C) =

Math
Straight linesAssume that you don't know the commission rate, but you do know the actual amount of daily commission you earned and the total dollar value of the shoes you sold. Based on these values, you can derive a formula for the commission rate. Using the slope-intercept form of a line, write an equation to calculate the commission y, based on sales, x. Hint: The y-intercept will be zero since you get no commission if you have no sales.
Math
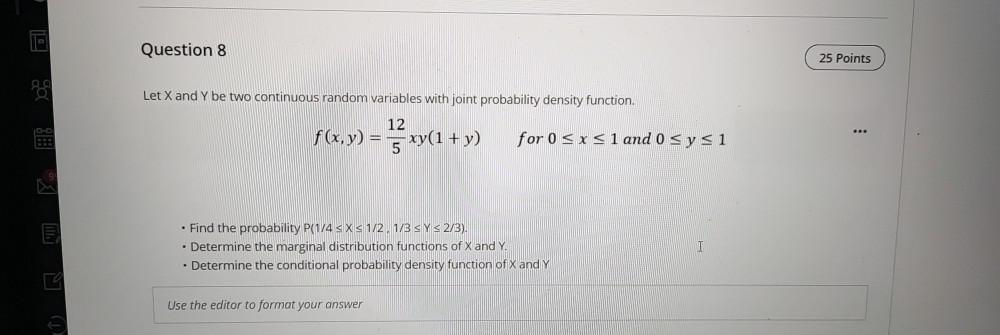
ProbabilityLet X and Y be two continuous random variables with joint probability density function
f(x,y) = 12/5xy(1+y) for 0 ≤x ≤1 and 0 ≤ y ≤ 1
• Find the probability P(1/4 ≤ X ≤1/2, 1/3 ≤ Y ≤ 2/3).
• Determine the marginal distribution functions of X and Y
• Determine the conditional probability density function of X and Y

Math
Basic MathSuppose that the local sales tax rate is 6% and you purchase a car for $18,500.
a. How much tax is paid?
b. What is the car's total cost?
The amount of tax paid is $ .

Math
Binomial theoremSuppose the binomial expansion of (2x – 3y)n includes the term –15120x4y3
The x4y3 term in the expansion will be
The x5y3 term in the expansion will be

Math
ProbabilityDifferent shapes are drawn on cards and then the cards are placed in a bag. The number of cards for each shape is shown in the table.
Shape octagon square circle
Number of cards 12 27 91
What is the probability that a randomly selected card has a circle drawn on it? Write your answer as a fraction in simplest form.