Math Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
Math
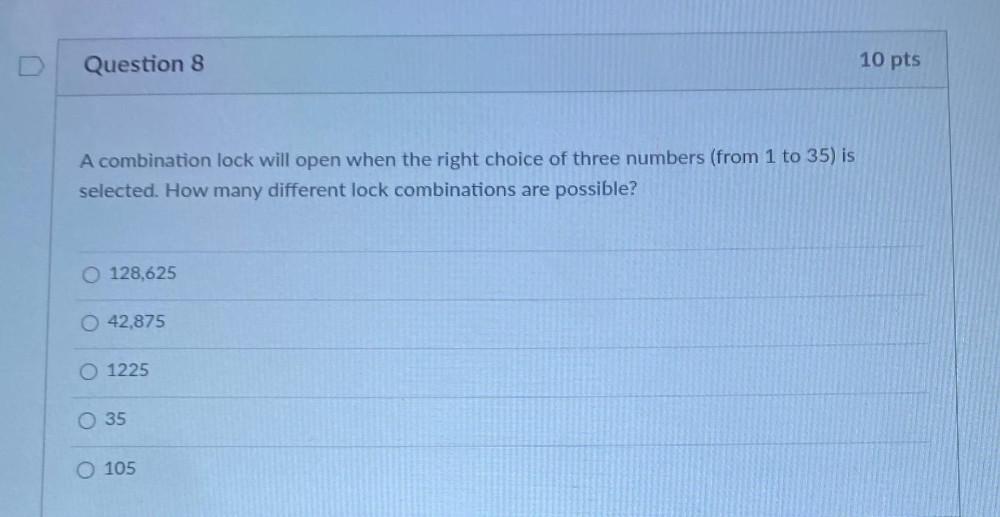
Permutations and CombinationsA combination lock will open when the right choice of three numbers (from 1 to 35) is selected. How many different lock combinations are possible?
128,625
42,875
1225
35
105

Math
Matrices & DeterminantsA certain experiment produces the data (1, 1.7), (2, 2.6), (3, 3.2), (4, 3.6), and (5, 3.9). Describe the model that produces a least-squares fit of these points by a function of the form y = β1*x+ β2*x^2. Such a function might arise, for example, as the revenue from the sale of x units of a product, when the amount offered for sale affects the price to be set for the product. Answer parts (a) through (c) below.
a. Give the design matrix, the observation vector, and the unknown parameter vector. Choose the correct design matrix X below.
The observation vector is y =
Choose the correct form of the parameter vector β below.
b. Find the associated least-squares curve for the data.
c. If a machine learned the curve you found in (b), what output would it provide for an input of x = 6?
Math
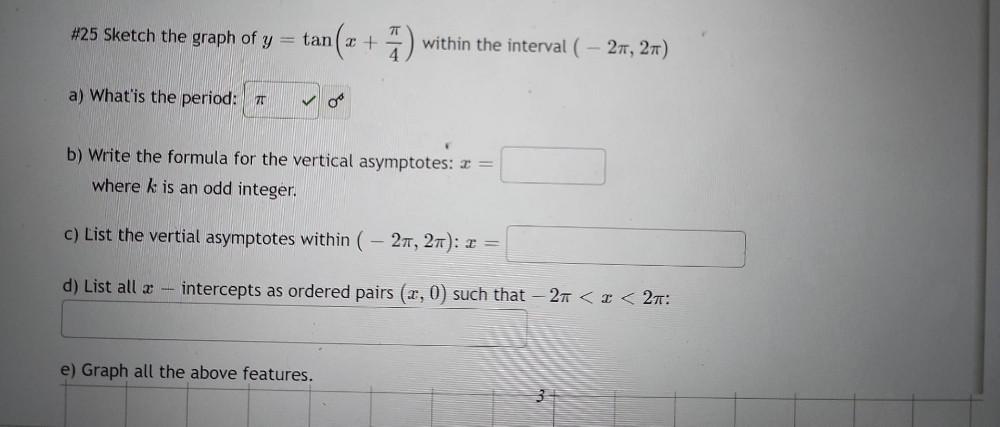
Trigonometric equationsSketch the graph of y = tan( x + π/4 ) within the interval ( – 2π, 2π)
a) What is the period?
b) Write the formula for the vertical asymptotes: x =
where k is an odd integer.
c) List the vertical asymptotes within ( - 2π, 2π ): x =
d) List all x intercepts as ordered pairs ( x,0) such that – 2π < x < 2π:
e) Graph all the above features.

Math
StatisticsYou are interested in estimating the the mean weight of the local adult population of female white-tailed deer (doe). From past data, you estimate that the standard deviation of all adult female white-tailed deer in this region to be 17 pounds. What sample size would you need to in order to estimate the mean weight of all female white-tailed deer, with a 95% confidence level, to within 5 pounds of the actual weight?
Sample Size: n≥

Math
Basic MathTranslate each of these statements into logical expressions using predicates, quantifiers, and logical connectives.
a) Something is not in the correct place.
b) All tools are in the correct place and are in excellent condition.
c) Everything is in the correct place and in excellent condition.
d) Nothing is in the correct place and is in excellent condition.
e) One of your tools is not in the correct place, but it is in excellent condition.
Math
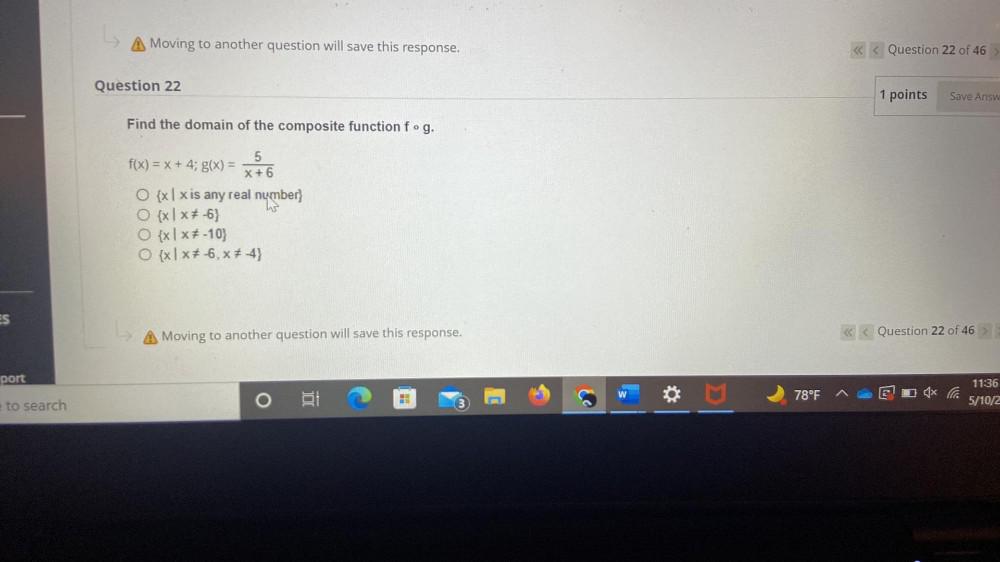
FunctionsFind the domain of the composite function f₀g.
f(x) = x + 4; g(x) = 5/x+6
{x | x is any real number}
{x | x ≠ -6}
{x| x ≠ -10)
{x | x≠ -6, x ≠ -4}
![Let the matrix below be the augmented matrix [A|B] of a linear system Ax = b. Write the most general solution (the sum of a particular one and the general solution of the homogeneous system) in parametric form. Write it in vector form. Give a basis of NulA.
0 2 0 0 2
0 0 1 0 3
0 0 0 1 2](https://media.kunduz.com/media/sug-question/raw/77898310-1658745324.8269083.jpeg?w=256)
Math
Matrices & DeterminantsLet the matrix below be the augmented matrix [A|B] of a linear system Ax = b. Write the most general solution (the sum of a particular one and the general solution of the homogeneous system) in parametric form. Write it in vector form. Give a basis of NulA.
0 2 0 0 2
0 0 1 0 3
0 0 0 1 2
Math
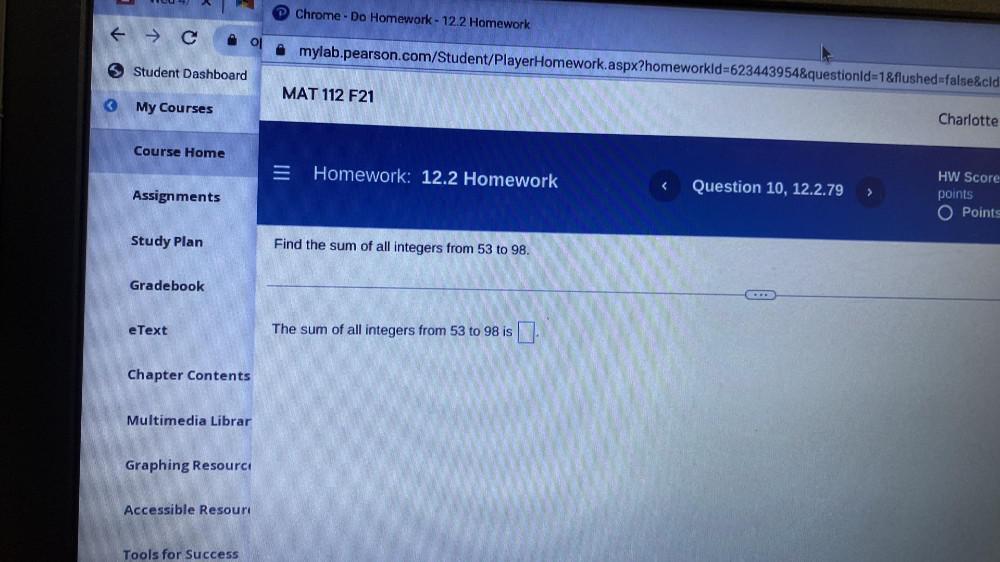
Sequences & SeriesFind the sum of all integers from 53 to 98.
The sum of all integers from 53 to 98 is ______________.
Math
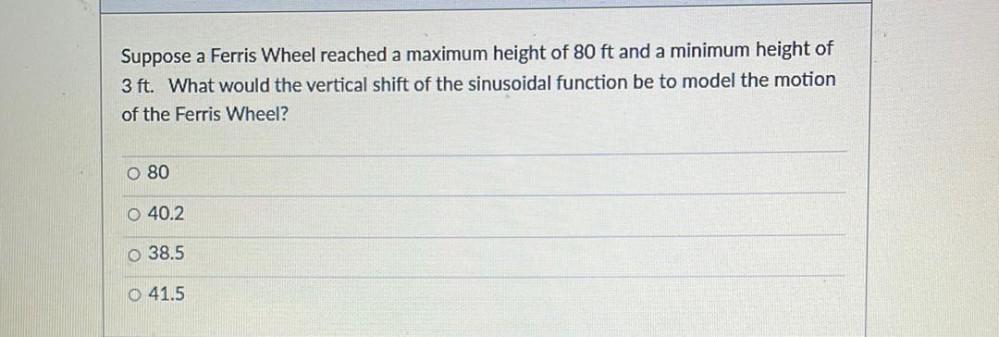
Basic MathSuppose a Ferris Wheel reached a maximum height of 80 ft and a minimum height of 3 ft. What would the vertical shift of the sinusoidal function be to model the motion of the Ferris Wheel?
80
40.2
38.5
41.5

Math
ProbabilityA six-sided number cube is tossed and a coin is flipped. The sample space is {1H, 2H, 3H, 4H, 5H, 6H, 1T, 2T, 3T, 4T, 5T, 6T}.
What is the probability of rolling an even number and flipping tails?
Enter your answer, as a fraction in simplest form, in the box.
Math
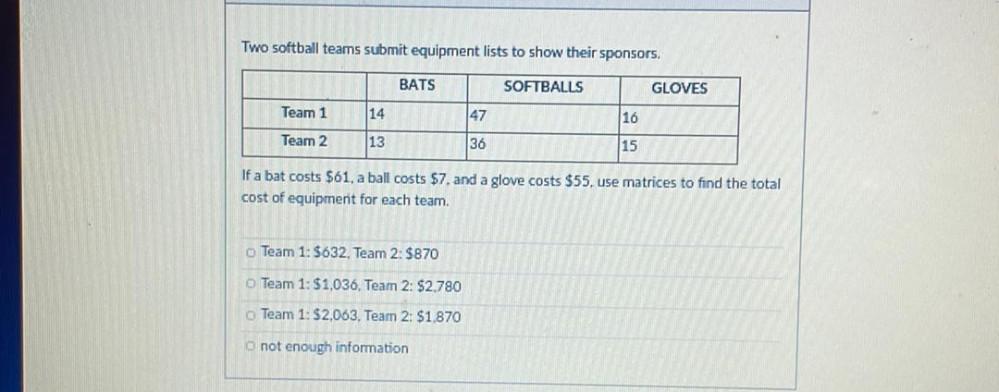
Basic MathTwo softball teams submit equipment lists to show their sponsors.
BATS SOFTBALLS GLOVES
TEAM 1 14 47 16
TEAM 2 13 36 15
If a bat costs $61, a ball costs $7, and a glove costs $55, use matrices to find the total cost of equipment for each team.
Team 1: $632, Team 2: $870
Team 1: $1,036, Team 2: $2,780
Team 1: $2,063, Team 2: $1,870
not enough information
Math
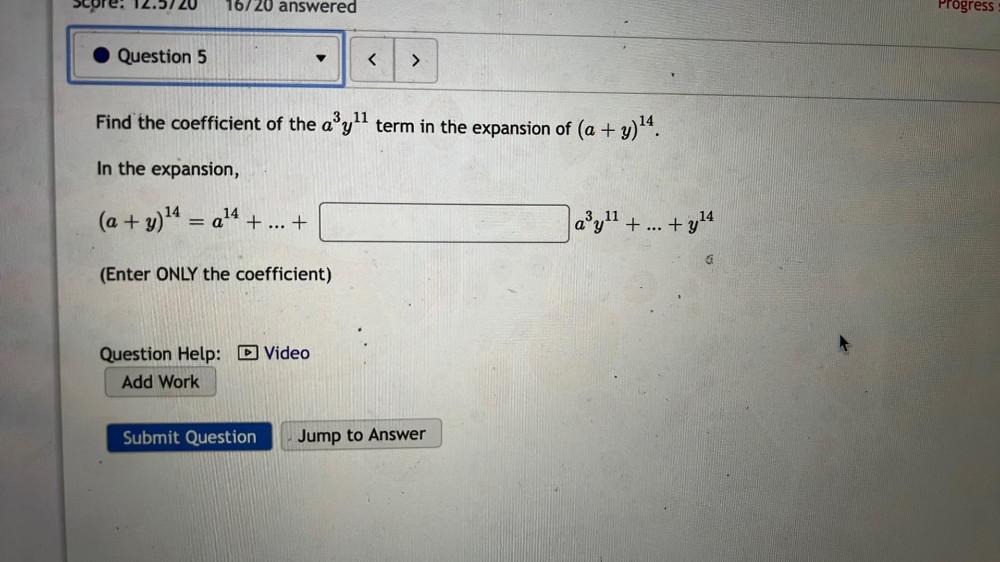
Binomial theoremFind the coefficient of the a³y¹¹ term in the expansion of (a + y)¹⁴.
In the expansion,
(a + y)¹⁴ = a¹⁴ + ... +___________ a³y¹¹ + ... +y¹⁴
(Enter ONLY the coefficient)
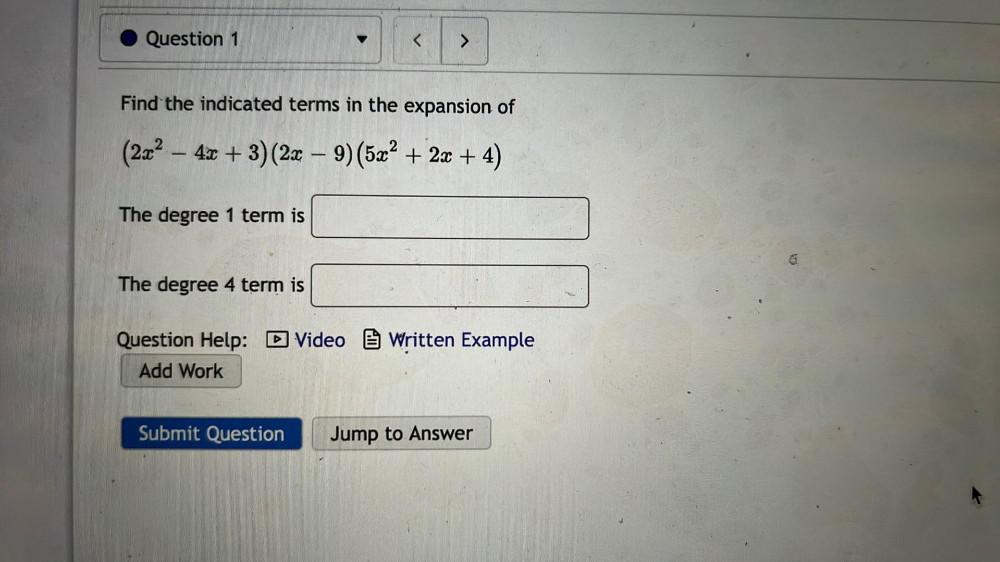
Math
Basic MathFind the indicated terms in the expansion of
(2x2 - 4x + 3)(2x – 9) (5x2 + 2x + 4)
The degree 1 term is
The degree 4 term is

Math
StatisticsSeventy percent of all Raleigh students believe that Friday should be a weekend day. You take a sample of 40 students and find that 30 believe that Friday should be a part of the weekend. What does the 70% represent?
1. Statistic
2. Parameter
3. Sample size
4. Population size
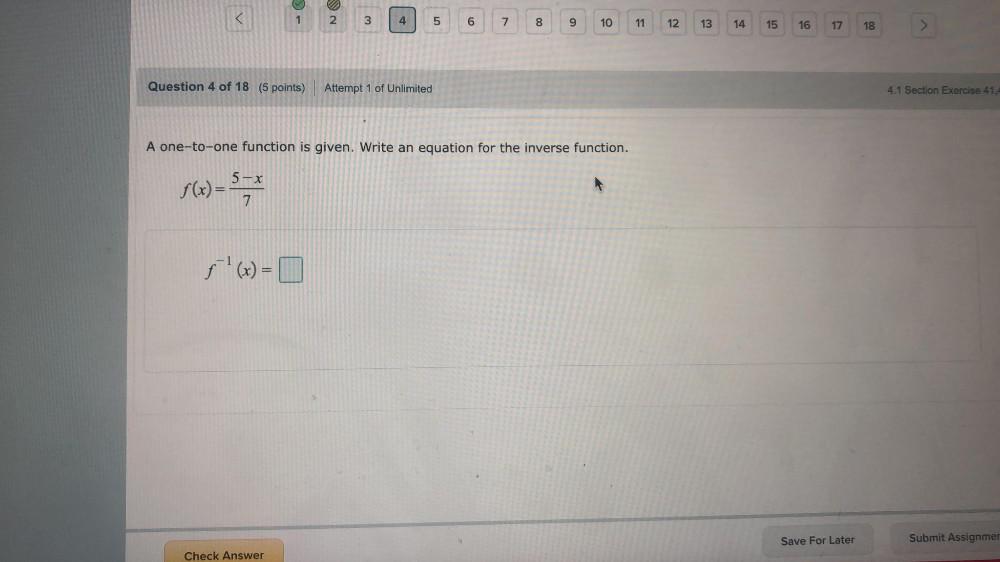
Math
Basic MathA one-to-one function is given. Write an equation for the inverse function.
f(x) = (5 - x)/ 7
f^-1(x) =

Math
Basic MathJocelyn is going to invest in an account paying an interest rate of 2.3% compounded continuously. How much would Jocelyn need to invest, to the nearest hundred dollars, for the value of the account to reach $550 in 15 years?
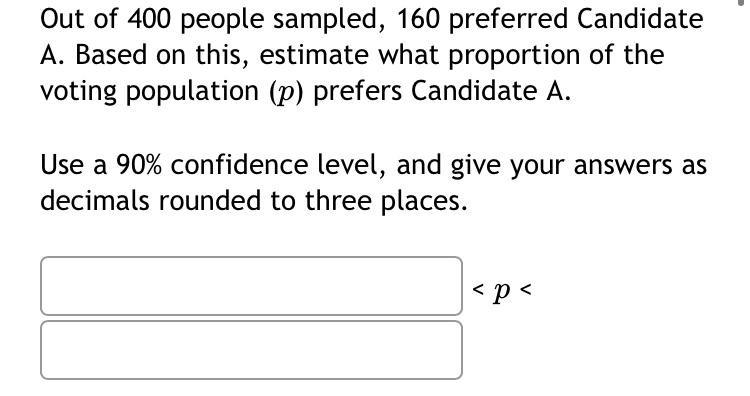
Math
StatisticsOut of 400 people sampled, 160 preferred Candidate
A. Based on this, estimate what proportion of the voting population (p) prefers Candidate A.
Use a 90% confidence level, and give your answers as decimals rounded to three places.
_________ < p < _________

Math
ProbabilityOut of 35 students, 14 pick apples as their favorite snack, 21 pick M&M's as their favorite snack, and 10 choose both. (Leave answers in fraction form. Do not
reduce.
a. Fill in the Venn diagram for this.
b. Find P(apple only) ________
c. Find P(apple and M&M's)________
d. Find P(student did not choose apple).________________
e. Find P(the student did not choose either)_______________
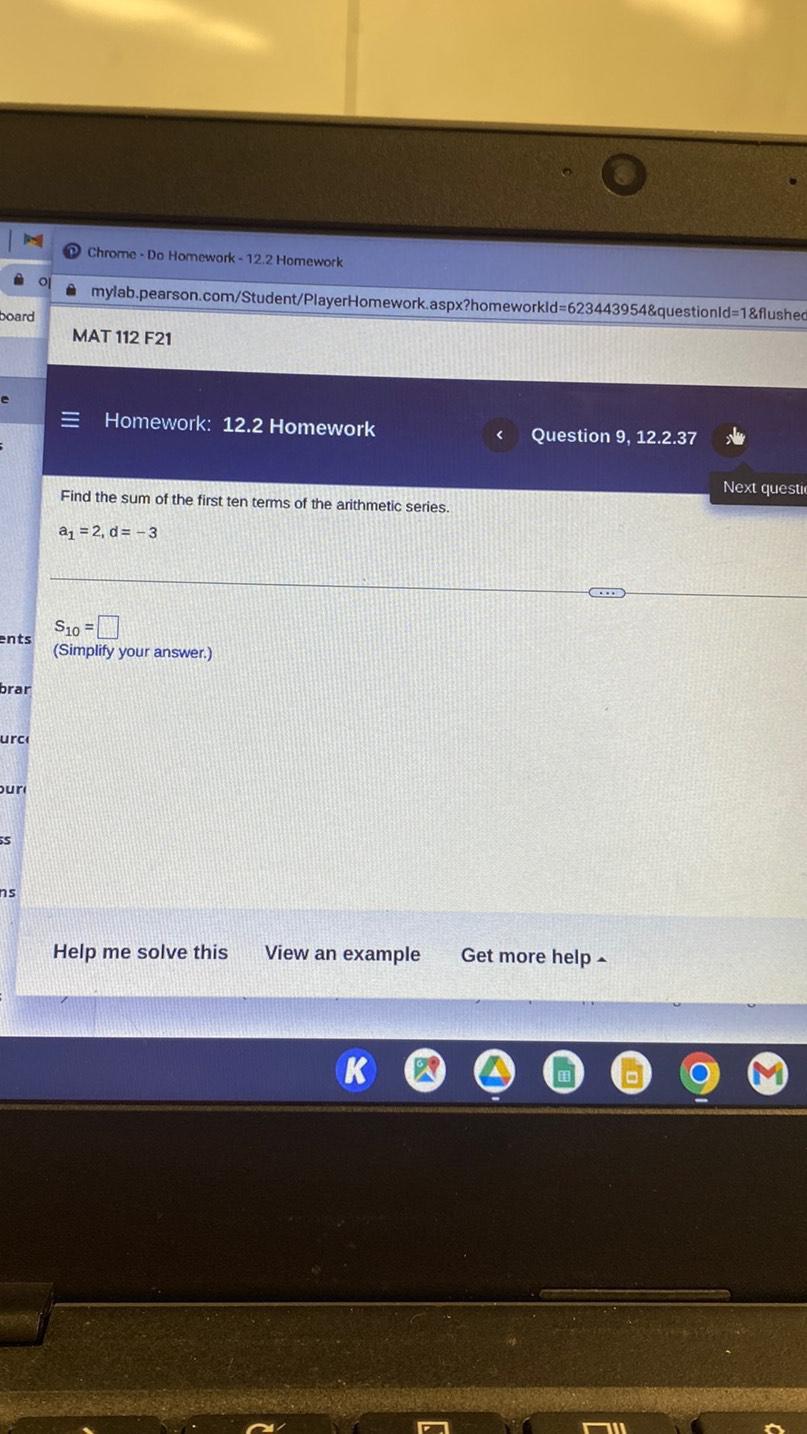
Math
Sequences & SeriesFind the sum of the first ten terms of the arithmetic series.
a1 = 2, d = -3
S10 = ______.

Math
StatisticsYou want to obtain a sample to estimate a population mean. Based on previous evidence, you believe the population standard deviation is approximately σ = 26.7. You would like to be 98% confident that your estimate is within 5 of the true population mean. How large of a sample size is required?
Do not round mid-calculation. However, you are encouraged to use a critical value accurate to three decimal places - this is important for the system to be able to give hints for incorrect answers.
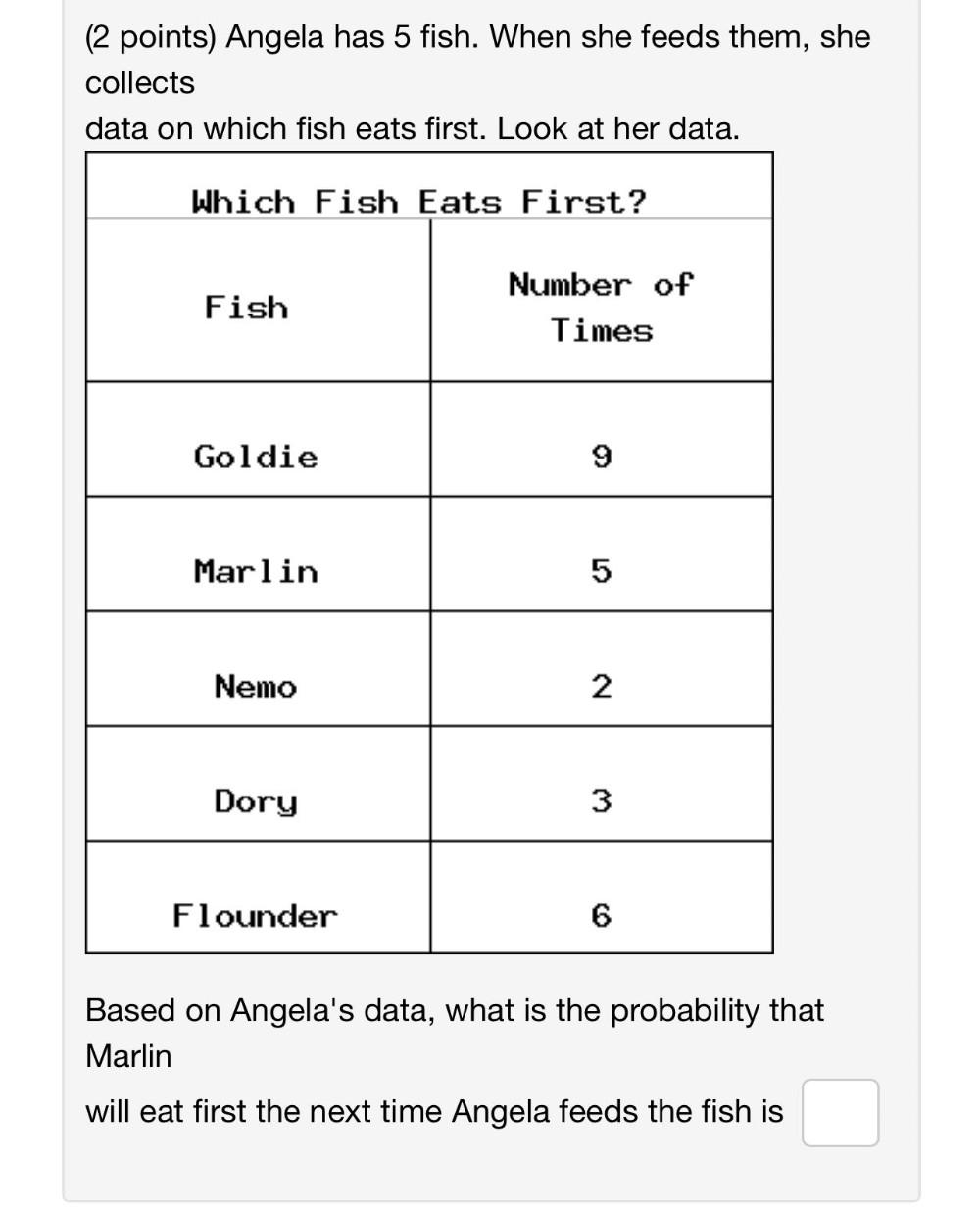
Math
ProbabilityAngela has 5 fish. When she feeds them, she collects data on which fish eats first. Look at her data.
Which Fish Eats First?
Fish Number of
Times
Goldie 9
Marlin 5
Nemo 2
Dory 3
Flounder 6
Based on Angela's data, what is the probability that Marlin will eat first the next time Angela feeds the fish is ▢
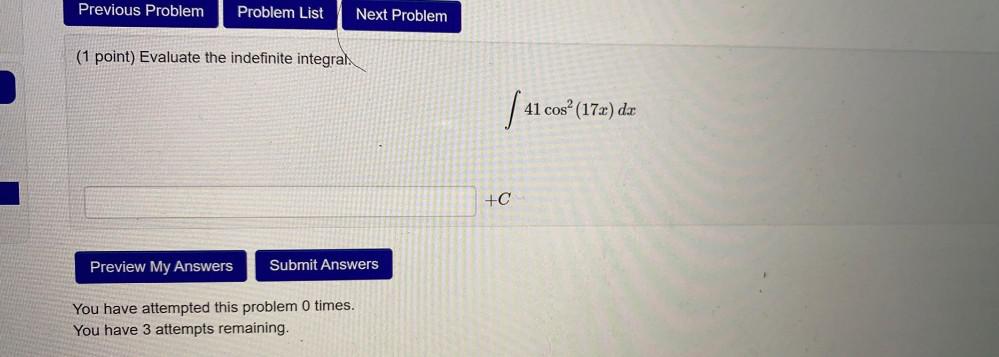
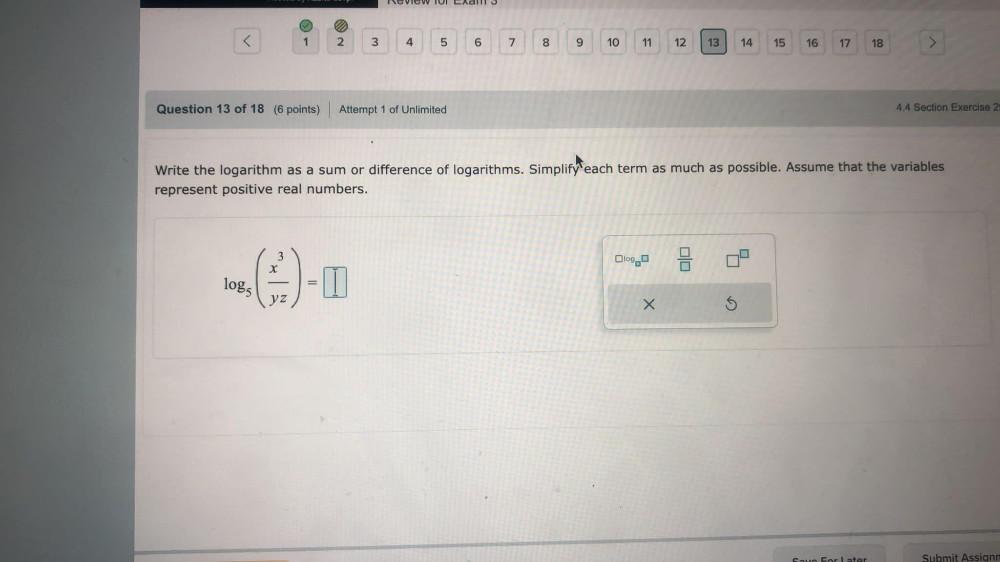
Math
LogarithmsWrite the logarithm as a sum or difference of logarithms. Simplify each term as much as possible. Assume that the variables represent positive real numbers.
log₅ (x³/yz).

Math
Inverse Trigonometric functionsHector missed the beginning of this lesson, and he is confused about domains for inverse functions. Explain why restrictions are needed. Describe specifically the restrictions that each trigonometric function (sine, cosine, and tangent) requires in order to find its inverse function.

Math
HyperbolaThe cross-section of a nuclear power plants cooling tower is in the shape of a hyperbola. Suppose the tower has a base diameter of 264 meters and the diameter at its narrowest point, 56 meters above the ground, is 88 meters. If the diameter at the top of the tower is 176 meters, how tall is the tower?
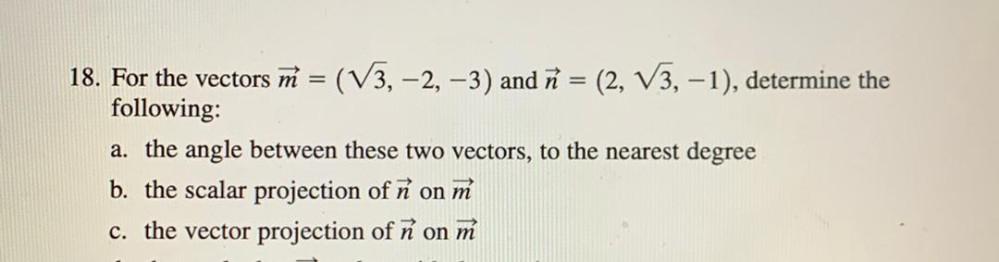
Math
VectorsFor the vectors M = (√3, -2, -3) and n = (2, √3, -1), determine the following:
a). the angle between these two vectors, to the nearest degree
b). the scalar projection of ñ on m
c). the vector projection of n on m
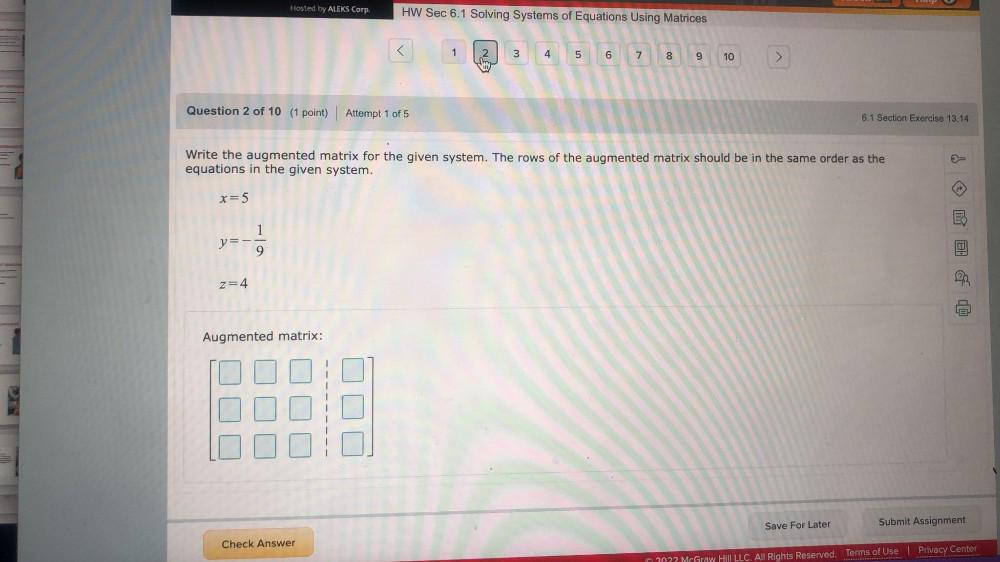
Math
Matrices & DeterminantsWrite the augmented matrix for the given system. The rows of the augmented matrix should be in the same order as the equations in the given system.
x=5
y= -(1/9)
z=4
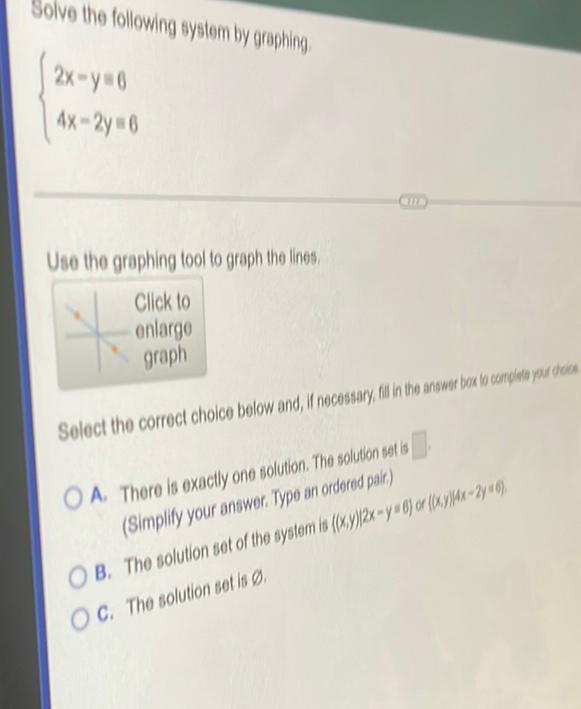
Math
Basic MathSolve the following system by graphing.
2x - y = 6
4x - 2y = 6
Use the graphing tool to graph the lines.
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A) There in exactly one solution. The solution set is _____.
(Simplify your answer. Type an ordered pair.)
B) The solution set of the system is ((x , y)|2x -y = 6) or {(x , y)|4x - 2y = 6.
C) The solution set is ∅.
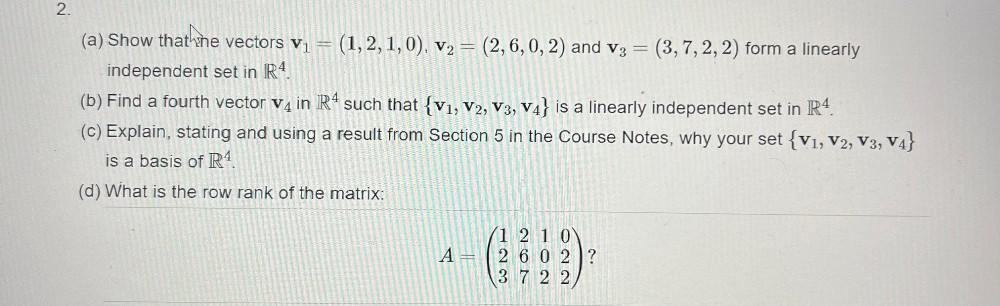
Math
Matrices & Determinants(a) Show that the vectors v1 = (1,2,1,0), v2 = (2,6,0,2) and v3 = (3,7,2,2) form a linearly independent set in R^4.
(b) Find a fourth vector v4 in R^4 such that {V1, V2, V3, V4} is a linearly independent set in R^4.
(c) Explain, stating and using a result from Section 5 in the Course Notes, why your set {v1, v2, v3, v4} is a basis of R4.
(d) What is the row rank of the matrix:
A= 1 2 1 0
2 6 0 2
3 7 2 2
![Write the expression as a sum and/or a difference of logarithms with all variables to the first degree.
log [9w(v + 4)]
(A) log 9+ log w+ log v + log 4
(B) log 9+ log w+ log (v + 4)
(C) log 9- log w-log (v + 4)
(D) 9log w+ log (v + 4)
(E) log (9w) + log (9v) + log 36](https://media.kunduz.com/media/sug-question/raw/77769747-1658744271.6231394.jpeg?w=256)
Math
LogarithmsWrite the expression as a sum and/or a difference of logarithms with all variables to the first degree.
log [9w(v + 4)]
(A) log 9+ log w+ log v + log 4
(B) log 9+ log w+ log (v + 4)
(C) log 9- log w-log (v + 4)
(D) 9log w+ log (v + 4)
(E) log (9w) + log (9v) + log 36
Math
Basic MathGraph the linear equation.
f(x) = - 3x + 5
Use the graphing tool to graph the linear equation.

Math
Basic MathA small radio transmitter broadcasts in a 38 mile radius. If you drive along a straight line from a city 49 miles north of the transmitter to a second city 52 miles east of the transmitter, during how much of the drive will you pick up a signal from the transmitter?
Math
Basic MathA plane flies 405 miles with the wind and 315 miles against the wind in the same length of time. If the speed of the wind is 20 mph, find the speed of the plane in still air.
The speed of the plane in still air is ___ mph
Math
Binomial theoremFind the indicated terms in the expansion of
(4x² + x - 2)(4x² + 5x – 10) (5x² + 4x + 3)
The degree 5 term is ___
The degree 1 term is ___

Math
Linear ProgrammingGraph the following inequality.
4x + 2y > -4
Use the graphing tool to graph the inequality.

Math
Basic MathDo each of the following:
1) Describe some of the similarities and differences among Euclidean, Spherical, and Hyperbolic geometries with respect to:
a) triangles
b) models for the geometries
c) parallels
Math
Permutations and CombinationsThere are 14 members of the scholastic bowl team, 8 of whom are boys and 6 of whom are girls. The coach wants to play 3 boys and 1 girl in the next round.
How many different teams of 3 boys and 1 girl could be formed to play the next round?
Math
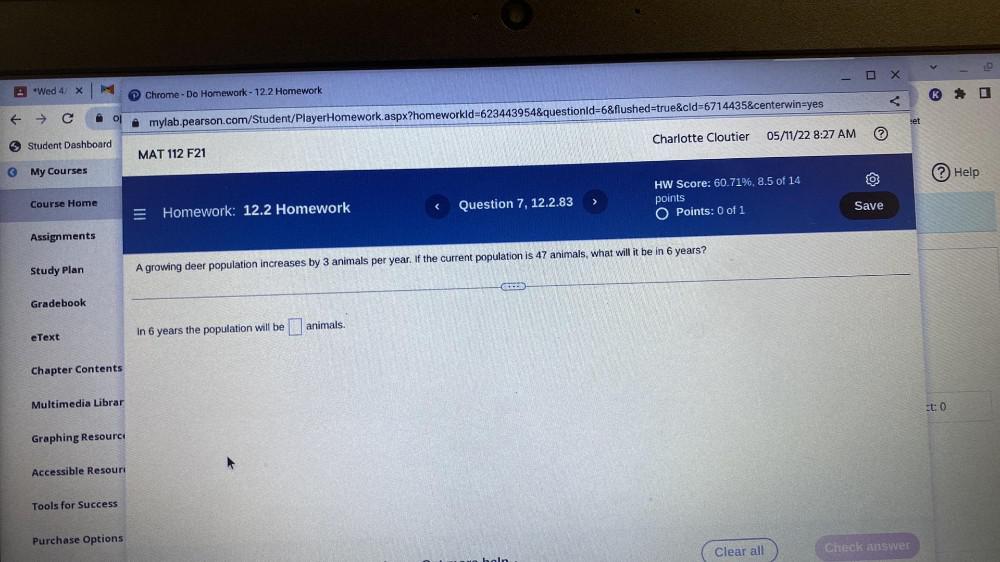
Basic MathA growing deer population increases by 3 animals per year. If the current population is 47 animals, what will it be in 6 years?
In 6 years the population will be _____ animals.
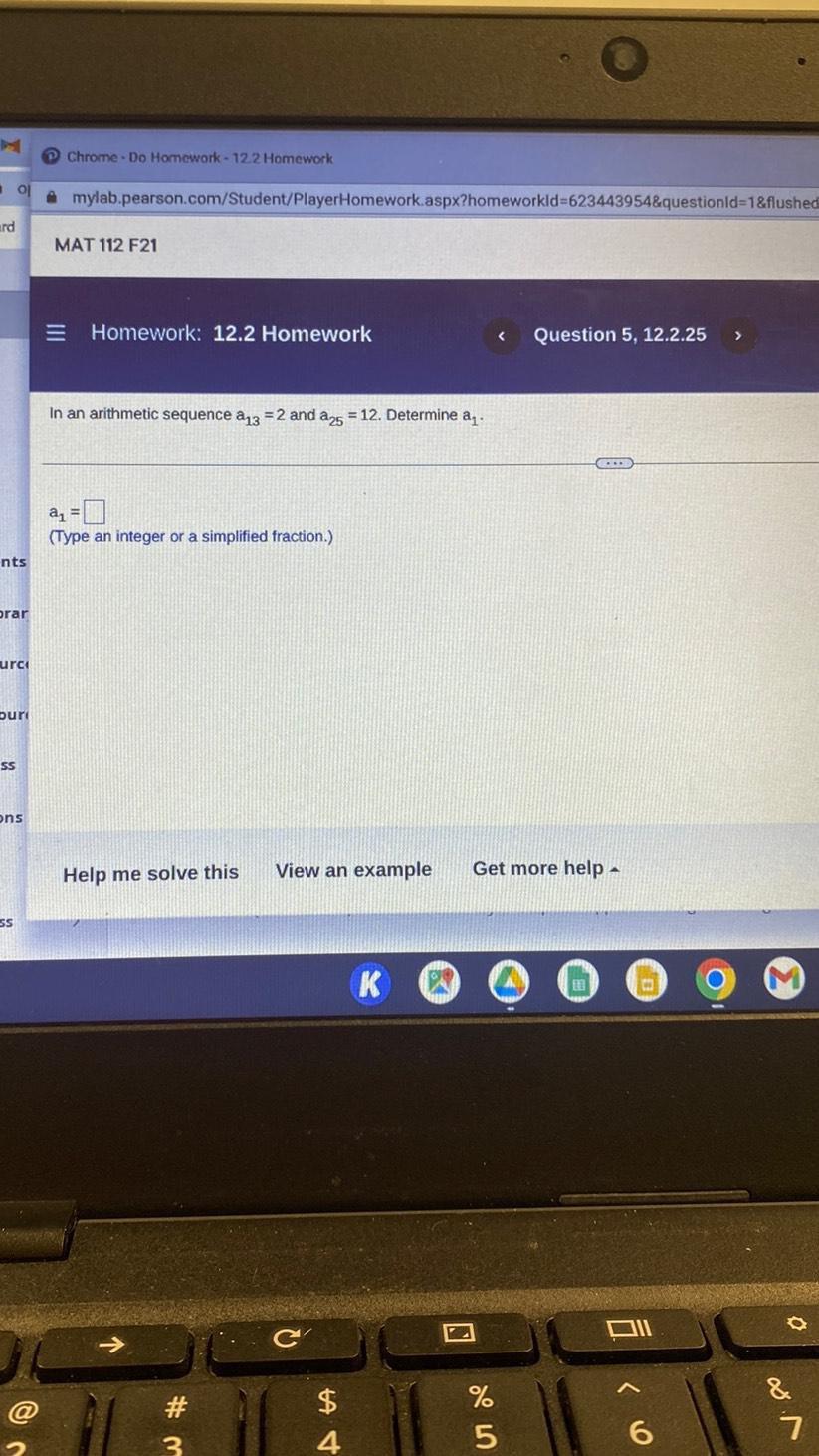
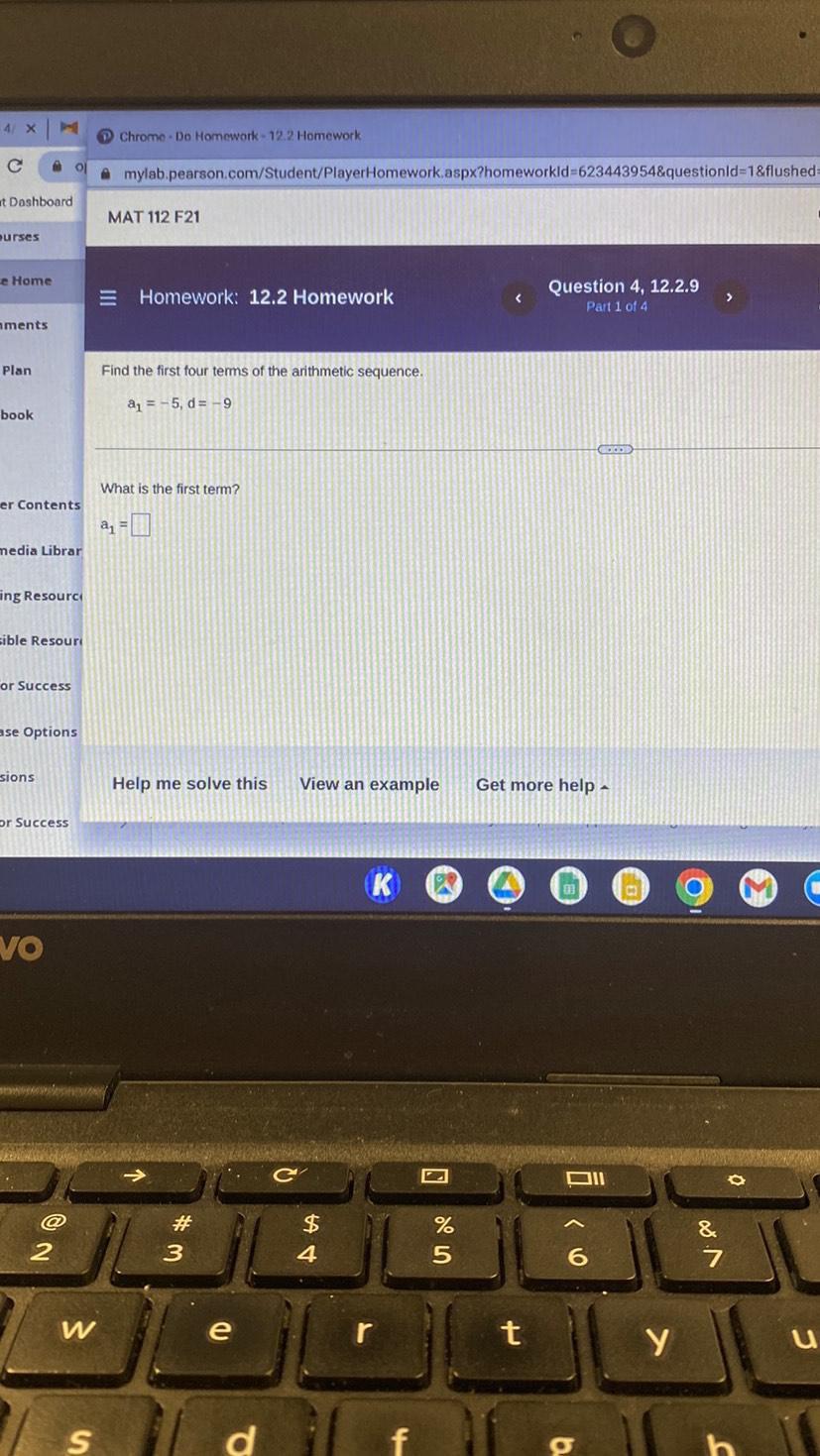
Math
Basic MathFind the first four terms of the arithmetic sequence.
a₁ = -5, d= -9
What is the first term?
a₁ = ▢

Math
Basic MathGraph the feasible region for the following system of inequalities. Tell whether the region is bounded or unbounded.
x + y ≤ 4
x - y ≥ 5

Math
Basic MathA political party is planning a ninety-minute television show. The show will have at least 9 minutes of direct requests for money from viewers. Three of the party's politicians will be on the show-a senator, a congresswoman, and a governor. The senator, a party "elder statesman," demands that he be on screen for at least twice as long as the governor. The total time taken by the senator and the governor must be at least twice the time taken by the congresswoman. Based on a pre-show survey, it is believed that 39, 44, and 49 (in thousands) viewers will watch the program for each minute the senator, congresswoman, and governor, respectively, are on the air. Find the time that should be allotted to each politician in order to get the maximum number of viewers. Find the maximum number of viewers.
The quantity to be maximized, z, is the number of viewers in thousands. Let x₁ be the total number of minutes allotted to the senator, x₂ be the total number of minutes allotted to the congresswoman, and x3 be the total number of minutes allotted to the governor. What is the objective function?
The senator should be allotted minutes.
(Simplify your answer.)
The congresswoman should be allotted minutes.
(Simplify your answer.)
The governor should be allotted minutes.
(Simplify your answer.)
The maximum number of viewers is
(Simplify your answer.)

Math
FunctionsLet f(x)=x²-9 and g(x) = 6 -x. Perform the composition or operation indicated.
(fg)(-1)

Math
StatisticsType the correct answer in each box Use numerals instead of words. If necessary, use / for the fraction bar(s).
Lucas has five buttons in a container. Each button is a different shape. There is a star, an oval, a hexagon, a circle, and a heart. He picks one button, replaces it, and then picks another button.
The sample size for this compound event is
Suppose one square-shaped button is added to the container. If Lucas repeats the same picking process, then the sample size would be
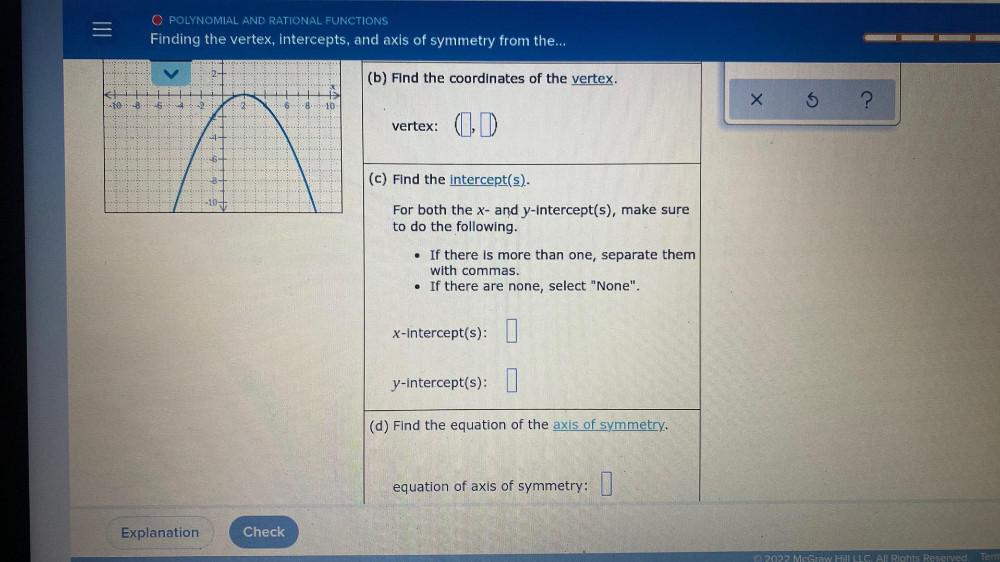
Math
Functions(b) Find the coordinates of the vertex.
(c) Find the intercept(s).
For both the x- and y-intercept(s), make sure to do the following. If there is more than one, separate them with commas. .If there are none, select "None".
x-intercept(s):
y-intercept(s):
(d) Find the equation of the axis of symmetry. equation of axis of symmetry:
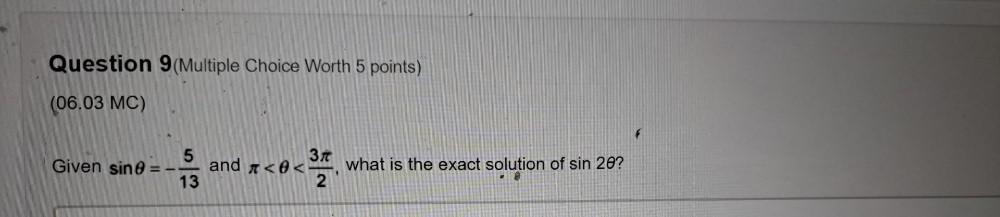

Math
Trigonometric equationsThe amount of daylight in a town can be modelled by the sinusoidal function
d(t)= 4.37 cos 0.017t + 12.52
where d(t) represents the hours of daylight and t represents the number of days since June 20, 2012. How many hours of daylight should be expected on June 20, 2013?
a) 16.80 hr
c) 16.84 hr
b) 16.88 hr
d) 16.92 hr
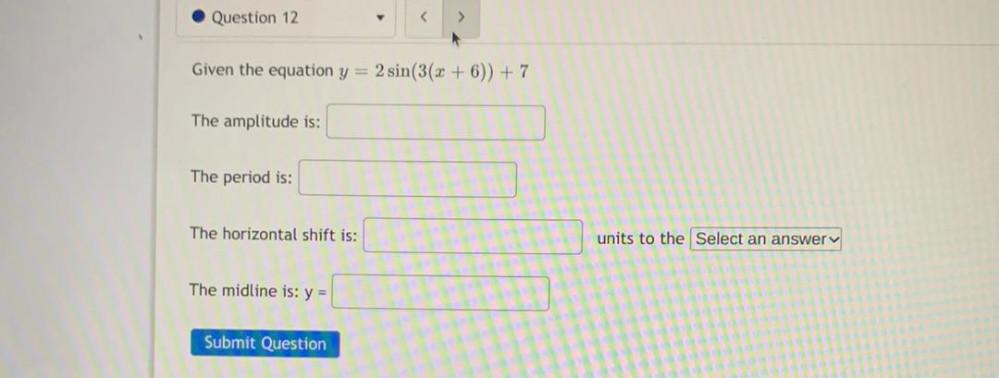
Math
Trigonometric equationsGiven the equation y = 2 sin(3(x + 6)) + 7
The amplitude is:
The period is:
The horizontal shift is:
The midline is: y =